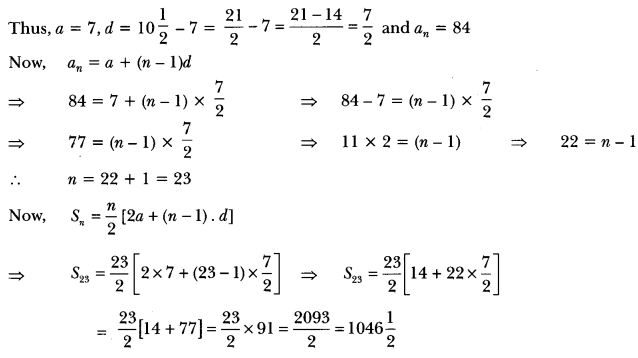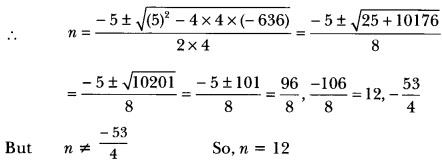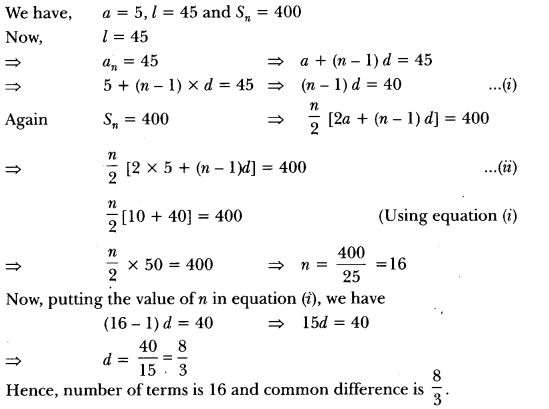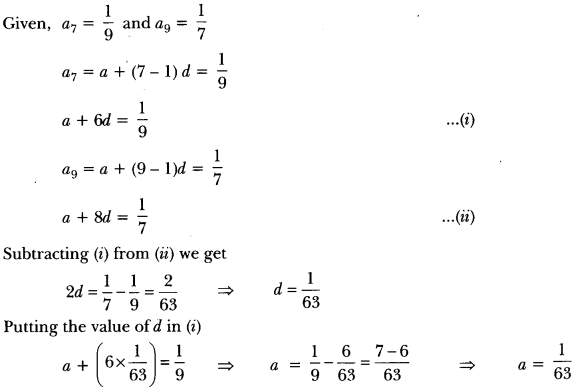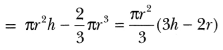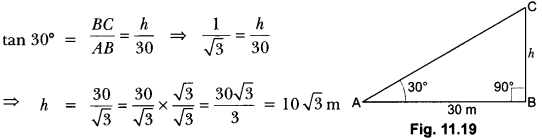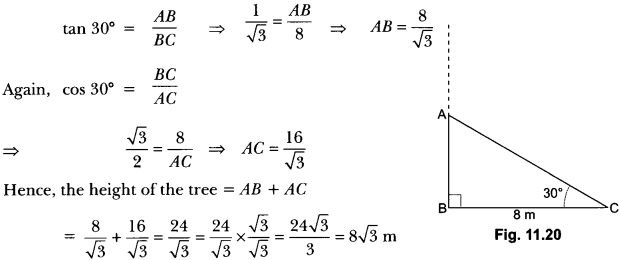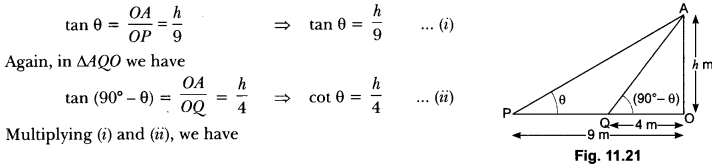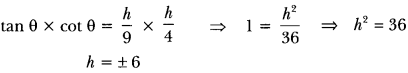Category: CBSE Class 10

Check the below Online Education NCERT MCQ Questions for Class 10 Economics Chapter 4 Extra Questions and Answers Globalisation and the Indian Economy Pdf free download. https://ncertmcq.com/extra-questions-for-class-10-social-science/

Online Education Globalisation and the Indian Economy Class 10 Extra Questions Economics Chapter 4

Globalisation And The Indian Economy Class 10 Extra Questions Question 1.
In which year had the Indian Government adopted the policy of liberalisation, privatisation and globalisation?
Answer:
Since 1991.

Class 10 Economics Chapter 4 Extra Questions Question 2.
Why the private sector was subjected to many controls and regulations?
Answer:
The private sector was subjected to many controls and regulations so: that wealth could not get concentrated in a few hands.

Extra Questions For Class 10 Economics Chapter 4 Question 3.
Point out the main features of economic reforms.
Answer:
The main features of economic reforms are

• Liberalisation
• Privatisation
• Globalisation.

Globalisation And The Indian Economy Extra Questions Question 4.
What is meant by the term LQP and LPG in economic reforms?
Answer:
LQP: The term LQP means Licence, Quota and Permit. This was the Indian Economic pattern before 1991
LPG: It is meant by Liberalisation, Privatisation and Globalisation. LPG replaced LQP in 1991.

Extra Questions Of Globalisation And The Indian Economy Question 5.
What is meant by Tariff?
Answer:
Tariff is meant by the tax or levy imposed on each unit of a commodity imported into the country.

Globalisation Class 10 Extra Questions Question 6.
Name a country which provides the advantage of being a cheap manufacturing location.
Answer:
China.

Class 10 Economics Chapter 4 Extra Questions And Answers Question 7.
Name two countries which are useful for their location to the markets in the USA and Europe.
Answer:
Mexico is close to the USA, and the Eastern European countries are close to Europe.

Globalisation And The Indian Economy Class 10 Extra Questions Answers Question 8.
What is meant by investment?
Answer:
The money that is spent to buy assets such as land, building, machines and other equipment is called investment.

Globalisation Extra Questions Question 9.
Why is foreign investment called foreign?
Answer:
Investment made by MNCs is called foreign investment.

Globalisation Class 10 Important Questions Question 10.
What is the basic utility of foreign trade?
Answer:
Foreign trade leads to connecting the markets or integration of markets in different countries.

Globalization Class 10 Extra Questions Question 11.
Define the form ‘Globalisation’.
Answer:
Globalisation is the process through which rapid integration is made possible. It is interconnection between countries.

Extra Questions Of Chapter 4 Economics Class 10 Question 12.
Give an example of trade barrier.
Answer:
Tax on import is an example of trade barrier.

Globalisation Class 10 Extra Questions And Answers Question 13.
Explain the term ‘Liberalisation’.
Answer:
Removing barriers or restrictions set by the government is what is known as liberalisation.

Extra Question Of Globalisation Class 10 Question 14.
What are the implications of fair globalisation?
Answer:
Fair globalisation would imply

• opportunities for all, and
• benefits of globalisation are shared and ensured for all equally.

Globalisation And The Indian Economy Class 10 Important Questions Question 15.
What is WTO?
Answer:
WTO stands for World Trade Organisation.

Question 16.
What is the main task of WTO
Answer:
The main task of WTO is to formulate rules and regulations with regard to trade among the different countries.

Question 17.
What is globalisation?
Answer:
Globalisation means integrating our economy with the world economy. Globalisation makes us economically interdependent at the global or international level. Globalisation also facilitates those who have capital to establish enterprises produce goods for sale and export them.

Question 18.
Define liberalisation?
Answer:
The term liberalisation contains two components

1. To allow private sector to run those activities which we restricted earlier only to public sector.
2. Realisation of all the rules and regulations which put restrictions in the growth of the private sector.
   Thus liberalisation is the process that provides more and more facilities to the private sector so that it can make fast progress.

Question 19.
Define sustainable economic development.
Answer:
Sustainable economic development is meant by the development that takes place without damaging the environment. This kind of development does not compromise on the needs of the future generation. Sustainable economic development, in fact, is an issue that has emerged from rapid industrialisation of the world in the past century. The need for sustainable development stems from the concern for environment.

Question 20.
What is WTO and when and why was it set up?
Answer:
WTO stands for the World Trade Organisation. It was set up in 1995 by the member countries of the United Nations. The main purpose of its setting up was to promote trade among the countries.

Question 21.
Describe the main steps that have been taken for globalisation of the economy?
Answer:
Following are the steps that have mainly been taken for the globalisation of the economy

• Devaluation of rupee.
• Full convertibility of rupee.
• Long-period trade policy for removal of restrictions.
• Encouragement to open competition.
• Modification of custom and tariff.

Question 22.
Point out the main objectives of new Economic policy.
Answer:
The main objectives of the new economic policy are the following

• Liberalisation of economy.
• Dispensing with too many controls.
• Expansion of private sector.
• Encouragement of foreign direct investment
• Controlling fiscal deficit.

Question 23.
Point out the significant advantage of globalisation?
Answer:
The significant advantages of globalisation are the following

• Globalisation provides scope’ to every nation to special. Specialize in the production of the commodity that it can produce most effectively.
• Commodities produced at low cost are made available at cheap prices to producers and consumers throughout the world.
• Due to the globalisation, consumers can get the commodities produced in any part of the World.
• Globalisation has provided the producers the scope to sell their goods throughout the world.
• Due to globalisation technology has spread fastly towards advancement.
• Globalisation has given scope for formation of multi-national companies and banks.

Question 24.
Explain with example how a MNC functions in another country.
Answer:
MNCs invest to buy up local companies and in turn expands production. MNCs, with huge wealth, can do this easily. To take an example, Cargill Foods, a very large American MNC, has bought over smaller Indian companies such as Parakh Foods.

Parakh Foods had built a large marketing network in parts of India, where its brand was well-reputed. Also, Parakh Foods had four oil refineries, whose control has now shifted to Cargill. Cargill is now the largest producer of edible oil in India, with a capacity to make5 million pouches daily.

Question 25.
Why do you think the company wants to develop India as a base for manufacturing car components for its global operations? Discuss the following factors:
(a) cost of labour and other resources in India.
(b) the presence of several local manufacturers who supply auto-parts to Ford Motors
(c) closeness to a large number of buyers in India and
Answer:
India provides Ford Motors an opportunity for market in other countries.
(a) Cost of labour and other resources, in India, is relatively very low

(b) Motor raw-material industries in India is very rich industries provide Ford Motors necessary auto parts at low price.

(c) India’s geographical location is good for Ford Motors markets close to other nations in the region.

Question 26.
Nearly all major multinationals are American, Japanese or European, such as Nike, Coca-Coia, Pepsi, Honda, Nokia. Can You guess why?
Answer:
Nearly all MNCs are American, Japanese, Europeans such as Coca-Cola, Pepsi, Honda, Nokia etc. This is because these countries are technologically more advanced. They have had expertise in the field, working at home. Now with a view to capture the world market, these companies are expanding ford Motors, an American company is one of the world’s largest automobile manufacturers with production spread over 140 plants in 26 countries of the world, Ford Motors came to India.

In 1995 and spent ₹ 1700 crores to set up a large plant near Chennai. This was done in collaboration with Mahindra and Mahindra, a major Indian manufacturer of jeeps and trucks. By the year 2004, Ford Motors was selling 27,000 cars in the Indian markets. An additional 24,000 cars were exported from India to south Africa, Mexico and Brazil. The company wants to develop ford India as a component supplying base for its global operations.

Question 27.
Write a short essay on WTO in your own words?
Answer:
WTO stands for the World Trade Organisation. It was set p in 1995 by the member countries of the United Nations. The foundation aim of the WTO was to promote trade among the member countries.

The headquarters of WTO is located in Geneva. It has significantly influenced the liberalisation as well as globalization process in most of the developing countries. WTO aims at conducting international trade among countries of the world in an open, uniform and nondiscriminatory manner, while facilitating trade among countries, WTO expects countries to follow what it wants.

WTO deals with three issues

1. Bilateral agreements
2. import quotas
3. export quotas.

All of these three issues are very significant for India as well as for all other developing countries. Bilateral agreements play crucial role in the trade relations among countries. In order to prevent competition from the producers of other countries with local manufacturers, it is common for countries to impose taxes on the imported goods.

WTO is in fact not only regulating the international trade of goods but also the services. All the members of WTO have to adopt laws and policies in order to comply with the WTO rules.

Question 28.
Point out the impact of the World Trade Organisation on the Indian Economy?
Answer:
The main impact of the World Trade Organisation on the Indian economy can be described in the following points

• It has provided an opportunity to India for trading with other member countries.
• India is now able to export its goods and services to other countries with less restriction from those countries.
• Thanks to the WTO that it is expected that the technology from developed countries will be available to India at a reduced cost.
• Since a major share of world trade is taking places among the developed countries themselves, the benefit of being a member of WTO to the developing countries, especially to India, is very limited.
• It is feared that once India abides by the rules and regulations of WTO, the prices of many essential and life-saving drugs may go up.
• It is alleged that WTO is being used by the developed countries to support globalisation in areas that are not directly related to trade. These rules often interfere in the management of the domestic economy of a country.

Question 29.
Point out the advantages as well as disadvantages of globalisation or to what extent globalisation is beneficial for the Indian economy? Give your own arguments.
Answer:
Globalisation means opening up the economic system for the other countries across the world. It provides opportunity for bilateral as well as free trade. It is actually integrating ones economy with the world economy. Globalisation takes place at various levels. It makes an economically interdependent world.

Argument in favour of the Globalisation

• Globalisation is the idea that has a support base from all the leading international organisations like UN, OECD, WTO.
• Because of the globalisation, the growth of trade between the nations increases the wealth of everyone.
• Due to the globalisation, the world prosperity is enhanced by greater exchange between nations and this also makes possible that everyone abides by the rules.

Question 30.
To what extent WTO can be beneficial for India?
Answer:

• WTO can be beneficial for India for the following reasons
• If India succeeds in producing quality goods, its market will naturally expand.
• WTO may help in rooting out the concern of labour. It will provide a high speed to the production process.
• It will make the Indian labourers realise that they have no alternative of hard work.
• In order to boost agricultural exports, India should make effort that the restrictions imposed on the export of agricultural products to developed countries due to domestic subsidies and barriers to trade be removed.
• A proper check on multilateral and multinational companies should also be kept so that they might not harm fabric industry of India.

Question 31.
Explain the various liberalisation measures undertaken by the Government of India.
Answer:
The liberalisation process that has been undertaken by the Indian government since 1991 are as follows

The Indian Government has opened many industrial activities for the private sector which were reserved for the public sector earlier.

Formerly, the private sector had to request to get prior permission from the Government for manufacturing a large number of goods. At present this system was done away with and only for the manufacturing of a few things like alcohol, industrial expertise, hazardous chemicals, cigarettes, electronics, drugs and pharmaceuticals.

The number of industries reserved for public sector has been reduced from 17 to 3.

Because of the liberalisation, the private sector has been freed from many regulations like

• permission to import raw materials
• licensing
• regulation on price and distribution
• restriction on investment by large business companies.

Question 32.
Describe the changes that have occurred in India due to the adoption of the policy of liberalisation and globalisation.
Answer:
Following are the changes which have occurred in India due to the adoption of the policy of liberalisation and globalisation:

• Communication sector has seen much progress.
• Telephone facilities have spread to the far village areas also.
• Colour televisions have become more cheaper.
• Food processing companies like Coca-Cola, Pepsi etc. have entered the country and are providing cold drinks and products as well.
• The share of our country in the world market in the field of goods and services has increased.
• It has provided the scope to do better with better quality.

Question 33.
Explain with examples that the top Indian companies have benefitted from competition. How has globalisation created new opportunities?
Answer:
Several of the top Indian companies have been able to benefit from the increased competition. They have invested in newer technology and production methods and raised their production standards. Some have gained from successful collaborations with foreign companies. Moreover, globalization has enabled some large Indian companies to emerge as multinationals themselves Tata Motors (automobiles), Infosys (l), Ranbaxy (medicines), Asian Paints (paints), Sundaram Fasteners (nuts and bolts) are some Indian companies which are spreading their operations worldwide.

Globalisation has also created new opportunities for companies providing services, particularly those involving information and communication technologies. The Indian company producing a magazine for the London based company and call centre and some examples. Besides, a host of services such as data entry, accounting, administrative tasks, engineering, etc. are now being done cheaply in countries such as India and are exported to the developed countries.

Question 34.
How can we make globalisation ‘fair?
Answer:
Since globalisation is now a reality, the question is how to make globalisation more fair’ Fair globalisation would create opportunities for all and also ensure that the benefits of globalisation are shared better.
The government can play a major role in making this possible.

Its policies must protect the interests, not only of the rich and the powerful but all the people in the country. For instance, the government can ensure that labour laws are properly implemented and the workers get their rights.

It can support small producers to improve their performance till the time they become strong enough to compete. If necessary, the government can use trade and investment barriers. It can negotiate at the WTO for “fairer rules. It can also align with other developing countries with similar interests to fight against the domination of developed countries in the WTO.

In the past few years, massive campaigns and representation by people’s organisations have influenced important decisions relating to trade and investments at the WTO. This has demonstrated that people also can play an important role in the struggle for fair globalisation.

Objective Type Questions

1. Choose true (✓) and false (✗) from the following

Question 1.
Globalisation has been an American phenomenon.
Answer:

Question 2.
Foreign investment is made by the multinational companies.
Answer:

Question 3.
WTO formulates trade rules among the nations.
Answer:

Question 4.
India has reverted to pre-1991 policies since 2001.
Answer:

2. Fill in the blanks:

Question 1.
Investment includes …………………………… such lands, building etc.
Answer:
assets.

Question 2.
MNCs are private companies, but …………………………… in infrastructure.
Answer:
large

Question 3.
Ford Motors is an American …………………………… .
Answer:
MNC

Question 4.
…………………………… toys are becoming popular in India.
Answer:
Chinese.

Extra Questions for Class 10 Social Science

Here we are providing Pair of Online Education for Arithmetic Progressions Class 10 Extra Questions Maths Chapter 5 with Answers Solutions, Extra Questions for Class 10 Maths was designed by subject expert teachers. https://ncertmcq.com/extra-questions-for-class-10-maths/

Online Education Extra Questions for Class 10 Maths Arithmetic Progressions with Answers Solutions

Extra Questions for Class 10 Maths Chapter 5 Arithmetic Progressions with Solutions Answers

Arithmetic Progressions Class 10 Extra Questions Very Short Answer Type

Arithmetic Progression Class 10 Extra Questions Question 1.
Which of the following can be the n^th term of a_n AP?
4n + 3, 3n² + 5, n² + 1 give reason.
Solution:
4n + 3 because n^th term of a_n AP ca_n only be a linear relation in n as a_n = a + (n – 1)d.

Arithmetic Progression Extra Questions And Answers Class 10 Pdf Question 2.
Is 144 a term of the AP: 3, 7, 11, …? Justify your answer.
Solution:
No, because here a = 3 a_n odd number and d = 4 which is even. so, sum of odd and even must be odd whereas 144 is a_n even number.

Class 10 Arithmetic Progression Extra Questions Question 3.
The first term of a_n AP is p and its common difference is q. Find its 10^th term.
Solution:
210 = a + 9d = p + 99.

Ap Extra Questions Class 10 Question 4.
For what value of k: 2k, k + 10 and 3k + 2 are in AP?
Solution:
Given numbers are in AP
∴ (k + 10) – 2k = (3k + 2) – (k + 10)
⇒ -k + 10 = 2k – 8 or 3k = 18 or k = 6.

Ap Class 10 Extra Questions Question 5.
If a_n = 5 – 11n, find the common difference.
Solution:
We have a_n = 5 – 11n
Let d be the common difference
d = a_n+1 – a_n
= 5 – 11(n + 1) – (5 – 11n)
= 5 – 11n – 11 -5 + 11n = -11

Class 10 Ap Extra Questions Question 6.
If n^th term of a_n AP is \(\frac{3+n}{4}\) find its 8^th term.
Solution:

Arithmetic Progression Extra Questions Question 7.
For what value of p are 2p + 1, 13, 5p – 3, three consecutive terms of AP?
Solution:
since 20 + 1, 13, 5p – 3 are in AP.
∴ second term – First term = Third term – second term
⇒ 13 – (2p + 1) = 5p – 3 – 13
⇒ 13 – 2p – 1 = 5p – 16
⇒ 12 – 2p = 5p – 16
⇒ -7p = – 28
⇒ p = 4

Extra Questions Of Ap Class 10 Question 8.
In a_n AP, if d = -4, n = 7, a, = 4 then find a.
Solution:
We know, a_n = a + (n – 1)d
Putting the values given, we get
⇒ 4 = a + (7 – 1)(-4) or a = 4 + 24
⇒ a = 28

Class 10 Maths Chapter 5 Extra Questions With Solutions Question 9.
Find the 25^th term of the AP: -5, \(\frac{-5}{2}\) , 0, \(\frac{-5}{2}\) ………
Solution:
Here, a = -5, b = –\(\frac{5}{2}\) – (-5) = \(\frac{5}{2}\)
We know,
a₂₅ = a + (25 – 1 )d
= (-5) + 24(\(\frac{5}{2}\)) = -5 + 60 = 55

Class 10 Maths Arithmetic Progression Extra Questions Question 10.
Find the common difference of an AP in which a₁₈ – a₁₄ = 32.
Solution:
Given, a₁₈ – a₁₄ = 32
⇒ (a + 17d) – (a + 13d) = 32
⇒ 17d – 13d = 32 or d = \(\frac{32}{4}\)

Important Questions Arithmetic Progression Class 10 With Solutions Pdf Question 11.
If 7 times the 7^th term of an AP is equal to 11 times its 11^th term, then find its 18^th term.
Solution:
Given, 7a₇= 11a₁₁
⇒ 7(a + 6d) = 11(a + 100) or 7a + 42d = 11a + 110d
⇒ 4a + 68d = 0 or a + 17d = 0
Now, a₁₈ = a + 17d = 0

Ap Questions Class 10 Question 12.
In an AP, if a = 1, a_n = 20, and s_n = 399, then find n.
Solution:
Given, An = 20
= 1 + (n – 1)d = 20
⇒ (n – 1) d = 19
s_n = \(\frac{n}{2}\) {2a + (n – 1)d}
⇒ 399 = \(\frac{n}{2}\){2 × 1 + 19}
⇒ \(\frac{399 \times 2}{21}\) = n
⇒ n = 38

Class 10 Maths Ch 5 Extra Questions Question 13.
Find the 9th term from the end (towards the first term) of the AP 5, 9, 13, …, 185.
Solution:
l = 185, d = 4
l₉ = l – (n – 1) d
= 185 – 8 × 4 = 153

Arithmetic Progressions Class 10 Extra Questions Short Answer Type 1

Ch 5 Maths Class 10 Extra Questions Question 1.
In which of the following situations, does the list of numbers involved to make an AP? If yes, give a reason.
(i) The cost of digging a well after every meter of digging, when it costs 150 for the first meter and rises by 50 for each subsequent meter.
(ii) The amount of money in the account every year, when 10,000 is deposited at simple interest at 8% per annum.
Solution:
(i) The numbers involved are 150, 200, 250, 300, …
Here 200 -150 = 250 – 200 = 300 – 250 and so on
∴ It forms a_n AP with a = 150, d = 50

(ii) The numbers involved are 10,800, 11,600, 12,400, …
which forms a_n AP with a = 10,800 and d = 800.

Extra Questions On Ap Class 10 Question 2.
Find the 20^th term from the last term of the AP: 3, 8, 13, …, 253.
Solution:
We have, last term = 1 = 253
And, common difference d = 2^nd term – 1^st term = 8 – 3 = 5
Therefore, 20^th term from end = 1 -(20 – 1) × d = 253 – 19 × 5 = 253 – 95 = 158.

Arithmetic Progression Class 10 Important Questions Question 3.
If the sum of the first p terms of an AP is ap² + bp, find its common difference.
Solution:
a_p = s_p – s_p-1 = (ap² + bp) -[a(p – 1)² + b(p – 1)]
= ap² + bp – (ap² + a – 2ap + bp – b)
= ap² + bp – ap² – a + 2ap – bp + b = 2ap + b-a .
= a₁ = 2a + b – a = a + b and a₂ = 4a + b – a = 3a + b
⇒ d = a₂ – a₁ = (3a + b) – (a + b) = 2a

Class 10 Maths Chapter 5 Extra Questions Question 4.
The first and the last terms of an AP are 5 and 45 respectively. If the sum of all its terms is 400, find its common difference.
Solution:
Let the first term be ‘a’ and common difference be ‘d’.
Given, a = 5, T_n = 45, s_n = 400 .
Tn = a + (m – 1)d
⇒ 45 = 5 + (m – 1)d
⇒ (n – 1) d = 40 ………(i)
s_n = \(\frac{n}{2}\) (a + T_n)
⇒ 400 = \(\frac{n}{2}\) (5 + 45)
⇒ n = 2 × 8 = 16 substituting the value of n in (i)
⇒ (16 – 1)d = 40
⇒ d = \(\frac{40}{15}\) = \(\frac{8}{3}\)

Extra Questions Of Arithmetic Progression Class 10 Question 5.
Find the number of natural numbers between 101 and 999 which are divisible by both 2 and 5.
Solution:
Natural numbers between 101 and 999 divisible by both 2 and 5 are 110, 120, … 990.
so, a1 = 110, d = 10, a_n = 990
We know, a_n = a₁ + (n – 1)d
990 = 110 + (n – 1) 10
(n – 1) = \(\frac{990-110}{10}\)
⇒ n = 88 + 1 = 89

Ap Important Questions Class 10 Question 6.
Find how many integers between 200 and 500 are divisible by 8.
Solution:
AP formed is 208, 216, 224, …, 496
Here, a_n = 496, a = 208, d = 8
a_n = a + (n – 1) d
⇒ 208 + (n – 1) x 8 = 496
⇒ 8 (n – 1) = 288
⇒ n – 1 = 36
⇒ n = 37

Extra Questions On Arithmetic Progression Class 10 Question 7.
The sum of the first n terms of an AP is 3n² + 6n. Find the nth term of this
Solution:
Given: s_n = 3n² +6n
s_n-1 = 3(n – 1)² + 6(n – 1)
⇒ 3(n² + 1 – 2n) + 6n – 6
⇒ 3m2 + 3 – 6n + 6n – 6 = 3n² – 3
The n^th term will be a_n
s_n = s_n-1 + a_n
a_n = s_n – s_n-1
⇒ 3n² + 6n – 3n² + 3
⇒ 6n + 3

Arithmetic Progression Class 10 Extra Questions With Solutions Question 8.
How many terms of the AP 18, 16, 14, …. be taken so that their sum is zero?
Solution:
Here, a = 18, d = -2, s_n = 0
Therefore, \(\frac{n}{2}\) [36 + (n – 1) (- 2)] = 0
⇒ n(36 – 2n + 2) = 0
⇒ n(38 – 2n) = 0
⇒ n = 19

Question 9.
The 4th term of an AP is zero. Prove that the 25^th term of the AP is three times its 11th term.
Solution:
∵ a₄ = 0 (Given)
⇒ a + 3d = 0
⇒ a = -3d
a₂₅ = a + 24d = – 3d + 24d = 21d
3a₁₁ = 3(a + 100) = 3(70) = 21d
∴ a₂₅ = 30₁₁
Hence proved.

Question 10.
If the ratio of sum of the first m and n terms of an AP is m² : n², show that the ratio of its mth and n^th terms is (2m – 1) : (2n – 1).
Solution:

Question 11.
What is the common difference of an AP in which a₂₁ – a₇ = 84?
Solution:
Given: a₂₁ – a₇ = 84
⇒ (a + 20d) – (a + 6d) = 84
⇒ 14d = 84
⇒ d = 6

Question 12.
For what value of n, are the n^th terms of two APs 63, 65, 67,… and 3, 10, 17,… equal?
Solution:
Let nth terms for two given series be a_n and a’_n
According to questions
a_n = a’_n
⇒ a + (n – 1)d = a + (n – 1)d’
⇒ 63 + (n – 1)2 = 3 + (n – 1)7
⇒ 5n = 65
⇒ n = 13.

Arithmetic Progressions Class 10 Extra Questions Short Answer Type 2

Question 1.
Which term of the AP: 3, 8, 13, 18, … , is 78?
Solution:
Let a_n be the required term and we have given AP
3, 8, 13, 18, …..
Here, a = 3, d = 8 – 3 = 5 and a_n = 78
Now, a_n = a + (n – 1)d
⇒ 78 = 3 + (n – 1) 5
⇒ 78 – 3 = (n – 1) × 5
⇒ 75 = (n – 1) × 5
⇒ \(\frac{75}{5}\) = n – 1
⇒ 15 = n – 1
⇒ n = 15 + 1 = 16
Hence, 16^th term of given AP is 78.

Question 2.
Find the 31^st term of an AP whose 11^th term is 38 and the 16^th term is 73.
Solution:
Let the first term be a and common difference be d.
Now, we have

Putting the value of d in equation (i), we have
a + 10 × 7 = 38
⇒ a + 70 = 38
⇒ a = 38 – 70
⇒ a = – 32
We have, a = -32 and d = 7
Therefore, a₃₁ = a + (31 – 1)d
⇒ a₃₁ = a + 30d
⇒ (-32) + 30 × 7
⇒ – 32 + 210
= a₃₁ = 178

Question 3.
An AP consists of 50 terms of which 3^rd term is 12 and the last term is 106. Find the 29^th term.
Solution:
Let a be the first term and d be the common difference.
since, given AP consists of 50 terms, so n = 50
a₃ = 12
⇒ a + 2d = 12 …(i)
Also, a₅₀ = 106
⇒ a + 490 = 106 … (ii)
subtracting (i) from (ii), we have
47d = 94
⇒ d = \(\frac{94}{47}\) = 2
Putting the value of d in equation (i), we have
a + 2 × 2 = 12
⇒ a = 12 – 4 = 8
Here, a = 8, d = 2
∴ 29th term is given by
a₂₉ = a + (29 – 1)d = 8 + 28 × 2
⇒ a₂₉ = 8 + 56
⇒ a₂₉ = 64

Question 4.
If the 8th term of an AP is 31 and the 15^th term is 16 more than the 11^th term, find the AP.
Solution:
Let a be the first term and d be the common difference of the AP.
We have, a₈ = 31 and a₁₅ = 16 + a₁₁
⇒ a + 7d = 31 and a + 14d = 16 + a + 10d
⇒ a + 7d = 31 and 4d = 16
⇒ a + 7d = 31 and d = 4
⇒ a + 7 × 4 = 31
⇒ a + 28 = 31
⇒ a= 3
Hence, the AP is a, a + d, a + 2d, a + 3d…..
i.e., 3, 7, 11, 15, 19, …

Question 5.
Which term of the arithmetic progression 5, 15, 25, …. will be 130 more than its 31^st term?
Solution:
We have, a = 5 and d = 10
∴ a₃₁ = a + 30d = 5 + 30 × 10 = 305
Let n^th term of the given AP be 130 more than its 31^st term. Then,
a_n = 130 + a₃₁
∴ a + (n – 1)d = 130 + 305
⇒ 5 + 10(n – 1) = 435
⇒ 10(n – 1) = 430
⇒ n – 1 = 43
⇒ n = 44
Hence, 44^th term of the given AP is 130 more than its 31^st term.

Question 6.
Which term of the progression \(20,19 \frac{1}{4}, 18 \frac{1}{2}, 17 \frac{3}{4}\), is the first negative term?
Solution:

Question 7.
Find the sum given below:
7 + 10 \(\frac{1}{2}\) + 14 +…+ 84
Solution:
Let a be the first term, d be the common difference and a_n be the last term of given AP.

Question 8.
In an AP: given l = 28, s = 144, and there are total 9 terms. Find a.
Solution:
We have, l = 28, s = 144 and n = 9
Now, l = a_n = 28
28 = a + (n – 1) d 28 = a + (9 – 1)d
⇒ 28 = a + 8d ……(i)
and S = 144
⇒ 141 = \(\frac{1}{2}\) [2a + (n – 1)d]
⇒ 144 = \(\frac{9}{2}\) [12a +(9 – 1) d]
\(\frac{144 \times 2}{9}\) = 2a + 8d
⇒ 32 = 2a + 8d
⇒ 16 = a + 4d … (ii)
Now, subtracting equation (ii) from (i), we get
4d = 12 or d = 3
Putting the value of d in equation (i), we have
a + 8 × 3 = 28
⇒ a + 24 = 28
⇒ a = 28 – 24
∴ a = 4.

Question 9.
How many terms of the AP: 9, 17, 25, … must be taken to give a sum of 636?
Solution:
Let sum of n terms be 636.
s_n = 636, a = 9, d = 17 – 9 = 8
⇒ \(\frac{n}{2}\)[2a + (n – 1) d] = 636
⇒ \(\frac{n}{2}\)[2 x 9 + (n – 1) × 8] = 636
⇒ \(\frac{n}{2}\) × 2[9+ (n – 1) 4] = 636
⇒ n[9 + 4n – 4] = 636
⇒ n[5 + 4n] = 636
⇒ 5n + 4n² = 636
⇒ 4n² + 5n – 636 = 0

Thus, the sum of 12 terms of given AP is 636.

Question 10.
How many terms of the series 54, 51, 48 ……. be taken so that, their sum is 513? Explain the
double answer.
Solution:
Clearly, the given sequence is an AP with first term a = 54 and common difference d = -3. Let
the sum of n terms be 513. Then,
s_n = 513
⇒ \(\frac{n}{2}\) {2a + (n – 1) d} = 513
⇒ \(\frac{n}{2}\) (108 + (n – 1) – 3) = 513
⇒ n[108 – 3n + 3) = 1026
⇒ -3n² + 111n = 1026
⇒ n² – 37n + 342 = 0
⇒ (n – 18) (n – 19) = 0
⇒ n = 18 or 19
Here, the common difference is negative. so, 19th term is given by
a₁₉ = 54 + (19 – 1) × – 3 = 0
Thus, the sum of 18 terms as well as that of 19 terms is 513.

Question 11.
The first term, common difference and last term of an AP are 12, 6 and 252 respectively. Find the sum of all terms of this AP.
Solution:
We have, a = 12, d = 6 and l = 252
Now, l = 252
⇒ a_n = 252
= l = a + (n – 1)d
⇒ 252 = 12 + (n – 1) × 6
⇒ 240 = (n – 1) × 6
⇒ n – 1 = 40 or n = 41
Thus, S_n = \(\frac{n}{2}\)(a + l)
⇒ S₄₁ = \(\frac{41}{2}\)(12 + 252) = \(\frac{41}{2}\) (264) = 41 × 132 = 5412

Question 12.
If the sum of first 7 terms of an AP is 49 and that of 17 terms is 289, find the sum of first n terms.
Solution:
We have, S₇ = 49
⇒ 49 = \(\frac{7}{2}\)[2a + (7 – 1) × d]
⇒ 49 × \(\frac{2}{7}\) = 2a + 6d
⇒ 14 = 2a + 6d
⇒ a + 3d = 7
and S₁₇ = 289
⇒ 289 = \(\frac{17}{2}\) [2a + (17 – 1)d]
⇒ 2a + 16d = \(\frac{289 \times 2}{17}\) = 34
⇒ a + 8d = 17
Now, subtracting equation (i) from (ii), we have
5d = 10 ⇒ d = 2
Putting the value of d in equation (i), we have
a + 3 × 2 = 7
⇒ a = 7 – 6 = 1
Here, a = 1 and d = 2
Now, s_n = \(\frac{n}{2}\) [2a + (n – 1) d]
= \(\frac{n}{2}\) [2 × 1 + (n – 1) × 2]
= \(\frac{n}{2}\)[2 + 2n – 2]
= \(\frac{n}{2}\) × 2n = n²

Question 13.
The first term of an AP is 5, the last term is 45 and the sum is 400. Find the number of terms and the common difference.
Solution:

Question 14.
If the seventh term of an AP is a and its ninth term is, find its 63^rd term.
Solution:

Question 15.
The sum of the 5^th and the 9^th terms of an AP is 30. If its 25^th term is three times its 8^th term, find the AP.
Solution:
a₅ + a₉ = 30
⇒ (a + 4d) + (a + 8d) = 30 = 2a + 12d = 30
⇒ a + 6d = 15
a = 15 – 6d …(i)
a₂₅ = 3a₈
⇒ a + 24d = 3(a + 7d)
á + 24d = 3a + 21d
⇒ 2a = 3d
Putting the value of a form (i), we have
2(15 – 6d) = 3d
⇒ 30 – 12d = 3d
⇒ 15d = 30
⇒ d = 2
So, a = 15 – 6 × 2 = 15 – 12 [From equation (i)]
⇒ a = 3
The AP will be 3, 5, 7, 9….

Question 16.
The sum of the first 7 terms of an AP is 63 and the sum of its next 7 terms is 161. Find the 28^th term of this AP.
Solution:
sum of first seven terms,

Question 17.
If the ratio of the sum of first n terms of two AP’s is (7n + 1): (4n + 27), find the ratio of their mth terms.
Solution:

Question 18.
Find the sum of the following series :
5 + (-41) + 9 + (-39) + 13 + (-37) + 17 + … + (-5) + 81 + (-3)
Solution:
The series can be rewritten as,
(5 + 9 + 13 + … +81) + (41 + (-39) + (-37) + … + (-5) + (-3))
For the series 5 + 9 + 13 + … 81
a = 5, d = 4 and a_n = 81
nth term = a + (n – 1)d = a_n
⇒ 5+ (n – 1)4 = 81
⇒ 4n = 80
⇒ n =
20 sum of 20 terms for this series.
s_n = \(\frac{20}{2}\) (5 + 81) = 860 …(i)
[∵ s_n = \(\frac{n}{2}\) (a + a_n)]
For the series (41) + (-39) + (-37)… + (-5) + (-3)
a = 41, d = 2 and and = -3
nth term = a + (n – 1)d = a_n.
⇒ -41 + (n – 1)2 = -3
⇒ 2n = 40
⇒ n = 20
sum of 20 terms for this series
s_n = \(\frac{20}{2}\) (-41 – 3) = – 440 …(ii)
By adding (i) and (ii), we get
sum of series = 860 – 440
= 420

Question 19.
Find the sum of all two digit natural numbers which are divisible by 4.
Solution:
Here a = 12, d = 4, a_n = 96
The formula is a_n = a + (n – 1)d
Therefore 96 = 12 + (n – 1) × 4
⇒ 96 = 8 + 4n
⇒ n = \(\frac{88}{4}\)
⇒ n = 22
Apply the formula for sum,
s_n = \(\frac{n}{2}\) [2a + (n – 1)d]
Hence, s₂₂ = 11/24 + 21 × 4] = 11[24 + 84]
= 11 × 108 = 1188.

Arithmetic Progressions Class 10 Extra Questions Long Answer Type

Question 1.
The sum of the 4^th and 8^th term of an AP is 24 and the sum of the 6th and 10th term is 44. Find the first three terms of the AP.
Solution:
We have, a₄ + a₈ = 24
⇒ a + (4 – 1)d + a + (8 – 1) d = 24
⇒ 2a + 3d + 7d = 24
⇒ 2a + 10d = 24
⇒ 2(a + 5d) = 24
∴ a + 5d = 12
and, a₆ + a₁₀ = 44
⇒ a + (6 – 1)d + a + (10 – 1) d = 44
⇒ 2a + 5d + 9d = 44
⇒ 2a + 14d = 44
⇒ a + 7d = 22
subtracting (i) from (ii), we have
2d = 10
∴d = \(\frac{10}{2}\) = 5
Putting the value of d in equation (i), we have
a + 5 × 5 = 12
⇒ a = 12 – 25 = -13
Here, a = -13, d = 5
Hence, first three terms are
-13, -13, + 5, -13 + 2 × 5 i.e., -13, -8, -3

Question 2.
The sum of the first n terms of an AP is given by s_n = 3n² – 4n. Determine the AP and the 12^th term.
Solution:
We have, s_n = 3n² – 4n …(i)
Replacing n by (n – 1), we get
s_n-1 = 3(n – 1)² – 4(n – 1) ….(ii)
We know, .
a_n = s_n – s_n-1 = {3n² – 4n} – {3(n – 1)² – 4(n – 1)}.
= {3n² – 4n} – {3n² + 3 – 6n – 4n + 4}
= 3n² – 4n – 3n² – 3 + 6n + 4n – 4 = 6n – 7
so, nth term a_n = 6n – 7
To get the AP, substituting n = 1, 2, 3… respectively in (iii), we get
a₁ = 6 × 1-7 = -1,
a₂ = 6 × 2 – 7 = 5
a₃ = 6 × 3 – 7 = 11,…
Hence, AP is – 1,5, 1:1, …
Also, to get 12th term, substituting n = 12 in (iii), we get
a₁₂ = 6 × 12 – 7 = 72 – 7 = 65

Question 3.
Divide 56 into four parts which are in AP such that the ratio of product of extremes to the product of means is 5 : 6.
Solution:
Let the four parts be a – 3d, a-d, a + d, a + 3d.
Given, (a – 3d) + (a – d) + (a + d) + (a + 3d) = 56

Question 4.
In an AP of 50 terms, the sum of first 10 terms is 210 and the sum of its last 15 terms is 2565. Find the AP.
Solution:
Let ‘a’ be the first term and ‘d be the common difference.

Question 5.
If s, denotes the sum of the first n terms of an AP, prove that s₃₀ = 3 (s₂₀ – s₁₀).
Solution:

Question 6.
A thief runs with a uniform speed of 100 m/minute. After one minute a policeman runs after the thief to catch him. He goes with a speed of 100 m/minute in the first minute and increases his speed by 10 m/minute every succeeding minute. After how many minutes the policeman will catch the thief?
Solution:
Let total time be n minutes
Total distance covered by thief = 100 n metres
Total distance covered by policeman = 100 + 110 + 120 + … + (n – 1) terms
∴ 100m = \(\frac{n-1}{2}\) [100(2) + (n – 2)10]
⇒ 200n = (n – 1)(180 + 10n)
⇒ 10²– 30n – 180 = 0
⇒ n² – 3n – 18 = 0
⇒ (n-6) (n + 3) = 0
⇒ n = 6
Policeman took (n – 1) = (6 – 1) = 5 minutes to catch the thief.

Question 7.
The houses in a row are numbered consecutively from 1 to 49. show that there exists a value of X such that sum of numbers of houses preceeding the house numbered X is equal to sum of the numbers of houses following X. Find value of X.
Solution:
The numbers of houses are 1, 2, 3, 4……….49.
The numbers of the houses are in AP, where a = 1 and d = 1
sum of n terms of an AP = \(\frac{n}{2}\)[2a + (n – 1)d]
Let X^th number house be the required house.
sum of number of houses preceding X^th house is equal to s_x-1 i.e.,

since number of houses is positive integer,
∴ X = 35

Question 8.
If the ratio of the 11^th term of an AP to its 18th term is 2:3, find the ratio of the sum of the first five terms to the sum of its first 10 terms.
Solution:

Arithmetic Progressions Class 10 Extra Questions HOTS

Question 1.
Find the sum of the first 15 multiples of 8.
Solution:
The first 15 multiples of 8 are
8, 16, 24, … 120
Clearly, these numbers are in AP with first term a = 8 and common difference, d = 16 – 8 = 8

Question 2.
Find the sum of all two digit natural numbers which when divided by 3 yield 1 as remainder.
Solution:
Two digit natural numbers which when divided by 3 yield 1 as remainder are:
10, 13, 16, 19, …, 97, which forms an AP.
with a = 10, d = 3, a_n = 97
a_n = 97 = a + (n – 1) d = 97
or 10 + (n – 1)3 = 97
⇒ (n – 1) = \(\frac{87}{3}\) = 29
⇒ n = 30
Now, s₃₀ = [2 × 10 + 29 × 3) = 15(20 + 87) = 15 × 107 = 1605

Question 3.
A sum of ₹700 is to be used to give seven cash prizes to students of a school for their overall academic performance. If each prize is ₹20 less than its preceding prize, find the value of each of the prizes.
Solution:
Let the prizes be a + 60, a + 40, a + 20, a, a – 20, a – 40, a – 60
Therefore, the sum of prizes is
a + 60 + a + 40 + a + 20 + a ta – 20 + a – 40 +a – 60 = 700
= 7a = 700
⇒ a = \(\frac{700}{7}\) = 100
Thus, the value of seven prizes are
100 + 60, 100 + 40, 100 + 20, 100, 100 – 20, 100 – 40, 100 – 60
i.e., ₹160, ₹140, ₹120, ₹100, ₹80, ₹60, ₹340

Question 4.
If the mth term of an AP is \(\frac{1}{n}\) and nth term is \(\frac{1}{m}\), then show that its (mn)th term is 1.
Solution:
Let a and d be the first term and common difference respectively of the given AP. Then
a_m = a + (m – 1) d
⇒ a + (m – 1)d = \(\frac{1}{n}\) …… (i)

Question 5.
If the sum of m terms of a_n AP is the same as the sum of its n terms, show that the sum of its (m + n) terms is zero.
Solution:
Let a be the first term and d be the common difference of the given AP.
Then, s_m = s_n

Question 6.
The ratio of the sums of m and n terms of a_n AP is m² : n². show that the ratio of the mth and nth terms is (2m – 1): (2n – 1).
Solution:
Let a be the first term and d the common difference of the given AP. Then, the sums of m and n terms are given by

Question 7.
The sum of n, 2_n, 3_n terms of a_n AP are s₁, s₂, and s₃ respectively. Prove that s₃ = 3(s₂ – s₁).
Solution:
Let a be the first term and d be the common difference of the AP

Question 8.
If a², b², c², are in AP, prove that \(\frac{a}{b+c}, \frac{b}{c+a}, \frac{c}{a+b}\) are in AP.
Solution:
since a², b², c², are in AP …(i)

Check the below Online Education NCERT MCQ Questions for Class 10 Economics Chapter 3 Extra Questions and Answers Money and Credit Pdf free download. https://ncertmcq.com/extra-questions-for-class-10-social-science/

Online Education for Money and Credit Class 10 Extra Questions Economics Chapter 3

Money And Credit Class 10 Extra Questions Question 1.
Who issues currency in India?
Answer:
The Reserve Bank of India issues currency in India.

Money And Credit Extra Questions Question 2.
Mention the form of modem currency
Answer:
Usually, there are two forms of modem currency. Those are (a) paper currency, (b) coins.

Class 10 Economics Chapter 3 Extra Questions Question 3.
What is Money Supply?
Answer:
Money supply refers to total money in circulation in any country at a given point of time.

Money And Credit Class 10 Important Questions Question 4.
What is paper money? What is its use?
Answer:
Money made of paper is called paper money. It is easy to carry

Money And Credit Class 10 Questions And Answers Question 5.
What do you know about Muhammad Yunns?
Answer:
Muhammad Yunus founded the Grameen Bank in Bangladesh. He got Nobel Peace prize in 2006.

Extra Questions For Class 10 Economics Chapter 3 Question 6.
What do you mean by a bank?
Answer:
A bank is an institution which deals with the transaction of money and credit.

Extra Questions Of Money And Credit Class 10 Question 7.
What is a commercial bank?
Answer:
A commercial bank is a financial institution which deals with money and credit with a view to earn profit.

Class 10 Economics Chapter 3 Extra Questions And Answers Question 8.
What is credit control?
Answer:
Credit control is the regulation of credit by the RBI for achieving certain objectives like price stability, growth and exchange rate stab ill ty.

Extra Questions Of Chapter Money And Credit Class 10 Question 9.
Define moral suasion?
Answer:
Moral suasion means persuasion, request and appeal by the RBI to the member-banks so to expand and control credit.

Class 10 Eco Ch 3 Extra Questions Question 10.
What eliminates the need for double coincidence wants?
Answer:
Money eliminates the double coincidence of wants.

Chapter 3 Economics Class 10 Extra Questions Question 11.
What is called the medium of exchange?
Answer:
Money as an intermediate in the exchange process is rightly called the medium of exchange.

Ch 3 Economics Class 10 Extra Questions Question 12.
How do we deposit money in the bank?
Answer:
We deposit money in the bank by opening an account. the money so deposited in the bank is credited to our account.

Class 10 Economics Ch 3 Extra Questions Question 13.
What will happen if all the depositors ask for their money from the bank?
Answer:
The bank will have to seek deposits from other sources or will have to ask its borrowers to give back the money.

Ncert Class 10 Economics Chapter 3 Extra Questions Question 14.
Explain the meaning of the collateral?
Answer:
Collateral is an asset the borrower owns (such as to land, livestock, building etc.) and uses this as a guarantee a lender until the loan is paid.

Economics Chapter 3 Class 10 Extra Questions Question 15.
What do you mean by terms of credit?
Answer:
Interest rate, collateral and documentation requirements, and the mode of repayment etc. comprise what is called th.e terms of Credit.

Question 16.
Explain how money acts as a medium of exchange?
Answer:
Money has a significant role in helping exchange or commodities. We sell our products in return to get money. We buy products by giving money for the products we want. Money acts as the intermediate, and thus eliminates the need of the double coincidence of wants.

Question 17.
Why rupee is used, in India, as a medium of exchange?
Answer:
As per law, it is only the Reserve Bank of India which issues paper notes. We find rupee as a paper note. No individual has been authorised to issue rupees in the form of paper currency Law recognises the use of rupees as a medium of making payment. It is used in settling transactions in India. No individual in India can legally refuse a payment made in rupees.

Question 18.
Why do the cheques constitute money- in the modem currency?
Answer:
We buy products by making payment through cash.

Question 19.
Give briefly the functions of money.
Answer:
Money, in the form of cash or cheques, is a medium of exchange. Its functions, briefly, are:

• it acts as a medium of exchange,
• it acts as a measure of value;
• it is source of store of value;
• it helps us transfer value;
• it acts as a standard for deferred payments.

Question 20.
Differentiate between demand deposits and fixed deposits
Answer:
Demand deposits can be written down from the bank without any notice; fixed deposits are withdrawn only at the time of maturity. Demand deposits are chequable; fixed deposits are not chequable. Demand deposit constitute a part of money supply while the fixed deposits come under the category of near money.

Question 21.
Why are demand deposits considered as money?
Answer:
M.Salim will write a cheque in the name of a person from whom he buys on a products. Then he will write the specific amount both in words and figures. On the right top of the cheque, he will specify the date, and down below in the right, he will sign the cheque.

Salim’s balance in his bank account decreases and Prem’s balance increases.

As the deposits in the bank can be withdrawn on demand, they act as money. One can issue a cheque and ask for money against one’s deposits in the bank. If you do not have deposits in the bank, you can not withdraw money. Supposing, Salim continues to get orders from traders. What would be his position after 6 years.

Question 22.
What are the reasons that make Swapna’s situation so risky? Discuss the following factors pesticides role of moneylenders; climate.
Answer:

• Salim is a small trader. He wants to buy stock so to sell it at the time of festival in the following month.
• The risk is that if he does not get credit, he would not able to buy stock and shall not earn profit.
• Salim was able to obtain credit from the bank against some security. He got the loan, had bought the stocks and earning profit when he sold the stock.

Salim would be able to make profit year after year his business will expand.

Swapna took loan from the moneylender and paid a higher rate of interest. But what she bought for her farming expenses, she did not obtain the desired result. Unfortunately, her crop failed. She was caught up in debit. She had to pay to the moneylender a high amount in the form of interesct.

Question 23.
Why should the people deposit money with bank
Answer:
People hold money as deposit with the bank. At a point of time, people need only some currency for their day-to-day needs. For instance, workers who receive their salaries at the end of each month have extra cash at the beginning of the month.

They deposit it with the banks by opening a bank account in their name. Banks accept the deposits and also pay an interest rate on the deposits. In this way people’s money is safe with the banks and it earns an interest. People also have the provision to withdraw the money as and when they require. Since the deposits in the bank accounts can be withdrawn on demand, these deposits are called demand deposits.

Demand deposits offer another interesting facility. It is this facility which lends it the essential characteristics of money (that of a medium of exchange). One would like to make payments by cheques instead of cash. For payment through cheque, the payer who has an account with the bank makes out a cheque for a specific amount. A cheque is a paper instructing the bank to pay a specific amount from the person’s account to the person in whose name the cheque has been made.

Question 24.
What does the bank do with the deposits it has?
Answer:
Banks has the deposits from the people. It keeps only a small proportion of their deposits as cash with themselves. For example, banks in India these days hold about 15 per cent of their deposits as cash. This is kept as provision to pay the depositors who might come to withdraw money from the bank on any day. Since, on any particular day, only some of its many depositors come to withdraw cash, the bank is able to manage with this cash.

Banks use the major portion of the deposits to extend loans. There is a huge demand for loans for various economic activities banks make use of the deposits to meet the loan requirement of the people. In this way, banks mediate between those who a surplus funds (the depositors) and those who are in need these funds (the borrowers). Banks charge a higher interest rate on loans than what they offer on deposits. The difference between what is charge from borrowers and what is paid to depositors is their main source of income.

Question 25.
What do you mean by terms of credit? Why do the lender aks for collateral against loan?
Answer:
Interest rate, collateral and documentation requirements, and the mode of repayment together comprise what is called the terms of credit. The terms of credit vary substantially from one another. Every loan agreement specific an interest which the borrower must pay me lender along with the repayment of the principal.

In addition, lenders may demand collateral (i.e. security against loan). Collateral is an asset that the borrower own, such as land, building, vehicle, livestock, deposits with the bank and uses this as guarantee to a lender until the loan is refunded. If the borrower fails to repay the loan, the lender has the right to sell the asset or collateral to obtain repayment payment such as land titles, deposits with banks livestock are some common examples of collateral used for borrowing.

Question 26.
What are formal and informal sector loans? Who supervises the functioning of formal sources of loans and how?
Answer:
Various types of loans can be grouped as formal sector loans and informal sector loans. Banks and cooperatives are examples of formal sector loans whereas informal sector loans include loans from money lenders, traders, employers, relatives and friends. The chart here refers to sources of credit for Rural Households in India in 2003.
Sources of Credit for Rural Households in India in 2003.

The Reserve Bank of India supervises the functioning of formal sources of loans. For instance, the banks maintain a minimum cash balance out of the deposits they receive. The RBI monitor that the banks actually maintain the cash balance. Similarly, the RBI sees that the banks give loans not just to profit-make into business and traders but also to small cultivators, small scale industries, to small borrowers etc. Periodically, banks have to submit information to the RBI on how much they are lending to whom, at what interest rate, etc.

Question 27.
Write a note on ‘Self Help Group’.
Answer:
In recent years, people have tried out some newer ways of providing loans to the poor. The idea is to organise rural poor, in particular women, into small Self Help Groups (SHGs) and pool (collect) their savings. A typical SHG has 15-20 members, usually belonging to one neighbourhood, who meet and save Regularly. Saving per member varies from ₹ 25 to ₹ 100 or more, depending on the ability of the people to save.

Members can take small loans from the group itself to meet their needs. The group charges interest on these loans but this is still less than what the moneylender charges. After a year or two, if the group is regular in savings, it becomes eligible for availing loan from the bank.

The SHGs help borrowers overcome the problem of lack of collateral. They can get timely loans for a variety of purposes and at a reasonable interest rate. Moreover, SHGs are the building blocks of organisation of the rural poor. Not only does it help women to become financially self-reliant, but the regular meetings of the group also provide a platform to discuss and act on a variety of social issues such as health, nutrition, domestic violence, etc.

Objectives Type Questions

1. Fil in the blanks with appropriate words

Question 1.
The Reserve Bank of India issue ………………….. currency.
Answer:
paper.

Question 2.
Banks are the ………………….. sources of credit.
Answer:
formal.

Question 3.
Money is an ………………….. of exchange.
Answer:
instrument.

Question 4.
………………….. are important in giving loans to the poorer.
Answer:
SHGs.

2. Choose the most appropriate answer:

Question 1.
The following eliminates the need for double coincidence of wants:
(a) barter
(b) money
(c) bank
(d) none of these
Answer:
(b) money

Question 2.
Money provides a medium of the following :
(a) Production
(b) consumption
(c) exchange
(d) Distribution.
Answer:
(c) exchange

Question 3.
Cheque is an instruction to the following
(a) Borrower
(b) Lender
(c) Bank
(d) None of these.
Answer:
(c) Bank.

Extra Questions for Class 10 Social Science

Here we are providing Online Education for Surface Areas and Volumes Class 10 Extra Questions Maths Chapter 13 with Answers Solutions, Extra Questions for Class 10 Maths was designed by subject expert teachers. https://ncertmcq.com/extra-questions-for-class-10-maths/

Online Education Extra Questions for Class 10 Maths Surface Areas and Volumes with Answers Solutions

Extra Questions for Class 10 Maths Chapter 13 Surface Areas and Volumes with Solutions Answers

Surface Areas and Volumes Class 10 Extra Questions Very Short Answer Type

Surface Area And Volume Class 10 Extra Questions Question 1.
What is the capacity of a cylindrical vessel with a hemispherical portion raised upward at the bottom?.
Solution:

Capacity of the given vessel
= capacity of cylinder – capacity of hemisphere

Class 10 Surface Area And Volume Extra Questions Question 2.
A solid cone of radius r and height h is placed over a solid cylinder having same base radius and height as that of a cone. What is the total surface area of the combined solid?

Solution:
The total surface area of the combined solid in Fig.
= curved surface area of cone + curved surface area of cylinder + area of the base.

Surface Area And Volume Class 10 Extra Questions With Solutions Pdf Question 3.
Two identical solid hemispheres of equal base radius r сm are struck together along their bases. What will be the total surface area of the combination?
Solution:
The resultant solid will be a sphere of radius r whose total surface area is 4πr².

Surface Area And Volume Extra Questions Question 4.
A solid ball is exactly fitted inside the cubical box of side a. What is the volume of the ball?
Solution:
Diameter of the solid ball = edge of the cube = a

Area Related To Circles Extra Questions Question 5.
If two cubes of edge 5 cm each are joined end to end, find the surface area of the resulting cuboid.
Solution:
Total length (l) = 5 + 5 = 10 cm
Breadth (b) = 5 cm, Height (h) = 5 cm
Surface Area = 2 (lb + bh + lh)
= 2(10 × 5 + 5 × 5 + 5 × 10) = 2 × 125 = 250 cm²

Area Related To Circle Class 10 Extra Questions Pdf Question 6.
A solid piece of iron in the form of a cuboid of dimension 49 cm × 33 cm × 24 cm is melted to form a solid sphere. Find the radius of sphere.
Solution:
Volume of iron piece = Volume of the sphere formed
= 49 × 33 × 24 = \(\frac{4}{3}\) πr²

r = 21 cm

Area Related To Circle Class 10 Extra Questions With Solutions Pdf Question 7.
A mason constructs a wall of dimensions 270 cm × 300 cm × 350 cm with the bricks each of size 22.5 cm × 11.25 cm × 8.75 cm and it is assumed that space is covered by the mortar. Find the number of bricks used to construct the wall.
Solution:
Space occupied with bricks = \(\frac{7}{8}\) × volume of the wall
= \(\frac{7}{8}\) × 270 × 300 × 350

Class 10 Maths Chapter 12 Extra Questions Question 8.
The radii of the ends of a frustum of a cone 40 cm high are 20 cm and 11 cm. Find its slant height.
Solution:

Area Related To Circle Difficult Questions Question 9.
Volume and surface area of a solid hemisphere are numerically equal. What is the diameter of hemisphere?
Solution:
As per question
Volume of hemisphere = Surface area of hemisphere
= \(\frac{2}{3}\)πr² = 3πr² = , units r = \(\frac{9}{2}\) units

Surface Areas and Volumes Class 10 Extra Questions Short Answer Type 1

Area Related To Circle Class 10 Extra Questions Question 1.
A cone, a hemisphere and a cylinder stand on equal bases and have the same height. What is the ratio of their volumes?
Solution:
Volume of a cone: Volume of a hemisphere: Volume of a cylinder

Area Related To Circle Class 10 Important Questions With Solutions Question 2.
What is the ratio of the volume of a cube to that of a sphere which will fit inside it?
Solution:
Let edge of the cube be ‘a’.
Then, diameter of the sphere that will fit inside the given cube = a
∴ Volume of the cube : Volume of the sphere

Ch 12 Maths Class 10 Extra Questions Question 3.
The slant height of the frustum of a cone is 5 cm. If the difference between the radii of its two circular ends is 4 cm, find the height of the frustum.
Solution:
Let r and R be radii of the circular ends of the frustum of the cone.
Then, R – r = 4, l = 5
We know, l² = (R – r)² + h²
⇒ 5² = 4² + h² or h² = 25 – 16 = 9
⇒ h = 3 cm

Areas Related To Circles Class 10 Important Questions Question 4.
If the slant height of the frustum of a cone is 10 cm and the perimeters of its circular base are 18 cm and 28 cm respectively. What is the curved surface area of the frustum?
Solution:
Let r and R be the radii of the two circular ends of the frustum of the cone.
Then, 2πr = 18 and 2πR = 28

Surface Area And Volume Class 10 Important Questions Question 5.
The slant height of a frustum of a cone is 4 cm and the perimeters (circumference) of its circular ends are 18 cm and 6 cm. Find the curved surface area of the frustum.
Solution:

We have, slant height, l = 4 cm
Let R and r be the radii of two circular ends respectively. Therefore, we have
⇒ 2πR = 18 = πR = 9
⇒ 2πr = 6 = πr = 3
∴ Curved surface area of the frustum = (πR + πr)l
= (9 + 3) × 4 = 12 × 4 = 48 cm²

Surface Area And Volume Extra Questions Class 10 Question 6.
A vessel is in the form of a hollow hemisphere mounted by a hollow 7 cm cylinder. The diameter of the hemisphere is 14 cm and the total height T of the vessel is 13 cm. Find the inner surface area of the vessel.
Solution:

Here, radius of hemisphere = radius of cylinder = r cm = 7 cm
and height of cylinder, h = (13 – 7) cm = 6 cm
Now, inner surface area of the vessel
= Curved surface area of the cylindrical part + Curved surface area of hemispherical part = (2πrh + 2πr2) = 2πr (h + r)
= 2 × \(\frac{22}{7}\) × 7 (6 + 7)
= 2 × 22 × 13 = 572 cm²

Extra Questions Of Surface Area And Volume Class 10 Question 7.
A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of T.
Solution:

We have,
Height
of cone is equal to its radius
i.e., h =r = 1 cm (Given)
Also, radius of hemisphere = r = 1 cm
Now, Volume of the solid
= Volume of the cone + Volume of the hemisphere

Surface Areas And Volumes Class 10 Extra Questions Question 8.
If the total surface area of a solid hemisphere is 462 cm², find its volume. [Take π = \(\frac{22}{7}\)]
Solution:
Given, total surface area of solid hemisphere = 462 cm²
⇒ 3πr² = 462 cm²
3 × \(\frac{22}{7}\) × r² = 462
r² = 49 ⇒ r = 7 cm
Volume of solid hemisphere = \(\frac{2}{3}\) πr³
= \(\frac{2}{3}\) × \(\frac{22}{7}\) × 7 × 7 × 7 = 718.67 cm³

Surface Areas and Volumes Class 10 Extra Questions Short Answer Type 2

Ch 13 Maths Class 10 Extra Questions Question 1.
Two cubes each of volume 64 cm³ are joined end to end. Find the surface area of the resulting cuboid.
Solution:

Let the length of each edge of the cube of volume 64 cm³ be x cm.
Then, Volume = 64 cm³
⇒ x² = 64
⇒ x² = 4³
⇒ x = 4 cm
4 cm The dimensions of cuboid so formed are
l = Length = (4 + 4) cm = 8 cm
b = Breadth = 4 cm and h = Height = 4 cm
∴ Surface area of the cuboid = 2 (lb + bh + lh)
= 2 (8 × 4 + 4 × 4 + 8 × 4)
= 2 (32 + 16 + 32)
= 160 cm²

Extra Questions Of Chapter 13 Class 10 Maths Question 2.
A cubical block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have? Find the surface area of the solid.
Solution:
The greatest diameter that a hemisphere can have = 7 cm = l
Radius of the hemisphere (R) = \(\frac{7}{2}\) cm
∴ Surface area of the solid after surmounting hemisphere
= 6l² – πR² + 2πR² = 6l² + πR²

Extra Questions On Surface Area And Volume Question 3.
The dimensions of a solid iron cuboid are 4.4 m × 2.6 m × 1.0 m. It is melted and recast into a hollow cylindrical pipe of 30 cm inner radius and thickness 5 cm. Find the length of the pipe.
Solution:
Let the length of pipe by h m.
Volume of cuboid = 4.4 × 2.6 × 1 m²
Inner and outer radii of cylindrical pipe are 30 cm, (30 + 5) cm = 35 cm

Extra Questions On Surface Area And Volume Class 10 Question 4.
A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy.
OR
A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius on its circular face. The total height of the toy is 15.5 cm. Find the total surface area of the toy.
Solution:

We have,
CD = 15.5 cm and OB = OD = 3.5 cm
Let r be the radius of the base of cone and h be the height of conical part of the toy.
Then, r = OB = 3.5 cm
h = OC = CD – OD = (15.5 – 3.5) cm = 12 cm

Class 10 Maths Chapter 13 Extra Questions Question 5.
A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter l of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.
Solution:
Here, we have
Edge of the cube = l = Diameter of the hemisphere
Therefore, radius of the hemisphere = \(\frac{l}{2}\)
∴ Surface area of the remaining solid after cutting out the hemispherical

Question 6.
A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4 m respectively, and the slant height of the top is 2.8 m, find the area of the canvas used for making the tent. Also, find the cost of the canvas of the tent at the rate of 500 per m². (Note that the base of the tent will not be covered with canvas).
Solution:
We have,
Radius of cylindrical base = \(\frac{4}{2}\) = 2 m
Height of cylindrical portion = 2.1 m
∴ Curved surface area of cylindrical portion = 2πrh
= 2 × \(\frac{22}{7}\) × 2 × 2.1 = 26.4 m²
Radius of conical base = 2 m
Slant height of conical portion = 2.8 m
∴ Curved surface area of conical portion = πrl
= \(\frac{22}{7}\) × 2 × 2.8 = 17.6m²
Now, total area of the canvas = (26.4 + 17.6)m² = 44 m²
∴ Total cost of the canvas used = ₹500 × 44 = ₹22,000

Question 7.
A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends (Fig). The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area.

Solution:
Let the radius and height of the cylinder be r сm and h cm respectively. Then,

Question 8.
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in Fig. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.

Solution:
We have, r = 3.5 cm and h = 10 cm
Total surface area of the article
= Curved surface area of cylinder + 2 × Curved surface area of hemisphere
= 2πrh + 2 × 2πr² = 2πr (h + 2r)
= 2 × \(\frac{22}{7}\) × 3.5 × (10 + 2 × 3.5)
= 2 × \(\frac{22}{7}\) × 3.5 × 17 = 374 cm²

Question 9.
Mayank made a bird-bath for his garden in the shape of a cylinder with a hemispherical depression at one end (Fig). The height of the cylinder is 1.45 m and its radius is 30 cm. 30 cm Find the total surface area of the bird-bath. [Take π = \(\frac{22}{7}\) ]
Solution:

Let h be height of the cylinder, and r be the common radius of the cylinder and hemisphere.
Then, the total surface area of the bird-bath
= Curved surface area of cylinder + Curved surface area of hemisphere
= 2πrh + 2πr² = 2πr (h + 2r)
= 2 × \(\frac{22}{7}\) × 30 (145 + 30) cm² = 33,000 cm² = 3.3 m²

Question 10.
A juice seller was serving his customers using glasses as shown in Fig. 13.16. The inner diameter of the cylindrical glass was 5 cm, but the bottom of the glass had a hemispherical raised portion which reduced the capacity of the glass. If the height of a glass was 10 cm, find the apparent capacity of the glass and its actual capacity. (Use π = 3.14).
Solution:

Since, the inner diameter of the glass = 5 cm and height = 10 cm,
the apparent capacity of the glass = πr²h
= (3.14 × 2.5 × 2.5 × 10) cm³ = 196.25 cm²
But the actual capacity of the glass is less by the volume of the hemisphere at the base of the glass.
i.e., it is less by \(\frac{2}{3}\) πr³
= \(\frac{2}{3}\) × 3.14 × 2.5 × 2.5 × 2.5 cm³
= 32.71 cm
So, the actual capacity of the glass
= Apparent capacity of glass – Volume of the hemisphere
= (196.25 – 32.71) cm³ = 163.54 cm³

Question 11.
Asphericalglassvesselhasacylindricalneck8cmlong, 2cmindiameter;the diameterofthespherical part is 8.5 cm. By measuring the amount of water it holds, a child finds its volume to be 345 cm³. Check whether she is correct, taking the above as the inside measurements, and π = 3.14.
Solution:

We have,
Radius of cylindrical neck = 1 cm and height of cylindrical neck = 8 cm
Radius of spherical part = 4.25 cm

∴ The answer found by the child is incorrect.
Hence, the correct answer is 346.51 cm”.

Question 12.
A metallic sphere of radius 4.2 cm is melted and recast into the shape of a cylinder of radius 6 cm. Find the height of the cylinder.
Solution:
We have,
Radius of sphere (r₁) = 4.2 cm, Radius of cylinder (r₂) = 6 cm
Let h cm be the height of cylinder.
Now, since sphere is melted and recast into cylinder
∴ Volume of sphere = Volume of cylinder

Hence, height of the cylinder is 2.744 cm.

Question 13.
Metallic spheres of radii 6 cm, 8 cm and 10 cm, respectively, are melted to form a single solid sphere. Find the radius of the resulting sphere.
Solution:
Letr be the radius of resulting sphere.
We have,
Volume of resulting sphere = Sum of the volumes of three given spheres

Hence, the radius of the resulting sphere is 12 cm.

Question 14.
A 20 m deep well with diameter 7 m is dug and the earth from digging is evenly spread out to form a platform 22 m by 14 m. Find the height of the platform.
Solution:
Here, radius of cylindrical well =\(\frac{7}{2}\)m
Depth of cylindrical well = 20 m
Let H metre be the required height of the platform.
Now, the volume of the platform = Volume of the earth dugout from the cylindrical well

∴ Height of the platform = 2.5 m

Question 15.
How many silver coins, 1.75 cm in diameter and of thickness 2 mm, must be melted to form a cuboid of dimensions 5.5 cm × 10 cm × 3.5 cm?
Solution:
We have,

Question 16.
A copper rod of diameter 1 cm and length 8 cm is drawn into a wire of length 18 m of uniform thickness. Find the thickness of the wire.
Solution:

The length of the new wire of the same volume = 18 m = 1800 cm
If r is the radius (in cm) of cross-section of the wire, its volume = π × r² × 1800 cm³
Therefore, π × r² × 1800 = 2π
i.e., r² = \(\frac{1}{900}\) i.e., r = \(\frac{1}{30}\)
So, the diameter of the cross section, i.e., the thickness of the wire is \(\frac{1}{15}\),
i.e., 0.67 mm (approx.).

Question 17.
A drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular, ends are 4 cm and 2 cm. Find the capacity of the glass.
Solution:

We have, R = 2 cm, r = 1 cm, h = 14 cm
∴ Capacity of the glass = Volume of the frustum

Question 18.
A fez, the cap used by the Turks, is shaped like the frustum of a cone (Fig). If its radius on the open side is 10 cm, radius at the upper base is 4 cm and its slant height is 15 cm, find the area of material used for making it.

Solution:
We have,
R = 10 cm, r = 4 cm, l = 15 cm
∴ Area of the material used for making the fez
= Surface area of frustum + Area of top circular section
= π(R + r) l +πr²
= \(\frac{22}{7}\)(10 + 4) × 15 + \(\frac{22}{7}\) × 4 × 4
= \(\frac{22}{7}\) × 14 × 15 + \(\frac{22}{7}\) × 16
= \(\frac{22}{7}\) (210 + 16) = \(\frac{4972}{7}\) = 710 \(\frac{2}{7}\) cm²

Question 19.
Two spheres of same metal weigh 1 kg and 7 kg. The radius of the smaller sphere is 3 cm. The two spheres are melted to form a single big sphere. Find the diameter of the new sphere.

Solution:

∴ Diameter of new sphere = 12 cm.

Question 20.
A farmer connects a pipe of internal diameter 20 cm from a canal into a cylindrical tank which is 10 m in diameter and 2 m deep. If the water flows through the pipe at the rate of 4 km per hour, in how much time will the tank be filled completely?
Solution:
Given, Diameter of tank = 10 m
Depth of tank (H) = 2 m
Internal diameter of pipe = 20 cm = \(\frac{2}{10}\) m
Rate of flow of water, ν = 4 km/h = 4,000 m/h
Internal radius of pipe, r =\(\frac{1}{10}\) m
Let ‘t be the time taken to fill the tank.
∴ Water flowing through pipe in t hours = Volume of tank
πr² × υ × t = πR²H

Question 21.
The largest possible sphere is carved out of a wooden solid cube of side 7 cm. Find the volume 22 of the wood left. [Use π = \(\frac{22}{7}\) ]
Solution:
Diameter of sphere carved out = side of cube = 7 cm
So, r = 3.5 cm
Volume of cube = a³ = 7³ = 343 cm³

Volume of wood left = 343 – 179.67 = 163.33 cm³

Question 22.
A hemispherical bowl of internal diameter 36 cm contains liquid. This liquid is filled into 72 cylindrical bottles of diameter 6 cm. Find the height of the each bottle, if 10% liquid is wasted in this transfer.
Solution:

Question 23.
A solid is composed of a cylinder with hemispherical ends. If the whole length of the solid is 100cm and the diameter of the hemispherical ends is 28cm. Find the cost of polishing the surface of the solid at the rate of 5 paise per sq.cm.
Solution:
We have
r = radius of cylinder = radius of hemispherical ends = \(\frac{28}{2}\) cm
h = height of the cylinder = 100 – 2 × 14 = 100 – 28 = 72 cm.
Total surface area
= Curved surface area of cylinder + 2 × Surface area of hemispherical ends = 2πrh + 2 × (2πr²)

Question 24.
A hemispherical tank, of diameter 3 m, is full of water. It is being emptied by a pipe at the rate of 3 \(\frac{4}{7}\) litre per second. How much time will it take to make the tank half empty? [Use π = \(\frac{22}{7}\)]
Solution:

Question 25.
The \(\frac{3}{4}\)th part of a conical vessel of internal radius 5 cm and height 24 cm is full of water. The water is emptied into a cylindrical vessel with internal radius 10 cm. Find the height of water in cylindrical vessel.
Solution:
Let the height of cylindrical vessel be h cm
According to question

Question 26.
A cylindrical tub, whose diameter is 12 cm and height 15 cm is full of ice cream. The whole ice cream is to be divided into 10 children in equal ice-cream cones, with conical base surmounted by hemispherical top. If the height of conical portion is twice the diameter of base, find the diameter of conical part of ice-cream cone.
Solution:
Volume of ice-cream in the cylinder = πr²h = (π(6)² × 15) cm³

Diameter of conical ice-cream cup = 6 cm

Question 27.
A conical vessel, with base radius 5 cm and height 24 cm, is full of water. This water is emptied into a cylindrical vessel of base radius 10 cm. Find the height to which the water will rise in the cylindrical vessel. [use π = \(\frac{22}{7}\)]
Solution:

⇒ h = 2 cm

Question 28.
The sum of the radius of base and height of a solid right circular cylinder is 37 cm. If the total surface area of the solid cylinder is 1628 sq. cm find the volume of the cylinder.
[Use π = \(\frac{22}{7}\)]
Solution:
Here
r + h = 37 and 2πr(r + h) = 1628

Question 29.
A sphere of diameter 12 cm, is dropped in a right circular cylindrical vessel, partly filled with water. If the sphere is completely submerged in water, the water level in the cylindrical vessel rises by 3\(\frac{3}{9}\) cm. Find the diameter of the cylindrical vessel.
Solution:

Question 30.
Water is flowing at the rate of 5 km/hour through a pipe of diameter 14 cm into a rectangular tank of dimensions 50 m × 44 m. Find the time in which the level of water in the tank will rise by 7 cm.
Solution:
Let the time taken by pipe be t hours.
∵ Speed = 5 km/h
∴ Length in t hours = 5000 t m.
According to question
Volume of water flown through pipe = Volume of water in tank
πr²h = l × b × h

⇒ t = 2
Hence required time is 2 hours.

Question 31.
The radius and height of a solid right circular cone are in the ratio of 5 : 12. If its volume is 314 cm³, find its total surface area. [Take π = 3.14]
Solution:
Given r : h = 5 : 12
Let r = 5x
⇒ h = 12x
Volume of cone = \(\frac{1}{3}\)π²h
314 = \(\frac{1}{3}\) × 3.14 (5x)² × 12x
⇒ x³ = \(\frac{314 \times 3}{3.14 \times 25 \times 12}\)
⇒ x³ = 1
⇒ x = 1
So, the value of r = 5 cm and h = 12 cm
Now, l = \(\sqrt{(12)^{2}+(5)^{2}}\) = 13 cm
TSA of cone = πr(l + r) = 3.14 × 5 (13 + 5)
= 3.14 × 90 = 282.6 cm²

Question 32.
A wire of diameter 3 mm is wound about a cylinder whose height is 12 cm and radius 5 cm so as to cover the curved surface of the cylinder completely. Find the length of the wire.
Solution:
CSA of cylinder = 2π(5) × 12
= 120 πcm²
Let length of wire = h cm
Radius of wire = \(\frac{3}{20}\) cm
According to question
CSA of wire = CSA of cylinder

Surface Areas and Volumes Class 10 Extra Questions Long Answer Type

Question 1.
From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm?
OR
From a solid right circular cylinder of height 2.4 cm and radius 0:7 cm, a right circular cone of same height and same radius is cut out. Find the total surface area of the remaining solid.

Solution:
We have,
0.7 cm Radius of the cylinder = 1.4/2 = 0.7 cm
Height of the cylinder = 2.4 cm
Also, radius of the cone = 0.7 cm
and height of the cone = 2.4 cm

∴ Total surface area of the remaining solid
= Curved surface area of cylinder + Curved surface area of the cone + Area of upper circular base of cylinder
= 2πrh + πrl + πr² = πr(2h + l + r)
= \(\frac{22}{7}\) × 0.7 × [2 × 2.4 + 2.5 + 0.7]
= 22 × 0.1 × (4.8 + 2.5 + 0.7)
= 2.2 × 8.0 = 17.6 cm² = 18 cm²

Question 2.
The decorative block shown in figure is made of two solids a cube and a hemisphere. The base of the block is a cube with edge 5 cm, and the hemisphere fixed on the top has a diameter of 4.2 cm. Find the total surface area of the block. (Use π = \(\frac{22}{7}\))
Solution:

The total surface area of the cube = 6 × (edge)²
= 6 × 5 × 5 cm² = 150 cm
∴ Total surface area of the block
= Total surface area of cube – Base area of hemisphere + Curved surface area of hemisphere
= 150 – πr² + 2πr² = (150 + πr²) cm²

cm² = (150 + 13.86) cm² = 163.86 cm

Question 3.
Rasheed got a playing top (lattu) as his birthday present, which surprisingly had no colour on it. He wanted to colour it with his crayons. The top is shaped like a cone surmounted by a hemisphere (Fig). The entire top is 5 cm in height and the diameter of the top is 3.5 cm. Find the area he has to colour. (Take π = \(\frac{22}{7}\)

Solution:
Total surface area of the top
= Curved surface area of hemisphere + Curved surface area of cone. Now, the curved surface area of hemisphere = 2πr²

Question 4.
A wooden toy rocket is in the shape of a cone mounted on a cylinder, in Fig. The height of the entire rocket is 26 cm, 6 cm while the height of the conical part is 6 cm. The base of the conical portion has a diameter of 5 cm, while the base diameter of the cylindrical portion is 3 cm. If the conical portion is to be painted orange and the cylindrical portion yellow, find the area of the rocket painted with each of these colours. (Take π = 3.14) 26 cm

Solution:
Denote radius, slant height and height of cone by r, l and h, respectively, and radius and height of cylinder by r’ and h’, respectively. Then r = 2.5 cm, h = 6 cm, r’ = 1.5 cm,
h’ = 26 – 6 = 20 and

Here, the conical portion has its circular base resting on the base of the cylinder, but the base of the cone is larger than the base of the cylinder. So, a part of the base of the cone (a ring) is to be painted. So, the area to be painted orange
= Curved surface area of the cone + Base area of the cone – Base area of the cylinder
= πrl + πr² – π(r’)²
= [(2.5 × 6.5) + (2.5)² – (1.5)²] cm²
= π[20.25] cm²
= 3.14 × 20.25 cm² = 63.585 cm²
Now, the area to be painted yellow
= Curved surface area of the cylinder + Area of one base of the cylinder
= 2πr’h’ + π(r’)² = πr’ (2h’ + r’)
= (3.14 × 1.5) (2 × 20 + 1.5) cm² = 4.71 × 41.5 cm² = 195.465 cm²

Question 5.
Rachel, an engineering student, was asked to make a model shaped like a cylinder with two cones attached at its two ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its length is 12 cm. If each cone has a height of 2 cm, find the volume of air contained in the model that Rachel made. (Assume the outer and inner dimensions of the model to be nearly the same.)
Solution:

Here, radius of cylindrical portion = \(\frac{3}{2}\)
Height of each cone = 2 cm
Height of cylindrical portion = 12 – 2 – 2 = 8 cm
Volume of the air contained in the model
= Volume of the cylindrical portion of the model + Volume of two conical K ends.

Question 6.
A gulab jamun, contains sugar syrup about 30% of its volume. Find approximately how much syrup would be found in 45 gulab jamuns, each shaped like a cylinder with two hemispherical ends with length 5 cm and diameter 2.8 cm (Fig).

Solution:
We have,
Radius of cylindrical portion and hemispherical portion of a gulab jamun
2.8/2 = 1.4 cm
Length of cylindrical portion = 5 – 1.4 – 1.4 = 2.2 cm
Volume of one gulab jamun
= Volume of the cylindrical portion + Volume of the hemispherical ends

Question 7.
A solid toy is in the form of a hemisphere surmounted by a right circular cone. EF The height of the cone is 2 cm and the diameter of the base is 4 cm. Determine the volume of the toy. If a right circular cylinder circumscribes the toy, find the difference of the volumes of the cylinder and the toy. (Take π = 3.14)

Solution:
Let BPC be the hemisphere and ABC be the cone standing on the base of the N
hemisphere (see Fig. 13.29).
The radius BO of the hemisphere (as well as of the cone) = 1/2 × 4 cm = 2 cm

Now, let the right circular cylinder EFGH circumscribe the given solid. The radius of the base of the right circular cylinder = HP = BO = 2 cm and its height is
EH = AO + OP = (2 + 2) cm = 4 cm
So, the required volume
= Volume of the right circular cylinder – Volume of the toy
= (3.14 × 2² × 4 – 25.12) cm³ = 25.12 cm³
Hence, the required difference of the two volumes = 25.12 cm³

Question 8.
A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand (Fig).

Solution:
We have,
Length of cuboid = 1 = 15 cm
Breadth of cuboid = b = 10 cm
Height of cuboid = h = 3.5 cm
And radius of conical depression = 0.5 cm
Depth of conical depression = 1.4 cm
Now, Volume of wood in the entire pen stand
= Volume of cuboid – 4 × Volume of a conical depression

Question 9.
A solid iron pole consists of a cylinder of height 220 cm and base diameter r = 8 cm 24 cm, which is surmounted by another cylinder of height 60 cm and radius 8 cm. Find the mass of the pole, given that 1 cm of iron has approximately 8 g mass. 60 cm (Use π = 3.14).
Solution:

Let r₁ and h₁ be the radius and height of longer cylinder, respectively, and r₂, h₂ be the respective radius and height of smaller cylinder mounted on the longer cylinder.
Then we have,
r₁ = 12 cm, h₁ = 220 cm
r₂ = 8 cm, h₂ = 60 cm
Now, Volume of solid iron pole
= Volume of the longer cylinder + Volume of smaller cylinder
= πr₁²h¹ + πr₂²h²
= 3.14 R (12)² × 220 + 3.14 R (8)² × 60
= 3.14 × 144 × 220 + 3.14 × 64 × 60
= 99475.2 + 12057.6 = 111532.8 cm³
Hence, the mass of the pole =(111532.8 × 8) grams
= \(\frac{111532.8 \times 8}{1000} \mathrm{kg}\) = 892.2624 kg

Question 10.
A solid consisting of a right circular cone of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is 60 cm and its height is 180 cm.
Solution:

We have,
Radius of cylinder = Radius of cone = Radius of hemisphere = 60 cm
∴ Height of cone = 120 cm
Height of cylindrical vessel = 120 + 60 = 180 cm

Question 11.
A container shaped like a right circular cylinder having diameter 12 cm and height 15 cm is full of ice cream. The ice cream is to be filled into cones of height 12 cm and & diameter 6 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice I cream.
Solution:

Question 12.
A cylindrical bucket, 32 cm high and with radius of base 18 cm, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, find the radius and slant height of the heap.
OR
A girl empties a cylindrical bucket, full of sand, of base radius 18 cm and height 32 cm, on the floor to form a conical heap of sand . If the height of this conical heap is 24 cm, then find its slant height correct up to one place of decimal.
Solution:
We have,
Radius of cylindrical bucket = 18 cm
Height of cylindrical bucket = 32 cm
And height of conical heap = 24 cm
Let the radius of conical heap be r cm
Volume of the sand = Volume of the cylindrical bucket
= πr²h = π × (18)² × 32
Now, Volume of conical heap = \(\frac{1}{3} \pi r^{2} h=\frac{1}{3} \pi r^{2} \times 24=8 \pi r^{2}\)
Here, volume of the conical heap will be equal to the volume of sand.
8πr² = π × (18)² × 32
r² = 18 × 18 × 4 = (18)² × (2)²
r² = (36)² or r = 36 cm

Question 13.
Selvi’s house has an overhead tank in the shape of a cylinder. This is filled by pumping water from a sump (an underground tank) which is in the shape of a cuboid. The sump has dimensions 1.57 m × 1.44 m × 95 cm. The overhead tank has its radius 60 cm and height 95 cm. Find the height of the water left in the sump after the overhead tank has been completely filled with water from the sump which had been full. Compare the capacity of the tank with that of the sump. (Use π = 3.14)
Solution:
The volume of water in the overhead tank equals the volume of the water removed from the sump.
Now, the volume of water in the overhead tank (cylinder) = πr²h
= 3.14 × 0.6 × 0.6 × 0.95 m³
The volume of water in the sump when full = l × b × h = 1.57 × 1.44 × 0.95 m³
The volume of water left in the sump after filling the tank
= [(1.57 × 1.44 × 0.95) – (3.14 × 0.6 × 0.6 x 0.95)] m³
= 1.57 × 0.95[1.44 – 2 × 0.6 × 0.6]
= 1.57 × 0.95 × 0.72
So, the height of the water left in the sump

Therefore, the capacity of the tank is half the capacity of the sump.

Question 14.
A container, opened from the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm, respectively. Find the cost of the milk which can completely fill the container, at the rate of ₹ 20 per litre. Also, find the cost of metal sheet used to make the container, if it costs ₹ 8 per 100 cm² (Take π = 3.14)
Solution:
We have, R = 20 cm, r = 8 cm, h = 16 cm

Now, cost of milk to fill the container completely at the rate of ₹20 per litre
= ₹ 20 x 10.44992 = ₹ 208.9984 ₹ 209
Also, Surface area = πl(R + r) + πr²
= 3.14 × 20 × (20 + 8) + 3.14 × 8 × 8
= 3.14 [560 + 64] = 3.14 × 624 = 1959.36 cm²
∴ Total cost of metal sheet used to make the container at the rate of ₹ 8 per 100 cm²
= ₹ \(\frac{8}{100}\) × 1959.36 = ₹ 156.75.

Question 15.
A metallic right circular cone 20 cm high whose vertical angle is 60° which is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained be drawn into a wire of diameter 1/16 cm, find the length of the wire.
Solution:
Let VAB be the metallic right circular cone of height 20 cm.
Suppose this cone is cut by a plane parallel to its base at a point O’ such that VO’ = O’ O i.e., O’ is the mid point of VO. Let r₁ andrą be the radii of circular ends of the frustrum ABB’A’. Now, in AVOA and VO’ A’, we have

Question 16.
In Fig, a cone of radius 10 cm is divided into two parts by drawing a plane through the mid-point of its axis, parallel to its base. Compare the volumes of the two parts.
Solution:
Let BC = r cm, DE = 10 cm
Since, B is the mid-point of AD and BC is parallel to DE, therefore C is the mid-point of AE.

Question 17.
The radii of the ends of a frustum of a cone 45 cm, high are 28 cm and 7 cm (Fig). Find its volume, the curved surface area and the total surface area[ Take π = \(\frac{22}{7}\) ]
Solution:

The frustum can be viewed as a difference of two right circular cones OAB and OCD (Fig. 13.37). Let the height (in cm) of the cone OAB be h₁ and its slant height l₁ ,i.e, OP = h₁ and OA = OB = l₁. Let h₂ be the height of cone OCD and l₂ its slant height.
We have, r₁ = 28 cm, r₂ = 7 cm
and the height of frustum (h) = 45 cm
Also, h₁ = 45 + h₂ …….. (i)
We first need to determine the respective heights h₁ and h₂ of the cone OAB and OCD.
Since the triangles OPB and OQD are similar, we have
\(\frac{h_{1}}{h_{2}}=\frac{28}{7}=\frac{4}{1}\) …….(ii)
From (i) and (ii), we get hy = 15 cm and h, = 60 cm.
Now, the volume of the frustum = Volume of the cone OAB – Volume of the cone OCD

The respective slant height l, and ly of the cones OCD and OAB are given by

Thus, the curved surface area of the frustum = πr₁l₁ – πr₂l₂
= \(\frac{22}{7}\) (28)(66.20) – \(\frac{22}{7}\)(7) (16.55)
= \(\frac{22}{7}\) × 7 × 16.55(16 – 1) = 5461.5 cm²
Now, the total surface area of the frustum
= Curved surface area of frustum + πr₁² + πr₂²
= 5461.5 cm² + \(\frac{22}{7}\)² cm² + \(\frac{22}{7}\)(7)² cm²
= 5461.5 cm² + 2464 cm² + 154 cm²
= 8079.5 cm²

Question 18.
An open metal bucket is in the shape of a frustum of a cone, mounted on a hollow cylindrical base made of the same metallic sheet (Fig). The diameters of the two circular ends of the bucket are 45 cm and 25 cm, the total vertical height of the bucket is 40 cm and that of the cylindrical base is 6 cm. Find the area of the metallic sheet used to make the bucket, where we do not take into account the handle of the bucket. Also, find the volume of water the bucket can hold. [Take π = \(\frac{22}{7}\)]

Solution:
The total height of the bucket = 40 cm, which includes the height of the base.
So, the height of the frustum of the cone = (40 – 6) cm = 34 cm.

Area of metallic sheet used
Curved surface area of frustum of cone + Area of circular base + Curved surface area of cylinder
= [π × 35.44 (22.5 + 12.5) + π × (12.5)² + 21 × 12.5 × 6] cm²
= \(\frac{22}{7}\) (1240.4 + 156.25 + 150) cm² = 4860.9 cm²
Now, the volume of water that the bucket can hold (also, known as the capacity of the bucket)

Question 19.
150 spherical marbles, each of diameter 1.4 cm, are dropped in a cylindrical vessel of diameter 7 cm containing some water, which are completely immersed in water. Find the rise in the level of water in the vessel.
Solution:
Diameter of spherical balls = 1.4 cm
Radius of spherical balls, r = 0.7 cm
Diameter of cylinder = 7 cm
Radius of cylinder = 3.5 cm
No. of spherical balls = 150
Let the rise in water be h cm.
Now, 150 × volume of a spherical ball = Volume of cylinder with height h.

Surface Areas and Volumes Class 10 Extra Questions HOTS

Question 1.
A well of diameter 3 m is dug 14 m deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 4 m to form an embankment. Find the height of the embankment.
Solution:

Here, radius of the well = \(\frac{7}{2}\) = 1.5 m
1.5 m Depth of the well = 14 m
Width of the embankment = 4 m
∴ Radius of the embankment = 1.5 + 4 = 5.5 m
Let h be the height of the embankment.
∴ Volume of the embankment
= Volume of the well (cylinder)

Question 2.
A hollow cone is cut by a plane parallel to the base at some height and the upper portion is removed. If the curved surface area of the remainder is of \(\frac{8}{9}\) the curved surface of the whole cone, find the ratio of the two parts into which the cone’s altitude is divided.
Solution:

In Fig, the smaller cone APQ has been cut off through the plane PQ || BC. Let r and R be the radii of the smaller and larger cone and l and L their slant heights respectively.
Here, in the adjoining figure
OQ = r, MC = R, AQ = l, AC = L.
Now, ∆AOQ ~ ∆AMC

Since, curved surface area of the remainder = \(\frac{8}{9}\) of the curved surface area of the whole cone,
therefore, we get,
CSA of smaller cone = \(\frac{1}{9}\) of the CSA of the whole cone


Hence, the required ratio of their heights = 1 : 2

Question 3.
The height of the cone is 30 cm. A small cone is cut off at the top by a plane parallel to the base. If its volume be \(\frac{1}{27}\) of the given cone, at what height above the base is the section made?
OR
The height of a cone is 30 cm. From its topside a small cone is cut by a plane parallel to its base. If volume of smaller cone is \(\frac{1}{27}\) of the given cone, then at what height it is cut from its base?
Solution:

Let the small cone APQ be cut off at the top by the plane PQ || BC
Let r and h be the radius and height of the smaller cone, respectively and also let the radius of larger cone = R

Hence, the smaller cone has been cut off at a height of (30 – 10) cm = 20 cm from the base.

Question 4.
Water in a canal, 6 m wide and 1.5 m deep, is flowing with a speed of 10 km/h. How much area will it irrigate in 30 minutes, if 8 cm of standing water is needed?
Solution:
We have, width of the canal = 6 m
Depth of the canal = 1.5 m
Now, length of water flowing per hour = 10 km
∴ Length of water flowing in half hour = 5 km = 5,000 m
∴ Volume of water flow in 30 minutes = 1.5 × 6 × 5,000 = 45,000 m³
Here, standing water needed is 8 cm = 0.08 m

= 562500 mo [1 hectare = 10000 m²]
= 56.25 hectares

Question 5.
A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one-fourth of the water flows out. Find 8 cm the number of lead shots dropped in the vessel.

Solution:
We have,
Height of conical vessel = h = 8 cm and its radius = r = 5 cm
Now, volume of cone = Volume of water in the cone

Question 6.
A right triangle with sides 3 cm and 4 cm is revolved around its hypotenuse. Find the volume of double cone thus generated. (Use π = 3.14).
Solution:

In the given Fig, ∆PQR is a right triangle, where PQ = 3 cm, PR = 4 cm and QR = 5 cm.
(by Pythagoras Theorem)
Let OQ = x ⇒ OR = 5 – x and OP = y
Now in right angled-triangle POQ, we have
PQ² = OQ² + OP²
⇒ (3)2 = x² + y² = y² = 9 – x² …..(i)
Also from right angled triangle POR, we have
OP² + OR² = PR²
⇒ y² + (5 – x)² = (4)²
⇒ y² = 16 – (5 – x)² ….. (ii)
From (i) and (ii), we get
9 – x² = 16 – (5 – x)²
⇒ 9 – x² = 16 – (25 + x² – 10x)
or 9 – x² = – 9 – x² + 10x
⇒ 10x = 18
⇒ x = \(\frac{9}{5}\)
∴ OR = 5 – x = 5 – \(\frac{9}{5}\) = \(\frac{16}{5}\)

Question 7.
A right circular cone is divided into three parts by trisecting its height by two planes drawn parallel to the base. Show that the volumes of the three portions starting from the top are in the ratio 1 : 7 : 19.
Solution:

From figure it is clear that
∆ACO” ~ ∆AEO’ [By AA similarity] and
∆ACO” ~ ∆AGO [By AA similarity]

Here we are providing Online Education for The Hack Driver Extra Questions and Answers Class 10 English Footprints Without Feet, Extra Questions for Class 10 English was designed by subject expert teachers. https://ncertmcq.com/extra-questions-for-class-10-english/

Online Education for The Hack Driver Extra Questions and Answers Class 10 English Footprints Without Feet

The Hack Driver Extra Questions and Answers Short Answer Type

The Hack Driver Extra Questions Question 1.
What job did the narrator get after graduation? Did he like his work?
Answer:
After doing his graduation, the narrator got the job of a junior assistant clerk in a law firm. No, he did not like his work. He had to serve a summons on the wanted people. He had to visit many dirty places. He never liked his work.

The Hack Driver Class 10 Extra Questions Question 2.
Why was he happy to go to New Mullion? Why did he go there?
Answer:
The narrator did not like the dirty and dark sides of the city life. He thought that he would find some pleasant sights in New Mullion. So, he was happy to go there.He went there to serve summons on Oliver Lutkins.

The Hack Driver Important Questions Question 3.
Why did the lawyer find the sight at the station’ “agreeable”?
Answer:
The narrator was disappointed to see the dirty roads and rows of wooden shops. But there was a man
who made the dull scene of the station agreeable by adding his cheerfulness.
He was the delivery man at the station.

Question 4.
How did the hack driver sketch the character of Lutkins?
Answer:
In fact, the hack driver was Lutkins himself. He sketched Lutkins as a very clever man who was good
at deceiving people. He never repaid the money he had taken from others.
He had a passion for Poker.

Question 5.
The narrator and the hack driver drove around together to find Lutkins.
(i) Which were the places they visited?
(ii) Why couldn’t they find Lutkins?
Answer:
(i) The hack driver took the narrator to almost all the places where Lutkins could be found. They visited Fritz’s shop, GustafFs shop, Gray’s stop, the pool room and Lutkins mother’s farmhouse.
(ii) They could not find Lutkins because the Hack driver was Lutkins himself.

Question  6.
What did the hack driver tell the narrator about Lutkins’ mother?
Answer:
The hack driver told the narrator that Lutkins’ mother was a real terror. She was nine feet tall, four feet thick and as quick as a cat.

Question 7.
How did Lutkins’ mother receive the narrator?
Answer:
Lutkins’ mother was not ready to tell them anything about Lutkins’. She tried to avoid their enquiry. When she ceune to know about the purposes of the narrator, she got furious. She went to the kitchen and came out with an iron rod. She marched towards them with a threat. They had to retreat from there.

Question 8.
What does the narrator describe as “pretty disrespectful treatment”?
Answer:
The narrator describes the treatment given to them by Lutkins’ mother as a pretty disrespected treatment. She insulted them. She marched towards them with a hot iron rod. She laughed at them when they retreated with a fear from there.

Question 9.
With what impression did the lawyer come back to the city?
Answer:
The lawyer returned to the city with a good impression. He liked the people of the village. He found them simple, wise and soft-spoken. He thought of practising law there. He was excited. He had found a treasure and a new way of life in New Mullion.

Question 10.
How did the people at the law firm receive him?
Answer:
The narrator could not find Lutkins. He could not serve the Summons on him so everyone at the firm was angry with him. They scolded and disgraced him,. His chief considered him as a useless fool. He was asked to go back to serve the summons on Lutkins.

Question 11.
Why was he sent back to New Mullion? Who went with him?
Answer:
The lawyer was sent back to New Mullion to serve summons on Lutkins. He had failed in his mission earlier. This time another man who had worked with Lutkins was also sent with him.

Question 12.
Who was the hack driver? What really hurt the feelings of the narrator in the end?
Answer:
The hack driver was Lutkins himself. He had driven the lawyer previous day. The narrator was really hurt when Lutkins and his mother were laughing at him as if he were a bright boy of seven.

Question 13.
How did the lawyer find the streets and shops of New Mullion?
Answer:
The lawyer found the streets of New Mullion muddy. With rows of wooden shops, either painted in sour brown or not painted at all. He was disappointed because he expected to see a sweet and simple country village.

Question 14.
Did the lawyer and the hack driver find Lutkins at Gustaffs barber shop? What did Gustaff say about Lutkins?
Answer:
No, they did not find Lutkins at Gustaffs barber shop. Gustaff told the hack driver that he had neither seen Lutkins nor he cared to see him. He asked him that if he finds Lutkins, he might collect the thirty , five dollars which Lutkins owes to him.

Question 15.
“Let’s go to a restaurant and I’ll buy your lunch,” the lawyer told the hack driver. Did they go to a restaurant to have lunch?
Answer:
The hack driver told the young lawyer that all the four restaurants in the town were bad. He suggested that only for half a dollar his wife would pack up the lunch for them and they would eat at Wade’s Hill. So they did not go to a restaurant.

Question 16.
Did Lutkin’s mother allow the lawyer to search her house to find Lutkins?
Answer:
The hack driver told Lutkins’ mother that the lawyer represented the court in the city and he had a legal right to search the home. She treated them quite disrespectfully but allowed to search the house. But they could not find Lutkin’s there.

Question 17.
“Really, I considered returning to New Mullion to practise law.” Why did the young lawyer think so?
Answer:
While returning, the young lawyer was too busy thinking about Bill Magnuson. He was so fascinated with Bill being “so deep and richly human” and others so soft-spoken, simple and wise that he thought of returning to New Mullion to practice law.

Question 18.
How did the lawyer feel after knowing that the hack driver was Oliver Lutkins himself?
Answer:
The law firm sent the lawyer again to New Mullion to serve the summons to Lutkins. The lawyer was
shocked and his feelings were hurt when the man told him that Bill or the hack driver was Lutkins himself.

Question 19.
“He was so open and friendly that I glowed with the warmth of his affection”. How did the young lawyer form this opinion about the hack driver?
Answer:
The young lawyer felt that the co-operating attitude and kindness shown to him was real, though the hack driver had to earn something out of it also. The lawyer bargained with the hack driver and had settled for two dollars an hour, but his wide smile made him think that he was one old friend.

Question 20.
Why is the lawyer sent to New Mullion? What does he first think about the place?
Answer:
The lawyer is sent to New Mullion to serve summons on a person named Oliver Lutkins, who was needed as a witness in a law case. He had expected the place to be a sweet and simple country village.

Question 21.
Who befriends him? Where does he take him?
Answer:
The lawyer was befriended by a delivery man who introduced himself as Bill. He told him that he knew Lutkins and would help the lawyer in finding him. He took him to all the possible places where Lutkins was’seen or was known to hang out. He took the lawyer to Fritz’s shop, where Lutkins was a frequent visitor to play poker; to GustafFs barber shop and then to Gray’s barber shop; to the poolroom and several other places before finally taking him to Oliver’s mother’s farm. However, so much of roaming around did not yield any result as they failed to find Oliver Lutkins.

Question 22.
What does he say about Lutkins?
Answer:
Bill told the lawyer that Lutkins was a clever fellow hard enough to catch. He was always up to something or the other. He owed money to many people, including Bill, and had never even paid anybody a cent. He also said that Oliver played a lot of pokers and was good at deceiving people.

Question 23.
What more does Bill say about Lutkins and his family?
Answer:
Bill told the lawyer that he knew Lutkin’s mother. He said that she was a terror. He narrated an incident when he took a trunk to her once and she almost took his skin off because he did not treat it like a box of eggs. He also said that she was very tall and fat. She was very quick and could talk a lot. He said that Oliver must have heard that somebody was chasing him and consequently, would have gone into hiding at his mother’s place.

Question 24.
Does the narrator serve the summons that day?
Answer:
No, the narrator does not serve the summon that day.

Question 25.
Who is Lutkins?
Answer:
The hack driver, who called himself Bill, is Oliver Lutkins.

The Hack Driver Extra Questions and Answers Long Answer Type

Question 1.
A person may appear humble but in actually he may not be so. Appearances can be deceptive. Explain with reference to the story ‘The Hack Driver’.
Answer:
Appearances are not always true. At times a person on first meeting appears to be friendly, co-operative,  understanding but as the time unfolds a different story is revealed. When the lawyer comes to the city for first time he is very happy to meet the hack driver. In fact the hack driver himself is Oliver Lutkins.

The hack driver seemed to be a simple country man ready to help. The hack driver showed affectionate behaviour. He left a favourable impression on the narrator’s mind. But very soon lawyer was able to realize that hack driver himself was Oliver Lutkins. It te so foolish to find that a wise person like a lawyer is befooled by a simple country man.

Question 2.
Intelligence or cleverness cannot be identified only on the basis of our work or profession but it comes from our inside. Explain it with reference to the chapter, ‘The Hack Driver’.
Answer:
Yes, it is quite right that intelligence and cleverness come automatically from our inside because it is our birth quality, it cannot be created, that’s why our intelligence or cleverness cannot be identified only on the basis of our work or profession. Many times in our daily life, we can find such examples. For example, a policeman is always considered brave and fighter because he has to face many difficulties daily and if he is not like that, he cannot defeat criminals, dacoits, burglars and cheaters. But sometimes we find some policemen opposite to it.

Some policemen nm away from the place where the people need them very much. Such policemen never think about their duty. They think only to save their lives. Such examples can easily be found in many different fields like medical, political. Some doctors don’t fulfill expectation of the common people, they think only for their families. So it is clear that our work or profession cannot disclose our internal quality like intelligence or cleverness. As we find in this story, the lawyer is not so clever or intelligent but the hackman is very cunning.

Question 3.
The hack driver appears to be humble, co-operative and friendly but as a matter of fact he is not. Explain in context of the story ‘The Hack Driver’ that appearances can be deceptive’.
Answer:
Appearances are not always true. At times a person on first meeting appears to be friendly, co-operative,  understanding but as the time unfolds a different story is revealed. When the lawyer comes to the city for first time he is very happy to meet the hack driver. In fact the hack driver himself is Oliver Lutkins.

The hack driver seemed to be a simple country man ready to help. The hack driver showed affectionate behaviour. He left a favourable impression on the narrator’s mind. But very soon lawyer was able to realize that hack driver himself was Oliver Lutkins. It te so foolish to find that a wise person like a lawyer is befooled by a simple country man.

Question 4.
The lawyer feels delighted in going to a country and enjoying going around it whole day. How does it portray the plight of town life? What values of the lawyer are reflected here?
Answer:
The lawyer is not happy the way he is treated by his law firm. He has no reputation there. He is taken to the task of serving the summons only. He is simple but hardworking. He believes that he can do better in his own village. Besides, he does not like the city life where people are selfish and boorish. On the other hand he finds the country life peaceful, close to the nature and the people there ready to extend a helping hand.

Question 5.
Give a brief character sketch of Oliver Lutkins.
Answer:
Oliver Lutkins was a jolly natured and fun loving person. He had a pleasant appearance. He impressed the lawyer at the railway station by his friendliness and simplicity. But he was not so simple and honest as he appeared to be. He knew about the lawyer’s ignorance and his purpose. He decided to be fool him. He introduced himself as Bill. He had a lot of fun out of his ignorance.

But Oliver had no other intention to befool the narrator besides having simple fun and enjoyment. He had a good understanding with the town folks who helped him in his plan. He loved poker. Lutkins never harmed anybody. He was very kind and well mannered too. He was a talented actor who made fun of an intelligent lawyer. He was very clever and sinart to plan at the moment and include everyone in his plan right before the narrator’s eyes.

Question 6.
Which were the places the narrator and the hack driver visited to search for Lutkins? How did they miss him narrowly everywhere?
Answer:
The narrator was a young lawyer and”was sent to New Mullion to serve a summon on Lutkins. The narrator did not recognise him. He met Bill, the hack driver at the station, who promised him to help in finding Lutkins. The hack driver first of all took him to Fritz. They learnt from him that he had gone to Gustaff s barber shop to have a shave. Reaching there, they learnt that Oliver had left for Gray’s barber shop. They missed him just by five minutes. The hack drove him to the poolroom. They missed him there too. After lunch the hack driver took the narrator to the farm of Lutkin’s mother. Lutkins could not be found there too. Thus, they missed him narrowly everywhere.

Question 7.
“Life is a serious matter; there is no place in it for humour or wit”. Discuss with reference to the story ‘The Hack Driver’.
Answer:
Life is certainly a serious matter. But it is wrong to say that there is no place for humour or wit in it. Life would be a great burden, if it had no humour or wit. There are so many tensions in life. We need a change from the monotony and dullness of the seriousness of life. Laughter is the best sauce of life. Wit and humour are its tools. However, we should be careful. We should not hurt the feelings of others by our sharp and biting wit. Let us laugh with others and not at them. Only then we can bid adieu to tension.

Question 8.
In life, people who easily trust others are sometimes made to look foolish. One should not be too trusting. Describe how Oliver Lutkins made a fool of the young lawyer.
Answer:
Appearances are not always true. At times a person on first meeting appears to be friendly, co-operative,  understanding but as the time unfolds a different story is revealed. When the lawyer comes to the city for first time he is very happy to meet the hack driver. In fact the hack driver himself is Oliver Lutkins.

The hack driver seemed to be a simple country man ready to help. The hack driver showed affectionate behaviour. He left a favourable impression on the narrator’s mind. But very soon lawyer was able to realize that hack driver himself was Oliver Lutkins. It te so foolish to find that a wise person like a lawyer is befooled by a simple country man.

Question 9.
When the lawyer reached New Mullion, did ‘Bill’ know that he was looking for Lutkins? When do you think Bill came up with his plan of fooling the lawyer?
Answer:
Lutkins act of taking the lawyer for a ride clearly indicates that he is a very cunning person. The way he tried to deal with the lawyer shows how quick he is in making plans to fool people. His idea not to disclose his true identity to unknown persons SIKJW how clever he is and it seems to be his regular practice to dupe people, especially the newcomers. As soon as the lawyer told Bill his purpose to visit to that place, Bill instantly knew how he would fool the lawyer.

Question 10.
Lutkins openly takes the lawyer all over the village. How is it that no one lets out the secret?
(Hint: Notice that the hack driver asks the lawyer to keep out of sight behind him when they go into Fritz’s.) Can you find other such subtle ways in which Lutkins manipulates the tour?
Answer:
Lutkins never allows the lawyer to the place where the imaginary Lutkins is supposed to be present at a given time. He asks him to keep out to sight, weaving vague stories about Lutkin’s vagabond nature. Bill also tries to scare away the lawyer, cooking up different stories about Lutkin’s mother. He did all this just to save himself from being summoned in the case.

Question 11.
Why do you think Lutkins’ neighbours were anxious to meet the lawyer?
Answer:
Lutkin’s neighbours were not anxious to meet a person who could be easily duped. They just wanted to enjoy the lawyer’s predicament.

Question 12.
After his first day’s experience with the hack driver the lawyer thinks of returning to New Mullion to practise law. Do you think he would have reconsidered this idea after his second visit?
Answer:
After his first day’s experience with the hack driver, the lawyer got a lesson for life that not to befriend anybody so easily. However, he realized during his second visit that he had been literally taken for a ride by the hack driver (who himself was Lutkins) and people of that town were just trying to enjoy the situation he was in. After becoming the laughing stock of the town, it is most likely that the lawyer would have reconsidered his initial idea of practising law in the village.

Question 13.
Do you think the lawyer was gullible? How could he have avoided being taken for a ride?
Answer:
The lawyer seems to be a simpleton and inexperienced person. He has yet to come to terms with the way the people in this world function. Being a lawyer, he could have easily avoided being duped by a stranger. Before visiting that village, he could have gathered important information regarding Lutkins. He could have taken a photograph of Lutkins along with him, most importantly, he should not have discussed his purpose of his visit with a total stranger, as it was a matter that involved law and security.

Question 14.
Do we come across persons like Lutkins only in fiction or do we encounter them in real life as well? You can give examples from fiction, or narrate an incident that you have read in the newspaper or an incident from real life.
Answer:
Yes, we do come across persons like Lutkins in fiction as well as in real life. Literature is full of instances where appearance is different from reality. In real life also we find that what appears may be quite contrary to what it turns out to be. That is why, it is said that all that glitters is not gold. A person who appears to be very gentle, may, later on, turns out to be a rogue. We read in newspapers many instances of so-called false holy men deceiving the people and turning out later as frauds.

Once I was taken for a ride. One night I got a telephonic message that my brother would be coming by morning flight. The person who was calling told me personally. He told me that my brother would be waiting for us at the airport. As my father was not feeling well, he asked me to go there to receive my brother. After reaching the airport, I looked for my brother, but he was nowhere to be found. I contacted the enquiry counter and was told that the flight was in. After two hours, I got a call on my mobile. It was my friend who laughed and said that they were successful in making me the first April fool!

Question 15.
Who is a ‘con man’, or a confidence trickster?
Answer:
A con man is a person who cheats others using confidence tricks. A con man poses as a sophisticated gentleman and takes his victim in full confidence. And then he cheats him in such a way that he comes to know about it only after he has been cheated.

Here we are providing Online Education for Some Applications of Trigonometry Class 10 Extra Questions Maths Chapter 9 with Answers Solutions, Extra Questions for Class 10 Maths was designed by subject expert teachers. https://ncertmcq.com/extra-questions-for-class-10-maths/

Online Education for Extra Questions for Class 10 Maths Some Applications of Trigonometry with Answers Solutions

Extra Questions for Class 10 Maths Chapter 9 Some Applications of Trigonometry with Solutions Answers

Some Applications of Trigonometry Class 10 Extra Questions Short Answer Type 1

Applications Of Trigonometry Class 10 Extra Questions With Solutions Question 1.
If a man standing on a platform, 3 metres above the surface of a lake observes a cloud and its reflection in the lake, then the angle of elevation of the cloud is equal to the angle of depression of its reflection.

Solution:
False, θ₁ ≠ θ₁ (Fig. 11.15)

Applications Of Trigonometry Hot Questions Question 2.
Find the angle of elevation of the sun when the shadow of a pole h m high is √3 h m long.
Solution:

In ∆ABC

θ = 30°

Application To Trigonometry Class 10 Extra Questions With Answers Question 3.
The height of a tower is 12 m. What is the length of its shadow when 10 Sun’s altitude is 45°?
Solution:

Let AB be the tower [Fig. 11.17].
Then, ∠C = 45°, AB = 12 m

∴ The length of the shadow is 12 m.

Some Applications Of Trigonometry Class 10 Extra Questions With Solutions Pdf Question 4.
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30° [Fig. 11.18].
Solution:
Let AB be the vertical pole and AC be the long rope tied to point C.
In right ∆ABC, we have

Therefore, height of the pole is 10 m.

Some Applications of Trigonometry Class 10 Extra Questions Short Answer Type 2

Applications Of Trigonometry Extra Questions Question 1.
The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.
Solution:
Let BC be the tower whose height is h metres and A be the point at a distance of 30 m from the
foot of the tower. The angle of elevation of the top of the tower from point A is given to be 30°.
Now, in right angle ∆CBA we have,

Hence, the height of the tower is 10 √3 m.

Some Applications Of Trigonometry Extra Questions Question 2.
A tree breaks due to storm and the broken part bends, so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
Solution:
In right angle ∆ABC, AC is the broken part of the tree (Fig. 11.20).
So, the total height of tree = (AB + AC)
Now in right angle ∆ABC,

Class 10 Maths Chapter 9 Extra Questions With Solutions Question 3.
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
Solution:

Let OA be the tower of height h metre and P, l be the two points at distance of 9 m and 4 m respectively from the base of the tower.
Now, we have OP = 9 m, OQ = 4 m,
Let ∠APO = θ, ∠AQO = (90° – θ)
and OA = h metre (Fig. 11.21)
Now, in ∆POA, we have


Height cannot be negative.
Hence, the height of the tower is 6 metre.

Applications Of Trigonometry Questions Question 4.
Determine the height of a mountain if the elevation of its top at an unknown distance from the base is 30° and at a distance 10 km further off from the mountain, along the same line, the angle of elevation is 15o. (Use tan 15° = 0.27)
Solution:
Let AB be the mountain of height h kilometres. Let C be a point at a distance of x km, from the base of the mountain such that the angle of elevation of the top at C is 30°. Let D be a point at a distance of 10 km from C such that angle of elevation at D is of 15°.
In MBC (Fig. 11.22), we have

Substituting x = √3h in equation (i), we get
⇒ 0.27 ( √3h + 10) = h
= 0.27 × √3h + 0.27 × 10 = h
⇒ 2.7 = h – 0.27 × √3h
⇒ 27 = h (1 – 0.27 × √3)
⇒ 27 = h (1 – 0.46)
⇒ h = \(\frac{2.7}{0.54}\) = 5
Hence, the height of the mountain is 5 km.

Applications Of Trigonometry Class 10 Extra Questions Question 5.
The shadow of a tower standing on a level ground is found to be 40 m longer when the Sun’s altitude is 30° than when it is 60°. Find the height of the tower.
Solution:
In Fig. 11.23, AB is the tower and BC is the length of the shadow when the Sun’s altitude is 60°, i.e., the angle of elevation of the top of the tower from the tip of the shadow is 60° and DB is the length of the shadow, when the angle of elevation is 30°.
Now, let AB be h m and BC be x m.
According to the question, DB is 40 m longer than BC.
So, BD = (40 + x) m
Now, we have two right triangles ABC and ABD.

Using (i) in (ii), we get (x √3 ) √3 = x + 40, i.e., 3x = x + 40
i.e., x = 20
So, h = 20 √3 [From (i)]
Therefore, the height of the tower is 20 √3 m.

Applications Of Trigonometry Class 10 Questions With Solutions Question 6.
From a point P on the ground, the angle of elevation of the top of a 10m tall building is 30°. A flag is hosted at the top of the building and the angle of elevation of the top of the flagstaff from P is 45o. Find the length of the flagstaff and the distance of the building from the point P. (You may take √3 = 1.732).
Solution:

In Fig. 11.24, AB denotes the height of the building, BD the flagstaff and P the given point. Note that there are two right triangles PAB and PAD. We are required to find the length of the flagstaff, i.e., BD and the distance of the building from the point P, i.e., PA.
Since, we know the height of the building AB, we will first consider the right ∆PAB.

i.e., x = 100(√3 – 1) = 7.32
So, the length of the flagstaff is 7.32 m.

Ch 9 Maths Class 10 Extra Questions Question 7.
A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, whereas for elder children, she wants to have a steep slide at a height of 3 m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?
Solution:
Let AC be a steep slide for elder children and DE be a slide for younger children. Then AB = 3 m and DB = 1.5 m (Fig. 11.25).
Now, in right angle ∆DBE, we have

So, the length of slide for elder children is 2 √3 m.

Applications Of Trigonometry Class 10 Important Questions Question 8.
A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
Solution:
Let AB be the horizontal ground and K be the position of the kite and its height from the ground is 60 m and let length of string AK be x m. (Fig. 11.26)
∠KAB = 60°
Now, in right angle ∆ABK we have

So, the length of string is 40 √3 m.

Some Applications Of Trigonometry Class 10 Extra Questions Question 9.
A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.
Solution:
Let AB be the building and PQ be the initial position of the boy (Fig. 11.27) such that
∠APR = 30°
and AB = 30 m
Now, let the new position of the boy be P’Q’ at a distance QQ’.
Here, ∠AP’R = 60°
Now, in ∆ARP, we have

Therefore, required distance, QQ = PP’ = PR – P’R
= 28.5 √3 – 9.5 √3 = 19√3
Hence, distance walked by the boy is 19√3 m.

Chapter 9 Maths Class 10 Extra Questions Question 10.
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45° respectively. If the bridge is at a height of 3 m from the banks, find
the width of the river.
Solution:
In Fig. 11.28, A and B represent points on the bank on opposite sides of the river, so that AB is the width of the river. P is a point on the bridge at a height of 3 m, i.e., DP = 3m. We are interested to determine the width of the river, which is the length of the side AB of the ∆APB.
In right ∆ADP, ∠A = 30°

∴ DB = 3m
Now, AB = BD + AD = 3 + 3 √3 = 3 (1 + √3) m
Therefore, the width of the river is 3(√3 + 1) m.

Class 10 Chapter 9 Maths Extra Questions Question 11.
As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
Solution:

Let AB be the lighthouse of height 75 m and P, Q be the position of the two ships whose angles of depression are 45° and 30°, respectively (Fig. 11.29). Let BP = x m and PQ = y m, we have
∠APB = 45° and ∠AQB = 30°
Now, in ∆ABP we have
tan 45° = \(\frac{AB}{BP}\)
⇒ 1 = \(\frac{70}{x}\)
⇒ x = 75 m …..(i)
Again, in ∆ABQ we have
tan 30° = \(\frac{AB}{BQ}\)
⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac{75}{x+y}\)
⇒ x + y = 75 √3 ……(ii)
From (i) and (ii), we have
75 + y = 75 √3
y = 75 √3 – 75
⇒ y = 75(√3 – 1)
Hence, the distance between two ships is 75(√3 – 1) metres.

Class 10 Applications Of Trigonometry Important Questions Question 12.
Two ships are there in the sea on either side of a light house in such a way that the ships and the light house are in the same straight line. The angles of depression of two ships as observed from the top of the light house are 60° and 45°. If the height of the light house is 200 m, find the distance between the two ships. (Use √3 = 1.73]
Solution:
Let the distance between the two ships be d.
Let the distance of one ship from the light house be x metres. Then, the distance of the other ship from the light house will be (d – x) metres.

Class 10 Maths Ch 9 Extra Questions Question 13.
The angle of elevation of an aeroplane from a point on the ground is 60°. After a flight of 30 seconds the angle of elevation becomes 30°. If the aeroplane is flying at a constant height of 3000 √3 m, find the speed of the aeroplane.
Solution:
Let A be point of observation and P and Q be positions of the plane. Let ABC be the line through A and it is given that angles of elevation from point A to two positions P and Q are 60° and 30°.
∠PAB = 60°, ∠QAB = 30°
Height = 3000 √3 m
So, in ∆ABP, we have

Some Applications Of Trigonometry Class 10 Important Questions Question 14.
From the top of a 60 m high building, the angles of depression of the top and the bottom of a tower are 45° and 60° respectively. Find the height of the tower. [Take √3 = 1.73]
Solution:
Let the height of the building be AE = 60 m, the height of the tower is ‘h’. The distance between the base of the building and the tower be ‘d’.
In ∆ADE,

⇒ AC = 34.60 m
Now, height of tower = AE – AC = 60 – 34.60 = 25.4 m

Question 15.
Two ships are approaching a light-house from opposite directions. The angles of depression of the two ships from the top of the light-house are 30° and 45°. If the distance between the two ships is 100 m, find the height of the light-house. (Use √3 = 1.732]
Solution:
Let AD be the light house and its height be h. The distance of one ship from the light house is x and that of other ship is 100 – x.
In ∆ADB,

= 50 × (1.732 – 1)
h = 36.6 m

Question 16.
Two men on either side of a 75 m high building and in line with base of building observe the angle of elevation of the top of the building as 30° and 60°. Find the distance between the two men. (Use √3 = 1.73)
Solution:

(i) In ∆ABM₁
\(\frac{A B}{B M_{1}}\) = tan 30° = \(\frac{1}{\sqrt{3}}\)
⇒ BM₁ = 75 √3 m

(ii) In ∆ABM₂
\(\frac{A B}{B M_{2}}\) = tan 60° = √3
⇒ BM2 = \(\frac{75}{\sqrt{3}}\) = 25 √3 m
∴ M₁ M₂ = M₁B + BM₂
= 75√3 + 25 √3 = 100 √3 m = 173 m
∴ Distance between two men = 173 m.

Question 17.
A moving boat is observed from the top of a 150 m high cliff moving away from the cliff. The angle of depression of the boat changes from 60° to 45° in 2 minutes. Find the speed of the boat in m/h.
Solution:

Let the speed of boat be x m/min
∴ CD = 2x
In ∆ABC
\(\frac{150}{y}\) = tan 60°
⇒ y =\(\frac{150}{\sqrt{3}}\) = 50√3 m
In ∆ABD
\(\frac{150}{y+2 x}\) = tan 45°
⇒ 150 = 50√3 + 2x
⇒ x = 25(3 – √3)
Speed = 25(3 – √3 ) m/min
∴ = 25 × 60 (3 – √3) m/h = 1500 (3 – √3) m/h

Some Applications of Trigonometry Class 10 Extra Questions Long Answer Type

Question 1.
From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60°, respectively. Find the height of the tower.
Solution:
Let AB be a building of height 20 m and BC be the transmission tower of height x m and D be any point on the ground (Fig. 11.36).
Here, ∠BDA = 45° and ∠ADC = 60°
Now, in ∆ADC, we have

⇒ x = 20√3 – 20 = 20 (√3 – 1) = 20 (1.732 – 1) = 20 × 0.732 = 14.64 m
Hence, the height of tower is 14.64 m.

Question 2.
A statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point, the angle of elevation of the bottom of the pedestal is 45°. Find the height of the pedestal.
Solution:
Let AB be the pedestal of height h metres and BC be the statue of height 1.6 m (Fig. 11.37).
Let D be any point on the ground such that,
∠BDA = 45° and ∠CDA = 60°
Now, in ∆BDA, we have


Hence, height of the pedestal is 0.8 (√3 + 1) m.

Question 3.
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
OR
From the top of a 7 m high building, the angle of elevation of the top of a tower is 60° and the angle of depression of its foot is 45°. Find the height of the tower. (Use √3 = 1.732]
Solution:

Let PQ be the building of height 7 metres and AB be the cable tower. Now it is given that the angle of elevation of the top A of the tower observed from the top P of building is 60° and the angle of depression of the base B of the tower observed from P is 45° (Fig. 11.38).
So, ∠APR = 60° and ∠QBP = 45°
Let QB = x m, AR = h m then, PR = x m
Now, in ∆APR, we have
tan 60° = \(\frac{AR}{PR}\)
⇒ √3 = \(\frac{h}{x}\)
⇒ √3x = h
⇒ h = √3x ……(i)
Again, in ∆PBQ we have
tan 45o = \(\frac{PQ}{QB}\)
⇒ 1 = \(\frac{7}{x}\)
⇒ x = 7 ……(ii)
Putting the value of x in equation (i), we have
h = √3 × 7 = 7 √3
i.e., AR = 7 √3 metres
So, the height of tower = AB = AR + RB = 7 √3 + 7 = 7(√3 + 1) m.

Question 4.
At a point, the angle of elevation of a tower is such that its tangent is \(\frac{5}{12}\) On walking 240 m to the tower, the tangent of the angle of elevation becomes \(\frac{3}{4}\). Find the height of the tower.
Solution:
In the Fig. 11.39, let AB be the tower, C and D be the positions of observation from where given that


Hence, the height of the tower is 225 metres.

Question 5.
A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After some time, the angle of elevation reduces to 30° (Fig. 11.40). Find the distance travelled by the balloon during the interval.
Solution:
Let A and B be two positions of the balloon and G be the point of observation. (eyes of the girl)
Now, we have
AC = BD = BQ – DQ = 88.2 m – 1.2 m = 87 m .
∠AGC = 60°, ∠BGD = 30°
Now, in ∆AGC, we have

Hence, the balloon travels 58 √3 metres.

Question 6.
A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.
Solution:
Let OA be the tower of height h, and P be the initial position of the car when the angle of depression is 30°.
After 6 seconds, the car reaches to such that the angle of depression at Q is 60°. Let the speed of the car be v metre per second. Then,
PQ = 6υ (∵ Distance = speed × time)
and let the car take t seconds to reach the tower OA from Q (Fig. 11.41). Then, OQ = υt metres.
Now, in ∆AQO, we have

Hence, the car will reach the tower from Q in 3 seconds.

Question 7.
In Fig. 11.42, ABDC is a trapezium in which AB || CD. Line segments RN and LM are drawn parallel to AB such that AJ = JK = KP. If AB = 0.5 m and AP = BQ = 1.8 m, find the lengths of AC, BD, RN and LM.
Solution:
We have,
AP = 1.8 m
AJ = JK = KP = 0.6 m
AK = 2AJ = 1.2 m
In ∆ARJ and ∆BNJ’ we have
AJ = BJ, ∠ARJ = ∠BNJ = 60°
and ∠AJR = ∠BJ’N = 90°
∴ ∆ARJ ≅ ∆BNJ
⇒ RJ = NJ (By AAS congruence criterion)
Similarly, ∆ALK ≅ ∆BMK”
⇒ LK = MK”
In ∆ARJ,


Since ∆ACP ≅ ∆BDQ
So, BD = AC = 2.0784 m
Now, RN = RJ + JJ + J’N
= 2RJ + AB [∵ RJ = J’ N and JJ = AB]
= 2 × 0.3464 +0.5 = 1.1928 m
Length of step LM = LK + KK + KM
= 2LK + AB [∵ LK = K M and KK = AB]
= 2 × 0.6928 + 0.5 = 1.8856 m
Thus, length of each leg = 2.0784 m = 2.1 m
Length of step RN = 1.1928 m = 1.2 m
and, length of step LM = 1.8856 m = 1.9 m

Question 8.
Two poles of equal heights are standing opposite to each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30°, respectively. Find the height of the poles and the distances of the point from the poles.
Solution:

Let AB and CD be two poles of equal height h metre and let P be any point between the poles, such that
∠APB = 60° and ∠DPC = 30°
The distance between two poles is 80m.(Given)
Let AP = x m, then PC = (80 – x) m.
h’m Now, in ∆APB, we have

Now, putting the value of x in equation (i), we have
h = √3 × 20 = 20 √3
Hence, the height of the pole is 20 √3 m and the distance of the point from first pole is 20 m and that of the second pole is 60 m.

Question 9.
A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30° (Fig. 11.44). Find the height of the tower and the width of the canal.
Solution:
Let height of the tower be h metres and width of the canal be x metres, so AB = h m and BC = x m
Now in ∆ABC, we have

Now, putting the value of x in equation (i), we have
h = √3 × 10 = 10√3
⇒ h = 10 73 m
Hence, height of the tower is 10 √3 m and width of the canal is 10 m.

Question 10.
A person standing on the bank of a river observes that the angle of elevation of the top of a tree standing on the opposite bank is 60°. When he moves 40 metres away from the bank, he finds the angle of elevation to be 30°. Find the height of the tree and the width of the river.
Solution:
Let AB be the tree of height metres standing on the bank of a river. Let C be the position of man standing on the opposite bank of the river such that BC = x m. Let D be the new position of the man. It is given that CD = 40 m and the angles of elevation of the top of the tree at C and D are 60° and 30°, respectively, i.e.,
∠ACB = 60° and ∠ADB = 30°.
In ∆ACB, we have


Hence, the height of the tree is 34.64 m and width of the river is 20 m.

Question 11.
The angles of elevation and depression of the top and bottom of a lighthouse from the top of a building, 60 m high, are 30° and 60° respectively. Find
(i) the difference between the heights of the lighthouse and the building.
(ii) distance between the lighthouse and the building.
Solution:
Let AB be the building and CE be the lighthouse (Fig. 11.46).
In right-angled ∆ABC,

= √3 DE = 20 √3
⇒ DE = 20
∴ (i) Difference between the heights of lighthouse and building = EC – DC = DE = 20 m
and (ii) Distance between the lighthouse and the building = BC = 34.64 m.

Question 12.
In Fig. 11.47, from the top of a building AB, 60 metres high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60°, respectively. Find
(i) the horizontal distance between AB and CD.
(ii) the height of the lamp post.
Solution:
Given AB is the building and CD is the vertical lamp post. Then, DE is the horizontal distance between AB and CD. Let CD = h metres.
Then
∠EDB = 30° and ∠ACB = 60°, AE = CD = h metres and EB = (60 -h) m
Now, in ∆ABC

⇒ 60 – h = 20, i.e., h = 40 m
∴ (i) Horizontal distance between AB and CD = 20 √3 m = 20 × 1.732 = 34.64 m
(ii) The height of lamp post = 40 m

Question 13.
A boy standing on a horizontal plane finds a bird flying at a distance an elevation of 30°. A girl standing on the roof of 20 metre high building, finds the angle of elevation of the same bird to be 45°. Both the boy and the girl are on opposite sides of the bird. Find the distance of bird from the girl.
Solution:
Let B be the position of bird. O and P be the positions of boy and girl respectively and PQ be the building
We have, ∠AOB = 30° and ∠BPM = 45°
Now, in ∆AOB we have

Hence, distance of bird from girl is 30 √2 m.

Question 14.
The angles of depression of the top and the bottom of a 8 m tall building from the top of a multi-storeyed building are 30° and 45°, respectively. Find the height of the multi-storeyed building and the distance between the two buildings.
Solution:
In Fig. 11.49, PC denotes the multi-storeyed building and AB denotes the 8 m tall building. We are interested to determine the height of the multi-storeyed building, i.e., PC and the distance between the two buildings, i.e., AC.
Let PD = x m
In right ∆PDB, we have

From (i), BD = [4(√3 + 1)] √3 = 4(3 + √3 )]
So, the height of the multi-storeyed building is {4( √3 + 1) +8} m = 4(3 + √3) m
and the distance between the two buildings is also 4(3 + √3) m.

Question 15.
The angle of elevation of the top of a tower at a distance of 120 m from a point A on the ground is 45°. If the angle of elevation of the top of a flagstaff fixed at the top of the tower, at A is 60°, then find the height of the flagstaff. [Use √3 = 1.73]
Solution:

Let CD be the tower which is at a distance of 120m from A.
BD = x be the length of flagstaff.

120 √3 = x + 120
= 120 × 1.73 – 120
x = 120 (1.73 – 1) = 120 × 0.73
x = 87.6 m

Question 16.
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
Solution:
Let AB be the building of height h m and CD be the tower of height 50 m. We have,
∠ACB = 30° and ∠DAC = 60°
Now, in ∆ACD, we have

Hence, the height of the building is 16\(\frac{2}{3}\)m.

Question 17.
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 5 m. From a point on the ground the angles of elevation of the top and bottom of the flagstaff are 60° and 30° respectively. Find the height of the tower and the distance of the point from the tower. (Take √3 = 1.732)
Solution:
Let height of tower be x m and distance of
point from tower be y m.


= x + 5 = 3x
⇒ x = \(\frac{5}{2}\) = 2.5
Height of tower = 2.5 m
Distance of point from tower = y = √3x
= (2.5 x 1.732) or 4.33 m

Question 18.
From the top of a tower, 100 m high, a man observes two cars on the opposite sides of the tower and in same straight line with its base, with angles of depression 30° and 45o. Find the distance between the cars.[Take √3 = 1.732]
Solution:
Let AQ be the tower of height 100m. Car B and Car Care in opposite direction and at distance
of x m and y m respectively.
In ∆ABO,

Distance between the cars = x + y
= 100 + 100√3 [From equation (i) and (ii)]
= 100 (1 + √3 )
= 100 (1 + 1.732) = 273.2 m

Some Applications of Trigonometry Class 10 Extra Questions HOTS

Question 1.
A man standing on the deck of a ship, which is 10 m above the water level, observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill.
Solution:
In Fig. 11.54, let C represents the position of the man on the deck of the ship, A represents the top of hill and D its base.
Now in right-angled triangle CWD,

Now, AD = AB + BD = 30 m + 10 m = 40 m.
Therefore, the distance of the hill from the ship = 17.3 m and the height of the hill = 40 m

Question 2.
A spherical balloon of radius r subtends an angle θ at the eye of an observer. If the angle of elevation of its centre is Ø, find the height of the centre of the balloon.
Solution:
In Fig. 11.55, O is the centre of balloon, whose radius OP = rand ∠PAQ = 0. Also, ∠OAB = Ø.
Let the height of the centre of the balloon be h. Thus OB = h.
Now, from ∆OAP,

Question 3.
From a window (h metres high above the ground) of a house in a street, the angles of elevation and depression of the top and the foot of another house on the opposite side of the street are θ and Ø respectively. Show that the height of the opposite house is h (1 + tan θ cot Ø).
Solution:
Let W be the window and AB be the house on the opposite side.
Then, WP is the width of the street (Fig. 11.56).
Let AP = h’ m

⇒ h’ = WP tan θ
⇒ h’ = h cot Ø tan θ
∴ Height of house = h’ + h
= h cot Ø tan θ + h = h (1 + tan θ cot Ø)

Question 4.
The angle of elevation of a jet plane from a point A on the ground is 60°. After a flight of 15 seconds, the angle of elevation changes to 30°. If the jet plane is flying at a constant height of
1500√3 m find the speed of the jet plane.
Solution:
Let P and Q be the two positions of the plane and let A be the point of observation. Let ABC be the horizontal line through A. It is given that angles of elevation of the plane in two positions P and Q from a point A are 60° and 30°, respectively,
Then, ∠PAB = 60°, ∠QAB = 30°
It is also given that PB = 1500√3 metres
In ∆ABP, we have

Question 5.
If the angle of elevation of a cloud from a point h metres above a lake is a and the angle of depression of its reflection in the lake is B, prove that the height of the cloud is \(\frac { h(tanß-tanα) }{ tan ß – tan α }\)

Solution:
Let AB be the surface of the lake and let P be a point of observation (Fig. 11.58) such that AP = h metres. Let C be the position of the cloud and C’ be its reflection in the lake. Then, CB = C’ B. Let PM be perpendicular from P on CB. Then, ∠CPM = a and ∠MPC’ = B.
Let CM = x.
Then, CB = CM + MB = CM + PA = x + h
In ∆CPM, we have

Question 6.
The shadow of a tower at a time is three times as long as its shadow when the angle of elevation of the sun is 60°. Find the angle of elevation of the sun at the time of the longer shadow.
Solution:
Let AB be the flagstaff and BC be the length of its shadow when the Sun rays meet the ground at an angle of 60°. Let o be the angle between the Sun rays and the ground when the length of the shadow of the flagstaff is BD. Let h be the height of the flagstaff (Fig. 11.59).
Let BC = x
∴ BD = 3x and CD = 2x
In ∆ABC, we have

Question 7.
From an aeroplane vertically above a straight horizontal plane, the angles of depression of two consecutive kilometre stones on the opposite sides of the aeroplane are found to be α and β. Show that the height of the aeroplane is = \(\frac { tanα.tanβ }{ tanα+tanβ }\)
Solution:
In Fig. 11.60, let P be the position of plane, A and B be the positions of two stones one kilometre apart. Angles of depression of stones A and B are a and ß respectively.
Let PC = h.
In right-angled triangle ACP, we have

Question 8.
The angle of elevation of a cliff from a fixed point is θ. After going up a distance of k metres towards the top of the cliff at an angle of Ø, it is found that the angle of elevation is α. Show that the height of the cliff is \(\frac {k(cos\phi-sin\phi cot\alpha)}{cot\theta-cot\alpha}\) metres.
Solution:
Let AB be the cliff and O be the fixed point such that ∠AOB = θ. Let ∠AOC = Ø and OC = k m.
From C, draw CD and CE perpendiculars on AB and OA, respectively. Now, ∠DCB = a. Let h be the height of the cliff AB.
In ∆COE, we have

Hence Proved.

Question 9.
The angle of elevation of the top of a tower from a point A due south of the tower is a and from B due east of the tower is β. if AB = d, show that the height of the tower is \(\frac {d}{\sqrt{{cot}^{2}}\alpha+{cot}^{2}\beta}\).
Solution:
Let OC be the tower. Let height of tower OC be h. A and B be two points due south and east of tower at O.
In ∠AOC, ∠O = 90°

Question 10.
From the top of a hill, the angles of depression of two consecutive kilometre stones due east are found to be 45° and 30° respectively. Find the height of the hill.
Solution:
Let the height of the hill be hm, C and D are two consecutive stones having distance 1000 m between them and AC = x m.
In ∆ABC,
tan 45° = \(\frac{h}{x}\)
⇒ x = h ….(i)
In ∆ABD,

Hence, the height of the hill = 500(√3 + 1)m.

Download NCERT Extra Questions for Class 10 Science for free: Here we are providing NCERT Extra Questions for Class 10 Science with Solutions Answers Chapter Wise Pdf free download. Students can get Class 10 Science NCERT Solutions, CBSE Class 10 Science Important Extra Questions and Answers designed by subject expert teachers.

Candidates who are studying under CBSE, UP, MP, Gujarat boards, and in search of NCERT Extra Questions Class 10 Science with Solutions Pdf reached the right page. Here, we have given NCERT Class 10th Science Extra Questions in pdf format. Students can get chapter-wise CBSE Extra Questions and Answers for 10th Class Science based on the NCERT syllabus which are designed by subject expert teachers from here.

NCERT Extra Questions for Class 10 Science with Answers Pdf

Available CBSE NCERT Chapter Wise Extra Questions for Class 10 Science with answers and solutions Pdf will surely encourage students to secure graceful marks in the board examinations. Access the below links & practice well for your science examination.

1. Chemical Reactions and Equations Class 10 Extra Questions
2. Acids Bases and Salts Class 10 Extra Questions
3. Metals and Non-metals Class 10 Extra Questions
4. Carbon and its Compounds Class 10 Extra Questions
5. Periodic Classification of Elements Class 10 Extra Questions
6. Life Processes Class 10 Extra Questions
7. Control and Coordination Class 10 Extra Questions
8. How do Organisms Reproduce Class 10 Extra Questions
9. Heredity and Evolution Class 10 Extra Questions
10. Light Reflection and Refraction Class 10 Extra Questions
11. Human Eye and Colourful World Class 10 Extra Questions
12. Electricity Class 10 Extra Questions
13. Magnetic Effects of Electric Current Class 10 Extra Questions
14. Sources of Energy Class 10 Extra Questions
15. Our Environment Class 10 Extra Questions
16. Management of Natural Resources Class 10 Extra Questions

NCERT Extra Questions for Class 10 Maths in PDF: Here we are providing NCERT Extra Questions for Class 10 Maths with Solutions Answers Chapter Wise Pdf free download. Students can get Class 10 Maths NCERT Solutions, CBSE Class 10 Maths Important Extra Questions and Answers designed by subject expert teachers.

To understand important SSC Maths concepts & solve any type of questions in the board exams, we have come up with an amazing & effective exam resource ie., class 10th maths extra questions and answers pdf. This NCERT extra questions of maths class 10 pdf cover all important topics chapterwise along with detailed solution steps. You can also Download CBSE class 10 maths extra questions with solutionss Pdf to revise the complete Syllabus and score more marks in your examinations.

Class 10 Maths Extra Questions with Solutions Answers

Make sure to download chapterwise Class 10 Maths NCERT CBSE Extra important questions solution pdf via available quick links for rigorous practice.

1. Real Numbers Class 10 Extra Questions
2. Polynomials Class 10 Extra Questions
3. Pair of Linear Equations in Two Variables Class 10 Extra Questions
4. Quadratic Equations Class 10 Extra Questions
5. Arithmetic Progressions Class 10 Extra Questions
6. Triangles Class 10 Extra Questions
7. Coordinate Geometry Class 10 Extra Questions
8. Introduction to Trigonometry Class 10 Extra Questions
9. Some Applications of Trigonometry Class 10 Extra Questions
10. Circles Class 10 Extra Questions
11. Constructions Class 10 Extra Questions
12. Areas Related to Circles Class 10 Extra Questions
13. Surface Areas and Volumes Class 10 Extra Questions
14. Statistics Class 10 Extra Questions
15. Probability Class 10 Extra Questions

We hope the given NCERT Extra Questions for Class 10 Maths with Solutions Answers Chapter Wise Pdf free download will help you. If you have any queries regarding CBSE Class 10 Maths Important Extra Questions and Answers, drop a comment below and we will get back to you at the earliest.