Category: CBSE Class 6

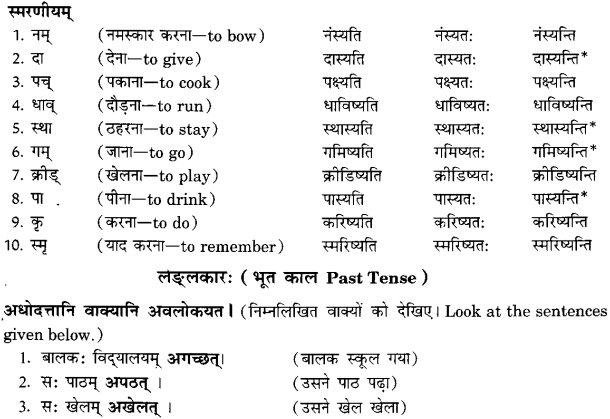
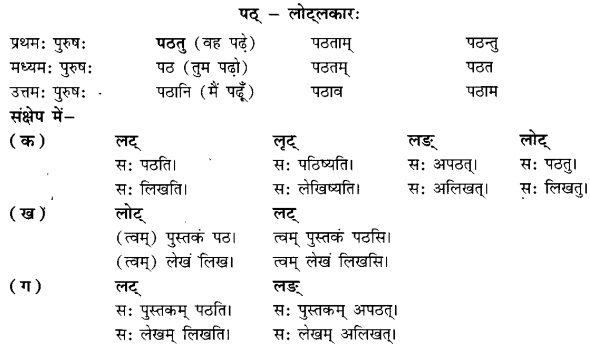
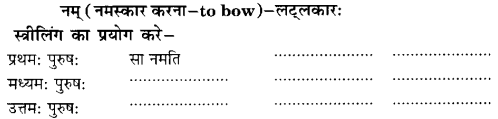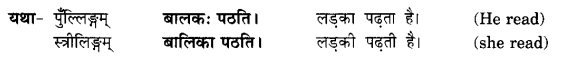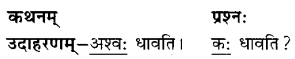We have given detailed NCERT Solutions for Class 6 Sanskrit Grammar Book चित्रवर्णनम् Questions and Answers come in handy for quickly completing your homework.

Sanskrit Vyakaran Class 6 Solutions चित्रवर्णनम्

प्रश्न 1.
प्रत्येकं चित्रं पश्यत। मुख्यवाक्यं पठित्वा मञ्जूषायाः सहायतया चतुर्पु वाक्येषु चित्रवर्णनम् कुरुत। (Look at the picture. Read the principal sentences and describe the picture in your sentences with help from the box.)

(क) एतत् वाटिकायाः चित्रम् अस्ति।

(पुष्पाणि, वृक्षाः, बालकाः, जनाः, चटकाः, वृक्षेषु, विकसन्ति, वाटिकायाम्, कूजन्ति, भ्रमणाय, अत्र वाटिकायाम्)
(i) ………..
(ii) ………..
(iii) ………….
(iv) ……….
(v) ……….
उत्तर:
(i) वाटिकायाम् पुष्पाणि विकसन्ति।
(ii) अत्र अनेके वृक्षाः सन्ति।
(iii) वृक्षेषु चटकाः कूजन्ति।
(iv) जनाः भ्रमणाय आगच्छन्ति।

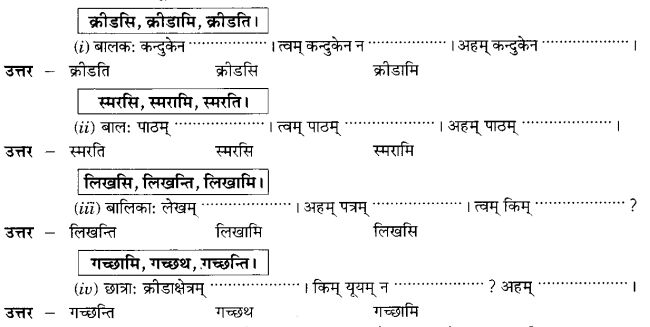
(ख) एतत् क्रीडाक्षेत्रस्य चित्रम् अस्ति।

(क्रीडाक्षेत्रे, कंदुकेन, पादकंदुकखेलम्, पादेन. क्षिपति, बालकाः, क्षिपति, खेलन्ति, कंदुकम्, प्रसन्नाः,सन्ति।)
(i) ……………….
(ii) ……………..
(iii) …………….
(iv) ………………
उत्तर:
(i) क्रीडाक्षेत्रे बालकाः खेलन्ति।
(ii) ते पादकंदुकखेलं खेलन्ति।
(iii) एक: बालकः पादेन कंदुकं क्षिपति।
(iv) बालकाः प्रसन्नाः सन्ति।

(ग) एतत् जंतुशालायाः चित्रम् अस्ति।

(व्याघ्राः, भल्लूकाः, चित्रकाः, मृगाः, मयूरः, सिंह, नृत्यति, गर्जति, जलचराः, उपवने, पञ्जरे, उच्चैः)
(i) ……………….
(ii) ……………..
(iii) …………….
(iv) ………………
उत्तर:
(i) जंतुशालायाम् व्याघ्राः, चित्रकाः, भल्लूकाः वानराः च सन्ति।
(ii) पञ्जरे सिंहः उच्चैः गर्जति।
(iii) उपवने मयूरः नृत्यति।
(iv) अत्र जलचराः अपि सन्ति।

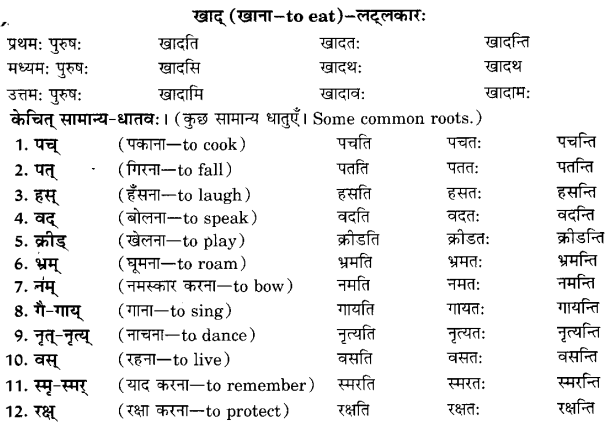
प्रश्न 2.
एकेन वाक्येन प्रत्येकम् चित्रं वर्णयत। (एक वाक्य में प्रत्येक चित्र का वर्णन कीजिए। Describe each picture in one sentence.)

उदाहरणम्-सिंहाः गर्जन्ति।

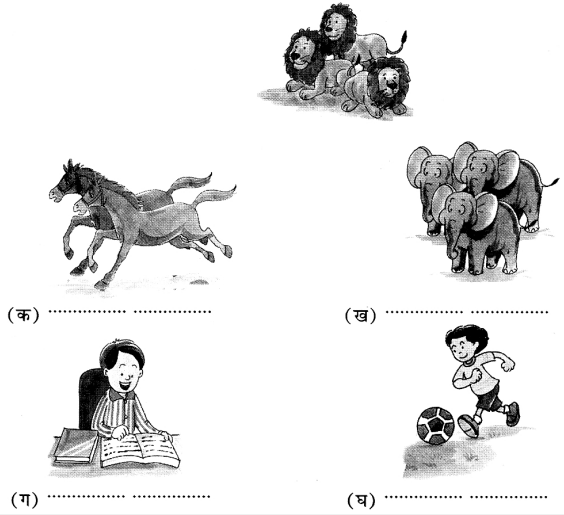
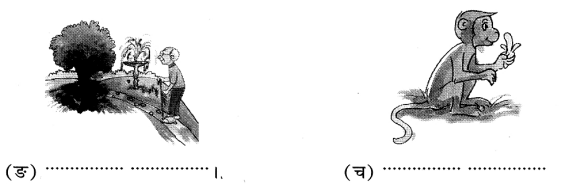
उत्तर:
(क) अश्वौ धावतः।
(ख) गजाः चलन्ति।
(ग) छात्रः पठति।
(घ) बालकः खेलति।
(ङ) वृदध/पितामहः भ्रमति।
(च) वानरः खादति।

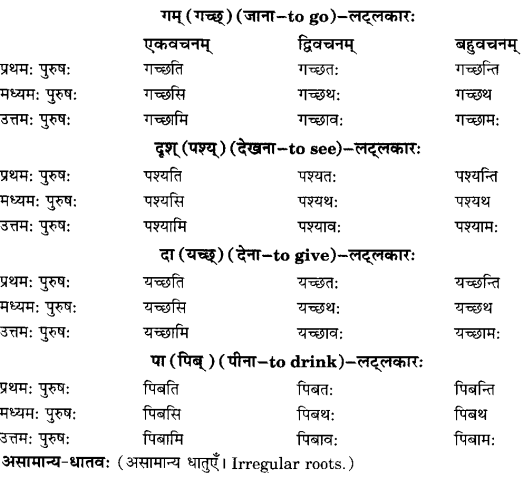
प्रश्न 3.
मञ्जूषातः उचितम् पदम् आदाय चित्रवर्णनम् पूरयत। (मञ्जूषा से उचित पद लेकर चित्र-वर्णन पूरा कीजिए। Complete the picture’s description with the help of words given in the box.)

(क) भोजनम्, चमसेन, बालिका, चषकः।

उत्तरम्-
(i) बालिका, (ii) भोजनम्, (iii) चमसेन, (iv) चषक:

(ख) नमति, बालिका, हस्ताभ्याम्, पितामहम्।

उत्तर:
(i) बालिकाः (ii) नमति (iii) पितामहम् (iv) हस्ताभ्याम्

(ग) दण्डेन, उपवनस्य, भ्रमति, वृक्षाः।

उत्तर:
(i) उपवनस्य (ii) वृक्षाः (iii) भ्रमति (iv) दण्डेन ।

Studying from CBSE Class 6 Sanskrit Notes helps students to prepare for the exam in a well-structured and organised way. Making NCERT Sanskrit Notes for Class 6 saves students time during revision as they don’t have to go through the entire textbook. In CBSE Notes, students find the summary of the complete chapters in a short and concise way. Students can refer to the NCERT Solutions for Class 6 Sanskrit (Ruchira Bhag 1), to get the answers to the exercise questions.

NCERT Sanskrit Notes for Class 6

1. शब्द परिचयः 1 Class 6 Notes
2. शब्द परिचयः 2 Class 6 Notes
3. शब्द परिचयः 3 Class 6 Notes
4. विद्यालयः Class 6 Notes
5. वृक्षाः Class 6 Notes
6. समुद्रतटः Class 6 Notes
7. बकस्य प्रतिकारः Class 6 Notes
8. सूक्तिस्तबकः Class 6 Notes
9. क्रीडास्पर्धा Class 6 Notes
10. कृषिकाः कर्मवीराः Class 6 Notes
11. पुष्पोत्सवः Class 6 Notes
12. दशमः त्वम असि Class 6 Notes
13. विमानयानं रचयाम Class 6 Notes
14. अहह आः च Class 6 Notes
15. मातुलचन्द्र Class 6 Notes

We hope students have found these CBSE Class 6 Sanskrit Notes useful for their studies. If you have any queries related to NCERT Sanskrit Notes for Class 6, drop your questions below in the comment box.

By going through these CBSE Class 6 Sanskrit Notes Chapter 10 कृषिकाः कर्मवीराः Summary, Notes, word meanings, translation in Hindi, students can recall all the concepts quickly.

Class 6 Sanskrit Chapter 10 कृषिकाः कर्मवीराः Summary Notes

कृषिकाः कर्मवीराः पाठ का परिचय

इस पाठ में हमारे अन्नदाता किसानों की कर्मठता और उनके संघर्षमय जीवन के विषय में बताया गया है। सर्दी-गर्मी के कष्टों को सहन करते हुए वे हम सब के लिए अन्न का उत्पादन करते हैं। अत्यधिक परिश्रम करने के उपरांत भी उन्हें निर्धनता का जीवन व्यतीत करना पड़ता है।

कृषिकाः कर्मवीराः Summary

इस पाठ में बताया गया है कि कृषक लोग ही सच्चे कर्मवीर हैं। सर्दी हो या गर्मी, कृषक कठोर परिश्रम करते हैं। गर्मी की ऋतु में शरीर पसीने से लथपथ हो जाता है और सर्दी में शरीर ठिठुरता है, परन्तु कृषक लोग कभी हल से तो कभी कुदाल से खेत को जोतते रहते हैं।

कृषक लोगों का जीवन कष्टमय होता है। वे स्वयं कष्ट उठाकर मानव मात्र की सेवा करते हैं। उनके पास न घर है, न वस्त्र हैं और न भोजन है। फिर भी वे मनुष्यों को सुख देने के लिए तत्पर रहते हैं। अतः कृषक ही सच्चे अर्थों में कर्मवीर हैं।

कृषिकाः कर्मवीराः Word Meanings Translation in Hindi

(क) सूर्यस्तपतु मेघाः वा वर्षन्तु विपुलं जलम्।
कृषिका कृषिको नित्यं शीतकालेऽपि कर्मठौ॥
ग्रीष्मे शरीरं सस्वेदं शीते कम्पमयं सदा।
हलेन च कुदालेन तौ तु क्षेत्राणि कर्षतः॥2॥

शब्दार्थाः (Word Meanings) :
सूर्यस्तपतु (सूर्य: + तपतु)-सूर्य तपाये (the Sun may burn), वर्षन्तु-बरसाएँ (may rain), विपुलम्-बहुत सारा (huge amount), कृषिका-किसान की स्त्री अथवा स्त्री किसान (a farmer’s wife or a lady farmer), कर्मठौ-काम में लगे हुए (active), सस्वेदम्-स्वेद (पसीने) से युक्त (full of sweat), कर्षत:-जुताई करते हैं (to plough), कृषिकः-किसान (farmer), कुदालेन-कुदाल से (with spade)

अन्वयः (Prose-order)
1. सूर्यः तपतु मेघाः वा विपुलं जलं वर्षन्तु। कृषिका कृषकः (च) शीतकाले अपि नित्यम् कर्मठौ (स्तः)।
2. ग्रीष्मे शरीरं सदा सस्वेदम् शीते (च) कम्पमयम् (अस्ति); तौ तु हलेन कुदालेन च क्षेत्राणि कर्षतः।

सरलार्थ :
चाहे, सूरज तपाये या बादल अत्यधिक बरसें किसान तथा उसकी पत्नी सदा सरदी में भी काम में लगे रहते हैं। गरमी में शरीर पसीने से भरा हुआ होता और ठंड में कंपनयुक्त अर्थात् काँपता रहता है किंतु फिर भी वे दोनों हल से अथवा कुदाल से खेतों को जोतते रहते हैं।

English Translation:
The Sun may burn or the clouds may pour huge amount of water, the farmer and his wife are always active even in winter, In summer the body is always full of sweat and in winter he shivers ie, it is shivering but they keep on ploughing the fields with their plough or with the spade.

(ख) पादयोन पदत्राणे शरीरे वसनानि नो।
निर्धनं जीवनं कष्टं सुखं दूरे हि तिष्ठति॥3॥
गृहं जीर्णं न वर्षासु वृष्टिं वारयितुं क्षमम्।
तथापि कर्मवीरत्वं कृषिकाणां न नश्यति॥4॥

शब्दार्थाः (Word Meanings) : पदत्राणे-जूते (shoes), पादयोः-पैरों में (on feet), वसनानि-वस्त्र (clothes), तिष्ठति-रहता है ( stays), जीर्णम्-पुराना (old), वृष्टिम्-बारिश को (rain), वारयितुम्-रोकने के लिए (to ward off), क्षमम्-समर्थ (able/capable), कर्मवीरत्वम्-कर्मठता (activity/active nature), न नश्यति-नष्ट नहीं होता (is not destroyed/ does not stop)।

अन्वयः (Prose-order)
3. पादयोः पदत्राणे न: (स्तः) शरीरे वसनानि न (सन्ति), निर्धनम् कष्टम् जीवनम् कष्टम्, सुखम् दूरे हि तिष्ठति।
4. जीर्णम् गृहम् वर्षासु वृष्टिं वारयितुम् क्षमम् न (अस्ति); तथापि कृषिकाणाम् कर्मवीरत्वं न नश्यति।

सरलार्थ : पैरों में जूते नहीं, शरीर पर कपड़े नहीं, निर्धन, कष्टमय जीवन है, सुख सदा दूर ही रहता है। घर टूटा-फूटा (पुराना) है, वर्षा के समय बारिश (अर्थात् बारिश का पानी अंदर आने से) रोकने में असमर्थ है। तो भी किसानों की कर्मनिष्ठा नष्ट नहीं होती अर्थात् वे कृषि के काम में लगे रहते हैं।

English Translation: There are no shoes on the feet, no clothes on the body. Life is full of poverty and there are difficulties and comforts stay far away. Their dwelling is old and during rains it is not able to keep off the rain i.e; the rain water (from seeping in.) but their activity (hardwork) does not stop.

(ग) तयोः श्रमेण क्षेत्राणि सस्यपूर्णानि सर्वदा।
धरित्री सरसा जाता या शुष्का कण्टकावृता॥5॥
शाकमन्नं फलं दुग्धं दत्त्वा सर्वेभ्य एव तौ।
क्षुधा-तृषाकुलौ नित्यं विचित्रौ जन-पालको॥6॥

शब्दार्थाः (Word Meanings):
तयोः-उन दोनों के (both of them), सस्यपूर्णानि-फसल से युक्त (full of crops), सर्वदा-हमेशा (always), धरित्री-धरा (earth/land), सरसा-रसपूर्ण। हरी-भरी (full of greenry), शुष्का-सूखी (dry), कण्टकावृता (कण्टक+आवृता)-काँटों से ढकी हुई (covered with thorns), शाकमन्नम् (शाकम्+अन्नम् )-सब्जी तथा अन्न (vegetables and grains), दत्त्वा-देकर (giving), क्षुधा-तृषाकुलौ (तृषा + आकुलौ)-भूख-प्यास से व्याकुल (distressed with hunger and thirst)।

अन्वयः (Prose-order)
5. तयोः श्रमेण क्षेत्राणि सर्वदा सस्यपूर्णानि (सन्ति), या धारित्री शुष्का कण्टकावृता (च आसीत्) (सा) सरसा जाता।
6. तौ सर्वेभ्यः एव शाकम् अन्नम् फलं दुग्धं (च) दत्त्वा नित्यं क्षुधा-तृषाकुलौ (स्तः) (तौ) विचित्रौ जनपालको (स्तः)।

सरलार्थ :
उन दोनों (किसान तथा उसकी पत्नी) के परिश्रम से खेत सदा फसलों से भर जाते हैं। धरती जो पहले सूखी व काँटों से भरी थी अब हरी-भरी हो जाती है। वे दोनों सब को सब्जी, अन्न, फल-दूध (आदि) देते हैं (किन्तु) स्वयं भूख-प्यास से व्याकुल रहते हैं। वे दोनों विचित्र (अनोखे) जन पालक हैं। (यह एक विडंबना है कि दूसरों की भूख मिटाने वाले स्वयं भूख का शिकार हैं।)

English Translation:
With the hard work of those two (the farmer and his wife) the fields are filled with crops. The land that was dry and full of thorns becomes fertile and full of greenry. They provide vegetables, grains, milk fruits to everybody but they themselves remain afflicted with hunger and thirst. These two are strange care-takers. (It is a paradox that those who alleviate the pangs of hunger of other people are themselves victims of hunger.)

By going through these CBSE Class 6 Sanskrit Notes Chapter 7 बकस्य प्रतिकारः Summary, Notes, word meanings, translation in Hindi, students can recall all the concepts quickly.

Class 6 Sanskrit Chapter 7 बकस्य प्रतिकारः Summary Notes

बकस्य प्रतिकारः पाठ का परिचय

इस पाठ में अव्यय पदों का प्रयोग आया है। अव्यय वे होते हैं, जिनमें लिंग, पुरुष, वचन, काल आदि के कारण कोई रूपांतर नहीं आता। वे अपने मूल रूप में प्रयुक्त होते हैं। यथा
(i) सः अपि गच्छति।
(ii) अहम् अपि गमिष्यामि।
(iii) ते अपि गमिष्यन्ति।

इन वाक्यों में ‘अपि’ में कोई परिवर्तन नहीं आया है। संस्कृत में ऐसे कई अव्यय हैं। यथा-एव (ही), च (और), तत्र (वहाँ), अत्र (यहाँ), कुत्र (कहाँ) आदि। पाठ में लङ्लकार (भूतकाल) के क्रियापद भी आए हैं। यथा- अवदत् (बोला) अयच्छत् (दिया) आदि।

बकस्य प्रतिकारः Summary

प्रस्तुत पाठ में अव्ययों के प्रयोग को कथा के माध्यम से दिखलाया गया है। गीदड़ और बगुला दो मित्र थे। दोनों मित्र एक वन में रहते थे। एक बार प्रात: गीदड़ ने बगुले से कहा-‘दोस्त, कल तुम मेरे साथ भोजन करो।’ गीदड़ का न्यौता पाकर बगुला प्रसन्न हुआ।

अगले दिन वह बगुला गीदड़ के निवास पर गया। गीदड़ कुटिल स्वभाव का था। उसने बगुले को एक थाली में खीर प्रदान की। गीदड़ बोला-‘दोस्त, इस पात्र में हम दोनों अब एक साथ खाते हैं।’ भोजन करते समय बगुले की चोंच थाली से भोजन लेने में समर्थ नहीं थी। इसलिए बगुला केवल खीर को देखता रहा। किन्तु गीदड़ सारी खीर खा गया। गीदड़ से ठगा गया बगुला सोचने लगा-जैसा व्यवहार इस गीदड़ ने मेरे साथ किया है वैसा मैं भी इसके साथ करूँगा। ऐसा सोचकर उसने गीदड़ से कहा-‘मित्र, तुम भी कल शाम को मेरे साथ भोजन करोगे। बगुले के निमन्त्रण से गीदड़ प्रसन्न हुआ।’

जब गीदड़ शाम को बगुले के निवास पर भोजन के लिए गया तब बगुले ने एक तंग मुँह के कलश में खीर प्रदान की और गीदड़ से कहने लगा-‘मित्र, हम दोनों साथ ही इस पात्र में भोजन करते हैं।’ बगुला कलश से चोंच के द्वारा खीर खाता है परन्तु गीदड़ का मुख कलश में प्रवेश नहीं करता। इसलिए बगुला सारी खीर खा लेता है और गीदड़ ईर्ष्यापूर्वक उसे देखता रहता है। शिक्षा-दुर्व्यवहार का फल दु:खदायक होता है। अतः सुख चाहने वाले मनुष्य को अच्छा व्यवहार करना चाहिए।

बकस्य प्रतिकारः Word Meanings Translation in Hindi

(क) एकस्मिन् वने शृगालः बकः च निवसतः स्म। तयोः मित्रता आसीत्। एकदा प्रातः शृगालः बकम् अवदत्-“मित्र! श्वः त्वं मया सह भोजनं कुरु।” शृगालस्य निमंत्रणेन बकः प्रसन्नः अभवत्।

शब्दार्थाः (Word Meanings) : एकस्मिन् वने-एक वन में (in a forest), शृगालः-गीदड़ सियार (jackal), बकः च-और बगुला (and a crane), निवसतः स्म-रहते थे lived (dual), तयो:-उन दोनों में (between them), आसीत्-था/थी (was), एकदा-एक बार (once), अवदत्-बोला (spoke/said), श्व:-आने वाला कल (tomorrow), मया सह-मेरे साथ (with me), भोजनं कुरु-भोजन करो (have dinner/meals), निमंत्रणेन-निमंत्रण से with (his) invitation, अभवत्-हुआ (became/was)

सरलार्थ :
एक वन में एक सियार और एक बगुला रहते थे। उन दोनों में मित्रता (दोस्ती) थी। एक दिन सवेरे सियार ने बगुले को कहा-“मित्र! कल तुम मेरे साथ खाना खाओ।” सियार के निमंत्रण से बगुला खुश हुआ।

English Translation:
There lived a jackal and a crane in a forest. There was friendship between the two of them. One morning the jackal said to the crane, ‘Friend! tomorrow you have dinner with me. The crane was happy with the jackal’s invitation.

(ख) अग्रिमे दिने सः भोजनाय शृगालस्य निवासम् अगच्छत्। कुटिलस्वभावः शृगालः स्थाल्यां काय क्षीरोदनम् अयच्छत्। बकम् अवदत् च-“मित्र! अस्मिन् पात्रे आवाम् अधुना सहैव खादावः।” भोजनकाले बकस्य चञ्चुः स्थालीतः भोजनग्रहणे समर्था न अभवत्। अतः बकः केवलं क्षीरोदनम् अपश्यत्। शृगालः तु सर्वं क्षीरोदनम् अभक्षयत्।

शब्दार्थाः (Word Meanings) :
अग्रिम दिवसे-अगले दिन (the next day), भोजनाय-भोजन के लिए (for dinner), निवासम्-निवास स्थान को (his residence), अगच्छत्-गया/गई (went), स्थाल्याम्-थाली में (in a dish), बकाय-बगुले के लिए, (for crane), क्षीरोदनम्-खीर (A sweet dish prepared with milk, rice, sugar etc.), अयच्छत्-दिया (to give), पात्रे-बर्तन में (in the vessel), अधुना-अब (now), सहैव (सह + एव)-साथ ही (together), बकस्य चञ्चुः-बगुले की चोंच (the crane’s beak), स्थालीतः-थाली से (from the dish), भोजनग्रहणे- भोजन ग्रहण करने में (to have dinner), समर्था-समर्थ (capable), अतः-इसलिए (therefore), केवलम्-केवल/सिर्फ़ (only), अपश्यत्-देखा/देखी (saw), अभक्षयत्-खाया। खायी (ate)

सरलार्थ:
अगले दिन वह भोजन के लिए सियार के निवास स्थान पर गया। कुटिल स्वभाव वाले सियार ने थाली में बगुले को खीर दी और बगुले से कहा-“मित्र, इस बर्तन में हम दोनों अब साथ ही खाते हैं।” भोजन के समय में बगुले की चोंच थाली से भोजन ग्रहण करने में समर्थ नहीं थी। अतः बगुला केवल खीर देखता रहा। सियार ने तो सारी खीर खा ली।

English Translation:
The next day he went to jackal’s house for dinner. The crooked jackal served the rice pudding to the crane in a flat dish and said to the crane — “Friend, let us now eat together in this vessel”. At the time of the meal the crane’s beak was unable to reach the food in the flat dish. Therefore the crane just kept looking at the milk pudding. The jackal ate up the entire milk pudding.

(ग) शगालेन वञ्चितः बकः अचिन्तयत्-“यथा अनेन मया सह व्यवहारः कृतः तथा अहम् अपि तेन सह व्यवहरिष्यामि।” एवं चिंतयित्वा सः शृगालम् अवदत्- “मित्र! त्वम् अपि श्वः सायं मया सह भोजनं करिष्यसि।” बकस्य निमंत्रणेन शृगालः प्रसन्नः अभवत्।

शब्दार्थाः (Word Meanings) :
शृगालेन-सियार द्वारा (by the jackal), वञ्चितः-ठगा गया . (deceived), अचिंतयंत्-सोचा (thought), यथा-जिस प्रकार (the way/like), अनेन-इसके द्वारा by this (jackal), व्यवहारः-व्यवहार (treatment, behaviour), कृतः-किया गया (has been done), तथा-उसी प्रकार (like that), अपि-भी (also/ too), तेन सह-उसके साथ (with him), व्यवहरिष्यामि-व्यवहार करूँगा (shall behave), एवम्-इस प्रकार (thus), चिंतयित्वा-सोच-समझकर (thinking properly), करिष्यसि-करोगे (will do)। .

सरलार्थ : सियार के द्वारा ठगे जाने पर बगुले ने सोचा, “जिस प्रकार इसने मेरे साथ बर्ताव किया है, उसी प्रकार मैं भी उसके साथ बर्ताव करूँगा।” ऐसा सोचकर उसने सियार से कहा-“दोस्त! तुम भी कल शाम मेरे साथ भोजन करोगे।” बगुले के निमंत्रण से सियार खुश हो गया।

English Translation: Having been cheated by the jackal the crane thought-“The way he has treated (behaved with) me, I too shall behave with him in the same manner.’ Thinking this he said to the jackal, ‘Friend, you too shall have dinner with me tomorrow evening. The jackal became happy with the crane’s invitation.

(घ) यदा शृगालः सायं बकस्य निवासं भोजनाय अगच्छत्, तदा बकः सङ्कीर्णमुखे कलशे क्षीरोदनम् अयच्छत् शृगालं च अवदत्-“मित्र! आवाम् अस्मिन् पात्रे सहैव भोजनं कुर्वः”। बकः कलशात् चञ्च्या क्षीरोदनम् अखादत्। परंतु शृगालस्य मुखं कलशे न प्राविशत्। अतः बकः सर्वं क्षीरोदनम् अखादत्। शृगालः च केवलम् ईjया अपश्यत्।

शब्दार्थाः (Word Meanings): यदा-जब (when), तदा-तब (then), सङ्कीर्णमुखे कलशे-तंग मुख वाले कलश में (in a pot with a narrow mouth), कुर्व:-(हम दोनों) करते हैं (we/both do), कलशात्-कलश से (from the pot), चञ्च्वा -चोंच से (with beak), प्राविशत्-प्रवेश किया (entered), ईर्ष्णया-ईर्ष्या से (jealously), अपश्यत्-देखा (saw)।

सरलार्थ :
जब सियार शाम को बगुले के निवास स्थान पर भोजन के लिए गया, तब बगुले ने छोटे मुख वाले कलश (सुराही) में खीर डाली (दी) और सियार से कहा-“दोस्त, हम दोनों इसी बर्तन में साथ ही भोजन करते हैं।” बगुले ने कलश से चोंच द्वारा खीर खाई। परंतु सियार का मुँह कलश में नहीं जा सका। इसलिए बगुला सारी खीर खा गया। सियार केवल ईर्ष्या से देखता रहा।

English Translation: When the jackal went to the crane’s residence for meals in the evening then the crane gave the rice pudding in a pot with a narrow mouth. And said to the jackal, “Friend! we shall eat together in this pot.” The crane ate the rice pudding with its beak. But the jackal’s mouth was unable to reach into the pot. Therefore the crane ate up all the rice pudding. The jackal just looked on jealously.

(ङ) शृगालः बकं प्रति यादृशं व्यवहारम् अकरोत् बकः अपि शृगालं प्रति तादृशं व्यवहारं कृत्वा प्रतीकारम् अकरोत्।

उक्तमपि- आत्मदुर्व्यवहारस्य फलं भवति दुःखदम्।
तस्मात् सद्व्यवहर्तव्यं मानवेन सुखैषिणा॥

शब्दार्थाः (Word Meanings) :
यादृशम् व्यवहारम्-जैसा व्यवहार (kind of behaviour), तादृशम्-वैसा (the same), कृत्वा-करके (having done), प्रतीकारम्-बदला (revenge), अकरोत्-किया (did), आत्मदुर्वव्यवहारस्य-अपने बुरे व्यवहार का (fall out of bad behaviour), फलम्-फल/परिणाम (result/fall out), दु:खद-दुखद/दुख देने वाला (causing misery), तस्मात्-इसलिए (therefore), सद्व्यवहर्तव्यम्-अच्छा व्यवहार करना चाहिए (should put on (do) good behaviour), मानवेन-मनुष्य द्वारा (by a person), सुखैपिणा-सुख चाहने वाले (wishing for happiness)।

सरलार्थः
सियार ने बगुले के प्रति जिस प्रकार का व्यवहार किया बगुले ने भी सियार के साथ वैसा ही व्यवहार करके बदला लिया। कहा भी गया है अपने बुरे व्यवहार का परिणाम दुखद ही होता है। इस कारण सुख चाहने वाले मानव को चाहिए कि वह सदा अच्छा व्यवहार करे।

English Translation: The way the jackal behaved with the crane the crane also behaved in the same way and took revenge. It also said, The fall out of one’s bad behaviour is always sorrowful. Therefore a person wishing for happiness should always do good behaviour.

अन्वयः- आत्मदुर्व्यवहारस्य फलं दु:खदम् भवति; तस्मात् सुखैषिणा मानवेन सद्व्यवहर्तव्यम्।

हमने सीखा
(i) अव्यय पदों का प्रयोग।
यथा-तदा, तथा, यदा, सह, एव, एवम्, प्रति, एकदा, प्रातः. सायं, अधुना, अद्य, श्वः।

(ii) लङ्लकार का प्रयोग भूतकाल की क्रिया दर्शाने के लिए किया जाता है। लङ्लकार में धातुरूप में धातु से पहले ‘अ’ लग जाता है।

By going through these CBSE Class 6 Sanskrit Notes Chapter 6 समुद्रतटः Summary, Notes, word meanings, translation in Hindi, students can recall all the concepts quickly.

Class 6 Sanskrit Chapter 6 समुद्रतटः Summary Notes

समुद्रतटः पाठ का परिचय

इस पाठ में तृतीया तथा चतुर्थी विभक्ति के शब्द-रूप का प्रयोग आया है। सरल शब्दों में ‘के द्वारा’, ‘से’ (with, by) के अर्थ में तृतीया विभक्ति पद तथा ‘के लिए’ (for) के अर्थ में चतुर्थी विभक्ति पद का प्रयोग किया जाता है। यथा

1. ‘कन्दुकेन’-गेंद से (with a ball), तरङ्गैः-लहरों से (with waves) (तृतीया)
2. ‘पर्यटनाय’–पर्यटन/घूमने के लिए (for excursion), पठनाय-पढ़ने के लिए (for study) (चतुर्थी)

वाक्य-प्रयोग

1. बालकः कन्दुकेन क्रीडति।
1. बच्चा गेंद से खेलता है।

2. सः पठनाय विद्यालयम् गच्छति।
2. वह पढ़ने के लिए विद्यालय जाता है।

समुद्रतटः Summary

इस पाठ में तृतीया व चतुर्थी विभक्ति के पदों का प्रयोग हुआ है। साथ ही इस पाठ में चित्रों के माध्यम से भारत के प्रसिद्ध समुद्रीय तटों का वर्णन है। चित्र में एक समुद्र तट को चित्रित किया गया है। यहाँ प्रणव नाम का एक बालक दोस्तों के साथ खेलता है। वह बालू (रेत) से घर बनाता है। दूसरे बालक गेंद से खेलते हैं। वे पैर से गेंद फेंकते हैं। कुछ बालक पानी की लहरों से क्रीडा करते हैं। दूसरे बालक लहरों के साथ उछलते हैं।

यहाँ अनेक नौकाएँ भी हैं। मल्लाहों के साथ सैलानी नौकाओं से समुद्र विहार करते हैं। हमारे देश में अनेक समुद्रतट हैं। इनमें बम्बई, गोवा, कन्याकुमारी अत्यधिक प्रसिद्ध हैं। विदेशी लोगों को गोवा तट अधिक रुचिकर लगता है। कोच्चि तट नारियल के फलों के लिए जाना जाता है। चेन्नई नगर का मेरीना तट देश के सागर तटों में सबसे लम्बा है। इस प्रकार भारत की तीनों दिशाओं में समुद्रतट हैं।

समुद्रतटः Word Meanings Translation in Hindi

(क) एषः समुद्रतटः। अत्र जनाः पर्यटनाय आगच्छन्ति। केचन तरङ्गैः क्रीडन्ति। केचन च नौकाभिः जलविहारं कुर्वन्ति। तेषु केचन कन्दुकेन क्रीडन्ति। बालिकाः बालकाः च बालुकाभिः बालुकागृहं रचयन्ति। मध्ये मध्ये तरङ्गाः बालुकागृह प्रवाहयन्ति। एषा क्रीडा प्रचलति एव। समुद्रतटा: न केवलं पर्यटनस्थानानि। अत्र मत्स्यजीविनः अपि स्वजीविकां चालयन्ति।

शब्दार्थाः (Word Meanings) :
समुद्रतट:-समुद्र का किनारा (shore), पर्यटनाय-घूमने के लिए (for excursion), आगच्छन्ति-आते हैं (come), केचन-कुछ (लोग) some (people), तरङ्गै -लहरों से (with waves), नौकाभिः-नौकाओं/नावों द्वारा (by boats), जलविहारम्-पानी में घूमना/खेल (make fun/roam around in water), तेषु केचन-उनमें से कुछ (some of them), बालुकाभिः -रेत से (with sand), बालुकागृहम्-रेत के घर (sand houselet), मध्ये मध्ये-बीच-बीच में (at some intervals), प्रवाहयन्ति-बहा ले जाती है (wash/carry away), प्रचलति एव-चलता ही रहता है। (keeps on going), मत्स्यजीविनः-मत्स्यजीवी/ मछुआरे (fishermen), स्वजीविकां चालयन्ति-अपनी आजीविका चलाते हैं, (carry on their livelihood)।

सरलार्थ :
यह समुद्र तट है। यहाँ लोग पर्यटन के लिए आते हैं। कुछ लहरों से क्रीडा करते हैं। कुछ नौकाओं द्वारा जलविहार करते हैं। उनमें से कुछ गेंद से खेलते हैं। लड़कियाँ और लड़के रेत से रेत के घर बनाते हैं। बीच-बीच में लहरें रेत का घर बहा ले जाती हैं। यह खेल चलता ही रहता है। समुद्र तट केवल पर्यटन-स्थल नहीं। यहाँ मछुआरे भी अपनी आजीविका चलाते हैं।

English Translation:
This is a beach. People come here for excursion. Some play with waves (of the sea). Some indulge in water sports by boats i.e, using boats. Among them some play with a ball. Girls and boys make sand castles (house) with sand. At intervals the waves wash away the sand-castle. This play keeps on going. The beaches are not mere tourist spots. Here the fishermen too earn their livelihood.

(ख) अस्माकं देशे बहवः समुद्रतटाः सन्ति। एतेषु मुम्बई-गोवा-कोच्चि-कन्याकुमारी विशाखापत्तनम्-पुरीतटाः अतीव प्रसिद्धाः सन्ति। गोवातटः विदेशिपर्यटकेभ्यः समधिकं रोचते। विशाखापत्तनम्-तटः वैदेशिकव्यापाराय प्रसिद्धः। कोच्चितटः नारिकेलफलेभ्यः ज्ञायते। मुम्बईनगरस्य जुहूतटे सर्वे जनाः स्वैरं विहरन्ति। चेन्नईनगरस्य मेरीनातटः देशस्य सागरतटेषु दीर्घतमः।

शब्दार्थाः (Word Meanings) :
अस्माकं-हमारे (our), देशे-देश में (in country), बहवः-अनेक (many), अतीव (अति + इव)-बहुत ज़्यादा (very much, excessive), प्रसिद्धाः -मशहर (famous), विदेशिपर्यटकेभ्यः -विदेशी सैलानियों के लिए (for foreign tourists), समधिकम्-बहुत ज्यादा (in excess), रोचते-अच्छा लगता है, (is favourite), वैदेशिकव्यापाराय-विदेशी व्यापार के लिए (foreign trade), नारिकेलफलेभ्यः-नारियल के लिए (for coconuts), ज्ञायते-जाना जाता है (is known), स्वैरं-अपनी इच्छानुसार (according to own will), विहरन्ति-घूमते हैं (roam around), देशस्य-देश का/के/की (of country), सागरतटेषु-समुद्री तटों में (among beaches), दीर्घतमः-सबसे बड़ा/लंबा (longest)।

सरलार्थ : हमारे देश में बहुत से समुद्रतट हैं। इनमें मुम्बई, गोवा, कोच्चि, कन्याकुमारी, विशाखापत्तनम् तथा पुरी का तट बहुत प्रसिद्ध है। गोवा का तट विदेशी पर्यटकों को बहुत ज़्यादा पसंद है। विशाखापत्तनम् का तट विदेशी व्यापार के लिए प्रसिद्ध है। कोच्चि का तट नारियल के लिए जाना जाता है। मुम्बई नगर के जुहू तट पर. सब लोग अपनी इच्छानुसार विहार करते हैं। चेन्नई का मेरीना तट देश के सभी तटों में सबसे लंबा है।

English Translation:
In our country there are many beaches. Among them the beaches at Mumbai, Goa, Kochi, Kanyakumari, Vishakhapattanam and Puri are very famous. The Goa beach is favourite with foreign tourists. The beach at Vishkhapattnam is famous for foreign trade. The Kochi-beach is known for coconuts. Everyone roams around according to one’s will at the Juhu beach of Mumbai city. The Marina beach of Chennai is the largest among all the beaches of the country.

(ग) भारतस्य तिसृषु दिशासु समुद्रतटाः सन्ति। अस्माद् एव कारणात् भारतदेशः प्रायद्वीपः इति कथ्यते। पूर्वदिशायां बगोपसागरः दक्षिणदिशायां हिंदमहासागरः पश्चिमदिशायां च अरबसागरः अस्ति। एतेषां त्रयाणाम् अपि सागराणां सङ्गमः कन्याकुमारीतटे भवति। अत्र पूर्णिमायां चन्द्रोदयः सूर्यास्तं च युगपदेव द्रष्टुं शक्यते।

शब्दार्थाः (Word Meanings) :
भारतस्य-भारत का/के/की (of India), तिसृषु दिशासु-तीनों दिशाओं में (in all three directions), अस्माद् एव कारणात्-इसी कारण से (for this very reason), प्रायद्वीप-प्रायद्वीप (तीन दिशाओं में समुद्र से घिरा) (peninsula), इति-ऐसा (thus/this), कथ्यते-कहा जाता है (is said), पूर्वदिशायाम्-पूर्व दिशा में (in the East), बङ्गोपसागर-बंगाल की खाड़ी (Bay of Bengal), दक्षिण दिशायाम्-दक्षिण दिशा में (in the Southern direction), एतेषां त्रयाणाम्-इन तीनों का (of these three), सङ्गमः-मिलने का स्थान (place, where rivers or oceans meet), पूर्णिमायाम्-पूर्णिमा पर (on Poornima, full moon), चंद्रोदयः-चाँद का उदय होना (Moon-rise), द्रष्टुम् शक्यते-देखा जा सकता है (can be seen), सागराणाम्-सागरों का (of the seas), कन्याकुमारी तटे-कन्याकुमारी के तट पर (on the beach of Kanyakumari), युगपदेव (युगपद् + एव)-एक साथ ही (at the same time, simultaneously)

सरलार्थ :
भारत की तीनों दिशाओं में समुद्रतट हैं। इसी कारण से भारत देश को प्रायद्वीप भी कहा जाता है। पूर्व दिशा में बंगाल की खाड़ी, दक्षिण दिशा में हिंद महासागर और पश्चिम दिशा में अरब सागर है। इन तीनों सागरों का संगम कन्याकुमारी के तट पर होता है। यहाँ पूर्णिमा के अवसर पर चन्द्रोदय और सूर्यास्त एक साथ ही देखा जा सकता है।

English Translation: There are beaches in all the three directions of India. For this very reason India is called a peninsula. In the east direction there is Bay of Bengal, in the South there is the Indian ocean and in the West there is the Arbian Sea. There is confluence of all these three at the Kanyakumari-beach. On the Full-Moon day it is possible to see both the Moon rise and the Sun-set at the same time.

हमने सीखा संस्कृत में संज्ञा शब्दों के लिंग पूर्व निर्धारित होते हैं। अकारान्त शब्दों में कुछ पुल्लिग और कुछ नपुंसकलिंग शब्द हैं। आकारान्त शब्द स्त्रीलिंग होते हैं। दोनों के रूप भिन्न हैं।

ध्यातव्यम्-तृतीया विभक्ति से अकारांत पुल्लिग तथा नपुंसकलिंग शब्दों के रूप में कोई भेद नहीं होता। यथा मित्र शब्द के रूप भी ‘बालक’ की भाँति होते हैं।

(घ) सः मित्रेण सह खेलति। (मित्र के साथ)

• सह (साथ) के योग में तृतीया विभक्ति पद का प्रयोग किया जाता है।
• ददाति (देना) के योग में चतुर्थी विभक्ति पद का प्रयोग किया जाता है।

 

By going through these CBSE Class 6 Sanskrit Notes Chapter 5 वृक्षाः Summary, Notes, word meanings, translation in Hindi, students can recall all the concepts quickly.

Class 6 Sanskrit Chapter 5 वृक्षाः Summary Notes

वृक्षाः पाठ का परिचय

पाठ का परिचय (Introduction of the Lesson) इस पाठ में अकारान्त शब्द के प्रथमा तथा द्वितीया विभक्ति के रूप का प्रयोग आया है। प्रथमा विभक्ति का शब्द रूप कर्तापद के लिए और द्वितीया विभक्ति का रूप कर्मपद के लिए प्रयोग में लाया जाता है। यथा

वृक्षाः Summary

इस पाठ में कवि ने वृक्षों के महत्त्व का चित्रण किया है। वृक्ष मनुष्य के मित्र हैं। वृक्ष मनुष्य के लिए सर्वथा उपयोगी एवं कल्याणकारी हैं। वृक्षों की शाखाओं पर बैठे हुए पक्षी कलरव करते हैं। ऐसा प्रतीत होता है मानो वृक्ष मानव के मनोरंजन के लिए मधुर गीत गा रहे हैं। वृक्ष केवल वायु का भक्षण करते हैं और जल पीते हैं, परंतु वे मनुष्यों को फल, छाया आदि प्रदान करते हैं। वस्तुतः वृक्ष मनुष्य के लिए हितकारी हैं।

वृक्षाः Word Meanings Translation in Hindi

(क) ‘बालकाः खेलन्ति’ वाक्य में ‘बालकाः’ कर्तापद (Subject) होने के कारण प्रथम विभक्ति में है।
(ख) ‘बालकाः पादकंदुकखेलम्-खेल खेलन्ति’ वाक्य में ‘पादकंदुकखेलम्’ कर्मपद (object) होने के कारण द्वितीया विभक्ति में है। हम सीख चुके हैं अकारान्त शब्द दो प्रकार के होते हैं।
(i) पुल्लिंग तथा
(ii) नपुंसकलिंग। दोनों के रूप नीचे दिए गए हैं।

ध्यातव्यम्-नपुंसकलिंग शब्दों के रूप प्रथमा तथा द्वितीया विभक्ति में एक समान होते हैं।

पाठ – शब्दार्थ एवं सरलार्थ ।

(क) वने वने निवसन्तो वृक्षाः।
वनं वनं रचयन्ति वृक्षाः।।।
शाखादोलासीना विहगाः।
तैः किमपि कूजन्ति वृक्षाः।2।

शब्दार्थाः (Word Meanings) : वने वने-प्रत्येक जंगल में (in each forest), निवसन्तः (निवसन्तो)-निवास करते रहते हैं (keep living), वनम्-जंगल (forest), रचयन्ति-रचना करते हैं (create), शखादोलासीनाः (शाखादोला + आसीनाः)-शाखा रूपी झूले पर बैठे हुए (sitting on the swing of branches), विहगाः-पक्षी (birds), तैः-उनके द्वारा अर्थात् पक्षियों द्वारा (through them by the birds), किमपि (किम् + अपि)-कुछ-कुछ (some), कूजन्ति-कूकते/कूकती हैं (chirping), वृक्षाः-पेड़ (trees)।

अन्वय : (Prose-order)

1. वृक्षाः वने वने निवसन्तोः, वृक्षाः वनम् वनम् रचयन्ति।
2. विहगाः शाखादोलासीन (सन्ति), वृक्षाः तैः किम् अपि कूजन्ति।

सरलार्थ :
1. वृक्ष प्रत्येक वन में निवास करते/रहते हैं, इस प्रकार वृक्ष कई जंगल बनाते रहते हैं।
2. पक्षी शाखा रूपी झूले पर बैठे हैं मानों वृक्ष उनके माध्यम से कुछ-कुछ कूक रहे हैं अर्थात् कह रहे हैं।

English Translation:
1. Trees dwell in every jungle, thus they form (make) many jungles.
2. The birds are sitting on the branches of trees and chirping.
It seems that trees are saying something through them (birds).

(ख) पिबन्ति पवनं जलं सन्ततम्। साधुजना इव सर्वे वृक्षाः।।
स्पृशन्ति पादैः पातालं च। .
नभः शिरस्सु वहन्ति वृक्षाः ।।

शब्दार्थाः (Word Meanings) : पिबन्ति-पीते/पीती हैं (drink), पवनं-वायु (air), सन्ततम्-लगातार (continually), साधुजनाः इव-सज्जनों की भाँति (like good noble people), सर्वे-सब (all), स्पृशन्ति-स्पर्श करते हैं (touch), पादैः-पैरों से (with foot), पातालं-जमीन के नीचे भाग (underground), नभः-आकाश को (the sky), शिरस्सु-सिरों पर (on their head), वहन्ति-ढोते (carry)।

अन्वय : (Prose-order)
3. वृक्षाः सन्ततम् पवनं जलम् च पिबन्ति। सर्वे वृक्षाः साधुजनाः इव (सन्ति)।
4. वृक्षाः पादैः पातालम् स्पृशन्ति शिरस्तु च नभः वहन्ति।

सरलार्थ :
3. वृक्ष हमेशा वायु और जल पीते हैं। सभी वृक्ष सज्जनों की भाँति होते हैं। अर्थात् वे सज्जनों के समान हमारा उपकार करते हैं।
4. वृक्ष पैरों से (जड़ों से) पाताल को छूते हैं और सिरों पर आकाश को ढोते हैं। अर्थात् वे महान हैं और अत्यधिक कार्यभार संभालते हैं।

English Translation:
3. Trees continually take water and air only. All trees are like noble persons. i.e., trees show kindness in many ways like noble persons.
4. Trees touch the underground with their feet in their roots. They carry the sky on their heads.

पयोदर्पणे स्वप्रतिबिम्बम्।
कौतुकेन पश्यन्ति वृक्षाः।5।

प्रसार्य स्वच्छायासंस्तरणम्।
कुर्वन्ति सत्कारं वृक्षाः।6।

शब्दार्थाः (Word Meanings) : पयोदर्पणे-जलरूपी दर्पण/शीशे में (in the mirror-like water), स्वप्रतिबिंबम्-अपनी परछाई को (own reflection), कौतुकेन-आश्चर्य से (with surprise/ wonder), पश्यन्ति-देखते हैं (see), प्रसार्य-फैलाकर (having spread), स्वच्छायासंस्तरण म्-(स्व+छाया+संस्तरणम्) अपने छाया रूपी बिस्तर को (their own shadow which is like a bed), कुर्वन्ति-करते/करती हैं (do), सत्कारम्-आदर-सत्कार (regards)।

अन्वय : (Prose-order)
5. वृक्षाः पयोदर्पणे स्वप्रतिबिम्बम् कौतुकेन पश्यन्ति।
6. वृक्षाः स्वच्छायासंस्तरणम् प्रसार्य सत्कारं कुर्वन्ति।

सरलार्थ :
5. वृक्ष जलरूपी आईने में अपना प्रतिबिम्ब आश्चर्य/कौतूहल से देखते हैं।
6. वृक्ष छाया रूपी अपन बिछौने को फैलाकर अर्थात् बिछाकर (सबका) आदर-सत्कार करते हैं।

English Translation:
5. Trees look at their own reflection in mirror like water.
6. Trees spread out their shadow like a bed and pay respect.
(give regards to those who come there.)

हमने सीखा
संस्कृत में संज्ञा शब्दों के लिंग पूर्व निर्धारित होते हैं। अकारान्त शब्दों में कुछ पुल्लिग और कुछ नपुंसकलिंग शब्द हैं। दोनों के शब्द रूप भिन्न होते हैं। यथा

केवल द्वितीया एकवचन में दोनों का रूप समान हैं, यथा- ‘पल्लवम्’ तथा ‘पर्णम्’। अतः शेष ‘रूपों से ही लिंग की पहचान संभव है। यथा ‘पल्लवाः’ पुल्लिग पद है और ‘पर्णानि’ नपुंसकलिंग।

ध्यातव्यम्-शेष विभक्तियों में अकारान्त पुल्लिग तथा नपुंसकलिंग के रूप एक समान होते हैं।
पर्ण

We have given detailed NCERT Solutions for Class 6 Sanskrit Grammar Book अव्ययपदानि Questions and Answers come in handy for quickly completing your homework.

Sanskrit Vyakaran Class 6 Solutions अव्ययपदानि

अभ्यासः

उत्तर:
(क) कुत्र
(ख) कदा
(ग) यदा-तदा
(घ) अद्य
(ङ) बहिः
(च) श्वः
(छ) सह
(ज) अधुना
(झ) प्रति
(ब) आम् ।अपि

प्रश्नः 2.
उचितेन अव्ययपदेन रिक्तस्थानपूर्तिं कुरुत। (उचित अव्यय-पद से रिक्त स्थान की पूर्ति कीजिए। Fill in the blanks with the suitable Indeclinable.)

प्रतिदिनम्, सायम्, श्वः।

(क)

(i) जनाः ……………….. भ्रमन्ति ।
(ii) अहं ……. ……. जन्तुशालाम् गमिष्यामि ।
(iii) किम् त्वम् …………………. खेलसि?
उत्तर:
(i) सायम्
(ii) श्वः
(iii) प्रतिदिनम्

शीघ्रम्, उच्चैः, शनैः-शनैः।

(ख)
(i) सिंहः …………………. गर्जति।
(ii) वृद्धः ……………….. चलति ।
(iii) अहम् ……………….. लिखामि।
उत्तर:
(i) उच्चैः
(ii) शनैः-शनैः
(iii) शीघ्रम्

नहि, आम्, च।

(ग)
(i) बालकाः बालिकाः …………. खेलन्ति।
(ii) …………..अहम् अपि खेलामि।
(iii) ………. अहं बहिः न गमिष्यामि।
उत्तर:
(i) च
(ii) आम्
(iii) नहि

प्रश्न: 3.
कोष्ठकात् उचितं विकल्पं चित्वा वाक्यपूर्तिं कुरुत। (कोष्ठक से उचित विकल्प चुनकर वाक्यों की पूर्ति कीजिए। Pick out the correct option from the bracket and complete the sentences.)

(i) यूयम् खेलितुम् ……………. गच्छथ? (कुतः, कुत्र, किम्)
(ii) ……….. प्रातः भवति खगाः …………. कूजन्ति। (यदा-तदा, यत्र-तत्र, शनैः-शनैः)
(iii) पितामही देवालयं ……………….. अगच्छत्। (विना, सह, प्रति)
(iv) आकाशे मेघाः ………….. गर्जन्ति। (उच्चैः , तीव्रम्, परस्परम्)
(v) ……. जनकः कार्यालयम् न गच्छति। (अद्य, हयः, श्वः)
उत्तर:
(i) कुत्र
(ii) यदा-तदा
(iii) प्रति
(iv) उच्चैः
(v) अद्य

एतानि वाक्यानि अवलोकयत। (इन वाक्यों को देखिए। Look at these sentences.)

1. किम् त्वम् अधुना संस्कृतम् पठसि?
2. आम्, अहम् अधुना संस्कृतम् पठामि।
3. छात्रा: कदा विद्यालयम् गच्छन्ति?
4. ते प्रातः विद्यालयम् गच्छन्ति ।
5. किम् त्वम् सायम् पठसि ?
6. नहि, अहम् सायम् क्रीडामि। उपर्युक्त वाक्यों में स्थूलाक्षरों में आए पद-अधुना, आम्, कदा, प्रातः, सायम्, नहि अव्यय हैं।

अव्यय वे पद होते हैं जिनका वाक्य-प्रयोग के समय रूप नहीं बदलता।

In the sentences given above the words in bold letters viz. अधुना, आम्, कदा, प्रातः, सायम्, नहि are all अव्यय-the Indeclinables. अव्यय are those words that do not change their form when used in a sentence. कुछ सामान्यतः प्रयोग में आने वाले अव्यय तथा उनका वाक्य-प्रयोग। (A few commonly used Indeclinables and their usage.)

We have given detailed NCERT Solutions for Class 6 Sanskrit Grammar Book क्रियापदानि तथा धातुरूपाणि Questions and Answers come in handy for quickly completing your homework.

Sanskrit Vyakaran Class 6 Solutions क्रियापदानि तथा धातुरूपाणि

अभ्यासः

प्रश्न 1.
(क) तालिकां पूरयत। (तालिका पूरी कीजिए। Complete the table.)

उत्तर:
प्रथम पुरुषः-धावति, धावन्ति, मध्यम पुरुष:धावसि, धावथ, उत्तम पुरुष:-धावामि, धावामः।

उत्तर:

(ख) रिक्तस्थानानि पूरयत। (रिक्त स्थान भरिए। Fill in the blanks.)

प्रश्न 2.
उदाहरणानुसारम् रिक्तस्थानानि पूरयत। (उदाहरण के अनुसार रिक्त स्थान भरिए। Fill in the blanks as per the example.)

प्रश्न 3.
रिक (रिक्त स्थान भरिए- Fill in the blanks.)

उत्तर:

उत्तर:

प्रश्न 4.
रेखाङ्कितक्रियापदम् संशोधयत- (रेखांकित क्रिया-पदों को शुद्ध कीजिए- Correct the underlined verbs.)

(क) सा दुग्धम् पिबिष्यति।। ……………….
(ख) अहम् बहिः खेलिष्यति। ……………
(ग) अहम् क्रीडितुम् गच्छिष्यामि। …………………..
(घ) त्वम् किं खादिष्यति? …………………..
(ङ) छात्र: लेखम् लिखिष्यति। …………………..
उत्तर:
(क) पास्यति
(ख) खेलिष्यामि
(ग) गमिष्यामि
(घ) खादिष्यसि
(ङ) लेखिष्यति प्रश्नः

प्रश्न 5.
उदाहरणम् अनुसृत्य वाक्यानि पुनः लिखत। (उदाहरण के अनुसार वाक्य को पुनः लिखिए। Rewrite the sentences as per the example.)

उदाहरणम् – बालकः खेलति। बालकः खेलिष्यति।

(क)
(i) सः किम् करोति? …………………..
(ii) अम्बा पचति। …………………..
(iii) अहम् नमामि। …………………..
(iv) वयम् धावामः। …………………..
(v) यूयम् क्रीडथ। …………………..
उत्तर:
(i) सः किम् करिष्यति?
(ii) अम्बा पक्ष्यति ।
(iii) अहम् नस्यामि ।
(vi) वयम् धाविष्यामः।
(v) यूयम् क्रीडिष्यथ।

(ख) उदाहरणम्- बालक: सत्यम् वदति। — बालकः सत्यम् अवदत् ।

(i) सा भोजनम् पचति । — ……………..
(ii) अजीजः गच्छति। — ……………..
(iii) सः मह्यम् यच्छति। — ……………..
(iv) सा त्वाम् वदति। — ……………..
(v) स्वामी सेवकम् पृच्छति। — ……………..
उत्तर:
(i) सा भोजनम् अपचत्।
(ii) अजीज: अगच्छत् ।
(iii) सः मह्यम् अयच्छत्।
(iv) सा त्वाम् अवदत् ।
(v) स्वामी सेवकम् अपृच्छत् ।

(ग) उदाहरणम् – बालक: खादतु। — बालकः खादति।

(i) सा लिखतु। — ……………..
(ii) छात्रः पठतु। — ……………..
(iii) बालिका क्रीडतु। — ……………..
(iv) अजीजः गच्छतु। — ……………..
(v) सः नमतु। — ……………..
उत्तर:
(i) सा लिखति।
(ii) छात्रः पठति।
(iii) बालिका क्रीडति ।
(iv) अजीजः गच्छति।
(v) सः नमति।

प्रश्न: 6.
निर्देशानुसारम् परिवर्तनम् कुरुत। (निर्देश के अनुसार परिवर्तन कीजिए ।Change as directed.)

उदाहरणम् – स: नमति। ( उ०पु०) अहम् नमामि।
(क) यूयम् धावथ। — (एकवचने) — ……………..
(ख) अहम् नमामि। — (द्विवचने) — ……………..
(ग) त्वम् वदसि। — (प्रथमपुरुषे) — ……………..
(घ) वयम् क्रीडिष्यामः। — (लट्लकारे) — ……………..
(ङ) युवाम् पठथः। — (लुट्लकारे) — ……………..
उत्तर:
(क) त्वम् धावसि।
(ख) आवाम् नमावः।
(ग) सः वदति।
(घ) वयम् क्रीडामः।
(ङ) युवाम् पठिष्यथः।

क्रियापदानि

अधोदत्तानि वाक्यानि अवलोकयत। (नीचे दिए गए वाक्यों को देखिए। Examine the sentences given below.)

उपरिलिखित वाक्यों में स्थूल शब्द क्रियापद हैं।
क्रियापद वे शब्द होते हैं जो क्रिया का बोध कराते हैं। प्रत्येक वाक्य में एक क्रियापद होता है। प्रत्येक क्रियापद धातु से बनता है और क्रिया के मूल रूप को धातु कहते हैं।

(In the sentences given at the beginning of the chapter the words in bold are verbs. The words which tell us about an action are called verbs. Simply put verbs are ‘doing’ words. Each sentence has a verb. Each verb is formed from a root.)

धातुरूपाणि

प्रत्येक धातु से अनेक क्रियापद बनते हैं। इसी को धातुरूप कहते हैं। नीचे ‘पठ्’ धातु के लट् लकार में रूप दिए गए हैं। लट् लकार का प्रयोग वर्तमान काल की क्रिया को दर्शाने के लिए किया जाता है।

(Many verb forms can be formed from a single root. This is called conjugation. Below are given the forms of the root पठ् in लट् लकार। लट् लकार is used to denote action in Present.

परिवर्तनशील-धातवः

(परिवर्तनशील धातुएँ, Roots that undergo a change.)

कुछ धातुएँ परिवर्तनशील होती हैं अर्थात् रूप चलाते समय उनमें परिवर्तन आता है; जैसे-गम् धातु का रूप चलाते समय ‘गच्छ्’ हो जाता है। (Some roots undergo a change, when they are conjugated e.g. the root गम् changes into गच्छ when conjugated.)

अवधेयम् – अंग्रेजी भाषा की तरह संस्कृत भाषा में भी कर्त्ता में लिङ्ग-भेद होने से क्रियापद में लिङ्ग भेद नहीं होता। (हिन्दी भाषा में क्रियापद में लिङ्ग-भेद होता है।)

(As in English, so also in Sanskrit there is no difference in the verb form whether the subject of the sentence is in Masculine or Feminine Gender.)

लट्लकारः
भविष्यत् काल-Future Tense

लृट् लकार का प्रयोग भविष्यत् काल की क्रिया को दर्शाने के लिए होता है। (लट् लकार is used to denote action in the future.)

उपर्युक्त वाक्यों में आए स्थूल पद-पठिष्यति, लेखिष्यति, खेलिष्यति-लृट् लकार के क्रियापद हैं जो क्रमश: पठ्, लिखु, खेल धातु से बने हैं। The words in bold are verbs of Future Tense (लुट्लकार)।

अवधेयम्-लुट लंकार में धातु के आगे लगने वाले प्रत्यय-ति, तः, अन्ति आदि वही होते हैं जो लट् लकार में धातु में जोड़े जाते हैं, किन्तु लृट् लकार में धातु और प्रत्यय के बीच ‘स्य’ अथवा ‘ष्य’ आ जाता है; यथा दा + स्य + ति = दास्यति; लिख + ष्य + ति = लेखिष्यति इत्यादि। (In लृट् लकार the root takes the same suffixes ति, तः, अन्ति etc., that are added in लट् लकार. But in लृट् लकार ‘स्य’ or ‘ष्य’ is inserted between the root and the suffix, when the root is conjugated.) नीचें कुछ धातुओं के लृट् लकार के रूप दिए गए हैं। (Given below is the conjugation of a few roots in लृट् लकार.)

उपर्युक्त वाक्यों में आए स्थूलपद-लङ्लकार के क्रियापद हैं जो क्रमशः गम्, पत्, खेल धातु से बने हैं। लङ्लकार का प्रयोग भूत काल की क्रिया को दर्शाने के लिए किया जाता है। लङ्लकार में धातु से पहले ‘अ’ जोड़ा जाता है। यथा- अवदत्, अनमत्, अलिखत् इत्यादि। उदाहरण रूप दिए गए क्रियापद प्रथम पुरुष एकवचन में हैं। अवलोकन हेतु लङ्लकार में पठ् धातु के तीनों पुरुषों के रूप नीचे दिए गए हैं यद्यपि इस कक्षा में प्रथम पुरुष, एकवचन के रूप पर ही ध्यान केंद्रित किया गया है।

उपर्युक्त वाक्यों में ‘पठ’, ‘आनय’, ‘लिख’ लोट् लकार, मध्यम पुरुष, एकवचन के रूप हैं। लोट्लकार का अधिकतम प्रयोग मध्यम पुरुष, एकवचन में होता है; कर्त्ता ‘त्वम्’ प्रायः लुप्त रहता है। अवलोकन हेतु पठ् धातु के लोट् लकार के रूप नीचे दिए गए हैं, यद्यपि सविस्तार चर्चा अगली कक्षाओं में होगी।

We have given detailed NCERT Solutions for Class 6 Sanskrit Grammar Book सर्वनाम शब्द-रूपाणि तथा वाक्यप्रयोगः Questions and Answers come in handy for quickly completing your homework.

Sanskrit Vyakaran Class 6 Solutions सर्वनाम शब्द-रूपाणि तथा वाक्यप्रयोगः

अभ्यासः

प्रश्न 1.
‘तत्’ सर्वनाम-शब्दस्य उचितेन रूपेण वाक्यानि पूरयत। (तत् सर्वनाम के उचित रूप द्वारा वाक्य पूरे कीजिए। Complete the sentences with the appropriate form of the pronoun तत्..)

उदाहरणम्-सुनील: धावति। —- सः पतति।

(क) सुदीप्तिः क्रीडति। ……. न पतति। (सः, सा, तत्)
(ख) बालकाः खादन्ति। …………………… हसन्ति अपि। (ते, ताः, सः)
(ग) फलम् पतति। ………………….. मधरम अस्ति । (सः, तत्, तम्)
(घ) छात्रौ गच्छतः। (ते, तौ, सा)
(ङ) बालिकाः गच्छन्ति। …………………. बसयानेन गच्छन्ति। (ते, सा, ता:)
उत्तर:
(क) सा
(ख) ते
(ग) तत्
(घ) तौ
(ङ) ताः

प्रश्न 2.
उदाहरणानुसारं सर्वनामपदं संशोध्य वाक्यानि पुनः लिखत। (उदाहरण के अनुसार सर्वनाम-पद शुद्ध करके वाक्य को पुनः लिखिए। Correct the pronoun and rewrite the sentences as per the example.)

उदाहरणम् – एषः कमलानि। — एतानि कमलानि।
(क) एतत् वृक्षः। — ………….
(ख) एषा पुस्तकम्। — ………….
(ग) एतत् बालिके। — ………….
(घ) एषः बालकाः। — ………….
(ङ) एषा: अध्यापिकाः। — ………….
उत्तर:
(क) एषः वृक्षः
(ख) एतत् पुस्तकम्,
(ग) एते बालिके
(घ) एते
(ङ) एषा अध्यापिका।

प्रश्न 3.
किम् सर्वनाम-शब्दरूप-सहायतया प्रश्नान् पूरयत। (किम् सर्वनाम शब्दरूप की सहायता से प्रश्न पूरे कीजिए। Complete the following questions with the help of किम् शब्दरूप.)


उत्तर:
(क) के, (ख) कम्, (ग) केन, (घ) कस्मै (ङ) कस्मात् (च) कस्य (छ) कस्मिन्

प्रश्न 4.
प्रदत्त सर्वनामपदेभ्यः उचितं विकल्पं चित्वा रिक्तस्थानानि पूरयत। (दिए गए सर्वनाम पदों में से उचित विकल्प चुनकर रिक्त स्थान भरिए। Fick out the appropriate option from among the pronouns given and fill in the blanks.)

(क)
(i) ………. छात्रस्य नाम तन्मयः अस्ति। (सः, तम्, तस्य)
(ii) गुरुः ………. छात्रम् वदति। (सा, तम्, तेन)
(ii) …………. छात्रात् कलमम् आनय। (तस्मात्, तेन, तस्मै)
(iv) ………. गृहे अहम् वसामि। (ते, तम्, तस्मिन्)
(v) …………. छात्राय पुस्तकम् यच्छ। (तस्मिन्, कस्मै, तस्मै)
उत्तर:
(i) तस्य
(ii) तम्
(iii) तस्मात्
(iv) तस्मिन्
(v) तस्मै

(ख)
(i) एतत् ………. गृहम्। (मम्, माम्, मम)
(ii) किम् एतत् ………. पुस्तकम्? (त्वम्, त्वाम्, तव)
(iii) त्वम् ………. मित्राय उपहारम् आनेष्यसि? (कम्, किम्, कस्मै)
(iv) सः बालकः ………. वृक्षात् अपतत्? (कः, कस्मात्, केन)
(v) व्याघ्राः …………. वने सन्ति? (के, किम्, कस्मिन्)
उत्तर:
(i) मम
(ii) तव
(iii) कस्मै
(iv) कस्मात्
(v) कस्मिन्

प्रश्न: 5.
अधोदत्तायां तालिकायां उचित सर्वनामपदैः रिक्तस्थानपूर्ति कुरुत। (निम्नलिखित तालिका में उचित सर्वनामपद द्वारा रिक्त स्थानों की पूर्ति कीजिए॥ Fill in the blanks in the table given below with the appropriate pronoun forms.)

बालक शब्द- संज्ञापद (पुंल्लिग) एकवचन रूपाणि निर्देशानुसार पूरयत

उत्तर:

अधोदत्तानि वाक्यानि अवलोकयत। (नीचे दिए गए वाक्यों को देखिए । Examine the sentences given below.)

1. विभा पठति । सा न लिखति।
2. अरविन्दः लिखति। सः न पठति ।
3. तत् फलम् मधुरम्।
4. एषः वृक्षः।
5. एषा वाटिका।
3. तत् फलम् मधुरम्।
6. एतत् फलम्।
उपर्युक्त वाक्यों में स्थूल अक्षरों में आए शब्द सर्वनाम हैं।

सर्वनाम वे शब्द होते हैं जो संज्ञा के स्थान पर प्रयोग में लाए जाते हैं।

अवधेयम् – संस्कृत में सर्वनाम शब्द का पूर्व निर्धारित लिङ्ग नहीं होता है। सर्वनाम शब्द जिस शब्द के साथ प्रयुक्त होता है उसी का लिङ्ग अपना लेता है। अतः सर्वनाम शब्दों के रूप तीनों लिङ्गों में चलते हैं। संज्ञा

In the sentences given at the beginning of the chapter the words in bold letters are Pronouns. Pronouns are words which are used in place of nouns. In San skrit, the pronoun takes the gender of the word with which it is used. Therefore, Pronouns are declined in all three genders.

शब्दरूप-सर्वनाम

तत्, एतत्, किम् सर्वनाम हैं। नीचे इनके रूप दिए गए हैं।

By going through these CBSE Class 6 Sanskrit Notes Chapter 14 अहह आः च Summary, Notes, word meanings, translation in Hindi, students can recall all the concepts quickly.

Class 6 Sanskrit Chapter 14 अहह आः च Summary Notes

अहह आः च पाठ का परिचय

प्रस्तुत पाठ एक कथा है। इसमें यह बताया गया है कि एक सरल स्वभाव वाला परिश्रमी कर्मचारी एक वृद्धा के द्वारा दिए हुए विचित्र उपाय से अपने चतुर मालिक की अद्भुत शर्त पूरी कर उससे अवकाश और वेतन का पूरा पैसा पाने में सफल हो जाता है। इस कथा द्वारा यह शिक्षा दी गई है कि परिश्रम और लगन से कठिन कार्य ही नहीं अपितु असंभव को भी संभव किया जा सकता है।

अहह आः च Summary

अजीज सरल स्वभाव वाला था। वह स्वामी की सेवा में लीन रहता था। एक दिन अजीज ने स्वामी से अवकाश माँगा। स्वामी ने उसे दो वस्तु ‘अरे, ओह’ लाने के लिए कहा। अजीज उन वस्तुओं की खोज में घर-घर भटकने लगा। एक बुढ़िया ने उसे दो अमूल्य वस्तुएँ दे दी। उन्हें लेकर वह स्वामी के पास आया। स्वामी ने एक पात्र को खोला। एक मधुमक्खी ने पात्र से निकल स्वामी को काट खाया। अचानक स्वामी के मुख से निकला-अरे। दूसरे पात्र को खोलने पर भी एक मक्खी ने स्वामी को काट लिया। पुनः स्वामी के मुख से निकला-ओह! अजीज परीक्षा में उत्तीर्ण हो चुका था। स्वामी ने उसे पूरे वेतन सहित अवकाश प्रदान कर दिया।

अहह आः च Word Meanings Translation in Hindi

(क) अजीज: सरलः परिश्रमी च आसीत्। सः स्वामिनः एव सेवायां लीनः आसीत्। एकदा सः गृहं गंतुम् अवकाशं वाञ्छति। स्वामी चतुरः आसीत्। सः चिंतयति- ‘अजीजः इव न कोऽपि अन्यः कार्यकुशलः। एष अवकाशस्य अपि वेतनं ग्रहीष्यति।’ एवं चिंतयित्वा स्वामी कथयति-‘अहं तुभ्यम् अवकाशस्य वेतनस्य च सर्वं धनं दास्यामि।’ परम् एतदर्थं त्वं वस्तुद्वयम् आनय-“अहह! आ:!” च इति।

शब्दार्थाः (Word Meanings):
स्वामिनः-स्वामी की (of master), सेवायां लीन:-सेवा में लीन (engaged in service), वाञ्छति-चाहता/चाहती है (wants), चिंतयति-सोचता/ सोचती है (thinks), ग्रहीष्यति-लेगा/लेगी (will take), दास्यामि-दूंगा/दूंगी (shall give), आनय-लाओं (bring), एतदर्थम्-इसके लिए (for this), अहह-कष्टसूचक अव्यय (Oh!), आ:-पीड़ासूचक (अव्यय) (ah!)।

सरलार्थ :
अजीज सरल स्वभाव वाला और मेहनती था। वह स्वामी की सेवा में ही लगा रहता था। एक बार वह घर जाने के लिए छुट्टी चाहता था। स्वामी (मालिक) चालाक था। वह सोचता है-‘अजीज जैसा कोई भी दूसरा कार्य कुशल नहीं है। यह छुट्टी का भी वेतन लेगा।’ यह सोचकर मालिक कहता है-“मैं तुम्हें छुट्टी और वेतन का सारा पैसा दूंगा।” परंतु तुम इसके लिए दो वस्तुएँ लाओ-‘अहह!’ और ‘आ:’ बस यह।

English Translation:
Ajeeja was a simpleton and hardworking. He was engaged in the service of his master. Once he wanted leave for going home. The master was clever. He thinks There is no skilful/expert person like Ajeeja.’ He will take wages for (the period of) leave also. Thinking this the master says—“I shall give you the (total) entire amount for your leave as also your wages.” But for this you bring two things—’Oh!’ and ‘Ah!’—that is it.

(ख) एतत् श्रुत्वा अजीजः वस्तुद्वयम् आनेतुं निर्गच्छति। सः इतस्ततः परिभ्रमति। जनान् पृच्छति। आकाशं पश्यति। धरां प्रार्थयति। परं सफलतां नैव प्राप्नोति। चिंतयति, परिश्रमस्य धनं सः नैव प्राप्स्यति। कुत्रचित् एका वृद्धा मिलति। सः तां सर्वां व्यथां श्रावयति। सा विचारयति-स्वामी अजीजाय धनं दातुं न इच्छति। सा तं कथयति-‘अहं तुभ्यं वस्तुद्वयम् ददामि।’ परं द्वयम् एव बहुमूल्यकं वर्तते। प्रसन्नः सः स्वामिनः समीपे आगच्छति।

शब्दार्थाः (Word Meanings) :
आनेतुम्-लाने के लिए (to bring), निर्गच्छति-निकलता है (exits/ comes out), इतस्तत: (इत: + ततः)-इधर-उधर- (here and there), पृच्छति-पूछता है (asks), धराम्-पृथ्वी को (the earth), प्राप्स्यति-पाएगा (will get), नैव (न+ एव)-नहीं (not/never), श्रावयति-सुनाता है (tells/relates), वस्तुद्वयम्-दो वस्तुएँ (two things), ददामि-देता/देती हूँ (shall give)।

सरलार्थ :
यह सुनकर अजीज दोनों वस्तुएँ लाने के लिए निकलता है। वह इधर-उधर घूमता है। लोगों से पूछता है। आकाश को देखता है। पृथ्वी से प्रार्थना करता है। किंतु सफलता प्राप्त नहीं करता। सोचता है, परिश्रम का धन वह नहीं पा सकेगा। कहीं पर एक बुढ़िया मिलती है। वह उसे सारी व्यथा सुनाता है। वह सोचती है-“स्वामी अजीज को धन नहीं देना चाहता।” वह उसे कहती है-“मैं तुम्हें दो वस्तुएँ देती हूँ। किंतु दोनों ही कीमती (बहुमूल्य) हैं।” प्रसन्न (होकर) वह मालिक के पास आता है।

English Translation:
Having heard this Ajeeja goes out to bring two things. He roams around here and there. He asks people. He looks at the sky. He requests the earth. But he does not get success. He thinks—’He shall never get the wages (money) of his labour.’ Somewhere he meets an old woman. He tells her his pain and agony. She thinks—“The master does not wish to pay money to Ajeeja’. She says to him-‘I am giving you two things. But both are precious (costly). Happily (at this) he comes back to his master.’

(ग) अजीजं दृष्ट्वा स्वामी चकितः भवति। स्वामी शनैः शनैः पेटिकाम् उद्घाटयति। पेटिकायां लघुपात्रद्वयम् आसीत्। प्रथमं सः एकं लघुपात्रम् उद्घाटयति। सहसा एका मधुमक्षिका निर्गच्छति। तस्य च हस्तं दशति। स्वामी उच्चै वदति-“अहह!” द्वितीयं लघुपात्रम् उद्घाटयति।
एका अन्या मक्षिका निर्गच्छति। सः ललाटे दशति। पीडितः सः अत्युच्चैः चीत्करोति-“आः” इति। अजीजः सफलः आसीत्। स्वामी तस्मै अवकाशस्य वेतनस्य च पूर्णं धनं ददाति।

शब्दार्थाः (Word Meanings) :
पेटिकाम्-पेटी को (box), लघुपात्रद्वयम्-दो छोटे पात्र (two small utensils), उद्घाटयति-खोलता है (opens), मधुमक्षिका-मधुमक्खी (honey bee), सहसा-अचानक (all of a sudden), दशति-डसती है (bites), हस्तम्-हाथ को (hand), ललाटे-मस्तक पर (on forehead), उच्चैः -जोर से (loudly), चीत्करोति-चिल्लाता है (cries out)।

सरलार्थ :
अजीज को देखकर स्वामी चकित होता है। स्वामी धीरे-धीरे पेटी खोलता है। पेटी में दो छोटे पात्र (बरतन) थे। पहले वह एक छोटा पात्र खोलता है। सहसा एक मधुमक्खी निकलती है और उसके हाथ को डसती है। मालिक ज़ोर से बोल उठता है-अहह (अरे!)। दूसरा छोटा पात्र खोलता है। एक दूसरी मक्खी निकलती है। वह मस्तक पर डसती है। व्यथित (होकर) वह बहुत ज़ोर से चिल्लाता है-‘आः’ ऐसा। अजीज सफल हुआ। स्वामी उसे (उसके लिए) अवकाश और वेतन के पूरे पैसे देता है।

English Translation:
Having seen Ajeeja Master gets surprised. Master opens the box slowly. There were two small pots in the box. First he opens one small pot. Suddenly a honey bee comes out of it and bites on his arm. He loudly says, “AHH!” Now he opens the other small pot. Another bee comes out. She bites on his forehead. Afflicted with pain he cries loudly, “AAH!” Ajeej became successful. Master gave him total amount for his leave and wages.

By going through these CBSE Class 6 Sanskrit Notes Chapter 12 दशमः त्वम असि Summary, Notes, word meanings, translation in Hindi, students can recall all the concepts quickly.

Class 6 Sanskrit Chapter 12 दशमः त्वम असि Summary Notes

दशमः त्वम असि पाठ का परिचय

इस पाठ में संख्यावाची पदों (पुल्लिग) से परिचय कराया गया है। पाठ में ‘क्त्वा’ प्रत्ययान्त पदों का प्रयोग भी है। यथा- दृष्ट्वा – देखकर, श्रुत्वा – सुनकर आदि। दस बालक स्नान के लिए नदी पर जाते हैं; स्नान के पश्चात् एक बालक गणना करता है किंतु स्वयं को गिनना भूल जाता है। अतः नौ बालक गिनता है। दूसरा बालक भी गणना में यही त्रुटि करता है। उन्हें लगता है कि उनमें से एक नदी में डूब गया है। वे बहुत दु:खी होते हैं। इसी बीच एक पथिक वहाँ आकर गणना में उनकी सहायता करता है। गिनने वाले को वह कहता है कि दसवें तुम हो। सभी प्रसन्न हो जाते हैं।

दशमः त्वम असि Summary

इस पाठ में संख्याओं का प्रयोग किया गया है। पाठ का सार इस प्रकार है एक बार दस बालक स्नान करने के लिए नदी पर गए। स्नान करने के पश्चात् एक बालक ने गिनना शुरू किया। उसने सभी बालकों को गिन लिया, परन्तु अपने आप को नहीं गिना। उसके अनुसार वहाँ नौ बालक थे। सभी ने निश्चय किया कि दसवाँ बालक नदी में डूब गया है।

तब एक यात्री वहाँ आया। उसने उनकी समस्या को सुनकर गिनना प्रारम्भ किया। अब पूरे दस बालक थे। यात्री ने समझाया कि गणना करने वाले बालक ने स्वयं को गिना नहीं। अपनी भूल पर सभी बालक अत्यधिक शर्मिन्दा हुए। अब वे प्रसन्न होकर अपने घर को चले गए।

दशमः त्वम असि Word Meanings Translation in Hindi

(क) एकदा दश बालकाः स्नानाय नदीम् अगच्छन्। ते नदीजले चिरं स्नानम् अकुर्वन्। ततः ते तीर्वा पारं गताः। तदा तेषां नायकः अपृच्छत्-अपि सर्वे बालका: नदीम् उत्तीर्णाः?

शब्दार्थाः (Word Meanings) :
एकदा-एक बार (once), दश-दस (ten), अगच्छन्-गए (went), चिरम्-देर तक (for long time), अकुर्वन्-किया (did), तीा -तैर कर (after swimming), अपृच्छत्-पूछा (asked), अपि सर्वे उत्तीर्णाः-क्या सब पार कर गए हैं? (have they all crossed?), नदीम्-नदी को (the river)।

सरलार्थ :
एक बार दस बालक स्नान के लिए नदी पर गए। उन्होंने देर तक नदी के जल में स्नान किया। फिर वे तैरकर नदी के पार गए। तब उनके नायक ने पूछा- क्या सभी बालक नदी पार कर गए हैं?’ अर्थात् क्या सभी नदी से बाहर आ गए हैं?

English Translation:
Once ten boys went to a river for bathing. They bathed in the river water for long. Then they crossed the river after swimming. Then their leader asked, ‘Have all boys crossed the river?’

(ख) तदा कश्चित् बालकः अगणयत्- एकः, द्वौ , त्रयः, चत्वारः, पञ्च, षट्, सप्त, अष्टौ, नव
इति। सः स्वं न अगणयत् अतः सः अवदत्- नव एव सन्ति।
दशमः न अस्ति। अपरः अपि बालकः पुनः अन्यान् बालकान् अगणयत् । तदा अपि नव एव
आसन्। अतः ते निश्चयम् अकुर्वन् यत् दशमः नद्यां मग्नः। ते दुःखिताः तूष्णीम् अतिष्ठन्।

वाक्य के आरंभ में अपि का प्रयोग होने से वाक्य प्रश्नात्मक हो जाता है।
यथा- अपि सर्वम् कुशलम्-क्या सब कुशल मंगल है? Is everything Ok?

शब्दार्थाः (Word Meanings) :
कश्चित्-कोई (someone), द्वौ-दो (two), त्रयः-तीन (three), चत्वार:-चार (four), पञ्च-पाँच (five), षट्-छः (six), सप्त-सात (seven), अगणयत्-गिना (counted), अष्ट-आठ (eight), नव-नौ (nine), स्वं-अपने आपको (himself), दशम्-दस (ten), अपरः-अन्य, दूसरा (other), अन्यान्-दूसरों को (to others), आसन-थे (were), पुन:-फिर से (again), नद्याम्-नदी में (in the river), मग्नः-डूब गया (drowned), तूष्णीम्-चुपचाप (silent), अतिष्ठान्-बैठ गए (sat down, stayed)।

सरलार्थ :
तब किसी बालक ने गणना की-“एक, दो, तीन, चार, पाँच, छः, सात, आठ, नौ इस तरह।” उसने अपने आपको (स्वयं को) नहीं गिना। अतः वह बोला-“नौ ही हैं, दसवाँ नहीं है।” दूसरे बालक ने भी अन्य बालकों को गिना। फिर भी नौ ही थे। अत: उन्होंने निश्चय किया कि दसवाँ नदी में डूब गया है। वे दुखी हो, चुपचाप बैठ गए।

English Translation:
Then a boy counted one, two, three, four, five, six, seven, eight, nine. He did not count himself. Hence he said—There are only nine. The tenth one is not their.’ Another boy also counted them. Then also there were the same nine. Hence they decided that the tenth had drowned in the river. They were distressed and stayed quiet.

(ग) तदा कश्चित् पथिकः तत्र आगच्छत्। सः तान् बालकान् दुःखितान् दृष्ट्वा अपृच्छत्-बालकाः!
युष्माकं दुःखस्य कारणं किम्? बालकानां नायकः अकथयत्- ‘वयं दश बालकाः स्नातुम्
आगताः। इदानीं नव एव स्मः। एकः नद्यां मग्नः’ इति।

शब्दार्थाः (Word Meanings) :
आगच्छत्-आया (came), पथिकः-पथिक/राहगीर (traveller), दृष्ट्वा -देखकर (having seen), युष्माकम्-तुम लोगों का (yours), अकथयत्-कहा (said), स्नातुम्-नहाने के लिए (to take bath), इदानीम्-अब (now), स्म:-हैं (हम) are (we)|

सरलार्थ :
तब कोई पथिक वहाँ आया। उसने उन बालकों को दुखी देखकर पूछा-“हे बच्चो! तुम लोगों के दुःख का कारण क्या है?” बालकों के नायक ने कहा-“हम दस लड़के स्नान के लिए आए थे। अब हम नौ ही हैं। एक नदी में डूब गया है।”

English Translation:
Then a traveller came there. Seeing them sad he asked, “Boys! what is the cause of your misery/unhappiness.?’ The leader of the boys said—“We ten boys, came to take a bath, Now we are only nine. One got drowned in the river.”

(घ) पथिकः तान् अगणयत्। तत्र दश बालकाः एव आसन्। सः नायकम् आदिशत् त्वं बालकान्
गणय। सः तु नव बालकान् एव अगणयत्। तदा पथिकः अवदत्-“दशमः त्वम् असि इति।”
तत् श्रुत्वा प्रहृष्टाः भूत्वा सर्वे गृहम् अगच्छन्।

शब्दार्थाः (Word Meanings) :
नायकम्-नायक को (to the leader), आदिशत्-आदेश दिया (gave instructions), गणय-गिनो count (you), दशमः-दसवाँ (tenth), असि-हो (तुम) are (you), श्रुत्वा-सुनकर (hearing/having heard), प्रहृष्टाः -प्रसन्न (happy), भूत्वा-होकर (keeping/having been)।

सरलार्थ :
पथिक ने उन्हें गिना। वहाँ दस बालक ही थे। उसने नायक को आदेश दिया-“तुम बालकों को गिनी। उसने तो नौ बालक ही गिने।” तब पथिक बोला-“दसवें तुम हो।” यह सुनकर सब खुश होकर घर चले गए।

English Translation:
The traveller counted them. There were ten boys only. He instructed the leader to count the boys. But he counted only nine boys. Then the traveller said—’you are the tenth.’ Hearing this they felt happy and went home.

अवधेयम् :
1. संस्कृत में एक से चार तक की गणना में संख्यावाची शब्दों में लिंग भेद होता है। पाँच से आगे
कोई लिंग भेद नहीं होता। यथा

2. ‘क्त्वा’ प्रत्ययान्त पद यथा कृत्वा (कृ+ क्त्वा) = करके; दृष्ट्वा (दृश् + क्त्वा) = देखकर; भूत्वा
(भू+ क्त्वा) = होकर आदि अव्यय होते हैं। अर्थात् लिंग, वचन काल आदि के कारण इनमें कोई रूपांतर नहीं होता। क्त्वा प्रत्यय केवल धातुओं में जोड़ा जाता है। धातु में लगने पर इसका केवल ‘त्वा’ शेष रहता है।

यथा— पठ् + क्त्वा = पठित्वा (पढ़कर)

अथवा अहं विद्यालये पठित्वा गृहं गच्छामि। दोनों वाक्यों में पुरुष व वचन का भेद होने पर भी
‘पठित्वा’ के रूप में कोई अंतर नहीं आया।
‘क्त्वा’ प्रत्यय का प्रयोग ‘करके’ के अर्थ में किया जाता है।