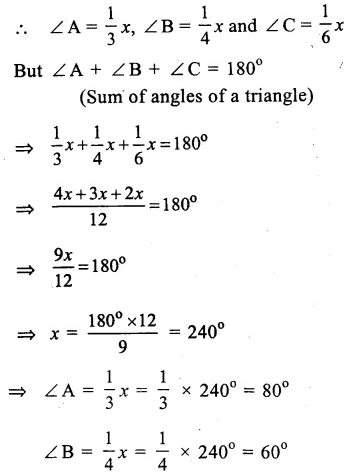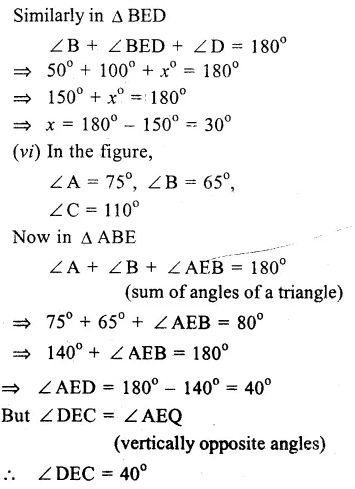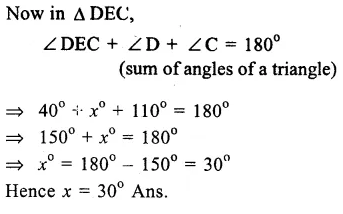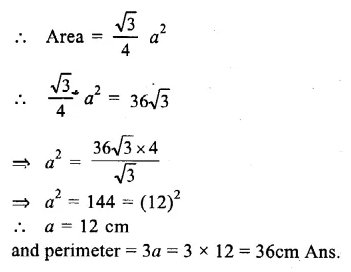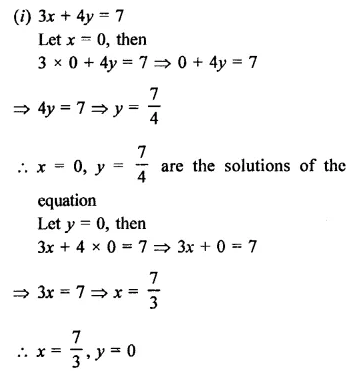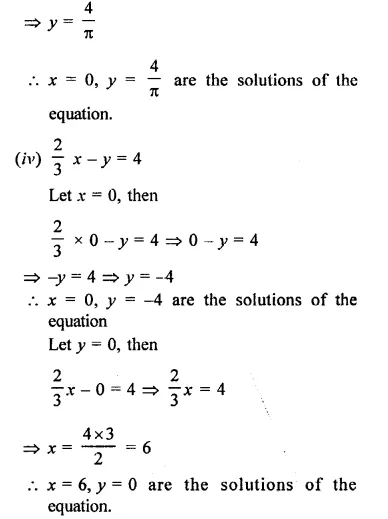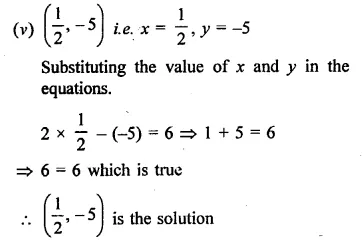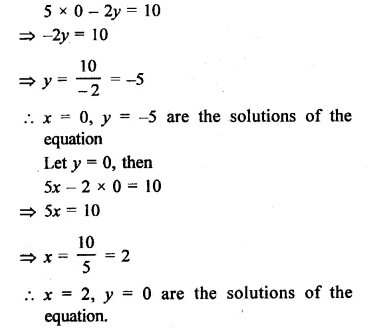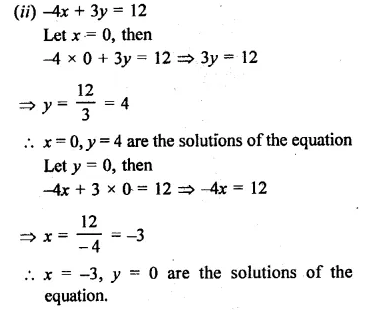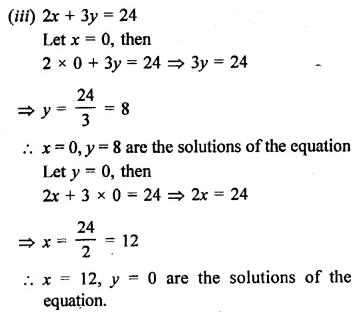NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules
These Solutions are part of NCERT Exemplar Solutions for Class 9 Science . Here we have given NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules
Question 1.
Which of the following correctly represents 360 g of water ?
(i) 2 moles of H2O
(ii) 20 moles of water
(iii) 6.022 x 1023 molecules of water
(iv) 1.2044 x 1025 molecules of water
(a) (i)
(b) (i) and (iv)
(c) (ii) and (iii)
(d) (ii) and (iv).
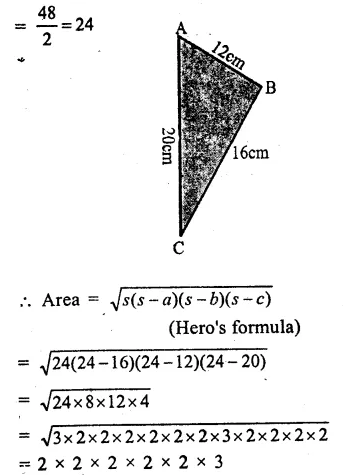
Mass of water
Correct Answer:
(d)

More Resources
- NCERT Exemplar Solutions for Class 9 Science
- NCERT Solutions for Class 9 Science
- Value Based Questions in Science for Class 9
- HOTS Questions for Class 9 Science
- Previous Year Question Papers for CBSE Class 9 Science
Question 2.
Which of the following statements is not true about atoms ?
(a) Atoms are not able to exist independently
(b) Atoms are the basic units from which molecules and ions are formed
(c) Atoms are always neutral in nature
(d) Atoms aggregate in large numbers to form the matter that we can see, feel or touch.
Correct Answer:
(a) Atoms of inert gas elements can exist independently. However, atoms of all other elements cannot exist independently.
Question 3.
The chemical symbol for nitrogen gas is :
(a) Ni
(b) N2
(c) N+
(d) N
Correct Answer:
(b).
Question 4.
The chemical symbol for sodium is :
(a) So
(b) Sd
(c) NA
(d) Na.
Correct Answer:
(d ).
Question 5.
Which of the following would weigh the maximum ?
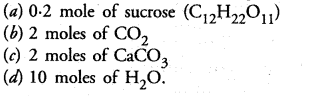
Correct Answer:
(c).
(a) 0.2 x 342 g = 68.4 g
(b) 2 x 44 g = 88 g
(c) 2 x 100 g = 200 g
(d) 10 x 18 g = 180 g.
Question 6.
Which of the following has maximum number of atoms ?
(a) 18 g of H2O
(b) 18 g of O2
(c) 18 g of CO2
(d) 18 g of CH4.
Correct Answer:
(d).
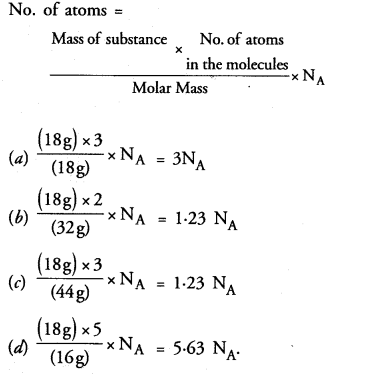
Question 7.
Which of the following contains maximum number of molecules ?
(a) 1g CO2
(b) 1g N2
(c) 1g H2
(d) 1g CH4.
Correct Answer:
(c).
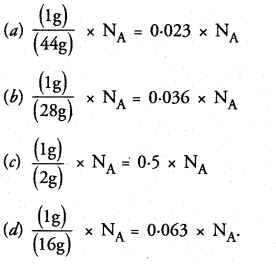
Question 8.
Mass of one atom of oxygen is :
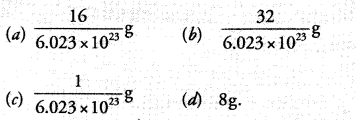
Correct Answer:
(a).
Question 9.
3.42 g of sucrose are dissolved in 18 g of water in a beaker. The number of oxygen atoms in the solution are
(a) 6.68 x 1023
(b) 6.09 x 10222
(c) 6.022 x 1023
(d) 6.022 x 1021.
Correct Answer:
(a).
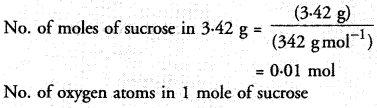
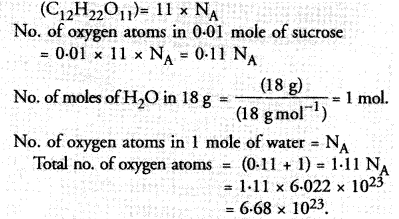
Question 10.
A change in the physical state can be brought about :
(a) only when energy is given to the system
(b) only when energy is taken out from the system
(c) when energy is either given to, or taken out from the system
(d) without any energy change.
Correct Answer:
(c).
Short Answer Questions
Question 11.
Which of the following represents a correct chemical formula ? Name it.
(a) CaCl
(b) BiPO4
(c) NaSO4
(d) NaS.
Answer:
(b). Both Bi and PO4 are trivalent ion (Bi3+ and PO43- ).
It is known as bismuth phosphate.
Question 12.
Write the chemical formulae for the following compounds :
(a) Copper (II) bromide
(b) Aluminium (III) nitrate
(c) Calcium (II) phosphate
(d) Iron (III) sulphide
(e) Mercury (II) chloride
(f) Magnesium (II) acetate.
Answer:
(a) CuBr2
(b) Al(NO3)3
(c) Ca3(PO4)2
(d) Fe2S3
(e) HgCl2
(f) Mg(CH2COO)2.
Question 13.
Write the chemical formulae of all the compounds that can be formed by the combination of following ions :
Cu2+, Na+, Fe3+, Cl–, SO42-, PO43- .
Answer:
For Cu2+ ion : CuCl2, CuSO4, Cu3(PO4)2
For Na+ ion : NaCl, Na2SO4, Na3PO4
For Fe3+ um :FeCl3, Fe2(SO4)3, FePO4.
Question 14.
Write the cations and anions present (if any) in the following compounds :
(a) CH3COONa
(b) NaCl
(c) H2
(d) NH4NO3.
Answer:
(a) CH3O– (anion), Na+ (cation)
(b) Na+ (cation), Cl– (anion)
(c) Molecular compound (no ions)
(d) NH4+(cation), NO3– (anion).
Question 15.
Give the formulae of the compounds formed from the following sets of elements :
(a) Calcium and fluorine
(b) Hydrogen and sulphur
(c) Nitrogen and hydrogen
(d) Carbon and chlorine
(e) Sodium and oxygen
(f) Carbon and oxygen.
Answer:
(a) CaF2
(b) H2S
(c) NH3
(d) CCl4
(e) Na2O
(f) CO and CO2.
Question 16.
Which of the following symbols of elements are incorrect ? Give their correct symbols :
(a) Cobalt Co
(b) Carbon C
(c) Aluminium Al
(d) Helium He
(e) Sodium So
Answer:
(a) Incorrect; correct symbol is Co
(b) Incorrect; correct symbol is C
(c) Incorrect; correct symbol is Al
(e) Incorrect; correct symbol is Na.
Question 17.
Give the chemical formulae for the following compounds and compute the ratio by mass of the combining elements in each one of them.
(a) Ammonia
(b) Carbon monoxide
(c) Hydogen chloride
(d) Aluminium fluoride
(e) Magnesium sulphide.
Answer:

Question 18.
State the number of atoms present in each of the following chemical species :
(a) CO32-
(b) PO43-
(c) P2O5
(d) CO.
Answer:
(a) Four
(b) Five
(c) Seven
(d) Two.
Question 19.
What is the fraction of mass of water (H2O) due to neutrons ?
Answer:
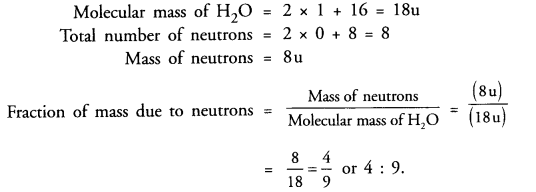
Question 20.
Does the solubility of a substance change with temperature ? Explain with the help of an example.
Answer:
In most of the cases, the solubility of a substance in a particular solvent such as water increases with the rise in temperature. For example, more of sugar can dissolve in a particular volume of water by increasing the temperature. .
Question 21.
Classify each of the following on the basis of their atomicity.
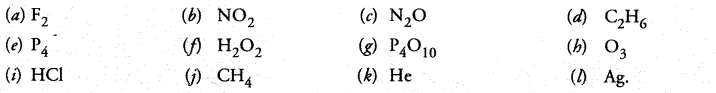
Answer:
(a) 2
(b) 3
(c) 3
(d) 8
(e) 4
(f) 4
(g) 14
(h) 3
(i) 2
(j) 5
(k) 1
(l) 1.
Question 22.
You are provided with a fine white coloured powder which is either sugar or salt. How would you identify it without tasting ?
Answer:
Dissolve both sugar and salt separately in water taken in two glass beakers. Pass electric current through both. In case, solution is conducting, it represents a salt dissolved in water. If it fails to conduct electricity, it represents a sugar solution.
Question 23.
Calculate the number of moles of magnesium present in a magnesium ribon weighing 12 g. Molar atomic mass of magnesium is 24 g mol-1.
Answer:
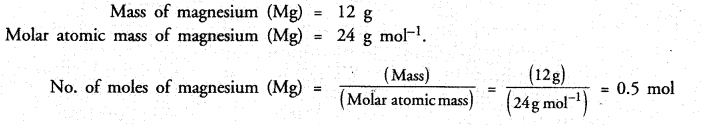
Long Answer Questions
Question 24.
Verify by calculating that :
(a) 5 moles of CO2 and 5 moles of H2O do not have the same mass.
(b) 240 g of calcium and 240 g magnesium elements have mole ratio of 3 : 5.
Answer:
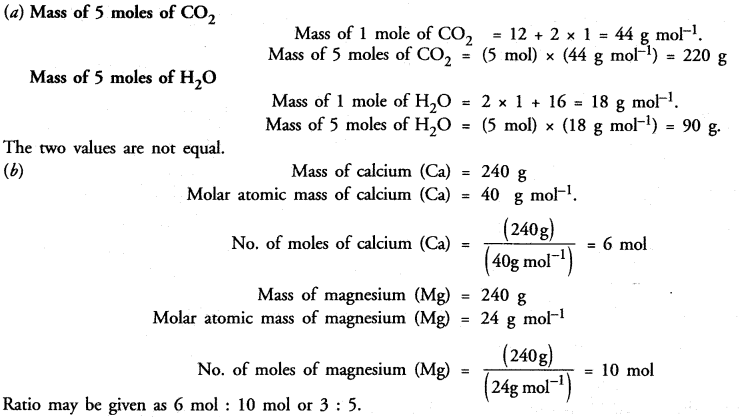
Question 25.
Find the ratio by mass of the combining elements in the following compounds :

Answer:
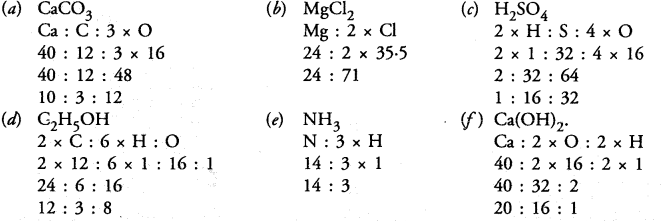
Question 26.
Calcium chloride when dissolved in water dissociates into its ions according to the following equation.
![]()
Calculate the number of ions obtained from CaCl2 when 222 g of it is dissolved in water.
Answer:

Question 27.
The difference in the mass of 100 moles each of sodium atoms and sodium ions is 5.48002 g. Compute the mass of an electron.
Answer:

Question 28.
Cinnabar (HgS) is a prominent ore of mercury. How many grams of mercury are present in 225 g of pure HgS ?
Answer:
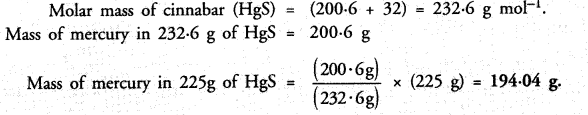
Question 29.
The mass of one steel screw is 4.11 g. Find the mass of one mole of these steel screws. Compare this value with the mass of the Earth (5.98 x 1024 kg). Which one of the two is heavier and by how many times ?
Answer:

Question 30.
A sample of vitamin C is known to contain 2.58 x 1024 oxygen atoms. How many moles of oxygen atoms are present in the sample ?
Answer:
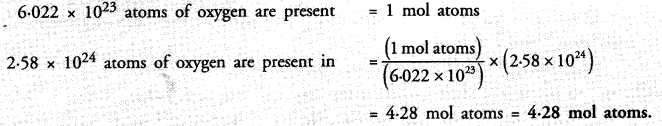
Question 31.
Raunak took 5 moles of carbon atoms in a container and Krish also took 5 moles of sodium atoms in another container of same weight.
(a) Whose container is heavier ?
(b) Whose container has more number of atoms ?
Answer:
(a) Molar atomic mass of carbon = 12 g
No. of moles of carbon carried by Raunak = 5
Mass of 5 moles of carbon = (12 x 5) = 60 g
Molar atomic mass of sodium = 23 g
No. of moles of sodium carried by Krish = 5
Mass of 5 moles of sodium = (23 x 5) = 115 g
This shows that the container carried by Krish is heavier.
(b) Since both the containers have same number of moles, the number of atoms present in these containers are also same i.e. 5 x NA atoms.
Question 32.
Fill in the missing data in the given table

Answer:

Question 33.
The visible universe is estimated to contain 1022 stars. How many moles of stars are present in the visible universe ?
Answer:
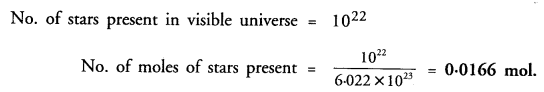
Question 34.
What is the SI prefix for each of the following multiples and submultiples of a unit ?
![]()
Answer:
(a) kilo
(b) deci
(c) centri
(d) micro
(e) nano
(f) pico
Question 35.
Answer:

Question 36.
Compute the difference in masses of 103 moles each of magnesium atoms and magnesium ions.
Answer:

Question 37.
Which has more number of atoms ?
100 g of N2 or 100 g of NH3
Answer:
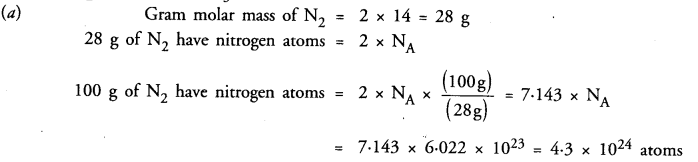
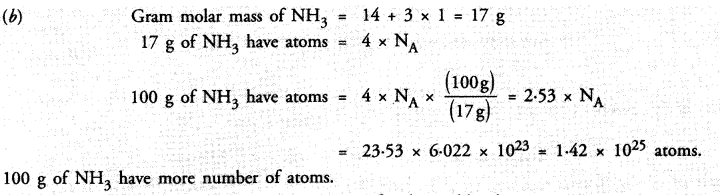
Question 38.
Compare the number of ions present in 5.85 g of sodium chloride.
Answer:
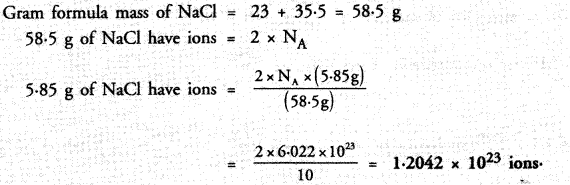
Question 39:
A gold sample contains 90% of gold and the rest copper. How many atoms of gold are present in one gram of this sample of gold ?
Answer:
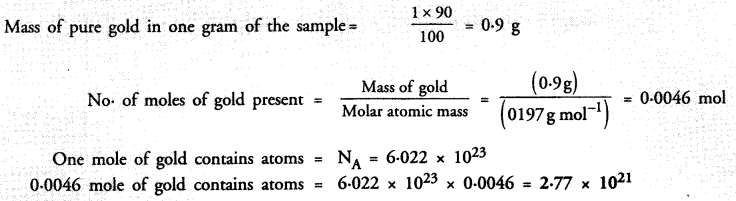
Question 40.
What are ionic and molecular compounds ? Give examples.
Answer:
Simple ionic compounds are of binary nature. It means that both the positive and negative ions have one atom only. The symbols of these ions are written side by side with their valencies at their bottom. A common factor if any, is removed to get a simple ratio of the valencies of the combining atoms. The criss-cross method is then applied to arrive at the final chemical formula of the compound. Let us write the formulae of a few simple ionic compounds. For example,
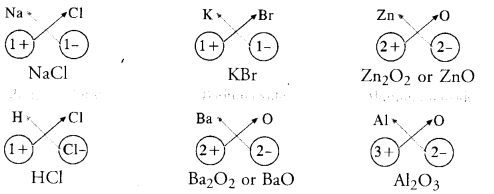
The molecular compounds also called covalent compounds. The compounds listed above are heteroatomic in nature. It means that different elements participate in these compounds. They may be homoatomic also which means that these are formed from the atoms of the same element. For example, hydrogen molecule (H2), chlorine molecule (Cl2), oxygen molecule (02), nitrogen molecule (N2), etc.

Question 41.
Compute the difference in masses of one mole each of aluminium atoms and one mole of its ions. (Mass of an electron is 9.1 x 10-28 g). Which one is heavier ?
Answer:

Question 42.
A silver ornament of mass ‘m’ gram is polished with gold equivalent to 1% of the mass of silver. Compute the ratio of the number of atoms of gold and silver in the ornament.
Answer:
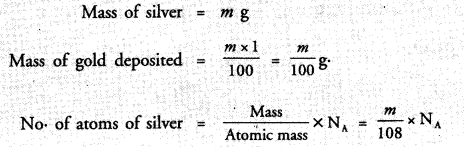
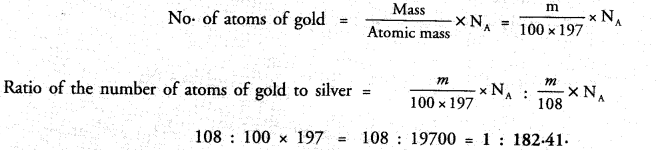
Question 43.
A sample of ethane (C2H6) gas has the same mass as 1.5 x 1020 molecules of methane (CH4). How many C2H6 molecules does the sample of gas contain ?
Answer:

Question 44.
Fill in the blanks
(a) In a chemical reaction, the sum of the masses of the reactants and products remains unchanged. This is called ………….. .
(b) A group of atoms carrying a fixed charge on them is called ………….. .
(c) The formula unit mass of Ca3(PO4)2 is ………….. .
(d) Formula of sodium carbonate is ………… and that of ammonium sulphate is …………… .
Answer:
(a) Law of conservation of mass
(b) Polyatomic ions
(c) 3 x Atomic mass of Ca + 2 x Atomic mass of P + 8 x Atomic mass of O.
3 x 40 + 2 x 31 + 8 x 16 = 120 + 62 + 128 = 310 u
(d) Na2CO3, (NH4)2SO4.
Question 45.
Complete the following crossword puzzle by using the name of the chemical elements. Use the data given in table.

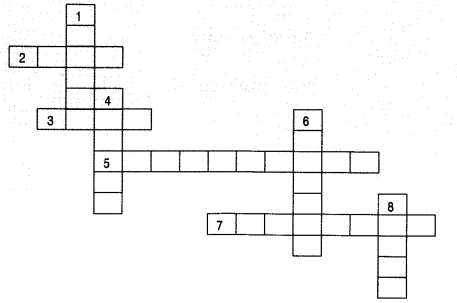
Answer:
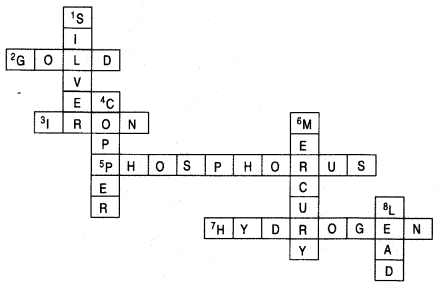
Question 46.
Write the formulae for the following and calculate the molecular mass for each one of them.
(a) Custic potash
(b) Baking powder
(c) Lime stone
(d) Caustic soda
(e) Ethanol
(f) Common salt.
Answer:
(a) KOH = 39 + 16 + 1 = 56 u
(b) NaHCO3 = 23 + 1 + 12 + 3 x 16 = 84 u
(c) CaCO3 = 12 + 12 x 3 x 16 = 100 u
(d) NaOH = 23 + 16 + 1 = 40 u
(e) C2H5OH = 2 x 12 + 6 x 1 + 16 = 46 u
(f) NaCl = 23 + 35.5 = 58.5 u
Question 47.
In photosynthesis, 6 molecules of carbon dioxide combine with an equal number of water molecules through a complex sereies of reactions to give a molecule of glucose having a molecular formula C6H12O6 and a molecule of oxygen with molecular formula O2. How many grams of water would be required to produce 18 g of glucose ? Compute the volume of water so consumed assuming the density of water to be 1 g cm-3.
Answer:
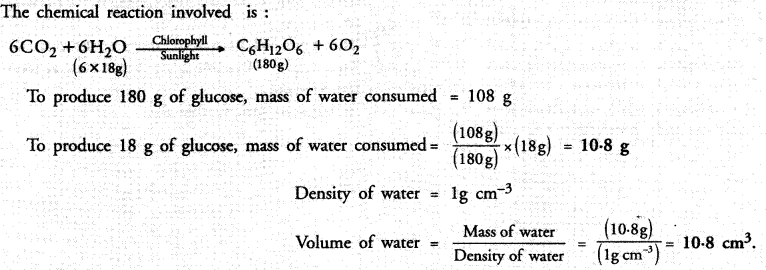
Hope given NCERT Exemplar Solutions for Class 9 Science Chapter 3 Atoms and Molecules are helpful to complete your science homework.
If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.