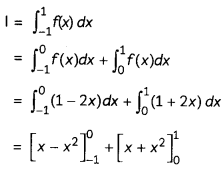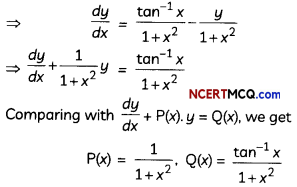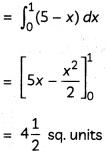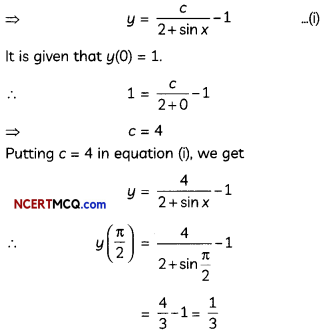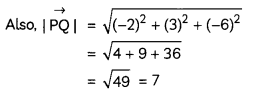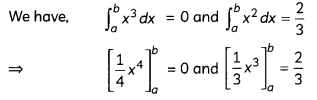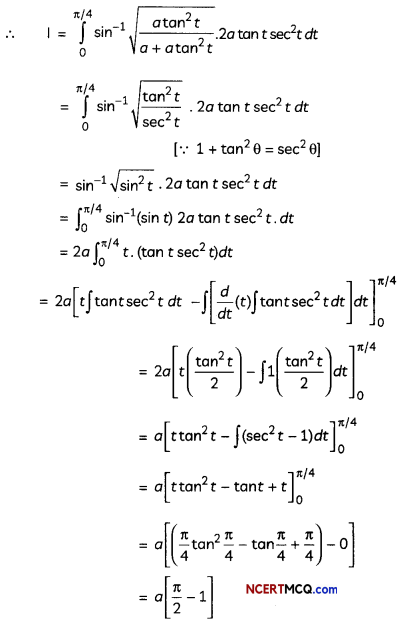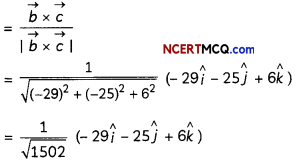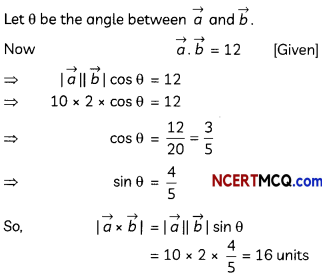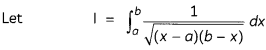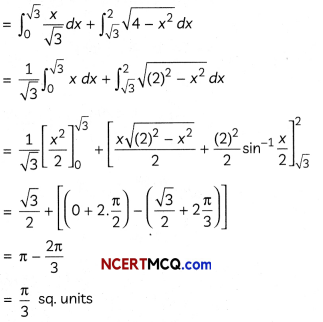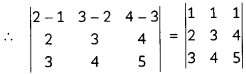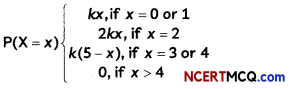Category: CBSE Sample Papers

Students can access the CBSE Sample Papers for Class 12 Chemistry with Solutions and marking scheme Term 2 Set 2 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Chemistry Term 2 Set 2 with Solutions

Time Allowed: 2 Hours
Maximum Marks: 35

General Instructions:

• There are 12 questions in this question paper with internal choice.
• SECTION A – Q. No. 1 to 3 are very short answer questions carrying 2 marks each.
• SECTION B – Q. No. 4 to 11 are short answer questions carrying 3 marks each.
• SECTION C- Q. No. 12 is case based question carrying 5 marks.
• All questions are compulsory.
• Use of log tables and calculators is not allowed.

Section – A
(Section A-Question No 1 to 3 are very short answer questions carrying 2 marks each.)

Question 1.
(A) Arrange the following amines in order of decreasing basic strength—Ethylamine, ammonia, tri ethylamine.
Answer:
Triethyl amine (C₂H₅)₃N> Ethyl amine C₂H₅NH₂> Ammonia NH₃
Explanation: More the number of alkyl groups, more the +1 effect so more the basic strength.

(B) Why aniline is acetylated first to prepare mono bromo derivative ? (2)
Answer:
Due to the strong activating effect of amino group, aromatic amines readily undergo electrophilic substitution reactions and it is difficult to stop the reaction the monosubstitution stage. Therefore, the acetyl group attached with aniline deactivates the aniline due to its electron withdrawing effect. Thus acetylation of aniline reduces its activation effect.

Question 2.
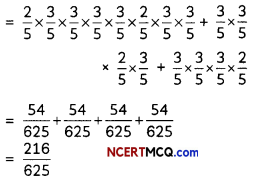
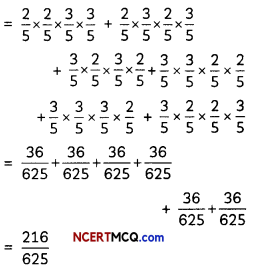
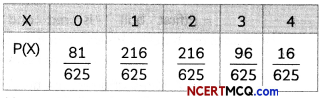
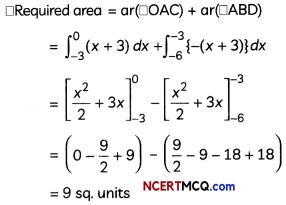
If the half-life period of a first-order reaction in A is 2 minutes, how long will it take to reach 25% of its initial concentration? (2)
Answer:

Question 3.
Draw the structure of the alcohol that could be oxidized to each compound. (2)
(i) 2-propanone
(ii) Cyclohexanone
Answer:

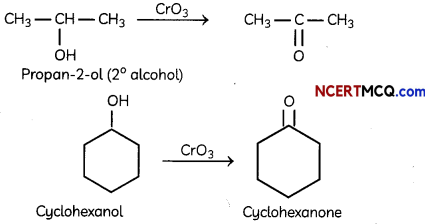
Section – B
(Section B-Question No 4 to 11 are short answer questions carrying 3 marks each.)

Question 4.
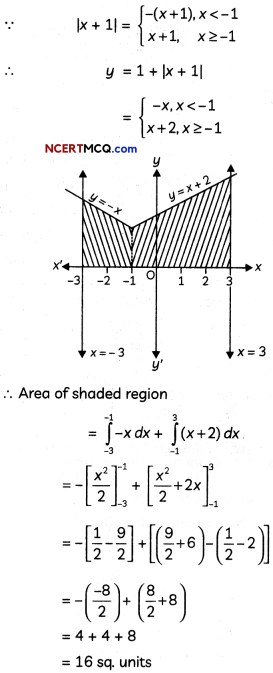
Using thermodynamic principles, explain: (3)
(A) Entropy has negative value for adsorption.
Answer:
The randomness of the overall process decreases due to the presence of a force of attraction between adsorbent and adsorbate due to which the gas molecules stick to the surface. So, Entropy has negative value for adsorption.

(B) Adsorption is a exothermic process?
Answer:
Adsorption is an exothermic process since surface particles of the adsorbent are unstable and when the adsorbate is adsorbed on the surface, the energy of adsorbent decreases, and this results in the evolution of heat. Therefore, adsorption is always exothermic.

(C) Relation between enthalpy and entropy at equilibrium.
Answer:
When ΔG becomes zero, adsorption equilibrium is established. Since it is an exothermic process, ΔH is negative. Since the adhering of gas molecules to the surface lowers the randomness, the ΔS is negative. So, ΔH and TΔS become equal at equilibrium to make ΔG zero. (ΔG = ΔH – TΔS)

Question 5.
The following table summarizes the oxidation states of the 3d series elements.

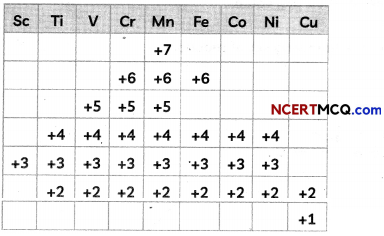
Account for the following questions related to the above table:
(A) Transition metals show variable oxidation state.
(B) At the beginning of the series, +3 oxidation state is stable but towards the end +2 oxidation state is stable.
(C) Mn has six different oxidation states from +2 to +7.
OR
Explain the trends in the properties of the members of the First series of transition elements:
(A) E⁰ (M²⁺/M) value for copper is positive (+0.34V)in contrast to the other members of the series.
(B) Cr²⁺ is reducing while Mn²⁺ is oxidising though both have d⁴ configuration.
(C) The oxidising power in the series increases in the order VO₂⁺ < Cr₂ O₇^2- < MnO₄^– (3)
Answer:
(A) Transition elements show variable oxidation states because their valence electrons are in two different sets of orbitals, that is (n-l)d and ns. The energy difference between these orbitals is very less, so both the energy levels can be used for bond formation. Thus, transition elements have variable oxidation states.

(B) The number of oxidation states increases with the number of electrons available, and it decreases as the number of paired electrons increases.
Explanation: In 3d series, first element Sc has only one oxidation state +3; the middle element Mn has six different oxidation states from + 2 to +7 because number of unpaired electrons is maximum but the last element Cu shows +1 and +2 oxidation states only because it has maximum number of paired electrons.

(C) The different oxidation states of manganese (Mn) are +2, +3, +4, +5, +6 and +7. Manganese with 3d⁵, 4s² as the outer electronic configuration, shows oxidation states ranging from +2(3d⁵) to + 7(3d⁰). The +2 oxidation state is very stable due to exactly half-filled 3d-orbital of higher stability.
OR
(A) Copper has high atomisation Δ_aH° and low hydration energy Δ_hydH°. Due to which the E° value is positive.
Explanation: The E_θ(M2+/M) value of a metal depends on the energy changes involved in the following:
1. Sublimation : The energy required for converting one mole of an atom from the solid state to the gaseous state.
M_(x) → M_(g) Δ_s H(Sublimation energy)

2. Ionization : The energy required to take out electrons from one mole of atoms in the gaseous state.
M_(x) → M_(g) Δ_i H(lonization energy)

3. Hydration: The energy released when one mole of ions hydrated.
M_(g) → M²⁺_(ag) Δ_hyd H(Hydration energy)
Now, copper has a high energy of atomization and low hydration energy. Hence, the E^Φ (M²⁺/M) value for copper is positive.

(B) Cr²⁺ is reducing agent as its configuration changes from d⁴ to d³, when it is oxidized to Cr³⁺ . On the other hand, the reduction of Mn³⁺ to Mn²⁺ results in the half-filled (d⁵) configuration which has extra stability hence Mn³⁺ acts as oxidizing agent.

(C) Greater the oxidation state, higher is the oxidising power.
Explanation: Oxidation state of V in VO₂⁺+ is 5, Cr in Cr₂O₇^2- is 6 and Mn in MnO₄^– is 7.

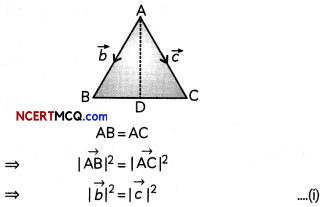
Question 6.
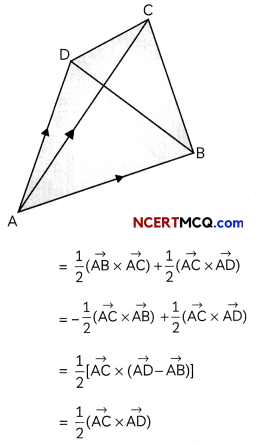
Based on valence bond theory, explain the bonding in the coordination entity [Co(NH₃)₆]³⁺. Also, comment on the geometry and spin of the given entity. (Atomic no. of Co = 27) (3)
Answer:
[Co(NH₃)₆³⁺
Co³⁺ = 3d⁶

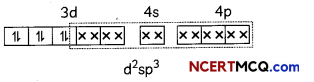
In this complexion, the oxidation state of cobalt is +3.
This complex involves the d²sp³ hybridisation. The six pairs of electrons, one from each NH₃ molecule, occupy the six hybrid orbitals. It proves that complex has octahedral geometry.

Question 7.
A metal complex having composition Cr(NH₃)₄Cl₂Br has been isolated in two forms A and B. The form A reacts with AgN03 to give a white precipitate readily soluble in dilute aqueous ammonia, whereas B gives a pale-yellow precipitate soluble in concentrated ammonia
(i) Write the formulae of isomer A and B
(ii) State the hybridisation of Cr in each of them.
OR
Give reason for each of the following:
(A) Co²⁺ is easily oxidised to Co³⁺ in presence of a strong ligand.
(B) CO is a stronger complexing reagent than NH₃.
(C) The molecular shape of Ni(CO)₄ is not the same as that of [Ni(CN)₄]^2- (3)
Answer:
(i) Formula of A → [Cr(NH₃)₄ Br Cl] Cl
Formula of B →[Cr(NH₃)₄ Cl₂] Br
Explanation: ‘A’ and ‘B’ are Ionisation isomers. ‘A’ has Cl as onion so it gives white ppt. with AgNO₃
Whereas ‘B’ has Br as onion so it gives pale yellow ppt. with AgNO₃.
(ii) Hybridisation state of Cr in each of them is d²sp³.
OR
(A) Co²⁺ ions can be easily oxidised to Co³⁺ ions because the crystal field stabilisation energy of Co³⁺ ions with a d⁶ configuration is higher than d⁷ configuration.
In presence of strong ligand, the d- orbitals of metal gets splits up into two set of orbitals that is t_2g and e_g. The half filled or fully filled t_2g is more stable than other configuration. This is because it gives maximum amount of low energy of t_2g orbital with electrons. Lower the energy, more is the stabilisation.

(B) Since CO can form a as well as n bond, whereas NH₃ has lone pair of electrons and can form a bond only. Therefore, CO is a better complexing reagent than NH₃.
Explanation: CO has empty π orbitals which overlap with filled d-orbitals (t_2g orbitals) of transition metals and form π bonds by back bonding. These π interaction increases the value of crystal field stabilisation energy (∆₀).
As NH₃ cannot from π bonds by back bonding, therefore, CO is a stronger ligand than NH₃.

(C) In [Ni(CO)₄], nickel is present in zero oxidation state {Ni = 3d⁸ 4s²} but in [Ni(CN)₄ ]^2-, oxidation state of Nickel is +2. So, Ni²⁺: 3d⁸ 4s⁰.
Explanation: Electronic configuration of:
Ni [Ar]4s², 3d⁸
So Ni (0): [Ar] 4s⁰, 3d¹⁰
CO ligand causes pairing of electrons and shifting of electrons from 4s to 3d.
[Ni(CO)⁴]

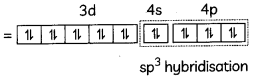
[Ni(CO)₄] has sp³ hybridisation and has tetrahedral shape.

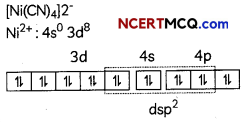
[Ni (CN₄)]^2- has dsp² hybridisation and has square planar shape.

Question 8.
The graphical representation of concentration of A Vs time is given for a general A → B,

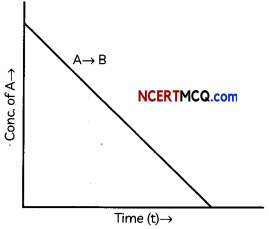
The following questions:
(a) What is the order of the reaction?
(b) What is the slope of the curve?
(c) State the units for the rate constant. (3)
Answer:
(A) Zero order reaction
(B) slope = – k
(C) Unit of k = mol L^-1 s^-1

Explanation: In case of a zero-order reaction, the rate of reaction is independent of the concentration of the reactant. The concentration [A]t of the reactant at a time t is given by [A]_t = – kt + [A]₀ (y = – mx +c) where [A]₀ is the initial concentration of the reactant and k is a rate constant.
When the concentration of the reactant is plotted against time, a straight line with the slope equal to – k is obtained.

Question 9.
Complete the following reactions:

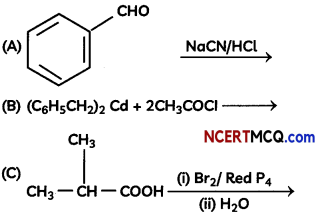
OR
Write chemical equations for the following reactions:
(A) Propanone is treated with diLute Ba(OH)₂.
(B) Acetophenone is treated with Zn(Hg)/ Conc. HCI
(C) Benzoyl chloride is hydrogenated in presence of Pd/BaSO₄. (3)
Answer:

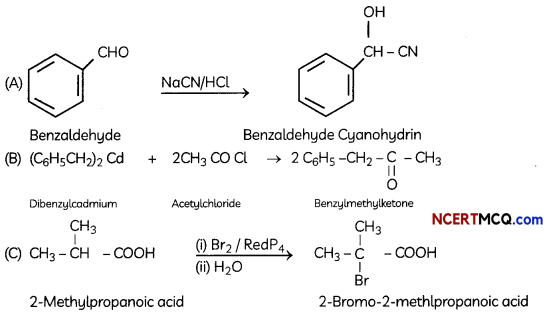
Explanation: Reaction is Hell-Vollard-Zelinsky reaction in which carboxylic acids react with chlorine or bromine in presence of small amount of red phosphorus to give a-halocarboxylic acids.
OR
(A)

Explanation: Aldol condensation is an organic reaction in which an enolate ion reacts with carboxyl compound to form β-hydroxy aldehyde or β-hydroxy ketone. Hydroxide functions as a base and therefore moves the acidic a-hydrogen producing the reactive enolate ion.

(B)

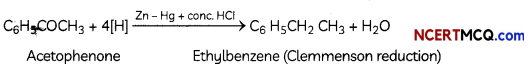
Explanation: The Clemmensen reduction is a reaction that is used to reduce aldehydes or ketones to alkanes using hydrochloric acid and zinc amalgam.

(C)

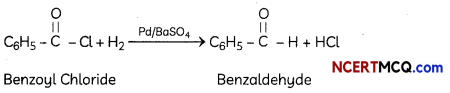
Explanation: Rosenmund reduction is the hydrogenation of an acyl chloride to an aldehyde, in presence of catalyst (Pd supported on barium sulphate). Barium sulphate partially poisons Pd metal and prevents over-reduction. Untreated Pd catalyst is too reactive.

Question 10.
(A) Account for the following:
(i) Cl- CH₂COOH is o stronger acid than CH₃COOH.
Answer:
(i) Cl group is an electron withdrawing creating less electron density on oxygen of carboxylic acid making the release of proton easier than acetate ion. Hence, Cl-CH₂COOH is a stronger acid than CH₃COOH.

Explanation: Chlorine due to its -1 effect increases the acidity of carboxylic acids by stabilising the conjugate base due to delocoalisation of the negative charge by resonance effect.

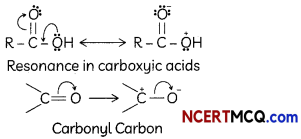
(ii) Carboxylic acids do not give reactions of the carbonyl group.
Answer:
Carboxylic acids do not give characteristic reaction of carbonyl group. This is because the lone pairs on oxygen atom attached to hydrogen atom in the -COOH group are involved in resonance thereby making the carbon atom less electrophilic Hence, carboxylic acids do not give characteristic reaction of carbonyl group.

Explanation:

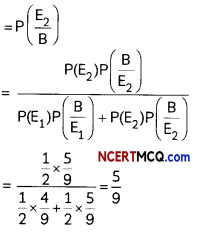
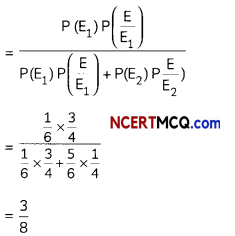
(B) Give simple chemical tests to distinguish Benzoic acid and Phenol. (3)
Answer:
Phenol and benzoic acid can be distinguished by ferric chloride test.
Ferric chloride test: Phenol reacts with neutral Fecl₃ to form an iron-phenol complex giving violet colouration. But benzoic acid reacts with neutral FeCl₃ to give a buff coloured ppt.

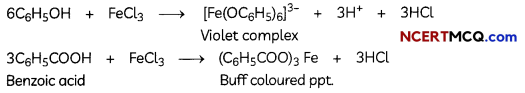
Question 11.
(A) Aniline is a weaker base than cyclohexylamine. Give reason.
(B) Amino group in aniline is ortho and para directing, Then why does aniline on nitration give substantial amount of m-nitroaniline?
(C) There are two test tubes (abetted A and B. Give suitable test to identify which test tube contains aniline and which contains methylamine.
OR
(A) Arrange the following in increasing order of their pK_a values:
(i) C₆H₅NH₂, C₂H₅NH₂, (C₂H₅) ₂NH, NH₃
(B) Identify the compounds A, B, C and D In the following set of reactions

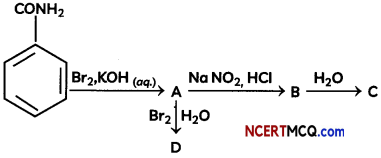
Answer:
(A) In aniline, benzene group is electron withdrawing in nature. Hence, it decreases the availability of electron pair on N-atom and is less basic. On the other hand, in cyclohexylamine, the cyclohexyl group is electron releasing in nature. Hence, this, increases the availability of electrons on N-atom and is more basic.

(B) Nitration is carried out in an acidic medium. In an acidic medium, aniline is protonated to give anilinium ion (which is meta-directing). Due to which aniline on nitration gives a substantial amount of m-nitroaniline.

(C) Nitrous acid Test – Treat aniline and methylamine with sodium nitrite with hydrochloric acid at zero degree Celsius.
In case of aniline: stable diazonium salt will be formed which will give phenol on hydrolysis.
In case of methylamine: unstable diazonium salt of aliphatic amine will be formed which will further get decompose into bubbles of nitrogen gas and methanol.
OR
(A) Increasing order of pKa value-
(C₂H₅)₂NH < C₂H₅NH₂ < NH₃ < C₆H₅NH₂
Explanation: Higher the pKa value, less the basic character.Diethylamine is the most basic due to maximum +1 effect (lowest pKa) and aniline is the least basic due to resonance (highest pKa).
(B)

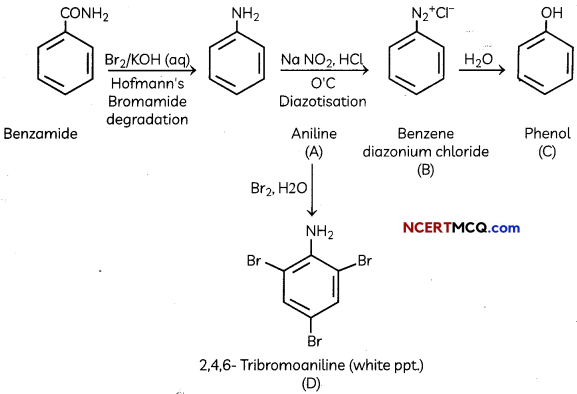
SECTION – C
(Section C-Question No 12 is case-based question carrying 5 marks.)

Question 12.
Read the passage given below and answer the questions that follow – (5)
Electrolysis, process by which electric current is passed through a substance to effect a chemical change. The process is carried out in an electrolytic cell, an apparatus consisting of positive and negative electrodes held apart and dipped into a solution containing positively and negatively charged ions. The substance to be transformed may form the electrode, may constitute the solution, or may be dissolved in the solution. Electric current (i.e., electrons) enters through the negatively charged electrode (cathode); components of the solution travel to this electrode, combine with the electrons, and are transformed (reduced). The products can be neutral elements or new molecules. Components of the solution also travel to the other electrode (anode), give up their electrons, and are transformed (oxidized) to neutral elements or new molecules.

Electrolysis is used extensively in metallurgical processes, such as in extraction (electrowinning) or purification (electrorefining) of metals from oresor compounds and in deposition of metals from solution (electroplating). Metallic sodium and chlorine gas are produced by the electrolysis of molten sodium chloride; electrolysis of an aqueous solution of sodium chloride yields sodium hydroxide and chlorine gas. Hydrogen and oxygen are produced by the electrolysis of water.

Michael Faraday discovered in 1833 that there is always a simple relationship between the amount of substance produced or consumed at an electrode during electrolysis and the quantity of electrical charge Q which passes through the cell.
(A) Name two metals which can be purified using electrolytic refining.
(B) What are the electrolysis products of an aqueous solution of sodium chloride?
(C) How much charge in terms of Faraday is required for the reduction of 1 mol of Cu²⁺ to Cu?
(D) How many moles of mercury will be produced by electrolysing 1.0 M Hg(NO₃)₂ solution with a current of 2.00 A for 3 hours? [Hg(NO₃)₂ = 200.6 g mol^-1].
OR
A steady current of 2 amperes was passed through two electrolytic cells X and Y connected in series containing electrolytes FeSO₄ and ZnSO₄ until 2.8 g of Fe deposited at the cathode of cell X. How long did the current flow?
(Molar mass: Fe = 56 g mol^-1, Zn = 65.3 g mol^-1, 1F = 96500 C mol^-1)
Answer:
(A) Na (Sodium) and K (Potassium)

(B) H₂ gas is liberated at cathode. Cl₂ gas is liberated at anode. NaOH is formed in the solution.
Explanation:

At anode: 2Cl^– → Cl₂ + 2e^–; At cathode: 2H⁺ + 2e^– → H₂

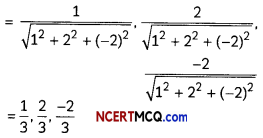
(C) Cu²⁺ + 2e- → Cu
Quantity of charge required for reduction of 1 mol of Cu²⁺ = 2F(F = Faraday)
Explanation: Faraday’s first law of electrolysis – The amount of any substance deposited or liberated at the electrode is directly proportional to the quantity of electricity passing through the electrolyte.

(D) Mass of mercury produced at the cathode,

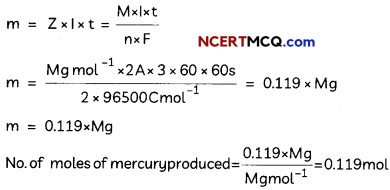
OR
(D) Current i = 2 A, Mass m of Fe = 2.8 g
Molar Mass M of Fe = 56 g mol^-1, 1F = 96500 c Fe2+ + 2e” -> Fe (Charge required = 2F)

Students can access the CBSE Sample Papers for Class 12 Physics with Solutions and marking scheme Term 2 Set 1 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Physics Standard Term 2 Set 1 with Solutions

Time Allowed: 2 Hours
Maximum Marks: 40

General Instructions:

• There are 12 questions in all. All questions are compulsory.
• This question paper has three sections: Section A, Section B, and Section C.
• Section A contains three questions of two marks each, Section B contains eight questions of three marks each, Section C contains one case study-based question of five marks.
• There is no overall choice. However, an internal choice has been provided in one question of two marks and two questions of three marks. You have to attempt only one of the chokes in such questions.
• You may use log tables if necessary but use of calculator is not allowed.

SECTION – A
(Section A consists 3 questions of 2 marks each.)

Question 1.
In a pure semiconductor crystal of Si, if antimony is added then what type of extrinsic semiconductor is obtained. Draw the energy band diagram of this extrinsic semiconductor so formed. (2)
Answer:
As given in the statement antimony is added to pure Si crystal, then an n-type extrinsic semiconductor would be so obtained Since antimony (Sb) is a pentavalent impurity. Energy level diagram of n-type semiconductor

Related Theory
Each pentavalent impurity atom donates one extra electron: it is known as donor. Most of the current is carried by negatively charged electrons, so, the semiconductors doped with donor type impurities are known as n-type semiconductors.

Question 2.
Consider two different hydrogen atoms. The electron in each atom is in an excited state. Is it possible for the electrons to have different energies but same orbital angular momentum according to the Bohr model? Justify your answer.
OR
Explain how does (A) photoelectric current and (B) kinetic energy of the photoelectrons emitted in a photocell vary if the frequency of incident radiation is doubled, but keeping the intensity same? Show the graphical variation in the above two cases. (2)
Answer:
No
Because according to Bohr’s model,
E_n = \(-\frac{13.6}{n^{2}}\) and electrons having different energies belong to different levels having different values of n.
So, their angular momenta will be different, as ‘
L = mvr = \(\frac{n h}{2 \pi}\)
OR
(A) The increase in the frequency of incident radiation has no effect on photoelectric current. This is because of incident photon of increased energy cannot eject more than one electron from the metal surface. f = photoelectric current f = frequency of incident radiation fo = threshold frequency

The kinetic energy of the photoelectron becomes more than the double of its original energy. As the work function of the metal is fixed, so incident photon of higher frequency and hence higher energy will impart more energy to the photo electrons.

Question 3.
Name the device which converts the change in intensity of illumination to change in electric current flowing through it. Plot l-V characteristics of this device for different intensities. State any two applications of this device.(2)
Answer:
Photodiodes are used to detect optical signals of different intensities by changing current flowing through them.

I-V Characteristics of a photodiode Applications of photodiodes:
1. In detection of optical signals.
2. In demodulation of optical signals.
3. In light operated switches.
4. In speed reading of computer punched cards.
5. In electronic counters
(any two out of these or any other relevant application)

SECTION – B
(Section B consists 8 questions of 3 marks each.)

Question 4.
Derive an expression for the frequency of radiation emitted when a hydrogen atom de-excites from LeveL n to Level (n – 1). Also show that for Large values of n, this frequency equals to classical frequency of revolution of an eLectron. (3)
Answer:
From Bohr’s theory, the frequency f of the radiation emitted when an electron de – excites from Level n₂ to Level, n₁ is given as,
f = \(\frac{2 \pi^{2} m k^{2} z^{2} e^{4}}{h^{3}}\left[\frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}}\right]\)
Given n₁ = n – 1 = n . derivation of it
f = \(\frac{2 \pi^{2} m k^{2} z^{2} e^{4}}{h^{3}} \frac{(2 n-1)}{(n-1)^{2} n^{2}}\)
For large n. 2n- 1 = 2n,n- 1 =n and z= 1
Thus, f = \(\frac{4 \pi^{2} m k^{2} e^{4}}{n^{3} h^{3}}\)
which is same as orbital. frequency of etectron in nth orbit.
f = \(\frac{v}{2 \pi r}=\frac{4 \pi^{2} m k^{2} e^{4}}{n^{3} h^{3}}\)

Question 5.
Explain with a proper diagram how an ac signal can be converted into dc ( pulsating) signal with output frequency as double than the input frequency using pnjunction diode. Give its input and output waveforms. (3)
Answer:
A junction diode aLlows current to pass only when it is forward biased. So, Wan alternating voltage is applied across a diode the current flows only in that part of the cycle when the diode is forward biased. This property is used to rectiy alternating voltages and the circuit used for this purpose is called a rectifier.

Explanation: A full wave rectifier converts ac signal into dc signaL During positive half of the cycle, diode 1 is forward biased and diode 2 is reverse biased. During negative half of the cycle, diode 1 is forward biased. Output voltage is obtained during both half cycles. This process is known as rectification.

Caution:
Output frequency double of input frequency is not possible in half wave rectifier. In half wove rectifier, there will be no output voltage, hence, diode will conduct during positive half cycle only.

Question 6.
How Long can an electric Lamp of 100 W be kept glowing by fusion of 2 kg of deuterium? Take the fusion reaction as ₁¹H+₁²H → ₂³He+n +3.27 MeV (3)
Answer:
Number of atoms present in 2 g of deuterium = 6 x10²³
Number of atoms present in 20 Kg of deuterium = 6 x 10²⁶
Energy released in fusion of 2 deuterium atoms = 3.27 MeV
Energy reLeased in fusion of 2.0 Kg of deuterium atoms

= \( \frac{3.27}{2}\) x 6 x 1026 MeV
= 9.81 x. 10²⁶ MeV
= 15.696 x 10¹³J
Energy consumed by bulb per sec = 100 J
Time for which bulb will glow
= \(\frac{15.696 \times 10^{13}}{100}\)
s = 4.97 x 10⁴ year

Question 7.
Define wavefront. Draw the shape of refracted wavefront when the plane incident wave undergoes refraction from optically denser medium to rarer medium. Hence prove Snell’s law of refraction. 3
Answer:
A locus of points, which oscillate in phase is called a wavefront. A wavefront is defined as a surface of constant phase.

Explanation: A wavefront is defined as the continuous locus of aLL such particles of the
medium which are vibrating in the same phase at any instant.

sin∠BAC=sini= \(\frac{\mathrm{BC}}{\mathrm{AC}}\)
From the right ΔAEC
sin ∠ECA =sin r = \(\frac{\mathrm{AE}}{\mathrm{AC}}\)
\(\frac{\sin i}{\sin r}=\frac{\mathrm{BC}}{\mathrm{AE}}=\frac{v_{1} \tau}{v_{2} \tau}\)
This is the Snells tow of refraction.

Question 8.
(A) Draw a ray diagram of compound microscope for the final image formed at least distance of distinct vision?
(B) An angular magnification of 30X is desired using an objective of focal length 1.25 cm and an eye piece of focal length 5 cm. How will you set up the compound microscope for the finaln image formed at least distance of distinct vision?
OR
(A) Draw a ray diagram of Astronomical Telescope for the final image formed at infinity.
(B) A small telescope has an objective lens of focal length 140 cm and an eyepiece of focal length 5.0 cm. Find the magnifying power of the telescope for viewing distant objects when
(i) the telescope is in normal adjustment,
(ii) the final image is formed at the least distance of distinct vision. (3)
Answer:
(A) Diagram of Compound Microscope for the final image formed at D:

(B) m₀ = 30, i₀ = 1.25 cm, f_e = 5 cm
when image is formed at least distance of aistinct vision,
D = 25 cm
Angular magnification of eyepiece
m_e = \(\left(1+\frac{D}{f_{e}}\right)=1+\frac{25}{5} \) = 6

Total Angular magnification, m = m₀m_e ⇒
m₀ = \(\frac{m}{m_{e}}=\frac{30}{6}\) = 5
As the objective lens forms the real image,
m₀= \(\frac{v_{0}}{u_{0}}\) – 5 ⇒ v₀ = -5u₀
using Lens equation, u_e = \(\frac{25}{6}\)

Thus, object is to be placed at 1.5 cm from the objective and separation between the two lenses should be
L = v₀ + |U_e| = 11.67 cm
OR
(A) Ray diagram of astronomical telescope when image is formed at infinity.

(B) (i) In normal adjustment: Magnifying power.
m=f₀/f_e=(140/5)= 28
(ii) When the final image is formed at the east distance of distinct vision (25 cm):
m = \(\frac{f_{o}}{f_{e}}\left(1+\frac{f_{e}}{D}\right)(28 \times 1.2)\) = 33.6

Question 9.
Light of waveLength 2000 Å falls on a metal surface of work function 4.2 eV.
(A) What is the kinetic energy (in eV) of the fastest electrons emitted from the surface?
(B) What will be the change in the energy of the emitted eLectrons if the intensity of Light with same waveLength is doubled?
(C) If the same Light faits on another surface of work function 6.5 eV, what will be the energy of emitted electrons? (3)
Answer:
λ = 2000 Å = (2000 x 10^-10)m
W₀ = 4.2 eV
h = 6.63 x 10^-34 Js

(A) Using Einstein’s photoelectric equation
K. E. = (6.2 – 4.2) eV = 2.0 eV

(B) The energy of the emitted electrons does not depend upon intensity of incident Light; hence the energy remains unchanged.

(C) For this surface, electrons will not be emitted as the energy of incident light (6.2 eV) is less than the work function (6.5 eV) of the surface.

Question 10.
The focal length of a convex lens made of glass of refractive index (1.5) is 20 cm. What will be its new focal length when placed in a medium of refractive index 1.25 ? Is focal length positive or negative? What does it signify? (3)
Answer:
Given a_μg = 1.5
Focal length of the given convex lens when it is placed in air is
f= + 20 cm
Refractive index of the given medium with respect to air is
a_μm = 1-25
New focal length of the given convex lens when placed in a medium is f’

New focal length is positive.
The significance of the positive sign of the focal length is that given convex lens is still converging in the given medium.

Question 11.
(A) Name the e.m. waves which are suitable for radar systems used In aircraft navigation. Write the range of frequency of these waves.
(B) If the Earth did not have atmosphere, would its average surface temperature be higher or lower than what it is now? Explain.
(C) An e.m. wave exerts pressure on the surface on which it is incident. Justify.
OR
(A) If the slits in Young’s double-slit experiment are identical, then intensity at any point on the screen may vary between zero and four times to the intensity due to single slit”. Justify the above statement through a relevant mathematical expression.
(B) Draw the intensity distribution as function of phase angle when diffraction of light takes place through coherently illuminated single slit. 3
Answer:
(A) Microwaves are suitable for the radar system used in aircraft navigation. Range of frequency of microwaves is 108 Hz to 1011 Hz.

(B) If the Earth did not have atmosphere, then there would be absence of greenhouse effect of the atmosphere. Due to this reason, the temperature of the earth would be lower than what it is now.

(C) An e.m. wave exerts pressure on the surface on which it is incident. Justify An e.m. wave carries a linear momentum with it and the linear momentum carried by a portion of wave having energy U, which is given by p = U/c, where U = potential energy and c = speed of light.
Thus, if the wave incident on a material surface is completely absorbed, it delivers potential energy U and momentum p = Uc to the surface.
If the wave is totally reflected, the momentum delivered is p = 2U/c because the momentum of the wave changes from p to -p.
Therefore, it follows that an e.m. waves incident on a surface exert a force and hence a pressure on the surface.
OR
(A) The total intensity at o point where the phase difference is Φ. is given by I = I₁ + I₂ + 2\( \sqrt{1_{1} I_{2}}\) Φ
Here I₁ and I₂ are the intensities of two individual sources which are equal.
When Φ is 0,I = 4I₁
When Φ is 90°, I = 0
Thus intensity on the screen varies between 4I₂ and 0.
(B) Intensity distribution as function of phase angle, when diffraction of light takes place through coherently illuminated single slit

SECTION – C
(Section C consists one case study-based question of 5 marks.)

Question 12.
CASE STUDY: MIRAGE IN DESERTS

To a distant observer, the light appears to be coming from somewhere below the ground. The observer naturally assumes that light is being reflected from the ground, say, by a pool of water near the tall object.
Such inverted images of distant tall objects cause an optical illusion to the observer. This phenomenon is called mirage.
This type of mirage is especially common in hot deserts. Based on the above facts, answer the following questions:
(A) Which of the following phenomena is prominently involved in the formation of mirage in deserts?
(i) Refraction, Total internal Reflection
(ii) Dispersion and Refraction
(iii) Dispersion and scattering of light
(iv) Total internal Reflection and diffraction.

(B) A diver at a depth 12 m inside water
\(\left(a_{\mu \omega}=\frac{4}{3}\right)\) sees the sky in a cone of semi-vertical angle

• sin^-1\(\frac{4}{3}\)
• tan^-1 \(\frac{4}{3}\)
• sin^-1 \(\frac{4}{3}\)
• 90°

(C) In an optical fibre, if n₁ and n₂ are the refractive indices of the core and cladding, then which among the following, would be a correct equation?
(i) n₁ < n₂
(ii) n₁ = n₂
(iii) n₁ < n₂
(iv) n₁ > n₂

(D) A diamond is immersed in such a liquid which has its refractive index with respect to air as greater than the refractive index of water with respect to air. Then the critical angle of diamond- liquid interface as compared to critical angle of diamond -water interface will:
(i) depend on the nature of the liquid only
(ii) decrease
(iii) remain the same
(iv) increase.

(E) The following figure shows a cross-section of a ‘light pipe’ made of a glass fiber of refractive index 1.68.
The outer covering of the pipe is made of a material of refractive index 1.44.
What is the range of the angles of the incident rays with the axis of the pipe for the following phenomena to occur. (5)

Answer:
(A)
(i) Refraction, Total internal reflection
Explanation: When Light passes from cold air to hot air, tight tends to bend from its path which is known as refraction. As the tight is refracted, it reaches to o point where it forms a 90° angle. Hence refraction and total internal reflection are involved in formation of mirages.

(B) (iii) sin^-1 \(\left(\frac{3}{4}\right)\)

(C) (iv) n₁ > n₂
The refractive index of the core should be greater than the refractive index of the dadding.

(D) (iv) increase
\(\mathrm{I}_{\mu d}=\frac{1}{\sin c}=\frac{\mu_{d}}{\mu_{1}}\)
μ₁ = μ_ω
Thus C>C’

(E) (ii) 0<i<60°, ^lμ₂ = \(\frac{1}{\sin C^{\prime}}\)
SinC’= \(\frac{1.44}{1.68}\) = 0.8571
⇒ C = 59°
Total, internat reflection wilL occur if the angle i > i’c,
i.e., if i’> 59° or when r < r_max where r_max = 90° – 59°= 31°.
Using Snell’s Law.

\(\frac{\sin i_{\max }}{\sin r_{\max }}\) = 1.68
sin i_max = 1.68 x sin r_max
= 1.68 x sin 31° = 1.68 x 0.5 150 = 0.8662
Thus all incident rays which make angles in the range 0 < i < 60° with the axis of the pipe wilt suffer total internal reftections in the pipe.

Students can access the CBSE Sample Papers for Class 12 Physics with Solutions and marking scheme Term 2 Set 9 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Physics Standard Term 2 Set 9 with Solutions

Time Allowed: 2 Hours
Maximum Marks: 40

General Instructions:

• There are 12 questions in all. All questions are compulsory.
• This question paper has three sections: Section A, Section B and Section C.
• Section A contains three questions of two marks each, Section B contains eight questions of three marks each, Section C contains one case study-based question of five marks.
• There is no overall choice. However, an internal choice has been provided in one question of two marks and two questions of three marks. You have to attempt only one of the chokes in such questions.
• You may use log tables if necessary but use of calculator is not allowed.

SECTION – A
(Section A contains 3 questions of 2 marks each.)

Question 1.
Number of protons and number of neutrons are same on either side of a nuclear reaction. Then how is it said that energy released in a nuclear reaction is due to conversion of mass.
OR
What is a p-n junction diode and define the term dynamic resistance for the junction diode? (2)
Answer:
Total binding energy of nuclei on one side of the nuclear reaction may not be equal to that on the other side of the reactions. This fact tells that only rest mass of neutrons and protons is same on each side of the reaction difference in total binding energy on both sides can be referred to as difference in total mass in a nuclear reaction.
OR
A p-n junction diode is a single crystal of Germanium or Silicon doped in such a manner that one half portion of it acts as a p-type semiconductor and other half acts as a n-type semiconductor. As soon as a p-n junction is formed, holes from p-region and electrons from n-region diffuse which results in development of potential barrier across the junction and opposes the further diffusion of holes and electrons through the junction.
The dynamic or alternating current resistance of diode is the ratio of small applied voltage to the corresponding change in current.
r_d = \(\frac{\Delta V}{\Delta l}\)
Above the threshold voltage, the diode characteristic is linear. In linear region, dynamic resistance is almost independent of voltage and Ohm’s law is obeyed.

Question 2.
Find the maximum intensity in case of interference of n identical waves each of intensity l0 if the sources are:
(A) Coherent
(B) Incoherent (2)
Answer:
(A) Coherent sources
Let the amplitude be A for each wave then,
A_R = (A + A + …)n times ,
= nA
lR ∝\(\) = n²l₀

(B) Incoherent Sources
l = l₀ + l₀…. )n times
= nl₀

Question 3.
State principle of reversibility of light. Define lateral shift. (2)
Answer:
Principle of reversibility of light states that if the final path of ray of light after it has suffered several reflections and refractions is reversed, it retraces its path exactly.

Lateral shift is the perpendicular distance between the incident and emergent rays when light is incident obliquely on a refracting slab with parallel faces.

SECTION – B
(Section B consists of 8 questions of 3 marks each.)

Question 4.
Answer the following questions:
(A) In a double slit experiment using light of wavelength 600 nm, the angular width of the fringe formed on a distant screen is 0.1°. Find the spacing between the two slits.
(B) Light of wavelength 5000 A propagating in air gets partly reflected from the surface of water. How will the wavelengths and frequencies of the reflected and refracted light be affected?
OR
(A) Describe any two characteristic features which distinguish between interference and diffraction phenomena. Derive the expression for the intensity at a point of the interference pattern in Young’s double slit experiment. (3)
Answer:
(A) Angular width (θ) of fringe in double-slit experiment is given by
θ = \(\frac{\lambda}{d}\)
Where d = Spacing between the slits.
Given: Wavelength of light,
λ = 600 nm
Angular width of fringe,
θ = 0.1°
= 0.1 × \(\frac{\lambda}{180}\) rad
= 0.0018 rad
∴ d = \(\frac{\lambda}{\theta}\)
d = \(\frac{600 \times 10^{-9}}{18 \times 10^{-4}}\) = 33.33 × 10^-5
⇒ d = 0.33 × 10^-3 m

(B) The frequency and wavelength of reflected wave will not change.
The refracted wave wiLl have same frequency, only wavelength will change.
The velocity of light v in water is given by
v = λf
where, v = Velocity of light
f = Frequency of light
λ = Wavelength of light As light ray in travelling from rarer (air) medium to denser medium, its speed will decrease. Hence wavelength (λ) will also decrease.

ReLated Theory
When a light ray traveLs from rarer medium to denser medium, then its speed and wavelength both will decrease.
(A)

A sources of monochromatic light illuminates two narrow slits S₁ and S₂. The two illuminated slits act as the two coherent sources. The two slits is very close to each other and at equal distance from source. The wave front S₁ and S₂ spread in all direction and superpose and produces dark and bright fringe on screen. Let the displacement of waves from Si and S2 at point P on screen at time t is:

y₁ = a₁sin ωt
y₂ = a₂ sin (ωt + Φ)
The resultant displacement at point P is given by
y = y₁ + y₂
= a₁ sin ωt + a₂ sin (ωt + Φ)
= a₁ sin ωt + a₂ sin ωt cos Φ
+ a₂ cos ωt sin Φ
= (a₁ + a₂ cos Φ) sin ωt + a₂ sin Φ cos ωt …………. (i)
Let, a₁ + a₂ cos Φ
= A cos Φ …………. (ii)
a₂ sin Φ = A sin Φ …………. (iii)

Therefore, equation (i) becomes
y = A cos θ sin ωt + A sin θ cos ωt
= A sin (ωt + θ)
This is the resultant displacement.
Now, squaring and adding equations (ii) and (iii)
A² cos² θ + A² sin²θ
= (a₁ + a₂ cos Φ)² + a₂² sin² Φ
A² = a₁² + a₂² + 2a₁ a₂ cos Φ

The is intensity of light is directly proportional to the square of the amplitude
i.e., I = a₁² + a₂² + 2a₁ a₂ cos Φ

This is the expression for intensity at a point of interference pattern.
or I = I₁+ I₂ + \(2 \sqrt{I_{1} I_{2}}\) cos Φ

Question 5.
(A) On what factor does the velocity of EM waves depends on?
(B) The magnetic field in a travelling
electromagnetic wave has a peak value of 20 nT. Find the peak value of electric field strength? (3)
Answer:
(A) The velocity of electromagnetic wave
depends on electric and magnetic properties of the medium.

(B) Here,
B₀ = 20nT
= 20 x 10^-9T,
c = 3 x 10⁸ m/s
E₀ = cB₀
= 3 x 10⁸ x 20 x 10^-9
= 6 V/m

Question 6.
(A) Draw graphs showing variation of photoelectric current with applied voltage for two incident radiations of equal frequency and different intensities. Mark the graph for the radiation of higher intensity.
(B) An α-particle and a proton are accelerated through the same potential difference. Find the ratio of their de Broglie wavelengths. (3)
Answer:
(A) Graph for photoelectric current (I) versus applied potential for radiations of same frequency and varying intensity.

(B)


Caution
Students are often confused in solving this problem. Here, de-Broglie wavelength is inversely proportional to the square root of mass and charge.

Question 7.
What are the important considerations required while fabricating a p-n junction diode to be used as a light emitting diode? (3)
Answer:
(A) There is a very little resistance to limit the current in LED. Therefore, a resistor must be used in series with the LED to avoid any damage to it.

(B) The reverse breakdown voltage of LEDs is very low, typically around 5 V. Therefore, care should be taken while fabricating a p-n junction diode so that the p-side should only attached positive side of the battery as LED easily get damaged by small reverse voltage.

(C) The semiconductors used for fabrication of visible LEDs must have at least band gap of 1.8 eV.

Question 8.
(A) What is the position of an object
relative to the objective of compound microscope? Where is its image formed?
(B) The magnifying power of objective of compound microscope is 5. If the magnifying power of microscope is 30, then what is the magnifying power of eyepiece? (3)
Answer:
(A) When object is placed slightly larger than f₀ then the final image is formed at infinity.

(B) M = M₀ x M_e
Here, M = 30
and M₀ = 5
M_e = \(\frac{\mathrm{M}}{\mathrm{M}_{o}}\)
= \(\frac{30}{5}\) = 6

Question 9.
(A) How does the de-Broglie wavelength of a charged particle change when accelerating potential increases?
(B) A proton and an a-particle have the same de-Broglie wavelength. Determine the ratio of:
(A) their accelerating potentials.
(B) their speeds. – (3)
Answer:
(A) λ ∝ \(\frac{1}{\sqrt{V}}\), WhenV increases, λ decreases.

(B) (i) The de-Broglie wavelength of a particle is given by
λ = \(\frac{h}{\sqrt{2 m q V}}\)
where, V is the accelerating potential of the particle.
It is given that
λ_proton = λ_alpha
⇒ \(\frac{h}{2 m_{p} q_{p} V_{p}}\) = \(\frac{h}{2 m_{\alpha} q_{\alpha} V_{\alpha}}\)
\(\sqrt{2 m_{\alpha} q_{\alpha} V_{\alpha}}\) = \(\sqrt{2 m_{p} q_{p} V_{p}}\)
On squaring both sides, we get
2m_αq_αV_α = 2m_pq_pV_p
⇒ \(\frac{V_{p}}{V_{\alpha}}\) = \(\frac{m_{\alpha} q_{\alpha}}{m_{p} q_{p}}\)
= \(\frac{4 m_{p} \times 2 q_{p}}{m_{p} q_{p}}\)
[∵m_a = 4m_p and q_α = 2q_p]
= \(\frac{8}{1}\)

(B) We can also write de-Broglie wavelength as:
λ = \(\frac{1}{2 \pi f C}\)

where h is Planck’s constant, m is mass of the particle and v is the speed of the particle.
It is given that
λ_proton = λ_alpha
We know
m_alpha = 4m_proton
∴ λ_alpha = \(\frac{h}{4 m_{\text {proton }} V_{\text {alpha }}}\)
⇒ Now L
\(\frac{h}{m_{\text {proton }} v_{\text {proton }}}\) = \(\)
\(\frac{h}{4 m_{\text {proton }} v_{\text {alpha }}}\) = 4

Question 10.
Distinguish between intrinsic semiconductors
and extrinsic semiconductors. 3
Answer:

Question 11.
(A) What is the maximum number of spectral lines emitted by a hydrogen atom when it is in the third excited state? (B) The velocity of electron in the first Bohr’s orbit of radius 0.5 A.U. is 2.25 x 106 m/s. Calculate the period of revolution of the electron in the same orbit
OR
What is a nuclear chain reaction? (3)
Answer:
(A) n = 4, number of maximum transition
= \(\frac{n}{2}\) (n – 1)
= 6

(B) Here, r = 0.5A.U.
= 0.5 × 1.5 × 10¹¹ m
[1 A.U. = 1.5 × 10¹¹ m]
v = 2.25 × 10⁶m/s
velocity of.electron in n^th orbit
\(\frac{1}{137}\) , \(\frac{c}{n}\)
Period of revolution
= \(\frac{2 \pi}{v}\)
= \(\frac{2 \pi r \times 137 \times n}{v}\)
= \(\frac{2 \times 3.14 \times 0.5 \times 1.5 \times 10^{11} \times 137 \times 1}{2.25 \times 10^{6}}\)
= 2.86 × 10⁸s
OR
The equation of fission of

These three secondary neutrons produced in the reaction may cause of fission of
three more (\({ }_{92}^{235} U\)) and give 9 neutrons, which in turn, may cause of nine more fission of (\({ }_{92}^{235} U\)) ar|d so on. Thus, a continuous ‘Nuclear Chain reaction would start. If there is no control on chain reaction then in a short time (~ 10^-6 sec.) a huge amount of energy will be released. (This is the principle of ‘Atom bomb’). If chain reaction is controlled then produced energy can be used for peaceful purposes. For examplenuclear reactor (Based on fission) generates electricity.

SECTION – C
(Section C consists one case study-based question of 5 marks.)

Question 12.
As the focal length of the lens varies from colour to colour, the magnification m = \(\)
produced by the lens also varies from colour to colour. Therefore, for little finite sized objects, the image due to different colours formed by the lens are of different sizes. The formation of images of different colours in different sizes is called lateral chromatic aberration.
Axial chromatic aberration

(A) An object is placed on the axis of a convex lens. Its image is formed 80 cm from the object. The magnification is 3. The focal length of the lens is:
(i) 15 cm
(ii) 20 cm
(iii) 40 cm
(iv) 45 cm

(B) The sun’s diameter is 1.4 x 10⁹ m and its distance from the earth is 10¹¹ m.
Determine the diameter of its image, formed by a convex lens of focal length 2 m.
(i) 0.7 cm
(ii) 1.4 cm
(iii) 2.8 cm
(iv) zero (i.e., point image)

(C) The combination of two lenses of focal lengths 20 cm and -20 cm in contact has the focal length of:
(i) 50 cm
(ii) Infinite
(iii) 10 cm
(iv) 60 cm

(D) Spherical aberration in thin lenses can be reduced by:
(i) Using monochromatic light
(ii) Increasing the size of the lens
(iii) Using a doublet combination
(iv) Using a circular annular mask over the lens.
(E) Two plano-convex lenses of equal focal lengths are arranged as shown. The ratio of combined focal length will be:

(i) 1:2:3
(ii) 1:1:1
(iii) 1:2:1
(iv) 2:1:2
Answer:
(A) (i)
Explanation:
m = \(\frac{v}{u}\)
v = 3u
u + v = 80 cm
> 4u = 80
u = 20 cm
v = 3 x 20 cm
= 60 cm
using \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\)
\(\frac{1}{f}\) = \(\frac{1}{60}-\frac{1}{(-20)}\)
f = 15 cm

Caution
Students are often confused about the sign convention. Remember that u is always negative.
(B) (Hi) 2.8 cm
Explanation: Magnification
m = \(\frac{h^{\prime}}{h}\)
= \(\frac{-v}{u}\)
or h’ \(\frac{-v}{u}\) x h
= \(\frac{-2 \times\left(1.4 \times 10^{9}\right)}{10^{11}}\)
= -2.8 cm

(C) (ii) Infinite
Explanation: Power = P₁
= \(\)
and p₂ = \(\)
= 5 D and -5D
Net power = 0
Therefore,
Focal length = \(\) = ∞

(D) (iv) Using a circular annular mask over the lens Explanation: In a thin lens, spherical aberration can be reduced by using a circular annular mask over the lens. It cuts off the marginal rays and focuses the par axial rays to a single point.

(E) (ii) 1:1:1
Explanation: The power of lens remains the same irrespective to the positioning of the lenses. So, the power and hence, their focal length in all three cases will remain the same.

Students can access the CBSE Sample Papers for Class 12 Maths with Solutions and marking scheme Term 2 Set 8 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Maths Term 2 Set 8 with Solutions

Time Allowed: 2 Hours
Maximum Marks: 40

General Instructions:

• This question paper contains three sections-A. B and C. Each part is compulsory.
• Section-A has 6 short answer type (SA1) questions of 2 marks each.
• Section-B has 4 short answer type (SA2) questions of 3 marks each.
• Section-C has 4 long answer type questions (LA) of 4 marks each.
• There is an Internal choice in some of the questions.
• Q14 is a case-based problem having 2 sub parts of 2 marks each.

Section – A
(Section – A has 6 short answer type (SA-1) questions of 2 marks each.)

Question 1.
Evaluate

Answer:
Let

= [0 – (-1 – 1)] + [(1 + 1) – 0]
= 2 + 2
= 4

Question 2.
Identify the functions P(x) and Q(x) from the linear differential equation (tan^-1 x – y) dx = (1 + x²) dy.
Or
Solve the differential equation \(\frac{d y}{d x}\) + 1 = e^x+y
Answer:
We have

Given, differential equation is
\(\frac{d y}{d x}\) + 1 = e^x+y ….(i)
Let x + y = t
On differentiating w.rt x, we get
1 + \(\frac{d y}{d x}=\frac{d t}{d x}\) ….(ii)

∴ From equation (i) and (ii),
\(\frac{d y}{d x}\) = e^x
⇒ e^-tdt = dx
On integrating both sides, we get
⇒ \(\frac{-e^{-t}}{e^{x+y}}\) = x + c
⇒ -1 = (x + c)e^x+y
⇒ (x + c)e^x+y = 0

Caution:
Do the necessary substitution. wherever needed.

Question 3.
Urn I contains 5 white and 4 blue balls. Urn II contains 4 white and 5 blue balls. One of the urn is selected at random and a ball is drawn from it. If the ball drawn is blue, what is the probability that it is drawn from Urn II? (2)
Answer:
Let E₁ and E₂ be the events of selecting Urn I
and Urn II respectively,
Also, let B be the event of drawing a blue ball
∴ P(E₁) = \(\frac{1}{2}\) and P(E₂) = \(\frac{1}{2}\)
Also, P = \(\left(\frac{B}{E_{1}}\right) \frac{4}{9}\) and P = \(\left(\frac{\mathrm{B}}{\mathrm{E}_{2}}\right) \frac{5}{9}\)

Using Bayes Theorem,
Required Probability

Question 4.
Find the intercepts made on the coordinate axes by the plane x + 2y – 2z = 9. Also, find the direction cosines of the normal to the plane. (2)
Answer:
Given Equationsof plane is:
x +2y – 2z = 9
Or
\(\frac{x}{9}+\frac{2 y}{9}-\frac{2 z}{9}\) = 1
Or
\(\frac{x}{9}+\frac{y}{\frac{9}{2}}+\frac{z}{\frac{-9}{2}}\) = 1

Thus, the intercepts made by the plane on the coordinate axes are 9, \(\frac{9}{2},-\frac{9}{2}\) respectively.
Now, direction ratios of the normal to the plane are (1, 2, -2).
Therefore, direction cosines of the normal to the plane

Question 5.
Two cards are drawn successively with replacement from a well-shuffled pack of 52 playing cards. Find the probability distribution of the number of queens. (2)
Answer:
Let X denotes the discrete random variable “the number of queens”. When two cards are drawn with replacement.
Then, X takes values 0,1, 2.
P(X = 0) = P(both cards are not queen)
= \(\frac{48}{52} \times \frac{48}{52}=\frac{144}{169}\)
P(X = 1) = P(one card is queen)
= \(\frac{4}{52} \times \frac{48}{52}+\frac{48}{52} \times \frac{4}{52}=\frac{24}{169}\)
P(X = 2) = P(both are queen cards)
= \(\frac{4}{52} \times \frac{4}{52}=\frac{1}{169}\)

So, the required probability distribution of X is

Question 6.
The dot products of a vector with the vectors î + ĵ – 3k̂, î + 3ĵ – 2k̂ and 2î + ĵ + 4k̂ are 0, 5 and 8 respectively. Find the vector. (2)
Answer:
Let the required vector be
\(\vec{a}\) = αî + βĵ + γk̂

Then, according to the question,
(αî + βĵ + γk̂). (î + 3ĵ – 2k̂) =0
⇒ α + 3β – 2γ = 5 …(ii)
and, (αî + βĵ + γk̂) ,(2î + ĵ + 4k̂) = 8
⇒ 2α + β + 4γ = 8 …(iii)
Solving equation (i), (ii) and (iii) we get
Thus, the required vector is î + 2ĵ + k̂

Section – B
(Section – B has 4 short answer type (SA-2) questions of 3 marks each.)

Question 7.
Evaluate ∫\(\frac{\sin 4 x}{\sin x}\)dx.
or
Evaluate ∫₀⁹ f(x) dx. (3)

Answer:
Let I = ∫\(\frac{\sin 4 x}{\sin x}\)dx.
= ∫\(\frac{2 \sin 2 x \cos 2 x}{\sin x}\) dx
[∵ sin 2θ = 2 sin θ cos θ]
= ∫\(\frac{2(2 \sin x \cos x) \cos 2 x}{\sin x}\) dx
= 4∫cos x cos 2x dx
= 4∫cos x(1 – 2 sin²x)dx
[∵ cos 2x = 1 – 2 sin²x]

Put sin x = t
⇒ cos x dx = dt
∴ I = 4∫(1 – 2t²) dt

Question 8.
A(-4, 7, 2),B(2, -5, 8) and C(-5, -1, 5) are three points. Find the equation of the line AB. If D is the foot of the perpendicular drawn from the point C to the Line AB, find the coordinates of D. (3)
Answer:
Equation of Line AB is

∴ Any point on this line is (λ – 4, – 2λ + 7, λ + 2).

Let it be the point D and is the foot of the perpendicular from C (-5, – 1, 5) on the line AB.
Now, direction ratios of CD = (λ, – 4 + 5, – 2λ + 7 + 1, λ + 2 – 5)
= {λ + 1, – 2λ + 8, λ – 3}

Since, CD is perpendicular to AB.
∴ (λ + 1) × 1 + (- 2λ + 8) × (- 2) + (λ – 3) × 1 = 0
⇒ 6λ – 18 = 0
⇒ λ = 3
Thus, the coordinates ofthe point Dare (3 – 4, -2 × 3 + 7, 3 + 2), i.e., (- 1, 1, 5).

Related Theory
Two lines with directions ratios a₁, b₁, c₁ and a₂, b₂, c₂ are perpendicular, if a₁a₂ + b₁b₂ + c₁c₂ = 0

Question 9.
Find the area of the region bounded by the curve y = |x – 5| and the Lines x = 0 and x = 1.
Or
Draw a rough sketch of the curve y = 1 + |x + 1|, x = -3, x = 3, y = 0 and find the area of the region bounded by them, using integration. (3)
Answer:
We have, y = |x – 5|

∴ Required area = ar(region OABC)

Given curves are y = 1 + |x + 1|, x = -3, x = 3 and y = 0

Question 10.
Using vectors show that the median of an isosceles triangle is perpendicular to the base. (3)
Answer:
Let ABC be an isosceles triangle with AB = AC.
Let the position vectors of B and C taking A as origin be \(\vec{b}\) and \(\vec{c}\).

We have,

Since, AD is median of ∆ABC
∴ D bisect the base BC
∴ Using mid-point formula,

So, angle between \(\overrightarrow{A D}\) and \(\overrightarrow{B C}\) is \(\frac{π}{2}\)
Thus, AD is perpendicular to BC.
Hence proved.

Section – C
(Section – C has 4 long answer type questions (LA) of 4 marks each.)

Question 11.
If y(x) is a solution of \(\left(\frac{2+\sin x}{1+y}\right)\) = -cos x and y(0) = 1, then find the value of y \(\frac{π}{2}\).
Answer:
Given \(\left(\frac{2+\sin x}{1+y}\right)\) = -cos x
⇒ \(\frac{d y}{1+y}=-\left(\frac{\cos x}{2+\sin x}\right)\)dx

On integrating both sides, we get cosx
∫\(\frac{1}{1+y}\)dy = -∫\(\frac{\cos x}{2+\sin x}\)dx
⇒ log(1 + y) = -log(2 + sin x) + log c
⇒ log(1 + y)(2 + sin x) = log c
⇒ (1 + y)(2 + sin x) = c

Question 12.
Two dice are thrown together and the total score is noted. The events E, F and G are “a total of 4”, “a total of 9 or more” and “a total which is divisible by 5” respectively. Calculate P(E), P(F) and P(G) and decide which pairs of events, if any, are independent.
Or
A bag contains 2 red and 3 black balls. Find the probability distribution of the number of red balls, if 4 balls are drawn out (i) with replacement from the bag. (ii) without replacement from the bag. (4)
Answer:
We have,
F = (3, 6), (4, 5), (4, 6), (5, 4), (5, 5), (5, 6), (6, 3), (6, 4), (6, 5), (6, 6)
G = (1, 4), (2, 3), (3, 2), (4,1), (4, 6), (5, 5), (6, 4)

∴ P(E) = \(\frac{3}{36}=\frac{1}{12}\)
P(F) = \(\frac{10}{36}=\frac{5}{18}\)
P(G) = \(\frac{7}{36}\)

Further, E ∩ F = Φ, E ∩ G = Φ and F ∩ G = {(4, 6), (5, 5), (6, 4)}
P(E ∩ F) = 0, P(F ∩ G) = \(\frac{3}{36}=\frac{1}{12}\)

Now, P(E) × P(F) = \(\frac{1}{12} \times \frac{5}{18}\)
= \(\frac{5}{216}\) ≠ P(E ∩ F)
⇒ E and F are not independent.

P(E) × P(G) = \(\frac{1}{12} \times \frac{7}{36}\)
= \(\frac{7}{432}\) ≠ P(E ∩ G)
⇒ E and G are not independent.

P(F) × P(G) = \(\frac{5}{18} \times \frac{7}{36}\)
= \(\frac{35}{648}\) ≠ P(F ∩ G)
⇒ E and G are not independent.
Thus, event E, F and G are not pair-wise independent.

Or

(i) Let X be the discrete random variable defined as the number of red balls, when four ball are drawn with replacement.
Then, X can take values 0,1, 2, 3, 4.
Now, ‘
P(X = 0) = P(allfour balls are black)
\(\frac{3}{5} \times \frac{3}{5} \times \frac{3}{5} \times \frac{3}{5}=\frac{81}{625}\)
P(X = 1) = P(1 red ball and 3 black balls)
= P(first ball is red and next three balls are black) + P(second ball is red and rest are black balls) + P(third ball is red and rest are black balls) + P(fourth ball is red and rest are black balls)

P(X = 2) = P(2 red balls and 2 black balls)
= P(first two are red balls, next two balls are black) + P(First, third ball are red) + P(second, fourth ball are red) + P(last two balls are red) + P(First, fourth balls are red) + P(second, third balls are red)

P(X = 3) = P(3 red balls and 1 black ball)
= P(first three balls are red) + P(second ball is black) + P(first ball is black) + P(third ball is black)

P(X = 4) = P(All four balls are red)
= \(\frac{2}{5} \times \frac{2}{5} \times \frac{2}{5} \times \frac{2}{5}=\frac{16}{625}\)

Thus, the probability distribution of X is:

(ii) Let X be the discrete random variable defined as the number of red balls, when four balls are drawn without replacement.
Then, X can take values 1, 2
P(X = 1) = P(1 red ball and 3 black balls)
= \(\frac{{ }^{2} C_{1} \times{ }^{3} C_{3}}{{ }^{5} C_{4}}=\frac{2 \times 1}{5}=\frac{2}{5}\)

P(X = 2) = P(2 red balls and 2 black balls)
= \(\frac{{ }^{2} C_{2} \times{ }^{3} C_{2}}{{ }^{5} C_{4}}=\frac{1 \times 3}{5}=\frac{3}{5}\)

Thus, the probability distribution of X is

Caution:
In part (ii). X cannot take O i.v1ue os there ore total of 3 block 1 and 2 red balls So on drawing four baILš. without replacement one of them wilt definitely be red.

Question 13.
Evaluate ∫x(logx)²dx. (4)
Answer:
Let I = ∫x(logx)²dx

Case-Based/Data-Based

Question 14.
Ranjana’s house is situated at Roop Nagar at point O. For going to Nita’s house, she first travels 10 km by bus in the East. Here at point A, a hospital is situated. From hospital, Ranjana takes an auto and goes 8 km in the North. Here at point B, a school is situated. From school, she travels by bus to reach Nita’s house at point C, which is at 30° East 12 km from point B.

Based on the above information, answer the following two questions:
(A) What is the vector distance between Ranjana’s house and school? (2)
(B) What is the vector distance from school to Nita’s house? (2)
Answer:
(A) Required distance, \(\overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{AB}}\)
[Using triangle law of vector addition]
= 10î + 8ĵ

(B) Required distance = \(\overrightarrow{\mathrm{BC}}\)

12 cos 30° î + 12 sin 30°ĵ = 12 × \(\frac{\sqrt{3}}{2}\)î + 12 × \(\frac{1}{2}\)ĵ
= 6√3 î + 6ĵ

Students can access the CBSE Sample Papers for Class 12 Maths with Solutions and marking scheme Term 2 Set 7 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Maths Term 2 Set 7 with Solutions

Time Allowed: 2 Hours
Maximum Marks: 40

General Instructions:

• This question paper contains three sections-A. B and C. Each part is compulsory.
• Section-A has 6 short answer type (SA1) questions of 2 marks each.
• Section-B has 4 short answer type (SA2) questions of 3 marks each.
• Section-C has 4 long answer type questions (LA) of 4 marks each.
• There is an Internal choice in some of the questions.
• Q14 is a case-based problem having 2 sub parts of 2 marks each.

Section – A
(Section – A has 6 short answer type (SA-1) questions of 2 marks each.)

Question 1.
The direction cosines of a line segment AB are \(\frac{-2}{\sqrt{17}}, \frac{3}{\sqrt{17}}, \frac{-2}{\sqrt{17}}\) If AB = \(\sqrt{17}\) and the coordinates of A are (3, -6, 10), then find coordinates of B. (2)
Answer:
Since, direction cosines of AB are \(\frac{-2}{\sqrt{17}}, \frac{3}{\sqrt{17}}, \frac{-2}{\sqrt{17}}\)
So, direction ratios of the Line AB are < -2, 3, -2>.
DR of the line AB = Coordinates of B – coordinates A
Let the coordinates of B be (x, y, z).
So, direction ratios of AB = <x – 3, y + 6, z – 10>
⇒ <-2, 3, -2> = <x – 3, y + 6, z – 10>
⇒ x – 3 = -2; y + 6 = 3; z – 10 = -2
⇒ x = 1; y = -3; z = 8
Thus, coordinates of B are (1, -3, 8).

Question 2.
A die is rolled. If the outcome is an even number, what is the probability that it is a prime number?
OR
A player has 7 cards in hand of which 5 are red and among these five, 2 are kings. A card is drawn at random. Find the probability that it is a king, if being known that it is red. (2)
Answer:
Sample space, S = { 1, 2, 3, 4, 5, 6}
Let A be the event of “getting an even number”, and B be the event of “getting a prime number”,
n (A) = {2, 4, 6}, n(B) = {2}, n (B ∩ A) = {2}
P(A) = \(\frac{3}{6}=\frac{1}{2}\)
And, P(B ∩ A) = \(\frac{1}{6}\)
[∵ 2 is the only even prime number from 1 to 6]
Now,
Required probability = P(B/A)
\(\frac{P(B \cap A)}{P(A)}=\frac{1 / 6}{1 / 2}=\frac{1}{3}\)

OR
Let A be the event of “card being red”, and B be the event of “card being king”.
P(A) = \(\frac{5}{7}\) And P(B ∩ A) = \(\frac{2}{7}\)
Now, required probability = P(B/A)
= \(\frac{P(B \cap A)}{P(A)}\)
= \(\frac{2 / 7}{5 / 7}=\frac{2}{5}\)

Question 3.
Find the vector and the cartesian equations of a line passing through the points (3, -2,-5) and (3, – 2, 6). (2)
Answer:
The direction ratios of the line passing through the points (3, -2, – 5) and (3, -2, 6) are (3 – 3, – 2 + 2, 6 + 5) i.e., (0, 0, 11).
Also, the required line passes through the point (3,-2,-5).
So, the cartesian equation of the required line is

And, its vector equation is
\(\vec{r}\) = (3î – 2ĵ – 5k̂) + λ(11k̂)

Question 4.
Evaluate ∫₀²| 1 – x | dx. (2)
Answer:

Question 5.
A die marked 1,2,3 in red and 4,5,6 in green is tossed. Let A be the event “the number is even” and B be the event “the number is red”. Are A and B independent? Give reasons for your answer. (2)
Answer:
We have, A = Event that the number is even.
∴ A = {2, 4, 6}
P(A) = \(\frac{3}{6}=\frac{1}{2}\)

Also, B = Event that the number is red.
∴ B = {1, 2, 3}
P(B) = \(\frac{3}{6}=\frac{1}{2}\)

And, A ∩ B = event that number is even and red
⇒ A ∩ B = {2}
P(A ∩ B) = \(\frac{1}{6}\)

∵P(A) × P(B) = \(\frac{1}{2} \times \frac{1}{2}=\frac{1}{4}\) ≠ P(A n B)
Hence, the two events A and B are not independent.

Question 6.
Sketch the region bounded by curves y = x² and y = |x|. (2)
Answer:

Hence, y = x² is an equation of parabola which open upwards, towards positive side of y-axis, with its vertex at the origin.

Section – B
(Section – B has 4 short answer type (SA-2) questions of 3 marks each.)

Question 7.
Find the area of the region bounded by the curve y² = 4x, the lines x = 1 and x = 4 and the x-axis in the first quadrant.
OR
Find the area of the region bounded by the curve y = |x + 3|, the lines x = -6 and x = 0. (3)
Answer:
y² = 4x represents a parabola whose vertex is at the origin, axis of symmetry is x-axis, focus on the positive direction of x-axis and it opens to the right

= \(\frac{4}{3}\)[(4)^3/2 – (1)^3/2]
= \(\frac{4}{3}\)(8 – 1)
= \(\frac{28}{3}\) sq.units
OR
We have, y = |x + 3|

Question 8.
Find the area of a parallelogram whose adjacent sides are determined by vectors \(\vec{a}\) = î – ĵ + 3k̂ and b = 2î – 7ĵ + k̂ respectively. (3)
Answer:
Let ABCD be the parallelogram with \(\overrightarrow{\mathrm{AB}}=\vec{a}\) = î – ĵ + 3k̂ and \(\overrightarrow{\mathrm{BC}}=\vec{b}\) = 2î – 7ĵ + k̂.

∴ Area of Parallelogram ABCD = \(|\overrightarrow{A B} \times \overrightarrow{B C}|\)
Now,
\(\overrightarrow{A B} \times \overrightarrow{B C}=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
1 & -1 & 3 \\
2 & -7 & 1
\end{array}\right|\)
= î(-1 + 21) – ĵ(1 – 6) + k̂(-7 + 2)
= 20î + 5ĵ – 5k̂

∴ \(|\overrightarrow{A B} \times \overrightarrow{B C}|=\sqrt{(20)^{2}+(5)^{2}+(-5)^{2}}\)
= \(\sqrt{450}\)
= 15√2

Question 9.
Evaluate ∫₀² x\(\sqrt{2-x}\)dx.
OR
Evaluate ∫\(\frac{\sin x}{1+\sin x}\) dx. (3)
Answer:
Let I = ∫₀² x\(\sqrt{2-x}\)dx.
Put 2 – x = t
⇒ -dx = dt
For x= 0, t= 2 – 0 = 2
For x = 2, t= 2 – 2 = 0

OR
Let I = ∫\(\frac{\sin x}{1+\sin x}\) dx
= ∫\(\frac{\sin x(1-\sin x)}{1-\sin ^{2} x}\)dx
= ∫\(\frac{\sin x-\sin ^{2} x}{\cos ^{2} x}\) dx
= ∫(tan x sec x – tan² x)dx
= ∫[tan x sec x – (sec² x – 1)] dx
= ∫(tan x sec x – sec² x + 1)dx
= sec x – tan x + x + C

Question 10.
Let \(\vec{a}, \vec{b}, \vec{c}\) be the three vectors such that | \(\vec{a}\) | = 3, | \(\vec{b}\) | = 4 and | \(\vec{c}\) | = 5 and each one of them being perpendicular to the sum of the other two. Find | \(\vec{a}+\vec{b}+\vec{c}\) |. (3)
Answer:
It is given that each vector is perpendicular to the sum of other two vectors.

Section – C
(Section – C has 4 long answer type questions (LA) of 4 marks each.)

Question 11.
Four defective bulbs are accidentally mixed with six good ones. If it is not possible to just look at a bulb and tell whether or not it is defective, then find the probability distribution of the number of defective bulbs, if four bulbs are drawn (without replacement) at random from this lot. (4)
Answer:
Let X be the discrete random variable defined as the number of defective bulbs.
Then, X can take values 0,1, 2, 3, 4.
Now, P(X = 0) = P (all the bulbs are good ones)

P(X = 1) = P(1 defective and three good ones)

P(X = 2) = P(2 defective and two good ones)

P(X = 3) = P(3 defective and one good one)

P(X = 4)= P (All the four defective bulbs)

Thus, the probability distribution of X is

Question 12.
Solve the differential equation:
\(\frac{d y}{d x}=\frac{x+y+7}{2 x+2 y+3}\)
OR
Solve the differential equation: du
sin x \(\frac{d y}{d x}\) + y cos x = x sin x
Answer:
Given differential equation is:
\(\frac{d y}{d x}=\frac{x+y+7}{2 x+2 y+3}\) …(i)

Put (x + y + 7) = z
⇒ 1 + \(\frac{d y}{d x}=\frac{d z}{d x}\)
Substituting these values in (i), we get

where, C₁ = 9C
or, 6y – 3x – 11 log (3x + 3y + 10) = C₂, where
C₂ = C₁ – 42.

which is the required solution of the given differential equation.
OR
The given differential equation can be rewritten dy
as \(\frac{d y}{d x}\) + cotx.y = x dx

It is a linear differential equation in the form
\(\frac{d y}{d x}\) + P(x).y = Q(x) dx
where, P(x) = cot x and Q(x) = x

Integrating Factor (I.F.) = e^∫Pdx
= e^{∫cot x dx}
= e^{logsin x}
= sin x

Thus, the solution to the given differential equation is:
y.(I.F.) = ∫Q(x).(I.F.)dx
⇒ y.sin x = ∫x.sin x dx
⇒ y.sin x = x∫sin x dx – ∫[\(\frac{d y}{d x}\)(x)∫sin xdx]dx
⇒ y. sin x = -x cos x + sin x +C
⇒ y. sin x + x cos x = sin x + C
which is the required solution of the given differential equation.

Question 13.
Evaluate ∫cos{2 cot^-1\(\sqrt{\frac{1-x}{1+x}}\)}dx. (4)
Answer:
Let I = ∫cos{2 cot^-1\(\sqrt{\frac{1-x}{1+x}}\)}dx.
Put x = cos t
⇒ dx = -sin t dt
I = -∫cos{2 cot^-1\(\sqrt{\frac{1-\cos t}{1+\cos t}}\)}sin tdt

CASE-BASED/DATA-BASED

Question 14.
Rohan and Rohit are two friends, and they are going to a road trip on their motorcycles. Their motorcycles are running at the speed more than the allowed speed on the road along the lines \(\vec{r}\) = λ(î + 2ĵ – k̂) and \(\vec{r}\) = 3î + 3ĵ + μ(2î + ĵ + k̂) respectively.

Based on the above information, answer the following two questions:
(A) Find the direction ratios of the line along which (i) motorcycle A is running (ii) motorcycle B is running. (2)
(B) Find the shortest distance between the two lines. (2)
Answer:
(A) (i) Direction ratios of the line along which the motorcycle A is running are <1, 2, – 1>.
(ii) Direction ratios of the line along which the motorcycle B is running are <2, 2, 1>.

(B) On comparing the given equations with equations \(\vec{r}=\overrightarrow{a_{1}}+\lambda \overrightarrow{b_{1}}\) and \(\vec{r}=\overrightarrow{a_{2}}+\lambda \overrightarrow{b_{2}}\)
we have
\(\overrightarrow{a_{1}}=\overrightarrow{0}\)
b₂ = î + 2î – k̂
\(\overrightarrow{a_{2}}\) = 3î + 3î
b₂ = 2i + ĵ + k̂

Students can access the CBSE Sample Papers for Class 12 Maths with Solutions and marking scheme Term 2 Set 6 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Maths Term 2 Set 6 with Solutions

Time Allowed: 2 Hours
Maximum Marks: 40

General Instructions:

• This question paper contains three sections-A. B and C. Each part is compulsory.
• Section-A has 6 short answer type (SA1) questions of 2 marks each.
• Section-B has 4 short answer type (SA2) questions of 3 marks each.
• Section-C has 4 long answer type questions (LA) of 4 marks each.
• There is an Internal choice in some of the questions.
• Q14 is a case-based problem having 2 sub parts of 2 marks each.

Section – A
(Section – A has 6 short answer type (SA-1) questions of 2 marks each.)

Question 1.
Evaluate ∫sin^-1\(\left(\sqrt{\frac{1-\cos 2 x}{2}}\right)\)dx. (2)
Answer:
Let I = ∫sin^-1\(\left(\sqrt{\frac{1-\cos 2 x}{2}}\right)\)dx

Question 2.
Check whether the differential equation (4x + 6y + 5)dx – (3x + 2y + 4) dy = 0 is homogeneous or not.
OR
Find the solution of \(\frac{d y}{d x}\) = 2^y-x. (2)
Answer:
We have.
(4x + 6y + 5)dx – (3x + 2y + 4)dy = 0

The given differential equation is not homogeneous.
OR

⇒ -2^y + 2^-x = c log 2
⇒ 2^-x – 2^y = k where k = c Log 2
Hence, the required solution is 2^-x – 2^y = k.

Question 3.
Find a unit vector in the direction of \(\overrightarrow{\mathrm{PQ}}\), where P and Q have coordinates (5, 0, 8) and (3, 3, 2) respectively. (2)
Answer:
We have, position vector of P = \(\overrightarrow{\mathrm{OP}}\) = 5î + 8k̂
and the position vector of Q = \(\overrightarrow{\mathrm{OQ}}\) = 3î + 3ĵ + 2k̂
\(\overrightarrow{\mathrm{PQ}}=\overrightarrow{\mathrm{OQ}}-\overrightarrow{\mathrm{OP}}\)
= (3î + 3ĵ + 2k̂) – (5î + 8k̂)
= -2î + 3ĵ – 6k̂

Now, unit vector in the direction of vector \(\overrightarrow{\mathrm{OP}}\)
= \(\frac{\overrightarrow{\mathrm{PQ}}}{\overrightarrow{\mid \mathrm{PQ}} \mid}\)
= \(\frac{1}{7}\)(-2î + 3ĵ – 6k̂)

Question 4.
Let \(\vec{a}\) and \(\vec{b}\) be two vectors such that |\(\vec{a}\)| = 3 and |\(\vec{a}\)| = \(\frac{\sqrt{2}}{3}\) Show that will be a unit vector, if the angle between them is \(\frac{\sqrt{2}}{3}\). (2)
Answer:
Let θ be the angle between the given two vectors \(\vec{a}\) and \(\vec{b}\).

Question 5.
Two dice are thrown. Find the probability that the numbers shown have a sum of 8, if it is known that the second die always exhibits 4. (2)
Answer:
Let A be the event of “occurrence of 4 always on second die” and B be the event of “occurrence of such numbers on both the dice whose sum is 8”.
∴ A = {(1,4), (2, 4), (3, 4), (4, 4), (5, 4), (6,4)}
And, B = {(2, 6), (3, 5), (4,4), (5, 3), (6, 2)}
∴P(A) = \(\frac{6}{36}=\frac{1}{6}\)
And P(B ∩ A) = \(\frac{1}{36}\)
Now,
Required Probability = P(B/A)
= \(\frac{P(B \cap A)}{P(A)}\)
= \(\frac{1 / 36}{1 / 6}=\frac{1}{6}\)

Question 6.
Two dice are rolled simultaneously. Find whether the following two events, are independent or not:
E = {(x, y): x + y = 11}; F = {(x, y): x ≠ 5} (2)
Answer:
We have,
E = {(x, y) : x + y = 11
∴ E = {(5, 6), (6, 5)}
Also, F = {(x, y) : x ≠ 5}
∴ F = {(1, 1), (1, 2), (1, 3),(1, 5), (1, 6), (2,1), (2, 2), (2, 4), (2, 5), (2, 6), (3, 1), (3, 3), (3, 4), (3, 5), (3, 6), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)} – {(5, 1), (5, 2), (5, 3) (5, 4), (5,5), (5, 6)}
n (E) = 2. n (F) = 30, n (E ∩ F) = 1

And,
P(E) = \(\frac{2}{36}=\frac{1}{18}\)
P(F) = \(\frac{30}{36}=\frac{5}{6}\)
and P(E ∩ F) = \(\frac{1}{36}\)

= P(E) × P(F)= \(\frac{1}{18} \times \frac{5}{6}=\frac{5}{108}\)
Since. P(E) × P(E) ≠ P(E ∩ F)
So, the two events E and F are not independent.

Section – B
(Section – B has 4 short answer type (SA-2) questions of 3 marks each.)

Question 7.
If ∫_a^bx³ dx = 0 and ∫_a^b x² dx = \(\frac{2}{3}\) Values of a and b.
OR
∫₁^ex³ logx dx (3)
Answer:

⇒ b⁴ – a⁴ = 0 and b³ – a³ = 2
Now, b⁴ – a⁴ = 0
⇒ (b² – a²)(b² + a²) = 0
⇒ (b – a) (b + a) (b² + a²) = 0
⇒ (b + a) (b² + a²) = 0 [∵ b ≠ a]
⇒ (b + a) = 0 [∵ b² + a² = 0]
⇒ a = -b
Substituting these values in b³ – a³ = 2, we get
a = -1,b = 1
OR
Let I = ∫₁^ex³ logx dx
= ∫₁^ex³ 1. logx dx
= log x∫1.dx – ∫[\(\frac{d}{d x}\)(log x).∫1dx]dx
(By Integration b parts formula)

= (e.log e – e) – (1 log 1 – 1)
= (e – e) – (0 – 1)
= 1

Question 8.
Find the cartesian equation of a line passing through (1, 2, 3) and parallel to the line \(\frac{x+2}{-1}=\frac{y+3}{7}=\frac{2 z-6}{3}\). (3)
Answer:
Given equation of line can be rewritten as
\(\frac{x+2}{-1}=\frac{y+3}{7}=\frac{2 z-6}{3}\)

∴ Its direction ratios: (-1, 7, \(\frac{3}{2}\))

Since, required line is parallel to the given line, so their direction ratios will be proportional.
∴ Direction ratios of required line = (-λ, 7λ, \(\frac{3}{2}\)λ)

Also the required line passes through the point (1, 2, 3).
∴ Cartesian equation of the required line is:

Question 9.
Solve the differential equation:
sin^-1\(\left(\frac{d y}{d x}\right)\) = x + y
OR
Solve the differential equation: du
tan x\(\frac{d y}{d x}\) + 2y = secx (3)
Answer:
Given differential equation can be rewritten as:
\(\frac{d y}{d x}\) = sin (x + y) …(i)
Put (x + y) = t

Differentiating w.r.t. x, we get
1 + \(\frac{d y}{d}=\frac{d t}{d}\)

Substituting these values in eq. (i), we get
\(\frac{d t}{d x}\) – 1 = sin t

⇒ \(\frac{d t}{d x}\) = 1 + sin t
or
\(\frac{d x}{d t}=\frac{1}{1+\sin t}\)
= \(\frac{1-\sin t}{\cos ^{2} t}\)
= (sec²t – tan t sec t)
⇒ dx = (sec²t -tan t sec t) dt

Integrating both sides, we get
∫dx = ∫ (sec² t – tan t sec t)dt
⇒ x = tan t – sec t + C
or, x = tan(x + y) – sec(x + y) + C
which is the required solution of the given differential equation.
OR
The given differential equation can be rewritten as:
\(\frac{d y}{d x}\) + 2cotx.y = cose cx

It is a linear differential equation in the form
\(\frac{d y}{d x}\) + P(x).y = Q(x) dx
where, P(x) = 2 cot x and Q(x) = cosec x

Integrating Factor (I.F.)
= e^∫P(x).dx
= e^{∫cot x.dx}
= e^2logsinx
= e^logsin2x
= sin² x

Thus, the solution to the given differential equation is:
y – (I.F.) = ∫Q(x).(I.F.)dx
⇒ y.sin²x= ∫ cosec x.sin2x dx
⇒ y .sin²x = ∫ sinx dx
⇒ y sin² x = – cos x + C
or y sin²x + cos x = C,
which is the required solution of the given differential equation.

Question 10.
Find the distance between the parallel planes \(\vec{r}\).(2î – 3ĵ + 6k̂) = 5 and \(\vec{r}\).(6î – 9ĵ + 18k̂) + 20 = 0. (3)
Answer:
Let \(\overrightarrow{r_{1}}\) be the position of any point on the plane \(\vec{r}\).(2î – 3ĵ + 6k̂) = 5
Then, \(\overrightarrow{r_{1}}\).(2î – 3ĵ + 6k̂) = 5
or \(\overrightarrow{r_{1}}\).(6î – 9ĵ + 18k̂) = 15

Now, the length of the perpendicular from \(\overrightarrow{r_{1}}\) to the other plane \(\vec{r}\).(6î – 9ĵ + 18k̂) + 20 = 0

Thus, the distance between the given parallel planes is \(\frac{5}{3}\) units.

Section – C
(Section – C has 4 long answer type questions (LA) of 4 marks each.)

Question 11.
Evaluate ∫₀^asin^-1\(\sqrt{\frac{x}{a+x}}\)dx. (4)
Answer:
Let I = ∫₀^asin^-1\(\sqrt{\frac{x}{a+x}}\)dx.
Put x = a tan² t
⇒ dx = 2a tan t sec² t dt

Question 12.
Using integration, find the area of the region bounded by a triangle whose vertices are A(2, 0), B(4, 5), C(6, 3).
OR
Sketch the bounded region and find the area bounded by the curve x = √y, the line x – y + 2 = 0 and the y-axis. (4)
Answer:
Given points are A(2, 0), B(4, 5) and C(6, 3).
We know, equation of a line with two given points, namely, (x₁, y₁) and (x₂, y₂) is given as:
y – y₁ = \(\left(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\right)\)(x – x₁)

Equation of side AB of triangle ABC is:
y – 0 = \(\frac{5-0}{4-2}\)(x – 2)
⇒ 2y = 5x – 10

Equation of side BC of triangle ABC is:
y – 5 = \(\frac{3-5}{6-4}\)(x – 4)
⇒ y = 9 – x

Equation of side AC of triangle ABC is:
y – 0 = \(\frac{3-0}{6-2}\)(x – 2)
⇒ 4y = 3x – 6

Now, required area of ∆ABC = ar(region APBA) + ar(region BPQB) – ar(region AQCA)

OR
x = √y, or x² = y is an equation of a parabola which open upwards with its vertex at origin.
To find the point of intersection of x² = y and x – y + 2 = 0, put y = x + 2 in x² = y.
∴ x² = x + 2
⇒ x² – x – 2 = 0
⇒ (x – 2) (x + 1) = 0
⇒ x = 2, -1
For x = 2, y = 4
For x = -1, y = 1
∴ Points of intersection are (2, 4) and (-1, 1). Also, the area common to the curve x² = y, line y = x + 2 and the y-axis is shown shaded in the figure.

Question 13.
A bag contains 5 red marbles and 3 black marbles. Three marbles are drawn one by one without replacement. What is the probability that at least one of the three marbles drawn be black, if the first marble is red? (4)
Answer:
Here, R = red marble and B = black marble For the condition that at least one of the three marbles drawn be black, if first marble is red, then following are the possibilities:
(A) Second marble is black and third is red (E₁)
(B) Second marble is black and third is also black (E₂)
(C) Second marble is red and third is black (E₃)

Case-Based/Data-Based

Question 14.
Three slogans on chart paper are to be placed on a school bulletin board at the points A, B and C displaying A, B and C The coordinates
of these points are A(2. 5, 1),B(3, – 3, 2)and C(- 2, 4, 7) respectiveLy. Let \(\vec{a}, \vec{b}\) and \(\vec{c}\) be the position vectors of A, B, and C respectively

Based on the above information, answer the following two questions:
(A) Find the unit vector in the direction of \(\vec{b} \times \vec{c}\) (2)
Answer:
Here,
\(\vec{b} \times \vec{c}=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
3 & -3 & 2 \\
-2 & 4 & 7
\end{array}\right|\)
= (- 21 – 8)î – (21 + 4)ĵ + (12 – 6)k̂
= – 29î – 25ĵ + 6k̂
So, unit vector in the direction of \(\vec{b} \times \vec{c}\)

(B) Find the area of ∆ABC. (2)
Answer:
Area of ∆ABC = \(\frac{1}{2}|\overrightarrow{A B} \times \overrightarrow{A C}|\)
Now, \(\overrightarrow{A B}\)=(3 – 2)î + (-3 – 5)ĵ + (2 – 1)k̂
= î – 8ĵ + k̂
and \(\overrightarrow{A C}\) =(-2 – 2)î + (4 – 5) ĵ+(7 – 1)k̂
= -4î – ĵ + 6k̂

Students can access the CBSE Sample Papers for Class 12 Maths with Solutions and marking scheme Term 2 Set 9 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Maths Term 2 Set 9 with Solutions

Time Allowed: 2 Hours
Maximum Marks: 40

General Instructions:

• This question paper contains three sections-A. B and C. Each part is compulsory.
• Section-A has 6 short answer type (SA1) questions of 2 marks each.
• Section-B has 4 short answer type (SA2) questions of 3 marks each.
• Section-C has 4 long answer type questions (LA) of 4 marks each.
• There is an Internal choice in some of the questions.
• Q14 is a case-based problem having 2 sub parts of 2 marks each.

Section – A
(Section – A has 6 short answer type (SA-1) questions of 2 marks each.)

Question 1.
Evaluate (2)

Answer:

Question 2.
Show that the solution of differential equation x dy – y dx = 0 represents a straight line.
OR
Write the general solution of the differential equation cos x sin y dx + sin x cos y dy = 0. (2)
Answer:
We have,
x dy – y dx = 0
or x dy = y dx
⇒ \(\frac{d y}{y}\) = \(\int \frac{d x}{x}\)
Integrating both sides, we get
⇒ \(\int \frac{d y}{y}\) = \(\int \frac{d x}{x}\)
⇒ log y = log x + log C,
where log C is constant of integration.
⇒ log y = log Cx
⇒ y = Cx
which is an equation of a straight line passing through the origin.
Hence proved.
OR
We have,
cos x sin y dx + sin x cos y dy = 0
or, cos x sin y dx = – sin x cos y dy
⇒ \(\frac{\cos x}{\sin x}\)dx = \(\frac{\cos y}{\sin y}\)dy
Integrating both sides, we get
\(\int \frac{\cos x}{\sin x}\) dx = –\(\int \frac{\cos y}{\sin y}\)dy
⇒ log |sin x| = – log |sin y| + log c [∵ \(\int \frac{f^{\prime}(x)}{f(x)}\)dx = log|f(x)| + C]
⇒ log (sin x. sin y) = log C
or, sin x sin y = C

Question 3.
For any two vectors \(\vec{a}\) and \(\vec{b}\), show that |\(\vec{a}\) + \(\vec{b}\)| ≤ |\(\vec{a}\)| + |\(\vec{b}\)|. (2)
Answer:
We have,

Question 4.
If |\(\vec{a}\)| = 10, |\(\vec{b}\)| = 2 and \(\vec{a} \cdot \vec{b}\) = 12, then find the value of \(|\vec{a} \times \vec{b}|\). (2)
Answer:

Question 5.
A man is known to speak truth 3 out of 4 times. He throws a die and reports that it is six. Find the probability it is actually a six. (2)
Answer:
Let E be the event that the man reports that six has occurred on throwing a die.
Also, let E₁ be the event “six has occurred” and E₂ be the event “six does not occurred”.
∴ P(E₁) = \(\frac{1}{6}\) and P(E₂) = \(\frac{5}{6}\)
Also,
P\(\left(\frac{E}{E_{1}}\right)\) = Probability that the man does not speaks truth = \(\frac{1}{4}\)
Now, using Bayes’ theorem,
Required probability = P\(\left(\frac{E_{1}}{E}\right)\)

Question 6.
In answering a question on a multiple choice test, a student either knows the answer or guesses. Let \(\frac{3}{4}\) be the probability that he knows the answer and \(\frac{1}{4}\) be the probability that he guesses. Assuming that a student who guesses at the answer will be correct with probability \(\frac{1}{4}\). What is the probability that the student knows the answer given that he answered it correctly? (2)
Answer:
Let E₁ be the event “the student knows the answer” and E₂ be the event “guesses the answer”.
Also, let A be the event “answer is correct”

Caution:
P\(\left(\frac{\mathrm{A}}{E_{1}}\right)\) = 1, as be knows the answer so his answer wili definitely be correct.

SECTION – B
(Section – B has 4 short answer type (SA-2) questions of 3 marks each.)

Question 7.
Evaluate \(\int \frac{x}{(x+2)(3-2 x)}\) dx.
OR
Evaluate (3)

Answer:

OR

Put x = a cos² t + b sin² t
⇒ dx = a(2 cos t) (- sin t) dt + b(2 sin t cos t) dt
= 2(b – a) sin t cos t dt
Also, x – a = (b – a) sin² t
and b – x = (b – a) cos² t
when x = b, t = \(\frac{\pi}{2}\); and when x = a, t = 0

Question 8.
Find the equation of the plane passing through the points (2, 1, – 3), (- 3, – 2, 1) and (2, 4, -1). (3)
Answer:
We know that the equation of the plane passing through three points (x,₁, y₁, z₁), (x₂, y₂, z₂) and (x₃, y₃, z₃) is given by:
\(\left|\begin{array}{ccc}
x-x_{1} & y-y_{1} & z-z_{1} \\
x_{2}-x_{1} & y_{2}-y_{1} & z_{2}-z_{1} \\
x_{3}-x_{1} & y_{3}-y_{1} & z_{3}-z_{1}
\end{array}\right|\) = 0 …….. (i)
Here,
(x₁, y₁, z₁) = (2, 1, – 3)
(x₂, y₂, z₂) = (- 3, – 2, 1)
and (x₃, y₃, z₃) = (2, 4, – 1)
Substituting these values in (i), we get

(x- 2) (- 6 – 12) – (y – 1) (- 10 – 0) + (z + 3) (- 15 + 0) = 0
⇒ 18 (x – 2) + 10(y – 1) – 15(z + 3) = 0
⇒ 18x + 10y – 15z – 19 = 0
Thus, the required equation of the p[ane is:
⇒ 18x + 10y – 15z – 19 = 0

Question 9.
Sketch the bounded region and find the area of the region bounded by the curve y = |x|, the x-axis and the ordinates x = -1 and x = 1.
OR
Find the area of the region bounded by the circle x² + y² = 4, the line x = √3y and the x-axis in the first quadrant. (3)
Answer:
Required area = ar(∆OAB) + ar(∆OCD)


OR
x² + y² = 4 represents a circle with centre at the origin and radius √4 i.e., 2 units; and the line x = √3y passes through the origin.

The line intersects the circle at point B (√3, 1) in the first quadrant.
∴ Required area = ar (∆OAB) + ar(region CAB)

Question 10.
If AC and BD are the diagonals of a quadrilateral ABCD, then show that its vector area is given by \(\frac{1}{2}(\overrightarrow{A C} \times \overrightarrow{B D})\). (3)
Answer:
Vector area of quadrilateral ABCD = Vector area of ∆ABC + Vector area of ∆ACD

Using triangle law of vector addition in ∆ABD]
Hence proved.

Section – C
(Section – C has 4 Long answer type questions (LA) of 4 marks each.)

Question 11.
Evaluate \(\int x \sin ^{-1}\left\{\frac{1}{2} \sqrt{\frac{2 a-x}{a}}\right\}\) (4)
Answer:

Question 12.
Consider an experiment of throwing two dice. Let E denote the event “odd number on the first die”, F denote the event” odd number on the second die” and G denote the event “sum of numbers on two dice is odd”. Show that E, F and G are pairwise independent events, but not mutually independent. (4)
Answer:
We have,
E = {(1, 1), (1. 2), (1, 3), (1, 4), (1, 5) (1, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (5,1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)}
F = [(1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1), (1, 3), (2, 3), (3, 3), (4, 3), (5, 3), (6, 3), (1, 5), (2, 5), (3, 5), (4, 5), (5, 5), (6, 5)}
and G = {(1, 2), (1, 4), (1, 6), (2, 1), (2, 3), (2, 5), (3, 2), (3, 4), (3, 6), (4,1), (4, 3), (4, 5), (5, 2), (5, 4), (5, 6), (6, 1), (6, 3), (6, 5)}
Further, E ∩ F = {(1,1), (1, 3), (1, 5), (3, 1), (3, 3), (3, 5), (5,1), (5, 3), (5, 5)
E ∩G = [(1, 2), (1, 4), (1, 6), (3, 2), (3, 4), (3, 6), (5, 2), (5, 4), (5, 6)]
And F ∩ G = {(2, 1), (2, 3), (2, 5), (4, 1), (4, 3), (4, 5), (6, 1), (6, 3), (6, 5)}

⇒ E and G are independent.
Thus, E, F and G are pairwise independent events.
Hence proved.
Now,
E ∩ F ∩ G = Φ
P(E ∩ F ∩ G) = O
Also,
P(E) × P(F) × P(G) = \(\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}\)
= \(\frac{1}{8}\) ≠ P(E ri Fri G)
Thus, E, F and G are not mutuatlly independent events.
Hence proved.

Question 13.
Show that the lines \(\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}\) and \(\frac{x-2}{3}=\frac{y-3}{4}=\frac{z-4}{5}\) are coplanar. Also,find the point of intersection. (4)
Answer:
Given lines are
\(\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}\)
and \(\frac{x-2}{3}=\frac{y-3}{4}=\frac{z-4}{5}\)
If two lines are coplanar, then
\(\left|\begin{array}{ccc}
x_{2}-x_{1} & y_{2}-y_{1} & z_{2}-z_{1} \\
a_{1} & b_{1} & c_{1} \\
a_{2} & b_{2} & c_{2}
\end{array}\right|\) = 0
Here,
(x₁, b₁, c₁) = (1, 2, 3)
(a₁, b₁, c₁) = (2, 3, 4)
(x₂, y₂, z₂) = (2, 3,4)
(a₂, b₂, c₂) = (3, 4, 5)

= 1(15 – 16) – 1(10 – 12) + 1(8 – 9)
= – 1 + 2 – 1 = 0
Hence, the given lines are coplanar.
Hence proved.
Now, any general point on the line
\(\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}\) = λ (say) is (2λ + 1, 3λ + 2, 4λ + 3)
Also, any general point on the line
\(\frac{x-2}{3}=\frac{y-3}{4}=\frac{z-4}{5}\) = µ(say) is (3µ + 2, 4µ + 3, 5µ + 4).
Since, the given two lines are coplanar, so they must be intersecting.
∴ 2λ + 1 = 3µ + 2;
3λ + 2 = 4µ + 3;
4λ + 3 = 5µ + 4
On solving these three equations, we get λ = – 1, µ = – 1.
Hence, the point of intersection of the given two lines is (- 1, – 1, – 1).

Related Theory:
Intersecting Lines are always coplanar.

CASE-BASED/DATA-BASED

Question 14.
The rate at which a body cools is proportional to the difference between the temperature of the body and that of the surrounding air. A body in air at 25°C will get cool from 100°C to 75°C in one minute.

Based on the above information, answer the following two questions:
(A) Find its temperature at the end of 3 minutes.
(B) After how many minutes, its temperature will be 58°C?
OR
The population of Swastik’s village increases continuously at the rate proportional to the number of its inhabitants present at any time. The population of the village was 20,000 in 1999 and 25,000 in the year 2004.

Based on the above information, answer the following two questions:
(A) What was the population of the Swastik’s village in the year 2009? (2)
(B) What will be the population of the village after 15 years from the year 1999? (2)
Answer:
Let the temperature of the body be T°C.
Then, according to the question, dT ,
\(\frac{d T}{d t}\) = k(T – 25)
⇒ \(\frac{d T}{\mathrm{~T}-25}\) = k dt
Integrating both sides, we get
log (T – 25) = kt + log C
⇒ log \(\frac{C}{\mathrm{~T}-25}\) = kt
or T – 25 = Ce^kt ………….. (i)
when t = 0, T = 100
Putting these values in (i), we get
100 – 25 = Ce⁰
⇒ C = 75
∴ T – 25 = 75e^kt …………….. (ii)
When t = 1, T = 75
Thus, from (ii), we get
T – 25 = \(\left(\frac{2}{3}\right)^{2}\)
or T = 25 + 75\(\left(\frac{2}{3}\right)^{t}\) ……… (iii)

(A) Putting t = 3, in eq. (iii), we get
T = 25 + 75\(\left(\frac{2}{3}\right)^{3}\)
= 25 + 75 × \(\frac{8}{27}\)
= 47.22°C

(B) Putting T = 58°C, in eq. (iii), we get
58 = 25 + 75\(\left(\frac{2}{3}\right)^{t}\)
⇒ \(\left(\frac{2}{3}\right)^{t}=\frac{33}{75}\)
or \(\left(\frac{2}{3}\right)^{t}=\frac{11}{25}\)
⇒ t = 2 minutes
OR
Let y be the populations of the Swastik’s village at any time t.
Then, according to the question, dy
\(\frac{d y}{d t}\)
where, k is an arbitrary constant.
⇒ \(\frac{d y}{y}\) = kdt
Integrating both sides, we get
log y = kt + C …(i)
Let the year 1999 be the initial year.
So, at t = 0, y = 20,000
putting these values in (i), we get
log 20000 = k(0) + C
⇒ C = log 20,000
∴ (i) becomes
log y = kt + log 20,000 …(ii)
So, in 2004, t = 5 and y = 25,000.
Putting these values in (ii), we get
log 25,000 = 5k + log 20,000
⇒ k = \(\frac{1}{5}\)log\(\left(\frac{5}{4}\right)\)
Hence, by (ii), we have

Students can access the CBSE Sample Papers for Class 12 Physics with Solutions and marking scheme Term 2 Set 11 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Physics Standard Term 2 Set 11 for Practice

Time Allowed: 2 Hours
Maximum Marks: 40

General Instructions:

• There are 12 questions in all. All questions are compulsory.
• This question paper has three sections: Section A, Section B and Section C.
• Section A contains three questions of two marks each, Section B contains eight questions of three marks each, Section C contains one case study-based question of five marks.
• There is no overall choice. However, an internal choice has been provided in one question of two marks and two questions of three marks. You have to attempt only one of the chokes in such questions.
• You may use log tables if necessary but use of calculator is not allowed.

SECTION – A
(Section A contains 3 questions of 2 marks each.)

Question 1.
Define the following terms:
(A) V-l characteristic of a forward biased diode.
(B) Reverse breakdown voltage. (2)

Question 2.
Which of the following is more stable and why (\({ }_{7}^{3} X\)) and (\({ }_{3}^{4} Y\))?
OR
How the width of depletion layer changes in p-n junction diode when the junction is forward biased and reverse biased? (2)

Question 3.
(A) Distinguish between an astronomical telescope and a terrestrial telescope?
(B) Find the magnification at least distance of distinct vision of a simple microscope having focal length 5 cm? (2)

SECTION – B
(Section B consists of 8 questions of 3 marks each.)

Question 4.
(A) In Young’s double slit experiment, what is the shape of interference fringes?
(B) The following table gives data about the single slit diffraction experiment:

Find the ratio of the widths of the slits used in the two cases. Would the ratio of the half angular widths of the first secondary maxima, in the two cases, be also equal to q? (3)

Question 5.
A deuteron and an alpha particle are accelerated with the same accelerating potential.
Which one of the two has:
(i) greater value of de-Broglie wavelength, associated with it, and
(ii) less kinetic energy ? Explain. (3)
OR
(A) Work function of aluminium is 4.2 eV. If two photons, each of energy 2.5 eV, are incident on its surface, will the emission of electrons take place? Justify your answer.
(B) Work function of caesium and platinum are 2.14 eV and 5.65 eV, respectively.
Which one of the two metals has higher threshold wavelength? Justify. (3)

Question 6.
How does a microwave oven work on the principle of EM waves? (3)

Question 7.
A 12.5 eV electron beam is used to bombard gaseous hydrogen at room temperature. Up to which energy level the hydrogen atoms would be excited? Calculate the wavelength of the first member of Lyman and first member of Balmer series. (3)

Question 8.
Find out the ratio of fringe width in Young’s double slit experiment when wavelength becomes four times. (3)

Question 9.
You are given three lenes L( L₂, L₃ each of focal length 15 cm. An object is kept at 20 cm in front of L₁, as shown. The final real image is formed at the focus T of L3. Find the separations between L₁ L₂ and L₃.

Plot a graph to show variation of the angle of deviation as a function of angle of incidence for light passing through a prism. Derive an expression for refractive index of the prism in terms of angle of minimum deviation and angle of prism. (3)

Question 10.
Draw a labelled diagram of experimental setup of Rutherford’s alpha particle scattering experiment and write two important inferences drawn from the experiment. (3)

Question 11.
Define wavefront. Use Huygens’ principle to verify the laws of refraction. (3)

SECTION – C
(Section C consists one case study-based question of 5 marks.)

Question 12.
As the world is advancing towards sustainable energy, solar cells play a crucial role for attaining that goal for the world. Solar panels used in industries, offices and homes are nothing but layers of conductors made of silicon to convert solar energy into electrical energy. As radiation strike the electron in the solar cell, the electron energy to jump from valence band to conduction band. This causes a motion of charge which generates electric current. Due to spontaneous reaction of the conversion, we can generate electrical energy during the daytime and store it in batteries which can be used in dark. The efficiency of semiconductors makes them a reliant source.

Based on the above facts, answer the following questions:

(A) What should be the band gap of a material for it to be used as a solar cell?
(i) 1-1.8 eV
(ii) 0.5-1.3 eV
(iii) 1-2 eV
(iv) None of the above

(B) A solar cell is a:
(i) p-n junction
(ii) n-type semiconductor
(iii) p-type semiconductor
(iv) Intrinsic semiconductor

(C) What is the difference between photodiode and solar cell?
(i) No external bias in photodiode
(ii) No external bias in solar cell
(iii) Larger surface area in photodiode
(iv) No difference

(D) Which of the following should not be the characteristic of a solar cell material?
(i) High absorption
(ii) High conductivity
(iii) High energy band
(iv) High availability

(E) Which of the following cannot be used as solar cells?
(i) Si
(ii) GaAs
(iii) CdS
(iv) PbS (5)

Students can access the CBSE Sample Papers for Class 12 Physics with Solutions and marking scheme Term 2 Set 12 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Physics Standard Term 2 Set 11 for Practice

Time Allowed: 2 Hours
Maximum Marks: 40

General Instructions:

• There are 12 questions in all. All questions are compulsory.
• This question paper has three sections: Section A, Section B and Section C.
• Section A contains three questions of two marks each, Section B contains eight questions of three marks each, Section C contains one case study-based question of five marks.
• There is no overall choice. However, an internal choice has been provided in one question of two marks and two questions of three marks. You have to attempt only one of the chokes in such questions.
• You may use log tables if necessary but use of calculator is not allowed.

SECTION – A
(Section A contains 3 questions of 2 marks each.)

Question 1.
What kind of fringes will be observed if we replace monochromatic light by white light?
OR
In a single-slit diffraction experiment, the width of the slit is made double the original width. How does this affect the size and intensity of the central diffraction band? (2)

Question 2.
How does the process of conduction takes place in n-type semiconductors and p-type semiconductors? (2)

Question 3.
How would the ionization energy change when electron in hydrogen atom is replaced by a particle of mass 100 times that of the electron but having the same charge? (2)

SECTION – B
(Section B consists of 8 questions of 3 marks each.)

Question 4.
A proton and an alpha particle are accelerated through the same potential? Which one of the two has:
(A) greater value of de-Broglie wavelength associated with it and
(B) less kinetic energy.
Give reasons to justify your answer. (3)

Question 5.
A convex lens made up of glass of refractive index 1.5 is dipped, in turn, in:
(A) a medium of refractive index 1.65,
(B) a medium of refractive index 1.33.
(i) Will it behave as a converging or a diverging lens in the two cases?
(ii) How will its focal length change in the two media? (3)

Question 6.
(A) Draw a labelled ray diagram showing the formation of a final image by a compound microscope at least distance of distinct vision.
(B) The total magnification produced by a compound microscope is 20. The magnification produced by the eye piece is 5. The microscope is focused on a certain object. The distance between the objective and eye-piece is observed to be 14 cm. If least distance of distinct vision is 20 cm, calculate the focal length of the objective and the eye-piece. (3)

Question 7.
A 12.3 eV electron beam is used to bombard gaseous hydrogen at room temperature. Up to which energy level the hydrogen atoms would be excited? Calculate the wavelength of the second member of Lyman series and second member of Balmer series. (3)

Question 8.
Induced electric field due to changing magnetic flux are more readily observed than induced magnetic field due to changing electric field. Why?
OR
State the laws of photoelectric emission. (3)

Question 9.
Why are Si and GaAs are preferred for making solar cells? Briefly explain working principle of a solar cell with the help of a necessary circuit diagram. (3)

Question 10.
What is a rectifier? Draw a labelled diagram
of Full-wave rectifier and its input and out¬put waveform. (3)

Question 11.
A composite prism ABC is made of two identical right-angled prisms ABD and ADC made of different materials of refractive indices √3 andm respectively. A ray of light is incident on face AB of the prism at 60° and the emergent ray grazes along the face AC. Find the value of n.

Consider two coherent sources S1 and S2 producing monochromatic waves to produce interference pattern. Let the displacement of the wave produced by S1 be given by Y1 = a cos ωt and the displacement by S2 be Y2 = a cos (ωt + Φ). Find out the expression for the amplitude of the resultant displacement at a point and show that the intensity at
that point will be I = 4a2 cos2 \(\frac{\phi}{2}\). Hence
establish the conditions for constructive and destructive interference. (3)

SECTION – C
(Section C consists one case study-based question of 5 marks.)

Question 12.
There wilt be a gain in the overall binding energy when we move from the heavy nuclei region to the middle region of the plot, hence release of energy when a heavy nucleus (A = 240) breaks into two roughly equal fragments, energy can be released. This process is called nuclear fission. Similarly, there will be gain in

(A) The binding energy per nucleon for the parent nucleus is E₁ and that for the daughter nuclei is E₂. Then A nucleus of mass M + Am is at rest and decays into two daughter nuclei of equal mass M/2 each. Speed of light is c.
(i) E1 = 2E2
(ii) E2 = 2E1
(iii) E1 > E2
(iv) E2 > E1
the overall binding energy, when we move from lighter nuclei to heavier nuclei, hence release of energy. When two or more lighter nuclei fuse together to form a heavy nucleus energy can be released. This process is called Nuclear Fusion. This is the energy source of sun.

(B) Solar energy is mainly caused due to:
(i) burning of hydrogen in the oxygen
(ii) fission of uranium present in the sun
(iii) fusion of protons during synthesis of heavier elements
(iv) gravitational contraction

(C) 200 MeV of energy may be obtained per fission of ²³⁵U. A reactor is generating
1000 KW of power. The rate of nuclear fission in the reactor is:
(i) 1000
(ii) 2 × 10⁸
(iii) 3.125 × 10¹⁶
(iv) 931
(D) Which type of reaction produces the most harmful radiation?
(i) Fusion reaction
(ii) Chemical reaction
(iii) Fission reaction
(iv) Photo-Chemical reaction

(E) The average energy released per fission of \(\begin{gathered}
235 \\
92
\end{gathered}\)U is: ,
(i) 200 eV 00
(ii) 200 MeV
(iii) 400 meV
(Vi) 200 GeV (5)

Students can access the CBSE Sample Papers for Class 12 Maths with Solutions and marking scheme Term 2 Set 11 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Maths Term 2 Set 11 for Practice

Time Allowed: 2 Hours
Maximum Marks: 40

General Instructions:

• This question paper contains three sections-A. B and C. Each part is compulsory.
• Section-A has 6 short answer type (SA1) questions of 2 marks each.
• Section-B has 4 short answer type (SA2) questions of 3 marks each.
• Section-C has 4 long answer type questions (LA) of 4 marks each.
• There is an Internal choice in some of the questions.
• Q14 is a case-based problem having 2 sub parts of 2 marks each.

Section – A
(Section – A has 6 short answer type (SA-1) questions of 2 marks each.)

Question 1.

Question 2.
Solve the differential equation
\(\frac{d y}{d x}\) + 2x = e^3x
OR
Find the particular solution of the differential equation cot\(\left(\frac{d y}{d x}\right)\) = a (- 1 ≤ a ≤ 1), given that

Question 3.
If \(\vec{b} \times \vec{c}=\vec{c} \times \vec{a} \neq \overrightarrow{0}\), then show that \(\vec{a}+\vec{b}=k \vec{c}\) = kc, where k is a scalar. (2)

Question 4.
Show that \(|\vec{a}| \vec{b}+|\vec{b}| \vec{a}\) is perpendicular \(|\vec{a}| \vec{b}-|\vec{b}| \vec{a}\), for any two non-zero vectors \(\vec{a}\) and \(\vec{b}\) (2)

Question 5.
Let X represents the difference between the number of heads and the number of tails obtained when a coin is tossed 6 times. What are the possible values of X? (2)

Question 6.
Find the probability of the occurrence of a number greater than 2 in a throw of a die1 if it is know that only even numbers can occur. (2)

SECTION – B
(Section – B has 4 short answer type (SA-2) questions of 3 marks each.)

Question 7.
Find the sine of the angle between the vectors
\(\vec{a}\) = 3î + ĵ + 2k̂ and \(\vec{b}\) = 2î – 2ĵ + 4k̂
OR
Using vectors, show that the angle in a semi-circle is a right angle. (3)

Question 8.
Evaluate \(\int \frac{2 x+1}{\sqrt{x^{2}+4 x+3}}\)dx. (3)

Question 9.
The lines \(\frac{x-2}{1}=\frac{y-3}{1}=\frac{z-4}{-k}\) and \(\frac{x-1}{k}=\frac{y-4}{2}=\frac{z-5}{1}\) are coplanar. Find k.
OR
Find the cartesian equation of a plane that passes through the point (3, – 6, 4) and normal to the line joining the points (2, – 1, 5) and (3, 4, – 1). (3)

Question 10.
Find the particular solution of the differential equation (1 + x²)\(\frac{d y}{d x}\) + 2xy = \(\frac{1}{1+x^{2}}\), given that y = 0 when x = 1. (3)

Section – C
(Section – C has 4 long answer type questions (LA) of 4 marks each.)

Question 11.
Prove that the lines x = ay + b = cz + d and x = αy + β = γz + δ are coplanar, if (γ – c) (αβ – bα) – (α – a) (cδ – dγ) = 0. (4)

Question 12.
Let X denotes the number of colleges where you will apply after your result and P(X = x) denotes your probability of getting admission in x number of colleges. It is given that

where k is a positive constant. Find the value of k. Also, find the probability that you will get admission in (A) exactly one college, (B) at most 2 colleges, (C) at least 2 colleges.
OR
Three persons A, B, C throw a die in succession till one gets a six and wins the game. Find their respective probabilities of winning, if A begins the game. (4)

Question 13.
Evaluate

CASE-BASED/DATA-BASED

Question 14.
Three friends, Anmol, Sanjay, and Sammer live in a same society. Location of their houses in the society is represented by the points A(-l, 0), B(l, 3) and C(3, 2) as shown in the figure.

Based on the above information, answer the following two questions:
(A) Find the equation of the lines AB, BC and CA. (2)
(B) Find the area of the region of ABCDA. (2)