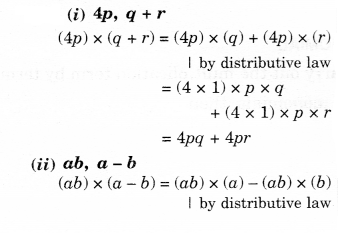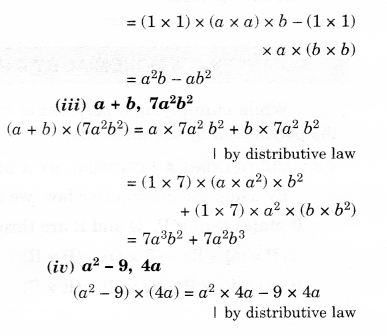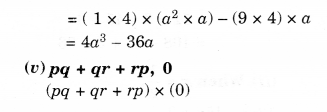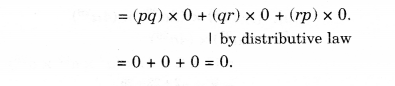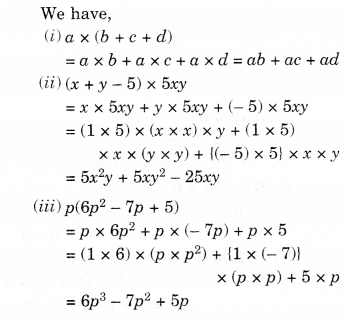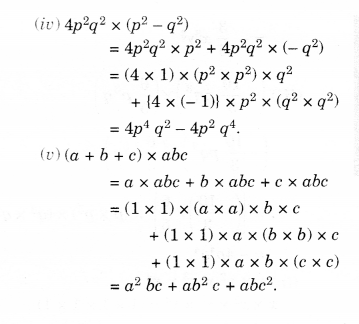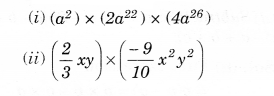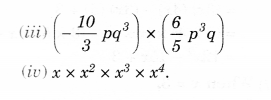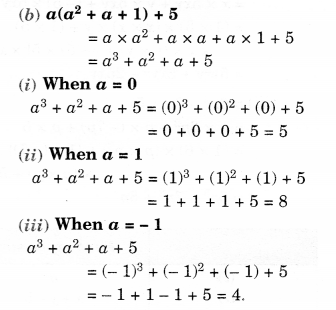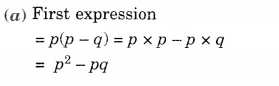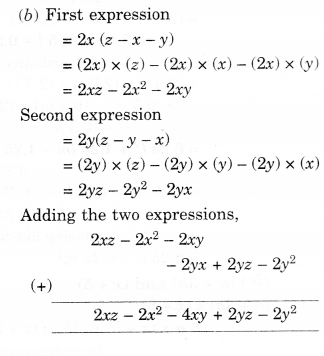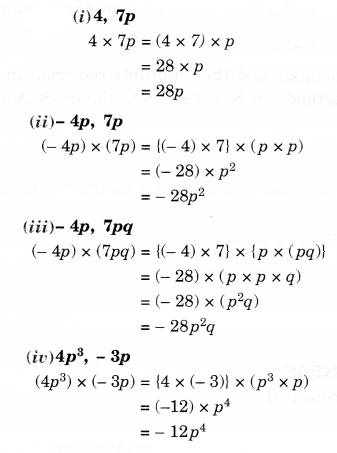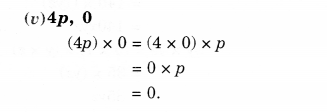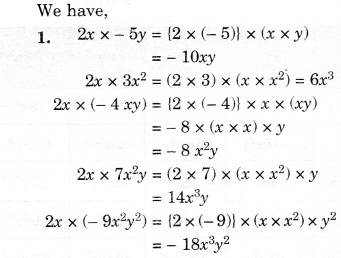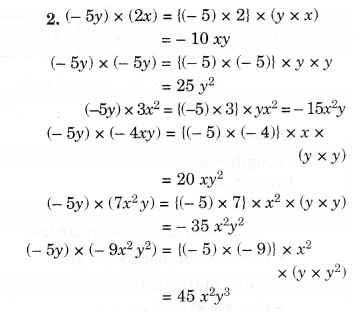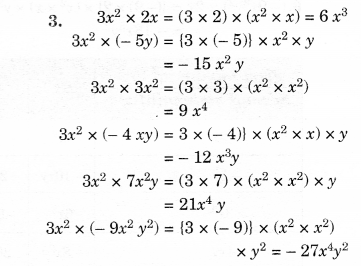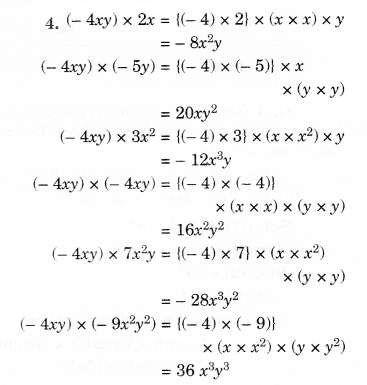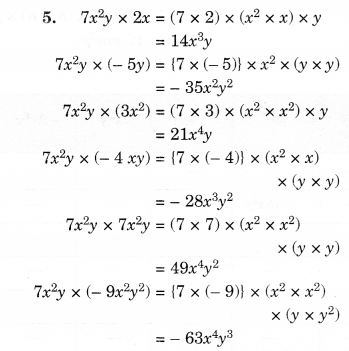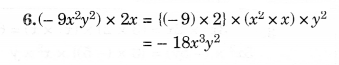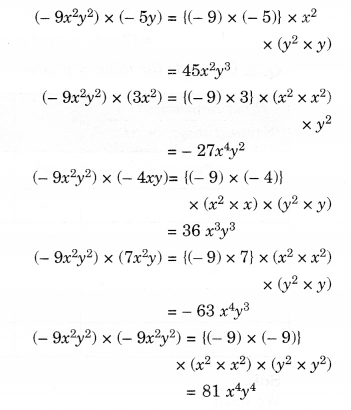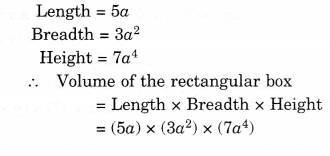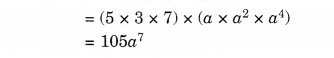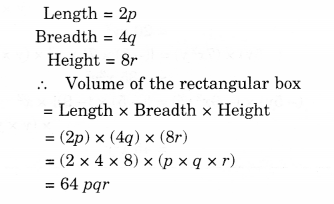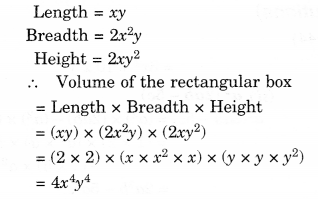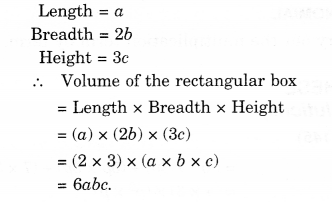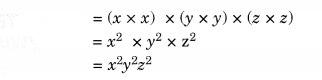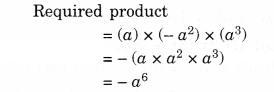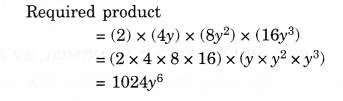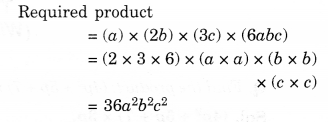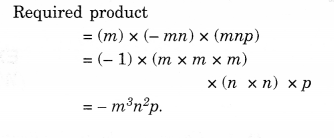NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.4 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.4.
- Algebraic Expressions and Identities Class 8 Ex 9.1
- Algebraic Expressions and Identities Class 8 Ex 9.2
- Algebraic Expressions and Identities Class 8 Ex 9.3
- Algebraic Expressions and Identities Class 8 Ex 9.5
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 8 |
| Subject | Maths |
| Chapter | Chapter 9 |
| Chapter Name | Algebraic Expressions and Identities |
| Exercise | Ex 9.4 |
| Number of Questions Solved | 3 |
| Category | NCERT Solutions |
NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.4
Question 1.
Multiply the binomials:
(i) (2x + 5) and (4x – 3)
(ii) (y – 8) and (3y – 4)
(iii) (2.5l – 0.5 m) and (2.5l + 0.5m)
(iv) (a + 3b) and (x + 5)
(v) \((2pq+3{ q }^{ 2 })\quad and\quad (3pq-2{ q }^{ 2 })\)
(vi) \((\frac { 3 }{ 4 } { a }^{ 2 }+3{ b }^{ 2 })\quad and\quad 4({ a }^{ 2 }-\frac { 2 }{ 3 } { b }^{ 2 })\)
Solution.
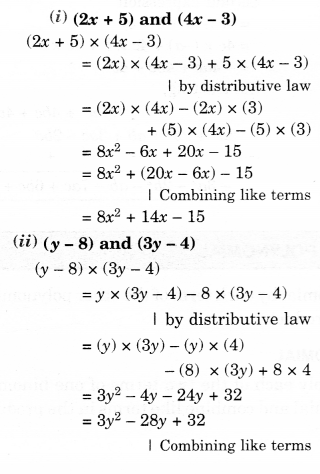

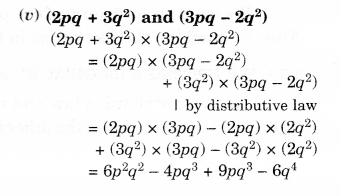

Question 2.
Find the product:
(i) (5 – 2x) (3 + x)
(ii) (x + 7y) (7x —y)
(iii) \(({ a }^{ 2 }+b)(a+{ b }^{ 2 })\)
(iv) \(({ p }^{ 2 }-{ q }^{ 2 })(2p+q)\)
Solution.
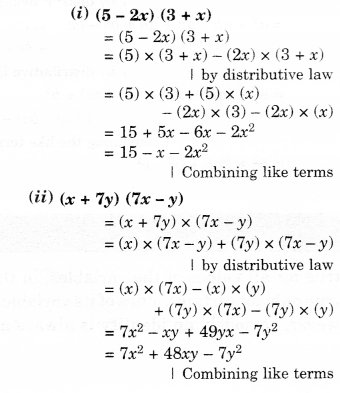

Question 3.
Simplify.
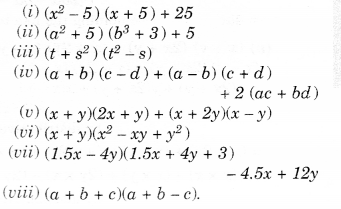
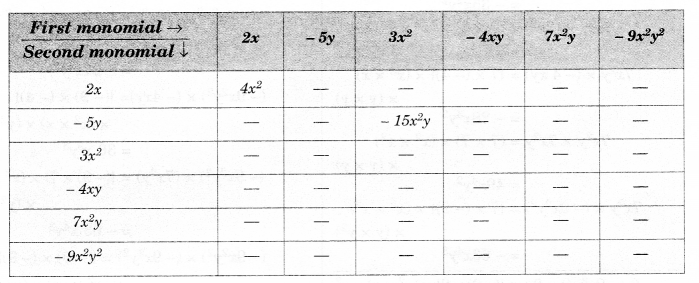
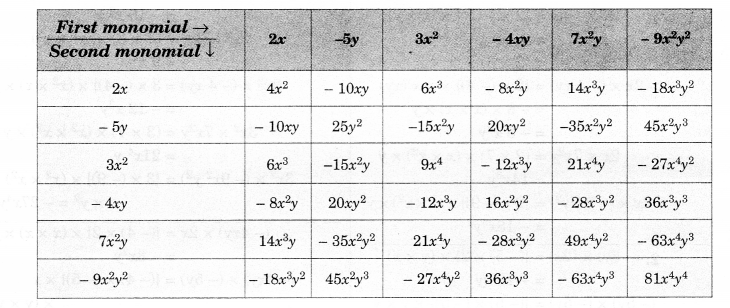
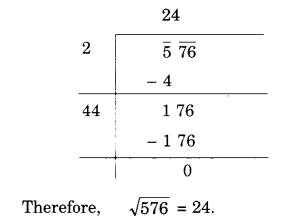
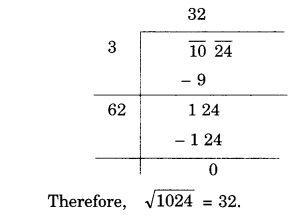
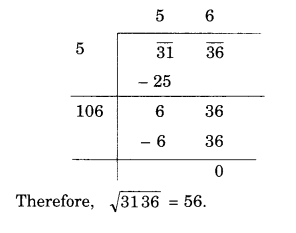
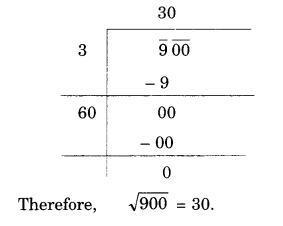
Solution.
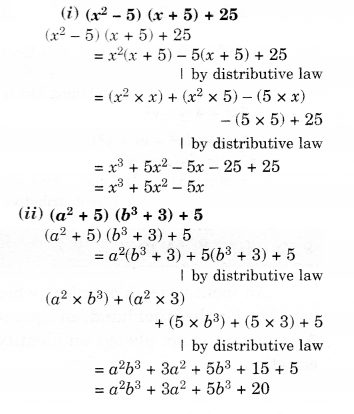

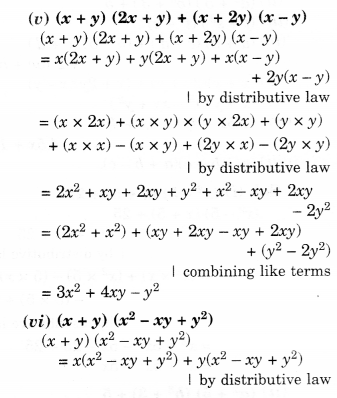
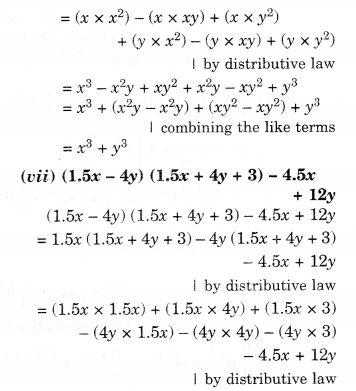

We hope the NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.4 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.4, drop a comment below and we will get back to you at the earliest.