Tag: RD Sharma Class 10 Maths Solutions

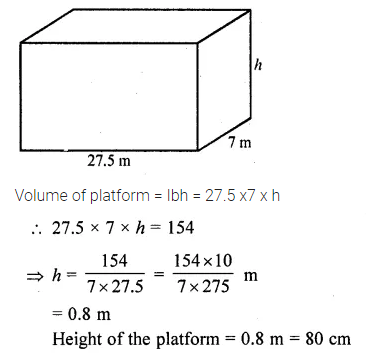
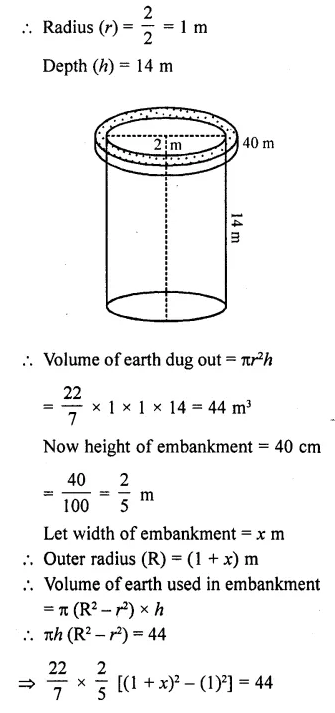
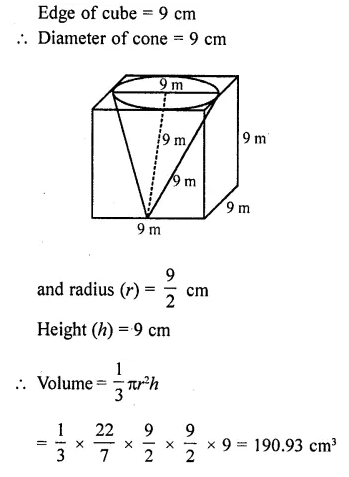
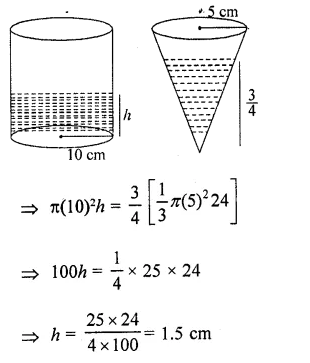
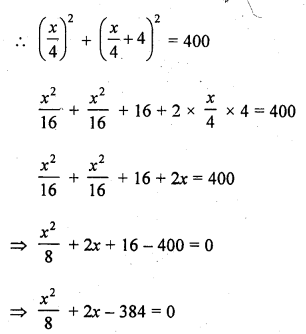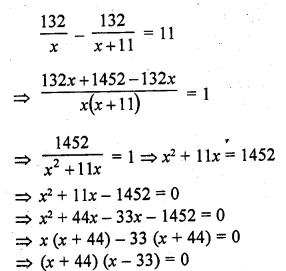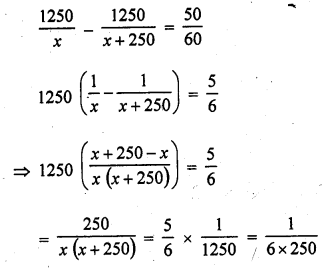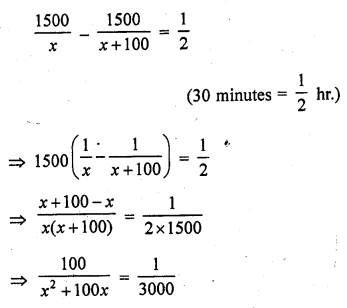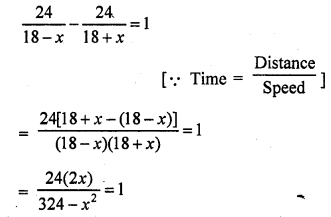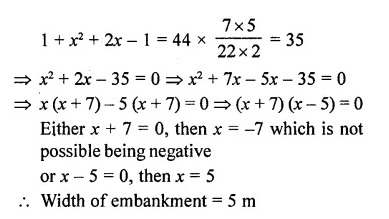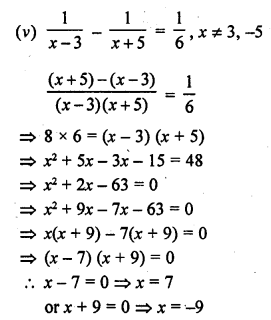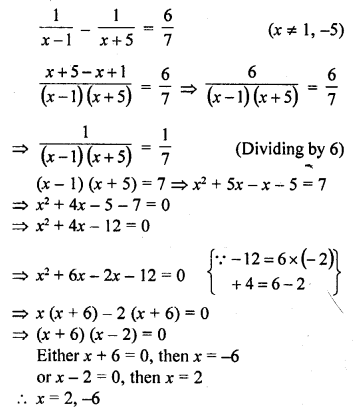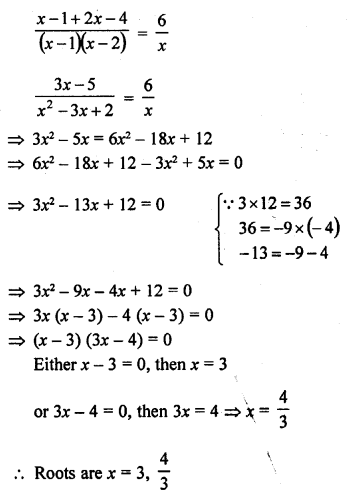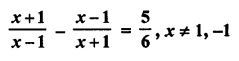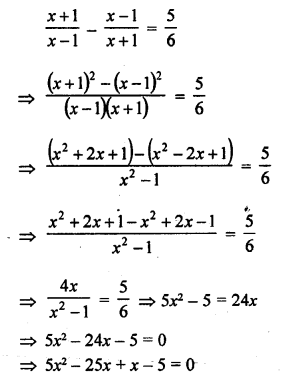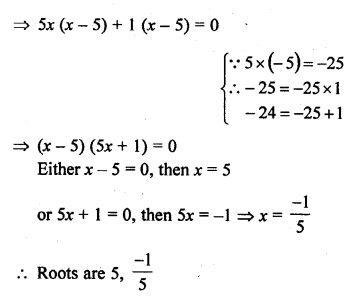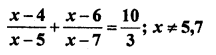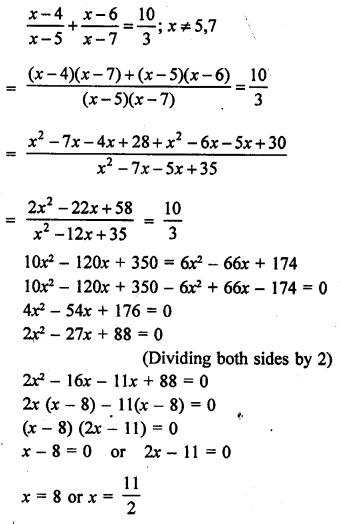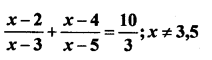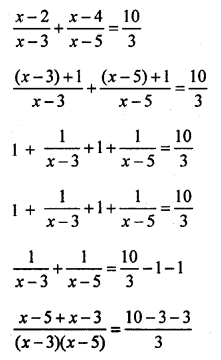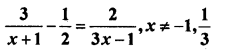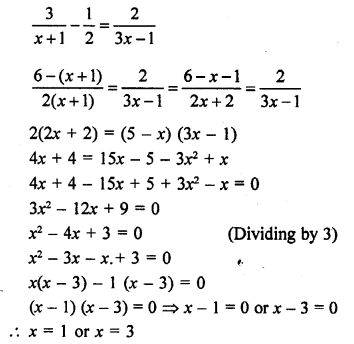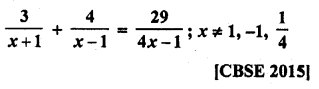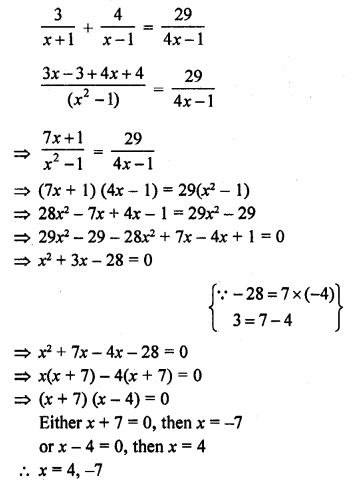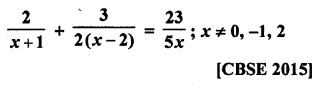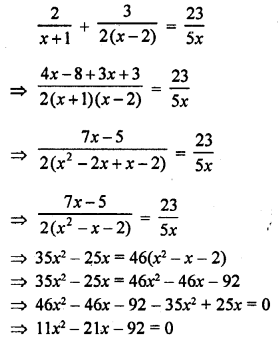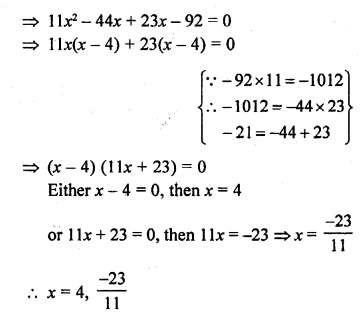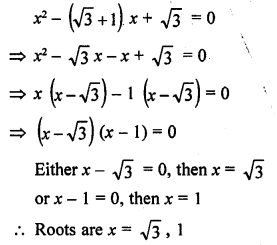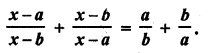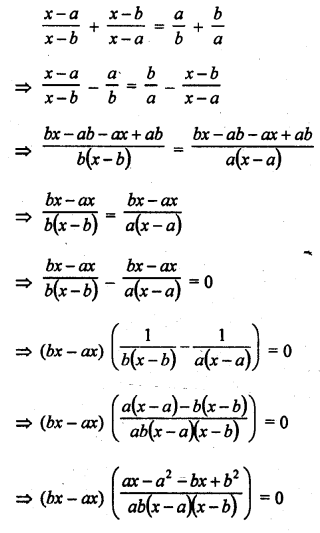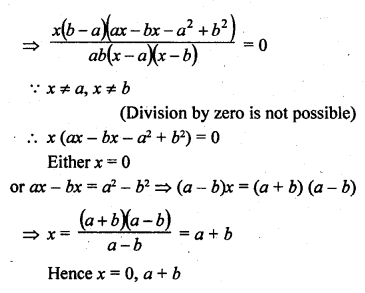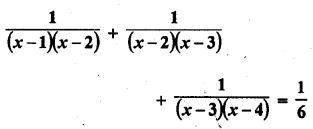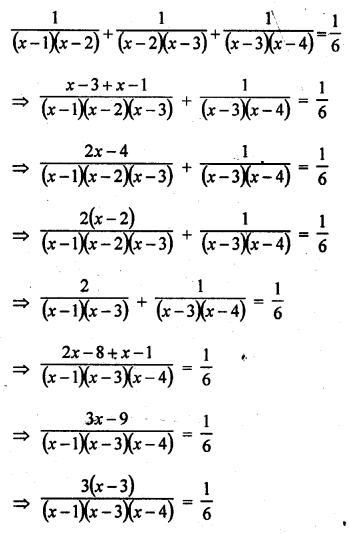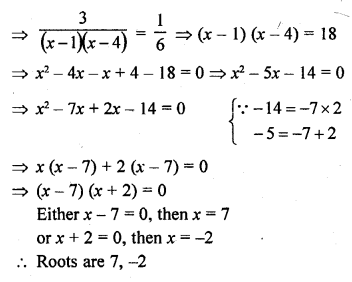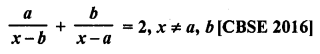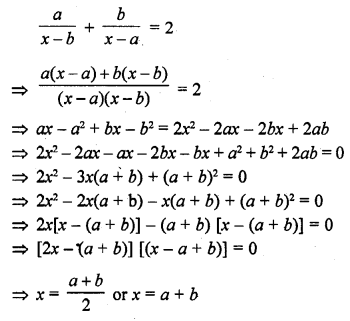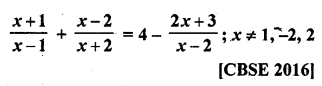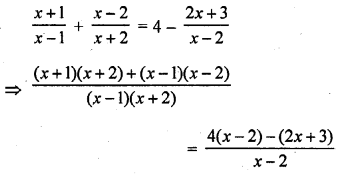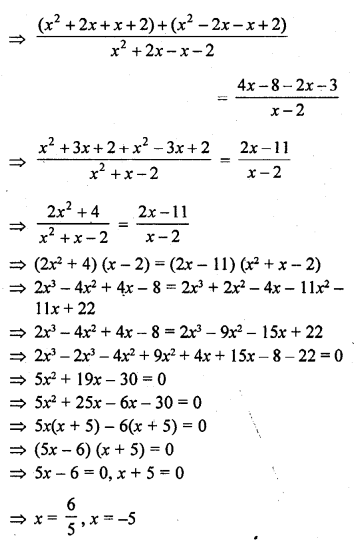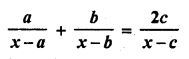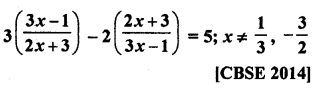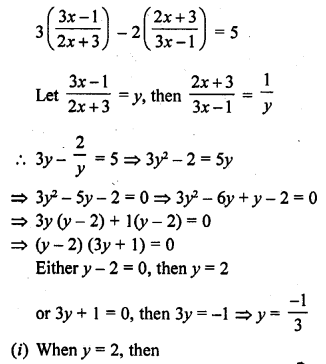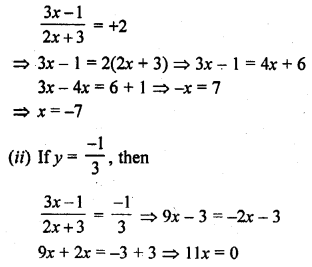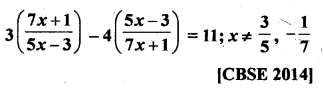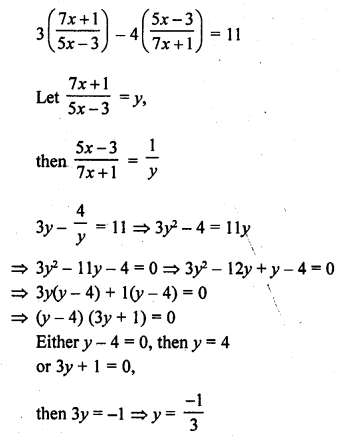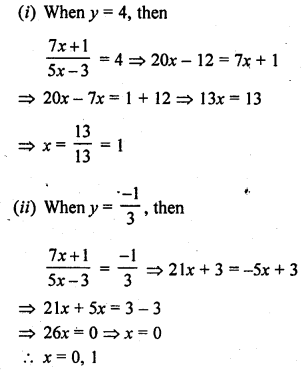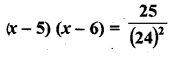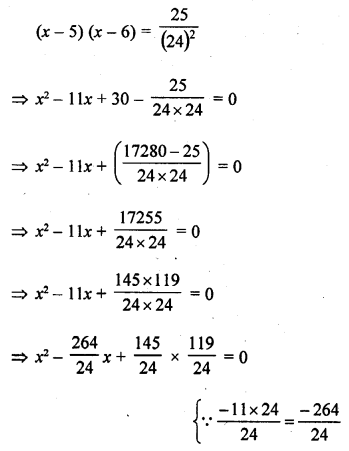RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12

Other Exercises

• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.1
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.2
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.4
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.5
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.6
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.7
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS

 

Question 1.
A takes 10 days less than the time taken by B to finish a piece of work. If both A and B together can finish the work in 12 days, find the time taken by B to finish the work. .
Solution:
Let B can do the work in = x days
A will do the same work in = (x – 10) days
A and B both can finish the work in = 12 days
According to the condition,

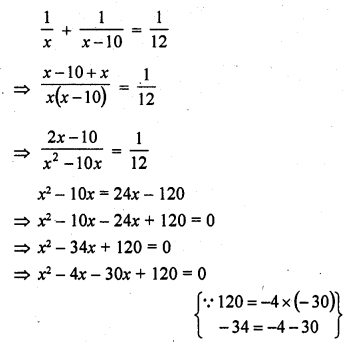
=> x (x – 4) – 30 (x – 4) = 0
=> (x – 4) (x – 30) = 0
Either x – 4 = 0, then x = 4
or x – 30 = 0, then x = 30
But x = 4 is not possible
B can finish the work in 30 days

Question 2.
If two pipes function simultaneously, a reservoir will be filled in 12 hours. One pipe fills the reservoir 10 hours faster than the other. How many hours will the second pipe take to fill the reservoir ?
Solution:
Two pipes can fill the .reservoir in = 12 hours
Let first pipe can fill the reservoir in = x hrs
Then second pipe will fill it in = (x – 10) hours
Now according to the condition,

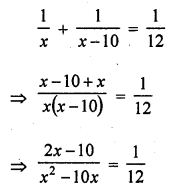
=> x² – 10x = 24x – 120
=> x² – 10x – 24x + 120 = 0
=> x² – 34x + 120 = 0
=> x² – 30x – 4x + 120 = 0
=> x (x – 30) – 4 (x – 30) = 0
=> (x – 30) (x – 4) = 0
Either x – 30 = 0, then x = 30
or x – 4 = 0 but it is not possible as it is < 10
The second pipe will fill the reservoir in = x – 10 = 30 – 10 = 20 hours

Question 3.
Two water taps together can fill a tank in 9\(\frac { 3 }{ 8 }\) hours. The tap of larger diameter takes 10 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank.
Solution:
Two taps can fill the tank in = 9\(\frac { 3 }{ 8 }\) = \(\frac { 75 }{ 8 }\) hr
Let smaller tap fill the tank in = x hours
Then larger tap will fill it in = (x – 10) hours
According to the condition,


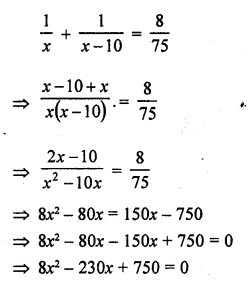
Smaller tap can fill the tank in = 25 hours
and larger tap can fill the tank in = 25 – 10 = 15 hours

Question 4.
Tw o pipes running together can fill a tank in 11\(\frac { 1 }{ 9 }\) minutes. If one pipe takes 5 minutes more than the other to fill the tank separately, find the time in which each pipe would fill the tank separately. [CBSE 2010]
Solution:

=> 9x (x – 20) + 25 (x – 20) = 0
=> (x – 20) (9x + 25) = 0
Either x = – 20 = 0, then x = 20 or 9x + 25 = 0 then 9x = -25
=> x = \(\frac { -25 }{ 9 }\) but it is not possible being negative
x = 20
Time taken by the two pipes = 20 minutes and 20 + 5 = 25 minutes

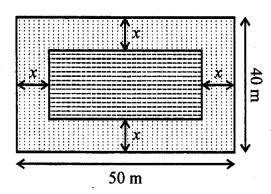
Question 5.
To fill a swimming pool two pipes are used. If the pipe of larger diameter used for 4 hours and the pipe of smaller diameter for 9 hours, only half of the pool can be filled. Find, how long it would take for each pipe to fill the pool separately, if the pipe of smaller diameter takes 10 hours more than the pipe of larger diameter to fill the pool? [CBSE 2015]
Solution:
Let pipe of larger diameter can fill the tank = x hrs
and pipe of smaller diameter can fill in = y hrs

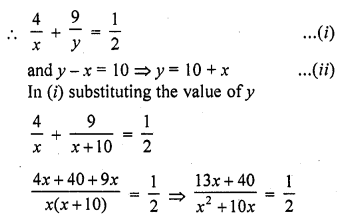
=> 26x + 80 = x² + 10x
=> x² + 10x – 26x – 80 = 0
=> x² – 16x – 80 = 0
=> x² – 20x + 4x – 80 = 0
=> x (x – 20) + 4 (x – 20) = 0
=> (x – 20) (x + 4) = 0
Either x – 20 = 0, then x = 20
or x + 4 = 0, then x = – 4 which is not possible
x = 20 and y = 10 + x = 10 + 20 = 30
Larger pipe can fill the tank in 20 hours and smaller pipe can fill in 30 hours.

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11

Other Exercises

• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.1
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.2
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.4
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.5
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.6
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.7
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS

Question 1.
The perimeter of a rectangular field is 82 m and its area is 400 m². Find the breadth of the rectangle.
Solution:
Perimeter of a rectangle field = 82 m
Length + Breadth = \(\frac { 82 }{ 2 }\) = 41 m
Let breadth = x m
Length = (41 – x) m
According to the condition,
Area = Length x breadth
400 = x (41 – x)
=> 400 = 4x – x²
=> x² – 41x + 400 = 0
=> x² – 16x – 25x + 400 = 0
=> x (x – 16) – 25 (x – 16) = 0
=> (x – 16) (x – 25) = 0
Either x – 16 = 0, then x = 16
or x – 25 = 0 then x = 25
25 > 16 and length > breadth
Breadth = 16 m

Question 2.
The length of a hall is 5 m more than its breadth. If the area of the floor of the hall is 84 m², what are the length and breadth of the hall ?
Solution:
Let breadth of the hall = x m
Then length = x + 5
Area of the floor = 84 m2
Now according to the condition,
x (x + 5) = 84
=> x² + 5x – 84 = 0
=> x² + 12x – 7x – 84 = 0
=> x (x + 12) – 7 (x + 12) = 0
=> (x + 12) (x – 7) = 0
Either x + 12 = 0, then x = -12 which is not possible being negative
or x – 7 = 0, then x = 7
Breadth of the hall = 7 m and length = 7 + 5 = 12 m

Question 3.
Two squares have sides x cm and (x + 4) cm. The sum of their areas is 656 cm². Find the sides of the squares.
Solution:
Side of first square = x cm
and side of the second square = (x + 4) cm
According to the condition,
x² + (x + 4)² = 656
=> x² + x² + 8x + 16 = 656
=> 2x² + 8x + 16 – 656 = 0
=> 2x² + 8x – 640 = 0
=> x² + 4x – 320 = 0 (Dividing by 2)
=> x² + 20x – 16x – 320 = 0
=> x (x + 20) – 16 (x + 20) 0
=> (x + 20) (x – 16) = 0
Either x + 20 = 0, then x = -20 which is not possible being negative
or x – 16 = 0, then x = 16
Side of first square = 16 cm
and side of second square = 16 + 4 = 20 cm

Question 4.
The area of a right angled triangle is 165 m². Determine its base and altitude if the latter exceeds the former by 7 m.
Solution:
Area of a right angled triangle = 165 m²
Let its base = x m
Then altitude = (x + 7) m
According to the condition,
\(\frac { 1 }{ 2 }\) x (x + 7) = 165
=> \(\frac { 1 }{ 2 }\) (x² + 7x) = 165
=> x² + 7x = 330
=> x² + 7x – 330 = 0
=> x² + 22x – 15x – 330 = 0
=> x (x + 22) – 15 (x + 22) = 0
=> (x + 22) (x – 15) = 0
Either x + 22 = 0, then x = -22 which is not possible being negative
or x – 15 = 0, then x = 15
Base = 15 m
and altitude = 15 + 7 = 22 m

Question 5.
Is it possible to design a rectangular mango grove whose length is twice its breadth and the area is 800 m² ? If so, find its length and breadth.
Solution:
Area of rectangular mango grove = 800 m²
Let breadth = x m
Then length = 2x m
According to the condition,
2x x x = 800
=> 2x² = 800
=> x² = 400 = (±20)²
Yes, it is possible,
x = 20, -20
But x = -20 is not possible being negative
Breadth = 20 m
and length = 20 x 2 = 40 m

Question 6.
Is it possible to design a rectangular park of perimeter 80 m and area 400 m² ? If so, find its length and breadth:
Solution:
Perimeter of rectangular park = 80 m
Length + Breadth = \(\frac { 80 }{ 2 }\) = 40 m
Let length = x m
Them breadth = 40 – x
According to the condition,
Area = Length x Breadth
x (40 – x) = 400
=> 40x – x² = 400
=> x² – 40x + 400 = 0
=> (x – 20)² = 0
=> x – 20 = 0
=> x = 20
Yes, it is possible
Length = 20 m
and breadth = 40 – x = 40 – 20 = 20 m

Question 7.
Sum of the areas of two squares is 640 m². If the difference of their perimeters is 64 m, find the sides of the two squares. [CBSE 2008]
Solution:
Let side of first square = x m
and of second squares = y m
According to the given conditions,
4x – 4y = 64
=> x – y = 16 ….(i)
and x² + y² = 640 ….(ii)
From (i), x = 16 + y
In (ii)
(16 + y)² + y² = 640
=> 256 + 32y + y² + y² = 640
=> 2y² + 32y + 256 – 640 = 0
=> y² + 16y – 192 = 0 (Dividing by 2)
=> y² + 24y – 8y – 192 = 0
=> y (y + 24) – 8 (y + 24) = 0
=> (y + 24)(y – 8) = 0
Either y + 24 = 0, then y = -24, which is not possible as it is negative
or y – 8 = 0, then y = 8
x = 16 + y = 16 + 8 = 24
Side of first square = 24 m
and side of second square = 8m

Question 8.
Sum of the areas of two squares is 400 cm². If the difference of their perimeters is 16 cm, find the sides of two squares. [CBSE 2013]
Solution:
Let perimeter of the first square = x cm
Then perimeter of second square = (x + 16) cm
Side of first square = \(\frac { x }{ 4 }\) cm
and side of second square = (\(\frac { x }{ 4 }\) + 4) cm
Sum of areas of these two squares = 400 cm²

Question 9.
The area of a rectangular plot is 528 m². The length of the plot (in metres) is one metre more then twice its breadth. Find the length and the breadth of the plot. [CBSE 2014]
Solution:
Area of a rectangular plot = 528 m²
Let breadth = x m
Then length = (2x + 1) m
x (2x + 1) = 528 (∴ Area = l x b)
2x² + x – 528 = 0
=> 2x² + 33x – 32x² – 528 = 0
=> x (2x + 33) – 16 (2x + 33) = 0
=> (2x + 33) (x – 16) = 0
Either 2x + 33 = 0 then 2x = – 33 => x = \(\frac { -33 }{ 2 }\) but it is not possible being negative
or x – 16 = 0, then x = 16
Length = 2x + 1 = 16 x 2 + 1 = 33 m
and breadth = x = 16 m

Question 10.
In the centre of a rectangular lawn of dimensions 50 m x 40 m, a rectangular pond has to be constructed so that the area of the grass surrounding the pond would be 1184 m². Find the length and breadth of the pond. [NCERT Exemplar]
Solution:
Given that a rectangular pond has to be constructed in the centre of a rectangular lawn of dimensions 50 m x 40 m. So, the distance between pond and lawn would be same around the pond. Say x m.

Now, length of rectangular lawn (l₁) = 50 m
and breadth of rectangular lawn (b₁) = 40 m
Length of rectangular pond (l₂) = 50 – (x + x) = 50 – 2x
Also, area of the grass surrounding the pond = 1184 m²
Area of rectangular lawn – Area of rectangular pond = Area of grass surrounding the pond
l₁ x b₁ – l₂ x b₂= 1184 [∵ area of rectangle = length x breadth]
=> 50 x 40 – (50 – 2x) (40 – 2x) = 1184
=> 2000 – (2000 – 80x – 100x + 4x²) = 1184
=> 80x + 100x – 4x² = 1184
=> 4x² – 180x + 1184 = 0
=> x² – 45x + 296 = 0
=> x² – 21x – 8x + 296 = 0 [by splitting the middle term]
=> x (x – 37) – 8 (x – 37) = 0
=> (x – 37) (x – 8) = 0
∴ x = 8
[At x = 37, length and breadth, of pond are -24 and -34, respectively but length and breadth cannot be negative. So, x = 37 cannot be possible]
Length of pond = 50 – 2x = 50 – 2(8) = 50 – 16 = 34 m
and breadth of pond = 40 – 2x = 40 – 2(8) = 40 – 16 = 24 m
Hence, required length and .breadth of pond are 34 m and 24 m, respectively.

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10

Other Exercises

• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.1
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.2
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.4
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.5
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.6
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.7
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS

Question 1.
The hypotenuse of a right triangle is 25 cm. The difference between the lengths of the other two sides of the triangle is 5 cm. Find the lengths of these sides.
Solution:
Length of the hypotenuse of a let right ∆ABC = 25 cm
Let length of one of the other two sides = x cm
Then other side = x + 5 cm

According to condition,
(x)² + (x + 5)² = (25)² (Using Pythagoras Theorem)
=> x² + x² + 10x + 25 = 625
=> 2x² + 10x + 25 – 625 = 0
=> 2x² + 10x – 600 = 0
=> x² + 5x – 300 = 0 (Dividing by 2)
=> x² + 20x – 15x – 300 = 0
=> x (x + 20) – 15 (x + 20) = 0
=> (x + 20) (x – 15) = 0
Either x + 20 = 0, then x = -20, which is not possible being negative
or x – 15 = 0, then x = 15
One side = 15 cm
and second side = 15 + 5 = 20 cm

Question 2.
The diagonal of a rectangular field is 60 metres more than the shorter side. If the longer side is 30 metres more than the shorter side, find the sides of the field.
Solution:
Let shorter side of the rectangular field = x m
Then diagonal = (x + 60) m
and longer side = (x + 30) m
According to the condition,
(Diagonal)² = Sum of squares of the two sides

=> (x + 60)² = x² + (x + 30)²
=> x² + 120x + 3600 = x² + x² + 60x + 900
=> 2x² + 60x + 900 – x² – 120x – 3600 = 0
=> x² – 60x – 2700 = 0
=> x² – 90x + 30x – 2700 = 0
=> x (x – 90) + 30 (x – 90) = 0
=> (x – 90) (x + 30) = 0
Either x – 90 = 0, then x = 90
or x + 30 = 0, then x = – 30 which is not possible being negative
Longer side (length) = x + 30 = 90 + 30= 120
and breadth = x = 90 m

Question 3.
The hypotenuse of a right triangle is 3√10 cm. If the smaller leg is tripled and the longer leg doubled, new hypotenuse will be 9√5 cm. How long are the legs of the triangle ?
Solution:
Let the smaller leg of right triangle = x cm
and larger leg = y cm
Then x² + y² = (3√10)² (Using Pythagoras Theorem)
x² + y² = 90 ….(i)
According to the second condition,
(3x)² + (2y)² = (9√5)²
=> 9x² + 4y² = 405 ….(ii)
Multiplying (i) by 9 and (ii) by 1

y = 9
Substituting the value of y in (i)
x² + (9)² = 90
=> x² + 81 = 90
=> x² = 90 – 81 = 9 = (3)²
x = 3
Length of smaller leg = 3 cm
and length of longer leg = 9 cm

Question 4.
A pole has to be erected at a point on the boundary of a circular park of diameter 13 metres in such a way that .the difference of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres. Is it the possible to do so? If yes, at what distances from the two gates should the pole be erected ?
Solution:
In a circle, AB is the diameters and AB = 13 m
Let P be the pole on the circle Let PB = x m,
then PA = (x + 7) m
Now in right ∆APB (P is in a semi circle)
AB² = AB² + AP² (Pythagoras Theorem)

(13)² = x² + (x + 7)²
=> x² + x² + 14x + 49 = 169
=> 2x² + 14x + 49 – 169 = 0
=> 2x²+ 14x – 120 = 0
=> x2 + 7x – 60 = 0 (Dividing by 2)
=> x² + 12x – 5x – 60 = 0
=> x (x + 12) – 5 (x + 12) = 0
=> (x + 12) (x – 5) = 0
Either x + 12 = 0, then x = -12 which is not possible being negative
or x – 5 = 0, then x = 5
P is at a distance of 5 m from B and 5 + 7 = 12 m from A

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9

Other Exercises

• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.1
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.2
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.4
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.5
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.6
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.7
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS

Question 1.
Ashu is x years old while his mother Mrs. Veena is x² years old. Five years hence Mrs. Veena will be three times old as Ashu. Find their present ages.
Solution:
Present age of Ashu = x years
and age of his mother = x² years
5 years hence,
age of Ashu will be = (x + 5) years
and age of his mother = (x² + 5) years
According to the question,
x² + 5 = 3 (x + 5)
=> x² + 5 = 3x + 15
=> x² + 5 – 3x – 15 = 0
=> x² – 3x – 10 = 0
=> x² – 5x + 2x – 10 = 0
=> x (x – 5) + 2 (x – 5) = 0
=> (x – 5) (x + 2) = 0
Either x – 5 = 0, then x = 5
or x + 2 = 0, then x = -2 which is not possible being negative
Present age of Ashu = 5 years
and age of his mother = x² = (5)² = 25 years

Question 2.
The sum of the ages of a man and his son is 45 years. Five years ago, the product of their ages was four times the man’s age at that time. Find their present ages.
Solution:
Sum of ages of a man and his son = 45 years
Let the present age of the man = x years
Then age of his son = (45 – x) years
5 years ago,
Age of the man was = (x – 5) years
and age of his son = (45 – x – 5) years = (40 – x) years
According to the condition,
(x – 5) (40 – x) = 4 (x – 5)
=> 40 – x = 4 [Dividing by (x – 5)]
=> x = 40 – 4 = 36
Age of the man = 36 years
and age of his son = 45 – 36 = 9 years

Question 3.
The product of Shikha’s age five years ago and her age 8 years later is 30, her age at both times being given in years. Find her present age.
Solution:
Let present age of Shikha = x years
5 years ago, her age was = (x – 5) years
and 8 years later, her age will be = (x + 8) years
According to the condition,
(x – 5) (x + 8) = 30
=> x² + 3x – 40 = 30
=> x² + 3x – 40 – 30 = 0
=> x² + 3x – 70 = 0
=> x² + 10x – 7x – 70 = 0
=> x (x + 10) – 7 (x + 10) = 0
=> (x + 10)(x – 7) = 0
Either x + 10 = 0, then x = -10 which is not possible being negative
or x – 7 = 0, then x = 7
Her present age = 7 years

Question 4.
The product of Ramu’s age (in years) five years ago and his age (in years) nine years later is 15. Determine Ramu’s present age.
Solution:
Let present age of Ramu = x years
5 years ago his age was = (x – 5) years
and 9 years later his age will be = (x + 9) years
According to the condition,
(x – 5) (x + 9) = 15
=> x² + 9x – 5x – 45 = 15
=> x² + 4x – 45 – 15 = 0
=> x² + 4x – 60 = 0
=> x² + 10x – 6x – 60 = 0
=> x (x + 10) – 6 (x + 10) = 0
=> (x + 10) (x – 6) = 0
Either x + 10 = 0, then x = -10 but it is not possible being negative
or x – 6 = 0, then x = 6
Present age of Ramu = 6 years

Question 5.
Is the following situation possible? If so, determine their present ages. The sum of the ages of two friends is 20 years. Four years ago, the product of their ages in years was 48.
Solution:
Sum of ages of two friends = 20 years
Let present age of one friend = x years
Age of second friend = (20 – x) years
4 years ago,
Age of first friend = x – 4
and age of second friend = 20 – x – 4 = 16 -x
According to the condition,
(x – 4) (16 – x) = 48
=> 16x – x² – 64 + 4x = 48
=> – x² + 20x – 64 – 48 = 0
=> – x² + 20x – 112 = 0
=> x² – 20x + 112 = 0
Here a = 1, b = – 20, c = 112
Discriminant(D) = b² – 4ac = (-20)² – 4 x 1 x 112
= 400 – 448 = – 48
∴ D < 0
Roots are not real
It is not possible

Question 6.
A girl is twice as old as her sister. Four years hence, the product of their ages (in years) will be 160. Find their present ages. [CBSE2010]
Solution:
Let age of sister = x years
Then age of girl = 2x years
4 years hence,
Girl’s age = 2x + 4
and sister’s age = x + 4
According to the condition,
(2x + 4) (x + 4) = 160
=> 2x² + 8x + 4x + 16 = 160
=> 2x² + 12x + 16 – 160 = 0
=> 2x²+ 12x – 144 = 0
=> x² + 6x – 12 = 0
=> x² + 12x – 6x – 72 = 0
=> x (x + 12) – 6 (x + 12) = 0
=> (x + 12) (x – 6) = 0
Either x + 12 = 0, then x = – 12 which is not possible being negative
or x – 6 = 0, then x = 6
Age of sister = 6 years
and age of girl = 2x = 2 x 6 = 12 years

Question 7.
The sum of the reciprocals of Rehman’s ages (in years) 3 years ago and 5 years from now is \(\frac { 1 }{ 3 }\). Find his present age. [NCERT]
Solution:
Let age of Rehman = x years
His age 3 years ago = x – 3
and age 5 years hence = x + 5
According to the condition,

=> x² + 2x – 15 = 6x + 6
=> x² + 2x – 15 – 6x – 6 = 0
=> x² – 4x – 21 =0
=> x² – 7x + 3x – 21 = 0
=> x (x – 7) + 3 (x – 7) = 0
=> (x – 7)(x + 3) = 0
Either x – 7 = 0, then x = 7
or x + 3 = 0 then x = – 3 which is not possible being negative
x = 7
His present age = 7 years

Question 8.
If Zeba were younger by 5 years than what she really is, then the square of her age (in years) would have been 11 more than 5 times her actual age. What is her age now? [NCERT Exemplar]
Solution:
Let the actual age of Zeba = x year .
Her age when she was 5 years younger = (x – 5) years
Now, by given condition,
Square of her age = 11 more than 5 times her actual age
(x – 5)² = 5 x actual age + 11
=> (x – 5)² = 5x + 11
=> x² + 25 – 10x = 5x + 11
=> x² – 15x + 14 = 0
=> x² – 14x – x + 14 = 0 [by splitting the middle term]
=> x (x – 14) – 1 (x – 14) = 0
=> (x – 1) (x – 14) = 0
=> x = 14
[Here, x ≠ 1 because her age is x – 5. So, x – 5 = 1 – 5= -4 i.e., age cannot be negative]
Hence, required Zeba’s age now is 14 years.

Question 9.
At present Asha’s age (in years) is 2 more than the square of her daughter Nisha’s age. When Nisha grows to her mother’s present age, Asha’s age would be one year less than 10 times the present age of Nisha. Find the present ages of both Asha and Nisha. [NCERT Exemplar]
Solution:
Let Nisha’s present age be x year.
Then, Asha’s present age = x² + 2 [by given condition]
Now, when Nisha grows to her mother’s present age i.e., after {(x² + 2) – x} years.
Then, Asha’s age also increased by [(x² + 2) – x] year.
Again by given condition,
Age of Asha = One years less than 10 times the present age of Nisha
(x² + 2) + {(x² + 2) – x} = 10x – 1
=> 2x² – x + 4 = 10x – 1
=> 2x² – 11x + 5 = 0
=> 2x² – 10x – x + 5 = 0
=> 2x (x – 5) – 1(x – 5) = 0
=> (x – 5) (2x – 1) = 0
∴ x = 5
[Here, x = \(\frac { 1 }{ 2 }\) cannot be possible, because at x = \(\frac { 1 }{ 2 }\), Asha’s age is 2\(\frac { 1 }{ 4 }\) years which is not possible]
Hence, required age of Nisha = 5 years
and required age of Asha = x² + 2 = (5)² + 2 = 25 + 2 = 27 years

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8

Other Exercises

• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.1
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.2
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.4
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.5
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.6
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.7
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS

Question 1.
The speed of a boat in still water is 8 km/hr. It can go 15 km upstream and 22 km downstream in 5 hours. Find the speed of the stream.
Solution:
Let the speed of stream = x km/h
and speed of boat in still water = 8 km/h
Distance covered up stream = 15 km
and downstream = 22 km
Total time taken = 5 hours
According to the conditions,

Question 2.
A train, travelling at a uniform speed for 360 km, would have taken 48 minutes less to travel the same distance if its speed were 5 km/hr more. Find the original speed of the train. [NCERT Exemplar]
Solution:
Let the original speed of the train = x km/h
Then, the increased speed of the train = (x + 5) km/h [by given condition]
and distance = 360 km
According to the question,

Question 3.
A fast train takes one hour less than a slow train for a journey of 200 km. If the speed of the slow train is 10 km/hr less than that of the fast train, find the speed of the two trains.
Solution:
Total journey = 200 km
Let the speed of fast train = x km/hr
Then speed of slow train = (x – 10) km/hr
According to the condition,

=> x (x – 50) + 40 (x – 50) = 0
=> (x – 50) (x + 40) = 0
Either x – 50 = 0, then x = 50
or x + 40 = 0, then x = -40 but it is not possible being negative
Speed of the fast train = 50 km/hr
and speed of the slow train = 50 – 40 = 10 km/hr

Question 4.
A passenger train takes one hour less for a journey of 150 km if its speed is increased by 5 km/hr from its usual speed. Find the usual speed of the train.
Solution:
Total journey = 150 km
Let the usual speed of the train = x km/hr
According to the condition,

=> x (x + 30) – 25 (x + 30) = 0
=> (x + 30) (x – 25) = 0
Either x + 30 = 0, then x = -30 but it is not possible being negative
or x – 25 = 0, then x = 25
Usual speed of the train = 25 km/hr

Question 5.
The time taken by a person to cover 150 km was 2.5 hrs more than the time taken in the return journey. If he returned at a speed of 10 km/hr more than the speed of going, what was the speed per hour in each direction ?
Solution:
Distance = 150 km
Let the speed of the person while going = x km/hr
Then the speed while returning = (x + 10) km/hr
According to the condition,


=> x (x + 30) – 20 (x + 30) = 0
=> (x + 30) (x – 20) = 0
Either x + 30 = 0, then x = -30 which is not possible being negative
or (x – 20) = 0 then x = 20
Usual speed of the man while going = 20 km/hr

Question 6.
A plane left 40 minutes late due to bad weather and in order to reach its destination, 1600 km away in time, it had to increase its speed by 400 km/hr from its usual speed. Find the usual speed of the plane.
Solution:
Distance = 1600 km
Let usual speed of the plane = x km/hr
Increased speed = (x + 400) km/hr
According to the condition,

is not possible being negative or x – 800 = 0, then x = 800
Usual speed of the plane = 800 km/hr

Question 7.
An aeroplane takes 1 hour less for a journey of 1200 km if its speed is increased by 100 km/hr from its usual speed. Find its usual speed.
Solution:
Distance = 1200 km
Let usual speed of the aeroplane = x km/hr
Increased speed = (x + 100) km/hr
According to the condition,

=> x (x + 400) – 300 (x + 400) = 0
=> (x + 400) (x – 300) = 0
Either x – 300 = 0, then x = 300
or x + 400 = 0, then x = -400 which is not possible being negative
Usual speed of the plane = 300 km/hr

Question 8.
A train travels at a certain average speed for a distance 63 km and then travels a distance of 72 km at an average speed of 6 km/hr more than the original speed. If it takes 3 hours to complete^total journey, what is its original average speed? [NCERT Exemplar]
Solution:
Let its original average speed be x km/h. Therefore
\(\frac { 63 }{ x }\) + \(\frac { 72 }{ x + 6 }\) = 3

Question 9.
A train covers a distance of 90 km at a uniform speed. Had the speed been 15 km/hr more, it would have taken 30 minutes less for the journey. Find the original speed of the train. [CBSE 2006C]
Solution:
Distance to be covered = 90 km
Let uniform-original speed = x km/h
Increased speed = (x + 15) km/hr
According to the condition,

=> x² + 60x – 45x – 2700 = 0
=> x (x + 60) – 45 (x + 60) = 0
=> (x + 60)(x – 45) = 0
Either x + 60 = 0, then x = -60 which is not possible being negative
or x – 45 = 0, then x = 45
Original speed of the train = 45 km/hr

Question 10.
A train travels 360 km at a uniform speed. If the speed had been 5 km/hr more, it would have taken 1 hour less for the same journey. Find the speed of the train.
Solution:
Total distance = 360 km
Let uniform speed of the train = x km/hr
Increased speed = (x + 5) km/hr
According to the condition,

=> x (x + 45) – 40 (x + 45) = 0
=> (x + 45) (x – 40) = 0
Either x + 45 = 0, then x = -45 but it is not possible being negative
or x – 40 = 0, then x = 40
Speed of the train = 40 km/hr

Question 11.
An express train takes 1 hour less than a passenger train to travel 132 km between Mysore and Bangalore (without taking into consideration the time they stop at intermediate stations). If the average speed of the express train is 11 km/hr more than that of the passenger train, find the average speeds of the two trains.
Solution:
Distance between Mysore and Bangalore = 132 km
Let the speed of the passenger train=x km/hr
Then speed of express train = x + 11
According to the condition,

Either x + 44 = 0, then x = -44 but it is not possible being negative
or x – 33 = 0, then x = 33
Speed of passenger train = 33 km/hr
and speed of express train = 33 + 11 = 44 km/hr

Question 12.
An aeroplane left 50 minutes later than its scheduled time, and in order to reach the destination, 1250 km away, in time, it had to increase its speed by 250 km/hr from its usual speed. Find its usual speed. (CBSE 2010)
Solution:
Distance = 1250 km
Usual speed = x km/hr
Increased speed = (x + 250) km/hr
According to the condition,

Question 13.
While boarding an aeroplane, a passenger got hurt. The pilot showing promptness and concern, made arrangements to hospitalise the injured and so the plane started late by 30 minutes to reach the destination, 1500 km away, in time, the pilot increased the speed by 100 km/hr. Find the original speed / hour of the plane. [CBSE 2013]
Solution:
Distance = 1500 km
Let the original speed of the aeroplane = x km/hr
Then increased speed = (x + 100) km/hr
According to the condition,

=> x² + 100x = 300000
=> x²+ 100x – 300000 = 0
=> x² + 600x – 500x – 300000 = 0
=> x (x + 600) – 500(x + 600) = 0
=> (x + 600) (x – 500) = 0
Either x + 600 = 0, then x = -600 which is not possible being negative
or x – 500 = 0, then x = 500
Original speed = 500 km/hr

Question 14.
A motorboat whose speed in still water is 18 km/h, takes 1 hour more to go 24 km upstream than to return downstream to the same spot. Find the speed of the stream. [CBSE 2014]
Solution:
Let speed of the stream be x km/hr,
Speed of the boat upstream = (18 – x) km/hr
and Speed of the boat downstream = (18 + x) km/hr
Distance = 24 km

48x = 324 – x²
x² + 48x – 324 = 0
x² + 54x – 6x – 324 = 0
x(x + 54) – 6(x + 54) = 0
(x – 6) (x + 54) = 0
x – 6 = 0 or x + 54 = 0
x = 6 or x = – 54
Since speed cannot be negative
Speed of stream, x = 6 km/hr

Question 15.
A car moves a distance of 2592 km with uniform speed. The number of hours taken for the journey is one-half the number representing the speed, in km/ hour. Find the time taken to cover the distance. [CBSE 2017]
Solution:
Distance = 2592 km
Let the speed of the car = x km/hr
and time taken = \(\frac { x }{ 2 }\) hour
We have, Distance = Speed x Time
2592 = x x \(\frac { x }{ 2 }\)
=> 2592 = \(\frac { { x }^{ 2 } }{ 2 }\)
=> x² = 2592 x 2
=> x = √5184
=> x = 72 km/hr
and thus time taken = \(\frac { x }{ 2 }\) h = \(\frac { 72 }{ 2 }\) = 36 hour

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1

Other Exercises

• RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1
• RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2
• RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3
• RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise
• RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS
• RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS

Question 1.
How many balls, each of radius 1 cm, can be made from a solid sphere of lead of radius 8 cm ?
Solution:

Question 2.
How many spherical bullets each of 5 cm in diameter can be cast from a rectangular block of metal 11dm x 1m x 5 dm?
Solution:
Volume of reactangular block of metal
(V₁) = 11 dm x 1 m x 5 dm
= 11 dm x 10 dm x 5 dm = 550 dm³
Diameter of spherical bullet = 5 cm

Question 3.
A spherical ball of radius 3 cm is melted and recast into three spherical balls. The radii of the two balls are 1.5 cm and 2 cm respectively. Determine the diameter of the third ball.
Solution:

Question 4.
2.2 cubic dm of brass is to be drawn into a cylindrical wire 0.25 cm in diameter. Find the length of the wire.
Solution:

Question 5.
What length of a solid cylinder 2 cm in diameter must be taken to recast into a hollow cylinder of length 16 cm, external diameter 20 cm and thickness 2.5 mm ?
Solution:
Length of hollow cylinder = 16 cm
External diameter = 20 cm
and thickness = 2.5 mm = 0.25 cm
∴External radius (R) = \(\frac { 20 }{ 2 }\) = 10 cm
and internal radius (r) = 10 – 0.25 = 9.75 cm
∴ Volume of the material used in hollow cylinder
= πh (R² – r²) = π x 16 (10² – 9.75²) cm²
= 16π (100.00 – 95.0625) = 16TC (4.9375) cm³
∴ Volume of solid cylinder = 16 x 4.93 75πcm3 Diameter = 2 cm
∴Radius (r) = \(\frac { 2 }{ 2 }\) = 1 cm
Let h be the height of the cylinder, then
πr²h = 16 x 4.9375π
⇒ π (1)² h = 16 x 4.93 75π
h = 16 x 4.9375 = 79
Hence height = 79 cm

Question 6.
A cylindrical vessel having diameter equal to its height is full of water which is poured into two identical cylindrical vessels with diameter 42 cm and jteight 21 cm which are filled completely. Find the diameter of the cylindrical vessel.
Solution:
Diameter of each small cylindrical vessels = 42 cm
∴Radius of each vessel (r) = \(\frac { 42 }{ 2 }\) = 21 cm
Height (h) = 21 cm
∴ Volume of each cylindrical vessal = πr²h = π (21 )2 (21) = 9261K cm³
and volume of both vessels = 2 x 9261π = 18522π cm³
Now volume of larger cylindrical vessel = 185 22π cm³
Let R be the radius of the vessel, then Height (H) = diameter = 2R,
∴Volume πR²H = πR² x 2R = 2πR²
∴ 2πR³ = 18522π
⇒ R³ = \(\frac { 18522 }{ 2 }\) = 9261
⇒ R³ = 9261 = (21 )³
∴ R = 21
∴Diameter = 2R = 2×21=42 cm

Question 7.
50 circular plates each of diameter 14 cm and thickness 0.5 cm are placed one above the other to form a right circular cylinder. Find its total surface area.
Solution:
Diameter of each circular plate = 14 cm
∴ Radius (r) = \(\frac { 14 }{ 2 }\) = 7 cm .
Thickness (h) = 0.5 cm
∴Height of 50 plates placing one above the other
= 0.5 x 50 = 25 cm
∴ Curved surface area of the cylinder so formed = 2πrh
= 2 x \(\frac { 2 }{ 7 }\) x 7 x 25 = 1100 cm2
and total surface area = curved surface area + 2 x base area
= 1100 + 2 x πr² =1100+ 2 x \(\frac { 22 }{ 2 }\) x 7 x 7
= 1100 + 308 = 1408 cm²

Question 8.
25 circular plates, each of radius 10.5 cm and thickness 1.6 cm, are placed one above the other to form a solid circular cylinder. Find the curved surface area and the volume of the cylinder so formed.
Solution:

Question 9.
Find the number of metallic circular discs with 1.5 cm base diameter and of height 0. 2 cm to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm. [NCERT Exemplar]
Solution:
Given that, lots of metallic circular disc to be melted to form a right circular cylinder. Here, a circular disc work as a circular cylinder.
Base diameter of metallic circular disc = 1.5 cm
∴Radius of metallic circular disc = \(\frac { 1.5 }{ 2 }\) cm [∵ diameter = 2 x radius]
and height of metallic circular disc i.e., = 0.2 cm
∴ Volume of a circular disc = π x (Radius)² x Height

Question 10.
How many spherical lead shots each of diameter 4.2 cm can be obtained from a solid rectangular lead piece with dimensions 66 cm x 42 cm x 21 cm. [NCERT Exemplar]
Solution:

Question 11.
How many spherical lead shots of diameter 4 cm can be made out of a solid cube of lead whose edge measures 44 cm. [NCERT Exemplar]
Solution:

Hence, the required number of spherical lead shots is 2541.

Question 12.
Three cubes of a metal whose edges are in the ratio 3:4:5 are melted and converted into a single cube whose diagonal is 12 \(\sqrt { 3 } \) cm. Find the edges of the three cubes. [NCERT Exemplar]
Solution:
Let the edges of three cubes (in cm) be 3x, 4x and 5x, respectively.
Volume of the cubes after melting is = (3x)³ + (4x)³ + (5x)³ = 216×3 cm³
Let a be the side of new cube so formed after melting. Therefore, a³ = 216x³
So, a = 6x,

Question 13.
A solid metallic sphere of radius 10.5 cm is melted and recast into a number of smaller cones, each of radius 3.5 cm and height 3 cm. Find the number of cones so formed. [NCERT Exemplar]
Solution:
The volume of the solid metallic sphere  = \(\frac { 4 }{ 3 }\) π(10.5)³ cm³
Volume of a cone of radius 3.5 cm and height 3 cm = \(\frac { 1 }{ 3 }\) π (3.5)² x 3 cm³
Number of cones so formed

Question 14.
The diameter of a metallic sphere is equal to 9 cm. It is melted and drawn into a long wire of diameter 2 mm having uniform cross-section. Find the length of the wire.
Solution:

Question 15.
An iron spherical ball has been melted and recast into smaller balls of equal size. If the radius of each of the smaller balls is  \(\frac { 1 }{ 4 }\) of the radius of the original ball, how many such balls are made ? Compare the surface area, of all the smaller balls combined together with that of the original ball.
Solution:
Let R be the radius of the original ball, then

Question 16.
A copper sphere of radius 3 cm is melted and recast into a right circular cone of height 3 cm. Find the radius of the base of the cone.
Solution:

Question 17.
A copper rod of diameter 1 cm and length 8 cm is drawn into a wire of length 18 m of uniform thickness. Find the thickness of the wire.
Solution:

Question 18.
The diameters of internal and external surfaces of a hollow spherical shell are 10 cm and 6 cm respectively. If it is melted and recast into a solid cylinder of length of 2 \(\frac { 2 }{ 3 }\) cm, find the diameter of the cylinder.
Solution:

Question 19.
How many coins 1.75 cm in diameter and 2 mm thick must be melted to form a cuboid 11 cm x 10 cm x 7 cm ?
Solution:

Question 20.
The surface area of a solid metallic sphere is 616 cm². It is melted and recast into a cone of height 28 cm. Find the diameter of the base of the cone so formed. (Use π = 22/7). [CBSE 2010]
Solution:

Question 21.
A cylindrical bucket, 32 cm high and with radius of base 18 cm, is filled with sand. This bucket is emptied out on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, find the radius and slant height of the heap. [CBSE 2012]
Solution:

Question 22.
A solid metallic sphere of radius 5.6 cm is melted and solid cones each of radius 2.8 cm and height 3.2 cm are made. Find the number of such cones formed. [CBSE 2014]
Solution:

Question 23.
A solid cuboid of iron with dimensions 53 cm x 40 cm x 15 cm is melted and recast into a cylindrical pipe. The outer and inner diameters of pipe are 8 cm and 7 cm respectively. Find the length of pipe. [CBSE 2015]
Solution:
Length of cuboid (l) = 53 cm
Breadth (b) = 40 cm
Height (h) = 15 cm

Volume =lbh= 53 x 40 x 15 cm³
= 31800 cm³
∴ Volume of cylindrical pipe = 31800 cm³
Inner diameter of pipe = 7 cm
and outer diameter = 8 cm
∴ Outer radius (R) = \(\frac { 8 }{ 2 }\) = 4 cm

Question 24.
The diameters of the internal and external surfaces of a holjow spherical shell are 6 cm and 10 cm respectively. If it is melted and recast into a solid cylinder of diameter 14 cm, find the height of the cylinder. [CBSE 2001C]
Solution:
Outer diameter of hollow spherical shell = 10 cm
and inner diameter = 6 cm
Outer radius (R) = \(\frac { 10 }{ 2 }\) = 5 cm 6
and inner radius (r) = \(\frac { 6 }{ 2 }\) = 3 cm

Question 25.
A hollow sphere of internal and external diameters 4 cm and 8 cm respectively is melted into a cone of base diameter 8 cm. Calculate the height of the cone.
Solution:

Question 26.
A hollow sphere of internal and external radii 2 cm and 4 cm respectively is melted into a cone of base radius 4 cm. Find the height and slant height of the cone. 
Solution:
Interval radius of hollow sphere  (r) = 2m
and external radius (R) = 4m

Question 27.
A spherical ball of radius 3 cm is melted and recast into three spherical balls. The radii of two of the balls are 1.5 cm and 2 cm. Find the diameter of the third ball.
Solution:
Radius of big spherical ball (R) = 3 cm
∴ Volume = \(\frac { 4 }{ 3 }\) πR³ = \(\frac { 4 }{ 3 }\) n x (3)³ cm³
= \(\frac { 4 }{ 3 }\) π x 27 = 36π cm³
Similarly volume of ball of radius (r₁) = 1.5 cm
∴ Volume = \(\frac { 4 }{ 3 }\) π( 1.5)³

Question 28.
A path 2 m wide surrounds a circular pond of diameter 40 m. How many cubic metres of gravel are required to grave the path to a depth of 20 cm ?
Solution:
Diamter of pond = 40 m
∴ Radius (r) = \(\frac { 40 }{ 2 }\) =20 m
Width of path = 2 m

Question 29.
A 16 m deep well with diameter 3.5 m is dug up and the earth from it is spread evenly to form a platform 27.5 m by 7 m. Find the height of the platform.
Solution:

Volume of platform = Ibh = 27.5 x7 x h

Question 30.
A well of diameter 2 m is dug 14 m deep. The earth taken out of it is spread evenly all around it to form an embankment of height 40 cm. Find the width of the embankment.
Solution:
Diameter of well = 2 m

Question 31.
A well with inner radius 4 m is dug 14 m deep. Earth taken out of it has been spread evenly all around a width of 3 m it to form an embankment. Find the height of the embankment.
Solution:

Question 32.
A well of diameter 3 m is dug 14 m deep. The earth taken out of it has>been spread evenly all around it to a width of 4 m to form an embankment. Find the height of the embankment.
Solution:

Question 33.
Find the volume of the largest right circular cone that can be cut out of a cube whose edge is 9 cm.
Solution:

Question 34.
A cylindrical bucket, 32 cm high and 18 cm of radius of the base, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, find the radius and slant height of the heap.
Solution:

Question 35.
Rain water, which falls on a flat rectangular surface of length 6 m and breadth 4 m is transferred into a cylindrical vessel of internal radius 20 cm. What will be the height of water in the cylindrical vessel if a rainfall of 1 cm has fallen ? [Use π = 22/7]
Solution:

Question 36.
The rain water from a roof of dimensions 22 m x 20 m drains into a cylindrical vessel having diameter of base 2 m and height 3.5 m. If the rain water collected from the roof just fills the cylindrical vessel, then find the rain in cm. [NCERT Exemplar]
Solution:

Question 37.
A conical flask is full of water. The flask has base-radius r and height h. The water is poured into a cylindrical flafisk of base- radius mr. Find the height of water in the cylindrical flask.
Solution:

Question 38.
A rectangular tank 15 m long and 11 m broad is required to receive entire liquid contents from a full cylindrical tank of internal diameter 21m and length 5 m. Find the least height of the tank that will serve the purpose.
Solution:

Question 39.
A hemispherical bowl of internal radius 9 cm is full of liquid. This liquid is to be fdled into cylindrical shaped small bottles each of diameter 3 cm and height 4 cm. How many bottles are necessary to empty the bowl ?
Solution:

Question 40.
A cylindrical tub of radius 12 cm contains water to a depth of 20 cm. A spherical ball is dropped into the tub and the level of the water is raised by 6.75 cm. Find the radius of the ball.
Solution:

Question 41.
500 persons have to dip in a rectangular tank which is 80 m long and 50 m broad. What is the rise in the level of water inthe tank, if the average displacement of water by a person is 0.04 m3 ?
Solution:

Question 42.
A cylindrical jar of radius 6 cm contains oil. Iron spheres each of radius 1.5 cm are immersed in the oil. How many spheres are necessary to raise the level of the oil by two centimetres ?
Solution:

Question 43.
A cylindrical tub of radius 12 cm contains water to a depth of 20 cm. A spherical form ball of radius 9 cm is dropped into the tub and thus the level of water is raised by h cm. What is the value of h ?
Solution:

Question 44.
Metal spheres, each of radius 2 cm, are packed into a rectangular box of internal dimension 16 cm x 8 cm x 8 cm when 16 spheres are packed the box is fdled with preservative liquid. Find the volume of this liquid. [Use π = 669/213]
Solution:

Question 45.
A vessel in the shape of a cuboid contains some water. If three identical spheres are immersed in the water, the level of water is increased by 2 cm. If the area of the base of the cuboid is 160 cm² and its height 12 cm, determine the radius of any of the spheres.
Solution:

Question 46.
150 spherical marbles, each of diameter 1.4 cm are dropped in a cylindrical vessel of diameter 7 cm contianing some water, which are completely immersed in water. Find the rise in the level of water in the vessel. [CBSE2014]
Solution:

Question 47.
Sushant has a vessel, of the form of an inverted cone, open at the top, of height 11 cm and radius of top as 2.5 cm and is full of water. Metallic spherical balls each of diameter 0.5 cm are put in the vessel due to which \((\frac { 2 }{ 5 } )\)² of the water in the vessel flows out. Find how many balls were put in the vessel. Sushant made the arrangement so that the water that flows out irrigates the flower beds. What value has been shown by Sushant? [CBSE 2014]
Solution:
Radius of vessel (R) = 2.5 cm
and height (h) = 11 cm

Question 48.
16 glass spheres each of radius 2 cm are packed into a cuboidal box of internal dimensions 16 cm x 8 cm x 8 cm and then the box is filled with water. Find the volume of water fdled in the box. |NCERT Exemplar]
Solution:
Given, dimensions of the cuboidal
= 16 cm x 8 cm x 8 cm
∴ Volume of the cuboidal =16x8x8
= 1024 cm³
Also, given radius of one glass sphere = 2cm
∴ Volume of one glass sphere = \((\frac { 4 }{ 3 } )\)πr³
= \((\frac { 4 }{ 3 } )\) x \((\frac { 22 }{ 7 } )\) x (2)³
= \((\frac { 704 }{ 21 } )\) = 33.523 cm³
Now, volume of 16 glass spheres = 16 x 33.523 = 536.37 cm³
∴ Required volume of water = Volume of cuboidal – Volume of 16 glass spheres
= 1024 – 536.37 = 487.6 cm³

Question 49.
Water flows through a cylindrical pipe, whose inner radius is 1 cm, at the rate of 80 cm/sec in an empty cylindrical tank, the radius of whose base is 40 cm. What is the rise of water level in tank in half an hour? [NCERT Exemplar]
Solution:
Given, radius of tank, r₁ = 40 cm
Let height of water level in tank in half an hour = h₁
Also, given internal radius of cylindrical pipe, r₁ = 1 cm
and speed of water = 80 cm/s /., in 1 water flow = 80 cm
∴In 30 (min) water flow = 80 x 60 x 30 = 144000 cm
According to the question,
Volume of water in cylindrical tank = Volume of water flow the circular pipe in half an hour
⇒ πr₁²h₁ = πr₂²h₂
⇒ 40 x 40 x h₁ = 1 x 1 x 14400
∴ h₁ = \((\frac {144000 }{ 40 x 40 } )\) = 90 cm
Hence, the level of water in cylindrical tank rises 90 cm in half an hour.

Question 50.
Water in a canal 1.5 m wide and 6 m deep is flowing with a speed of 10km/hr. How much area will it irrigate in 30 minutes if 8 cm of standing water is desired ?
Solution:

Question 51.
A famer runs a pipe of internal diameter 20 cm from the canal into a cylindrical tank in his field which is 10 m in diameter and 2 m deep. If water flows through the pipe at the rate of 3 km/h, in how much time will the tank be filled ?
Solution:

Question 52.
A cylindrical tank full of water is emptied by a pipe at the rate of 225 litres per minute. How much time will it take to empty half the tank, if the diameter of its base is 3 m and its height is 3.5 m? [Use π = 22/7] [ [CBSE 2014]
Solution:

Question 53.
A cylindrical tank full of water is emptied by a pipe at the rate of 225 litres per minute. How much time will it take to empty half the tank, if the diameter of its base is 3 m and its height is 3.5 m? [Use π  = 22/7] [CBSE 2014]
Solution:

Question 54.
Water flows at the rate of 15 km/hr through a pipe of diameter 14 cm into a cuboidal pond which is 50 m long and 44 m wide. In what time will the level of water in the pond rise by 21 cm?
[NCERT Exemplar]
Solution:
Given, length of the pond = 50 m and width of the pond = 44 m

Question 55.
A canal is 300 cm wide and 120 cm deep. The water in the canal is flowing with a speed of 20 km/h. How much area will it irrigate in 20 minutes if 8 cm of standing water is desired? [NCERT Exemplar]
Solution:
Volume of water flows in the canal in one hour = width of the canal x depth of the canal x speed of the canal water
= 3 x 1.2 x 20 x 1000 m³ = 72000 m³
In 20 minutes the volume of water
= \(\frac { 72000\times 20 }{ 60 }\) m³ = 24000 m³
Area irrigated in 20 minutes, if 8 cm,
i. e., 0.08 m standing water is required
= \((\frac { 2 }{ 5 } )\)
= \((\frac { 2 }{ 5 } )\) m²
= 300000 m²= 30 hectares.

Question 56.
The sum of the radius of base and height of a solid right circular cylinder is 37 cm. If the total surface area of the solid cylinder is 1628 cm2, find the volume of cylinder. (Use re = 22/7) [CBSE 2016]
Solution:
Let the radius and height of cylinder be r and h respectively.
r + h = 37 cm …(i) [given]
Total surface area of cylinder = 1628 cm²
2πr(r + h) = 1628
⇒ 2πr(37) = 1628

Question 57.
A tent of height 77 dm is in the form a right circular cylinder of diameter 36 m and height 44 dm surmounted by a right circular cone. Find the cost of the canvas at ₹3.50 per m². [Use π = 22/7]
Solution:
Total height of the tent = 77 dm
Height of the cylindrical part (h₁) = 44 dm = 4.4 m
Height of conical part (h₂) = 77 – 44 = 33 dm = 3.3 m
Diameter of the base of the tent = 36 m

Question 58.
The largest sphere is to be curved out of a right circular cylinder of radius 7 cm and height 14 cm. Find the volume of the sphere.
Solution:
Largest sphere to be curved must have its diameter = diameter of cylinder = height of cylinder

Question 59.
A right angled triangle whose sides are 3 cm, 4 cm and 5 cm is revolved about the sides containing the right angle in two ways. Find the difference in volumes of the two cones so formed. Also, find their curved surfaces.
Solution:
In ∆ABC, ∠B = 90°
and sides are 3 cm, 4 cm and 5 cm
Here diagonal is 5 cm

(i) When it is revolved along BC i.e., 4 cm side, then
Radius of the base of the cone (r₁) = 3 cm
and height (h₁) = 4 cm and slant height l = 5 cm
∴ Volume = \((\frac { 2 }{ 5 } )\) πr2h = \((\frac { 1 }{ 3 } )\) π x 3 x 3 x 4 cm³
= 12π cm³
and surface area = πrl = π x 3 x 5 cm2 = 157π cm2
(ii) When it is revolved along 3 cm side, then
r = 4 cm and h = 3 cm and l = 5 cm
∴ Volume = \((\frac { 1 }{ 3 } )\) πr2h =-\((\frac { 1 }{ 3 } )\) π x 4 x 4 x 3 cm3
= 16πcm³
and curved surface area = πrl
= π x 4 x 5 = 20n cm²
∴ Difference of their volumes = I6π- 12π = 4πcm³

Question 60.
A 5 m wide cloth is used to make a conical tent of base diameter 14 ir. and height 24 m. Find the cost of cloth used at the rate of ₹25 per metre. [Use π = 22/7] [CBSE 2014]
Solution:
Diameter of base of conical tent = 14 m
Radius (r) = \((\frac { 14 }{ 3 } )\)= 7 cm
Height (h) = 24 m

Question 61.
The volume of a hemi-sphere is 2425 \((\frac { 1 }{ 2 } )\) cm³, find its curved surface area. [2012]
Solution:

Question 62.
The difference between the outer and inner curved surface areas of a hollow right circular cylinder 14 cm long is 88 cm². If the volume of nretal used in making the cylinder is 176 cm³, find the outer and inner diameters of the cylinder. [CBSE 2010]
Solution:
Height of hollow right cylinder = 14 cm
Difference between outer and inner curved surface area = 88 cm²
and volume of metal used =176 cm³

Question 63.
The internal and external diameters of a hollow hemispherical vessel are 21 cm and 25.2 cm respectively. The cost of painting 1 cm² of the surface is 10 paise. Find the total cost to paint the vessel ail over.
Solution:
Outer diameter of the hemispherical vessel = 25.2 cm
and inner diameter = 21 cm

Question 64.
Prove that the surface area of a sphere is equal to the curved surface area of the circumscribed cylinder.
Solution:
Let r be the radius of the sphere, then surface area = 4πr² ….(i)
Then radius of the circumscribed cylinder = radius of the sphere = r

Question 65.
If the total surface area of a solid hemisphere is 462 cm², find its volume (Take π = 22/7).
Solution:

Question 66.
Water flows at the rate of 10 m / minutes through a cylindrical pipe 5 mm in diameter. How long would it take to fill a conical vessel whose diameter at the base is 40 cm and depth 24 cm? [NCERT Exemplar]
Solution:
Given, speed of water flow = 10 m min^-1 = 1000 cm/min

Question 67.
A solid right circular cone of height 120 cm and radius 60 cm is placed in a right circular cylinder full of water of height 180 cm such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is equal to the radius of the cone. [NCERT Exemplar]
Solution:
(i) Whenever we placed a solid right circular cone in a right circular cylinder with full of water, then volume of a solid right circular cone is equal to the volume of water failed from the cylinder.
(ii) Total volume of water in a cylinder is equal to the volume of the cylinder.
(iii) Volume of water left in the cylinder = Volume of the right circular cylinder – Volume of a right circular cone.

Now, given that
Height of a right circular cone = 120 cm
Radius of a right circular cone = 60 cm
∴Volume of a right circular cone = \((\frac { 1 }{ 3 } )\)πr² x h
= \((\frac { 1 }{ 3 } )\) x \((\frac { 22 }{ 7 } )\) x 60 x 60 x 120
=\((\frac { 22 }{ 7 } )\) x 20 x 60 x 120
= 144000π cm³
∴Volume of a right circular cone = Volume of water failed from the cylinder = 1440007c cm3 [from point (i)]
Given that, height of a right circular cylinder = 180 cm
and radius of a right circular cylinder = Radius of a right circular cone = 60 cm
∴Volume of a right circular cylinder = πr² x h
= π x 60 x 60 x 180 = 64800071 cm3 So, volume of a right circular cylinder = Total volume of water in a cylinder = 64800071 cm3 [from point (ii)]
From point (iii),
Volume of water left in the cylinder = Total volume of water in a cylinder – Volume of water failed from the cylinder when solid cone is placed in it
= 648000π- 144000π
= 504000π = 504000 x \((\frac { 22 }{ 7 } )\) = 1584000 cm³ 1584000
= \((\frac { 1584000 }{ (10)6 } )\) m³ = 1.584 m³
Hence, the required volume of water left in the cylinder is 1.584 m³.

Question 68.
A heap of rice in the form of a cone of diameter 9 m and height 3.5 m. Find the volume of rice. How much canvas cloth is required to cover the heap? [NCERT Exemplar]
Solution:
Given that, a heap of rice is in the form of a cone.
Height of a heap of rice i.e., cone (h) = 3.5m
and diameter of a heap of rice i. e., cone = 9 m
Radius of a heap of rice i.e., cone (r) = \((\frac { 9 }{ 2 } )\) m

Question 69.
A cylindrical bucket of height 32 cm and base radius 18 cm is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the concial heap is 24 cm, find the radius and slant height of the’ heap. [NCERT Exemplar]
Solution:
Given, radius of the base of the bucket = 18 cm
Height of the bucket = 32 cm
So, volume of the sand in cylindrical bucket
= πr²h = π (18)²x 32= 10368π
Also, given height of the conical heap (h) = 24 cm
Let radius of heap be r cm
Then, volume of the sand in the heap = \((\frac { 1 }{ 3 } )\) πr²h

Question 70.
A hemispherical bowl of internal radius 9 cm is full of liquid. The liquid is to be filled into cylindrical shaped bottles each of radius 1.5 cm and height 4 cm. How many bottles are needed to empty the bowl? [NCERT Exemplar]
Solution:
Given, radius of hemispherical bowl, r = 9cm
and radius of cylindrical bottles, R = 1.5 cm
and height, h = 4 cm
∴Number of required cylindrical bottles

Question 71.
A factory manufactures 120,000 pencils daily. The pencils are cylindrical in shape each of length 25 cm and circumference of base as 1.5 cm. Determine the cost of colouring the curved surfaces of the pencils manufactured in one day at ₹0.05 per dm². [NCERT Exemplar]
Solution:
Given, pencils are cylindrical in shape.
Length of one pencil = 25 cm
and circumference of base = 1.5 cm

Now, cost of colouring 1 dm2 curved surface of the pencils manufactured in one day = ₹0.05
∴ Cost of colouring 45000 dm2 curved surface = ₹2250

Question 72.
The\((\frac { 3 }{ 4 } )\)th part of a conical vessel of internal radius 5 cm and height 24 cm is full of water. The water is emptied into a cylindrical vessel with internal radius 10 cm. Find the height of water in cylindrical vessel.
Solution:
Let height of water in cylindrical vessel = h cm
Volume of water (in cylinder) = \((\frac { 3 }{ 4 } )\) Volume of water (in come)
∵ Volume of cylinder = nr²h & Volume of cone = \((\frac { 1 }{ 3 } )\) πr²h

Hence, height of water in cylindrical vessel (h) = 1.5 cm

Hope given RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.5

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.5

Other Exercises

• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.1
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.2
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.4
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.5
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.6
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.7
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS

Question 1.
Write the discriminant of the following quadratic equations :
(i) 2x² – 5x + 3 = 0
(ii) x² + 2x + 4 = 0
(iii) (x – 1) (2x – 1) = 0
(iv) x² – 2x + k = 0, k ∈ R
(v) √3 x² + 2√2 x – 2√3 = 0
(vi) x² – x + 1 = 0
Solution:

Question 2.
In the following, determine whether the given quadratic equations have real roots and if so, And the roots :
(i) 16x² = 24x + 1
(ii) x² + x + 2 = 0
(iii) √3 x² + 10x – 8√3 = 0
(iv) 3x² – 2x + 2 = 0
(v) 2x² – 2√6 x + 3 = 0
(vi) 3a²x² + 8abx + 4b² = 0, a ≠ 0
(vii) 3x² + 2√5 x – 5 = 0
(viii) x² – 2x + 1 = 0
(ix) 2x² + 5√3 x + 6 = 0
(x) √2 x² + 7x + 5√2= 0 [NCERT]
(xi) 2x² – 2√2 x + 1 = 0 [NCERT]
(xii) 3x² – 5x + 2 = 0 [NCERT]
Solution:

Question 3.
Solve for x :

Solution:

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.3
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.4
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.5
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex VSAQS
• RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS

Mark the correct alternative in each of the following:
Question 1.
Which of the following is not a measure of central tendency :
(a) Mean
(b) Median
(c) Mode
(d) Standard deviation
Solution:
Standard deviation is not a measure of central tendency. Only mean, median and mode are measures. (d)

Question 2.
The algebraic sum of the deviations of a frequency distribution from its mean is
(a) always positive
(b) always negative
(c) 0
(d) a non-zero number
Solution:
The algebraic sum of the deviations of a frequency distribution from its mean is zero
Let x₁, x₂, x₃, …… x_n are observations and \(\overline { X }\) is the mean

Question 3.
The arithmetic mean of 1, 2, 3, ….. , n is

Solution:
Arithmetic mean of 1, 2, 3, …… n is

Question 4.
For a frequency distribution, mean, median and mode are connected by the relation
(a) Mode = 3 Mean – 2 Median
(b) Mode = 2 Median – 3 Mean
(c) Mode = 3 Median – 2 Mean
(d) Mode = 3 Median + 2 Mean
Solution:
The relation between mean, median and mode is: Mode = 3 Median – 2 Mean (c)

Question 5.
Which of the following cannot be determined graphically ?
(a) Mean
(b) Median
(c) Mode
(d) None of these
Solution:
Mean cannot be determind graphically, (a)

Question 6.
The median of a given frequency distribution is found graphically with the help of
(a) Histogram
(b) Frequency curve
(c) Frequency polygon
(d) Ogive
Solution:
Median of a given frequency can be found graphically by an ogive, (d)

Question 7.
The mode of a frequency distribution can be determined graphically from
(a) Histogram
(b) Frequency polygon
(c) Ogive
(d) Frequency curve
Solution:
Mode of frequency can be found graphically by an ogive, (c)

Question 8.
Mode is
(a) least frequent value
(b) middle most value
(c) most frequent value
(d) None of these
Solution:
Mode is the most frequency value of observation or a class, (c)

Question 9.
The mean of n observations is \(\overline { X }\) . If the first item is increased by 1, second by 2 and so on,
then the new mean is

Solution:
Mean of n observations = \(\overline { X }\)
By adding 1 to the first item, 2 to second item and so on, the new mean will be
Let x₁, x₂, x_3,…..  x_n are the items whose mean is \(\overline { X }\) , then mean of
(x₁+ 1) + (x₂ + 2) + (x₃ + 3) + …… (x_n + n)

Question 10.
One of the methods of determining mode is
(a) Mode = 2 Median – 3 Mean
(b) Mode = 2 Median + 3 Mean
(c) Mode = 3 Median – 2 Mean
(d) Mode = 3 Median + 2 Mean
Solution:
Mode = 3 Median – 2 Mean (c)

Question 11.
If the mean of the following distribution is 2.6, then the value of y is

(a) 3
(b) 8
(c) 13
(d) 24
Solution:

Question 12.
The relationship between mean, median and mode for a moderately skewed distribution is
(a) Mode = 2 Median – 3 Mean
(b) Mode = Median – 2 Mean
(c) Mode = 2 Median – Mean
(d) Mode = 3 Median – 2 Mean
Solution:
The relationship between mean, median and mode is Mode = 3 Median – 2 Mean, (d)

Question 13.
The mean of a discrete frequency distribution x_i /f_i ; i= 1, 2, …… n is given by

Solution:

Question 14.
If the arithmetic mean of x, x + 3, x + 6, x + 9, and x + 12 is 10, then x =
(a) 1
(b) 2
(c) 6
(d) 4
Solution:

Question 15.
If the median of the data : 24, 25, 26, x + 2, x + 3, 30, 31, 34 is 27.5, then x =
(a) 27
(b) 25
(c) 28
(d) 30
Solution:

Question 16.
If the median of the data : 6, 7, x – 2, x, 17, 20, written in ascending order, is 16. Then x =
(a) 15
(b) 16
(c) 17
(d) 18
Solution:

Question 17.
The median of first 10 prime numbers is
(a) 11
(b) 12
(c) 13
(d) 14
Solution:

Question 18.
If the mode of the data : 64,60, 48, x, 43, 48, 43, 34 is 43, then x + 3 =
(a) 44
(b) 45
(c) 46
(d) 48
Solution:
Mode of 64, 60, 48, x, 43, 48, 43, 34 is 43
∵ By definition mode is a number which has maximum frequency which is 43
∴ x = 43
∴ x + 3 = 43 + 3 = 46 (c)

Question 19.
If the mode of the data : 16, 15, 17, 16, 15, x, 19, 17, 14 is 15, then x =
(a) 15
(b) 16
(c) 17
(d) 19
Solution:
Mode of 16, 15, 17, 16, 15, x, 19, 17, 14 is 15
∵By definition mode of a number which has maximum frequency which is 15
∴ x = 15 (a)

Question 20.
The mean of 1, 3, 4, 5, 7, 4 is m. The number 3, 2, 2, 4, 3, 3, p have mean m – 1 and median q. Then p + q =
(a) 4
(b) 5
(c) 6
(d) 7
Solution:

Question 21.
If the mean of a frequency distribution is 8.1 and Σf_ix_i = 132 + 5k, Σf_i = 20, then k =
(a) 3
(b) 4
(c) 5
(d) 6
Solution:

Question 22.
If the mean of 6, 7, x, 8, y, 14 is 9, then
(a)x+y = 21
(b)x+y = 19
(c) x -y = 19
(d) v -y = 21
Solution:

Question 23.
The mean of n observations is \(\overline { x }\) If the first observation is increased by 1, the second by 2, the third by 3, and so on, then the new mean is

Solution:

Question 24.
If the mean of first n natural numbers is \(\frac { 5n }{ 9 }\) then n =
(a) 5
(b) 4
(c) 9
(d) 10
Solution:

Question 25.
The arithmetic mean and mode of a data are 24 and 12 respectively, then its median is
(a) 25
(b) 18
(c) 20
(d) 22
Solution:
Arithmetic mean = 24
Mode = 12
∴ But mode = 3 median – 2 mean
⇒ 12 = 3 median – 2 x 24
⇒ 12 = 3 median =-48
⇒ 12 + 48 = 3 median
⇒ 3 median = 60
Median = \(\frac { 60 }{ 3 }\) = 20 (c) 

Question 26.
The mean of first n odd natural number is

Solution:

Question 27.
The mean of first n odd natural numbers is \(\frac { n2 }{ 81 }\) , then n = 81
(a) 9
(b) 81
(c) 27
(d) 18
Solution:

Question 28.
If the difference of mode and median of a data is 24, then the difference of median and mean is
(a) 12
(b) 24
(c) 8
(d) 36
Solution:
Difference of mode and median = 24
Mode = 3 median – 2 mean
⇒ Mode – median = 2 median – 2 mean
⇒ 24 = 2 (median – mean)
⇒ Median – mean = \(\frac { 24 }{ 2 }\) = 12 (a)

Question 29.
If the arithmetic mean of 7, 8, x, 11, 14 is x, then x =
(a) 9
(b) 9.5
(c) 10
(d) 10.5
Solution:

Question 30.
If mode of a series exceeds its mean by 12, then mode exceeds the median by
(a) 4
(b) 8
(c) 6
(d) 10
Solution:
Mode of a series = Its mean + 12
Mean = mode – 12
Mode = 3 median – 2 mean
Mode = 3 median – 2 (mode -12)
⇒ Mode = 3 median – 2 mode + 24
⇒ Mode + 2 mode – 3 median = 24
⇒ 3 mode – 3 median = 24
⇒ 3 (mode – median) = 24
⇒ Mode – medain = \(\frac { 24 }{ 3 }\) = 8 (b)

Question 31.
If the mean of first n natural number is 15, then n =
(a) 15
(b) 30
(c) 14
(d) 29
Solution:

Question 32.
If the mean of observations x₁, x₂, …, x_n is \(\overline { x }\) , then the mean of x₁ + a, x₂ + a,…, x_n + a is

Solution:

Question 33.
Mean of a certain number of observations is \(\overline { x }\) If each observation is divided by m (m ≠ 0) and increased by n, then the mean of new observation is

Solution:
Mean of some observations = \(\overline { x }\)
If each observation is divided by m and increased by n
Then mean will be = \(\frac { \overline { x } }{ m }\) +n

Question 34.
If u_i= \(\frac { xi-25\quad }{ 10 }\) Σf_iu_i = 20, Σf_i = 100, then \(\overline { x }\)
(a) 23
(b) 24
(c) 27
(d) 25
Solution:

Question 35.
If 35 is removed from the data : 30, 34, 35, 36, 37, 38, 39, 40, then the median increases by
(a) 2
(b) 1.5
(c) 1
(d) 0.5
Solution:

Question 36.
While computing mean of grouped data, we assume that the frequencies are
(a) evenly distributed over all the classes.
(b) centred at the class marks of the classes.
(c) centred at the upper limit of the classes.
(d) centred at the lower limit of the classes.
Solution:
In computing the mean of grouped data, the frequencies are centred at the class marks of the classes. (b)

Question 37.

Solution:

Question 38.
For the following distribution:

the sum of the lower limits of the median and modal class is
(a) 15
(b) 25
(c) 30
(d) 35
Solution:

Now, \(\frac { N }{ 2 }\) = \(\frac { 66 }{ 2 }\) = 33, which lies in the interval 10-15.
Therefore, lower limit of the median class is 10.
The highest frequency is 20, which lies in the interval 15-20.
Therefore, lower limit of modal class is 15.
Hence, required sum is 10 + 15 = 25. (b)

Question 39.
For the following distribution:

the modal class is
(a) 10-20
(b) 20-30
(c) 30-40
(d) 50-60
Solution:

Here, we see that the highest frequency is 30, which lies in the interval 30-40. (c)

Question 40.
Consider the following frequency distribution:

The difference of the upper limit of the median class and the lower limit of the modal class is
(a) 0
(b) 19
(c) 20
(d) 38
Solution:

Here, \(\frac { N }{ 2 }\) = \(\frac { 67 }{ 2 }\) = 33.5 which lies in the interval 125-145.
Hence, upper limit of median class is 145.
Here, we see that the highest frequency is 20 which lies in 125-145.
Hence, the lower limit of modal class is 125.
∴ Required difference = Upper limit of median class – Lower limit of modal class
= 145 – 125 = 2 (C)

Question 41.
In the formula \(\overline { X }\) = a + \(\frac { \Sigma fidi }{ \Sigma fi }\) for finding the mean of grouped data di’s are deviations from a of
(a) lower limits of classes
(b) upper limits of classes
(c) mid-points of classes
(d) frequency of the class marks
Solution:
We know that, d_i = x_i – a
i .e , d_i‘s are the deviation from a mid-points of the classes. (c)

Question 42.
The abscissa of the point of intersection of less than type and of the more than type cumulative frequency curves of a grouped data gives its
(a) mean
(b) median
(c) mode
(d) all the three above
Solution:
Since, the intersection point of less than ogive and more than ogive gives the median on the abscissa. (b)

Question 43.
Consider the following frequency distribution:

The upper limit of the median class is
(a) 17
(b) 17.5
(c) 18
(d) 18.5
Solution:
Given, classes are not continuous, so we make continuous by subtracting 0.5 from lower limit and adding 0.5 to upper limit of each class.

Here, \(\frac { N }{ 2 }\) = \(\frac { 57 }{ 2 }\) = 28.5, which lies in the interval 11.5-17.5.
Hence, the upper limit is 17.5.

Hope given RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 15 Statistics Ex VSAQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 15 Statistics VSAQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.3
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.4
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.5
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex VSAQS
• RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS

Question 1.
Define Mean.
Solution:
The mean of a set of observations is equal to their sum divided by the total number of observations. Mean is also called an average.

Question 2.
What is the algebraic sum of deviations of a frequency distribution about its mean ?
Solution:
The algebraic sum of deviation of a frequency distribution about its mean is zero.

Question 3.
Which measure of central tendency is given by the x-coordinates of the point of intersection of the ‘more than’ ogive and ‘less than’ ogive ? (C.B.S.E. 2008)
Solution:
Median is given by the x-coordinate of the point of intersection of the more than ogive and less than ogive.

Question 4.
What is the value of the median of the data using the graph in the following figure of less than ogive and more than ogive ?

Solution:
Median = 4, because the coordinates of the point of intersection of two ogives at x-axis is 4.

Question 5.
Write the empirical relation between mean, mode and median.
Solution:
The empirical relation is Mode = 3
Median – 2 Mean

Question 6.
Which measure of central tendency can be determined graphically ?
Solution:
Median can be determinded graphically.

Question 7.
Write the modal class for the following frequency distribution:

Solution:
The modal class is 20-25 as it has the maximum frequency of 75 in the given distribution.

Question 8.
A student draws a cumulative frequency curve for the marks obtained by 40 students of a class as shown below. Find the median marks obtained by the students of the class.

Solution:
Median marks
Here N = 40, then \(\frac { N }{ 2 }\) = \(\frac { 40 }{ 2 }\) = 20
From 20 on y-axis, draw a line parallel to the x-axis meeting the curve at P and from P, draw a perpendicular on x-axis meeting it at M. Then M is the median which is 50.

Question 9.
Write the median class for the following frequency distribution:

Solution:

Here N = 100, then \(\frac { N }{ 2 }\) = 50
Which lies in the class 40-50 (∵32 < 50 < 60)
∴ Required class interval is 40-50

Question 10.
In the graphical representation of a frequency distribution, if the distance between mode and mean isk times the distance between median and mean, then write the value of k.
Solution:
We know that
Mode = 3 median – 2 mean ….(i)
Now mode – mean = k (median – mean) , ….(ii)
But mode – mean = 3 median – 2 mean [from (i)]
⇒ Mode – mean = 3 (median – mean) ….(iii)
Comparing (ii) and (iii)
k = 3

Question 11.
Find the class marks of classes 10-25 and 35-55. (C.B.S.E. 2008)
Solution:

Question 12.
Write the median class of the following distribution :

Solution:


Here n = 50
∴ Median = \(\frac { n + 1 }{ 2 }\) = \(\frac { 5 + 1 }{ 2 }\) = 25.5 which lies in the class 30-40
Hence median class = 30-40.

Hope given RD Sharma Class 10 Solutions Chapter 15 Statistics VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3. You must go through NCERT Solutions for Class 10 Maths to get better score in CBSE Board exams along with RS Aggarwal Class 10 Solutions.

Other Exercises

• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.1
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.2
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.4
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.5
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.6
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.7
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS
• RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS

Solve the following quadratic equations by factorization.
Question 1.
(x – 4) (x + 2) = 0
Solution:
(x – 4) (x + 2) = 0
Either x – 4 = 0, then x = 4
or x + 2, = 0, then x = -2
Roots are x = 4, -2

Question 2.
(2x + 3) (3x – 7) = 0
Solution:

Question 3.
3x² – 14x – 5 = 0 (C.B.S.E. 1999C)
Solution:

Roots are x = 5, \(\frac { -1 }{ 3 }\)

Question 4.
9x² – 3x – 2 = 0
Solution:

Question 5.

Solution:

Question 6.
6x² + 11x + 3 = 0
Solution:

Question 7.
5x² – 3x – 2 = 0
Solution:

Question 8.
48x² – 13x – 1 =0
Solution:

Roots are x = \(\frac { 1 }{ 3 }\) , \(\frac { -1 }{ 16 }\)

Question 9.
3x² = – 11x – 10
Solution:

Question 10.
25x (x + 1) = -4
Solution:

Question 11.
16x – \(\frac { 10 }{ x }\) = 27 [CBSE 2014]
Solution:

Question 12.

Solution:

Question 13.
x – \(\frac { 1 }{ x }\) = 3, x ≠ 0 [NCERT, CBSE 2010]
Solution:

Question 14.

Solution:

Question 15.

Solution:

Question 16.
a²x² – 3abx + 2b² = 0
Solution:

Question 17.
9x² – 6b²x – (a⁴ – b⁴) = 0 [CBSE 2015]
Solution:

Question 18.
4x² + 4bx – (a² – b²) = 0
Solution:

Question 19.
ax² + (4a² – 3b)x- 12ab = 0
Solution:

Question 20.
2x² + ax – a² = 0
Solution:

Question 21.

Solution:

x² = 16
x = ±4

Question 22.

Solution:

Question 23.

Solution:

Question 24.

Solution:

Roots are 4, \(\frac { -2 }{ 9 }\)

Question 25.

Solution:

Question 26.

Solution:

Question 27.

Solution:

Question 28.

Solution:

Question 29.

Solution:

Question 30.

Solution:

Question 31.

Solution:

Question 32.

Solution:

Question 33.

Solution:

Question 34.

Solution:

Question 35.

Solution:

Question 36.

Solution:

Question 37.

Solution:

Question 38.

Solution:

Question 39.

Solution:

Question 40.

Solution:

Question 41.
x² – (√2 + 1) x + √2 = 0
Solution:

Question 42.
3x² – 2√6x + 2 = 0 [NCERT, CBSE 2010]
Solution:

Question 43.
√2 x² + 7x + 5√2 = 0
Solution:

Question 44.
\(\frac { m }{ n }\) x² + \(\frac { n }{ m }\) = 1 – 2x
Solution:

Question 45.

Solution:

Question 46.

Solution:

Question 47.

Solution:

Question 48.

Solution:

Question 49.

Solution:

Question 50.
x² + 2ab = (2a + b) x
Solution:

Question 51.
(a + b)² x² – 4abx – (a – b)2 = 0
Solution:

Question 52.
a (x² + 1) – x (a² + 1) = 0
Solution:

Question 53.
x² – x – a (a + 1) = 0
Solution:

Question 54.
x² + (a + \(\frac { 1 }{ a }\)) x + 1 = 0
Solution:

Question 55.
abx² + (b² – ac) x – bc = 0 (C.B.S.E. 2005)
Solution:

Question 56.
a²b²x² + b²x – a²x – 1 = 0 (C.B.S.E. 2005)
Solution:

Question 57.

Solution:

Question 58.

Solution:

Question 59.

Solution:


⇒ x = 0
x = 0, -7

Question 60.

Solution:

Question 61.

Solution:

Question 62.

Solution:

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6

Other Exercises

• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.3
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.4
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.5
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex VSAQS
• RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS

Question 1.
Draw an ogive by less than method for the following data :

Solution:

Take numbers of rooms along the x-axis and c.f along the y-axis
Plot the points (1, 4), (2, 13), (3, 35), (4, 63), (5, 87), (6, 99), (7, 107), (8, 113), (9, 118) and (10, 120) on the graph and join them and with free hand to get an ogive as shown. This is the less than ogive.

Question 2.
The marks scored by 750 students in an examination are given in the form of a frequency distribution table:

Prepare a cumulative frequency table by less than method and draw on ogive.
Solution:

Take marks along ,t-axis and no. of students (c.f) along 3 -axis. Now plot the points (640, 16), (680, 61), (720, 217), (760, 501), (800, 673), (840, 732) and (880, 750) on the graph and join them with free hand. This is the less than ogive.

Question 3.
Draw an ogive to represent the following frequency distribution:

Solution:
Representing the classes in exclusive form :


Represent class intervals along x-axis and c.f. along y-axis. Now plot the points (4.5, 2), (9.5, 8), (14.5, 18), (19.5, 23) and (24.5, 26) on the graph and join then in free hand to get an ogive as shown.

Question 4.
The monthly profits (in Rs.) of 100 shops are distributed as follows:

Draw the frequency polygon for it.
Solution:


Represent profits per shop along x-axis and no. of shop (c.f.) along y-axis.
Plot the points (50, 12), (100, 30), (150, 57), (200, 77), (250, 94) and (300, 100) on the graph and join them with ruler. This is the cumulative polygon as shown.

Question 5.
The following distribution gives the daily income of 50 workers of a factory:

Convert the above distribution to a less than type cumulative frequency distribution and draw its ogive.
Solution:


Now plot the points (120, 12), (140, 26), (160, 34), (180, 40) and (200,50) on the graph and join them with free hand to get an ogive which is less than.

Question 6.
The following table gives production yield per hectare of wheat of 100 farms of a village:

Draw ‘less than’ ogive and ‘more than’ ogive.
Solution:
(i) Less than

Now plot the points (55, 2), (60, 10), (65, 22), (70, 46), (75, 84) and (80, 100) on the graph and join them in free hand to get a less than ogive.
(ii) More than

Now plot the points (50, 100), (55, 84), (60, 46), (65, 22), (70, 10), (75, 2) and (80, 0) on the graph and join than in free hand to get a more than ogive as shown below :

Question 7.
During the medical check-up of 35 students of a class, their weights were recorded as follows :

Draw a less than type ogive for the given data. Hence, obtain the median weight from the graph and verify the result by using the formula. (C.B.S.E. 2009)
Solution:

Plot the points (38, 0), (40, 3), (42, 5), (44, 9), (46, 14), (48, 28), (50, 32), (52, 35) on the graph and join them in free hand to get an ogive as shown.
Here N = 35 which is odd
∴ \(\frac { N }{ 2 }\) = \(\frac { 25 }{ 2 }\) = 17.5
From 17.5 on y-axis draw a line parallel to x-axis meeting the curve at P. From P, draw PM ⊥ x-axis
∴ Median which is 46.5 (approx)
Now N = 17.5 lies in the class 46 – 48 (as 14 < 17.5 < 28)
∴ 46-48 is the median class
Here l= 46, h = 2,f= 14, F= 14

Question 8.
The annual rainfall record of a city for 66 days is given in the following tab

Calculate the median rainfall using ogives of more than type and less than type. [NCERT Exemplar]
Solution:
We observe that, the annual rainfall record of a city less than 0 is 0. Similarly, less than 10 include the annual rainfall record of a city from 0 as well as the annual rainfall record of a city from 0-10. So, the total annual rainfall record of a city for less than 10 cm is 0 + 22 = 22 days. Continuing in this manner, we will get remaining less than 20, 30, 40, 50 and 60.
Also, we observe that annual rainfall record of a city for 66 days is more than or equal to 0 cm. Since, 22 days lies in the interval 0-10. So, annual rainfall record for 66 – 22 = 44 days is more than or equal to 10 cm. Continuing in this manner we will get remaining more than or equal to 20, 30 , 40, 50, and 60.
Now, we construct a table for less than and more than type.

To draw less than type ogive we plot the points (0,0), (10,22), (20,32), (30, 40), (40, 55), (50, 60), (60, 66) on the paper and join them by free hand.
To draw the more than type ogive we plot the points (0, 66), (10, 44), (20, 34), (30, 26), (40, 11), (50, 6) and (60, 0) on the graph paper and join them by free hand.

∵ Total number of days (n) = 66
Now, \(\frac { n }{ 2 }\) = 33
Firstly, we plot a line parallel to X-axis at intersection point of both ogives, which further intersect at (0, 33) on Y- axis. Now, we draw a line perpendicular to X-axis at intersection point of both ogives, which further intersect at (21.25, 0) on X-axis. Which is the required median using ogives.
Hence, median rainfall = 21.25 cm.

Question 9.
The following table gives the height of trees:

Draw ‘less than’ ogive and ‘more than’ ogive.
Solution:
(i) First we prepare less than frequency table as given below:

Now we plot the points (7, 26), (14, 57), (21, 92), (28, 134), (35, 216), (42, 287), (49, 341), (56, 360) on the graph and join then in a frequency curve which is ‘less than ogive’
(ii) More than ogive:
First we prepare ‘more than’ frequency table as shown given below:

Now we plot the points (0, 360), (7, 341), (14, 287), (21, 216), (28, 134), (35, 92), (42, 57), (49, 26), (56, 0) on the graph and join them in free hand curve to get more than ogive.

Question 10.
The annual profits earned by 30 shops of a shopping complex in a locality give rise to the following distribution:

Draw both ogives for the above data and hence obtain the median.
Solution:

Now plot the points (5, 30), (10, 28), (15, 16), (20, 14), (25, 10), (30, 7) and (35, 3) on the graph and join them to get a more than curve.
Less than curve:

Now plot the points (10, 3), (15, 7), (20, 10), (25, 14), (30, 16), (35, 28) and (40, 30) on the graph and join them to get a less them ogive. The two curved intersect at P. From P, draw PM 1 x-axis, M is the median which is 22.5
∴ Median = Rs. 22.5 lakh

Hope given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.