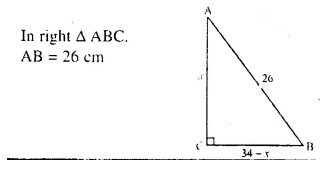
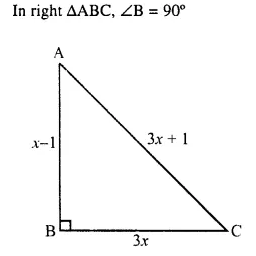
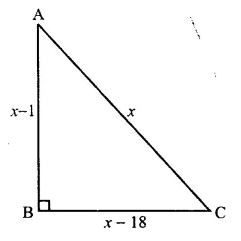
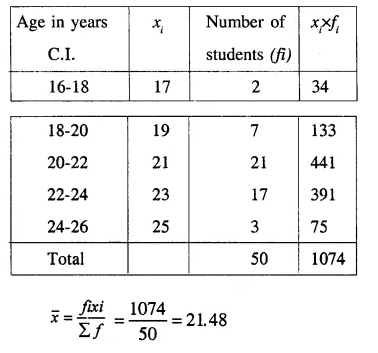
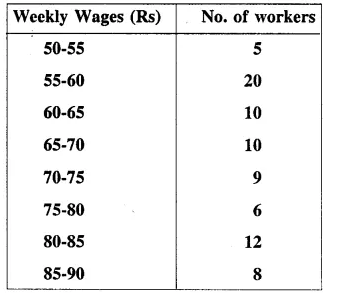
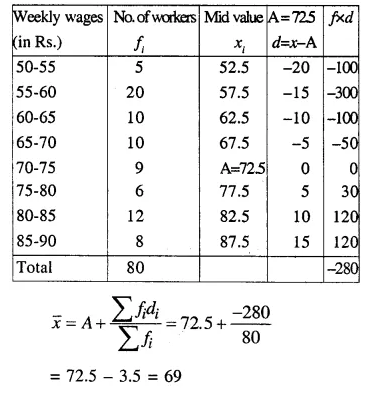
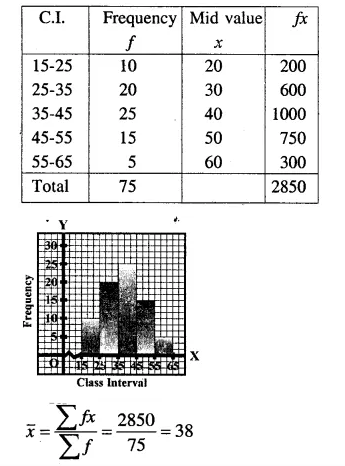
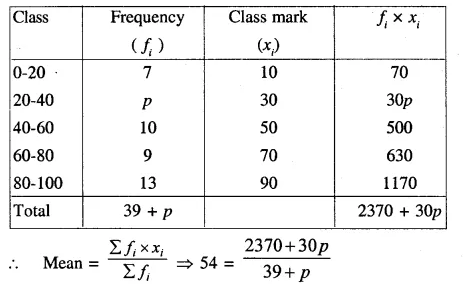
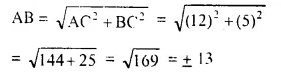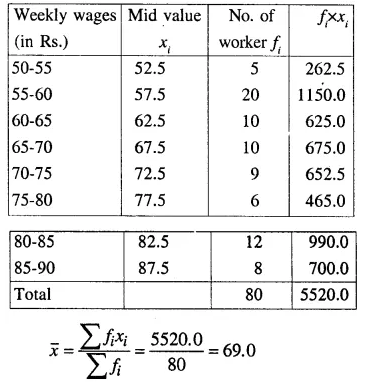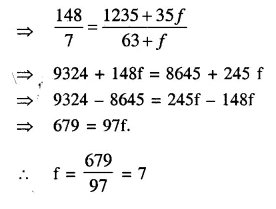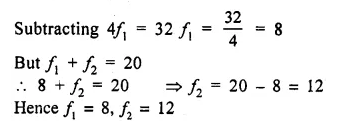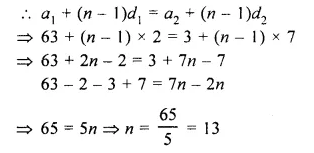Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11A
These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11A
Other Exercises
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11A
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11B
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11C
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11D
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Additional Questions
Question 1.
Find, which of the following sequence form a G.P. :
(i) 8, 24, 72, 216, ……
(ii) \(\\ \frac { 1 }{ 8 } \),\(\\ \frac { 1 }{ 24 } \),\(\\ \frac { 1 }{ 72 } \),\(\\ \frac { 1 }{ 216 } \)
(iii) 9, 12, 16, 24,…..
Solution:
(i) 8, 24, 72, 216,……
Here, a = 8
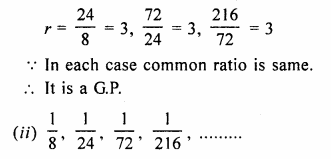

Question 2.
Find the 9th term of the series :
1, 4, 16, 64,…….
Solution:
In G.P. 1, 4, 16, 64,….
Here first term (a) = 1
and common ratio (r) = \(\\ \frac { 4 }{ 1 } \) = 4,
T9 = arn – 1 = 1 x 49 – 1 = 1 x 48 = 48
= 4 x 4 x 4 x 4 x 4 x 4 x 4 x 4
= 65536
Question 3.
Find the seventh term of the G.P. :
1 , √3, 3, 3√3…….
Solution:
G.P. is 1 , √3, 3, 3√3
Here first term (a) = 1
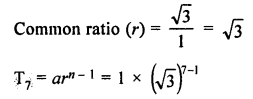
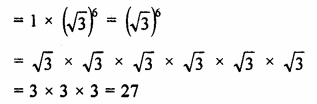
Question 4.
Find the 8th term of the sequence :
\(\\ \frac { 3 }{ 4 } \),\(1 \frac { 1 }{ 2 } \),3……
Solution:
G.P. = \(\\ \frac { 3 }{ 4 } \),\(1 \frac { 1 }{ 2 } \),3…….
= \(\\ \frac { 3 }{ 4 } \),\(\\ \frac { 3 }{ 2 } \),3…….
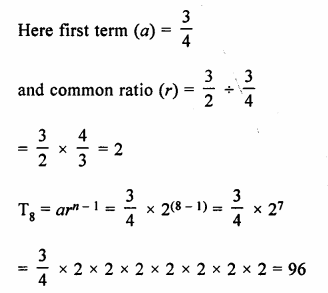
Question 5.
Find the 10th term of the G.P. :
12, 4, \(1 \frac { 1 }{ 3 } \),……
Solution:
G.P. = 12, 4, \(1 \frac { 1 }{ 3 } \),……..
= 12, 4, \(\\ \frac { 4 }{ 3 } \),…..
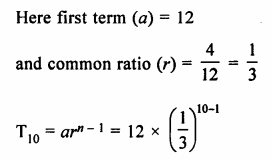
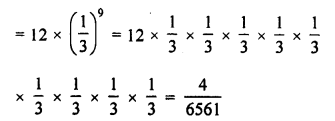
Question 6.
Find the nth term of the series :
1, 2, 4, 8 …….
Solution:
1, 2, 4, 8,……
Here, a = 1,r = \(\\ \frac { 2 }{ 1 } \) = 2
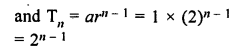
Question 7.
Find the next three terms of the sequence :
√5, 5, 5√5…..
Solution:
√5, 5, 5√5……
Here a = √5 and r = \(\frac { 5 }{ \surd 5 }\) = √5

Question 8.
Find the sixth term of the series :
22, 23, 24,….
Solution:
22, 23, 24,……
Here, a = 22, r = 23 ÷ 22 = 23 – 2 = 21 = 2
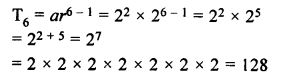
Question 9.
Find the seventh term of the G.P. :
√3 + 1, 1, \(\frac { \surd 3-1 }{ 2 } \),…….
Solution:
√3 + 1, 1, \(\frac { \surd 3-1 }{ 2 } \),…….
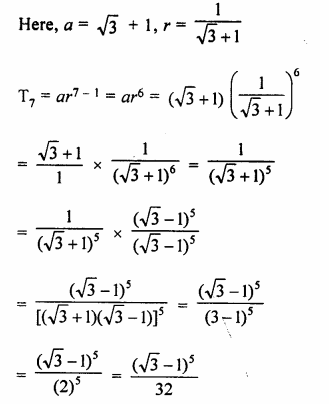
Question 10.
Find the G.P. whose first term is 64 and next term is 32.
Solution:
First term of a G.P. (a) = 64
and second term (ar) = 32
G.P. will be 64, 32, 16, 8, 4, 2, 1,…….
Question 11.
Find the next three terms of the series:
\(\\ \frac { 2 }{ 27 } \),\(\\ \frac { 2 }{ 9 } \),\(\\ \frac { 2 }{ 3 } \),…..
Solution:
G.P. is \(\\ \frac { 2 }{ 27 } \),\(\\ \frac { 2 }{ 9 } \),\(\\ \frac { 2 }{ 3 } \),…..
a = \(\\ \frac { 2 }{ 27 } \)
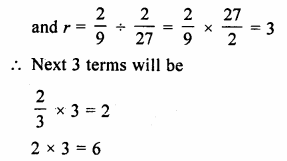
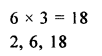
Question 12.
Find the next two terms of the series
2 – 6 + 18 – 54…..
Solution:
G.P. is 2 – 6 + 18 – 54 +………
Here a = 2 and r = \(\\ \frac { -6 }{ 2 } \) = – 3
Next two terms will be
– 54 x ( – 3) = + 162
162 x ( – 3) = – 486
Next two terms are 162 – 486
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 11 Geometric Progression Ex 11A are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.