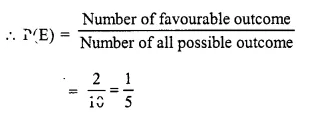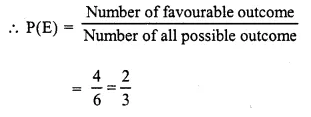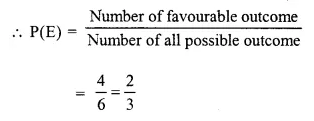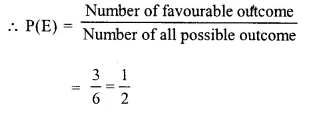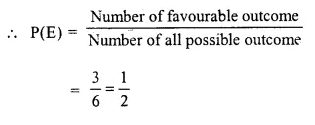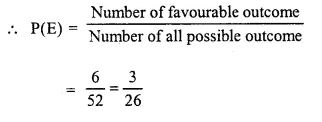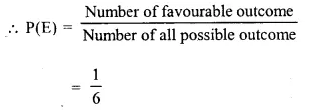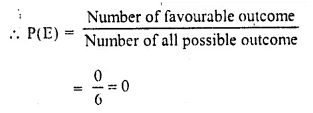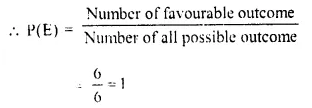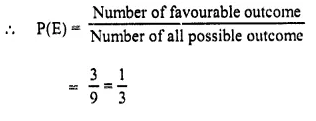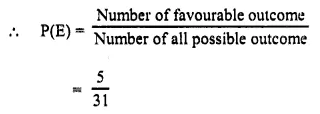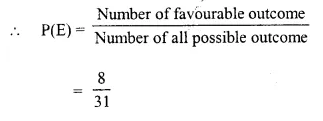Check the below Online Education NCERT MCQ Questions for Class 10 Sanskrit Chapter 8 विचित्रः साक्षी with Answers Pdf free download. MCQ Questions for Class 10 Sanskrit with Answers were prepared based on the latest exam pattern. We have provided विचित्रः साक्षी Class 10 Sanskrit MCQs Questions with Answers to help students understand the concept very well.
Students can also read NCERT Solutions for Class 10 Sanskrit Chapter 8 Questions and Answers at LearnInsta. Here all questions are solved with a detailed explanation, It will help to score more marks in your examinations.
उचितं पदं चित्वा प्रश्ननिर्माणं कुरुत
Question 1.
आरक्षिणि निजपक्षं प्रस्तुतवति।।
(i) किम्
(ii) कस्मिन्
(iii) कानि
(iv) कस्य
Answer
Answer: (ii) कस्मिन्
Question 2.
शवः प्रावारकम् अपसार्य निवेदितवान्।
(i) कम्
(ii) किम्
(iii) कः
(iv) काम्
Answer
Answer: (ii) किम्
Question 3.
त्वं वर्षत्रयस्य कारादण्ड लप्स्यसे।
(i) किम्
(ii) कम्
(iii) काम्
(iv) कति
Answer
Answer: (ii) कम्
Question 4.
न्यायाधीशः अतिथिम् ससम्मानं मुक्तवान्।
(i) कः
(ii) कम्
(iii) कथम्
(iv) केन
Answer
Answer: (iii) कथम्
Question 5.
मति वैभवशालिनः जनाः दुष्कराणि कर्माणि प्रकुर्वते।
(i) कः
(ii) के
(iii) कीदृशाः
(iv) काः
Answer
Answer: (iii) कीदृशाः
Question 6.
नीति युक्तिं समालम्ब्य लीलयैव प्रकुर्वते।
(i) कया
(ii) कैव
(iii) किम्
(iv) कुत्र
Answer
Answer: (i) कया

Question 7.
अभियुक्तः अतीव कृशकायः आसीत्।
(i) कः
(ii) कीदृशः
(ii) किम्
(iv) कथम्
Answer
Answer: (ii) कीदृशः
Question 8.
कश्चित् कर्मचारी समागत्य न्यवेदयत्।
(i) कः
(ii) कीदृशः
(iii) की
(iv) कम्
Answer
Answer: (i) कः
Question 9.
अन्येद्युः तौ न्यायालये स्व-स्व-पक्षं पुनः स्थापितवन्तौ।
(i) के
(ii) कुत्र/कस्मिन्
(iii) कदा
(iv) कदा
Answer
Answer: (ii) कुत्र/कस्मिन्
Question 10.
निशान्धकारे पदयात्रा न शुभावहा।
(i) कुत्र
(ii) कस्मिन्
(iii) का
(iv) कः
Answer
Answer: (ii) कस्मिन्
Question 11.
ग्रामस्य आरक्षी एव चौरः आसीत्।
(i) कः
(ii) कस्य
(iii) किम्
(iv) कथम्
Answer
Answer: (ii) कस्य
Question 12.
जनाः वराकम् अतिथिम् चौरं मत्वा भर्स्यन्।।
(i) कम्
(ii) कीदृशम्
(iii) किम्
(iv) कः
Answer
Answer: (ii) कीदृशम्
Question 13.
प्रबुद्धाः ग्रामवासिनः स्वगृहात् निष्क्रम्य तत्रागच्छन्।
(i) के
(ii) काः
(iii) कीदृशाः
(iv) कः
Answer
Answer: (iii) कीदृशाः
Question 14.
तत् तनयः पठनाय स्वगृहात् निष्क्रम्य तत्रागच्छन्।
(i) कस्मै
(ii) किमर्थम्
(iii) काय
(iv) कात्
Answer
Answer: (ii) किमर्थम्
Question 15.
चौरः एव उच्चैः क्रोशितुमारभत।।
(i) कः
(ii) किम्
(iii) कस्मै
(iv) काः
Answer
Answer: (i) कः
Question 16.
उभौ शवं स्कन्धेन वहन्तौ न्यायाधिकरणं प्रति प्रस्थितौ।
(i) कः
(ii) को
(iii) किम्
(iv) कथम्
Answer
Answer: (ii) को
Question 17.
एतेन आरक्षिणा अध्वनि यदुक्तं तत् वर्णयामि।
(i) कया
(ii) केन
(iii) का
(iv) कीदृशाः
Answer
Answer: (ii) केन
Question 18.
असौ तौ अग्रिमेदिने उपस्थातुम् आदिष्टवान्।
(i) कदा
(ii) कथम्
(iii) कीदृशे
(iv) के
Answer
Answer: (i) कदा
Question 19.
भारवतः शवस्य स्कन्धेन वहनं तत्कृते दुष्करम् आसीत्।
(i) कथम्
(ii) कम्
(iii) कीदृशम्
(iv) किम्
Answer
Answer: (iii) कीदृशम्
Question 20.
बकिमचन्द्रः उभाभ्यां पृथक्-पृथक् विवरणं श्रुतवान्।
(i) काभ्याम्
(ii) काम्
(iii) केषाम्
(iv) कीदृशीम्
Answer
Answer: (i) काभ्याम्
Question 21.
इदानीम् निजकृत्यस्य फलं भुझ्व।
(i) कदा
(ii) काम्
(iii) किम्
(iv) कस्याम्
Answer
Answer: (i) कदा
Question 22.
सर्वम् वृत्तम् अवगत्य सः तम् निर्दोषम् अमन्यत।
(i) कम्
(ii) किम्
(iii) काम्
(iv) कथम्
Answer
Answer: (ii) किम्
Question 23.
इति प्रोच्य आरक्षी उच्चैः अहसत्।
(i) कथम्
(ii) कैः
(iii) के
(iv) कः
Answer
Answer: (i) कथम्
Question 24.
पदातिक्रमेण संचलन् सायं अभवत्।
(i) केन
(ii) किमर्यम्
(iii) कम्
(iv) कीदृशम्
Answer
Answer: (i) केन
Question 25.
तनूजस्य रुग्णतामाकर्ण्य पिता व्याकुलः व्यातः।
(i) कः.
(ii) कीदृशः
(iii) कम्
(iv) कथम्
Answer
Answer: (ii) कीदृशः

अधोलिखितं गद्याशं पठित्वा निर्देशानुसारं प्रश्नान् उत्तरत
(क) कश्चन निर्धनो जनः भूरि परिश्रम्य किञ्चिद् वित्तमुपार्जितवान्। तेन वित्तेन स्वपुत्रम् एकस्मिन् महाविद्यालये प्रवेशं दापयितुं सफलो जातः। तत्तनयः तत्रैव छात्रावासे निवसन् अध्ययने संलग्नः समभूत्। एकदा स पिता तनूजस्य रुग्णतामाकर्ण्य व्याकुलो जातः पुत्रं द्रष्टुं च प्रस्थितः। परमर्थकार्येन पीडितः स बसयानं विहाय पदातिरेव प्राचलत्। पदातिक्रमेण संचलन् सायं समयेऽप्यसौ गन्तव्याद् दूरे आसीत्। “निशान्धकारे प्रसृते विजने प्रदेशे पदयात्रा न शुभावहा।’ एवं विचार्य स पार्श्वस्थिते ग्रामे रात्रिनिवासं कर्तुं कञ्चिद् गृहस्थमुपागतः। करुणापरो गृही तस्मै आश्रयं प्रायच्छत्।
Question 1.
कीदृशः जनः परिश्रमं करोति?
Answer
Answer: निर्धनम्
Question 2.
सः कम् महाविद्यालये प्रवेशं दापयितुं सफलः जातः?
Answer
Answer: स्वपुत्रम्
Question 3.
निर्धनस्य पुत्रः कुत्र निवसन् अध्ययने संलग्नः समभूत्?
Answer
Answer: छात्रावासे
Question 4.
रात्रिनिवासं कर्तुम् सः कम् उपागतः?
Answer
Answer: सः पावस्थिते ग्रामे रात्रिनिवासम् कर्तुम् कञ्चित् गृहस्थमुपागतः।
Question 5.
कः तस्मै आश्रयं प्रायच्छत्?
Answer
Answer: करुणापरो गृही तस्मै आश्रयं प्रायच्छत्।
Question 6.
‘निर्धनः जनः’ अत्र विशेषणपदं किम्?
Answer
Answer: निर्धनः
Question 7.
‘उपार्जितवान्’ इति क्रियापदस्य कर्तृपदं किम्?
Answer
Answer: जनः
Question 8.
‘पिता’ इति कर्तृपदस्य क्रियापदं किमस्ति?
Answer
Answer: प्रस्थितः
Question 9.
गद्यांशे ‘अधिकम्’ इत्यस्य पदस्य कः पर्यायः लिखितः?
Answer
Answer: (क) भूरि
(ख) विचित्रा दैवगतिः। तस्यामेव रात्रौ तस्मिन् गृहे कश्चन चौरः गृहाभ्यन्तरं प्रविष्टः। तत्र निहितामेकां मञ्जूषाम् आदाय पलायितः। चौरस्य पादध्वनिना प्रबुद्धोऽतिथिः चौरशङ्कया तमन्वधावत् अगृह्णाच्च, परं विचित्रमघटत। चौरः एव उच्चैः क्रोशितुमारभत “चौरोऽयं चौरोऽयम्” इति। तस्य तारस्वरेण प्रबुद्धाः ग्रामवासिनः स्वगृहाद् निष्क्रम्य तत्रागच्छन् वराकमतिथिमेव च चौरं मत्वाऽभर्त्सयन्। यद्यपि ग्रामस्य आरक्षी एव चौर आसीत्। तत्क्षणमेव रक्षापुरुषः तम् अतिथिं चौरोऽयम् इति प्रख्याप्य कारागृहे प्राक्षिपत्।
Question 1.
दैवगतिः कीदृशी अस्ति?
Answer
Answer: विचित्रा
Question 2.
गृहाभ्यान्तरं कः प्रविष्टः?
Answer
Answer: चौरः
Question 3.
कः उच्चैः क्रोशितुम् आरभत?
Answer
Answer: चौरः
Question 4.
ग्रामवासिनः किम् अकुर्वन्?
Answer
Answer: तस्य नरस्य तारस्वरेण प्रबुद्धाः ग्रामवासिनः स्वगृहात् निष्क्रम्य तत्रागच्छन् वराकमतिथिमेव च चौरं मत्वा अभर्त्सयन्।
Question 5.
चौरस्य पादध्वनिना प्रबुद्धोऽतिथिः किम् अकरोत्?
Answer
Answer: चौरस्य पादध्वनिना प्रबुद्धोऽतिथिः चौरशङ्कया तमन्वधावत् अगृह्णाच्च।
Question 6.
‘विचित्रा दैवगतिः’ अत्र विशेषणपदं किम्?
Answer
Answer: विचित्रा
Question 7.
‘प्रविष्टः’ इति क्रियापदस्यं कर्तृपदं किम्?
Answer
Answer: चौरः
Question 8.
‘दिवसे’ इति पदस्य विपर्ययपदं किम् प्रयुक्तम्?
Answer
Answer: रात्रौ
Question 9.
‘उच्चस्वरेण’ इत्यस्य पदस्य अत्र कः पर्यायः आगतः?
Answer
Answer: तारस्वरेण
(ग) अग्रिमे दिने स आरक्षी चौर्याभियोगे तं न्यायालयं नीतवान्। न्यायाधीशो बंकिमचन्द्रः वा उभाभ्यां पृथक्-पृथक् विवरणं श्रुतवान्। सर्वं वृत्तमवगत्य स तं निर्दोषम् अमन्यत आरक्षिणं च दोषभाजनम्। किन्तु प्रमाणाभावात् स निर्णेतुं नाशक्नोत्। ततोऽसौ तौ अग्रिमे दिने उपस्थातुम् आदिष्टवान्। अन्येयुः तौ न्यायालये स्व-स्व-पक्षं पुनः स्थापितवन्तौ। तदैव कश्चिद् तत्रत्यः कर्मचारी समागत्य न्यवेदयत् यत् इतः क्रोशद्वयान्तराले कश्चिज्जनः केनापि हतः। तस्य मृतशरीरं राजमार्ग निकषा वर्तते। आदिश्यतां किं करणीयमिति। न्यायाधीशः आरक्षिणम् अभियुक्तं
च तं शवं न्यायालये आनेतुमादिष्टवान्।
Question 1.
न्यायाधीशस्य नाम किमासीत्?
Answer
Answer: बंकिमचन्द्रः
Question 2.
शवं न्यायालये आनेतुम् कः आदिष्टवान्?
Answer
Answer: न्यायाधीशः
Question 3.
अग्रिमे दिने क: चौर्याभियोगे तं न्यायालयं नीतवान्?
Answer
Answer: आरक्षी
Question 4.
कर्मचारी समागत्य किं न्यवेदयत्?
Answer
Answer: कर्मचारी समागत्य न्यवेदयत् यत् इतः क्रोशद्वयान्तराले कश्चिज्जनः केनापि हतः। तस्य मृतशरीरं राजमार्ग निकषा वर्तते।
Question 5.
न्यायाधीशः कं किं च आदिष्टवान्?
Answer
Answer: न्यायाधीशः आरक्षिणम् अभियुक्तं च तं शवं न्यायालये आनेतुमादिष्टवान्।
Question 6.
‘नीतवान्’ इति क्रियापदस्य कर्तृपदं किम्?
Answer
Answer: आरक्षी
Question 7.
‘अग्रिमे दिने’ अत्र विशेष्यपदं कि प्रयुक्तम्?
Answer
Answer: दिने
Question 8.
‘न्यायाधीशः’ इति कर्तृपदस्य क्रियापदम् किम्?
Answer
Answer: श्रुतवान्
Question 9.
अनुच्छेदे ‘समीपम्’ इति पदस्य अर्थे किं पदम् आगतम्?
Answer
Answer: निकषा
(घ) आदेशं प्राप्य उभौ प्राचलताम्। तत्रोपेत्य काष्ठपटले निहितं पटाच्छादितं देहं स्कन्धेन वहन्तौ न्यायाधिकरणं प्रति प्रस्थितौ। आरक्षी सुपुष्टदेह आसीत्, अभियुक्तश्च अतीव कृशकायः। भारवतः शवस्य स्कन्धेन वहनं तत्कृते दुष्करम् आसीत्। स भारवेदनया क्रन्दति स्म। तस्य क्रन्दनं निशम्य मुदित आरक्षी तमुवाच-रे दुष्ट! तस्मिन् दिने त्वयाऽहं चोरिताया मञ्जूषाया ग्रहणाद् वारितः। इदानीं निजकृत्यस्य फलं भुक्ष्व। अस्मिन् चौर्याभियोगे त्वं वर्षत्रयस्य कारादण्डं लप्स्यसे” इति प्रोच्य उच्चैः अहसत्। यथाकथञ्चिद् उभौ शवमानीय एकस्मिन् चत्वरे स्थापितवन्तौ।
Question 1.
आरक्षी कीदृशः आसीत्?
Answer
Answer: सुपुष्टदेहः
Question 2.
अभियुक्तः कीदृशः आसीत्?
Answer
Answer: कृशकायः
Question 3.
सः कथं क्रन्दति स्म?
Answer
Answer: भारवेदनया
Question 4.
अभियुक्तस्य क्रन्दनं श्रुत्वा प्रसन्नः आरक्षी तम् किम् उवाच?
Answer
Answer: अभियुक्तस्य क्रन्दनं श्रुत्वा प्रसन्नः आरक्षी तम् उवाच-‘रे दुष्ट! तस्मिन् दिने त्वयाऽहं चोरितायाः मञ्जूषायाः ग्रहणाद् वारितः। इदानीं निजकृत्यस्य फलं भुझ्व। अस्मिन् चौर्याभियोगे त्वं वर्षत्रस्य कारादण्ड लप्स्यसे।”
Question 5.
उभौ कथं प्राचलताम्?
Answer
Answer: आदेशं प्राप्य उभौ प्राचलताम्।
Question 6.
‘प्रस्थितौ’ इति क्रियापदस्य कर्तृपदं किम्?
Answer
Answer: उभौ
Question 7.
‘सुपुष्टदेहः’ इति पदस्य विपरीतपदं गद्यांशे किम् प्रयुक्तम्?
Answer
Answer: कृशकायः
Question 8.
‘एकस्मिन्’ इति विशेषणपदस्य विशेष्यपदं किम?
Answer
Answer: चत्वरे
Question 9.
अनुच्छेदे ‘त्वया’ इति कर्तृपदस्य क्रियापदं किम्?
Answer
Answer: वारितः
(ङ) न्यायाधीशेन पुनस्तौ घटनायाः विषये वक्तुमादिष्टौ। आरक्षिणि निजपक्षं प्रस्तुतवति आश्चर्यमघटत् स शवः प्रावारकमपसार्य न्यायाधीशभिवाद्य निवेदितवान्-मान्यवर! एतेन आरक्षिणा अध्वनि यदुक्तं तद् वर्णयामि ‘त्वयाऽहं चोरितायाः मञ्जूषायाः ग्रहणाद् वारितः, अतः निजकृत्यस्य फलं भुक्ष्व। अस्मिन् चौर्याभियोगे त्वं वर्षत्रयस्य कारादण्डं लप्स्यसे’ इति।
Question 1.
आरक्षी किम् प्रस्तुतवान्?
Answer
Answer: निजपक्षम्
Question 2.
न्यायाधीशः कस्याः विषये वक्तम् आदिशति?
Answer
Answer: घटनायाः
Question 3.
चौरः कस्याः ग्रह्णात् वारितः?
Answer
Answer: मञ्जूषायाः
Question 4.
न्यायाधीशेन पुनस्तौ किम् आदिष्टौ?
Answer
Answer: न्यायाधीशेन पुनस्तौ घटनायाः विषये वक्तुमादिष्टौ।
Question 5.
एतेन आरक्षिणा मार्गे किम् उक्तम्?
Answer
Answer: एतेन आरक्षिणा मार्गे उक्तम्-‘त्वयाऽहं चोरितायाः मञ्जूषायाः ग्रहणाद् वारितः, अतः निजकृत्यस्य फलं भुक्ष्व। अस्मिन् चौर्याभियोगे त्वं वर्षत्रयस्य कारादण्डं लप्स्यसे’ इति।
Question 6.
‘निवेदितवान्’ इति क्रियापदस्य कर्तृपदं किम्?
Answer
Answer: शवः
Question 7.
‘मार्गे’ इति पदस्य पर्यायपदं किं प्रयुक्तम्?
Answer
Answer: अध्वनि
Question 8.
‘न्यायाधीशेनः’ इति कर्तृपदस्य क्रियापदं किम्?
Answer
Answer: आदिष्टौ
Question 9.
अनुच्छेदे ‘परपक्षम्’ इति पदस्य कः विपर्ययः आगतः?
Answer
Answer: निजपक्षम्
अधोलिखितं पद्याशं पठित्वा निर्देशानुसारं प्रश्नान् उत्तरत
दष्कराण्यपि कर्माणि मतिवैभवशालिनः।
नीतिं युक्तिं समालम्ब्य लीलयैव प्रकुर्वते॥
Question 1.
कीदृशाः जनाः दुष्कराणि कर्माणि अपि कुर्वन्ति?
Answer
Answer: मतिवैभवशालिनः
Question 2.
जनाः दुष्कराणि कर्माणि कथम् कुर्वन्ति?
Answer
Answer: लीलयैव
Question 3.
का समालम्ब्य मतिवैभवशालिनः कार्याणि कुर्वन्ति?
Answer
Answer: नीतिम्/युक्तिम्
Question 4.
मतिवैभवशालिनः दुष्कराणि कर्माणि कथम् कुर्वन्ति?
Answer
Answer: मतिवैभवशालिनः जनाः दुष्कराणि कर्माणि नीतिं युक्तिं समालम्ब्य लीलयैव कुर्वन्ति।
Question 5.
लीलया के कार्याणि कुर्वन्ति?
Answer
Answer: लीलया मतिवैभवशालिनः कार्याणि कुर्वन्ति।
Question 6.
‘दुष्कराणि’ इति विशेषणपदस्य विशेष्यपदं किम्?
Answer
Answer: कर्माणि
Question 7.
प्रकुर्वते’ इति क्रियापदस्य कर्तृपदं किम्?
Answer
Answer: मतिवैभवशालिन:
Question 8.
‘सुकराणि’ इति पदस्य विपर्ययपदं पद्यांशे किमस्ति?
Answer
Answer: दुष्कराणि
Question 9.
श्लोके ‘सरलतया’ पदस्य कः पर्यायः आगतः?
Answer
Answer: लीलया
वाक्येषु रेखाकितपदानां स्थाने प्रश्नवाचकं पदं प्रयुज्य प्रश्ननिर्माणं कुरुत
(क) निर्धनः जनः वित्तम् उपार्जितवान्।
(ख) वित्तेन स्वपुत्रम् महाविद्यालये प्रवेशं दापयितुं सफलः जातः।
(ग) छात्रावासे निवसन् अध्ययने संलग्नः समभूत्।
(घ) तस्य पिता तनूजस्य रुग्णतामकर्ण्य व्याकुलः अभवत्।
(ङ) सः बसयानं विहाय पदातिरेव प्राचलत्।
(च) विचित्रा दैवगतिः भवति।
(छ) निशान्धकारे प्रसृते विजने प्रदेशे पदयात्रा न शुभावहा।
(ज) रात्रिनिवासं कर्तुं सः कञ्चिद् गृहस्थमुपागतः।
(झ) रात्रौ गृहे कश्चन चौरः गृहाभ्यन्तरं प्रविष्टः।
(ञ) चौरस्य पादध्वनिना अतिथिः प्रबुद्धः।
(ट) चौरस्य तारस्वरेणं ग्रामवासिनः अपि प्रबुद्धाः।
(ठ) ते सर्वे गृहात् निष्क्रम्य अतिथिमेव चौरं मत्वाऽभर्त्सयन्।
(ड) रक्षापुरुषः अतिथिम् कारागृहे प्राक्षिपत्।
(ढ) आरक्षी अतिथिम् न्यायालयं नीतवान्।
(ण) न्यायाधीशः विवरणं श्रुतवान्।
(त) प्रमाणाभावात् न्यायाधीशः निर्णेतुं नाशक्नोत्।
(थ) अन्येयुः तौ न्यायालये स्व-स्व-पक्षं पुनः स्थापितवन्तौ।
(द) एकः मृतशरीरं राजमार्ग निकषा वर्तते।
(ध) न्यायाधीशः तं शवं न्यायालये आनेतुमादिष्टवान्।
(न) आरक्षी सुपुष्टदेहः आसीत्।
(प) अभियुक्तः अतीव कृशकायः आसीत्।
(फ) सः भारवेदनया क्रन्दति स्म।
(ब) तस्य क्रन्दनं श्रुत्वा मुदितः आरक्षी तमुवाच।
(भ) उभौ शवम् आनीय चत्वरे स्थापितवन्तौ।
(म) न्यायाधीशेन पुनस्तौ घटनायाः विषये वक्तुमादिष्टौ।।
Answer
Answer:
(क) किम्
(ख) केन
(ग) कस्मिन्
(घ) कस्य
(ङ) किम्
(च) कीदृशी
(छ) कीदृशे
(ज) किम्
(झ) कुत्र
(ञ) केन
(ट) के
(ठ) कस्मात्
(ड) कम्
(ढ) कुत्र।
(ण) कः
(त) कस्मात्
(थ) कदा
(द) कुत्र
(ध) कुत्र
(न) कीदृशः
(प) कीदृशः
(फ) कया
(ब) कीदृशः
(भ) कम्
(म) केन
अधोलिखितस्य श्लोकस्य प्रदत्ते अन्वये रिक्तस्थानानि पूरयत-
दुष्कराष्यपि कर्माणि मतिवैभवशालिनः।
नीतिं युक्तिं समालम्ब्य लीलयैव प्रकुर्वते॥
अन्वयः-मति वैभव शालिनः (जना) (i) …………… युक्तिं (ii) ……………. दुष्कराणि (iii) …………….. कर्माणि (iv) …………….. एव प्रकुर्वते।
मञ्जूषा- लीलया, नीति, अपि, समालम्ब्य
Answer
Answer:
(i) नीतिं
(ii) समालम्ब्य
(iii) अपि
(iv) लीलया
अधोलिखितश्लोकस्य भावार्थम् मञ्जूषातः उचितपदानि चित्वा पूरयत-
दुष्कराष्यपि कर्माणि मतिवैभवशालिनः।
नीतिं युक्तिं समालम्ब्य लीलयैव प्रकुर्वते॥
भावार्थ:- अस्य भावोऽस्ति यत् बुद्धि (i) ………………. युक्ताः जनाः उत्तम (ii) …………………. युक्तेः च आधारं नीत्वा (iii) …………… अपि कार्याणि लीलया एव (iv) …………. तेषु ते कदापि कठिनतामपि न अनुभवन्ति।
मञ्जूषा- प्रकुर्वन्ति, धनेन, कठिनतमानि, नीतेः
Answer
Answer:
(i) धनेन
(ii) नीते:
(iii) कठिनतमानि
(iv) प्रकुर्वन्ति
अधोलिखानि वाक्यानि कथाक्रमानुसार पुनः लेखनीयानि
I. (क) तेन वित्तेन तत्पुत्रम् महाविद्यालये प्रवेशं दापयितुं सफलः जातः।
(ख) तत्र निवसन् अध्ययने संलग्नः समभूत्।
(ग) पिता पुत्रं द्रुष्टुं च प्रस्थितः।
(घ) कश्चन निर्धनः जनः वित्तमुपार्जितवान्।
(ङ) सः बसयानं विहाय पदातिरेव प्राचलत्।
(च) एकदा तस्य पुत्रः रुग्णः अभवत्।
(छ) तत् तनयः छात्रावासे वसति स्म।
(ज) पुत्रस्य रुग्णतामाकर्ण्य सः व्याकुलः सञ्जातः।
Answer
Answer:
(क) कश्चन निर्धनः जनः वित्तमुपार्जितवान्।।
(ख) तेन वित्तेन तत्पुत्रम् महाविद्यालये प्रवेशं दापयितुं सफलः जातः।
(ग) तत् तनयः छात्रावासे वसति स्म।
(घ) तत्र निवसन् अध्ययने संलग्नः समभूत्।
(ङ) एकदा तस्य पुत्रः रुग्णः अभवत्।
(च) पुत्रस्य रुग्णतामाकर्ण्य सः व्याकुलः सञ्जातः।
(छ) पिता पुत्रं द्रुष्टुं च प्रस्थितः।
(ज) सः बसयानं विहाय पदातिरेव प्राचलत्।
II. (क) सः पुत्रं द्रष्टुम् पदातिरेव प्राचलत्।
(ख) तस्मिन् गृहे कश्चन चौरः गृहाभ्यन्तरं प्रविष्टः।
(ग) चौरः एव उच्चैः क्रोशितुमारभत।
(घ) कश्चन निर्धनः जनः वित्तम् उपार्जितवान्।
(ङ) रात्रिनिवासं कर्तुम् कञ्चिद् गृहस्थमुपागतः।
(च) एकदा तस्य पुत्रः रुग्णः जातः।
(छ) चौरस्य पादध्वनिना अतिथिः प्रबुद्धः।
(ज) ग्रामवासिनः वराकमतिथिमेव चौरं मत्वाऽभर्त्सयन्।
Answer
Answer:
(क) कश्चन निर्धनः जनः वित्तम् उपार्जितवान्।
(ख) एकदा तस्य पुत्रः रुग्णः जातः।।
(ग) सः पुत्रं द्रष्टुम् पदातिरेव प्राचलत्।
(घ) रात्रिनिवासं कर्तुम् कञ्चिद् गृहस्थमुपागतः।
(ङ) तस्मिन् गृहे कश्चन चौरः गृहाभ्यन्तरं प्रविष्टः।
(च) चौरस्य पादध्वनिना अतिथिः प्रबुद्धः।
(छ) चौरः एव उच्चैः क्रोशितुमारभत।
(ज) ग्रामवासिनः वराकमतिथिमेव चौरं मत्वाऽभर्त्सयन्।
III. (क) तस्मिन् दिने त्वयाऽहं चोरितायाः मञ्जूषायाः ग्रहणाद् वारितः।
(ख) न्यायाधीशः उभाभ्यां पृथक्-पृथक् विवरणं श्रुतवान्।
(ग) न्यायाधीशेन पुनः तौ घटनायाः विषये वक्तुमादिष्टौ।
(घ) न्यायाधीशः प्रामाणाभावात् निर्णेतुम् नाशक्नोत्।
(ङ) स शवः प्रावारकमपसार्य न्यायाधीशम् सत्यं निवेदितवान्।
(च) अन्येधुः तौ न्यायालये स्व-स्व-पक्षं पुनः स्थापितवन्तौ।
(छ) न्यायाधीशः आरक्षिणे कारादण्डम् आदिश्य तं जनं ससम्मानं मुक्तवान्।
(ज) न्यायाधीशः आरक्षिणम् अभियुक्तं च तं शवं न्यायालये आनेतुम् आदिष्टवान्।
Answer
Answer:
(क) न्यायाधीशः उभाभ्यां पृथक्-पृथक् विवरणं श्रुतवान्।
(ख) न्यायाधीशः प्रामाणाभावात् निर्णेतुम् नाशक्नोत्।
(ग) अन्येधुः तौ न्यायालये स्व-स्व-पक्षं पुनः स्थापितवन्तौ।
(घ) न्यायाधीशः आरक्षिणम् अभियुक्तं च तं शवं न्यायालये आनेतुम् आदिष्टवान्।
(ङ) तस्मिन् दिने त्वयाऽहं चोरितायाः मञ्जूषायाः ग्रहणाद् वारितः।
(च) न्यायाधीशेन पुनः तौ घटनायाः विषये वक्तुमादिष्टौ।
(छ) स शवः प्रावारकमपसार्य न्यायाधीशम् सत्यं निवेदितवान्।
(ज) न्यायाधीशः आरक्षिणे कारादण्डम् आदिश्य तं जनं ससम्मानं मुक्तवान्।
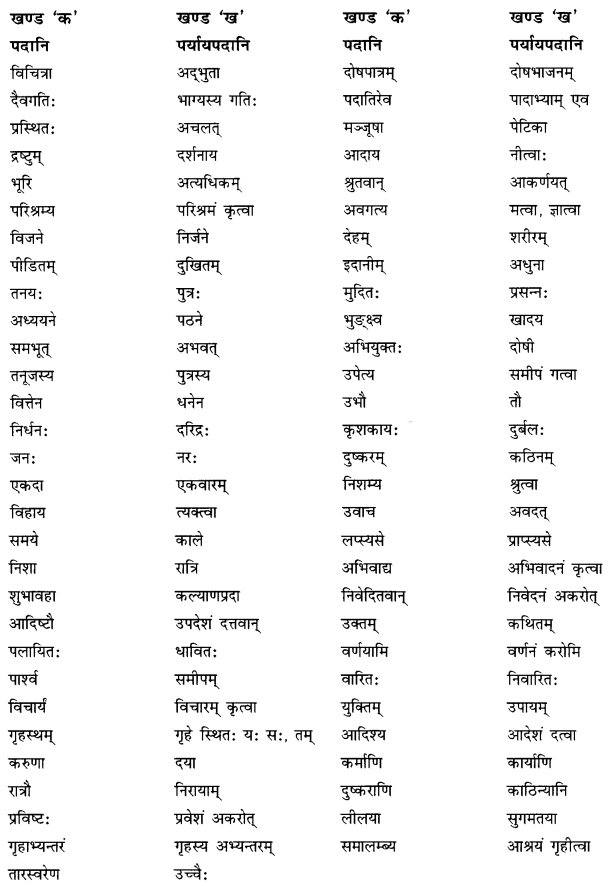
अधोलिखितपदानां तेषाम् पर्यायपदैः च मेलनं कुरुत
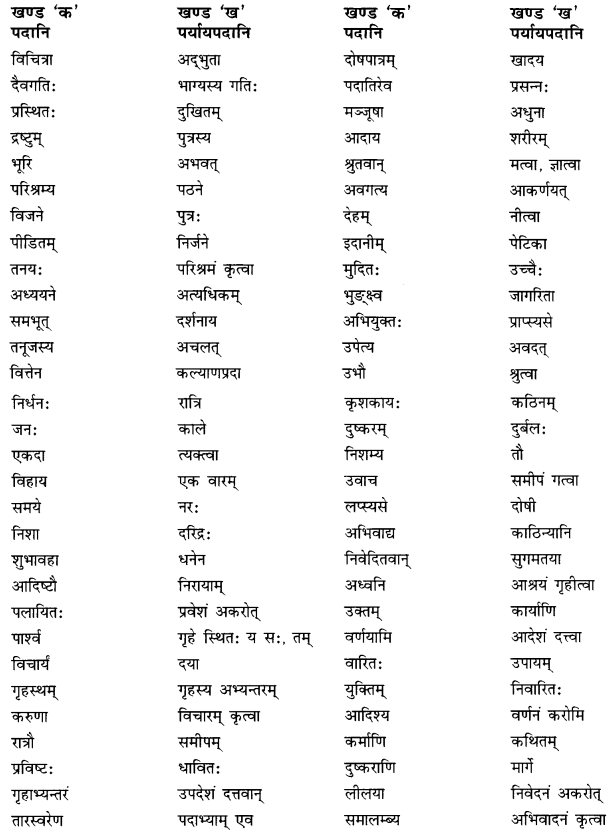
Answer
Answer:
विशेषण-विशेष्यपदानि योजयत
विशेषणपदानि – विशेष्यपदानि
(क) निर्धनो – (i) प्रदेशे
(ख) भूरि – (ii) दिने
(ग) विजने – (iii) विवरणं
(घ) अग्रिम – (iv) शवस्य
(ङ) पृथक-पृथकं – (v) आरक्षी
(च) स्व-स्व – (vi) पक्षं
(छ) भारवतः – (vii) परिश्रम्य
(ज) मुदित – (viii) जनः
Answer
Answer:
विशेषणपदानि – विशेष्यपदानि
(क) निर्धनो – (viii) जनः
(ख) भूरि – (vii) परिश्रम्य
(ग) विजने – (i) प्रदेशे
(घ) अग्रिम – (ii) दिने
(ङ) पृथक-पृथकं – (iii) विवरणं
(च) स्व-स्व – (vi) पक्षं
(छ) भारवतः – (iv) शवस्य
(ज) मुदित – (v) आरक्षी
संस्कृतेन वाक्यप्रयोगं कुरुत

Answer
Answer:
(क) वृद्धः पिता स्वपुत्रान् कृषिकर्मणः सञ्चलनाय भूयोभूयः प्रेरयति।
(ख) आलसाः पुत्राः शृण्वन्ति।
(ग) अपरः पुत्रः तथैव आदिष्टः।
(घ) एकैकं दण्ड पुत्रेभ्यः दत्तवान्।
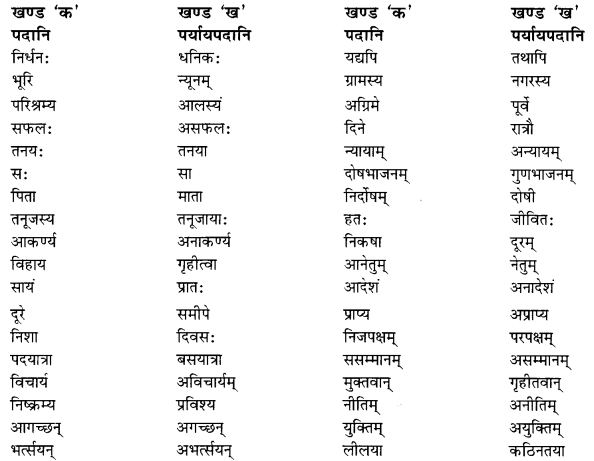
अधोलिखितपदानां तेषाम् विपर्ययपदानि सह मेलनं कुरुत
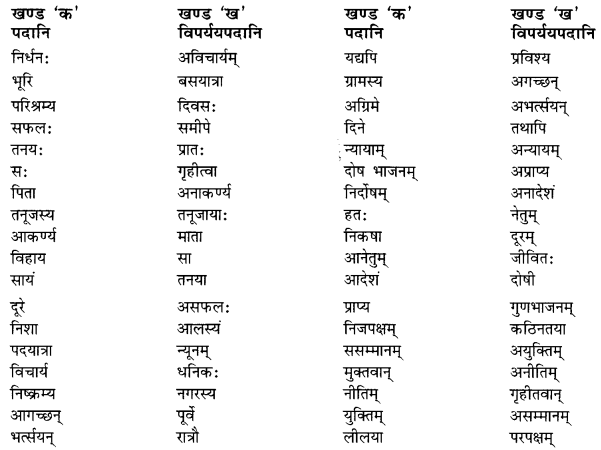
Answer
Answer:
We hope the given NCERT MCQ Questions for Class 10 Sanskrit Chapter 8 विचित्रः साक्षी with Answers Pdf free download will help you. If you have any queries regarding CBSE Class 10 Sanskrit विचित्रः साक्षी MCQs Multiple Choice Questions with Answers, drop a comment below and we will get back to you soon.