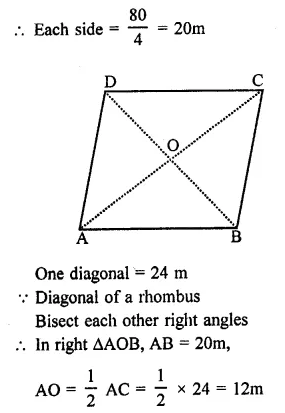
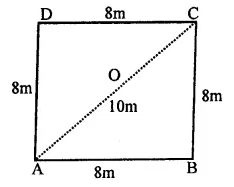
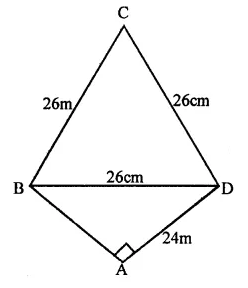
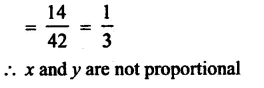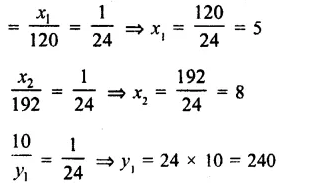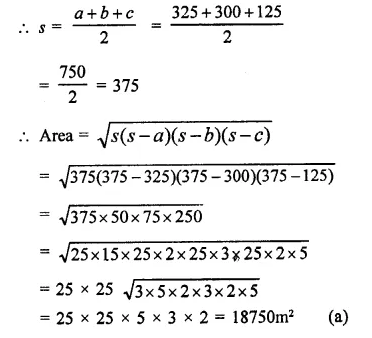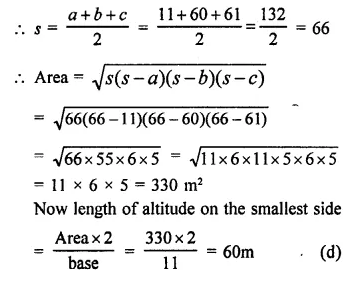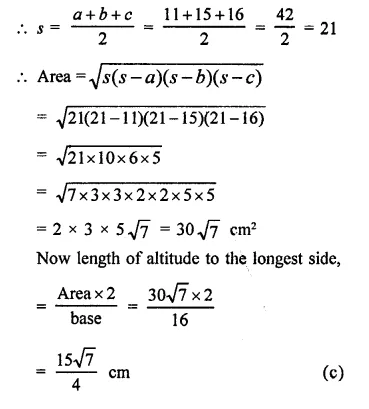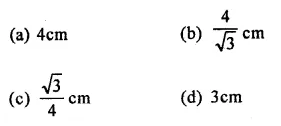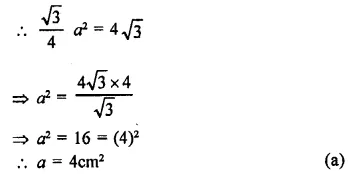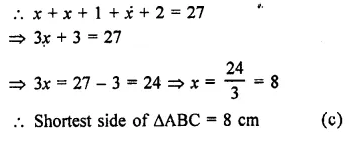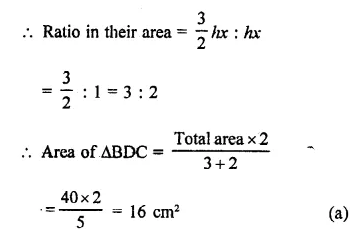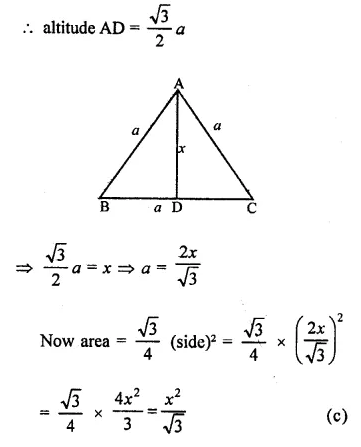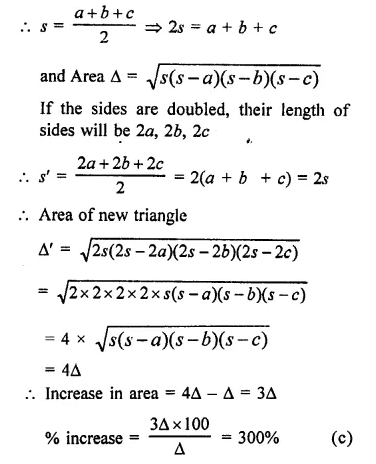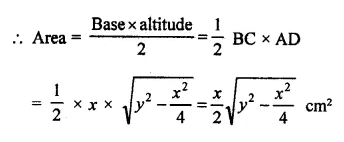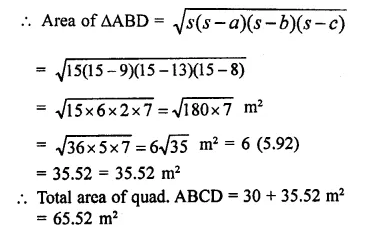NCERT Exemplar Solutions for Class 9 Science Chapter 9 Force and Laws of Motion
These Solutions are part of NCERT Exemplar Solutions for Class 9 Science . Here we have given NCERT Exemplar Solutions for Class 9 Science Chapter 9 Force and Laws of Motion
MULTIPLE CHOICE QUESTIONS
Question 1.
Which of the following statement is not correct for an object moving along a straight path in an accelerated motion ?
(a) Its speed keeps changing
(b) Its velocity always changes
(c) It always goes away from the earth
(d) A force is always acting on it.
Answer:
(c).
More Resources
- NCERT Exemplar Solutions for Class 9 Science
- NCERT Solutions for Class 9 Science
- Value Based Questions in Science for Class 9
- HOTS Questions for Class 9 Science
- Previous Year Question Papers for CBSE Class 9 Science
Question 2.
According to the third law of motion, action and reaction
(a) always act on the same body
(b) always act on different bodies in opposite directions
(c) have same magnitude and directions
(d) act on either body at normal to each other.
Answer:
(b).
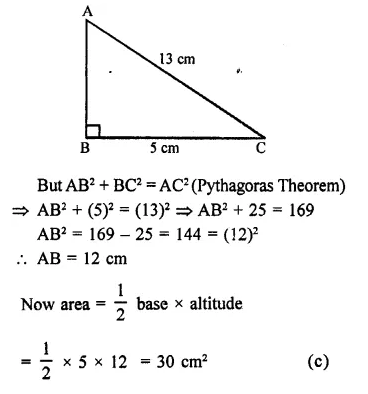
Question 3.
A goalkeeper in a game of football pulls his hands backwards after holding the ball shot at the goal. This enables the goal keeper to
(a) exert larger force on the ball
(b) reduce the force exerted by the ball on hands
(c) increase the rate of change of momentum
(d) decrease the rate of change of momentum.
Answer:
(b) Explanation :
![]()
Question 4.
By pulling his hands backwards, he increases the time to reduce the momentum of the ball. Hence, less force is exerted on his hands. The inertia of an object tends to cause the object
(a) to increase its speed
(b) to decrease its speed
(c) to resist any change in its state of motion
(d) to decelerate due to friction.
Answer:
(c).
Question 5.
A passenger in a moving train tosses a coin which falls behind him, it means that motion of the train is
(a) accelerated
(b) uniform
(c) retarded
(d) along circular tracks.
Answer:
(a).
Question 6.
An object of mass 2 kg is sliding with a constant velocity of 4 m s-1 on a frictionless horizontal table. The force required to keep the object moving with the same velocity is
(a) 32 N
(b) 0 N
(c) 2 N
(d) 8 N.
Answer:
(b) Explanation : No force is needed to keep the object moving with constant velocity.
Question 7.
Rocket works on the principle of conservation of
(a) mass
(b) energy
(c) momentum
(d) velocity.
Answer:
(c).
Question 8.
A water tanker filled up to 2/3 of its height is moving with a uniform speed. On sudden application of the brake, the water in the tank would
(a) move backward
(b) move forward
(c) be unaffected
(d) rise upwards.
Answer:
(b) Explanation : It is due to inertia of motion.
SHORT ANSWER QUESTIONS
Question 9.
There are three solids made up of aluminium, steel and wood, of the same shape and same volume. Which of them would have highest inertia? (CBSE 2012)
Answer:
Density of steel is more than that of aluminium and wood, so its mass is greater than the solids made of aluminium and wood. Inertia depends on the mass of object. Hence, steel has the highest inertia.
Question 10.
Two balls of the same size but of different materials, rubber and iron are kept on the smooth surface of a moving trains. The brakes are applied suddenly to stop the train. Will the balls start rolling ? If so, in which direction ? Will they move with the same speed ? Justify your answer. (CBSE Sample Paper)
Answer:
When train slows down, balls remain in motion due to inertia of motion. Hence, balls start rolling in the forward direction. Since mass of both the balls are different, so they move with different speed.
Question 11.
Two identical bullets are fired one by a light rifle and another by a heavy rifle with the same force. Which rifle will hurt the shoulder more and why ? (CBSE 2012)
Answer:
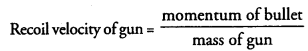
Recoil velocity of light rifle is more than that of heavy rifle. Therefore, light rifle will
hurt the shoulder more than heavy rifle.
Question 12.
A horse continues to apply a force in order to move a cart with a constant velocity. Explain why ?
Answer:
The cart will move with a constant velocity if no net external force acts on it. When horse applies a force on the cart, frictional force, also acts between the tyres of the cart and the road to oppose its motion. The cart will move with constant velocity only if the force applied by the horse is equal to the frictional force.
Question 13.
A ball of mass m is thrown vertically upward with an initial speed Its speed decreases continuously till it becomes zero. Thereafter, the ball begins to fell downward and attains the speed v again before striking the ground. It implies that the magnitude of initial and final momentum of the ball are same. Yet, it is not example of conservation of momentum. Explain why ?
(CBSE Sample Paper)
Answer:
Momentum of the system is conserved only if no external force acts on the system. However, in the given example, gravitational force acts on the ball when it moves upward or when it falls downward. Therefore, it is not the example of conservation of momentum.
Question 14.
Velocity versus time graph of a ball of mass 50 g rolling on a concrete floor is shown in Fig. 1
Calculate the acceleration and frictional force of the floor on the ball.
Answer:
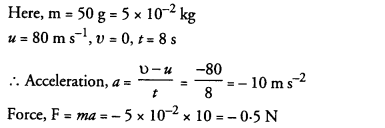
This force is known as retarding force or the frictional force of the floor on the ball.
Question 15.
A truck of mass M is moved under a force F. If the truck is then loaded with an object equal to the mass of the truck and the driving force is halved, then how does the acceleration change ?
Answer:
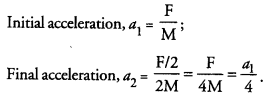
Question 16.
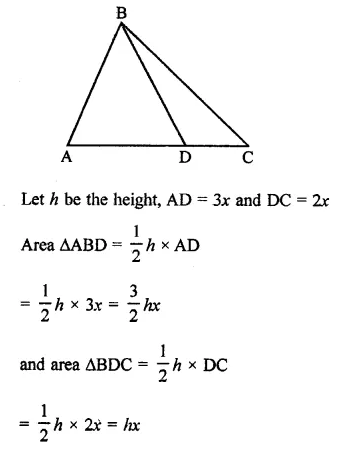
Two friends on roller-skates are standing 5 metres apart facing each other. One of them throws a ball of 2 kg towards the other, who catches it. How will this activity affect the position of the two ? Explain.
Answer:
When one boy throws a ball towards the other boy, he moves in the backward direction to conserve the linear momentum. On the other hand, the second boy will move away from the first boy after receiving momentum from the ball. Therefore, the distance between two friends will increase.
Question 17.
Water sprinkler used for grass lawns begins to rotate as soon as the water is supplied. Explain the principle on which it works.
Answer:
Water sprinkler works on Newton’s third law of motion.
LONG ANSWER QUESTIONS
Question 18.
Using second law of motion, derive the relation between force and acceleration. A bullet of 10 g strikes a sand-bag at a speed of 103 ms-1 and gets embedded after travelling 5 cm. Calculate
(i) the resistive force exerted by the sand on the bullet
(ii) the time taken by the bullet to come to rest.
Answer:
According to this law, the change in momentum of a body per unit time (i.e. rate of change of momentum) is directly proportional to the unbalanced force acting on the body and the change in momentum takes place in the direction of the unbalanced force on the body.
Consider a body of mass moving with initial velocity Let a force acts on the body for time so that the velocity of the body after time is .
Initial momentum of the body, pi = mu
Final momentum of the body, pf = mv
Now, change in momentum of the body = pf — pi = mv – mu = m(v-u)

Thus, force acting on the body is directly proportional to (i) its mass (m) and (ii) its acceleration (a).
Eqn. (1) gives the mathematical form of Newtons second law of motion. The force given by eqn (1) acts on the body.
Newton’s second law of motion in vector form
We know, force ( F ) and acceleration ( a ) are vector quantities, whereas mass ( m) is a scalar quantity. Therefore, Newton’s second law of motion can be written in vector form as
![]()
This relation shows that the direction of force applied on the body is same as that of the acceleration produced in the body.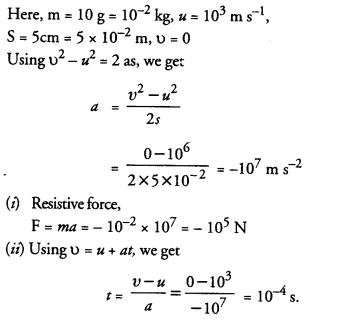
Question 19.
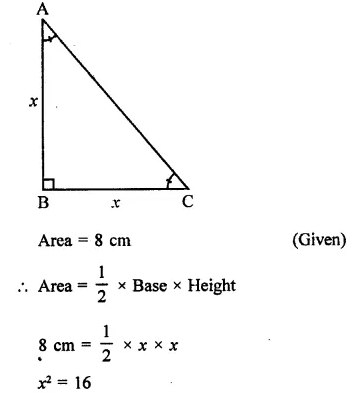
Derive the unit of force using the second law of motion. A force of 5 N produces an acceleration of 8 m s-2 on a mass m1 and an acceleration of 24 m s-2 on a mass m2. What acceleration would the same force provide if both the masses are tied together ?
Answer:
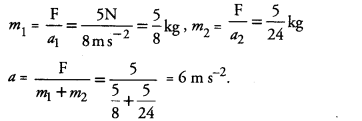
Question 20.
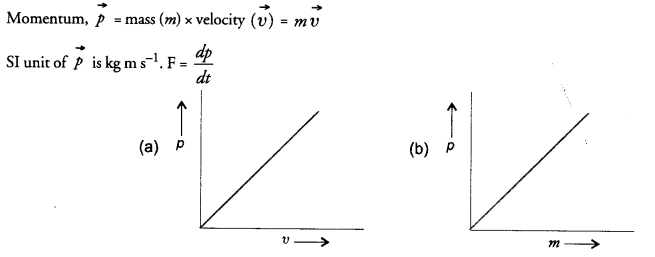
What is momentum ? Write its SI unit. Interpret force in terms of momentum. Represent the following graphically
(a) momentum versus velocity when mass is fixed.
(b) momentum versus mass when velocity is constant.
Answer:
Hope given NCERT Exemplar Solutions for Class 9 Science Chapter 9 Force and Laws of Motion are helpful to complete your science homework.
If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.