Prasanna

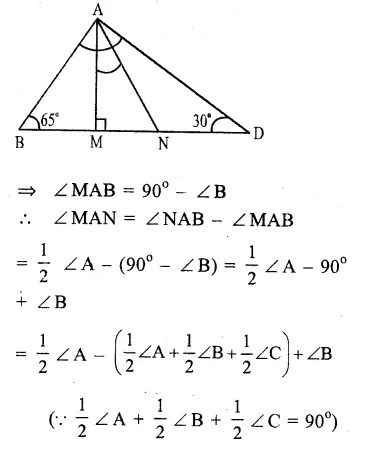
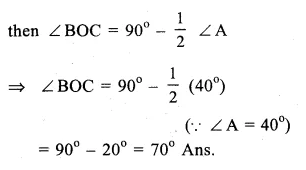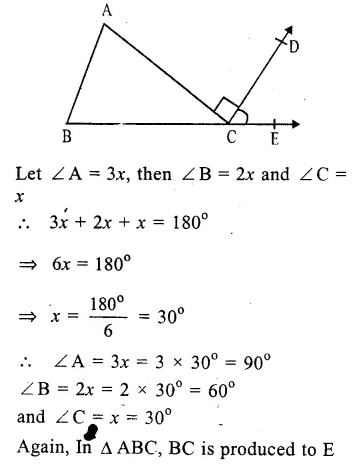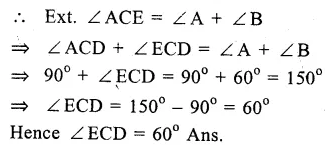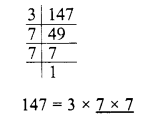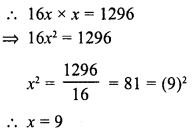RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.2

Other Exercises

• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.1
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.2
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.3
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.4
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials VSAQS
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials MCQS

Question 1.
If f(x) = 2x³ – 13x² + 17x + 12, find
(i) f (2)
(ii) f (-3)
(iii) f(0)
Solution:
f(x) = 2x³ – 13x² + 17x + 12
(i) f(2) = 2(2)³ – 13(2)² + 17(2) + 12
= 2 x 8-13 x 4+17 x 2+12
= 16-52 + 34 + 12
= 62 – 52
= 10
(ii) f(-3) = 2(-3)³ – 13(-3)² + 17 x (-3) + 12
= 2 x (-27) – 13 x 9 + 17 x (-3) + 12
= -54 – 117 -51 + 12
= -222 + 12
= -210
(iii) f(0) = 2 x (0)³ – 13(0)² + 17 x 0 + 12
= 0-0 + 0+ 12 = 12

Question 2.
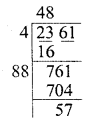
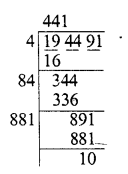
Verify whether the indicated numbers are zeros of the polynomials corresponding to them in the following cases: [NCERT]

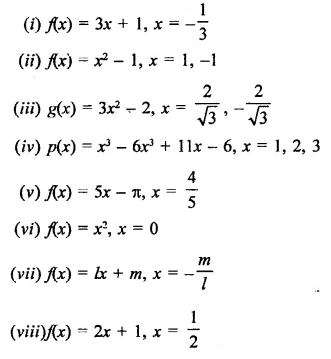
Solution:

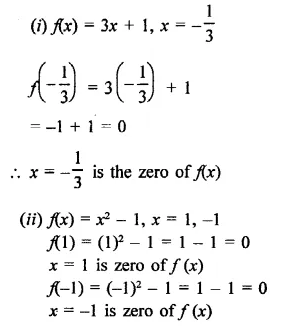
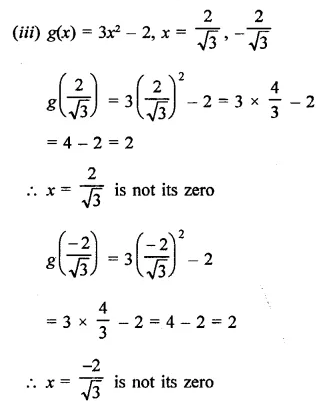
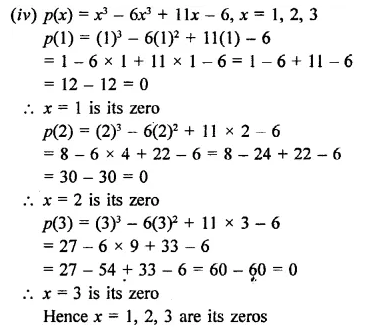
Question 3.
If x = 2 is a root of the polynomial f(x) = 2x²-3x + la, find the value of a.
Solution:
p(x) = 2x² – 3x + 7a
∵ x = 2 is its zero, then
p(0) = 0
∴ p( 2) = 2(2)² – 3×2 + la = 0
⇒2 x 4-3 x2 + 7a = 0
⇒ 8 – 6 + 7o = 0
⇒2 + 7a = 0
⇒ 7a = -2 ⇒ a =\(\frac { -2 }{ 7 }\)
∴ Hence a = \(\frac { -2 }{ 7 }\)

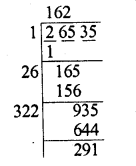
Question 4.
If x = –\(\frac { 1 }{ 2 }\) is a zero of the polynomial p(x) = 8x³ – ax² – x + 2, find the value of a.
Solution:

Question 5.
If x = 0 and x = -1 are the roots of the polynomial f(x) = 2x³ – 3x² + ax + b, find the value of a and b.
Solution:
f(x) = 2x³ – 3x² + ax + b
∵ x = 0 and x = -1 are its zeros
∴ f(0) = 0 and f(-1) = 0
Now, f(0) = 0
⇒  2(0)³ – 3(0)² + a x 0 + b = 0
⇒ 0-0 + 0 + b= 0
∴ b = 0
and f(-1) = 0
⇒ 2(-1)³ – 3(-1)² + a(-1) + b = 0
⇒  2 x (-1) – 3 x 1 + a x (-1) + b = 0
⇒ -2 -3-a + b = 0
⇒ -2-3-a + 0 = 0
⇒ -5- a = 0=>a =-5
Hence a = -5, b = 0

Question 6.
Find the integral roots of the polynomial f(x) = x³ + 6x² + 11x + 6.
Solution:
f(x) = x³ + 6x² + 11x + 6
Construct = 6 = ±1, ±2, +3, ±6
If x = 1, then
f(1) = (1)³ + 6(1)² + 11 x 1 + 6
= 1+ 6+11+ 6 = 24
∵  f(x) ≠ 0, +0
∴ x = 1 is not its zero
Similarly, f(-1) = (-1)³ + 6(-1)² + 11(-1) + 6
= -1 + 6 x 1-11+6
=-1+6-11+6
= 12-12 = 0
∴  x = -1 is its zero
f(-2) = (-2)³ + 6(-2)² + 11 (-2) + 6
= -8 + 24 – 22 + 6
= -30 + 30 = 0
∴ x = -2 is its zero
f(-3) = (-3)³ + 6(-3)² + 11 (-3) + 6
= -27 + 54 – 33 + 6 = 60 – 60 = 0
∴  x = -3 is its zero
x = -1, -2, -3 are zeros of f(x)
Hence roots of f(x) are -1, -2, -3

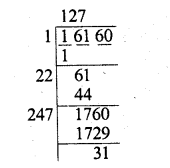
Question 7.
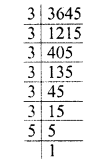
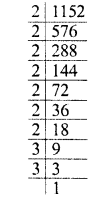
Find the rational roots of the polynomial f(x) = 2x³ + x² – 7x – 6.
Solution:

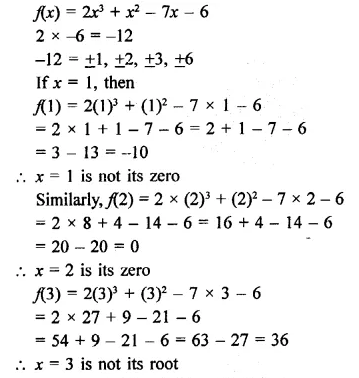
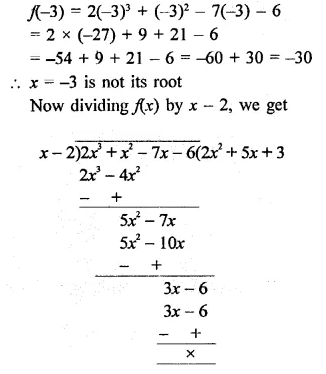
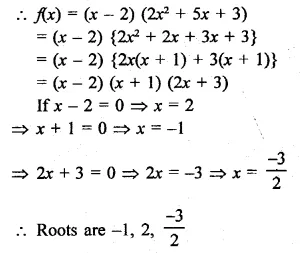
Hope given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2

Other Exercises

• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.1
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.3
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.5
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.6
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.8
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.9

Question 1.
The following numbers are not perfect squares. Give reason :
(i) 1547
(ii) 45743
(iii) 8948
(iv) 333333

Solution:
We know that if the units digit is 2, 3, 7 or 8 of a number, then the number is not a perfect square.

(i) ∴ 1547 has 7 as units digit.
∴ It is not a perfect square.

(ii) 45743 has 3 as units digit
∴ It is not a perfect square.

(iii)  ∴ 8948 has 8 as units digit
∴ It is not a perfect square.

(iv)  ∴ 333333 has 3 as units digits
∴ It is not a perfect square.

Question 2.
Show that the following numbers are not perfect squares :
(i) 9327
(ii) 4058
(iii) 22453
(iv) 743522

Solution:
(i) 9327
∴ The units digit of 9327 is 7
∴ This number can’t be a perfect square.

(ii) 4058
∴ The units digit of 4058 is 8
∴ This number can’t be a perfect square.

(iii) 22453
∴ The units digit of 22453 is 3
.∴ This number can’t be a perfect square.

(iv) 743522
∴ The units digit of 743522 is 2
∴ This number can’t be a perfect square.

Question 3.
The square of which of the following numbers would be an odd number ?
(i) 731
(ii) 3456
(iii) 5559
(iv) 42008
Solution:
We know that the square of an odd number is odd and of even number is even. Therefore
(i) Square of 731 would be odd as it is an odd number.
(ii) Square of 3456 should be even as it is an even number.
(iii) Square of 5559 would be odd as it is an odd number.
(iv) The square of 42008 would be an even number as it is an even number.
Therefore suqares of (i) 731 and (ii) 5559 will be odd numbers.

Question 4.
What will be the units digit of the squares of the following numbers ?
(i) 52
(ii) 977
(iii) 4583
(iv) 78367
(v) 52698
(vi) 99880
(vii) 12796
(viii) 55555
(ix) 53924

Solution:

(i) Square of 52 will be 2704 or (2)² = 4
∴ Its units digit is 4.

(ii) Square of 977 will be 954529 or (7)² = 49 .
∴ Its units digit is 9

(iii) Square of 4583 will be 21003889 or (3)² = 9
∴ Its units digit is 9

(iv) IS 78367, square of 7 = 7² = 49
∴ Its units digit is 9

(v) In 52698, square of 8 = (8)² = 64
∴ Its units digit is 4

(vi) In 99880, square of 0 = 0² = 0
∴ Its units digit is 0

(vii) In 12796, square of 6 = 6² = 36
∴ Its units digit is 6

(viii) In In 55555, square of 5 = 5² = 25
∴ Its units digit is 5

(ix) In 53924, square pf 4 = 4² = 16
∴ Its units digit is 6

Question 5.
Observe the following pattern
1 + 3 = 2²
1 + 3 + 5 = 3²
1+34-5 + 7 = 4²
and write the value of 1 + 3 + 5 + 7 + 9 +…………upto n terms.
Solution:
The given pattern is
1 + 3 = 2²
1 + 3 + 5 = 3²
1+3 + 5 + 7 = 4²
1+3 + 5 + 7 + 9 +……………… upto n terms (number of terms)² = n²

Question 6.
Observe the following pattern :
2² – 1² = 2 + 1
3² – 2² = 3 + 2
4² – 3² = 4 + 3
5² – 4² = 5 + 4
Find the value of
(i) 100² – 99²
(ii) 111² – 109²
(iii) 99² – 96²
Solution:
From the given pattern,
2² – 1² = 2 + 1
3² – 2² = 3 + 2
4² – 3² = 4 + 3
₅² – 4² = 5 + 4
Therefore
(i) 100²-99° = 100 + 99

(ii) 111² – 109² = 111² – 110²– 109²
= (111² – 110²) + (110² – 109²)
= (111 + 110) + (110+ 109)
= 221 + 219 = 440

(iii) 99² – 96² = 99² – 98² + 98² – 97² + 97² – 96²
= (99² – 98²) + (98² – 97²) + (97² – 96²)
= (99 + 98) + (98 + 97) + (97 + 96)
= 197 + 195 + 193 = 585

Question 7.
Which of the following triplets are Pythagorean ?
(i) (8, 15, 17)
(ii) (18, 80, 82)
(iii) (14, 48, 51)
(iv) (10, 24, 26)
(vi) (16, 63, 65)
(vii) (12, 35, 38)
Solution:
A pythagorean triplet is possible if (greatest number)² = (sum of the two smaller numbers)

(i) 8, 15, 17
Here, greatest number =17
∴ (17)² = 289
and (8)² + (15)² = 64 + 225 = 289
∴ 8² + 152 = 172
∴ 8, 15, 17 is a pythagorean triplet

(ii) 18, 80, 82
Greatest number = 82
∴ (82)² = 6724
and 18² + 80² = 324 + 6400 = 6724
∴ 18² + 80² = 82²
∴ 18, 80, 82 is a pythagorean triplet

(iii) 14, 48, 51
Greatest number = 51
∴ (51)² = 2601
and 14² + 48² = 196 + 2304 = 25 00
∴ 51²≠ 14² + 48²
∴ 14, 48, 51 is not a pythagorean triplet

(iv) 10, 24, 26
Greatest number is 26
∴ 26² = 676
and 102 + 242 = 100 + 576 = 676
∴ 26² = 10² + 24²
∴ 10, 24, 26 is a pythagorean triplet

(vi) 16, 63, 65
Greatest number = 65
∴ 65² = 4225
and 16² + 63² = 256 + 3969 = 4225
∴ 65² = 16² + 63²
∴ 16, 63, 65 is a pythagorean triplet

(vii) 12, 35, 38
Greatest number = 38
∴ 38² = 1444
and 12² + 35² = 144 + 1225 = 1369
∴ 38² ≠12² + 35²
∴ 12, 35, 38 is not a pythagorean triplet.

Question 8.
Observe the following pattern

Solution:
From the given pattern

Question 9.
Observe the following pattern

and find the values of each of the following :
(i) 1 + 2 + 3 + 4 + 5 +….. + 50
(ii) 31 + 32 +… + 50
Solution:
From the given pattern,

Question 10.
Observe the following pattern

and find the values of each of the following :
(i) 1² + 2² + 3² + 4² +…………… + 10²
(ii) 5² + 6² + 7² + 8² + 9² + 10² + 12²
Solution:
From the given pattern,

Question 11.
Which of the following numbers are squares of even numbers ?
121,225,256,324,1296,6561,5476,4489, 373758
Solution:
We know that squares of even numbers is also are even number. Therefore numbers 256, 324,1296, 5476 and 373758 have their units digit an even number.
∴ These are the squares of even numbers.

Question 12.
By just examining the units digits, can you tell which of the following cannot be whole squares ?

1. 1026
2. 1028
3. 1024 
4. 1022
5. 1023
6. 1027

Solution:
We know that a perfect square cam at ends with the digit 2, 3, 7, or 8
∴ By examining the given number, we can say that 1028, 1022, 1023, 1027 can not be perfect squares.

Question 13.
Write five numbers for which you cannot decide whether they are squares.
Solution:
A number which ends with 1,4, 5, 6, 9 or 0
can’t be a perfect square
2036, 4225, 4881, 5764, 3349, 6400

Question 14.
Write five numbers which you cannot decide whether they are square just by looking at the unit’s digit.
Solution:
A number which does not end with 2, 3, 7 or 8 can be a perfect square
∴ The five numbers can be 2024, 3036, 4069, 3021, 4900

Question 15.
Write true (T) or false (F) for the following statements.
(i) The number of digits in a square number is even.
(ii) The square of a prime number is prime.
(iii) The sum of two square numbers is a square number.
(iv) The difference of two square numbers is a square number.
(vi) The product of two square numbers is a square number.
(vii) No square number is negative.
(viii) There is not square number between 50 and 60.
(ix) There are fourteen square number upto 200. 

Solution:
(i) False : In a square number, there is no condition of even or odd digits.
(ii) False : A square of a prime is not a prime.
(iii) False : It is not necessarily.
(iv) False : It is not necessarily.
(vi) True.
(vii) True : A square is always positive.
(viii) True : As 7² = 49, and 8² = 64.
(ix) True : As squares upto 200 are 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196 which are fourteen in numbers.

Hope given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry VSAQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry VSAQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.1
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.2
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.3
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.4
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry VSAQS
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry MCQS

Question 1.
Write the equation representing x-axis.
Solution:
The equation of x-axis is, y = 0.

Question 2.
Write the equation representing y-axis.
Solution:
The equation of y-axis is, x = 0.

Question 3.
Write the equation of a line passing through the point (0, 4) and parallel to x-axis.
Solution:
The equation of the line passing through the point (0,4) and parallel to x-axis will be y = 4.

Question 4.
Write the equation of a line passing through the point (3, 5) and parallel to x-axis.
Solution:
The equation of the line passing through the point (3, 5) and parallel to x-axis will be y = 5.

Question 5.
Write the equation of a line parallel toy-axis and passing through the point (-3, -7).
Solution:
The equations of the line passing through the point (-3, -7) and parallel to y-axis will be x = -3.

Question 6.
A line passes through the point (-4, 6) and is parallel to x-axis. Find its equation. A line passes through the point (-4, 6) and is parallel to x-axis. Find its equation.
Solution:
A line parallel to x-axis and passing through the point (-4, 6) will be y = 6.

Question 7.
Solve the equation 3x – 2 = 2x + 3 and represent the solution on the number line.
Solution:
3x – 2 = 2x + 3
⇒  3x – 2x = 3 + 2 (By terms formation)
⇒  x = 5
∴ x = 5
Solution on the number line is

Question 8.
Solve the equation 2y – 1 = y + 1 and represent it graphically on the coordinate plane.

Solution:
2y – 1 = y + 1
⇒ 2y – y = 1 +1
⇒  y = 2
∴ It is a line parallel to x-axis at a distance of 2 units above the x-axis is y = 2.

Question 9.
If the point (a, 2) lies on the graph of the linear equation 2x – 3y + 8 = 0, find the value of a.
Solution:
∵ Points (a, 2) lies on the equation
2x – 3y + 8 = 0
∴ It will satisfy the equation,
Now substituting the value of x = a, y = 2 in the equation
⇒ 2a – 3 x 2+ 8= 0
⇒ 2a + 2= 0
⇒ 2a = -2
⇒ a = \(\frac { -2 }{ 2 }\) = -1
∴ a = -1

Question 10.
Find the value of k for which the point (1, -2) lies on the graph of the linear equation, x – 2y + k = 0.
Solution:
∵ Point (1, -2) lies on the graph of the equation x – 2y + k = 0
∴ x = 1, y = -2 will satisfy the equation
Now substituting the value of x = 1, y = -2 in it
1-2 (-2) + k = 0
⇒  1 + 4 + k = 0
⇒  5+ k = 0 ⇒  k =-5
∴  k = -5

Hope given RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.5

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.5

Other Exercises

• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.1
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.3
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.5
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.6
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.8
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.9

Question 1.
Find the square root of each of the long division method.
(I) 12544
(ii) 97344
(iii) 286225
(iv) 390625
(v) 363609
(vi) 974169
(vii) 120409
(viii) 1471369
(ix) 291600
(x) 9653449
(xi) 1745041
(xii) 4008004
(xiii) 20657025
(xiv) 152547201
(jcv) 20421361
(xvi) 62504836
(xvii) 82264900
(xviii) 3226694416
(xix)6407522209
(xx) 3915380329
Solution:
<

Question 2.
Find the least number which must be subtracted from the following numbers to make them a perfect square :
(i) 2361
(ii) 194491
(iii) 26535
(iv) 16160
(v) 4401624
Solution:
(i) 2361
Finding the square root of 2361

We get 48 as quotient and remainder = 57
∴ To make it a perfect square, we have to subtract 57 from 2361
∴ Least number to be subtracted = 57
(ii) 194491
Finding the square root of 194491

We get 441 as quotient and remainder = 10
∴ To make it a perfect square, we have to subtract 10 from 194491
∴ Least number to be subtracted = 10
(iii) 26535
Finding the square root of 26535

We get 162 as quotient and 291 as remainder
∴ To make it a perfect square, we have to subtract 291 from 26535
∴ Least number to be subtracted = 291
(iv)16160
Finding the square root of 16160

We get 127 as quotient and 31 as remainder
∴ To make it a perfect square, we have to subtract 31 from 16160
∴ Least number to be subtracted = 31
(v) 4401624
Find the square root of 4401624

We get 2098 as quotient and 20 as remainder
∴ To make it a perfect square, we have to subtract 20 from 4401624
∴ Least number to be subtracted = 20

Question 3.
Find the least number which must be added to the following numbers to make them a perfect square :
(i) 5607
(ii) 4931
(iii) 4515600
(iv) 37460
(v) 506900
Solution:
(i) 5607

Finding the square root of 5607, we see that 74² = 5607- 131 =5476 and 75² = 5625
∴ 5476 < 5607 < 5625
∴ 5625 – 5607 = 18 is to be added to get a perfect square
∴ Least number to be added = 18
(ii) 4931

Finding the square root of 4931, we see that 70²= 4900
∴ 71² = 5041 4900 <4931 <5041
∴ 5041 – 4931 = 110 is to be added to get a perfect square.
∴ Least number to be added =110
(iii) 4515600

Finding the square root of 4515600, we see
that 2124² = 4511376
and 2 1 25² = 45 1 56 25
∴ 4511376 <4515600 <4515625
∴ 4515625 – 4515600 = 25 is to be added to get a perfect square.
∴ Least number to be added = 25
(iv) 37460

Finding the square root of 37460
that 193² = 37249, 194² = =37636
∴ 37249 < 37460 < 37636
∴ 37636 – 37460 = 176 is to be added to get a perfect square.
∴ Least number to be added =176
(v) 506900

Finding the square root of 506900, we see that
711² = 505521, 712² = 506944
∴ 505521 < 506900 < 506944
∴ 506944 – 506900 = 44 is to be added to get a perfect square.
∴ Least number to be added = 44

Question 4.
Find the greatest number of 5 digits which is a perfect square.
Solution:
Greatest number of 5-digits = 99999 Finding square root, we see that 143 is left as remainder

∴ Perfect square = 99999 – 143 = 99856 If we add 1 to 99999, it will because a number of 6 digits
∴ Greatest square 5-digits perfect square = 99856

Question 5.
Find the least number of four digits which is a perfect square.
Solution:
Least number of 4-digits = 10000
Finding square root of 1000
We see that if we subtract 39

From 1000, we get three digit number
∴ We shall add 124 – 100 = 24 to 1000 to get a
perfect square of 4-digit number
∴ 1000 + 24 = 1024
∴ Least number of 4-digits which is a perfect square = 1024

Question 6.
Find the least number of six-digits which is a perfect square.
Solution:
Least number of 6-digits = 100000

Finding the square root of 100000, we see that if we subtract 544, we get a perfect square of 5-digits.
So we shall add
4389 – 3900 = 489
to 100000 to get a perfect square
Past perfect square of six digits= 100000 + 489 =100489

Question 7.
Find the greatest number of 4-digits which is a perfect square.
Solution:
Greatest number of 4-digits = 9999

Finding the square root, we see that 198 has been left as remainder
∴ 4-digit greatest perfect square = 9999 – 198 = 9801

Question 8.
A General arranges his soldiers in rows to form a perfect square. He finds that in doing so, 60 soldiers are left out. If the total number of soldiers be 8160, find the number of soldiers in each row.
Solution:
Total number of soldiers = 8160 Soldiers left after arranging them in a square = 60
∴ Number of soldiers which are standing in a square = 8160 – 60 = 8100

Question 9.
The area of a square field is 60025 m². A man cycle along its boundry at 18 km/hr. In how much time will be return at the starting point.
Solution:
Area of a square field = 60025 m²

Question 10.
The cost of levelling and turfing a square lawn at Rs. 250 per m² is Rs. 13322.50. Find the cost of fencing it at Rs. 5 per metre ?
Solution:
Cost of levelling a square field = Rs. 13322.50
Rate of levelling = Rs. 2.50 per m²

and perimeter = 4a = 4 x 73 = 292 m Rate of fencing the field = Rs. 5 per m
∴ Total cost of fencing = Rs. 5 x 292 = Rs. 1460

Question 11.
Find the greatest number of three digits which is a perfect square.
Solution:
3-digits greatest number = 999

Finding the square root, we see that 38 has been left
∴ Perfect square = 999 – 38 = 961
∴ Greatest 3-digit perfect square = 961

Question 12.
Find the smallest number which must be added to 2300 so that it becomes a perfect square.
Solution:
Finding the square root of 2300

We see that we have to add 704 – 700 = 4 to 2300 in order to get a perfect square
∴ Smallest number to be added = 4

Hope given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.9

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.9

Other Exercises

• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.1
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.3
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.5
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.6
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.8
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.9

Using square root table, find the square roots of the following :

Question 1.
7
Solution:

Question 2.
15
Solution:

Question 3.
74
Solution:

Question 4.
82
Solution:

Question 5.
198
Solution:

Question 6.
540
Solution:

Question 7.
8700
Solution:

Question 8.
3509
Solution:

Question 9.
6929
Solution:

Question 10.
25725
Solution:

Question 11.
1312
Solution:

Question 12.
4192
Solution:

Question 13.
4955
Solution:

Question 14.
\(\frac {99 }{ 144 }\)
Solution:

Question 15.
\(\frac {57 }{ 169 }\)
Solution:

Question 16.
\(\frac {101 }{ 169 }\)
Solution:

Question 17.
13.21
Solution:

Question 18.
21.97
Solution:

Question 19.
110
Solution:

Question 20.
1110
Solution:

Question 21.
11.11
Solution:

Question 22.
The area of a square field is 325 m². Find the approximate length of one side of the field.
Solution:

Question 23.
Find the length of a side of a square, whose area is equal to the area bf the rectangle with sides 240 m and 70 m.
Solution:

Hope given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.9 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.2

Other Exercises

• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.1
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.2
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.3
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.4
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles VSAQS
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles MCQS

Question 1.
In the figure, OA and OB are opposite rays:
(i) If x = 25°, what is the value of y?
(ii) If y = 35°, what is the value of x?

Solution:
(i) If x = 25°
∴ 3x = 3 x 25° = 75°
But ∠AOC + ∠BOC = 180° (Linear pair)
⇒ ∠AOC + 75° = 180°
⇒ ∠AOC = 180° – 75°
⇒ ∠AOC = 105°
∴ 2y + 5 = 105° ⇒ 2y= 105° – 5° = 100°
⇒ y = \(\frac { { 100 }^{ \circ } }{ 2 }\)  = 50°
∴ If x = 25° then y = 50°
(ii) If y = 35°, then ∠AOC = 2y + 5
∴ 2y + 5 = 2 x 35° + 5 = 70° + 5 = 75°
But ∠AOC + ∠BOC = 180° (Linear pair)
⇒ 75° + ∠BOC = 180°
⇒ ∠BOC = 180°-75°= 105°
∴ 3x = 105° ⇒ x = \(\frac { { 105 }^{ \circ } }{ 3 }\) = 35°
∴ x = 35°

Question 2.
In the figure, write all pairs of adjacent angles and all the linear pairs.

Solution:
In the given figure,
(i) ∠AOD, ∠COD; ∠BOC, ∠COD; ∠AOD, ∠BOD and ∠AOC, ∠BOC are the pairs of adjacent angles.
(ii) ∠AOD, ∠BOD and ∠AOC, ∠BOC are the pairs of linear pairs.

Question 3.
In the figure, find x, further find ∠BOC, ∠COD and ∠AOD.

Solution:
In the figure,
AOB is a straight line
∴ ∠AOD + ∠DOB = 180° (Linear pair)
⇒ ∠AOD + ∠DOC + ∠COB = 180°
⇒ x+ 10° + x + x + 20 = 180°
⇒ 3x + 30° = 180°
⇒ 3x= 180° -30°= 150°
⇒ x = \(\frac { { 150 }^{ \circ } }{ 3 }\) = 50°
∴ x = 50°
Now ∠BOC =x + 20° = 50° + 20° = 70°
∠COD = x = 50°
and ∠AOD = x + 10° = 50° + 10° = 60°

Question 4.
In the figure, rays OA, OB, OC, OD and OE have the common end point O. Show that ∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA = 360°.

Solution:
Produce AO to F such that AOF is a straight line
Now ∠AOB + ∠BOF = 180° (Linear pair)

⇒ ∠AOB + ∠BOC + ∠COF = 180° …(i)
Similarly, ∠AOE + ∠EOF = 180°
⇒ ∠AOE + ∠EOD + ∠DOF = 180° …(ii)
Adding (i) and (ii)
∠AOB + ∠BOC + ∠COF + ∠DOF + ∠EOD + ∠AOE = 180° + 180°
⇒ ∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA = 360°
Hence proved.

Question 5.
In the figure, ∠AOC and ∠BOC form a linear pair. If a – 2b = 30°, find a and b.

Solution:
∠AOC + ∠BOC = 180° (Linear pair)
⇒ a + 6 = 180° …(i)
and a – 2b = 30° …(ii)
Subtracting (ii) from (i), 3b = 150°
⇒ b = \(\frac { { 150 }^{ \circ } }{ 3 }\) = 50°
and a + 50° = 180°
⇒ a= 180°-50°= 130°
∴ a = 130°, b = 50°

Question 6.
How many pairs of adjacent angles are formed when two lines intersect in a point?
Solution:
If two lines AB and CD intersect each other at a point O, then four pairs of linear pairs are formed i.e.
∠AOC, ∠BOC; ∠BOC, ∠BOD; ∠BOD, ∠AOD and ∠AOD, ∠AOC

Question 7.
How many pairs of adjacent angles, in all, can you name in the figure.

Solution:
In the given figure 10 pairs of adjacent angles are formed as given below:
∠AOB, ∠BOC; ∠AOB, ∠BOD; ∠AOC, ∠COD; ∠AOD, ∠BOE; ∠AOB, ∠BOE; ∠AOC, ∠COF; ∠BOC, ∠COD; ∠BOC, ∠COE; ∠COD, ∠DOE and ∠BOD, ∠DOE

Question 8.
In the figure, determine the value of x.

Solution:
In the figure
∠AOC + ∠COB + ∠BOD +∠AOD = 360 (angles at a point )

⇒ 3x + 3x + x + 150° = 360°
⇒ 7x – 360° – 150° = 210°
⇒ x = \(\frac { { 210 }^{ \circ } }{ 7 }\) = 30°
∴ x = 30°

Question 9.
In the figure, AOC is a line, find x.

Solution:
In the figure,
∠AOB + ∠BOC = 180° (Linear pair)
⇒ 70° + 2x = 180°
⇒ 2x = 180° – 70°
⇒ 2x = 110°⇒x = \(\frac { { 110 }^{ \circ } }{ 2 }\) = 55°
∴ x = 55°

Question 10.
In the figure, POS is a line, find x.

Solution:
In the figure, POS is a line
∴ ∠POQ + ∠QOS = 180° (Linear pair)
⇒ ∠POQ + ∠QOR + ∠ROS = 180°
⇒ 60° + 4x + 40° = 180°
⇒ 4x + 100° – 180°
⇒ 4x = 180° – 100° = 80°
⇒ x = \(\frac { { 80 }^{ \circ } }{ 4 }\) =20°
∴ x = 20°

Question 11.
In the figure, ACB is a line such that ∠DCA = 5x and ∠DCB = 4x. Find the value of x.

Solution:
ACB is a line, ∠DCA = 5x and ∠DCB = 4x
∠ACD + ∠DCB = 180° (Linear pair)
⇒ 5x + 4x = 180° ⇒ 9x = 180°
⇒ x = \(\frac { { 180 }^{ \circ } }{ 9 }\) = 20°
∴ x = 20°
∴ ∠ACD = 5x = 5 x 20° = 100° and ∠DCB = 4x = 4 x 20° = 80°

Question 12.
Given ∠POR = 3x and ∠QOR = 2x + 10°, find the value ofx for which POQ will be a line.

Solution:
∠POR = 3x and ∠QOR = 2x + 10°
If POQ is a line, then
∠POR + ∠QOR = 180° (Linear pair)
⇒ 3x + 2x + 10° = 180°
⇒ 5x = 180° – 10° = 170°
⇒ x = \(\frac { { 170 }^{ \circ } }{ 5 }\) = 34°
∴ x = 34°

Question 13.
What value ofy would make AOB, a line in the figure, if ∠AOC = 4y and ∠BOC = (6y + 30).

Solution:
In the figure,
AOB is a line if
∠AOC + ∠BOC = 180°
⇒ 6y + 30° + 4y= 180°
⇒ 10y= 180°-30°= 150°
150°
⇒ y = \(\frac { { 150 }^{ \circ } }{ 10 }\) = 15°
∴ y = 15°

Question 14.
In the figure, OP, OQ, OR and OS are four rays. Prove that: ∠POQ + ∠QOR + ∠SOR + ∠POS = 360° [NCERT]

Solution:
In the figure, OP, OQ, OR and OS are the rays from O
To prove : ∠POQ + ∠QOR + ∠SOR + ∠POS = 360°
Construction : Produce PO to E

Proof: ∠POQ + ∠QOE = 180° (Linear pair)
Similarly, ∠EOS + ∠POS = 180°
Adding we get,
∠POQ + ∠QOR + ∠ROE + ∠EOS + ∠POS = 180° + 180° ,
⇒ ∠POQ + ∠QOR + ∠ROS + ∠POS = 360° Hence ∠POQ + ∠QOR + ∠SOR + ∠POS = 360°

Question 15.
In the figure, ray OS stand on a line POQ. Ray OR and ray OT are angle bisectors of ∠POS and ∠SOQ respectively. If ∠POS = x, find ∠ROT. [NCERT]

Solution:
Ray OR stands on a line POQ forming ∠POS and ∠QOS

OR and OT the angle bisects of ∠POS and ∠QOS respectively. ∠POS = x
But ∠POS + ∠QOS = 180° (Linear pair)
⇒ x + ∠QOS = 180°
⇒ ∠QOS = 180° – x
∵ OR and OT are the bisectors of angle

Question 16.
In the figure, lines PQ and RS intersect each other at point O. If ∠POR : ∠ROQ = 5 : 7. Find all the angles. [NCERT]

Solution:
Lines PQ and PR, intersect each other at O
∵ Vertically opposite angles are equal
∴ ∠POR = ∠QOS and ∠ROQ = ∠POS
∠POR : ∠ROQ = 5:7
Let ∠POR = 5x and ∠ROQ = 7x
But ∠POR + ∠ROQ = 180° (Linear pair)
∴ 5x + 7x = 180° ⇒ 12x = 180°
⇒ x = \(\frac { { 180 }^{ \circ } }{ 12 }\) = 15°
∴ ∠POR = 5x = 5 x 15° = 75°
and ∠ROQ = 7x = 7 x 15° = 105°
But ∠QOS = POR = 75° (Vertically opposite angles)
and ∠POS = ∠ROQ = 105°

Question 17.
In the figure, a is greater than b by one third of a right-angle. Find the values of a and b.

Solution:
In the figure,
∠AOC + ∠BOC = 180° (Linear pair)
⇒ a + b =180° …(i)
But a = b + \(\frac { 1 }{ 3 }\) x 90° = b + 30°
⇒ a – b = 30° …(ii)
Adding (i) and (ii)
210°
2a = 210° ⇒ a = \(\frac { { 210 }^{ \circ } }{ 2 }\) = 105°
and 105° + b = 180°
⇒ b = 180° – 105°
∴ b = 75°
Hence a = 105°, b = 75°

Question 18.
In the figure, ∠AOF and ∠FOG form a linear pair.
∠EOB = ∠FOC = 90° and ∠DOC = ∠FOG = ∠AOB = 30°

(i) Find the measures of ∠FOE, ∠COB and ∠DOE.
(ii) Name all the right angles.
(iii) Name three pairs of adjacent complementary angles.
(iv) Name three pairs of adjacent supplementary angles.
(v) Name three pairs of adjacent angles.
Solution:
In the figure,
∠AOF and ∠FOG form a linear pair
∠EOB = ∠FOC = 90°
∠DOC = ∠FOG = ∠AOB = 30°

(i) ∠BOE = 90°, ∠AOB = 30°
But ∠BOE + ∠AOB + ∠EOG = 180°
⇒ 30° + 90° + ∠EOG = 180°
∴∠EOG = 180° – 30° – 90° = 60°
But ∠FOG = 30°
∴ ∠FOE = 60° – 30° = 30°
∠COD = 30°, ∠COF = 90°
∴ ∠DOF = 90° – 30° = 60°
∠DOE = ∠DOF – ∠EOF
= 60° – 30° = 30°
∠BOC = BOE – ∠COE
= 90° – 30° – 30° = 90° – 60° = 30°
(ii) Right angles are,
∠AOD = 30° + 30° + 30° = 90°
∠BOE = 30° + 30° + 30° = 90°
∠COF = 30° + 30° + 30° = 90°
and ∠DOG = 30° + 30° + 30° = 90°
(iii) Pairs of adjacent complementaiy angles are ∠AOB, ∠BOD; ∠AOC, ∠COD; ∠BOC, ∠COE
(iv) Pairs of adjacent supplementary angles are ∠AOB, ∠BOG; ∠AOC, ∠COG and ∠AOD, ∠DOG
(v) Pairs of adjacent angles are ∠BOC, ∠COD; ∠COD, ∠DOE and ∠DOE, ∠EOF.

Question 19.
In the figure, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that ∠ROS = \(\frac { 1 }{ 2 }\)(∠QOS – ∠POS). [NCERT]

Solution:
Ray OR ⊥ ROQ. OS is another ray lying between OP and OR.

To prove : ∠ROS = \(\frac { 1 }{ 2 }\)(∠QOS – ∠POS)
Proof : ∵ RO ⊥ POQ
∴ ∠POR = 90°
⇒ ∠POS + ∠ROS = 90° …(i)
⇒ ∠ROS = 90° – ∠POS
But ∠POS + ∠QOS = 180° (Linear pair)
= 2(∠POS + ∠ROS) [From (i)]
∠POS + ∠QOS = 2∠ROS + 2∠POS
⇒ 2∠ROS = ∠POS + ∠QOS – 2∠POS
= ∠QOS – ∠POS
∴ ROS = \(\frac { 1 }{ 2 }\) (∠QOS – ∠POS)

Hope given RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4

Other Exercises

• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.1
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.3
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.5
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.6
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.8
• RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.9

Question 1.
Write the possible unit’s digits of the square root of the following numbers. Which of these numbers are odd square roots ?
(i) 9801
(ii) 99856
(iii) 998001
(iv) 657666025
Solution:
(i)  In \(\sqrt { 9801 }\) ∴ the units digits is 1, therefore, the units digit of the square root can be 1 or 9
(ii) In \(\sqrt { 799356 }\) ∴ the units digit is 6
∴ The units digit of the square root can be 4 or 6
(iii) In \(\sqrt { 7998001 }\) ∴ the units digit is 1
∴ The units digit of the square root can be 1 or 9
(iv) In 657666025
∴ The unit digit is 5
∴ The units digit of the square root can be 5

Question 2.
Find the square root of each of the following by prime factorization.
(i) 441
(ii) 196
(iii) 529
(iv) 1764
(v) 1156
(vi) 4096
(vii) 7056
(viii) 8281
(ix) 11664
(x) 47089
(xi) 24336
(xii) 190969
(xiii) 586756
(xiv) 27225
(xv) 3013696
Solution:

Question 3.
Find the smallest number by which 180 must be multiplied so that it becomes a perfect square. Also, find the square root of the perfect square so obtained.
Solution:
Factorising 180,

180 = 2 x 2 x 3 x 3 x 5
Grouping the factors in pairs we see that factor 5 is left unpaired.
∴ Multiply 180 by 5, we get the product 180 x 5 = 900
Which is a perfect square
and square root of 900 = 2 x 3 x 5 = 30

Question 4.
Find the smallest number by which 147 must be multiplied so that it becomes a perfect square. Also, find the square root of the number so obtained.
Solution:
Factorising 147,

147 = 3 x 7×7
Grouping the factors in pairs of the equal factors, we see that one factor 3 is left unpaired
∴ Multiplying 147 by 3, we get the product 147 x 3 = 441
Which is a perfect square
and its square root = 3×7 = 21

Question 5.
Find the smallest number by which 3645 must be divided so that it becomes a perfect square. Also, find the square root of the resulting number.
Solution:
Factorising 3645

3645 = 3 x 3 3 x 3 x 3 x 3 x 5
Grouping the factors in pair of the equal factors, we see t at one factor 5 is left unpaired
∴ Dividing 3645 by 5, the quotient 729 will be the perfect square and square root of 729 = 27

Question 6.
Find the smallest number by which 1152 must be divided so that it becomes a perfect square. Also, find the square root of the number so obtained.
Solution:
Factorsing 1152,

1152 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3
Grouping the factors in pairs of the equal factors, we see that factor 2 is left unpaired.
∴ Dividing by 2, the quotient 576 is a perfect square .
∴ Square root of 576, it is 24

Question 7.
The product of two numbers is 1296. If one number is 16 times the others find the numbers.
Solution:
Product of two numbers = 1296
Let one number = x
Second number = 16x

∴ First number = 9
and second number = 16 x 9 = 144

Question 8.
A welfare association collected Rs. 202500 as donation from the residents. If each paid as many rupees as there were residents find the number of residents.
Solution:
Total donation collected = Rs. 202500
Let number of residents = x
Then donation given by each resident = Rs. x
∴ Total collection = Rs. x x x

Question 9.
A society collected Rs. 92.16. Each member collected as many paise as there were members. How many members were there and how much did each contribute?
Solution:
Total amount collected = Rs. 92.16 = 9216 paise
Let the number of members = x
Then amount collected by each member = x
paise

∴ Number of members = 96
and each member collected = 96 paise

Question 10.
A school collected Rs. 2304 as fees from its students. If each student paid as many paise as there were students in the school, how many students were there in the school ?
Solution:
Total fee collected = Rs. 2304
Let number of students = x
Then fee paid by each student = Rs. x
∴ x x x = 2304 => x² = 2304
∴ x = \(\sqrt { 2304 }\)

Question 11.
The area of a square field is 5184 m². A rectangular field, whose length is twice its breadth has its perimeter equal to the perimeter of the square field. Find the area of the rectangular field.
Solution:
The area of a square field = 5184 m²
Let side of the square = x

∴ side of square= 72 m
∴ Perimeter, of square field = 72 x 4 m = 288 m
Perimeter of rectangle = 288 m
Let breadth of rectangular field (b) = x
Then length (l) = 2x
∴ Perimeter = 2 (l + b)
= 2 (2x + x) = 2 x 3x = 6x
= 2 (2x + x) = 2 x 3x = 6x

∴ Length of rectangular field = 2x = 2 x 48 = 96 m
and breadth = 48 m
and area = l x b = 96 x 48 m²
= 4608 m²

Question 12.
Find the least square number, exactly divisible by each one of the numbers :
(i) 6, 9,15 and 20
(ii) 8,12,15 and 20
Solution:

LCM of 6, 9, 15, 20 = 2 x 3 x 5 x 3 x 2 = 180
=2 x 2 x 3 x 3 x 5
We see that after grouping the factors in pairs, 5 is left unpaired
∴ Least perfect square = 180 x 5 = 900

We see that after grouping the factors,
factors 2, 3, 5 are left unpaired
∴ Perfect square =120 x 2 x 3 x 5 = 120 x 30 = 3600

Question 13.
Find the square roots of 121 and 169 by the method of repeated subtraction.
Solution:

Question 14.
Write the prime factorization of the following numbers and hence find their square roots. ^
(i) 7744
(ii) 9604
(iii) 5929
(iv) 7056
Solution:
Factorization, we get:
(i) 7744 = 2 x 2 x 2 x 2 x 2 x 2 x 11 x 11

Grouping the factors in pairs of equal factors,

Question 15.
The students of class VIII of a school donated Rs. 2401 for PM’s National Relief Fund. Each student donated as many rupees as the number of students in the class. Find the number of students in the class.
Solution:
Total amount of donation = 2401
Let number of students in VIII = x
∴ Amount donoted by each student = Rs. x

Question 16.
A PT teacher wants to arrange maximum possible number of 6000 students in a Held such that the number of rows is equal to the number of columns. Find the number of rows if 71 were left out after arrangement.
Solution:
Number of students = 6000
Students left out = 71
∴ Students arranged in a field = 6000 – 71=5929

Hope given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.