Raju – Page 30 – NCERT MCQ

RS Aggarwal Class 7 Solutions Chapter 1 Integers Ex 1C

January 23, 2023

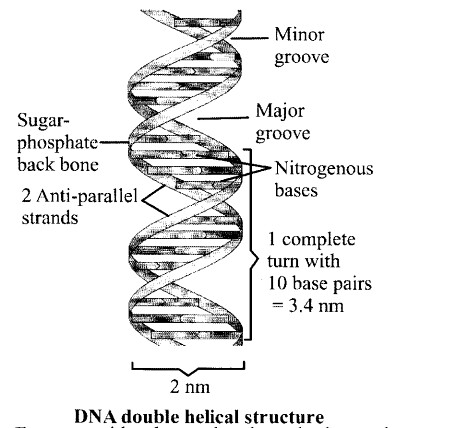
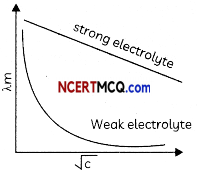
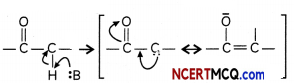
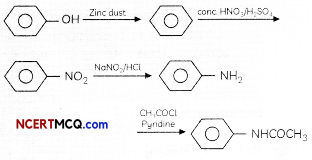
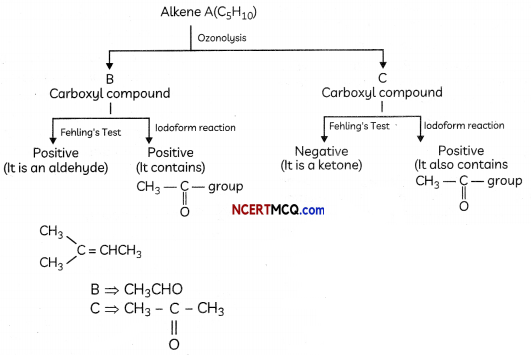
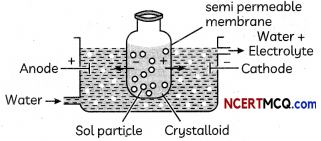
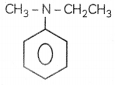
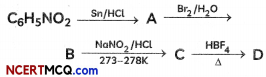
RS Aggarwal Class 7 Solutions Chapter 1 Integers Ex 1C

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 1 Integers Ex 1C.

Other Exercises

Question 1.
Solution:
(i) 65 by -13 = 65 ÷ (-13) = -5
(ii) -84 by 12 = -84 ÷ 12 = -7
(iii) -76 by 19 = -76 ÷ 19 = -4
(iv) -132 by 12 = -132 ÷ 12 = -11
(v) -150 by 25 = -150 ÷ 25 = -6
(vi) -72 by -18= -72 ÷ (-18)
(vii) -105 by -21 = -105 ÷ (-21) = 5
(viii) -36 by -1 = -36 ÷ (-1) = 36
(ix) 0 by -31 = 0 ÷ (-31) = 0
(x) -63 by 63 = -63 ÷ 63 = -1
(xi) -23 by -23 = -23 ÷ (-23)
(xii) -8 by 1 = -8 ÷ 1 = -8

Question 2.
Solution:
(i) 72 ÷ (………) = -4
⇒ 72 ÷ (-4) = -18
72 + (-18) = -4
(ii) -36 ÷ (………) = -4
⇒ -36 ÷ (-4) = 9
-36 ÷ (9) = -4
(iii) (………) ÷ (-4) = 24
⇒ -4 x 24 = -96
(-96) ÷ (-4) = 24
(iv) (……….) ÷ 25 = 0
(…….) ÷ 25 = 0 {0 ÷ a = 0}
(v) (………) ÷ (-1) = 36
⇒ 36 x (-1) = -36
(-36) ÷ (-1) = 36
(vi) (………..) + 1 = 37
⇒ (-37) x 1 = -37
(-37) ÷ 1 = -37
(vii) 39 ÷ (……….) = -1
⇒ 39 ÷ (-1) = -39
39 ÷ (-39) = -1
(viii) 1 ÷ (………) = -1
⇒ -1 ÷ 1 = -1
1 ÷ (-1) = -1
(ix) -1 + (………) = -1
-1 ÷ (1) = -1

Question 3.
Solution:
(i) True : as zero divided by non zero integer is zero.
(ii) False : as division by zero is not meaning full
(iii) False : as (-5) ÷ (-1) = 5 (product will be positive)
(iv) True : as -a ÷ 1 = -a
(v) False : as (-1) ÷ (-1) = 1
(vi) True.

Hope given RS Aggarwal Solutions Class 7 Chapter 1 Integers Ex 1C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 1 Integers Ex 1B

January 23, 2023

RS Aggarwal Class 7 Solutions Chapter 1 Integers Ex 1B

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 1 Integers Ex 1B.

Other Exercises

Question 1.
Solution:
(i) 16 by 9 = 16 x 9 = 144
(ii) 18 by -6 = 18 x (-6) = -108
(iii) -36 by -11 = 36 x (-11) = -396
(iv) -28 by 14 = -28 x 14 = -392
(v) -53 by 18 = -53 x 18 = -954
(vi) -35 by 0 = -35 x 0 = 0
(vii) 0 by -23 = 0 x (-23) = 0
(viii) -16 by -12 = (-16) x (-12) = 192
(ix) -105 by -8 = -105 x (-8) = 840
(x) -36 by -50 = (-36) x (-50) = 1800
(xi) -28 by -1 = (-28) x (-1) = 28
(xii) 25 by -11 = 25 x -11 = -275

Question 2.
Solution:
(i) 3 x 4 x (-5) = 12 x (-5) = -60 = 60
(ii) 2 x (-5) x (-6) = (-10) x (-6) = 60
(iii) (-5) x (-8) x (-3) = 40 x (-3) = -120
(iv) (-6) x 6 x (-10) = (-36) x (-10) = 360
(v) 7 x (-8) x 3 =(-56) x 3 = -168
(vi) (-7) x (-3) x 4 = 21 x 4 = 84

Question 3.
Solution:
(i) (-4) x (-5) x (-8) x (-10) = (4 x 5) x (8 x 10)
{Number of negative integers is even}
= 20 x 80 = 1600
(ii) (-6) x (-5) x (-7) x (-2) x (-3)
Here number of negative integers is odd
= (-1) [6 x 5 x 7 x 2 x 3]
= (-1) (1260) = -1260
(iii) (-60) x (-10) x (-5) x (-1)
Here number of negative integers is even
= 60 x 10 x 5 x 1
= 3000
(iv) (-30) x (-20) x (-5)
Here number of negative integers is odd
= (-1) (30 x 20 x 5) = -1 x 3000 = -3000
(v) (-3) x (-3) x (-3) x …6 times
Here number of negative integers is even
= 3 x 3 x 3 x 3 x 3 x 3 = 729
(vi) (-5) x (-5) x (-5) x …5 times
Here number of negative integers is odd
= (-1) (5 x 5 x 5 x 5 x 5)
= (-1) (3125) = – 3125
(vii) (-1) x (-1) x (-1) x …200 times
Here number of negative integers is even
= 1 x 1 x 1 x 1 x 200 times = 1
(viii) (-1) x (-1) x (-1) x …171 times
Here number of negative integers is odd
= (-1) x (1 x 1 x 1 x ……… 171 times)
= -1 x 1 = -1

Question 4.
Solution:
Number of negative integers = 90
which is positive and 9 integers are positive
The sign of the product will be positive

Question 5.
Solution:
Number of negative integers = 103 which is negative
Product will be negative

Question 6.
Solution:
(i) (- 8) x 9 + (- 8) x 7
= (-8) {9 + 7}
= -8 x 16 = -128
(ii) 9 x (-13) + 9 x (-7)
= 9 x (-13 – 7)
= 9 x (-20) = – 180
(iii) 20 x (-16) + 20 x 14 = 20 x {-16 + 14}
= 20 x (-2)= -40
(iv) (-16) x (-15) + (-16) x (-5)
= (-16) x {-15 – 5}
= (-16) x (-20) = 320
(v) (-11) x (-15)+ (-11) x (-25)
-(-11) x {-15 – 25}
= (-11) x (-40) = -440
(vi) 10 x (-12)+ 5 x (-12)
= (-12) {10 + 5} = (-12) x 15 = -180
(vii) (-16) x (-8) + (-4) x (-8)
= (-8){-16 – 4} = (-8) x (-20) = 160
(viii) (-26) x 72 + (-26) x 28
= (-26) (72 + 28) = (-26) x 100 = -2600

Question 7.
Solution:
(i) (-6) x (………) = 6 ⇒ (-6) x (-1) = 6
(ii) (-18) x (………) = (-18) ⇒ (-18) x (1) = (-18)
(iii) (-8) x (-9) = (-9) x (……….) ⇒ (-8) x (-9) = (-9) x (-8) (By Commutative Law of Multiplication)
(iv) 7 x (-3) = (-3) x (……….) ⇒ 7 x (-3) = (-3) x (7) (By Commutative Law of Multiplication)
(v) {(-5) x 3} x (-6) = (………) x {3 x (-6)} ⇒ {(-5) x 3} x (-6) = (-5) x {3 x (-6)} (By Associative Law of Multiplication)
(vi) (-5) x (……….) = 0 ⇒ (-5) x (0) = 0 (By Property of Zero)

Question 8.
Solution:
Number of questions in a test =10
Marks awarded for every correct answer = 5
and marks deducted for every wrong answer = 2 (-2 is given)
(i) Ravi gets 4 correct and 6 incorrect answers
Total marks obtained by him = 4 x 5 – 6 x 2 = 20 – 12 = 8
(ii) Reenu gets 5 correct and 5 incorrect answers
Total marks obtained by her = 5 x 5 – 5 x 2 = 25 – 10= 15
(iii) Heena gets 2 correct and 5 incorrect answers
She gets marks = 2 x 5 – 5 x 2 = 10 – 10 = 0

Question 9.
Solution:
(i) True: As product of a positive and a negative integer is negative.
(ii) False: The product of two negative integers is positive.
(iii) True.
(iv) False: As multiplication of an integer and (-1) is negative.
(v) True as a x b = b x a.
(vi) True as (a x b) x c = a x (b x c)
(vii) False: It is not possible except integer 1.

Hope given RS Aggarwal Solutions Class 7 Chapter 1 Integers Ex 1B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A

January 23, 2023

RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 16 Co-ordinate Geometry Ex 16A.

Other Exercises

Question 1.
Solution:
(i) A (9, 3) and B (15, 11)
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A 1

Question 2.
Solution:
Distance from origin O (0, 0) and the given points (x, y) = √(x² + y²)
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A 4

Question 3.
Solution:
Points A (x, -1), B (5, 3) and AB = 5 units
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A 6

Question 4.
Solution:
Points A (2, -3), B (10, y) and AB = 10
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A 7

Question 5.
Solution:
Points P (x, 4), Q (9, 10) and PQ = 10
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A 8

Question 6.
Solution:
Point A (x, 2) is equidistant from B (8, -2 and C (2, -2)
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A 9

Question 7.
Solution:
A (0, 2) is equidistant from B (3, p) and C ip, 5)
Then AB = AC
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A 10

Question 8.
Solution:
Let point P (x, 0) is on x-axis and P is equidistant from A (2, -5) and B (-2, 9)
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A 11

Question 9.
Solution:
Let the points on x-axis be P (x,, 0) and Q (x2, 0) and A (11, -8)
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A 12
or x – 5 = 0, then x = 5
Points are (17, 0) and (5, 0)

Question 10.
Solution:
Let point P (0, y) is on the y-axis, then
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A 13

Question 11.
Solution:
P (x, y) is equidistant from A (5, 1) and B (-1, 5)
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A 14

Question 12.
Solution:
P (x, y) is equidistant from A (6, -1) and B (2, 3)
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A 15

Question 13.
Solution:
Let the coordinates of the points be O (x, y)
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A 16

Question 14.
Solution:
Points A (4, 3) and B (x, 5) lie on a circle with centre O (2, 3)
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A 17

Question 15.
Solution:
Point C (-2, 3) is equidistant from points A (3, -1) and B (x, 8)
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A 18

Question 16.
Solution:
Point P (2, 2) is equidistant from the two points A (-2, k) and B (-2k, -3)
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A 19

Question 17.
Solution:
(i) Let point P (x, y) is equidistant from A (a + b, b – a) and B (a – b, a + b), then
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A 21

Question 18.
Solution:
We know that if the sum of any two of these distances is equal to the distance of the third, then the points are collinear.
Now, (i) Let the points are A (1, -1), B (5, 2), C (9, 5)
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A 22

Question 19.
Solution:
The points are A (7, 10), B (-2, 5) apd C (3, -4)
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A 26

Question 20.
Solution:
Points are A (3, 0), B (6, 4) and C (-1, 3)
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A 27

Question 21.
Solution:
Points are A (5, 2), B (2, -2) and C (-2, t)
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A 28

Question 22.
Solution:
Points are A (2, 4), B (2, 6) and C (2 + √3, 5)
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A 29

Question 23.
Solution:
Let the points are A (-3, -3), B (3, 3), C (-3√3, 3√3)
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A 30

Question 24.
Solution:
Points are A (-5, 6), B (3, 0), C (9, 8)
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A 31

Question 25.
Solution:
Points are O (0, 0), A (3, √3) and B (3, -√3)
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A 33

Question 26.
Solution:
(i) Points are A (3, 2), B (0, 5), C (-3, 2), D (0, -1)
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A 34

Question 27.
Solution:
Points are A (-3, 2), B (-5, -5), C (2, -3), D (4, 4)
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A 37

Question 28.
Solution:
Points are A (3, 0), B (4, 5), C (-1, 4) and D (-2, -1)
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A 39

Question 29.
Solution:
Points are A (6, 1), B (8, 2), C (9, 4) and D (7, 3)
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A 41

Question 30.
Solution:
Points are A (2, 1), B (5, 2), C (6, 4) and D (3, 3)
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A 43

Question 31.
Solution:
Points are A (1, 2), B (4, 3), C (6, 6) and D (3, 5)
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A 44

Question 32.
Solution:
(i) Points are A (-4, -1), B (-2, -4), C (4, 0) and D (2, 3)
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A 46

Question 33.
Solution:
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A 50

Question 34.
Solution:
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16A 53

Hope given RS Aggarwal Solutions Class 10 Chapter 16 Co-ordinate Geometry Ex 16A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16D

January 23, 2023

RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16D

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 16 Co-ordinate Geometry Ex 16D.

Other Exercises

Very-Short-Answer Questions
Question 1.
Solution:
Points are A (-1, y), B (5, 7) and centre O (2, -3y).
Points A and B lie on the circle with centre O.
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16D 1
or y + 1 = 0, then y = -1
y = -1, 7

Question 2.
Solution:
Point A (0, 2) is equidistant from B (3, p) and also from C (p, 5)
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16D 2

Question 3.
Solution:
Three vertices of a rectangle ABCD are B (4, 0), C (4, 3) and D (0, 3)
Its diagonal are equal.
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16D 3

Question 4.
Solution:
Point P (k – 1, 2) is equidistant from two points A (3, k) and B (k, 5)
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16D 4

Question 5.
Solution:
Let P (x, 2) divides the join of A (12, 5) and B (4, -3) in the ration m : n.
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16D 6

Question 6.
Solution:
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16D 7

Question 7.
Solution:
Vertices of ∆ABC are A (7, -3), B (5, 3) and C (3, -1)
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16D 9

Question 8.
Solution:
Point C (k, 4) divides the join of A (2, 6) and B (5, 1) in the ratio 2 : 3
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16D 11

Question 9.
Solution:
Let a point P (x, 0) on x-axis is equidistant from two points A (-1, 0) and B (5, 0)
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16D 12

Question 10.
Solution:
Distance between two points
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16D 13

Question 11.
Solution:
The points (3, a) lies on the line 2x – 3y = 5
It will satisfy it.
2 x 3 – 3 x a = 5
6 – 3a = 5 => 3a = 6 – 5 = 1
a = \(\frac { 1 }{ 3 }\)

Question 12.
Solution:
Points A (4, 3) and B (x, 5) lie on the circle with centre O (2, 3)
OA = OB
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16D 14

Question 13.
Solution:
P (x, y) is equidistant from the point A (7, 1) and B (3, 5)
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16D 15

Question 14.
Solution:
O (0, 0) is the centroid of ∆ABC whose vertices are A (a, b), B (b, c) and C (c, a)
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16D 17

Question 15.
Solution:
Coordinates of centroid
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16D 18

Question 16.
Solution:
Let point P (4, 5) divides the join of A (2, 3) and B (7, 8) in the ratio m : n
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16D 19

Question 17.
Solution:
Points are given A (2, 3), B (4, k) and C (6, -3)
Points are collinear.
RS Aggarwal Class 10 Solutions Chapter 16 Co-ordinate Geometry Ex 16D 20

Hope given RS Aggarwal Solutions Class 10 Chapter 16 Co-ordinate Geometry Ex 16D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12B

January 21, 2023

RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12B

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 12 Circles Ex 12B.

Other Exercises

Very-Short-Answer Questions
Question 1.
Solution:
In the given figure, a circle touches the sides AB, BC, CD and DA of a quadrilateral ABCD at P, Q, R and S respectively.
AB = 6 cm, BC = 9 cm, CD = 8 cm.
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12B 1
To find : The length of side AD.
A circle touches the sides of a quadrilateral ABCD.
AB + CD = BC + AD
=> 6 + 8 = 9 + AD
=> 14 = 9 + AD
=> AD = 14 – 9 = 5 cm

Question 2.
Solution:
In the given figure, PA and PB are two tangents to the circle with centre O.
∠APB = 50°
To find : Measure of ∠OAB.
Construction : Join OB.
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12B 2
In ∆APB,
PA = PB (tangents of the circle)
∠PAB = ∠PBA
But, ∠PAB + ∠PBA + ∠APB = 180° (Angles of a triangle)
=> ∠PAB + ∠PAB + 50° = 180°
=> 2∠PAB = 180° – 50° = 130°
∠PAB = 65°
But ∠OAP = 90° (OA is radius and PA is tangent)
∠OAB = 90° – 65° = 25°

Question 3.
Solution:
In the given figure, O is the centre of a circle.
PT and PQ are tangents to the circle from an external point P.
R is any point on the circle. RT and RQ are joined.
∠TPQ = 70°
To find : ∠TRQ
Construction : Join TO and QO.
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12B 3
∠TPQ = 70°
∠TOQ = 180° – 70° = 110° (OT and OQ are perpendicular on TP and QP)
Now, ∠TOQ is on the centre and ∠TRQ is on the remaining part of the circle.
∠TRQ = \(\frac { 1 }{ 2 }\) x ∠TOQ = \(\frac { 1 }{ 2 }\) x 110° = 55°

Question 4.
Solution:
In the given figure, common tangents AB and CD to the two circles with centres O1 and O2 intersect each other at E.
To prove : AB = CD.
Proof : EA and EC are tangents to the circle O1
EA = EC …(i)
Similarly, EB and ED are tangents to the circle O2.
EB = ED …(ii)
Adding (i) and (ii),
EA + EB = EC + ED
=> AB = CD
Hence, AB = CD

Question 5.
Solution:
In the given figure, PT is the tangent to the circle with centre O at P.
PQ is a chord of the circle and ∠TPQ = 70°.
To find : The measure of ∠POQ.
PT is tangent and OP is the radius.
∠OPT = 90°
But ∠QPT = 70°
∠OPQ = 90° – 70° = 20°
In ∆OPQ,
OP = OQ (radii of the same circle)
∠OQP = ∠OPQ = 20°
and ∠POQ = 180° – (∠OPQ + ∠OQP)
= 180° – (20° + 20°)
= 180° – 40° = 140°

Short-Answer Questions
Question 6.
Solution:
In the given figure, ∆ABC is circumscribed a circle with centre O and radius 2 cm.
Point D divides BC in such a way that
BD = 4 cm, DC = 3 cm, OD = 2 cm
Area of ∆ABC = 21 cm²
To find : AB and AC.
Construction : Join OA, OB, OC, OE and OF.
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12B 4
BD and BF are tangents to the circle.
BF = BD = 4 cm.
Similarly, CD and CE are tangents.
CE = CD = 3 cm
and AF and AE are tangents
AE = AF = x (suppose)
Now, area of ∆ABC = \(\frac { 1 }{ 2 }\) x Perimeter of ∆ABC x Radius
21 = \(\frac { 1 }{ 2 }\) (AB + BC + CA) x OD
=> 21 x 2 = [4 + 3 + 3+ x + x + 4) x 2
=> 42 = (14 + 2x) x 2
=> 14 + 2x = \(\frac { 42 }{ 2 }\) = 21
=> 2x = 21 – 14 = 7
x = \(\frac { 7 }{ 2 }\) = 3.5
AB = AF + FB = 3.5 + 4 = 7.5 cm
AC = AE + CE = 3.5 + 3 = 6.5 cm

Question 7.
Solution:
Given : Two concentric circles with centre O and radii 5 cm and 3 cm respectively.
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12B 5
AB is chord of larger circle which touches the smaller circle at C.
To find : The length of chord AB.
Construction : Join OA and OC.
AB is tangent and OC is radius of the smaller circle.
OC ⊥ AB and OC bisects AB at C. (AB is chord and OC ⊥ AB)
In right ∆OAC,
OA² = OC² + AC² (Pythagoras Theorem)
=> (5)² = (3)² + AC²
=> 25 = 9 + AC²
=> AC² = 25 – 9 = 16 = (4)²
=> AC = 4
and AB = 2 x AC = 2 x 4 = 8cm

Question 8.
Solution:
Given : AB is the tangent to the circle with centre O at point P.
PL ⊥ AB
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12B 6
To prove : PL passes through O.
Let PQ ⊥PT where Q lies on the circle.
∠QPT = 90°
Let PQ does not pass through the centre O.
Join PO and produce it to meet the circle at L.
PO being the radius of the circle drawn from the point of contact P.
OP ⊥ AB
=> ∠OPB = 90° => ∠LPB = 90°
But, PQ ⊥ AB
∠QPB = 90°
It is possible only if L and Q coincide each other.
Hence, PQ passes through the centre and is perpendicular from the point of contact.

Question 9.
Solution:
In the given figure, two tangents RQ and RP are drawn from the external point R to the circle with centre O.
∠PRQ = 120°
To prove : OR = PR + RQ
Construction : Join OP and OQ.
Also join OR.
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12B 7

Question 10.
Solution:
In the given figure, a circle is inscribed in a ∆ABC touches the sides AB, BC and CA at D, E and F respectively.
AB = 14 cm, BC = 8 cm and CA = 12 cm.
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12B 9
To find : The length of AD, BE and CF.
Let AD = x, BE = y and CF = z
AD and AF are the tangents to the circle from A.
AD = AF = x
Similarly,
BE and BD are tangents
BD = BE = y
and CF and CE are the tangents
CE = CF = z
Now, AB + BC + CA = 14 + 8 + 12 = 34
=> (x + y) + (y + z) + (z + x) = 34
=> 2 (x + y + z) = 34
=> x + y + z = 17 …(i)
But x + y = 14 cm …(ii)
y + z = 8 cm …(iii)
z + x = 12 cm …(iv)
Subtracting (iii), (iv) and (ii) from (i) term by term
x = 17 – 8 = 9 cm
y = 17 – 12 = 5 cm
z = 17 – 14 = 3 cm
Hence, AD = 9 cm, BE = 5 cm and CF = 3 cm.

Question 11.
Solution:
In the given figure, O is the centre of the circle.
PA and PB are the tangents.
To prove : AOBP is a cyclic quadrilateral.
Proof: OA is radius and PA is tangent
OA ⊥ PA
=> ∠OAP = 90° ….. (i)
Similarly, OB is radius and PB is tangent.
OB ⊥ PB
=> ∠OBP = 90° ….. (ii)
Adding (i) and (ii),
∠OAP + ∠OBP = 90° + 90° = 180°
But these are opposite angles of the quadrilateral AOBP.
Quadrilateral AOBP is a cyclic.

Question 12.
Solution:
In two concentric circles with centre O, a chord AB of the laiger circle touches the smaller circle at C.
AB = 8 cm and radius of larger circle = 5 cm
Join OA, OC
To find, the radius of smaller circle,
AB is the tangent and OC is the radius
OC ⊥ AB
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12B 10
AC = CB = \(\frac { 8 }{ 2 }\) = 4 cm
OA = 5 cm
In right ∆OCA,
OA² = OC² + AC² (Pythagoras Theorem)
(5)² = OC² + (4)²
OC² = (5)² – (4)² = 25 – 16 = 9 = (3)²
OC = 3
Radius of smaller circle = 3 cm

Question 13.
Solution:
In the given figure, PQ is a chord of a circle with centre O.
PT is the tangent ∠QPT = 60°.
To find : ∠PRQ.
Construction : Take a point M on the alternate segment.
Join MP and MQ.
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12B 11
∠MPQ = ∠QPT = 60° (Angles in the alternate segment)
∠PMQ + ∠PRQ = 180° (Opposite angles of a cyclic quadrilateral)
=> 60° + ∠PRQ = 180°
∠PRQ = 180° – 60° = 120°
Hence, ∠PRQ = 120°

Question 14.
Solution:
In the given figure,
PA and PB are the two tangents to the circle.
With centre O, OA and AB are joined
∠APB = 60°
To find : The measure of ∠OAB
PA and PB are tangents to the circle from P
PA = PB
∠PAB = ∠PBA
But ∠APB = 60°
∠PAB + ∠PBA = 180° – 60° = 120°
2 ∠PAB = 120°
∠PBA = 60°
OA is radius and PA is tangent.
OA ⊥ PA
∠OAP = 90°
=> ∠OAB + ∠PAB = 90°
=> ∠OAB + 60° = 90°
=> ∠OAB = 90° – 60° = 30°
Hence, ∠OAB = 30°

Question 15.
Solution:
Since, tangents drawn from an external point are equally inclined to the line joining centre to that point.
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12B 12

Hope given RS Aggarwal Solutions Class 10 Chapter 12 Circles Ex 12B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS

January 21, 2023

RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 12 Circles MCQS.

Other Exercises

Choose the correct answer in each of the following questions.
Question 1.
Solution:
Number of tangents drawn from an external point to a circle is 2. (b)

Question 2.
Solution:
In the given figure, RQ is tangent to the circle with centre O.
SQ = 6 cm, QR = 4 cm
OR = √(OQ² + QR²) (In right ∆OQR)
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 1

Question 3.
Solution:
In the given figure, PT is tangent to the circle with centre O and radius OT = 7 cm, PT = 24 cm
OT is the radius and PT is the tangent OT ⊥ PT
Now, in right ∆OTP,
OP² = OT² + PT²
OP² = (7)² + (24)²
OP² = 49 + 576 = 625 = (25)²
OP = 25 cm (c)

Question 4.
Solution:
Two diameters cannot be parallel. (d)

Question 5.
Solution:
A chord subtends a right angle at its centre
Radius of the circle = 10 cm
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 2

Question 6.
Solution:
In the given figure, PT is tangent to the circle with centre O and radius
OT = 6 cm OP = 10 cm
OT is the radius and PT is the tangent
OT ⊥ TB
Now, in right ∆OPT,
OP² = OT² + PT² (Pythagoras Theorem)
⇒ (10)² = (6)² + PT²
⇒ 100 = 36 + PT²
⇒ PT² = 100 – 36 = 64 = (8)².
PT = 8 cm (a)

Question 7.
Solution:
In the given figure, point P is 26 cm away from the centre O of the circle.
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 3
Length of tangent PT = 24 cm
Let radius = r
In right ∆OPT,
OP² = PT² + OT²
⇒ 26² = 24² + r²
⇒ r² = 26² – 24² = 676 – 576 = 100 = (10)²
r = 10
Radius = 10 cm (a)

Question 8.
Solution:
PQ is tangent to the circle with centre O at P. ∆OPQ is an isosceles triangle.
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 4
∠OQP = ?
∆OPQ is an isosceles triangle
OP = PQ
∠POQ = ∠OQP
But OP is radius and PQ is tangent
OP ⊥ PQ ⇒ ∠OPQ = 90°
∠POQ + ∠OQP = 90°
⇒ ∠POQ = ∠OQP = \(\frac { 90 }{ 2 }\) = 45°
Hence, ∠OQP = 45° (b)

Question 9.
Solution:
In the given figure, AB and AC are tangents to the circle with centre O such that ∠BAC = 40°, ∠BOC = ?
AB and AC are tangents and OB and OC are radii.
OB ⊥ AB and OC ⊥ AC
⇒ ∠OBA = 90° and ∠OCA = 90°
In quadrilateral ∆BOC,
∠BAC + ∠BOC = 180°
⇒ 40° + ∠BOC = 180°
⇒ ∠BOC = 180° – 40° = 140° (d)

Question 10.
Solution:
A chord AB subtends an angle of 60° at the centre of a circle with centre O.
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 5
TA and TB are tangents drawn to the circle.
Then, ∠ATB = 180° – ∠AOB = 180° – 60° = 120° (d)

Question 11.
Solution:
In the given figure, O is the centre of the two concentric circles of radii 6 cm and 10 cm.
AB is a chord of the outer circle and touches the inner circle at P.
OP = 6 cm, OA = 10 cm
OP is radius and APB is tangent to the inner circle.
OP ⊥ AB and P is the mid point of AB.
In right ∆OPA,
OA² = OP² + AP²
⇒ 10² = 6² + AP²
⇒ 100 = 36 + AP²
⇒ AP²= 100 – 36 = 64 = (8)²
AP = 8 cm
and AB = 2 x AP = 2 x 8 = 16 cm (c)

Question 12.
Solution:
In the given figure, AB and AC are tangents to a circle with centre O and radius 8 cm.
OA = 17 cm.
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 6

Question 13.
Solution:
In the given figure, O is the centre of the circle, AT is tangent, AOC is the diameter and ∠ACB = 50°
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 7
We have to find the measure of ∠BAT
AB is chord and AT is the tangent
∠ACB = ∠BAT (Angles in the alternate segment)
= 50° (b)

Question 14.
Solution:
O is the centre of circle, PQ is a chord, PT is tangent.
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 8
∠POQ = 70°, then ∠TPQ = ?
Take a point R on the major segment and join PR and QR
arc PQ subtends ∠POQ at the centre and ∠PRQ at the remaining part of the circle
∠PRQ = \(\frac { 1 }{ 2 }\) ∠POQ = \(\frac { 1 }{ 2 }\) x 70° = 35°
But ∠TPQ = ∠PRQ (Angles in the alternate segment)
∠TPQ = 35° (a)

Question 15.
Solution:
In the given figure, AT is the tangent to the circle with centre O and OA is its radius OT = 4 cm, ∠OTA = 30°
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 9
Now, we have to find the length of AT

Question 16.
Solution:
In the given figure, PA and PB are the two tangents to the circle with centre O, which subtends ∠AOB = 110°
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 11
Now, we have to find the measure ∠APB
OA and OB are the radii of the circle and AP and BP are the tangents
OA ⊥ AP and OB ⊥ BP
∠A = ∠B = 90°
In quadrilateral OAPB,
∠A + ∠B = 90° + 90°= 180°
∠AOB + ∠APB = 180°
⇒ 110° + ∠APB = 180°
⇒ ∠APB = 180° – 110° = 70° (c)

Question 17.
Solution:
In the given figure, in ∆ABC,
BC = ?
AF and AE are the tangents to the circle from A.
AE = AF = 4 cm CE = AC – AE = 11 – 4 = 7 cm
Similarly, CD and CE are tangents
CD = CE = 7 cm
and BF and BD are tangents BD = BF = 3 cm
BC = BD + CD = 3 + 7 = 10 cm (b)

Question 18.
Solution:
In the given figure, ∠AOD = 135°
We know that if a circle is inscribed in a quadrilateral, the opposite sides subtends supplementary angles.
∠AOD + ∠BOC = 180°
135° + ∠BOC = 180°
⇒ ∠BOC = 180° – 135° = 45° (b)

Question 19.
Solution:
In the given figure, PQ is a chord of a circle with centre O and PT is a tangent at P to the circle such that ∠QPT = 50°.
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 12
Then, we have to find ∠POQ.
PT is the tangent and OP is the radius
OP ⊥ PT ⇒ ∠OPT = 90°
∠OPQ = ∠OPT – ∠QPT = 90° – 50° = 40°
In ∆OPQ,
OP = OQ (radii of the same circle)
∠OPQ = ∠OQP = 40°
and ∠POQ = 180° – (∠OPQ + ∠OQP)
= 180° – (40° + 40°)
= 180°- 80° = 100° (a)

Question 20.
Solution:
In the given figure, PA and PB are two tangents to the circle with centre O.
∠APB = 60° then ∠OAB
Join OB.
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 13
PAOB is a cyclic quadrilateral.
∠APB + ∠AOB = 180°
OA is radius and PA is tangent
OA ⊥ AP ⇒ ∠OAP = 90°
PA = PB (Tangents to the circle)
∠PAB = ∠PBA
But, ∠PAB + ∠PBA = 180° – 60° = 120°
∠PAB = ∠PBA = \(\frac { 120 }{ 2 }\) = 60°
∠OAB = 90° – 60° = 30° (b)

Question 21.
Solution:
Two tangents inclined at an angle of 60° are drawn to a circle of radius 3 cm.
Join OA, OB and OP.
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 14

Question 22.
Solution:
In the given figure, PQ and PR are tangents drawn from an external point P to a circle with centre A.
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 16
∠QPA = 27°, ∠QAR = ?
AP bisects ∠QPR and ∠QPA = 27°
∠QPR = 2 x 27° = 54°
But ∠QPR + ∠QAR = 180° (QARP is a cyclic quadrilateral)
⇒ 54° + ∠QAR = 180°
⇒ ∠QAR = 180° – 54° = 126° (c)

Question 23.
Solution:
In the given figure, PA and PB are two tangents drawn from an external point P to a circle with centre C and radius 4 cm.
PA ⊥ PB, then length of tangent is = ?
Join GA and CB.
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 17
CAand CB are radii and PA, PB are tangents to the circle.
CA ⊥ PA and CB ⊥ PB But, ∠APB = 90°
∠ACB = 180° – 90° = 90°
PA = PB tangents of a circle
CAPB is a square
PA = PB = radius = 4 cm (b)

Question 24.
Solution:
In the given figure, PA and PB are tangents to the circle with centre O such that ∠APB = 80°.
Join OP
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 18
Now, in right ∆OAP, ∠A = 90°
∠AOP = 90° – 40° = 50° (b)

Question 25.
Solution:
In the given figure, O is the centre of a circle. AB is the tangent to the circle at point P.
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 19
∠APQ = 58°, ∠PQB = ?
∠QPR = 90° (Angle in a semi circle)
But, ∠RPB + ∠QPR + ∠APQ = 180° (Angles on one side of a line)
⇒ ∠RPB + 90° + 58° = 180°
⇒ ∠RPB + 148° = 180°
⇒ ∠RPB = 180° – 148° = 32°
∠PQR or ∠PQB = ∠RPB (Angles in the alternate segment)
⇒ ∠PQB = 32° (a)

Question 26.
Solution:
In the given figure, O is the centre of the circle. AB is tangent to the circle at P.
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 20
∠PAO = 30°
∠CPB + ∠ACP = ?
∠CPD = 90° (Angle in a semi circle)
∠DPA + ∠CPB = 90°
But, ∠DPA = ∠ACP (Angles in alternate segment)
∠CPB + ∠ACP = 90° (b)

Question 27.
Solution:
In the given figure, PQ is the tangent to the circle at A.
∠PAB = 67°, ∠AQB = ?
Join BC.
∠BAC = 90° (Angle in a semi circle)
But, ∠PAB + ∠BAC + ∠CAQ = 180°
⇒ 67° + 90° + ∠CAQ = 180°
⇒ 157° + ∠CAQ = 180°
∠CAQ = 182° – 157° = 23°
∠ACB = ∠PAB (Angles in the alternate segment)
∠ACB = 67°
In ∆ACQ,
Ext. ∠ACB = ∠CAQ + ∠AQC
⇒ 67° = 23° + ∠AQC
⇒ ∠AQC = 67° – 23° = 44°
⇒ ∠AQB = 44° (d)

Question 28.
Solution:
In the given figure, two circles touch each other at C. AB is the common tangent.
∠ACB = ?
Draw a tangent from C which meets AB at P.
PA and PC are tangents to the first circle.
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 21
PA = PC
∠PAC = ∠PCA …(i)
Similarly, PB = PC
∠PCB = ∠PBC …(ii)
Adding, ∠PAC + ∠PBC = ∠PCA + ∠PCB
⇒ ∠PAC + ∠PBC = ∠ACB
But, ∠PAC + ∠PBC + ∠ACB = 180° (Angles of a triangle)
∠ACB = 90° (c)

Question 29.
Solution:
In the given figure O is the centre of the circle with radius 5 cm P is a point out side the circle and OP = 13 cm
PQ and PR are the tangents to the circle drawn from P
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 22
We have to find the area of quad. PQOR
OQ is radius and PQ is the tangent
OQ ⊥ QP
In ∆OPQ,
OP² = OQ² + PQ² (Pythagoras Theorem)
⇒ (13)² = (5)² + PQ²
⇒ 169 = 25 + PQ²
⇒ PQ² = 169 – 25 = 144 = (12)²
PQ = 12 cm
PQ = PR = 12 cm
Now, diagonal OP bisects the quad. PQOR into two triangles equal in areas.
Now, area of ∆PQO = \(\frac { 1 }{ 2 }\) x PQ x OQ
= \(\frac { 1 }{ 2 }\) x 12 x 5 = 30 cm²
Area of quad. PQOR = 2 x area ∆PQO = 2 x 30 = 60 cm² (a)

Question 30.
Solution:
In the given figure,
PQR is a tangent drawn at Q to the circle with centre O.
AB is a chord parallel to PR such that ∠BQR = 70°
Then, we have to find ∠AQB
Join QO and produce it to AB meeting it at L.
OQ ⊥ PR ⇒ LQ ⊥ PR
QL bisects AB at L
QA = QB
∆QAB is an isosceles triangle
∠LQA = ∠LQB
∠LQA = ∠LQR – ∠BQR = 90° – 70° = 20°
∠AQB = 2 x 20° = 40° (c)

Question 31.
Solution:
Length of a tangent to the circle from an external point = 10 cm
Radius (r) = 5 cm OP = ?
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 23
OQ is radius and QP is tangent
OQ ⊥ QP
In right ∆OPQ,
OP² = OQ² + QP² (Pythagoras Theorem) = (5)² + (10)² = 25 + 100 = 125
OP = √125 cm (d)

Question 32.
Solution:
In the figure, O is the centre of the circle BOA is its diameter and PT is tangent at P which meets BA produced at T. ∠PBO = 30°.
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 24
We have to find ∠PTA
In ∆BOP,
OB = OP (radii of the same circle)
∠APB = ∠PBO = 30°
But, OP is radius and PT is the tangent
OP ⊥ PT ⇒ ∠OPT = 90°
∠BPT = ∠BPO + ∠OPT = 30° + 90° = 120°
Now, in ∆PBT,
∠BPT + ∠PBA + ∠PTA = 180° (sum of angles of a triangle)
⇒ 120° + 30° + ∠PTA = 180°
⇒ 150° + ∠PTA = 180°
⇒ ∠PTA = 180° – 150° = 30° (b)

Question 33.
Solution:
In the given figure, a circle touches the side DF of a AEDF at H and touches ED and EF on producing at K and M respectively.
EK = 9 cm.
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 25
Perimeter of ∆EDF.
DH and DK are tangents to the circle.
DH = DK
Similarly, ∠FH = ∠FM and EK = EH = 9 cm
EK = ED + DK ⇒ ED + DH = 9 cm…(i)
Similarly, EH = EF = FH = EF + FM = 9 cm …(ii)
Adding (i) and (ii)
ED + DH + EF + FH = 9 + 9 cm (DH + HF = DF)
ED + DF + FE = 18 cm
Perimeter of ∆EDF = 18 cm (d)

Question 34.
Solution:
In the given figure, PA and PB are two tangents drawn from an external point P which inclined at an angle of 45°.
OA and OB are radii of the circle.
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 26
To find ∠AOB
AOBP is a cyclic quadrilateral
∠AOB + ∠APB = 180°
⇒ ∠AOB + 45° = 180°
⇒ ∠AOB = 180° – 45° = 135° (b)

Question 35.
Solution:
In the given figure, O is the centre of the circle PQL and PRM are the tangents from P drawn to the circle meeting it at Q and R respectively ∠SQL = 50°, and ∠SRM = 60°
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 27
Now, we have to find ∠QSR,
Join OQ, OR and OS OQ is radius and QP is tangent
OQ ⊥ QP
Similarly, OR ⊥ RP
∠1 = 90° – 50° = 40° and ∠2 = 90° – 60° = 30°
OS = OQ (radii of the same circle)
∠3 = ∠1 = 40°
Similarly OS = OR
∠2 = ∠4 = 30°
∠QSR = ∠3 + ∠4 = 40° + 30° = 70° (d)

Question 36.
Solution:
In the given figure, a ∆PQR is drawn to inscribe a circle with centre O and radius 6 cm.
OT is radius.
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 28
QT = 12 cm, TR = 9 cm
Area ∆PQR =189 cm²
PQ = ?
QK = QT = 12 cm
RS = RT = 9 cm
Let PK = PS = x cm
PQ = 12 + x
PR = 9 + x cm
Area of A = \(\frac { 1 }{ 2 }\) x r x Perimeter of ∆PQR
⇒ 189 = \(\frac { 1 }{ 2 }\) x 6 x (PQ + QR + RP)
⇒ 189 = 3 (12 + x + 21 + 9 + x)
⇒ 63 = 42 + 2x
⇒ 2x = 63 – 42 = 21
x = 10.5
AB = 10.5 + 12 = 22.5 cm (c)

Question 37.
Solution:
In the given figure, QR is a common tangent to two given circles touching each other externally at point T.
A tangent PT is drawn from T which intersects QR at P.
PT = 3.8 cm, QR = ?
PT and PQ are tangents to the first circle.
PQ = PT …(i)
Similarly, PT and PR tangents to the second circle.
PR = PT …(ii)
From (i) and (ii),
PQ = PR = PT = 3.8 cm
QR = 3.8 + 3.8 = 7.6 cm (d)

Question 38.
Solution:
In the figure, quadrilateral ABCD is circumscribed touches the circle at P, Q, R and S
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 29
AP = 5 cm, BC = 7 cm, CS = 3 cm AB = ?
Tangents drawn from the external point to the circle are equal
AQ = AP = 5 cm
CR = CS = 3 cm
BQ = BR
Now, BR = BC – CR = 7 – 3 = 4 cm
BQ = 4 cm
Now, AB = AQ + BQ = 5 + 4 = 9 cm (a)

Question 39.
Solution:
In the given figure, quad. ABCD is circumscribed touching the circle at P, Q, R and S
AP = 6 cm, BP = 5 cm, CQ = 3 cm and DR = 4 cm.
Now, we have to find the perimeter of the quad. ABCD.
We know that tangents from an external point to the circle are equal.
AP = AS = 6 cm
BP = BQ = 5 cm
CQ = CR = 3 cm
DR = DS = 4 cm
AB = AP + BP = 6 + 5 = 11 cm
BC = BQ + CQ = 5 + 3 = 8 cm
CD = CR + DR = 3 + 4 = 7 cm
and DA = AS + DS = 6 + 4 = 10 cm
Perimeter of the quad. ABCD
= AB + BC + CD + DA
= (11 + 8 + 7 + 10) cm
= 36 cm (c)

Question 40.
Solution:
In the given figure, O is the centre of the circle, AB is chord and AT is the tangent at A.
∠AOB = 100°, ∠BAT = ?
Take a point P on the major segment of the circle and join AP and BP.
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 30
Arc AB subtends ∠AOB at the centre and ∠APB at the remaining part of the circle.
∠APB = \(\frac { 1 }{ 2 }\) ∠AOB = \(\frac { 1 }{ 2 }\) x 100° = 50°
Now, ∠BAT = ∠APB (Angles in the alternate segment)
∠BAT = 50° (b)

Question 41.
Solution:
In a right ∆ABC, right angled at B
BC = 12 cm, AB = 5 cm
A circle is inscribed in it touching its sides at P, Q and R.
Join OP, OQ and OR.
AC² = AB² + BC² (Pythagoras Theorem)
= 5² + 12² = 25 + 144 = 169 = (13)²
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 31

Question 42.
Solution:
In the given figure, a circle is inscribed in a quadrilateral ABCD touching its sides, AB, BC, CD and DA at P, Q, R and S respectively
Radius OS = 10 cm
BC = 38 cm, PB = 27 cm
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 32
AD ⊥ DC
Length of CD = ?
Join OR and OS
BP and BQ are tangents to the circle
BQ = BP = 27 cm
BC = 38 cm
QC = 38 – 27 = 11 cm
CQ and CR are the tangents to the circle
CR = CQ = 11 cm
DR and DS are the tangents to the circle
DR = DS
AD ⊥ CD
OS is the radius and AD is the tangent
OS ⊥ AD
Similarly, OR ⊥ DC
OSDR is a square whose each side is equal to the radius = 10 cm
DR = DS = 10 cm
CD = CR + DR = 11 + 10 = 21 cm (d)

Question 43.
Solution:
In the given figure, ∆ABC is a right angled triangle, right angle at ∠B.
BC = 6 cm, AB = 8 cm
A circle with centre O is inscribed inside the triangle ABC
OP ⊥ AB and OQ ⊥ BC and OR ⊥ AC
OP = OQ = OR = x cm
OPBQ is a square
In right ∆ABC,
AC² = AB² + BC² (Pythagoras Theorem)
= (8)² + (6)² = 64 + 36 = 100 = (10)²
AC = 10 cm
Tangents drawn from the external point to the circle are equal
BP = BQ = x
CQ = CR = 6 – x
AP = AR = 8 – x
AR + CR = AC
⇒ 8 – x + 6 – x = 10
⇒ 14 – 2x = 10
⇒ 2x = 14 – 10 = 4
x = 2
Hence r = 2cm (a)

Question 44.
Solution:
A quadrilateral ABCD is circumscribed to a circle with centre O.
AB = 6 cm, BC = 7 cm, CD = 4 cm, AD = 7 cm
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 33
ABCD circumscribed to a circle.
AB + CD = BC + AD
⇒ 6 + 4 = 7 + AD
⇒ 10 = 7 + AD
AD = 10 – 7 = 3 cm (a)

Question 45.
Solution:
In the given figure, PA and PB are the tangents to the circle with centre O from P
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 34
PA = 5 cm, ∠APB = 60°
PA = PB = 5 cm
In ∆APB, ∠P = 60° and PA = PB
PAB is an equilateral triangle
AB = AP = BP = 5 cm (b)

Question 46.
Solution:
In the given figure, DE and DF are tangents to the circle from an external point D.
A is the centre of the circle.
DF = 5 cm and DE ⊥ DF, radius of the circle = 3
Join EA and FA.
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 35
AE and AF are the radius of the circle and DE and BF are the tangents.
AE ⊥ DE and AF ⊥ DF
∠EAF = 180° – ∠EDF = 180° – 90° = 90°
AEDF is a square.
AE = 5 cm
Radius of the circle = 5 cm (c)

Question 47.
Solution:
In the given figure, three circles with centre A, B and C are drawn touching each other externally
AB = 5 cm, BC = 7 cm and CA = 6 cm
Let r1, r2, r3 be the radii of three circles respectively
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 36

Question 48.
Solution:
In the given figure, AP, AQ and BC are tangents to the circle.
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 37
AB = 5 cm, AC = 6 cm, BC = 4 cm
Length of AP = ?
BP and BR are the tangents to the circle.
BP = BR
Similarly, CR and CQ are tangents
CR = CQ
S and AP and AQ are tangents
AP = AQ
AP = AB + BP = AB + BR
AQ = AC + CQ = AC + CR
AP + AQ = AB + BR + AC + CR = AB + BR + CR + AC
AP + AP = AB + BC + AC
2AP = 5 + 4 + 6 = 15 cm
AP = \(\frac { 15 }{ 2 }\) = 7.5 cm (d)

Question 49.
Solution:
In the given figure, O is the centre of two concentric circles of radii 5 cm and 3 cm respectively.
From external point P, PA and PB are tangents are drawn to the external circle and internal circle respectively
PA = 12 cm, PB = ?
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 38
OA and OB are the radii
OA ⊥ AP and OB ⊥ BP
Now, in right ∆OAP,
OP² = OA² + AP² (Pythagoras Theorem)
= (5)² + (12)²
= 25 + 144 = 169 = (13)²
OP = 13 cm
and in right ∆OBP,
OP² = OB² + BP²
(13)² = (3)² + BP²
⇒ 169 = 9 + BP²
⇒ PB² = 169 – 9 = 160
PB = √160 = √(16 x 10) = 4√10 cm (c)

True/False Type
Question 50.
Solution:
(a) It is true that no tangent can be drawn from a point inside the circle.
(b) It is true, that one and only one tangent can be drawn from a point on the circle.
(c) True. If a point P is outside the circle, two tangents can be drawn to the circle.
(d) No, only two parallel tangents can be drawn which are parallel to a given line. (d)

Question 51.
Solution:
(a) It is true as a tangent intersects (touches) the circle exactly at one point.
(b) It is true that common point to the circle where the tangent touches the circle is called point of contact.
(c) It is true that the radius through the point of contact of a tangent is perpendicular to it.
(d) False as a straight line can meet at the most two points. (d)

Question 52.
Solution:
(a) It is true, that a secant is a line which intersects the circle at two points.
(b) It is true, as a tangent intersects the circle at only one point.
(c) It is true that the point at which a tangent touches the circle is called a point of contact.
(d) It is false, as no tangent can be drawn from a point in side the circle.

Assertion and Reason Type
Each question consists of two statements, namely, Assertion (A) and Reason (R).
For selecting the correct answer, use the following code :
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is a correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not a correct explanation of Assertion (A).
(c) Assertion (A) is true and Reason (R) is false.
(d) Assertion (A) is false and Reason (R) is true.
Question 53.
Solution:
In Assertion (A):
In right ∆OPQ, OP ⊥ PQ
RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS 39
OQ² = OP² + PQ² = (12)² + (16)² = 144 + 256 = 400 = (20)²
OQ = 20 cm, which is true
In Reason (R):
It is also with respect to (A) (a)

Question 54.
Solution:
Assertion (A):
The statement is true
In Reason (R):
It is also true but not with respect to (A) (b)

Question 55.
Solution:
In Assertion (A):
In the figure, ABCD is a quad, which is circumscribed a given circle.
Sum of opposite sides are equal
AB + CD = BC + AD
It is not true that AB + BC = AD + DC
In Reason (R):
It is true but not with respect to Assertion (A) (d)

Hope given RS Aggarwal Solutions Class 10 Chapter 12 Circles MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

NCERT Solutions for Class 11 Biology Chapter 9 Biomolecules

July 11, 2022

NCERT Solutions for Class 11 Biology Chapter 9 Biomolecules

These Solutions are part of NCERT Solutions for Class 11 Biology. Here we have given NCERT Solutions for Class 11 Biology Chapter 9 Biomolecules.

Question 1.
What are macromolecules? Give examples.
Solution:
Biomolecules i.e. chemical compounds found in living organisms are of two types. One, those which have molecular weights less than one thousand and are usually referred to as macromolecules or simply as biomolecules while those which are found in the acid-insoluble fraction are called macromolecules or as biomacromolecules.

The molecules in the insoluble fraction with the exception of lipids are polymeric substances. Then why do lipids, whose molecular weights do not exceed 800, come under acid-insoluble fractions i.e., macromolecular fractions?

Question 2.
Illustrate a glycosidic, peptide and a phospho-diester bond.
Solution:
(a) Glycosidic bond: It is a bond formed between two monosaccharide molecules in a polysaccharide. This bond is formed between two carbon atoms of two adjacent monosaccharides.

(b) Peptide bond: Amino acids are linked by a peptide bond which is between the carboxyl (- COOH) group of one amino acid and the amino (- NH₂) group of the next amino acid which is formed by the dehydration process.

(c) Phosphodiester bond: This is the bond present between the phosphate and hydroxyl group of sugar which is called an ester bond. As this ester bond is present on either side, it is called a phosphodiester bond.

Question 3.
What is meant by the tertiary structure of proteins?
Solution:
Tertiary structure of protein : When the individual peptide chains of secondary structure of protein are further extensively coiled and folded into sphere-like shapes with the hydrogen bonds between the amino and carboxyl group and various other kinds of bonds cross-linking on-chain to another they form tertiary structure. The ability of proteins to carry out specific reactions is the result of their primary, secondary and tertiary structure.
NCERT Solutions for Class 11 Biology Chapter 9 Biomolecules 1

protein molecular weight calculator. Molecular mass is the most fundamental characteristics for proteins and peptides.

Question 4.
Find and write down structures of 10 interesting small molecular weight biomolecules. Find if there is any industry which manufactures the compounds by isolation. Find out who are the buyers?
Solution:

NCERT Solutions for Class 11 Biology Chapter 9 Biomolecules 3

Fat is being manufactured by many companies in pharmaceuticals business as well as in food business. Vitamins come in many combination and are being used as supplementary medicines. Lactose is made by companies in manufacturing baby food. All of us are buyers of fat, protein and lactose.

Question 5.
Proteins have primary structures. If you are given a method to know which amino acid is at either of two termini (ends) of a protein, can you connect this information to purity or homogeneity of a protein?
Solution:
The primary structure of proteins is described as the type, number, and order of amino acids in the chain. A protein is imagined as a line whose left end represents the first and right end represents the last amino acid. But in fact, this is not so simple. Actually, the number of amino acids in between the two termini determines the purity or homogeneity of a protein.

Question 6.
Find out and make a list of proteins used as therapeutic agents. Find other applications of proteins (e.g., Cosmetics, etc.)
Solution:
Haemoglobin, Insulin, thyroxine, growth hormone, other hormones of the adenohypophysis, serum albumen, serum globulin, fibrinogen, etc. are used as the therapeutic agents. Proteins are also used for the synthesis of food supplements, film, paint, plastic, etc.

Question 7.
Explain the composition of triglyceride.
Solution:
Triglycerides are esters of three molecules of fatty acids and one molecule of glycerol.
NCERT Solutions for Class 11 Biology Chapter 9 Biomolecules 5

Question 8.
Can you describe what happens when milk is converted into curd or yoghurt, from your understanding of proteins.
Solution:
Conversion of milk into curd is the digestion of milk protein casein. Semi digested milk is the curd. In the stomach, renin converts milk protein into paracasein which then reacts with Ca⁺⁺ ion to form calcium paracaseinate which is called the curd or yoghurt.

Question 9.
Can you attempt building models of biomolecules using commercially available atomic models (Ball and Stick model)?
Solution:
Yes, the Three-dimensional structure of cellulose can be made using balls and sticks. Similarly, models of other bimolecular can be made
NCERT Solutions for Class 11 Biology Chapter 9 Biomolecules 6

Question 10.
Attempt titrating an amino acid against a weak base and discover the number of dissociating (ionizable) functional groups in the amino acid.
Solution:
When an amino acid is titrated with weak base then its-COOH group also acts as weak acid. So it forms a salt with weak base then the pH of the resulting solution is near 7, so there is no sudden change. Number of dissociating functional groups are two, one is amino group (NH2) and another is carboxylic group ( – COOH). In the titration, amino acid acts as an indicator. Amino acids in solution acts as basic or acidic as situation demands. So these are also called amphipathic molecules.

Question 11.
Draw the structure of the amino acid, alanine.
Solution:

Question 12.
What are gums made of? Is fevicol different?
Solution:
Gums are categorized into secondary metabolites or biomolecules. Thousands of compounds one present in plant-fungal and microbial cells. They are derived from these things. But is different. Fevicol has not derived from paper written cells.

Question 13.
Find out a qualitative test for proteins, fats and oils, amino acid and test any fruit juice, saliva, sweat and urine for them.
Solution:
Qualitative Tests for proteins, amino acids, and fats:
Biuret Test: Biuret test for protein identifies the presence of protein by producing violet colour of solution. Biuret H2NCONHCONH2 reacts with copper ion in a basic solution and gives violet colour.
Liebermann-Burchard Test for cholesterol:
This is a mixture of acidic anhydride and sulphuric acid. This gives a green colour when mixed with cholesterol.
Grease Test for oil: Certain oils give a translucent stain on clothes. This tesi can be used to show presence of fat in vegetable oils. These tests can be performed to check presence of proteins and amino acids and fats in any of the fluid mentioned in the question.

Question 14.
Find out how much cellulose is made by all the plants in the biosphere and compare it with how much of paper is manufactured by man and hence what is the consumption of plant material by man annually. What a loss of vegetation?
Solution:
According to a 2006 report from the UN, forests store about 312 billion tons of carbon in their biomass alone. If you add to that the carbon in deadwood, litter, and forest soil, the figure increases to about 1.1 trillion tons! The UN assessment also shows that the destruction of forests adds almost 2.2 billion tons of carbon to the atmosphere each year, the equivalent of what the U.S. emits annually. Many climate experts believe that the preservation and restoration of forests offers one of the least expensive and best ways to fight against climate change.
Although it is difficult to get exact data about the quantum of cellulose produced by plants, but above information can give some idea. About 10% of cellulose is used in paper making. The percentage is less but wrong practice of cutting wood and re-plantation makes the problem complicated. Usually older trees are cut for large quantity of cellulose and re-plantation is limited to selected species of plants. Selected species disturb the biodiversity as it leads to monoculture.
Add to this the problem of effluents coming out of a paper factory and the problem further aggravates.

Question 15.
Describe the important properties of enzymes.
Solution:
Properties of enzymes

Enzyme catalysis hydrolysis of ester, ether, peptide, c-c, c-halids, or P-N bonds.
Enzymes catalysis removal of the group from the substrate by mechanisms other than hydrolysis of leaving double bonds.
Enzymes generally function in a narrow range of temperature and p^H.
Activity declines both below and above optimum temperature and p^H.
The higher the affinity of the enzyme for its substrate the greater is its catalytic activity.
The activity of an enzyme is also sensitive to the presence of specific chemicals that bind to the enzyme.
For eg: Inhibitors that shuts off enzyme activity and Co-factors that facilitate catalytic activity.
Enzymes retain their identity at the end of the reaction.

VERY SHORT ANSWER QUESTIONS

Question 1.
Which organic compound is commonly called animal starch?
Solution:
Glycogen

Question 2.
Name the biomolecules of life.
Solution:
Carbohydrates, Lipids, Proteins, Enzymes, and nucleic acids.

Question 3.
Name one basic amino acid.
Solution:
Lysine.

Question 4.
Name one heteropolysaccharide.
Solution:
Chitin

Question 5.
Name the biomolecules present in the acid-insoluble fraction.
Solution:
Protein, polysaccharide, nucleic acid, and lipids.

Question 6.
Name the bond formed between sugar molecules.
Solution:
Glycosidic bond.

Question 7.
Name three pyrimidines.
Solution:
Thymine, cytosine, and uracil

Question 8.
Which enzyme does catalyse covalent bonding between two molecules to form a large molecule?
Solution:
Ligases.

Question 9.
On reaction with iodine, starch turns blue-black, why?
Solution:
The appearance of blue colour with the addition of iodine is due to its reaction with amylose fraction of starch.

Question 10.
Which type of bonds are found in proteins and polysaccharides?
Solution:
Peptides bond in protein and glycosidic bonds in polysaccharides.

Question 11.
Name one neutral amino acid.
Solution:
Valine.

Question 12.
Where does histone occur?
Solution:
Chromosomes.

Question 13.
Name two different kinds of metabolism.
Solution:
Anabolism and catabolism.

SHORT ANSWER QUESTIONS

Question 1.
Which type of bonds are found in nucleic acids?
Solution:
Phosphodiester bond.

Question 2.
What are the monosaccharides present in DNA and RNA? (Chikmagalur 2004)
Solution:
Deoxyribose in DNA and Ribose in RNA.

Question 3.
What are fatty acids? Give two examples.
Solution:
Fatty acids are compounds which have a carboxyl group attached to an R-group, which could be a methyl (CH3), or ethyl (C2H5) group or a higher number of CH2 groups e.g., Linoleic acid, Palmitic acid.

Question 4.
What are co-enzymes? Give two examples.
Solution:
Coenzymes are the non-protein organic ^compounds bound to the apoenzyme in a conjugate enzyme, their association with the apoenzyme is only transient, e.g., Nicotinamide adenine dinucleotide (NAD). Flavin adenine dinucleotide (FAD), Nicotinamide adenine dinucleotide phosphate (NADP).

Question 5.
(i) What is meant by complementary base pairing?
(ii) What is the distance between two successive bases in a strand of DNA?
(iii) How many base pairs are present in one turn of the helix of a DNA strand?
Solution:
(i) Complementary base pairing is the type of
pairing in DNA, where a purine always pairs with a pyrimidine, i.e., adenine pairs with thymine (A=T) and guanine pairs with cytosine (G=C).
(ii) 0.34 nm or 34 A is the distance between two successive bases in the strand of DNA
(iii) 10 base pairs

Question 6.
Differentiate between DNA and RNA.
Solution:
The main differences between DNA add RNA are as following
NCERT Solutions for Class 11 Biology Chapter 9 Biomolecules 8
Question 7.
What la a prosthetic group? Give an example.
Solution:
The non-protein part of a conjugated protein is called a prosthetic group. For example in a nucleoprotein (nucleic acid is the prosthetic group).

Question 8.
Differentiate between essential amino acids and non-essential amino acids.
Solution:

Question 9.
Differentiate between Structural Proteins and Functional Proteins.
Solution:

Question 10.
What is activation energy?
Solution:
Activation Energy: An energy barrier is required for the reactant molecules for their activation. So this energy with enzyme-substrate reaction is called Activation energy.
NCERT Solutions for Class 11 Biology Chapter 9 Biomolecules 12

The activation energy is low for reactions with catalysts [enzymes] than those with Non enzymatic reactions.

Question 11.
What are the components of enzymes?
Solution:
Enzymes are made up of protein as well as non – protein parts. The protein part is called an apoenzyme and the non-protein part is a coenzyme. These two together are called a holoenzyme.

LONG ANSWER QUESTIONS

Question 1.
How many classes are enzymes divided into? Name all the classes.
Solution:
Enzymes are divided into 6 classes. Namely

Oxidoreductases/dehydrogenases: Enzymes which catalyze oxidoreduction between two substrates
Transferases: Enzymes catalyzing a transfer of group between a pair of substrates.
Hydrolases: Enzymes catalyzing the hydrolysis of ester, ether, peptide, glycosidic, C-C-C-halide or P.N bonds.
Lyases: Enzymes catalyze the removal of groups from – substrates by mechanisms other than hydrolysis leaving double bonds.
Lyases: Enzymes catalyzing the interconversion of optical geometric or positional isomers.
Ligases: Enzymes catalyzing the linking together of 2 compounds.

Question 2.
Distinguish between the primary, secondary, and tertiary structures of proteins.
Solution:

Question 3.
Explain the effect of the following factors on enzyme activity:
(i) Temperature
(ii) pH.
Solution:
Temperature: An enzyme is active within a narrow range of temperature. The temperature at which an enzyme shows its highest activity is called optimum temperature.

It generally corresponds to the body temperature of warm blood animals e.g., 37°C in human beings. Enzyme activity decreases above and below this temperature. Enzyme becomes inactive below minimum temperature and beyond maximum temperature.

Low temperature present inside cold storage prevents spoilage of food. High temperature destroys enzymes by causing their denaturation.
NCERT Solutions for Class 11 Biology Chapter 9 Biomolecules 15

The relation between temperature and enzyme controlled reaction velocity

pH – Every enzyme has an optimum pH when it is most effective.

A rise or fall in pH reduces enzyme activity by changing the degree of ionisation of its side chains. A change in pH may also reverse the reaction.

Most of the intracellular enzymes function near-neutral pH with the exception of several digestive enzymes which work either in acidic range of pH or alkaline range of pH. pH for trypsin is 8.5.

Question 4.
Discuss the B-DNA helical structure with the help of a diagram.
Solution:

Watson & Crick suggested the double-helical structure of DNA in 1953.
The backbone of the DNA molecule is made up of deoxyribonucleotide units joined by a phosphodiester bond.
The DNA molecule consists of two chains wrapped around each other.
The two helical strands are bound to each other by Hydrogen Bonds.
Purines bind with pyrimidines A = T, C = G
The pairing is specific and the two chains are complementary.
One strand has the orientation 5’ → 3’ and other has 3’ → 5’.
Both polynucleotides strands remain separated with a 20A° distance.
The coiling is right-handed.

NCERT Solutions for Class 11 Biology Chapter 9 Biomolecules 16

Question 5.
What are different kinds of enzymes? Mention with enzyme examples.
Solution:
Enzymes with substrate bonds are broken and changed to different kinds as

Oxidoreductases: eg Alcohol dehydrogenase, oxidation, Reduction occurs
Transferases: transfer a particular group to another substrate, eg. transavninase
Hydrolases: cleave their substrates by hydrolysis of a covalent bond e.g. Urease, amylase.
Lyases: break the covalent bond eg. Deaminase
Isomerase: by changing the bonds they make isomers. eg: Aldolase.
Ligase: These bind two substrate molecules eg: DNA ligase, RNA ligase

We hope the NCERT Solutions for Class 11 Biology at Work Chapter 9 Biomolecules, help you. If you have any query regarding NCERT Solutions for Class 11 Biology at Work Chapter 9 Biomolecules, drop a comment below and we will get back to you at the earliest.

CBSE Sample Papers for Class 12 Chemistry Term 2 Set 1 with Solutions

July 8, 2022

Students can access the CBSE Sample Papers for Class 12 Chemistry with Solutions and marking scheme Term 2 Set 1 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Chemistry Term 2 Set 1 with Solutions

Time Allowed: 2 Hours
Maximum Marks: 35

General Instructions:

There are 12 questions in this question paper with internal choice.
SECTION A – Q. No. 1 to 3 are very short answer questions carrying 2 marks each.
SECTION B – Q. No. 4 to 11 are short answer questions carrying 3 marks each.
SECTION C- Q. No. 12 is case based question carrying 5 marks.
All questions are compulsory.
Use of log tables and calculators is not allowed.

Section – A
(Section A-Question No 1 to 3 are very short answer questions carrying 2 marks each.)

Question 1.
Arrange the following in the increasing order of their property indicated (any 2):
(a) Benzoic acid, Phenol, Picric acid, Salicylic acid (pka values).
Answer:
Picric acid < salicylic acid < benzoic acid <phenol

Explanation:

Picric acid (2,4,6 – Trinitrophenol) – Presence of electron-withdrawing group (-NO₂) increases the acidic character.
Salicylic acid (2-Hydroxy benzoic acid) – Stability of salicylate ion due to intramolecular H-bonding.
Benzoic acid (C₆H₅COOH) – More stability of benzoate ion due to resonance which is prominent on carboxylate ion.
Phenol (C₆H₅OH) – Stability of phenoxide ion due to resonance.

(b) Acetaldehyde, Acetone, Methyl tert butyl ketone (reactivity towards NH₂OH).
Answer:
Methyl tert – butyl ketone < acetone< Acetaldehyde

Explanation:

More the steric hinderance, difficult is the attack of nucleophile.
Methyl tert-butyl ketone < Acetone < Acetaldehyde.
(Max. steric hinderance) (Min. steric hinderance)

we can calculate the dilution of tube by dilution factor formula and…View the full answer.

Question 2.
Solutions of two electrolytes ‘A’ and ‘B’ are diluted. The Am of ‘B’ increases 1.5 times while that of A increases 25 times. Which of the two is a strong electrolyte? Justify your answer. Graphically show the behavior of ‘A’ and ‘B’. (2)
Answer:
B is a strong electrolyte. The molar conductivity increases slowly with dilution as there is no increase in number of ions on dilution as strong electrolytes are completely dissociated.
CBSE Sample Papers for Class 12 Chemistry Term 2 Set 1 with Solutions 1

Related Theory:
For strong electrolytes number of ions remains same at oil concentrations due to their complete dissociation. The ions become far apart from one another and their interionic forces decrease Hence, molar conductivity increases slowly with increase in dilution.

For weak electrolytes degree of dissociation increases with an increase in dilution, so molar conductivity increases maximum near-infinite dilution.

Question 3.
Give reasons to support the answer
(a) Presence of Alpha hydrogen in aldehydes and ketones is essential for aldol condensation.
Answer:
The alpha hydrogen atoms are acidic in nature due to presence of electron withdrawing carbonyl. group. These can be easily removed by a bose and the carbanion formed is resonance stabilized.

Explanation:
CBSE Sample Papers for Class 12 Chemistry Term 2 Set 1 with Solutions 2

(b) 3 -Hydroxy pentan-2-one shows positive Tollen’s test. (2)
Answer:
Tollen’s reagent is o weak oxidizing agent not capable of breaking the C-C bond in ketones . Thus ketones cannot be oxidized using Totlen’s reagent itseLf gets reduced to Ag.

Explanation:
3-Hydroxy pentan-2-one does not give Tollen’s test

Related Theory:
Aldehydes have a proton attached to the carbonyl carbon which can be abstracted, aUowing them to be easily oxidized to form carboxylic acids. The lack of this hydrogen, makes ketones generally inert to these oxidation conditions i.e with mild oxidizing agents Like Tollen’s reagent.

Section – B
(Section B-Question No 4 to 11 are short answer questions carrying 3 marks each.)

Question 4.
Account for the following:
(a) Aniline cannot be prepared by the ammonolysis of chlorobenzene under normal conditions.
(b) N-ethylethanamine boils at 329.3K and butanamine boils at 350.8K, although both are isomeric in nature.
(c) Acylation of aniline is carried out in the presence of pyridine.
OR
Convert the following:
(a) Phenol to N-phenylethanamide.
(b) Chloroethane to methanamine.
(c) Propanenitrile to ethanol. (3)
Answer:
(a) in case of chlorobenzene, the C—Cl bond is quite difficult to break as it acquires a partial double bond character due to conjugation.
So Under the normal conditions, ammonolysis of chlorobenzene does not yield aniline.

(b) Primary and secondary amines are engaged in intermolecular association due to hydrogen bonding between nitrogen of one and hydrogen of another molecule. Due to the presence of two hydrogen atoms, the intermolecular association is more in primary amines than in secondary amines as there is one hydrogen atom available for hydrogen bond formation in it

(c) During the acylation of aniline, stronger base pyridine is added. This done in order to remove the HCl so formed during the reaction and to shift the equilibrium to the right hand side.

(a) Phenol into IM-pherylethanamide
CBSE Sample Papers for Class 12 Chemistry Term 2 Set 1 with Solutions 3

(b) Chloroethane to methanamine
CBSE Sample Papers for Class 12 Chemistry Term 2 Set 1 with Solutions 4

Related Theory:
(a) Since aryl halides do not undergo nucleophilic substitution reactions due to resonance effect causing partial double bond character of C-X bond, so a of chiorobenzene cannot be substituted with ammonia (nucleophite).

(b) N-ethyl ethanamine CH₃CH₂NCH₂CH₃ is a secondary amine whereas butanamine (CH₃CH₂CH₂CH₂NH₂) is a primary amine. Since intermolecular hydrogen bonding is more in 1° amines than those in 2° amines so boiling points of 1° amines are higher than those of2°amines.

(c) Pyridine is used to remove the side product formed in the acylation reaction i.e., HCl from the reaction mixture. Being a strong base, it acts as an acceptor for the acid by-product formed in the reaction.

Question 5.
Answer the following questions:
(a) [Ni(H₂O)₆]²⁺ (ag) is green in colour whereas [Ni(H₂O)₄ (en)]²⁺ (aq) is blue in colour, give reason in support of your answer.
(b) Write the formula and hybridization of the following compound: tris(ethane-1,2-diamine) cobalt(III) sulphate
OR
In a coordination entity, the electronic configuration of the central metal ion is t₂g³eg¹
(a) Is the coordination compound a high spin or low spin complex?
(b) Draw the crystal field splitting diagram for the above complex.
Answer:
(a) The colour of coordination compound depends upon the type of ligand and d-d transition taking place.
H₂O is weak field ligand, which causes small splitting, leading to the d-d transition corresponding green colour, however due to the presence of (en) which is strong field ligand , the splitting is increased . Due to the change in t_2g – eg splitting the colouration of the compound changes from green to blue. :

(b) Formula of the compound is [Co(H₂NCH₂CH₂NH₂)₃]₂ (SO₄)₃
The hybridisation of the compound is: d₂sp³
OR
(a) As the fourth electron enters one of the eg orbitals giving the configuration t_2g³ eg¹, which indicates ∆₀< P hence forms high spin complex.

(b)
CBSE Sample Papers for Class 12 Chemistry Term 2 Set 1 with Solutions 6

Related Theory:
(a) The cause of the cotour of coordination compounds can be explained by Crystal Field Theory. The colours exhibited by transition- metal complexes are caused by

excitation of an electron from a lower-energy d orbital to a higher-energy d orbital, which is called a d-d transition,
The specific ligands(strong or weak) coordinated to the central metal atom.

(b) According to Valence Bond Theory (VBT), Co(en)₃]₂(SO₄)₃ forms inner orbital complex involving d²sp³ hybridization.
OR
Related Theory:
(a) According to Crystal Field Theory (CFT), given configuration t2g3 eg1 shows that splitting energy ∆o is less than pairing energy P(∆o < P) causing no pairing of electrons, so high spin complex will be formed.

Question 6.
Account for the following:
(a) Ti(IV) is more stable than Ti(II) or Ti(III).
(b) In case of transition elements, ions of the same charge in a given series show progressive decrease in radius with increasing atomic number.
(c) Zinc is a comparatively a soft metal, iron and chromium are typically hard. 3
Answer:
(a) Ti is having electronic configuration [Ar] 3d² 4s². Ti (IV) is more stable as Ti⁴⁺ acquires nearest noble gas configuration on loss of 4 e^–.

(b) In the case of transition elements, ions of the same charge in a given series show progressive decrease in radius with T increasing atomic number.

As the new electron enters a d orbital each time the nuclear charge increases by unity. The shielding effect of a d electron is not that effective, hence the net electrostatic attraction between the nuclear charge and the outermost electron increases and the ionic radius decreases.

(c) Iron and Chromium are having high enthalpy of atomization due to the presence of unpaired electrons, which accounts for their hardness. However, Zinc has low enthalpy of atomization as it has no unpaired electron. Hence zinc is comparatively a soft metal.

Related Theory:
(a) By losing its four electrons of 3d² 4s², Ti⁴⁺ attains stable configuration of the nearest noble gas with the complete octet.

Caution:
(b) Students should read the question carefully. Question is asking about the trend of ionic radii of transition metal ions and not about the trend of atomic radii of transition metal atoms because both the trends are different.

Related Theory:
(c) Zn has completely filled d-orbital, hence it cannot form metallic bonds (less enthalpy of atomization),while Cr has half filled d-orbital (3d⁵) and Fe has partially filled d-orbital (3d⁶) and can form metallic bonds (high enthalpies ofatomization). Since metallic bonds make a metal hard, Cr and Fe are hard metals and Zn is a soft metal.

Question 7.
An alkene ‘A’ (Mol. formula C₅H₁₀) on ozonolysis gives a mixture of two compounds ‘B’ and ‘C’. Compound ‘B’ gives positive Fehling’s test and also forms iodoform on treatment with I₂ and NaOH. Compound ‘C’ does not give Fehling’s test but forms an iodoform. Identify the compounds A, B and C. Write the reaction for ozonolysis and formation of iodoform from B and C. (3)
Answer:
Compound A is an alkene, on ozonolysis, it will give carbonyl compounds. As both B and C have >C=0 group, B gives positive Fehling’s test so it is an aldehyde and it gives iodoform test so it has CH₃C=0 group. This means the aldehyde is acetaldehyde. C does not give Fehling’s test, so it is a ketone. It gives a positive iodoform test so it is a methyl ketone means it has CH₃C=0 group

Compound A (C₅H₁₀) on ozonlysis gives B (CH₃CHO) + C (CH₃COR) SO “C” is CH₃COCH₃
CBSE Sample Papers for Class 12 Chemistry Term 2 Set 1 with Solutions 19

CH₃CHO + 2Cu²⁺ + 5OH → CH₃COO^– + Cu₂0 (red ppt) + 3H₂O
CH₃COCH₃ + 2Cu²⁺ + 5OH^– → No reaction
CH₃CHO + 3I₃ + 3 NaOH → CHI₃ (yellow ppt) + 3HI + HCOONa
CH₃COCH₃ + 3I₂ + 3 NaOH → CHI₃ (yellow ppt) + 3HI + CH₃COONa

A = CH₃CH = C(CH₃)₂
B = CH₃CHO
C = CH₃COCH₃

Related Theory:
Alkenes on ozonolysis give carbonyl compounds > C = O group.
CBSE Sample Papers for Class 12 Chemistry Term 2 Set 1 with Solutions 7

Question 8.
Observe the figure given below and answer the questions that follow: semi-permeable membrane
CBSE Sample Papers for Class 12 Chemistry Term 2 Set 1 with Solutions 8
(a) Which process is represented in the figure?
Answer:
electrodialysis

Explanation:
Electrodialysis is a process by which a colloidal solution is purified under the influence of electric field.

(b) What is the application of this process?
Answer:
purification of colloidal solution.

Explanation:
During this process of purification, the colloidal solution containing ionic impurities is put in bag of parchment paper under electric field so that ions can pass through the parchment paper but colloidal solution does not.

(c) Can the same process occur without applying electric field? Why is the electric field applied? (3)
Answer:
Yes. Dialysis is a very slow process to increase its speed electric field is applied.

Explanation:
Electrodialysis is faster process than normal dialysis under the influence of electric field.

Question 9.
What happens when reactions:
(a) N-ethylethanamine reacts with benzenesulphonyl chloride.
(b) Benzylchloride is treated with ammonia followed by the reaction with Chloromethane.
(c) Aniline reacts with chloroform in the presence of alcohoLic potassium hydroxide.
OR
(a) Write the tUPAC name for the following organic compound:
CBSE Sample Papers for Class 12 Chemistry Term 2 Set 1 with Solutions 9
(b) Complete the following: (3)

Answer:
(a) When N-ethylethanamine reacts with benzenesulphonyt chloride. N.N-diethylbenzenesutphonamide is formed.
(b) When benzytchloride is treated with ammonia , Benzytamine is formed which on reation with Chioromethane yields a secondary amine. N-methylbenzytamine.
(C) When aniLine reacts with chloroform in the presence of alcoholic potassium hydroxide. phenyl isocyanides or phenyt isonitrite is formed.
OR
(i) N-Ethyt-N-methytbenzenamine or N-EthyL-N-ethytaniline

(ii)
CBSE Sample Papers for Class 12 Chemistry Term 2 Set 1 with Solutions 11

Related Theory:
(a) The reaction of the benzene suiphonyl chionde (Hinsbergs reagent) with secondary amines like N-Ethylethanamine gibes a suiphonamide product (N, N-Diethylbenzenesulphonomide) that is NOT soluble ¡n alkall
CBSE Sample Papers for Class 12 Chemistry Term 2 Set 1 with Solutions 12

(b) Benzy chloride (C₆H₅CH₂Cl) undergoes nucleophilic substitution with ammonia (NH₃) to give Benzylamine (CH₅CH₂NH,) which on reaction with chtorornethane (CH₃Cl) undergoes alkylation to give N-methyl benzyiomine, a secondary amine.
CBSE Sample Papers for Class 12 Chemistry Term 2 Set 1 with Solutions 13

(c) Carbyl amine reaction/Ho ffmonWs carbytomines test/Isocyonide test: Aliphotic or aromatic primary amines on heating with chloroform and alcoholic KOH give foul smelting alkyt isacyariides or carbytamines. This test is not given by secondary or tertiary amines.
CBSE Sample Papers for Class 12 Chemistry Term 2 Set 1 with Solutions 14

Related Theory:
(a) It is a tertiary amine so alkyl groups attached to N atoms will be named first in their alphabetical order followed by the name of parent amine (with the largest olkyl group).

(b) Compound C and D given in the question are from the deleted portion of Chapter 13- Amines

Question 10.
Represent the cell in whkh the following reaction takes place. The value of E° for the cell ¡s 1.260 V. What is the value of E?
2Al_(s) + 3Cd²⁺_(0.1M) → 3Cd_(s) + 2Al³⁺_(0.01M)
Answer:
Al_(s)/Cd²⁺_(0.1M)//Al³⁺_(0.01M)/Cd_(s)
2Al_(s) + 3Cd²⁺_(0.1M) → 3Cd_(s) + 2Al³⁺_(0.01M)

E_cell = E°_cell\(\frac{-0.059}{n}\)log\(\frac{\left[\mathrm{Al}^{3+}\right]^{2}}{\left[\mathrm{Cd}^{2+}\right]^{3}}\)

E_cell = 1.26 – \(\frac{0.059}{6}\)log\(\frac{(0.01)^{2}}{(0.1)^{3}}\)
= 1.26 – \(\frac{0.059}{6}\)(-1)
= 1.26 + 0.009
= 1.269 V

Caution:
Students generally forget to put powers of stoichiometric coefficients on concentration of ions in Nernst equation so see the stoichiometric coefficients carefully and try to avoid the very common mistake.

NERNST Equation:
E°_cell = E_cell – \(\frac{0.059}{n}\) log\(\frac{[P]^{x}}{[R]^{y}}\)

Question 11.
(a) Why are fluorides of transition metals more stable in their higher oxidation state as compared to the lower oxidation state?
(b) Which one of the following would feel attraction when placed in magnetic field: Co²⁺, Ag⁺, Ti⁴⁺, Zn²⁺
(c) It has been observed that first ionization energy of 5d series of transition elements are higher than that of 3d and Ad series, explain why?
OR
On the basis of the figure given below, answer the following questions:
CBSE Sample Papers for Class 12 Chemistry Term 2 Set 1 with Solutions 15
(a) Why Manganese has Lower melting point than Chromium?
(b) Why do transition metals of 3d series have Lower melting points as compared to 4d series?
(c) In the third transition series, identify and name the metal with the highest melting point. (3)
Answer:
(a) The ability of fluorine to stabilize the highest Oxidation state is attributed to the higher lattice energy or high bond enthalpy.

(b) Co²⁺ has three unpaired electrons so it would be paramagnetic in nature, hence Co²⁺ ion would be attracted to magnetic field.

(c) The transition elements of 5d series have intervening 4f orbitals. There is greater effective nuclear charge acting on outer valence electrons due to the weak shielding by 4f electrons. Hence first ionisation energy of 5d series of transition elements are higher than that of 3d and 4d series.

(a) Manganese is having lower melting point as compared to chromium, as it has highest number of unpaired electrons, weak interatomic metal bonding, hence no delocalisation of electrons.

(b) There is much more frequent metal – metal bonding in compounds of the heavy transition metals i.e., 4d and 5d series, which accounts for lower melting point of 3d series.

Related Theory:
(a) Transition metal fluorides in their higher oxidation station state forms smaller cation due to which lattice enthalpy increases and so the stability increases.

(b) Magnetic moment {μ = \(\sqrt{n(n+2)}\)}of Co²⁺ is maximum due to the presence three unpaired electrons so attracted by external magnetic field.

(c) First ionisation stionisation enthalpies of 5d elements are higher than those of 3d or 4d elements this is due to the greater effective nuclear charge acting on outer valence electrons because of weak shielding by Af electrons causing lanthanoid contraction.

Related Theory:
(a) Manganese has 5 electrons in its d-orbital with half-filled stable configuration so delocalization of the electrons. Hence these electrons are not free to participate in metallic bonding. Manganese has less heat of atomization and hence its melting point is also low.

(b) The size of 4d-series transition metal elements is Consequently, the melting point of elements larger than 3d-series transition metal elements of 3d-series is lower than the elements of (atomic size increases down the group) so force 4d-series. of attraction of nucleus towards outermost electrons becomes Less. Hence the outer most valence electron is available for strong metallic bond formation so a large amount of heat energy is required to break this type of metallic bond.

Section – C
(Section C-Question No 12 is case-based question carrying 5 marks.)

Question 12.
Case Study-1
Read the passage given below and answer the questions that follow.
Are there nuclear reactions going on in our bodies?
There are nuclear reactions constantly occurring in our bodies, but there are very few of them compared to the chemical reactions, and they do not affect our bodies much. All of the physical processes that take place to keep a human body running are chemical processes. Nuclear reactions can lead to chemical damage, which the body may notice and try to fix.

The nuclear reaction occurring in our bodies is radioactive decay. This is the change of a less stable nucleus to a more stable nucleus. Every atom has either a stable nucleus or an unstable nucleus, depending on how big it is and on the ratio of protons to neutrons. The ratio of neutrons to protons in a stable nucleus is thus around 1:1 for small nuclei (Z < 20). Nuclei with too many neutrons, too few neutrons, or that are simply too big are unstable. They eventually transform to a stable form through radioactive decay. Wherever there are atoms with unstable nuclei (radioactive atoms), there are nuclear reactions occurring naturally. The interesting thing is that there are small amounts of radioactive atoms everywhere: in your chair, in the ground, in the food you eat, and yes, in your body.

The most common natural radioactive isotopes in humans are carbon-14 and potassium-40. Chemically, these isotopes behave exactly like stable carbon and potassium. For this reason, the body uses carbon-14 and potassium-40 just like it does normal carbon and potassium; building them into the different parts of the cells, without knowing that they are radioactive. In time, carbon-14 atoms decay to stable nitrogen atoms and potassium-40 atoms decay to stable calcium atoms.

Chemicals in the body that relied on having a carbon-14 atom or potassium-40 atom in a certain spot will suddenly have a nitrogen or calcium atom. Such a change damages the chemical. Normally, such changes are so rare, that the body can repair the damage or filter away the damaged chemicals.

The natural occurrence of carbon-14 decay in the body is the core principle behind carbon dating. As long as a person is alive and still eating, every carbon-14 atom that decays into a nitrogen atom is replaced on average with a new carbon-14 atom. But once a person dies, he stops replacing the decaying carbon-14 atoms. Slowly the carbon-14 atoms decay to nitrogen without being replaced, so that there is less and less carbon-14 in a dead body. The rate at which carbon-14 decays is constant and follows first order kinetics. It has a half-life of nearly 6000 years, so by measuring the relative amount of carbon-14 in a bone, archeologists can calculate when the person died.

All living organisms consume carbon, so carbon dating can be used to date any living organism, and any object made from a living organism. Bones, wood, leather, and write in continuation to above line paper can be accurately dated, as long as they first existed within the last 60,000 years. This is all because of the fact that nuclear reactions naturally occur in living organisms.

(source: The textbook Chemistry: The Practical Science by Paul B. Kelter, Michael D. Mosher and Andrew Scott states)
(a) Why is Carbon -14 radioactive while Carbon -12 not? (Atomic number of Carbon: 6)
(b) Researchers have uncovered the youngest known dinosaur bone, dating around 65 million years ago. How was the age of this fossil estimated?
(c) Which are the two most common radioactive decays happening in human body?
(d) Suppose an organism has 20 g of Carbon -14 at its time of death. Approximately how much Carbon -14 remains after 10,320 years? (Given antilog 0.517 = 3.289)
OR
(d) Approximately how old is a fossil with 12g of Carbon -14 If it initially possessed 32 g of Carbon -14? (Given tog 2,867 = 0.4280) (5)
Answer:
(a) Ratio of neutrons to protons is 2.3:1 which is not the stable ratio of 1:1

(b) Age of fossils can be estimated by C-14 decay. All living organisms have C-14 which decays without being replaced back once the organism dies.

(d) t = \(\frac{2.303}{k}\) log\(\left(\frac{\mathrm{Co}}{\mathrm{Ct}}\right)\)
Co = 20 g Ct = ?
t = 10320 gears k = \(\frac{0.693}{6000}\) (half-Life given in passage) substituting in equation:
10320 = \(\frac{2.303}{\left(\frac{0.693}{6000}\right)}\)log\(\frac{20}{\mathrm{Ct}}\)
0.517 = Log\(\frac{20}{\mathrm{Ct}}\) antiLog (0.517) = \(\frac{20}{\mathrm{Ct}}\)
3.289 = \(\frac{20}{\mathrm{Ct}}\)
Ct = 6.17 g.
OR
t = \(\frac{2.303}{k}\)log\(\left(\frac{\mathrm{Co}}{\mathrm{Ct}}\right)\)
Co = 32g Ct = 12
t =? k = \(\frac{0.693}{6000}\) (half Life given in passage)
substituting in equation:
CBSE Sample Papers for Class 12 Chemistry Term 2 Set 1 with Solutions 16

(d) All nuclear reactions in radioactive decaj are of FIRST ORDER.
Formula used:
CBSE Sample Papers for Class 12 Chemistry Term 2 Set 1 with Solutions 17
Formula used:

Online Education for Class 6 Geography Chapter 4 Extra Questions and Answers Maps

April 20, 2022

Here we are providing Online Education for Class 6 Geography Chapter 4 Extra Questions and Answers Maps was designed by subject expert teachers. https://ncertmcq.com/extra-questions-for-class-6-social-science/

Online Education for Maps Class 6 Extra Questions Geography Chapter 4

Class 6 Geography Chapter 4 Extra Questions Question 1.
What are political maps?
Answer:
Maps showing different countries and states of the world with their boundaries are called political maps.

Maps Class 6 Extra Questions Question 2.
Who was the first to represent the earth as a sphere?
Answer:
An Egyptian geographer was the first who represented: the earth as a sphere.

Class 6 Geography Chapter 4 Worksheet Question 3.
How do we draw maps in present times?
Answer:
Nowadays, maps are drawn on computers. These maps are very accurate.

Ncert Class 6 Geography Chapter 4 Extra Questions Question 4.
What are the limitations of a globe?
Answer:
When we want to study only a part of the earth, or about the states, districts, towns or villages of our country, globes are of little help. They only help us to study about the earth as a whole.

Class 6 Geography Chapter 4 Questions And Answers Question 5.
What are physical maps?
Answer:
Maps which show natural features of the earth, such as mountains, plateaus, plains, rivers and oceans, are called physical maps.

Class 6 Geography Chapter 4 Question 6.
What are the components of a map? Write about each of them.
Answer:
The three components of a map are distance, direction and symbol.

1.Distance: Maps are drawings which reduce the entire world or a part of it to fit on a sheet of paper. This reduction is done very carefully so that distances between the places are kept true. It is possible only when a small distance on the map represents a large distance on the ground.

Therefore that scale is chosen, which is a ratio between the actual distance on the ground and the distance shown on the map, eg. suppose the distance between your home and school is 10 km and on the map you show it as 2 cm. Therefore, the scale of your drawing will be 1 cm – 5 km.

2. Direction: Most maps contain an arrow marked with the letter ‘N at the upper right. It is called the north line and the arrow show’s the north direction. With the help of this line, we can find the other directions – south, east and west.

3. Symbols: We cannot draw the actual size and shape of different features like buildings, railway lines etc on the map, so they are shown with different symbols. The symbols give much information in a limited space. With the use of these symbols, maps can be easily drawn and are simple to read. The symbols can be read by all. Sometimes colours are used on the maps for the same pin-pose, e.g. blue colour represents water bodies.

Multiple Choice Questions

1. Which one of the following statements is true about a map?
(а) It is a true model of the earth
(b) A map is used to show various features of the earth
(c) It is a representation of the earth’s surface or a part of it drawn on a flat surface with the help of a scale
(d) It is used to show a small area.
Answer:
(c) It is a representation of the earth’s surface or a part of it drawn on a flat surface with the help of a scale

2. Which one of the following is used to show the natural features (land, river, etc.) of the earth?
(a) Thematic map
(b) Physical -map
(c) Political map
(d) Road map
Answer:
(b) Physical -map

3. Cities, towns, etc. are shown on which one of the following maps?
(a) Political maps
(b) Weather maps
(c) Road maps
(d) City maps
Answer:
(a) Political maps

4. Which one of the following maps focuses on specific information?
(a) Physical map
(b) Political map
(c) Weather map
(d) Thematic map
Answer:
(d) Thematic map

5. Which one of the following is different from the other three, with reference to the components of maps?
(a) Distance
(b) Title
(c) Direction
(d) Symbol
Answer:
(b) Title

6. Which one of the following terms is used for the ratio between the actual distance on the ground and the distance shown on the map?
(a) Direction
(b) Plan
(c) Scale
(d) Sketch
Answer:
(c) Scale

7. On which one of the following maps, the large areas like continents, etc. are shown with the help of a small scale?
(a) Small scale map
(b) Large scale map
(c) Globe
(d) Sketch
Answer:
(a) Small scale map

8. Which one of the following statements is true about the large scale map?
(а) It shows continents, countries, oceans, etc.
(b) It shows small areas (village or town) by using large scale
(c) It shows less information
(d) It is drawn on a small piece of paper
Answer:
(b) It shows small areas (village or town) by using large scale.

Important Definitions/ Words:

→ Map: It is a representation of the earth’s surface or a part of it on a flat surface.

→ Atlas: It is a collection of maps bound into a volume. Generally, these maps are drawn on a small scale.

→ Cartography; It is the science of map-making.

→ Scale: It is the ratio between the actual distance on the ground and the distance shown on the map.

→ Cardinal points: The four major directions North, South, East and West are called Cardinal points.

→ Symbols: It is not possible to draw on the map the actual shape and size of different features. So they are shown by symbols. Symbols give information in a limited space.

→ Conventional symbols: There is an international agreement regarding the use of symbols.

→ Sketch: It is a drawing mainly based on memory and not to scale.

→ Plan: It is a drawing of a small area on a large scale.

Extra Questions for Class 6 Social Science

Class 9 History Chapter 1 Extra Questions and Answers The French Revolution

April 20, 2022

Online Education for The French Revolution Class 9 Extra Questions History Chapter 1

Question 1.
What led to the end of monarchy in France?
Answer:
The French Revolution prepared the ground for the culmination of monarchy in India.

Question 2.
What is the Bastille?
Answer:
The Bastille is the fortress prison which belonged the French King, Louis XVI. Its fall was the indication that the Revolution in France has begun.

Question 3.
Who was the king in France at the time revolution in 1789?
Answer:
Louis XVI.

Question 4.
To what does the Old Regime refer?
Answer:
The Old Regime is usually used to describe the society and institutions of France before 1789.

Question 5.
Mention the sections of society which constituted the third estate.
Answer:
Big businessmen, merchants, court officials, lawyers etc. Down below were the peasants, artisans, labourers, servants.

Question 6.
What were the tithes?
Answer:
The tithe was a type of tax, extracted by the church from the peasant during pre-revolution times.

Question 7.
What do you mean by subsistence crisis?
Answer:
Subsistence crisis is an extreme situation where the basic means of livelihood are in danger.

Question 8.
Name the book written by John Locke?
Answer:
Two Treatises on Government.

Question 9.
Who was Montesquieu? Name the book he wrote.
Answer:
Montesquieu was a French philosopher. The name of the book which he wrote was the Spirit of the Laws.

Question 10.
What was the Estates General?
Answer:
The Estate’s General was a political body to which the three estates sent their representatives.

Question 11.
The image ‘the broken chain’ refers to something. Explain the image.
Answer:
The image ‘the broken chain’ refers to a situation of being free.

Question 12.
What does the image sceptre mean?
Answer:
Sceptre means the symbol of royal power.

Question 13.
What does the image ‘the eye within a triangle radiating lighf signify?
Answer:
The image ‘the eye within a triangle radiating light implies that the all-seeing eye is knowledge and die rays of the sun will drive away the clouds of ignorance.

Question 14.
What does red Phrygian cap mean?
Answer:
The red Phrygian cap means that one who wears it is free, and not a slave.

Question 15.
What does the image ‘the winged woman mean?
Answer:
It means the personification of law.

Question 16.
Explain the meaning of the image ‘the law tablet’.
Answer:
The image ‘the law tablet means that the law is the same for all and all are equal before law.

Question 17.
When was monarchy abolished and Republic instituted in France?
Answer:
Monarchy was abolished and the Republic was instituted on September 21, 1792.

Question 18.
What is guillotine?
Answer:
Guillotine is a device, instituted in the regime of Robespierre, consisting of two poles and a blade. With it/ the guilty were beheaded.

Question 19.
What are ‘citbyen’ and ‘citoyenne’?
Answer:
The terms used for he-citizen and she-citizen respectively in 1794.

Question 20.
What led to the subsistence crisis in France on the eve of revolution in 1789?
Answer:
The population in France rose from 23 million in 1715 to 28 million in 1789. This led to a rapid increase in the demand for foodgrains. Production of grains could not keep pace with the demand. So the price of bread which was the staple diet of the majority rose rapidly. Most workers were employed as labourers in workshops whose owners fixed their wages, but wages did not keep pace with the rise in prices. So the gap between the poor and the rich widened. This led to a subsistence crisis, something that occurred frequently in France during the Old Regime.

Question 21.
Why did the King Louis XIV call the meeting of the Estates-General? ‘
Answer:
The king wanted to increase the taxes. So he called for the meeting of the Estates-General in May 1789.

Question 22.
What were the main features of the Constitution of 1791?
Answer:
The following were the main features of thp Constitution of 1791:

The power to make laws was given to the National Assembly.
The National Assembly was to be indirectly elected: the ordinary citizens would elect the electors, and the electors, members of the National Assembly.
Voting power was given to the active citizens who paid taxes equal to three days of a labourer’s (/) wages; the electors were those who paid more taxes.
A Declaration of Rights of Man and Citizen was a part of the constitution. These rights included right to life, freedom of opinion, equality before law etc.

Question 23.
Explain the meaning of the painting of the Declaration of Rights of Man and Citizen (see figure on p. 39) by reading only the symbols.
Answer:
The Declaration of the Rights of Man and Citizen (figure painted by the artist Le Barbier in 1790) represents France on the right, and on the left, symbolises the law. The Declaration states rights of man and citizen.

Question 24.
Who was Qlympe de Gouges ?
Answer:
Olympe de Gouges was one of the most important of the politically active women in revolutionary France. She protested against the Constitution and the Declaration of Rights of Man and Citizen as they excluded women from basic rights that each human being was entitled to.

So in 1791, she wrote a Declaration of the Rights of Woman and Citizen, which she addressed to the Queen and to the members of the National Assembly, demanding that they act upon it.

Question 25.
Describe briefly the legacy of the French Revolution.
Answer:
The ideas of liberty and democratic rights were the most important legacy of the French Revolution. These spread from France to the rest of Europe during the nineteenth century, where feudal systems were abolished. Colonised peoples reworked the idea of freedom from bondage into their movements to create a sovereign nation-state.

Question 26.
Describe the causes of the French Revolution.
Answer:
There are three types of the causes relating to the French Revolution. These are intellectual, social and political causes :

I. Intellectual Causes-

Liberty-Human Rights/Natural Rights.
The sovereignty of the people.
Equality meant equal rights for all and tinder the Law. Liberals also wanted freedom from a state-controlled economy. Property was seen as sacred. These were middle-class property owners by and large.

II. Social Causes- A. The Estates System

First Estate: The Clergy-1% of population, with 10% of land. They had wealth, land, privileges and they levied a tax on the peasantry, the tithe, which generally went to some remote bishop or monastery rather than the local parish priest.
Second Estate: The Nobility-2-5% of population with 20% of the land. They also had great wealth and taxed the; peasantry: There was a “feudal” resurgence in 18th century.
Third Estate: Everyone Else-95-97% of the population. There were some few rich members, the artisans and all the peasantry. These were also class divisions.

The Bourgeoisie-8% of the population, about 2.3 million people, with 20% of Land. They often bought land and exploited the peasants on it. In Third Estate, the most important group politically was the. Bourgeoisie.

The Peasants-With 40% of the land, formed the vast majority of population. There was population growth in this period; perhaps 3,00,000 people added over the century. Peasants paid the most tax: aristocrats did not pay. Peasants farmed the land, and regard it as their own, but it was hot legally theirs. What they wanted was to own their own property. This was radical only at to start with. Later it was to be conservative desire.

The Urban Poor of Paris-Artisans- factory workers, journeymen. They were very poor probably less involved in politics. Artisans had different, interests than the bourgeoisie, but they played important role at several points. They were the most politicized group of poor people, possibly due to high literacy.

III. Political Causes-Some of these problems were:

Economic Weakness-The Revocation of Edict of Nantes 1685 had struck, a blow at French commerced. The economy tottered for the next hundred years.
Taxation Problems-The richest were not taxed: i.e. the Nobles and Clergy. Taxes were indirect on the poorest part of population-the Taille on peasant produce – the Gabele-on salt -various trade tariffs
Dependence on loans- The banking system was not able to cope with the fiscal problems. It was” the need for King to raise taxes that led to the calling of the Estates-General.
Cost of Mid Century Wars The Seven Years War 1756-63 cost a lot.
The Cost of Versailles and the Royal household etc.
Bankruptcy of the State-By 1780s the government was nearly bankrupt. Half of government income was going on paying debts (annual deficit 126 Million Livres). (debt was almost 4 Billion Livres).

Question 27.
Compare the manifesto drafted by. Olympe de Gouges with the declaration of Rights of Man and Citizen.
Answer:
Olympe de Gouges (1748-1793), a revolutionary woman drafted a manifesto for women’s rights.
This can be reproduced as under:

Woman is born free and remains equal to man in rights.
The goal of all political associations is the preservation of the natural rights of women and men. These rights are liberty, property, Security, and above all resistance to oppression.
The source of all sovereignty resides in the nation, which is nothing but the union of women and men.
The law should be expression of the general will; all female and male citizens should have a say either personally or by their representatives in its formulation; it should be the same for all.
No woman is an exception; she is accused, arrested, and -detained in cases determined by law. Women, like men, obey this rigorous law.

Question 28.
Bring out the effects, of the French Revolution.
Answer:
The Trench Revolution, though it seemed a failure in 1799 and appeared nullified by 1815, had far-reaching results. In France the bourgeois arid landowning classes emerged as the dominant power. Feudalism was dead; social order and contractual relations were consolidated by the Code Napoleon. The Revolution unified France and enhanced the power of the national state.

Although some historians view the Reign of Terror as an ominous precursor of modern totalitarianism, others, argue that this ignores the vital role the Revolution played in establishing the precedents of such democratic institutions as elections, representative government, and constitutions. The failed attempts of the urban lower middle classes to secure economic and political gains foreshadowed the class conflicts of the 19th century.

Objective Type Questions

1. Fill in the blanks with the appropriate words given in brackets:

Question 1.
The fortress prison ……………………….. fell to the revolutionaries, (the Bastille, the Versailles)
Answer:
the Bastille

Question 2.
The ……………………………. constituted the first estate (clergy, nobility).
Answer:
clergy

Question 3.
Livre constituted a unit of currency in ……………………………. (America, France)
Answer:
France

Question 4.
Louis XVI became king of France in ……………………………. (1715,1774).
Answer:
1774

Question 5.
The philosopher ……………………………. had an impact on the French Revolution. (Rousseau, Marx)
Answer:
Rousseau

Question 6.
Napoleon was defeated in 1815 at ……………………………. (Waterloo, Als case)
Answer:
Waterloo.

2. Choose true (✓) or false (✗) in the following sentences:

Question 1.
The Declaration of Rights Of Man and Citizen is related to the American War of independence.
Answer:
(✗)

Question 2.
One Indian leader, Tipu Sultan, responded to the ideas coming from revolutionary Frartce, the other was Swami Vivekananda.
Answer:
(✗)

Question 3.
Slavery was finally abolished in France in 1848.
Answer:
(✓)

Question 4.
Robespierre was the leader of the Jacobians.
Answer:
(✓)

Question 5.
Marseillaise is the national anthem of France,
Answer:
(✓)

Question 6.
France became Republic in 1789.
Answer:
(✗).

3. Choose the correct answer from the alternatives given:

Question 1.
The French Revolution occurred in:
(a) 1776
(b) 1789
(c) 1814
(d) 1830
Answer:
(b) 1789

Question 2.
The reign of terror period belongs to:
(a) 1789-1790
(b) 1790-1791
(c) 1792-1793
(d) 1794-1795
Answer:
(c) 1792-1793

Question 3.
Directory was an executive body consisting of the following:
(a) 3 members
(b) 4 members
(c) 5 members
(d) 6 members
Answer:
(c) 5 members

Question 4.
Women got franchise in the following year:
(a) 1945
(b) 1946
(c) 1947
(d) 1948
Answer:
(b) 1946

Question 5.
At the time of French Revolution, the emperor was:
(a) Louis XIII
(b) Louis XIV
(c) Louis XV
(d) Louis XVI
Answer:
(d) Louis XVI

Question 6.
Old Regime belonged to the following period:
(a) Before 1789
(b) After 1789
(c) Before and after 1979
(d) None of the above.
Answer:
(a) Before 1789

Question 7.
France became Republic in:
(a) 1791
(b) 1792
(c) 1793
(d) 1794
Answer:
(b) 1792

Question 8.
One of the following participated in the French Revolution:
(a) Rousseau
(b) Robespierre
(c) Roosevelt
(d) Ramsay Mac Donald
Answer:
(b) Robespierre.

Extra Questions for Class 9 Social Science

Class 10 Civics Chapter 1 Extra Questions and Answers Power Sharing

April 20, 2022

Check the below Online Education NCERT MCQ Questions for Class 10 Civics Chapter 1 Extra Questions and Answers Power Sharing Pdf free download. https://ncertmcq.com/extra-questions-for-class-10-social-science/

Online Education for Power Sharing Class 10 Extra Questions Civics Chapter 1

Power Sharing Class 10 Extra Questions Pdf Download Question 1.
Why did the Dutch-speaking people resent in Belgium?
Answer:
Because the minority French-speaking community of is Belgium was relatively rich and powerful.

Class 10 Civics Chapter 1 Extra Questions Question 2.
Why was the conflict more acute in Brussels?
Answer:
The conflict between the two communities was more acute in Brussels because the Dutch-speaking people constituted a majority in the country, but a minority in the capital.

Power Sharing Class 10 Extra Questions Question 3.
Who are the majority and minority social groups of Sri Lanka?
Answer:
Sinhla speaking people 74% Tamils 18% er ar Christians – 7%.

Power Sharing Extra Questions Question 4.
Define majoritarianism.
Answer:
A belief that the majority community should be able to rule a country in whichever way it wants, by disregarding the wishes and needs of the minority.

Class 10 Political Science Chapter 1 Extra Questions And Answers Question 5.
When was the demand for independent Tamil state raised?
Answer:
By 1980s several political organizations were formed demanding an independent Tamil Eelam in north-eastern Sri Lanka.

Extra Questions For Class 10 Civics Chapter 1 Question 6.
Why was Belgium Constitution amended four times?
Answer:
Between 1970 -1993, the constitution of Belgium was amended four times so as to work out an arrangement that would enable everyone to live together within the same country.

Extra Questions Of Power Sharing Question 7.
What do you mean by “Community government”?
Answer:

The “Community government” in Belgium is elected by people belonging to one language community Dutch, French and German-speaking no matter where they live.
This government has the power regarding cultural, educational and language-related issues.

Civics Class 10 Chapter 1 Extra Questions Question 8.
What is civil war?
Answer:
A violent conflict between opposing groups within a country that becomes so intense that it appears like a war.

Power Sharing Extra Question Answer Question 9.
What is the main difference between prudential reasons and moral reasons?
Answer:
While prudential reasons stress its beneficial consequences, moral reasons emphasise the intrinsic worth of power-sharing.

Power Sharing Class 10 1 Mark Questions Question 10.
Which government can be called legitimate?
Answer:
A legitimate government is one where groups through participation, acquire a stake in the system.

Class 10 Power Sharing Extra Questions Question 11.
What do you mean by prudential?
Answer:
Prudential means based on prudence or on careful calculation contrasted with those decisions based purely on moral considerations.

Class 10 Civics Chapter 1 Extra Questions And Answers Question 12.
Define ‘horizontal distribution of power’.
Answer:
When power is shared among different organs of government, such as legislature, executive and judiciary, this is called horizontal distribution of power because it allows different organs of government placed at the same level to exercise different powers.

Power Sharing Class 10 Important Questions Question 13.
What do you understand by federal government?
Answer:
When power is shared among governments at different levels, for example, a general government for the entire country and governments at the provincial, sub-national or regional level. Such a general government for the whole country is called federal government.

Class 10 Civics Ch 1 Extra Questions Question 14.
Describe ‘federal division of power’.
Answer:
In those countries where there are different levels of governments, the constitution clearly lays down the powers of different levels of governments. This is called federal division of power.

Extra Question Answer Of Power Sharing Class 10 Question 15.
Explain ‘Vertical division of power’.
Answer:
The federal division of power can be extended to levels of government lower than he state government such as the municipality and panchayat. All such divisions involving higher and lower levels of government are called “vertical division of power”.

Ncert Class 10 Civics Chapter 1 Extra Questions Question 16.
Why the provision of “reserved constituencies” have been made in our country?
Answer:
Arrangements such as provision of reserved constituencies in and the parliament of our country is meant to give space in the government and administration to diverse social groups who otherwise feel alienated from the government.

Power Sharing Class 10 Question Answers Pdf Question 17.
Describe the ethnic composition of Belgium.
Answer:
The ethnic composition of Belgium, a small country in Europe is very complex. Of the country’s total population, 59 per cent live in the Flemish region and speak Dutch language.

Another 40 per cent live in the Wallonia region and speak French. Remaining I per cent of the Belgians speak German. In the capital city Brussels, 80 per cent people speak French while 20 percent are Dutch-speaking.

Civics Chapter 1 Class 10 Extra Questions Question 18.
What was the main reason of tension between the Dutch and the French-speaking people of Belgium?
Answer:

The minority French-speaking community of Belgium was relatively rich and powerful,
This was resented by the Dutch-speaking community who got the benefit of economic development and education much later.
This led to tensions between the Dutch and the rrench speaking communities during the 1950s and 1960s.

Class 10th Civics Chapter 1 Extra Questions Question 19.
How was the majoritarian dominance established in Sri Lanka?
Answer:

Sri Lanka got independence in 1948. The leaders of Sinhla community wished to secure dominance over government by virtue of their majority.
The democratically elected government adopted a series of majoritarian measures to establish Sinhala supremacy in Sri Lanka.
In 1956, an Act was passed to recognize Sinhala as the only official language, thus disregarding Tamil
The Sinhala speaking people were given preference in university position and government jobs.

Extra Questions Of Civics Class 10 Chapter 1 Question 20.
Explain the outcomes of Belgian model of governance?
Answer:

The Belgian model is very complicated even for the Belgian people. But these arrangements have so far worked well, They helped avoid civic strife between the two major communities and a possible division of the country on linguistic lines.
When many countries of Europe came together to form the European Union, Brussels who chosen as its headquarters.

Question 21.
“Belgium and Sri Lanka both are democracies, yet they dealt with the question of power-sharing differently.” Justify.
Answer:

Belgium and Sri Lanka, both are democratic Yet they dealt with the question of power-sharing differently
In Belgium, the leaders have realized that the unity of the country is possible only by respecting the feelings and interests of different communities and regions.
Such a realization resulted in mutually acceptable arrangements for sharing power.
Sri Lanka shows us a contrasting example. It shows us that if a majority community wants to force its dominance over others and refuses to share power, it can undermine the unity of the country.

Question 22.
Write a short note on checks and balances.
Answer:
Power-sharing among different organs of government, such as the legislature, executive and judiciary allows different organs of government placed at the same level to exercise different power. Such a separation ensures that none of the organs can exercise unlimited power.

Each organ checks the others. This results in balance of power among various institutions. For example, even though the ministers and government officials exercise power, they are responsible to the parliament or state legislatures. Similarly, although the judges are appointed by the executive, but they can check the functioning of executive or laws made by legislatures. This arrangement is also called a system of checks and balances.

Question 23.
What do you mean by Pressure groups or interest groups?
Answer:
Pressure groups or interest groups are those organized groups which influence the government decisions. They demonstrate the demands of the industrialists, traders, farmers, working-class and other professional people.
They use various methods with a view to influencing public opinion.

They organize big demonstrations and rallies and get newspapers columns written by prominent people to arouse public opinion for or against a particular Bill or Law. Makenzie defined it as, “the organized groups possessing both formal structure and real common interests, in so far as they influence the decisions of public bodies.”

Question 24.
Analyse the results of majoritarian dominance in Sri Lanka.
Answer:

In 1956, the Government of Sri Lanka passed an Act to recognize Sinhla as official language. The state declared to protect and foster Buddhism. The governments followed preferential policies that favoured Sinhla applicants for university positions and government jobs. All these, government measures, coming after one another, gradually increased the feeling of alienation among Sri Lankan Tamils.
They felt that none of the major political parties led by the Buddhist Sinhalese were sensitive to their language and culture.
They fell that the constitution and government policies denied them equal political rights, discriminated against them in getting jobs and other opportunities and ignored their interests,
It resulted in strained relations between the Sinhalese and Tamil communities.
The Sri Lankan Tamils launched parties and started struggling for the recognition of Tamil as an official language, for regional autonomy and equality of opportunity in securing education and jobs.
Their demand for more autonomy to provinces with more Tamil populations was repeatedly denied. By 1980s, several political organizations were formed demanding an independent Tamil Eelam in north-eastern Sri Lanka.

Question 25.
How did the Belgian leaders solve the problems of regional differences and cultural diversities?
Answer:

The Belgian leaders recognized the existence of regional differences and cultural diversities.
They amended their constitution four times between 1970 to 1993, so as to work out an arrangement that would enable everyone to live together within the same country.

The arrangement is very innovative. Some important elements of the Belgian model is a follows:

(a) Constitution prescribes that the number of Dutch and French-speaking ministers shall be equal in the central government. Some special laws require the support of majority of members from each linguistic group. Thus, no single community can make decisions unilaterally.

(b) Many powers of the central government have been given to state governments for the two regions of the country. The state governments are not subordinate to the central goverment.

(c) Brussels has a separate government in which both the communities have equal representation. The French-speaking people accepted equal representation in Brussels because the Dutch-speaking community has accepted equal representation in the central government.

(d) Apart from the central and the state government there is a third kind of government. This ‘community government7 is elected by people belonging to one language community Dutch, French and German-speaking- no matter where they live. This government has the power regarding cultural, educational and language-related issues.

Question 26.
Why power sharing is desirable for democracy?
Answer:
(a) Prudential Reasons: Two different sets of reasons can be given in favour of power-sharing. Firstly power-sharing is good because it helps to reduce the possibility of conflict between social groups. Since social conflict often leads to violence and political instability, power-sharing is a good way to ensure the stability of political order.

Imposing the will of majority community over others may look like an attractive option in the short run, but in the long run it undermines the unity of the nation. Tyranny of the majority is not just oppressive for the minority; it often brings rum to the majority as well.

(b) Moral Reasons: There is a second, deeper, reason why power sharing is good for democracies. Power-sharing is the very spirit of democracy, A democratic rule involves sharing power with those attected by its exercise, and who have to live with its effects.

People have a right to be consulted on how they are to be governed. A legitimate government is one where groups, through participation, acquire a stake in the system. While prudential reasons stress its beneficial consequences, moral reasons emphasise the intrinsic worth of power-sharing.

Question 27.
“The idea of power-sharing had emerged in opposition to the notions of undivided political power.” Justify.
Answer:

The idea of power-sharing has emerged in opposition to the notions of undivided, political power.
For a long time it was believed that all power of a government must reside in one person or group of persons located one place.
It was felt that if power to decide is dispersed, it would not be possible to take quick decisions and to enforce them.
But these notions have changed with the emergence of democracy. One basic principle of democracy is that people are the source of all political power.
In a democracy, people rule themselves through institutions of self-governance.
In a good democratic government, due respect is given to diverse groups and views that exist in a society and everyone has a voice in the shaping of public policies. Therefore it follows that in a democracy political power should be distributed among as many citizens as possible.

Question 28.
“Power can be shared among governments at different levels.” How?
Answer:

Power can be shared among governments at different levels: for example, a general government for the entire country and governments at the provincial, sub-national or regional level. Such a general government for the entire country is usually called federal government.
In India, we refer to it as the Central government. The governments at the provincial or regional level are called by different names in different countries. In India, we call them State governments.
This system is not followed in all the countries. There are many countries where there are no provincial or state governments.
But in those countries, where there are different levels of governments, the constitution clearly lays down the powers of different levels of government. This is what they did in Belgium, but was refused in Sri Lanka. This is called federal division of power.
The same principle can be extended to levels of government lower than the State government, such as the municipality and panchayat. All such divisions of power involving higher and lower levels of government are called vertical division of power.

Question 29.
How can we share power among different social groups?
Answer:
Power can be shared among governments at different levels, such as the religious and groups. ‘Community government in Belgium is a good example of this arrangement. In some countries, there are constitutional and legal arrangements whereby socially weaker sections and women are represented in the legislatures and administration. There is a system of ‘reserved constituencies’ in assemblies and the parliament of our country.

This type of arrangements is meant to give space in the government and administration to diverse social groups who otherwise would feel alienated from the government. This method is used to give minority communities a fair share of power.

Objective Type Questions

Four Choices are given to the following questions.
Choose the correct option as your answer.

Question 1.
When the power is shared among different organs of government this is called:
(a) Vertical distribution of power
(b) Horizontal distribution of power
(c) Triangular distribution of power
(d) None of these.
Answer:
(b) Horizontal distribution of power

Question 2.
Although the judges are appointed by the executive, but they can check the functioning executive laws made by the legislatures This arrangement is also called:
(a) A system checks
(b) A system of balances
(c) A system of checks and balances
(d) None of these.
Answer:
(c) A system of checks and balances

Question 3.
What is the population of Belgium
(a) 35 lakh
(b) 58 lakh
(c) 80 lakh
(d) more than 1 crore
Answer:
(d) more than 1 crore

Question 4.
How many people speak Dutch in Belgium:
(a) 59
(b) 40
(c) 8
(d) 10
Answer:
(a) 59

Questions 5.
What is the percentage of people living in Waillona region and speaking French?
(a) 59
(b) 20
(c) 40
(d) 10
Answer:
(c) 40

Question 6.
Which community is relatively rich and powerful in Belgium?
(a) Dutch
(b) French
(c) Danish
(d) Spanish
Answer:
(b) French

Question 7.
Who constituted a majority in Belgium :
(a) The French
(b) The Dutch
(c) The Spanish
(d) Anglo-Indians
Answer:
(c) The Spanish

Questions 8.
What is the percentage of Sinhla speakers in Sri Lanka:
(a) 74%
(b) 18%
(c) 7%
(d) 55%.
Answer:
(a) 74%

Questions 9.
Tamil natives of Sri Lanka in:
(a) Indian Tamils
(b) Anglo Tamils
(c) Muslim Tamils
(d) Sri Lanka Tamils.
Answer:
(d) Sri Lanka Tamils.

Questions 10.
How many people in Sri Lanka speak Tamil:
(a) 18%
(b) 74%
(c) 55%
(d) 7%.
Answer:
(a) 18%

Question 11.
What is the official language of Sri Lanka:
(a) Tamil
(b) Sinhla
(c) Hindi
(d) English
Answer:
(b) Sinhla

Question 12.
Which community in Sri Lanka is in majority:
(a) Tamil
(b) Christian
(c) Sinhla
(d) Indians
Answer:
(c) Sinhla

Question 13.
In which year several political organization were formed demanding an independent Tamil:
(a) 1980s
(b) 1990s
(c) 1970s
(d) 1950s
Answer:
(a) 1980s

Question 14.
How many times was the Belgian constitution ainended between 1970¬1991 :
(a) Three times
(b) Eight times
(c) Ten times
(d) four times
Answer:
(d) four times

Question 15.
Both Belgium and Sri Lanka are
(a) Democracies
(b) Autocracies
(c) Monarchies
(d) None of these
Answer:
(a) Democracies.