Category: CBSE Class 10

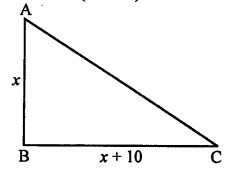
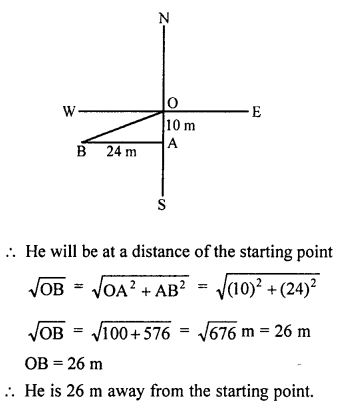
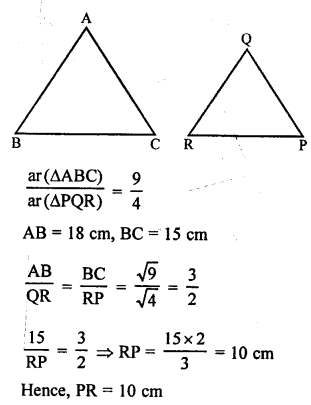
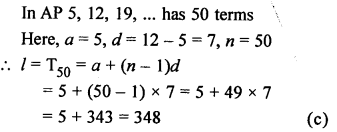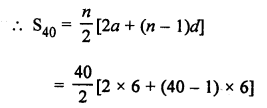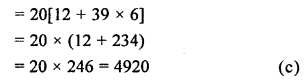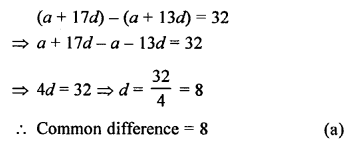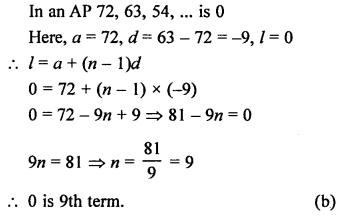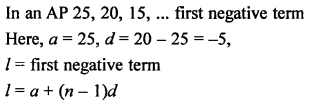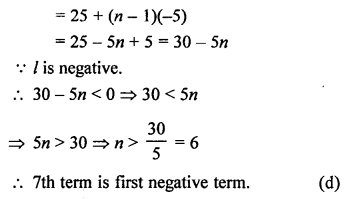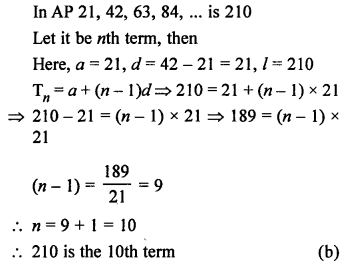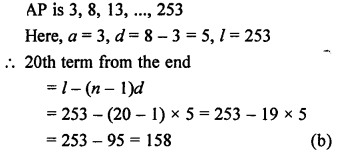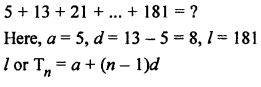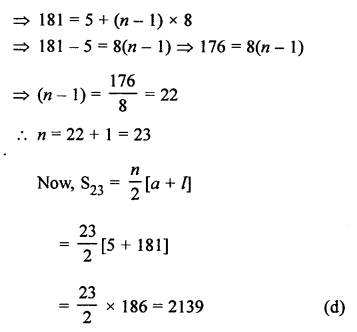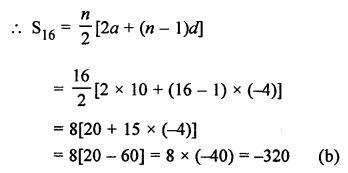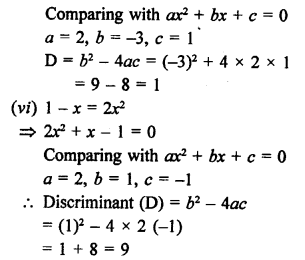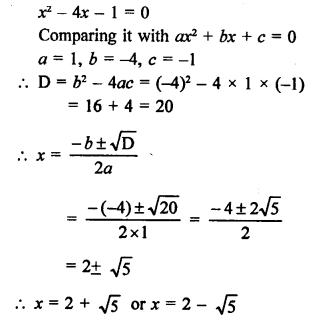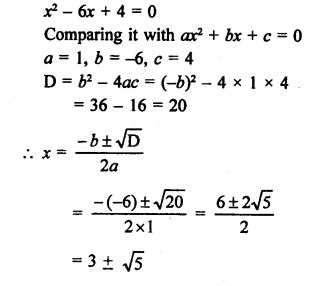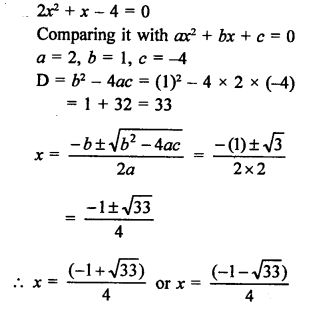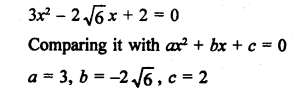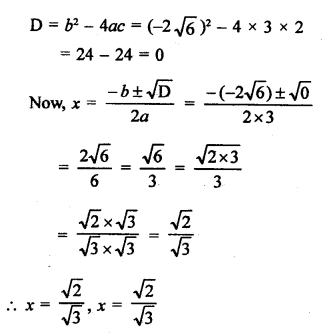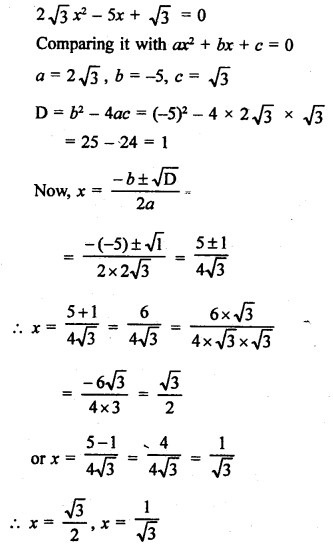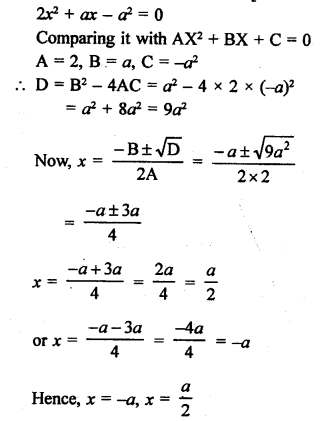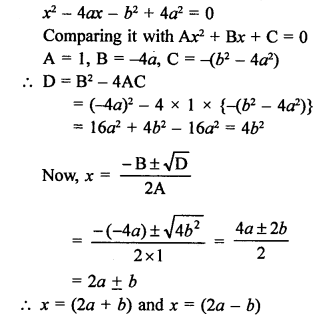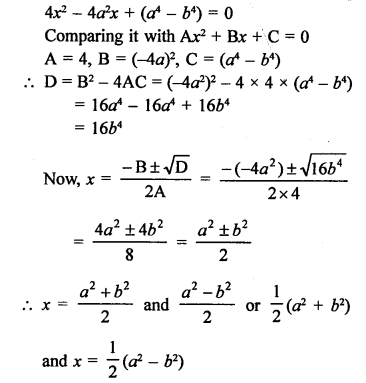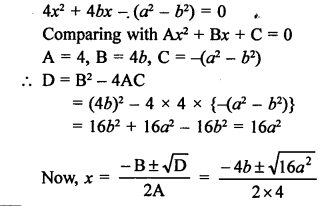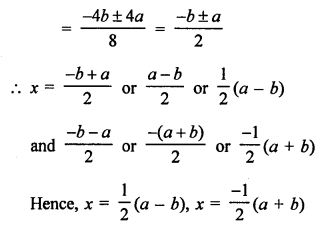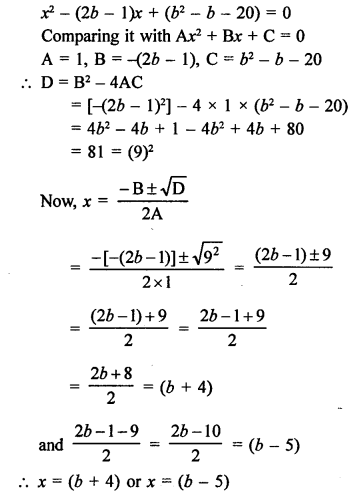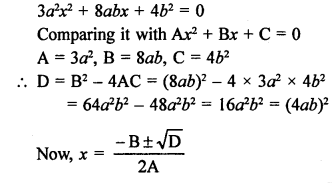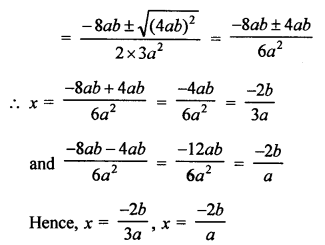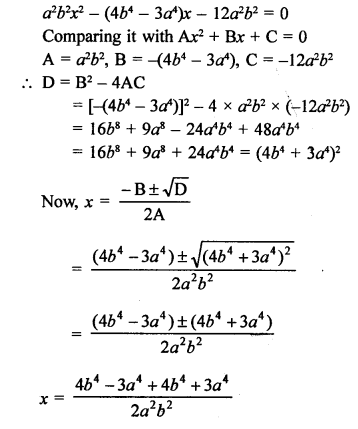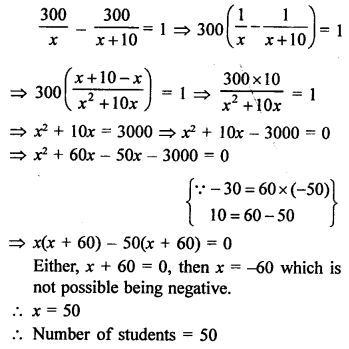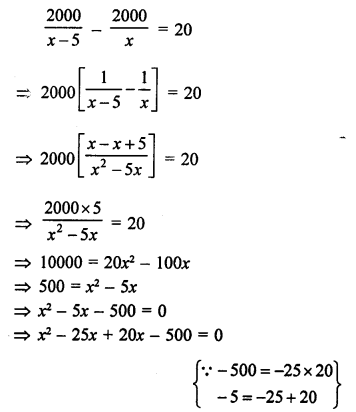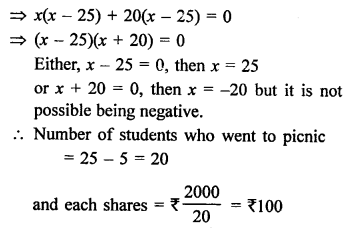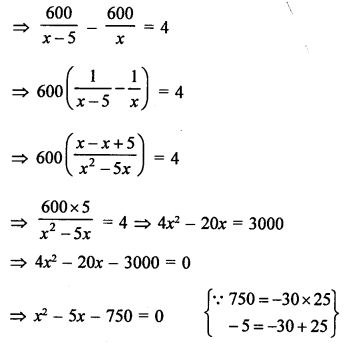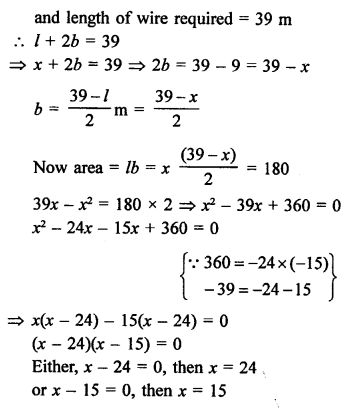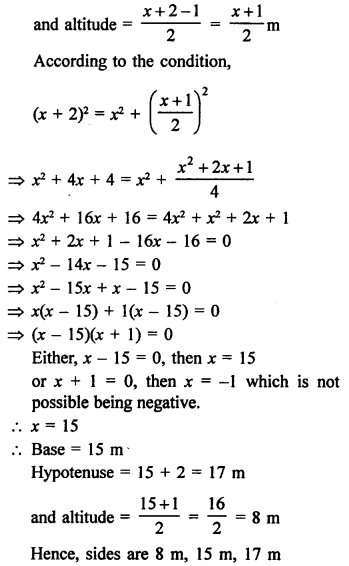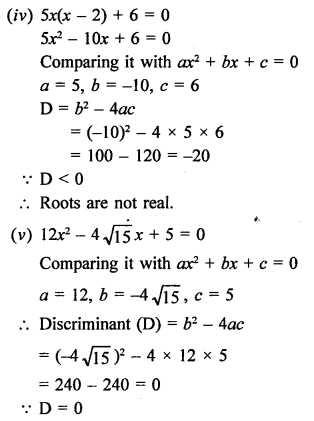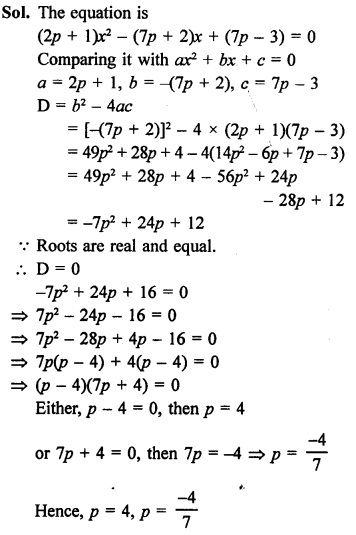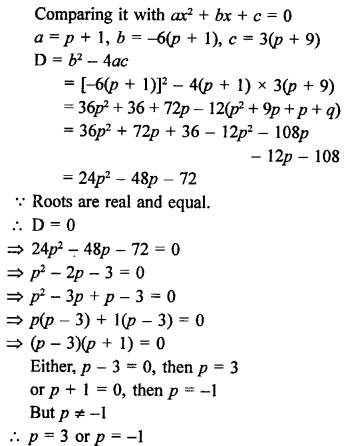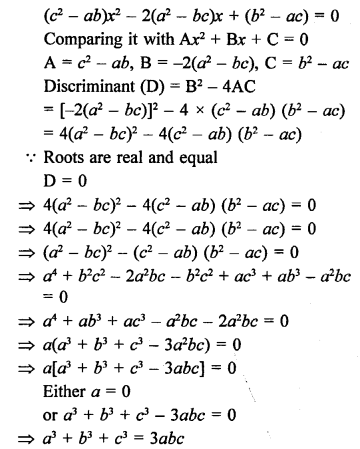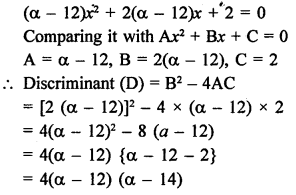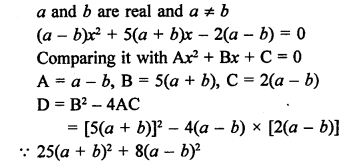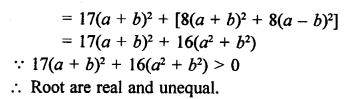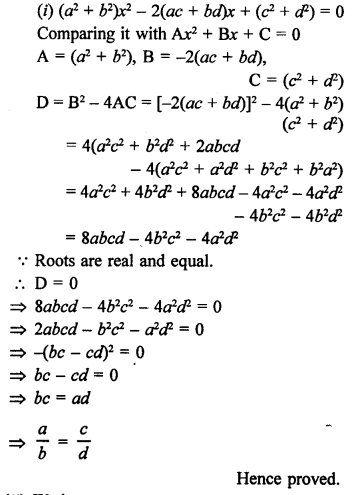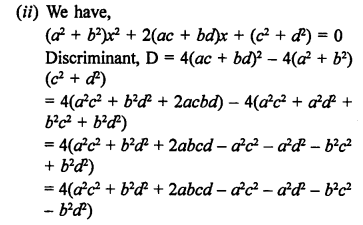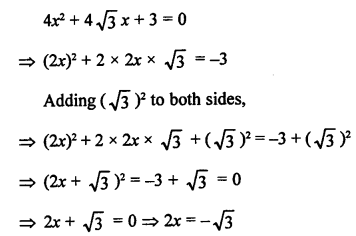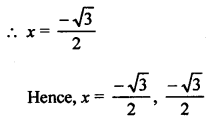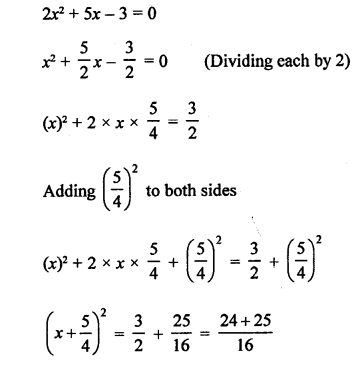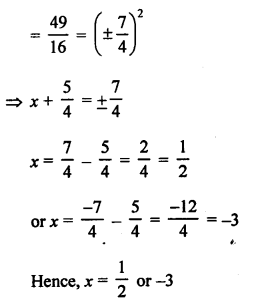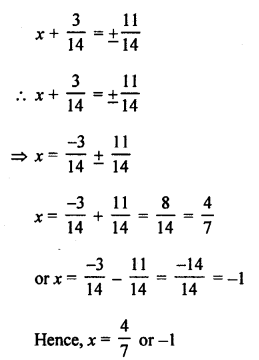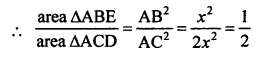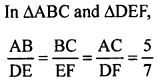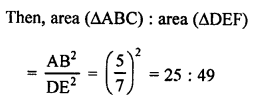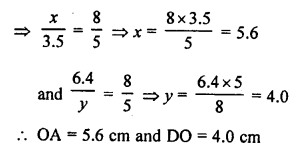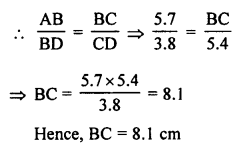RS Aggarwal Class 10 Solutions Chapter 12 Circles MCQS

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 12 Circles MCQS.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 12 Circles Ex 12A
• RS Aggarwal Solutions Class 10 Chapter 12 Circles Ex 12B
• RS Aggarwal Solutions Class 10 Chapter 12 Circles MCQS
• RS Aggarwal Solutions Class 10 Chapter 12 Circles Test Yourself

Choose the correct answer in each of the following questions.
Question 1.
Solution:
Number of tangents drawn from an external point to a circle is 2. (b)

Question 2.
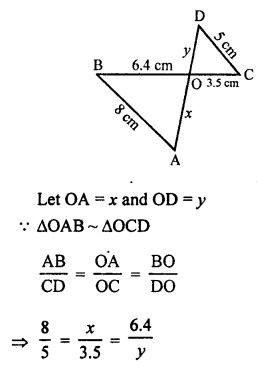
Solution:
In the given figure, RQ is tangent to the circle with centre O.
SQ = 6 cm, QR = 4 cm
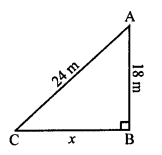
OR = √(OQ² + QR²) (In right ∆OQR)

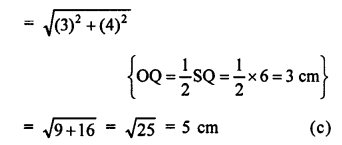
Question 3.
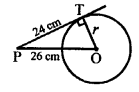
Solution:
In the given figure, PT is tangent to the circle with centre O and radius OT = 7 cm, PT = 24 cm
OT is the radius and PT is the tangent OT ⊥ PT
Now, in right ∆OTP,
OP² = OT² + PT²
OP² = (7)² + (24)²
OP² = 49 + 576 = 625 = (25)²
OP = 25 cm (c)

Question 4.
Solution:
Two diameters cannot be parallel. (d)

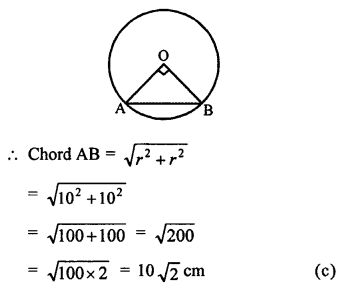
Question 5.
Solution:
A chord subtends a right angle at its centre
Radius of the circle = 10 cm

Question 6.
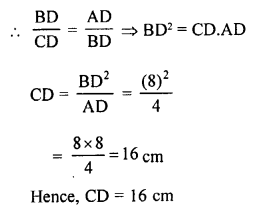
Solution:
In the given figure, PT is tangent to the circle with centre O and radius
OT = 6 cm OP = 10 cm
OT is the radius and PT is the tangent
OT ⊥ TB
Now, in right ∆OPT,
OP² = OT² + PT² (Pythagoras Theorem)
⇒ (10)² = (6)² + PT²
⇒ 100 = 36 + PT²
⇒ PT² = 100 – 36 = 64 = (8)².
PT = 8 cm (a)

Question 7.
Solution:
In the given figure, point P is 26 cm away from the centre O of the circle.

Length of tangent PT = 24 cm
Let radius = r
In right ∆OPT,
OP² = PT² + OT²
⇒ 26² = 24² + r²
⇒ r² = 26² – 24² = 676 – 576 = 100 = (10)²
r = 10
Radius = 10 cm (a)

Question 8.
Solution:
PQ is tangent to the circle with centre O at P. ∆OPQ is an isosceles triangle.

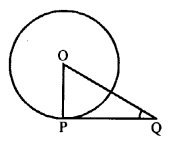
∠OQP = ?
∆OPQ is an isosceles triangle
OP = PQ
∠POQ = ∠OQP
But OP is radius and PQ is tangent
OP ⊥ PQ ⇒ ∠OPQ = 90°
∠POQ + ∠OQP = 90°
⇒ ∠POQ = ∠OQP = \(\frac { 90 }{ 2 }\) = 45°
Hence, ∠OQP = 45° (b)

Question 9.
Solution:
In the given figure, AB and AC are tangents to the circle with centre O such that ∠BAC = 40°, ∠BOC = ?
AB and AC are tangents and OB and OC are radii.
OB ⊥ AB and OC ⊥ AC
⇒ ∠OBA = 90° and ∠OCA = 90°
In quadrilateral ∆BOC,
∠BAC + ∠BOC = 180°
⇒ 40° + ∠BOC = 180°
⇒ ∠BOC = 180° – 40° = 140° (d)

Question 10.
Solution:
A chord AB subtends an angle of 60° at the centre of a circle with centre O.

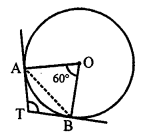
TA and TB are tangents drawn to the circle.
Then, ∠ATB = 180° – ∠AOB = 180° – 60° = 120° (d)

Question 11.
Solution:
In the given figure, O is the centre of the two concentric circles of radii 6 cm and 10 cm.
AB is a chord of the outer circle and touches the inner circle at P.
OP = 6 cm, OA = 10 cm
OP is radius and APB is tangent to the inner circle.
OP ⊥ AB and P is the mid point of AB.
In right ∆OPA,
OA² = OP² + AP²
⇒ 10² = 6² + AP²
⇒ 100 = 36 + AP²
⇒ AP²= 100 – 36 = 64 = (8)²
AP = 8 cm
and AB = 2 x AP = 2 x 8 = 16 cm (c)

Question 12.
Solution:
In the given figure, AB and AC are tangents to a circle with centre O and radius 8 cm.
OA = 17 cm.

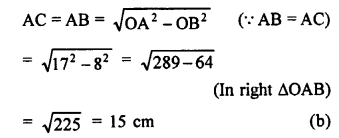
Question 13.
Solution:
In the given figure, O is the centre of the circle, AT is tangent, AOC is the diameter and ∠ACB = 50°

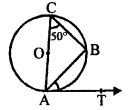
We have to find the measure of ∠BAT
AB is chord and AT is the tangent
∠ACB = ∠BAT (Angles in the alternate segment)
= 50° (b)

Question 14.
Solution:
O is the centre of circle, PQ is a chord, PT is tangent.

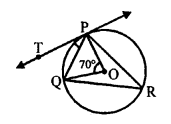
∠POQ = 70°, then ∠TPQ = ?
Take a point R on the major segment and join PR and QR
arc PQ subtends ∠POQ at the centre and ∠PRQ at the remaining part of the circle
∠PRQ = \(\frac { 1 }{ 2 }\) ∠POQ = \(\frac { 1 }{ 2 }\) x 70° = 35°
But ∠TPQ = ∠PRQ (Angles in the alternate segment)
∠TPQ = 35° (a)

Question 15.
Solution:
In the given figure, AT is the tangent to the circle with centre O and OA is its radius OT = 4 cm, ∠OTA = 30°

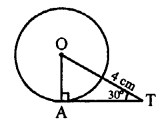
Now, we have to find the length of AT

Question 16.
Solution:
In the given figure, PA and PB are the two tangents to the circle with centre O, which subtends ∠AOB = 110°

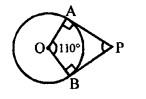
Now, we have to find the measure ∠APB
OA and OB are the radii of the circle and AP and BP are the tangents
OA ⊥ AP and OB ⊥ BP
∠A = ∠B = 90°
In quadrilateral OAPB,
∠A + ∠B = 90° + 90°= 180°
∠AOB + ∠APB = 180°
⇒ 110° + ∠APB = 180°
⇒ ∠APB = 180° – 110° = 70° (c)

Question 17.
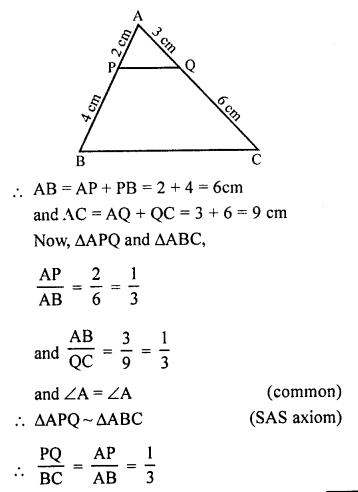
Solution:
In the given figure, in ∆ABC,
BC = ?
AF and AE are the tangents to the circle from A.
AE = AF = 4 cm CE = AC – AE = 11 – 4 = 7 cm
Similarly, CD and CE are tangents
CD = CE = 7 cm
and BF and BD are tangents BD = BF = 3 cm
BC = BD + CD = 3 + 7 = 10 cm (b)

Question 18.
Solution:
In the given figure, ∠AOD = 135°
We know that if a circle is inscribed in a quadrilateral, the opposite sides subtends supplementary angles.
∠AOD + ∠BOC = 180°
135° + ∠BOC = 180°
⇒ ∠BOC = 180° – 135° = 45° (b)

Question 19.
Solution:
In the given figure, PQ is a chord of a circle with centre O and PT is a tangent at P to the circle such that ∠QPT = 50°.

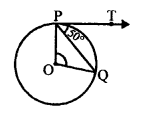
Then, we have to find ∠POQ.
PT is the tangent and OP is the radius
OP ⊥ PT ⇒ ∠OPT = 90°
∠OPQ = ∠OPT – ∠QPT = 90° – 50° = 40°
In ∆OPQ,
OP = OQ (radii of the same circle)
∠OPQ = ∠OQP = 40°
and ∠POQ = 180° – (∠OPQ + ∠OQP)
= 180° – (40° + 40°)
= 180°- 80° = 100° (a)

Question 20.
Solution:
In the given figure, PA and PB are two tangents to the circle with centre O.
∠APB = 60° then ∠OAB
Join OB.

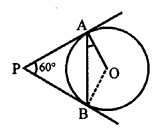
PAOB is a cyclic quadrilateral.
∠APB + ∠AOB = 180°
OA is radius and PA is tangent
OA ⊥ AP ⇒ ∠OAP = 90°
PA = PB (Tangents to the circle)
∠PAB = ∠PBA
But, ∠PAB + ∠PBA = 180° – 60° = 120°
∠PAB = ∠PBA = \(\frac { 120 }{ 2 }\) = 60°
∠OAB = 90° – 60° = 30° (b)

Question 21.
Solution:
Two tangents inclined at an angle of 60° are drawn to a circle of radius 3 cm.
Join OA, OB and OP.

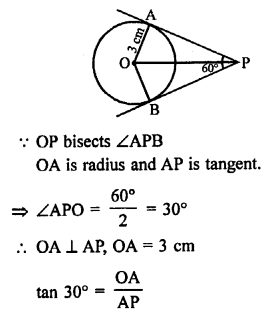
Question 22.
Solution:
In the given figure, PQ and PR are tangents drawn from an external point P to a circle with centre A.

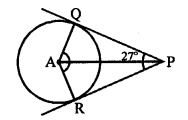
∠QPA = 27°, ∠QAR = ?
AP bisects ∠QPR and ∠QPA = 27°
∠QPR = 2 x 27° = 54°
But ∠QPR + ∠QAR = 180° (QARP is a cyclic quadrilateral)
⇒ 54° + ∠QAR = 180°
⇒ ∠QAR = 180° – 54° = 126° (c)

Question 23.
Solution:
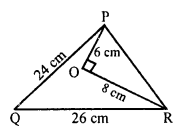
In the given figure, PA and PB are two tangents drawn from an external point P to a circle with centre C and radius 4 cm.
PA ⊥ PB, then length of tangent is = ?
Join GA and CB.

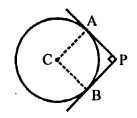
CAand CB are radii and PA, PB are tangents to the circle.
CA ⊥ PA and CB ⊥ PB But, ∠APB = 90°
∠ACB = 180° – 90° = 90°
PA = PB tangents of a circle
CAPB is a square
PA = PB = radius = 4 cm (b)

Question 24.
Solution:
In the given figure, PA and PB are tangents to the circle with centre O such that ∠APB = 80°.
Join OP

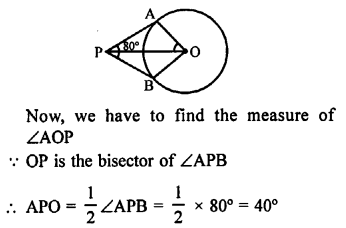
Now, in right ∆OAP, ∠A = 90°
∠AOP = 90° – 40° = 50° (b)

Question 25.
Solution:
In the given figure, O is the centre of a circle. AB is the tangent to the circle at point P.

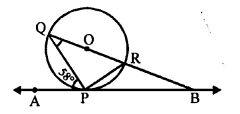
∠APQ = 58°, ∠PQB = ?
∠QPR = 90° (Angle in a semi circle)
But, ∠RPB + ∠QPR + ∠APQ = 180° (Angles on one side of a line)
⇒ ∠RPB + 90° + 58° = 180°
⇒ ∠RPB + 148° = 180°
⇒ ∠RPB = 180° – 148° = 32°
∠PQR or ∠PQB = ∠RPB (Angles in the alternate segment)
⇒ ∠PQB = 32° (a)

Question 26.
Solution:
In the given figure, O is the centre of the circle. AB is tangent to the circle at P.

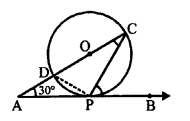
∠PAO = 30°
∠CPB + ∠ACP = ?
∠CPD = 90° (Angle in a semi circle)
∠DPA + ∠CPB = 90°
But, ∠DPA = ∠ACP (Angles in alternate segment)
∠CPB + ∠ACP = 90° (b)

Question 27.
Solution:
In the given figure, PQ is the tangent to the circle at A.
∠PAB = 67°, ∠AQB = ?
Join BC.
∠BAC = 90° (Angle in a semi circle)
But, ∠PAB + ∠BAC + ∠CAQ = 180°
⇒ 67° + 90° + ∠CAQ = 180°
⇒ 157° + ∠CAQ = 180°
∠CAQ = 182° – 157° = 23°
∠ACB = ∠PAB (Angles in the alternate segment)
∠ACB = 67°
In ∆ACQ,
Ext. ∠ACB = ∠CAQ + ∠AQC
⇒ 67° = 23° + ∠AQC
⇒ ∠AQC = 67° – 23° = 44°
⇒ ∠AQB = 44° (d)

Question 28.
Solution:
In the given figure, two circles touch each other at C. AB is the common tangent.
∠ACB = ?
Draw a tangent from C which meets AB at P.
PA and PC are tangents to the first circle.

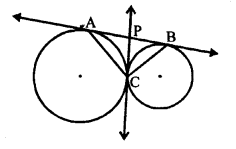
PA = PC
∠PAC = ∠PCA …(i)
Similarly, PB = PC
∠PCB = ∠PBC …(ii)
Adding, ∠PAC + ∠PBC = ∠PCA + ∠PCB
⇒ ∠PAC + ∠PBC = ∠ACB
But, ∠PAC + ∠PBC + ∠ACB = 180° (Angles of a triangle)
∠ACB = 90° (c)

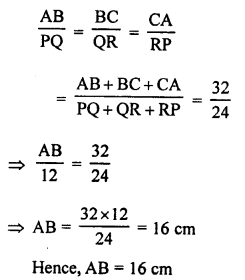
Question 29.
Solution:
In the given figure O is the centre of the circle with radius 5 cm P is a point out side the circle and OP = 13 cm
PQ and PR are the tangents to the circle drawn from P

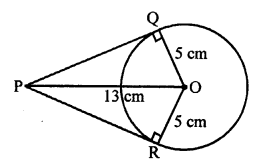
We have to find the area of quad. PQOR
OQ is radius and PQ is the tangent
OQ ⊥ QP
In ∆OPQ,
OP² = OQ² + PQ² (Pythagoras Theorem)
⇒ (13)² = (5)² + PQ²
⇒ 169 = 25 + PQ²
⇒ PQ² = 169 – 25 = 144 = (12)²
PQ = 12 cm
PQ = PR = 12 cm
Now, diagonal OP bisects the quad. PQOR into two triangles equal in areas.
Now, area of ∆PQO = \(\frac { 1 }{ 2 }\) x PQ x OQ
= \(\frac { 1 }{ 2 }\) x 12 x 5 = 30 cm²
Area of quad. PQOR = 2 x area ∆PQO = 2 x 30 = 60 cm² (a)

Question 30.
Solution:
In the given figure,
PQR is a tangent drawn at Q to the circle with centre O.
AB is a chord parallel to PR such that ∠BQR = 70°
Then, we have to find ∠AQB
Join QO and produce it to AB meeting it at L.
OQ ⊥ PR ⇒ LQ ⊥ PR
QL bisects AB at L
QA = QB
∆QAB is an isosceles triangle
∠LQA = ∠LQB
∠LQA = ∠LQR – ∠BQR = 90° – 70° = 20°
∠AQB = 2 x 20° = 40° (c)

Question 31.
Solution:
Length of a tangent to the circle from an external point = 10 cm
Radius (r) = 5 cm OP = ?

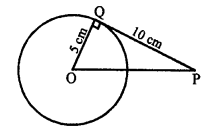
OQ is radius and QP is tangent
OQ ⊥ QP
In right ∆OPQ,
OP² = OQ² + QP² (Pythagoras Theorem) = (5)² + (10)² = 25 + 100 = 125
OP = √125 cm (d)

Question 32.
Solution:
In the figure, O is the centre of the circle BOA is its diameter and PT is tangent at P which meets BA produced at T. ∠PBO = 30°.

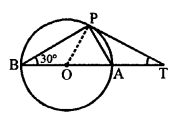
We have to find ∠PTA
In ∆BOP,
OB = OP (radii of the same circle)
∠APB = ∠PBO = 30°
But, OP is radius and PT is the tangent
OP ⊥ PT ⇒ ∠OPT = 90°
∠BPT = ∠BPO + ∠OPT = 30° + 90° = 120°
Now, in ∆PBT,
∠BPT + ∠PBA + ∠PTA = 180° (sum of angles of a triangle)
⇒ 120° + 30° + ∠PTA = 180°
⇒ 150° + ∠PTA = 180°
⇒ ∠PTA = 180° – 150° = 30° (b)

Question 33.
Solution:
In the given figure, a circle touches the side DF of a AEDF at H and touches ED and EF on producing at K and M respectively.
EK = 9 cm.

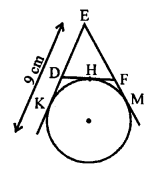
Perimeter of ∆EDF.
DH and DK are tangents to the circle.
DH = DK
Similarly, ∠FH = ∠FM and EK = EH = 9 cm
EK = ED + DK ⇒ ED + DH = 9 cm…(i)
Similarly, EH = EF = FH = EF + FM = 9 cm …(ii)
Adding (i) and (ii)
ED + DH + EF + FH = 9 + 9 cm (DH + HF = DF)
ED + DF + FE = 18 cm
Perimeter of ∆EDF = 18 cm (d)

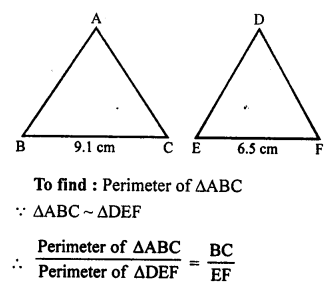
Question 34.
Solution:
In the given figure, PA and PB are two tangents drawn from an external point P which inclined at an angle of 45°.
OA and OB are radii of the circle.

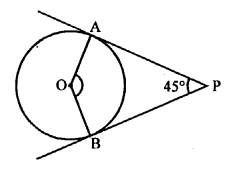
To find ∠AOB
AOBP is a cyclic quadrilateral
∠AOB + ∠APB = 180°
⇒ ∠AOB + 45° = 180°
⇒ ∠AOB = 180° – 45° = 135° (b)

Question 35.
Solution:
In the given figure, O is the centre of the circle PQL and PRM are the tangents from P drawn to the circle meeting it at Q and R respectively ∠SQL = 50°, and ∠SRM = 60°

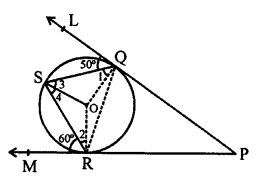
Now, we have to find ∠QSR,
Join OQ, OR and OS OQ is radius and QP is tangent
OQ ⊥ QP
Similarly, OR ⊥ RP
∠1 = 90° – 50° = 40° and ∠2 = 90° – 60° = 30°
OS = OQ (radii of the same circle)
∠3 = ∠1 = 40°
Similarly OS = OR
∠2 = ∠4 = 30°
∠QSR = ∠3 + ∠4 = 40° + 30° = 70° (d)

Question 36.
Solution:
In the given figure, a ∆PQR is drawn to inscribe a circle with centre O and radius 6 cm.
OT is radius.

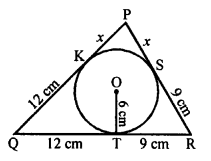
QT = 12 cm, TR = 9 cm
Area ∆PQR =189 cm²
PQ = ?
QK = QT = 12 cm
RS = RT = 9 cm
Let PK = PS = x cm
PQ = 12 + x
PR = 9 + x cm
Area of A = \(\frac { 1 }{ 2 }\) x r x Perimeter of ∆PQR
⇒ 189 = \(\frac { 1 }{ 2 }\) x 6 x (PQ + QR + RP)
⇒ 189 = 3 (12 + x + 21 + 9 + x)
⇒ 63 = 42 + 2x
⇒ 2x = 63 – 42 = 21
x = 10.5
AB = 10.5 + 12 = 22.5 cm (c)

Question 37.
Solution:
In the given figure, QR is a common tangent to two given circles touching each other externally at point T.
A tangent PT is drawn from T which intersects QR at P.
PT = 3.8 cm, QR = ?
PT and PQ are tangents to the first circle.
PQ = PT …(i)
Similarly, PT and PR tangents to the second circle.
PR = PT …(ii)
From (i) and (ii),
PQ = PR = PT = 3.8 cm
QR = 3.8 + 3.8 = 7.6 cm (d)

Question 38.
Solution:
In the figure, quadrilateral ABCD is circumscribed touches the circle at P, Q, R and S

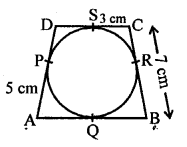
AP = 5 cm, BC = 7 cm, CS = 3 cm AB = ?
Tangents drawn from the external point to the circle are equal
AQ = AP = 5 cm
CR = CS = 3 cm
BQ = BR
Now, BR = BC – CR = 7 – 3 = 4 cm
BQ = 4 cm
Now, AB = AQ + BQ = 5 + 4 = 9 cm (a)

Question 39.
Solution:
In the given figure, quad. ABCD is circumscribed touching the circle at P, Q, R and S
AP = 6 cm, BP = 5 cm, CQ = 3 cm and DR = 4 cm.
Now, we have to find the perimeter of the quad. ABCD.
We know that tangents from an external point to the circle are equal.
AP = AS = 6 cm
BP = BQ = 5 cm
CQ = CR = 3 cm
DR = DS = 4 cm
AB = AP + BP = 6 + 5 = 11 cm
BC = BQ + CQ = 5 + 3 = 8 cm
CD = CR + DR = 3 + 4 = 7 cm
and DA = AS + DS = 6 + 4 = 10 cm
Perimeter of the quad. ABCD
= AB + BC + CD + DA
= (11 + 8 + 7 + 10) cm
= 36 cm (c)

Question 40.
Solution:
In the given figure, O is the centre of the circle, AB is chord and AT is the tangent at A.
∠AOB = 100°, ∠BAT = ?
Take a point P on the major segment of the circle and join AP and BP.

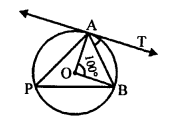
Arc AB subtends ∠AOB at the centre and ∠APB at the remaining part of the circle.
∠APB = \(\frac { 1 }{ 2 }\) ∠AOB = \(\frac { 1 }{ 2 }\) x 100° = 50°
Now, ∠BAT = ∠APB (Angles in the alternate segment)
∠BAT = 50° (b)

Question 41.
Solution:
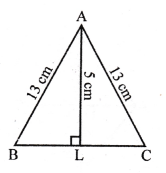
In a right ∆ABC, right angled at B
BC = 12 cm, AB = 5 cm
A circle is inscribed in it touching its sides at P, Q and R.
Join OP, OQ and OR.
AC² = AB² + BC² (Pythagoras Theorem)
= 5² + 12² = 25 + 144 = 169 = (13)²

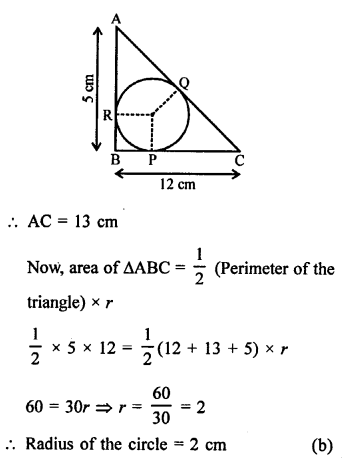
Question 42.
Solution:
In the given figure, a circle is inscribed in a quadrilateral ABCD touching its sides, AB, BC, CD and DA at P, Q, R and S respectively
Radius OS = 10 cm
BC = 38 cm, PB = 27 cm

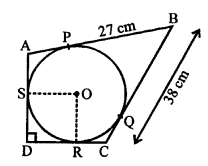
AD ⊥ DC
Length of CD = ?
Join OR and OS
BP and BQ are tangents to the circle
BQ = BP = 27 cm
BC = 38 cm
QC = 38 – 27 = 11 cm
CQ and CR are the tangents to the circle
CR = CQ = 11 cm
DR and DS are the tangents to the circle
DR = DS
AD ⊥ CD
OS is the radius and AD is the tangent
OS ⊥ AD
Similarly, OR ⊥ DC
OSDR is a square whose each side is equal to the radius = 10 cm
DR = DS = 10 cm
CD = CR + DR = 11 + 10 = 21 cm (d)

Question 43.
Solution:
In the given figure, ∆ABC is a right angled triangle, right angle at ∠B.
BC = 6 cm, AB = 8 cm
A circle with centre O is inscribed inside the triangle ABC
OP ⊥ AB and OQ ⊥ BC and OR ⊥ AC
OP = OQ = OR = x cm
OPBQ is a square
In right ∆ABC,
AC² = AB² + BC² (Pythagoras Theorem)
= (8)² + (6)² = 64 + 36 = 100 = (10)²
AC = 10 cm
Tangents drawn from the external point to the circle are equal
BP = BQ = x
CQ = CR = 6 – x
AP = AR = 8 – x
AR + CR = AC
⇒ 8 – x + 6 – x = 10
⇒ 14 – 2x = 10
⇒ 2x = 14 – 10 = 4
x = 2
Hence r = 2cm (a)

Question 44.
Solution:
A quadrilateral ABCD is circumscribed to a circle with centre O.
AB = 6 cm, BC = 7 cm, CD = 4 cm, AD = 7 cm

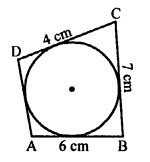
ABCD circumscribed to a circle.
AB + CD = BC + AD
⇒ 6 + 4 = 7 + AD
⇒ 10 = 7 + AD
AD = 10 – 7 = 3 cm (a)

Question 45.
Solution:
In the given figure, PA and PB are the tangents to the circle with centre O from P

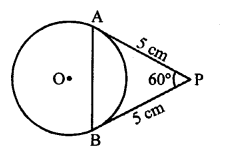
PA = 5 cm, ∠APB = 60°
PA = PB = 5 cm
In ∆APB, ∠P = 60° and PA = PB
PAB is an equilateral triangle
AB = AP = BP = 5 cm (b)

Question 46.
Solution:
In the given figure, DE and DF are tangents to the circle from an external point D.
A is the centre of the circle.
DF = 5 cm and DE ⊥ DF, radius of the circle = 3
Join EA and FA.

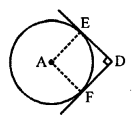
AE and AF are the radius of the circle and DE and BF are the tangents.
AE ⊥ DE and AF ⊥ DF
∠EAF = 180° – ∠EDF = 180° – 90° = 90°
AEDF is a square.
AE = 5 cm
Radius of the circle = 5 cm (c)

Question 47.
Solution:
In the given figure, three circles with centre A, B and C are drawn touching each other externally
AB = 5 cm, BC = 7 cm and CA = 6 cm
Let r1, r2, r3 be the radii of three circles respectively

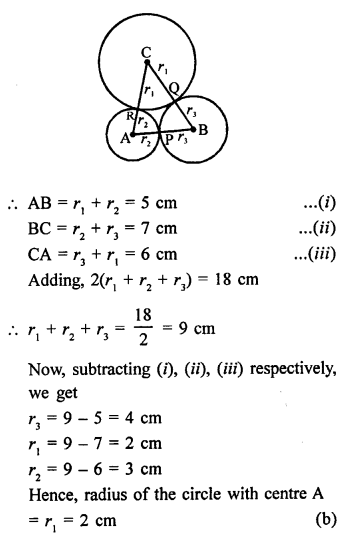
Question 48.
Solution:
In the given figure, AP, AQ and BC are tangents to the circle.

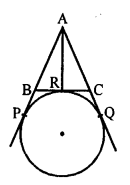
AB = 5 cm, AC = 6 cm, BC = 4 cm
Length of AP = ?
BP and BR are the tangents to the circle.
BP = BR
Similarly, CR and CQ are tangents
CR = CQ
S and AP and AQ are tangents
AP = AQ
AP = AB + BP = AB + BR
AQ = AC + CQ = AC + CR
AP + AQ = AB + BR + AC + CR = AB + BR + CR + AC
AP + AP = AB + BC + AC
2AP = 5 + 4 + 6 = 15 cm
AP = \(\frac { 15 }{ 2 }\) = 7.5 cm (d)

Question 49.
Solution:
In the given figure, O is the centre of two concentric circles of radii 5 cm and 3 cm respectively.
From external point P, PA and PB are tangents are drawn to the external circle and internal circle respectively
PA = 12 cm, PB = ?

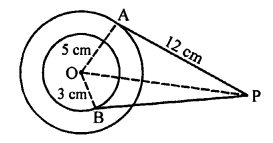
OA and OB are the radii
OA ⊥ AP and OB ⊥ BP
Now, in right ∆OAP,
OP² = OA² + AP² (Pythagoras Theorem)
= (5)² + (12)²
= 25 + 144 = 169 = (13)²
OP = 13 cm
and in right ∆OBP,
OP² = OB² + BP²
(13)² = (3)² + BP²
⇒ 169 = 9 + BP²
⇒ PB² = 169 – 9 = 160
PB = √160 = √(16 x 10) = 4√10 cm (c)

True/False Type
Question 50.
Solution:
(a) It is true that no tangent can be drawn from a point inside the circle.
(b) It is true, that one and only one tangent can be drawn from a point on the circle.
(c) True. If a point P is outside the circle, two tangents can be drawn to the circle.
(d) No, only two parallel tangents can be drawn which are parallel to a given line. (d)

Question 51.
Solution:
(a) It is true as a tangent intersects (touches) the circle exactly at one point.
(b) It is true that common point to the circle where the tangent touches the circle is called point of contact.
(c) It is true that the radius through the point of contact of a tangent is perpendicular to it.
(d) False as a straight line can meet at the most two points. (d)

Question 52.
Solution:
(a) It is true, that a secant is a line which intersects the circle at two points.
(b) It is true, as a tangent intersects the circle at only one point.
(c) It is true that the point at which a tangent touches the circle is called a point of contact.
(d) It is false, as no tangent can be drawn from a point in side the circle.

Assertion and Reason Type
Each question consists of two statements, namely, Assertion (A) and Reason (R).
For selecting the correct answer, use the following code :
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is a correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not a correct explanation of Assertion (A).
(c) Assertion (A) is true and Reason (R) is false.
(d) Assertion (A) is false and Reason (R) is true.
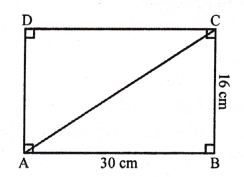
Question 53.
Solution:
In Assertion (A):
In right ∆OPQ, OP ⊥ PQ

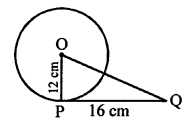
OQ² = OP² + PQ² = (12)² + (16)² = 144 + 256 = 400 = (20)²
OQ = 20 cm, which is true
In Reason (R):
It is also with respect to (A) (a)

Question 54.
Solution:
Assertion (A):
The statement is true
In Reason (R):
It is also true but not with respect to (A) (b)

Question 55.
Solution:
In Assertion (A):
In the figure, ABCD is a quad, which is circumscribed a given circle.
Sum of opposite sides are equal
AB + CD = BC + AD
It is not true that AB + BC = AD + DC
In Reason (R):
It is true but not with respect to Assertion (A) (d)

Hope given RS Aggarwal Solutions Class 10 Chapter 12 Circles MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 11 Arithmetic Progressions MCQS

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions MCQS

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11A
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11B
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11C
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11D
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions MCQS

Choose the correct answer in each of the following questions.
Question 1.
Solution:

Question 2.
Solution:

Question 3.
Solution:

Question 4.
Solution:

Question 5.
Solution:

Question 6.
Solution:

Question 7.
Solution:

Question 8.
Solution:

Question 9.
Solution:

Question 10.
Solution:

Question 11.
Solution:

Question 12.
Solution:

Question 13.
Solution:

Question 14.
Solution:
Sum of first n odd natural numbers = (n)²
Sum of first 20 odd natural numbers = (20)² = 400 (c)

Question 15.
Solution:
First 40 positive integers divisible by 6 are 6, 12, 18, 24, … to 40 terms
Here, a = 6, d = 6, n = 40

Question 16.
Solution:

Question 17.
Solution:

Question 18.
Solution:
In an AP,
a₁₈ – a₁₄ = 32
Let a be the first term and d be the common difference, then

Question 19.
Solution:

Question 20.
Solution:

Question 21.
Solution:

Question 22.
Solution:

Question 23.
Solution:

Question 24.
Solution:

Question 25.
Solution:
Sum of first 16 terms of AP 10, 6, 2, …
Here, a = 10, d = 6 – 10 = -4, n = 16

Question 26.
Solution:

Question 27.
Solution:

Question 28.
Solution:
In an AP, T₁₇ = T₁₀ + 21
Let a be the first term and d be the common difference, then

Question 29.
Solution:

Question 30.
Solution:

Hope given RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 10 Quadratic Equations Ex 10C

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10C.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10A
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10B
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10C
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10D
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10E
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Test Yourself

Find the discriminant of each of the following equations:
Question 1.
Solution:

Find the roots of each of the following equations, if they exist, by applying the quadratic formula:
Question 2.
Solution:

Question 3.
Solution:

x = 3 + √5 or x = 3 – √5

Question 4.
Solution:

Question 5.
Solution:

Question 6.
Solution:

Question 7.
Solution:

Question 8.
Solution:

Question 9.
Solution:

Question 10.
Solution:

Question 11.
Solution:

Question 12.
Solution:

Question 13.
Solution:

Question 14.
Solution:

Question 15.
Solution:

Question 16.
Solution:
x² + x + 2 = 0
Comparing it with ax² + bx + c = 0
a = 1, b = 1, c = 2
D = b² – 4ac = (1)² – 4 x 1 x 2 = 1 – 8 = -7
D < 0
There are no real roots.

Question 17.
Solution:

Question 18.
Solution:

Question 19.
Solution:

Question 20.
Solution:
3x² – 2x + 2 = 0
Comparing it with ax² + bx + c = 0
a = 3, b = -2, c = 2
D = b² – 4ac = (-2 )² – 4 x 3 x 2 = 4 – 24 = -20
D < 0
Roots are not real.

Question 21.
Solution:

Question 22.
Solution:

Question 23.
Solution:

Question 24.
Solution:

Question 25.
Solution:

Question 26.
Solution:

Question 27.
Solution:

x = (a + 2b) and x = (a – 2b)

Question 28.
Solution:

Question 29.
Solution:

Question 30.
Solution:

Question 31.
Solution:

Question 32.
Solution:

Question 33.
Solution:

Question 34.
Solution:

Question 35.
Solution:

Question 36.
Solution:

Hope given RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 10 Quadratic Equations Ex 10E

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10E.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10A
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10B
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10C
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10D
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10E
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Test Yourself

PROBLEMS ON NUMBERS
Question 1.
Solution:
Let natural number be = x
According to the condition,
x² + x = 156
⇒ x² + x – 156 = 0
⇒ x² + 13x – 12x – 156 = 0
⇒ x (x + 13) – 12 (x + 13) = 0
⇒ (x + 13) (x – 12) = 0
Either, x + 13 = 0, then x = -13 but it is not a natural number
or x – 12 = 0, then x = 12
Hence, required number = 12

Question 2.
Solution:
Let the natural number be x,
Then according to the condition,
x + √x = 132
Let √x = y, then
y² + y = 132
⇒ y² + y – 132 = 0
⇒ y² + 12y – 11y – 132 = 0
⇒ y (y + 12) – 11 (y + 12) = 0
⇒ (y + 12) (y – 11) = 0
Either, y + 12 = 0, then y = -12 but it is not a natural number.
or y – 11 = 0 ⇒ y = 11
√x = 11 ⇒ x = 121
Hence, required number =121

Question 3.
Solution:
Sum of two natural numbers = 28
Let first number = x
Then second number = 28 – x
According to the condition,
x (28 – x) = 192
⇒ 28x – x² = 192
⇒ x² – 28x + 192 = 0
⇒ x² – 16x – 12x + 192 = 0
⇒ x (x – 16) – 12 (x – 16) = 0
⇒ (x – 16)(x – 12) = 0
Either, x – 16 = 0, then x = 16
or x – 12 = 0, then x = 12
Required natural numbers are 16 and 12

Question 4.
Solution:
Let first integer = x
Then second = x + 1
According to the condition,
(x)² + (x + 1)² = 365
⇒ x² + x² + 2x + 1 = 365
⇒ 2x² + 2x + 1 – 365 = 0
⇒ 2x² + 2x – 364 = 0
⇒ x² + x – 182 = 0
⇒ x² + 14x – 13x – 182 = 0
⇒ x(x + 14) – 13(x + 14) = 0
⇒ (x + 14)(x – 13) = 0
Either, x + 14 = 0, then x = -14 but it is negative.
or x – 13 = 0, then x = 13
First number = 13
and second number = 13 + 1 = 14
Hence, the numbers are 13, 14

Question 5.
Solution:
Let first odd number = x
Then second consecutive odd number = x + 2
According to the condition,
x² + (x + 2)² = 514
⇒x² + x² + 4x + 4 = 514
⇒ 2x² + 4x + 4 – 514 = 0
⇒ 2x² + 4x – 510 = 0
⇒ x² + 2x – 255 = 0
⇒ x² + 17x – 15x – 255 = 0
⇒ x (x + 17) – 15 (x + 17) = 0
⇒ (x + 17) (x – 15) = 0
Either, x + 17 = 0, then x = -17 but it is not positive.
or x – 13 = 0, then x = 13
First odd number = 13
and second number = 13 + 2 = 15
Hence, the number are 15, 17

Question 6.
Solution:
Let first positive even number = x
Then second even number = x + 2
According to the condition, x² + (x + 2)² = 452
⇒ x² + x² + 4x + 4 = 452
⇒ 2x² + 4x + 4 – 452 = 0
⇒ 2x² + 4x – 448 = 0
⇒ x² + 2x – 224 = 0
⇒ x² + 16x – 14x – 224 = 0
⇒ x (x + 16) – 14 (x + 16) = 0
⇒ (x + 16) (x – 14) = 0
Either, x + 16 = 0, then x = 16 which is not positive.
or x – 14 = 0, then x = 14
First even number = 14
and second number = 14 + 2 = 16
Hence, the numbers are 14, 16

Question 7.
Solution:
Let first positive integer = x
Then second integer = x + 1
According to the condition,
x (x + 1) = 306
⇒ x² + x – 306 = 0
⇒ x² + 18x – 17x – 306 = 0
⇒ x (x + 18) – 17 (x + 18) = 0
⇒ (x + 18)(x – 17) = 0
Either, x + 18 = 0, then x = -18 which is not positive.
or x – 17 = 0, then x = 17
First number =17
and second integer = 17 + 1 = 18
Hence, the numbers are 17, 18

Question 8.
Solution:
Let first natural number = x
Then second number = x + 3
According to the condition,
x (x + 3) = 504
⇒ x² + 3x – 504 = 0
⇒ x² + 24x – 21x – 504 = 0
⇒ x(x + 24) – 21(x + 24) = 0
⇒ (x + 24)(x – 21) = 0
Either x + 24 = 0, then x = -24 but it is not positive.
or x – 21 =0, then x = 21
First natural number = 21
and second number = 21 + 3 = 24
Hence, two required numbers are 21, 24

Question 9.
Solution:
Let first multiple of 3 = 3x
and second = 3x + 3
According to the condition,
3x (3x + 3) = 648
⇒ 9x² + 9x – 648 = 0
⇒ x² + x – 72 = 0
⇒ x² + 9x – 8x – 72 = 0
⇒ x (x + 9) – 8 (x + 9) = 0
⇒ (x + 9)(x – 8) = 0
Either, x + 9 = 0, then x = -9 which is negative.
or x – 8 = 0, then x = 8
First multiple of 3 = 3 x 8 = 24
and second = 24 + 3 = 27
Hence, numbers are 24, 27

Question 10.
Solution:
Let first positive odd integer = x
Then second = x + 2
According to the condition,
x (x + 2) = 483
⇒ x² + 2x – 483 = 0
⇒ x² + 23x – 21x – 483 = 0
⇒ x (x + 23) – 21(x + 23) = 0
⇒ (x + 23)(x – 21) = 0
Either, x + 23 = 0, then x = -23 which is negative.
or x – 21 =0, then x = 21
First odd number = 21
and second = 21 + 2 = 23
Hence, numbers are 21, 23

Question 11.
Solution:
Let first positive even integer = 2x
Then second even integer = 2x + 2
According to the condition,
2x (2x + 2) = 288
⇒ 4x² + 4x – 288 = 0
⇒ x² + x – 12 = 0
⇒ x² + 9x – 8x – 72 = 0
⇒ x (x + 9) – 8 (x + 9) = 0
⇒ (x + 9) (x – 8) = 0
Either, x + 9 = 0, then x = -9 which is negative.
or x – 8 = 0, then x = 8
First even integer = 2 x 8 = 16
and second even integer = 16 + 2 = 18
Hence, required integers are 16, 18

Question 12.
Solution:
Sum of two natural numbers = 9
Let first number = x
Then second number = 9 – x
According to the condition,

Question 13.
Solution:
Sum of two natural numbers = 15
Let first number = x
Then second number = 15 – x
According to the condition,

Question 14.
Solution:
Difference of two natural numbers = 3
Let first number = x
Then second number = x + 3
According to the condition,

Either, x + 7 = 0, then x = -7 which is negative.
or x – 4 = 0, then x = 4.
First number = 4
and second number = 4 + 3 = 7
Hence, the numbers are 4, 7

Question 15.
Solution:
Difference of two natural numbers = 5
Let first number = x
Then second number = x – 5
According to the condition,

⇒ x (x – 7) + 2 (x – 7) = 0
⇒ (x – 7) (x – 2) = 0
Either, x – 7 = 0, then x = 7
or x + 2 = 0, then x = -2 which is negative
First number = 7
and second number = 7 – 5 = 2
Hence, numbers are 7, 2

Question 16.
Solution:
Let first number = 7x
Then second number = 7x + 7
According to the condition,
(7x)² + (7x + 7)² = 1225
⇒ 49x² + 49x² + 49 + 98x = 1225
⇒ 98x² + 98x + 49 – 1225 = 0
⇒ 98x² + 98x – 1176 = 0
⇒ x² + x – 12 = 0 (Dividing by 98)
⇒ x² + 4x – 3x – 12 = 0
⇒ x (x + 4) – 3 (x + 4) = 0
⇒ (x + 4) (x – 3) = 0
Either, x + 4 = 0, then x = -4 which is negative.
or x – 3 = 0, then x = 3
First number 3 x 7 = 21
and second number = 21 + 7 = 28
Hence, numbers are 21, 28

Question 17.
Solution:
Let the natural number = x
According to the condition,

⇒ 8x² – 64x – x + 8 = 0
⇒ 8x (x – 8) – 1 (x – 8) = 0
⇒ (x – 8) (8x – 1) = 0
Either, x – 8 = 0, then x = 8
or 8x – 1 = 0, then 8x = 1 ⇒ x = \(\frac { 1 }{ 8 }\) which is not a natural number.
Required natural number = 8

Question 18.
Solution:
Let first part = x
Then second part = 57 – x
According to the condition,
x (57 – x) = 680
⇒ 57x – x² = 680
⇒ x² – 57x + 680 = 0
⇒ x² – 40x – 17x + 680 = 0
⇒ x (x – 40) – 17 (x – 40) = 0
⇒ (x – 40) (x – 17) = 0
Either, x – 40 = 0, then x = 40
or x – 17 = 0, then x = 17
If first part is 40, then second part = 57 – 40 = 17
Parts are 40, 17 or 17, 40

Question 19.
Solution:
Let first part = x
Then second part = 27 – x
According to the condition,

⇒ 81x – 3x² = 540
⇒ 3x² – 81x + 540 = 0
⇒ x² – 27x + 180 = 0
⇒ x² – 12x – 15x + 180 = 0
⇒ x(x – 12) – 15(x – 12) = 0
⇒ (x – 12)(x – 15) = 0
Either, x – 12 = 0, then x = 12
or x – 15 = 0, then x = 15
If first part is 12, then
second part = 27 – 12 = 15
Parts are 12, 15 or 15, 12

Question 20.
Solution:
Let first part (larger) = x
Then second part = 16 – x
According to the condition,
2(x²) – (16 – x)² = 164
⇒ 2x² – (256 + x² – 32x) = 164
⇒ 2x² – 256 – x² + 32x – 164 = 0
⇒ x² + 32x – 420 = 0
⇒ x² + 42x – 10x – 420 = 0
⇒ x (x + 42) – 10 (x + 42) = 0
⇒ (x + 42) (x – 10) = 0
either x + 42 = 0, then x = -42 which is negative.
or x – 10 = 0, then x = 10
First part =10
and second part =16 – 10 = 6
Hence, parts are 10 and 6

Question 21.
Solution:
Let a and b be the two natural numbers.
According to the condition,
a² + b² = 25(a + b) and a² + b² = 50(a – b)
25(a + b) = 50(a – b)
⇒ a + b = 2(a – b)
⇒ a + b = 2a – 2b
⇒ 2a – a = 2b + b
⇒ a = 3b
Now, a² + b² = 25(a + b)
⇒ (3b)² + b² = 25(3b + b)
⇒ 9b² + b² = 25 x 4b
⇒ 10b² = 100b
⇒ b² = 10b
⇒ b² – 10b = 0
⇒ b(b – 10) = 0
Either, b = 0 which is not possible
or b – 10 = 0, then b = 10
a = 3b = 3 x 10 = 30
Numbers are 30 and 10

Question 22.
Solution:
Let the two natural numbers be a and b.
According to the condition,
a² – b² = 45 and b² = 4a
⇒ a² – 4a = 45
⇒ a² – 4a – 45 = 0
⇒ a² – 9a + 5a – 45 = 0
⇒ a(a – 9) + 5 (a – 9) = 0
⇒ (a – 9) (a + 5) = 0
Either, a – 9 = 0, then a = 9
or a + 5 = 0, then a = -5 which is not a natural number.
a = 9
and b² = 4a = 4 x 9 = 36 = (6)²
b = 6
Hence, numbers are 9, 6

Question 23.
Solution:
Let three consecutive positive integers be x, x + 1 and x + 2
According to the condition,
x² + (x + 1) (x + 2) = 46
⇒ x² + x² + 3x + 2 – 46 = 0
⇒ 2x² + 3x – 44 = 0
⇒ 2x² – 8x + 11x – 44 = 0
⇒ 2x (x – 4) + 11 (x – 4) = 0
⇒ (x – 4) (2x + 11) = 0
Either, x – 4 = 0, then x = 4
or 2x + 11 = 0, then 2x = -11 ⇒ x = \(\frac { -11 }{ 2 }\)
But it is not a natural number.
x = 4
Hence, three consecutive numbers are 4, 5, 6.

Question 24.
Solution:
Let the digits of a two digit number be x and y
Let one’s digit = x
and ten’s digit = y
Number = x + 10y
According to the condition,
x + 10y = 4(x + y)
and x + 10y = 2xy
Now, x + 10y = 4x + 4y
⇒ 10y – 4y = 4x – x
⇒ 3x = 6y
⇒ x = 2y …(i)
x + 10y = 2xy
⇒ 2y + 10y = 2 x 2y x y
⇒ 12y = 4y²
⇒ 3y = y²
⇒ y² – 3y = 0
⇒ y (y – 3) = 0
Either, y = 0, which is not possible,
or y – 3 = 0, then y = 3
x = 2y = 2 x 3 = 6
and number = x + 10y = 6 + 10 x 3 = 6 + 30 = 36

Question 25.
Solution:
Let the ones digit of a two digit number = x
and ten’s digit = y
Number = x + 10y
By reversing the digits,
the One’s digit = y
and ten’s digit = x
Number = y + 10x
According to the condition,
x + 10y + 45 = y + 10x
⇒ 10y – y + x – 10x = -45
9y – 9x = -45
⇒ x – y = 5
⇒ x = y + 5
and xy = 14
⇒ (y + 5) x y = 14
⇒ y² + 5y – 14 = 0
⇒ y² + 7y – 2y – 14 = 0
⇒ y (y + 7) – 2(y + 7) = 0
⇒ (y + 7)(y – 2) = 0
Either, y + 7 = 0, then x = -7 which is negative, so not possible.
or y – 2 = 0, then y = 2
x = y + 5 = 2 + 5 = 7
Number = x + 10y = 7 + 10 x 2 = 7 + 20 = 27

Question 26.
Solution:
Let numerator = x
Then denominator = x + 3

⇒ x² + 5x – 2x – 10 = 0
⇒ x (x + 5) – 2 (x + 5) = 0
⇒ (x + 5)(x – 2) = 0
Either x + 5 = 0, then x = -5 which not possible being negative,
or x – 2 = 0, then x = 2
Fraction = \(\frac { x }{ x + 3 }\) = \(\frac { 2 }{ 2 + 3 }\) = \(\frac { 2 }{ 5 }\)

Question 27.
Solution:
Let the denominator of a fraction = x
Then its numerator = x – 3

Question 28.
Solution:
Let the number = x
According to the condition,

SOME GENERAL PROBLEMS
Question 29.
Solution:
Let number of students = x
According to the given condition,

x² = (x + 25)(x – 24)
x² = x² + (25 – 24) x + 25 x (-24)
x² = x² + x – 600
x = 600
Number of students = 600

Question 30.
Solution:
Total number of apples = 300
Let number of students = x
Then according to the condition,

Question 31.
Solution:
Total number of marks = 40
Let marks in Mathematics = x
Then marks in English = 40 – x
According to the given condition,
(x + 3)(40 – x – 4) = 360
(x + 3)(36 – x) = 360
⇒ 36x – x² + 108 – 3x = 360
⇒ -x² + 33x + 108 – 360 = 0
⇒ -x² + 33x – 252 = 0
⇒ x² – 33x + 252 = 0
⇒ x² – 21x – 12x + 252 = 0
⇒ x(x – 21) – 12(x – 21) = 0
⇒ (x – 21)(x – 12) = 0
Either, x – 21 =0, then x = 21
or x – 11 = 0, then x = 11
Marks obtain in Mathematic and English = (21 and 19) or (12 or 28)

Question 32.
Solution:
Total budget = ₹ 2000
Let number of students = x
5 students failed to attend
Remaining students = x – 5
According to the condition,

Question 33.
Solution:
Let original price of each book = ₹ x
and total amount = ₹ 600
Commission in price = ₹ 5 per book
According to the condition,

⇒ x² – 30x + 25x – 750 = 0
⇒ x(x – 30) + 25(x – 30) = 0
⇒ (x – 30)(x + 25) = 0
Either, x – 30 = 0, then x = 30
or x + 25 = 0, then x = -25 which is not possible being negative.
Original price of each book = ₹ 30
and number of books = \(\frac { 600 }{ 30 }\) = 20

Question 34.
Solution:
Total expenses on tour = ₹ 10800
Let number of days = x
According to the condition,

⇒ x(x + 24) – 20(x + 24) = 0
⇒ (x + 24)(x – 20) = 0
Either, x + 24 = 0, then x = -24 which is not possible being negative,
or x – 20 = 0, then x = 20
Number of days of tour = 20 days

Question 35.
Solution:
Total marks obtained = 28
Let marks in Mathematics = x
Then marks in Science = 28 – x
According to the condition,
(x + 3)(28 – x – 4) = 180
⇒ (x + 3)(24 – x) = 180
⇒ 24x – x² + 72 – 3x = 180
⇒ -x² + 21x – 180 + 72 = 0
⇒ x² – 21x + 108 = 0
⇒ x² – 12x – 9x + 108 = 0
⇒ x(x – 12) – 9(x – 12) = 0
⇒ (x – 12)(x – 9) = 0
Either, x – 12 = 0, then x = 12
or x – 9 = 0, then x = 9
Marks obtained in Mathematics and Science = (12, 16) or (9, 19)

Question 36.
Solution:
Amount = ₹ 180
Let number of pens purchased = x
According to the condition,

⇒ x(x + 15) – 12(x + 15) = 0
⇒ (x + 15) (x – 12) = 0
Either, x + 15 = 0, then x = -15 which is not possible being negative,
or x – 12 = 0, then x = 12
Number of pens purchased = 12

Question 37.
Solution:
S.P. of an article = ₹ 75
Gain % = C.P. of the article
Let gain % = x %
According to the condition,

⇒ x² + 150x – 50x – 7500 = 0
⇒ x(x + 150) – 50(x + 150) = 0
⇒ (x + 150) (x – 50) = 0
Either, x + 150 = 0, then x = -150 which is not possible being negative,
or x – 50 = 0, then x = 50
Cost price of the article = ₹ 50

PROBLEMS ON AGES
Question 38.
Solution:
(i) Let present age of son = x years
His age 1 year ago = (x – 1) years
His father’s age = (x – 1) x 8
According to the condition,
(x – 1) x 8 + 1 = x2
⇒ 8x – 8 + 1 = x2
⇒ x² – 8x + 7 = 0
⇒ x² – x – 7x + 7 = 0
⇒ (x – 1)(x – 7) = 0
Either, x – 1 = 0, then x = 1 which is not possible.
or x – 7 = 0, then x = 7
Son’s age = 7 years
and his father’s age = (7)² = 49 years
(ii) Let the age of the son = x years
and the age of father = 3.5x years
According to the condition,
(x)² + (3.5x)² = 1325
⇒ x² + 12.25x² = 1325
⇒ 13.25x² = 1325
⇒ x² = 100
⇒ x = 10
Hence, the age of the son = 10 years
and the age of father 3.5 x 10 = 35 years

Question 39.
Solution:
Present age of Meena = x years
3 years ago her age = (x – 3) years
and 5 years hence, her age = (x + 5) years
According to the condition,

(x – 7) (x + 3) = 0
Either, x – 7 = 0, then x = 7
or x + 3 = 0, then x = -3 which is not possible being negative.
Her age = 7 years

Question 40.
Solution:
Sum of ages of a boy and his brother = 25 years
Let age of the boy = x years
Then age of his brother = (25 – x) years
According to the condition,
x (25 – x) = 126
⇒ 25x – x² – 126 = 0
⇒ x² – 25x + 126 = 0
⇒ x² – 18x – 7x + 126 = 0
⇒ x (x – 18) – 7 (x – 18) = 0
⇒ (x – 18) (x – 7) = 0
Either, x – 18 = 0, then x = 18
or x – 7 = 0, then x = 7
Age of boy = 7 years or 18 years
and age of his brother = 18 years or 7 years.

Question 41.
Solution:
Let present age of Tanvy = x years
Then 5 years ago her age = x – 5 years
8 years hence, her age = x + 8 years
According to the condition,
(x – 5) (x + 8) = 30
⇒ x² + 3x – 40 = 30
⇒ x² + 3x – 40 – 30 = 0
⇒ x² – 10x + 7x – 70 = 0
⇒ x (x – 10) + 7 (x – 10) = 0
⇒ (x – 10) (x + 7) = 0
Either, x – 10 = 0, then x = 10
or x + 7 = 0, then x = -7 which is not possible being negative.
Her present age = 10 years

Question 42.
Solution:
2 years ago,
Let son’s age = x years
and his father’s age = 3x²
Present age of son = (x + 2) years
and his father’s age = 3x² + 2
3 years hence, son’s age will be = x + 2 + 3 = x + 5 years
and age of his father = 3x² + 2 + 3 = (3x² + 5) years
According to the condition,
3x² + 5 = 4(x + 5)
⇒ 3x² + 5 = 4x + 20
⇒ 3x² – 4x + 5 – 20 = 0
⇒ 3x² – 4x – 15 = 0
⇒ 3x² – 9x + 5x – 15 = 0
⇒ 3x (x – 37) + 5 (x – 3) = 0
⇒ (x – 3)(3x + 5) = 0
Either, x – 3 = 0, then x = 3
or 3x + 5 = 0, then 3x = -5 ⇒ x = \(\frac { -5 }{ 3 }\) which is not possible being negative.
x = 3
Son’s present age = 3 + 2 = 5 years
and his father’s age = 3x² + 2
= 3 x (3)² + 2
= 27 + 2 = 29 years

PROBLEMS ON TIME AND DISTANCE
Question 43.
Solution:
Distance travelled = 150 km
Let the average speed of the truck = x km/hr

⇒ x (x – 60) + 10 (x – 60) 0
⇒ (x – 60) (x + 10) = 0
Either, x – 60 = 0, then x = 60
or x + 10 = 0, then x = -10 which is not possible being negative.
Original speed of the truck = 60 km/h

Question 44.
Solution:
Distance covered = 1500 km
Let original speed of the plane = x km/h

⇒ x² + 600x – 500x – 300000 = 0
⇒ x(x + 600) – 500(x + 600) = 0
⇒ (x + 600) (x – 500) = 0
Either, x + 600 = 0, then x = -600 which is not possible being negative.
or x – 500 = 0, then x = 500
Original speed of the plane = 500 km/hr
Yes, his promptness was appreciable.

Question 45.
Solution:
Distance covered by a train = 480 km
Let uniform speed = x km/h

⇒ x² – 40x + 32x – 1280 = 0
⇒ x(x – 40) + 32(x – 40) = 0
⇒ (x – 40) (x + 32) = 0
Either, x – 40 = 0, then x = 40
or x + 32 = 0, then x = -32 which is not possible being negative.
Speed of the train = 400 km/hr

Question 46.
Solution:
Distance covered = 54 km and then 63 km
Let first average speed = x km/hr
and next speed = (x + 6) km/hr
Total time taken = 3 hours
According to the condition,

⇒ x² – 33x – 108 = 0
⇒ x² – 36x – 3x – 108 = 0
⇒ x (x – 36) + 3 (x – 36) = 0
⇒ (x – 36) (x + 3) = 0
Either, x – 36 = 0, then x = 36
or x + 3 = 0, then x – 3 which is not possible being negative.
Speed of the train = 36 km/hr.

Question 47.
Solution:
Distance travelled by a train =180 km
Let the uniform speed = x km/hr

⇒ x² + 45x – 36x – 1620 = 0
⇒ x (x + 45) – 36 (x + 45) = 0
⇒ (x + 45) (x – 36) = 0
Either, x + 45 = 0, then x = -45 which is not possible being negative,
or (x – 36) = 0, then x = 36
Uniform speed of the train = 36 km/hr.

Question 48.
Solution:
Distance travelled = 300 km
Let the original speed of train be x km

⇒ 300x + 1500 – 300x = 2x² + 10x
⇒ 2x² + 10x – 1500 = 0
⇒ x² + 5x – 750 = 0 (Dividing by 2)
⇒ x² + 30x – 25x – 750 = 0
⇒ x (x + 30) – 25 (x + 30) = 0
⇒ (x + 30) (x – 25) = 0
Either, x + 30 = 0 ⇒ x = -30 (Rejected ∵ speed cannot be negative)
or x – 25 = 0 ⇒ x = 25
Speed of the train = 25 km/hr

Question 49.
Solution:
Distance = 300 km
Let the speed of the passenger = x km/hr

⇒ x (x + 30) – 25 (x + 30) = 0
⇒ (x + 30) (x – 25) = 0
Either, x + 30 = 0, then x = -30 which is not possible being negative,
or x – 25 = 0, then x = 25
Speed of the train = 25 km/hr.

Question 50.
Solution:
Distance between Mumbai and Pune = 192 km
Let the speed of Deccan Queen = x km/hr
and speed of another train = (x – 20) km/hr
According to the condition,

Question 51.
Solution:
Distance travelled = 24 km up and down
Speed of motor boat in still water = 18 km/hr
Let speed of stream = x km/hr
According to the condition,

⇒ x (x + 54) – 6 (x + 54) = 0
⇒ (x + 54) (x – 6) = 0
Either, x + 54 = 0, then x = -54 which is not possible being negative,
or x – 6 = 0, then x = 6
Speed of stream = 6 km/hr

Question 52.
Solution:
Speed of a boat in still water = 8 km/hr
Let speed of water in stream = x km/hr
Total time taken = 5 hours
According to the condition,

Question 53.
Solution:
Speed of motorboat in still water = 9 km/hr
Let speed of water = x km/hr
Total time taken = 3 hours
According to the condition,

PROBLEMS ON TIME AND WORK AND PIPES AND CISTERN
Question 54.
Solution:
Let B finishes the work in = x days
Then A will finish it in = (x – 10) days
According to the condition,
(A + B)’s one day’s work

⇒ x² – 30x – 4x + 120 = 0
⇒ x (x – 30) – 4 (x – 30) = 0
⇒ (x – 30)(x – 4) = 0
Either, x – 30 = 0, then x = 30
or x – 4 = 0, then x = 4
But x = 4 is not possible
x = 30
B can finish the work in 30 days
and A can in 30 – 10 = 20 days.

Question 55.
Solution:
2 pipes can fill a cistern in 3\(\frac { 1 }{ 13 }\) = \(\frac { 40 }{ 13 }\) minutes
Let one pipe can fill it in = x minute
Then second will fill it in = (x + 3) minutes

⇒ 13x (x – 5) + 24 (x – 5) = 0
⇒ (x – 5) (13x + 24) = 0
Either, x – 5 = 0, then x = 5
or 13x + 24 = 0
⇒ 13x = -24
⇒ x = \(\frac { -24 }{ 13 }\) which is not possible being negative.
x = 5
First pipe can fill the tank in 5 minutes
and second pipe will fill it in 5 + 3 = 8 minutes.

Question 56.
Solution:
Two pipes can fill a tank together in = 11\(\frac { 1 }{ 9 }\) = \(\frac { 100 }{ 9 }\) minutes
Let first pipe can fill it in = x minute
Then second pipe will fill it in = (x + 5) min
According to the condition,

⇒ 9x² – 155x – 500 = 0
⇒ 9x² – 180x + 25x – 500 = 0
⇒ 9x (x – 20) + 25(x – 20) = 0
⇒ (x – 20) (9x + 25) = 0
Either, x – 20 = 0, then x = 20
or 9x + 25 = 0, then 9x = -25 ⇒ x = \(\frac { -25 }{ 9 }\)
But it is not possible being negative.
First pipe will fill it in 20 minutes
and second will fill in = 20 + 5 = 25 minutes-

Question 57.
Solution:
Two water taps together can fill a tank in = 6 hours
Let first tap of larger diameter can fill it in x hour
Then second tap will fill it in (x – 9) hour
According to the condition,

PROBLEMS ON AREA AND GEOMETRY
Question 58.
Solution:
Let breadth of a rectangle (b) = x cm
Then length (l) = 2x cm
Area = l x b = 2x x x
2x x x = 288
⇒ 2x² = 288
⇒ x² = 144 = (12)²
x = 12
Length = 2x = 2 x 12 = 24 cm
and breadth = x = 12 cm

Question 59.
Solution:
Let breadth of a rectangular field (b) = x m
Then its length (l) = 3x m
Area = l x b = 3x x x = 3x²
3x² = 147
⇒ x² = 49 = (7)²
x = 7
Length = 3x = 3 x 7 = 21 m
and breadth = x = 7 m

Question 60.
Solution:
Let breadth of a hall (b) = x m
Then its length (l) = (x + 3) m
Area = l x b = (x + 3) x x = x² + 3x
x² + 3x = 238
⇒ x² + 3x – 238 = 0
⇒ x² + 11x – 14x – 238 = 0
⇒ x (x + 17) – 14 (x – 17) = 0
⇒ (x + 17) (x – 14) = 0
Either, x + 17 = 0, then x = -17 which is not possible being negative.
or x – 14 = 0, then x = 14
Breadth = 14 m
and length = 14 + 3 = 17 m

Question 61.
Solution:
Perimeter of a rectangular plot = 62 m
and area = 228 m²
Let length of plot = x m
Then width = \(\frac { 62 }{ 2 }\) – x = 31 – x
Area = l x b = x (31 – x)
x (31 – x) = 228
⇒ 31x – x² = 228
⇒ x² – 31x + 228 = 0
⇒ x² – 19x – 12x + 228 = 0
⇒ x (x – 19) – 12 (x – 19) = 0
⇒ (x – 19) (x – 12) = 0
Either, x – 19 = 0, then x = 19
or x – 12 = 0, then x = 12
If length is 19 m, then breadth = 31 – 19 = 12 m
and if length is 12 m then breadth = 31 – 12 = 19 m
which is not possible as length > breadth
Dimensions are (19, 12) m

Question 62.
Solution:
Area of path around it = 120 m²
Length of a rectangular field (l) = 16 m
and breadth (b) = 10 m
Let a path of x m wide be made around it, then its
Outer length (L) = (16 + 2x) m
and breadth (B) = (10 + 2x) m
Area of path = L x B – l x b
= (16 + 2x) (10 + 2x) – 16 x 10
⇒ 160 + 52x + 4x² – 160 = 120
⇒ 4x² + 52x – 120 = 0
⇒ x² + 13x – 30 = 0 (Dividing by 4)
⇒ x² + 15x – 2x – 30 = 0
⇒ x (x + 15) – 2 (x + 15) = 0
⇒ (x + 15) (x – 2) = 0
Either, x + 15 = 0, then x = -15 which is not possible being negative,
or x – 2 = 0, then x = 2
Width of path = 2 m

Question 63.
Solution:
The sum of areas of two squares = 640 m²
and difference between their perimeters = 64 m
Let 4 sides of first square = x m
Then perimeter = 4x
Perimeter of second square = 4x – 64
and side = \(\frac { 4x – 64 }{ 4 }\) = (x – 16) m
Now sum of their areas,
x² + (x – 16)² = 640
⇒ x² + x² – 32x + 256 = 640
⇒ 2x² – 32x + 256 – 640 = 0
⇒ 2x² – 32x – 384 = 0
⇒ x² – 16x – 192 = 0
⇒ x² – 24x + 8x – 192 = 0
⇒ x (x – 24) + 8 (x – 24) = 0
⇒ (x – 24) (x + 8) = 0
Either, x – 24 = 0, then x = 24
or x + 8 = 0, then x = -8 which not possible being negative,
x = 24
Side of first square = 24 m
and side of second square = 24 – 16 = 8 m

Question 64.
Solution:
Let side of a square = x m
Then length of rectangle = 3x m
and width = (x – 4) m

Now area of square = x² m²
and area of rectangle = l x b = (3x) x (x – 4) m²
According to the condition,
x² = 3x (x – 4)
⇒ x² = 3x² – 12x
⇒ 3x² – 12x – x2 = 0
⇒ 2x² – 12x = 0
⇒ 2x (x – 6) = 0
⇒ x – 6 = 0
⇒ x = 6m
Side of square = 6 m
and length of rectangle = 3 x 6 m = 18m
and width = x – 4 = 6 – 4 = 2m

Question 65.
Solution:
Area of a rectangular garden = 180 sq m
Let length of garden = x m

Question 66.
Solution:
Area of a right triangle = 600 cm²
Let altitude = x cm
Then base = (x + 10) cm

Area = \(\frac { 1 }{ 2 }\) base x altitude
600 = \(\frac { 1 }{ 2 }\) x (x + 10) x
x² + 10x = 1200
⇒ x² + 10x – 1200 = 0
⇒ x² + 40x – 30x – 1200 = 0
⇒ x (x + 40) – 30 (x + 40) = 0
⇒ (x + 40) (x – 30) = 0
Either, x + 40 = 0, then x = -40 which is not possible being negative.
or x – 30 = 0, then x = 30
Altitude = 30 cm
Base = 30 + 10 = 40 cm

Question 67.
Solution:
Area of right triangle = 96 sq. m
Let altitude of the triangle = x m
Then base = 3x m
Area = \(\frac { 1 }{ 2 }\) x base x altitude
96 = \(\frac { 1 }{ 2 }\) x 3x x x
⇒ 3x² = 96 x 2
x² = 64 = (8)²
x = 8 m
Base = 3x = 3 x 8 = 24m
and altitude = x = 8 m

Question 68.
Solution:
Area of right triangle = 165 sq m
Let altitude = x m
Then base = – (x + 7) m
Area = \(\frac { 1 }{ 2 }\) x base x altitude
165 = \(\frac { 1 }{ 2 }\) x x x (x + 7)
330 = x² + 7x
⇒ x² + 7x – 330 = 0
⇒ x² + 22x – 15x – 330 = 0
⇒ x (x + 22) – 15 (x + 22) = 0
⇒ (x + 22) (x – 15) = 0
Either, x + 22 = 0, then x = -22 which is not possible being negative,
or x – 15 = 0, then x = 15
Altitude = x + 7 = 15 + 7 = 22m
and base = x = 15 m

Question 69.
Solution:
In a right triangle,
Hypotenuse = 20 m
Difference of other two sides = 4 m
Let first side = x m
Then second side = (x + 4) m
According to the condition,
(x)² + (x + 4)² = (20)²
⇒ x² + x² + 8x + 16 = 400
⇒ 2x² + 8x + 16 – 400 = 0
⇒ 2x² + 8x – 384 = 0
⇒ x² + 4x – 192 = 0
⇒ x² + 16x – 12x – 192 = 0
⇒ x (x + 16) – 12 (x + 16) = 0
⇒ (x + 16) (x – 12) = 0
Either, x + 16 = 0, then x = -16 which is not possible being negative,
or x – 12 = 0, then x = 12
First side = 12 m
Second side = x + 4= 12 + 4 = 16 m

Question 70.
Solution:
In a right triangle, let base = x m
Length of hypotenuse = (x + 2) m

Question 71.
Solution:
Let shorter side of a right triangle = x m
Then hypotenuse = (2x – 1) m
and longer side = (x + 1) m
According to the condition,
(2x – 1)² = x² + (x + 1)² (Use of Pythagoras Theorem)
⇒ 4x² – 4x + 1 = x² + x² + 2x + 1
⇒ 4x² – 4x + 1 – x² – x² – 2x – 1 = 0
⇒ 2x² – 6x = 0
⇒ 2x (x – 3) = 0
⇒ x – 3 = 0
⇒ x = 3
Shorter side = 3 m
Hypotenuse = 2x – 1 = 3 x 2 – 1 = 6 – 1 = 5 m
and longer side = x + 1 = 3 + 1 = 4m
Sides 3 m, 4 m, 5 m

Hope given RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10E are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 10 Quadratic Equations Ex 10D

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10D.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10A
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10B
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10C
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10D
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10E
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Test Yourself

Question 1.
Solution:

Question 2.
Solution:

Question 3.
Solution:
x² + px – q² = 0
Comparing it with ax² + bx + c = 0
a = 1, b = p, c = -q²
Discriminant (D) = b² – 4ac
= (p)² – 4 x 1 x (-q²)
= p² + 4 q²
p and q are of two powers
p² + 4q² is always greater than 0
The roots are real for all real values of p and q.

Question 4.
Solution:
The quadratic equation is 3x² + 2kx + 27 = 0
Comparing it with ax² + bx + c = 0
a = 3, b = 2k, c = 27
Discriminant (D) = b² – 4ac
= (2k)² – 4 x 3 x 27
= (2k)² – 324
Roots are real and equal
(2k)² – 324 = 0
⇒ (2k)² – (18)² = 0
⇒ (k)² – (9)² = 0
⇒ (k + 9) (k – 9) = 0
Either k + 9 = 0, then k = -9
or k – 9 = 0, then k = 9
Hence, k = 9, -9

Question 5.
Solution:
The quadratic equation is
kx (x – 2√5) x + 10 = 0
kx² – 2√5 kx + 10 = 0
Comparing it with ax² + bx + c = 0
a = k, b = -2√5 k, c = 10
D = b² – 4ac = (-2 k)² – 4 x k x 10 = 20k² – 40k
Roots are real and equal.
D = 0
20k² – 40k = 0
⇒ k² – 2k = 0
⇒ k (k – 2) = 0
Either, k = 0 or k – 2 = 0, then k = 2
k = 0, k = 2

Question 6.
Solution:
The quadratic equation is 4x² + px + 3 = 0
Comparing it with ax² + bx + c = 0
a = 4, b = p, c = 3
D = b² – 4ac = p² – 4 x 4 x 3 = p²- 48
Roots are real and equal.
D = 0
⇒ p² – 48 = 0
⇒ p² = 48 = (±4√3)²
⇒ P = ± 4√3
P = 4√3, p = -4√3

Question 7.
Solution:
The quadratic equation is 9x² – 3kx + k = 0
Comparing it with ax? + bx + c = 0
a = 9, b = -3k, c = k
D = b² – 4ac = (-3k)² – 4 x 9 x k = 9k² – 36k
Roots are real and equal.
D = 0
9k² – 36k = 0
⇒ 9k (k – 4) = 0
Either, k = 0 or k – 4 = 0, then k = 4
The value of k is non-zero.
k = 4

Question 8.
Solution:
(i) The equation is (3k + 1) x² + 2(k + 1) x + 1 = 0
Comparing it with ax² + bx + c = 0
a = (3k + 1), b = 2(k + 1), c = 1
D = b² – 4 ac
= [2(k + 1)]² – 4(3k + 1) x 1
= 4k² + 4 + 8k – 12k – 4
= 4k² – 4k
= 4k (k – 1)
Roots are real and equal.
Either, k = 0 or k – 1 = 0, then k = 1
k = 0, k = 1
(ii) x² + k(2x + k – 1) + 2 = 0
⇒ x² + 2kx + (k² – k + 2) = 0
Here, a = 1, b = 2k, c = (k² – k + 2)
Discriminant (D) = b² – 4ac = (2k)² – 4 x 1 x (k² – k + 2)
= 4k² – 4k² + 4k – 8
= 4k – 8
Roots are real and equal.
D = 0
⇒ 4k – 8 = 0
⇒ k = 2
Hence, k = 2

Question 9.
Solution:

Question 10.
Solution:
The given quadratic equation is
(p + 1) x² – 6(p + 1) x + 3(p + 9) = 0, p ≠ -1

Question 11.
Solution:
-5 is a root of 2x² + px – 15 = 0
x = -5 will satisfy it
Now, substituting the value of x = -5
⇒ 2(-5)² + p(-5) – 15 = 0
⇒ 50 – 5p – 15 = 0
⇒ 35 – 5p = 0
⇒ 5p = 35
⇒ P = 7
In quadratic equation p(x² + x) + k = 0
⇒ 7 (x² + x) + k = 0 (p = 7)
⇒ 7x² + 7x + k = 0
Comparing it with ax² + bx + c = 0
a = 7, b = 7, c = k
D = b² – 4ac = (7)² – 4 x 7 x k
= 49 – 28k
Roots are real and equal.
49 – 28k = 0
⇒ 28k = 49
k = \(\frac { 49 }{ 28 }\) = \(\frac { 7 }{ 4 }\)

Question 12.
Solution:
3 is a root of equation x² – x + k = 0
It will satisfy it
Now, substituting the value of x = 3 in it
(3)² – (3) + k = 0
⇒ 9 – 3 + k = 0
⇒ 6 + k = 0
⇒ k = -6
Now in the equation, x² + k (2x + k + 2) + p = 0
x² + (-6)(2x – 6 + 2) + p = 0
⇒ x² – 12x + 36 – 12 + p = 0
⇒ x² – 12x + (24 + p) = 0
Comparing it with ax² + bx + c = 0
a = 1, b = -12, c = 24 + p
D = b² – 4ac
= (-12)² – 4 x 1 x (24 + p)
= 144 – 96 – 4p = 48 – 4p
Roots are real and equal.
D = 0
48 – 4p = 0
⇒ 4p = 48
⇒ p = 12
Hence, p = 12

Question 13.
Solution:
-4 is a root of the equation x² + 2x + 4p = 0
Then it will satisfy the equation
Now, substituting the value of x = -4
(-4)² + 2(-4) + 4p = 0
16 – 8 + 4p = 0
⇒ 8 + 4p = 0
⇒ 4p = -8
⇒ p = -2
In the quadratic equation x² + px (1 + 3k) + 7(3 + 2k) = 0
⇒ x² – 2x (1 + 3k) + 7(3 + 2k) = 0
Comparing it with ax² + bx + c = 0
a = 1, b = -2 (1 + 3k), c = 7 (3 + 2k)
D = b² – 4ac
= [-2(1 + 3k)]² – 4 x 1 x 7(3 + 2k)
= 4(1 + 9k² + 6k) – 28(3 + 2k)
= 4 + 36k² + 24k – 84 – 56k
= 36k² – 32k – 80
Roots are equal.
D = 0
⇒ 36k² – 32k – 80 = 0
⇒ 9k² – 8k – 20 = 0
⇒ 9k² – 18k + 10k – 20 = 0
⇒ 9k (k – 2) + 10(k – 2) = 0
⇒ (k – 2) (9k + 10) = 0
Either, k – 2 = 0, then k = 2
or 9k + 10 = 0, then 9k = -10 ⇒ k = \(\frac { -10 }{ 9 }\)
k = 2, k = \(\frac { -10 }{ 9 }\)

Question 14.
Solution:

Question 15.
Solution:

Question 16.
Solution:
The quadratic equation is 2x² + px + 8 = 0
Comparing it with ax² + bx + c = 0
a = 2, b = p, c = 8
D = b² – 4ac = p² – 4 x 2 x 8 = p² – 64
Roots are real.
D ≥ 0
p² – 64 ≥ 0
⇒ p² ≥ 64 ≥ (±8)²
p ≥ 8 or p ≤ -8

Question 17.
Solution:

Roots are equal
D = 0
⇒ 4(α – 12) (α – 14) = 0
⇒ α – 14 = 0 {(α – 12) ≠ 0}
⇒ α = 14
Hence, α = 14

Question 18.
Solution:
9x² + 8kx + 16 = 0
Comparing it with ax² + bx + c = 0
a = 9, b = 8k, c = 16
D = b² – 4ac
= (8k)² – 4 x 9 x 16 = 64k² – 576
Roots are real and equal.
D = 0
64k² – 576 = 0
64k² = 576
⇒ k² = 9 = (±3)²
k = 3, k = -3

Question 19.
Solution:

Question 20.
Solution:

Question 21.
Solution:

Question 22.
Solution:

Hope given RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 10 Quadratic Equations Ex 10B

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10B.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10A
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10B
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10C
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10D
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10E
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Test Yourself

Solve each of the following equations by using the method of completing the square:
Question 1.
Solution:
x² – 6x + 3 = 0
=> x² – 2 x 3 x x = -3

Question 2.
Solution:

Question 3.
Solution:

Question 4.
Solution:

Question 5.
Solution:

Question 6.
Solution:

Question 7.
Solution:

Question 8.
Solution:

Question 9.
Solution:

Question 10.
Solution:

Question 11.
Solution:

Question 12.
Solution:

Question 13.
Solution:

Question 14.
Solution:

Question 15.
Solution:

Question 16.
Solution:

Hope given RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4D

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4C.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4A
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4B
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4C
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4D
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4E
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles MCQS
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Test Yourself

Question 1.
Solution:
For the given triangle to be right-angled, the sum of the squares of the two smaller sides must be equal to the square of the largest side.
(i) 9 cm, 16 cm, 18 cm
Longest side = 18
Now (18)² = 324
and (9)² + (16)² = 81 + 256 = 337
324 ≠ 337
It is not a right triangle.
(ii) 1 cm, 24 cm, 25 cm
Here longest side = 25 cm
(25)² = 625
and (7)² x (24)² = 49 + 576 = 625
625 = 625
It is a right triangle
(iii) 1.4 cm, 4.8 cm, 5 cm
Here longest side = 5 cm
(5)² = 25
and (1.4)² + (4.8)² = 1.96 + 23.04 = 25.00 = 25
25 = 25
It is a right triangle
(iv) 1.6 cm, 3.8 cm, 4 cm
Here longest side = 4 cm
(4 )² = 16
and (1.6)² + (3.8)² = 2.56 + 14.44 = 17.00 = 17
16 ≠ 17
It is not a right triangle
(v) (a- 1) cm, 2√a cm, (a + 1) cm
Here longest side = (a + 1) cm
(a + 1)² = a² + 2a + 1
and (a – 1)² + (2 √a )² = a² – 2a + 1 + 4a = a² + 2a + 1
a² + 2a + 1 = a² + 2a + 1
It is a right triangle.

Question 2.
Solution:
A man goes 80 m from O to east side and reaches A, then he goes 150 m due north from A and reaches B.
Join OB.

In right ∆OAB,
OB² = OA²+² (Pythagoras Theorem) = (80)² + (150)² = 6400 + 22500 = 28900
⇒ OB = √28900 = 170

He is 170 m away from the starting point.

Question 3.
Solution:
A man goes 10 m due south from O and reaches A and then 24 m due west from A and reaches B.
Join OB.

Question 4.
Solution:
Length of a ladder = 13 m
Height of the window = 12 m
Distance between the foot of the ladder and building.
In the figures,

AB is ladder, A is window of building AC
AB² = AC² + BC² (Pythagoras Theorem)
⇒ (13)² = (12)² + x²
⇒ 169 = 144 + x²
⇒ x² = 169 – 144 = 25 = (5)²
x = 5
Hence, distance between foot of ladder and building = 5 m.

Question 5.
Solution:
Let length of ladder AB = x m
Height of window AC = 20 m
and distance between the foot of the ladder and the building (BC) = 15 m

AB² = AC² + BC² (Pythagoras Theorem)
⇒ x² = 20² + 15² = 400 + 225 = 625 = (25)²
x = 25
Length of ladder = 25 m

Question 6.
Solution:
Height of first pole AB = 9 m
and of second pole CD = 14 m

Let distance between their tops CA = x m
From A, draw AE || BD meeting CD at E.
Then EA = DB = 12 m CE = CD – ED = CD – AB = 14-9 = 5 m
In right ∆AEC,
AC² = AE² + CE² = 122 + 52 = 144 + 25 = 169 = (13)²
AC = 13
Distance between their tops = 13 m

Question 7.
Solution:
Height of the pole AB = 18 m
and length of wire AC = 24 m

Distance between the base of the pole and other end of the wire
BC = x m (suppose)
In right ∆ABC,
AC² = AB² + BC² (Pythagoras Theorem)
(24)² = (18)² + x²
⇒ 576 = 324 + x²
⇒ x² = 576 – 324 = 252

Question 8.

Solution:
In ∆PQR, O is a point in it such that
OP = 6 cm, OR = 8 cm and ∠POR = 90°
PQ = 24 cm, QR = 26 cm
To prove : ∆PQR is a right angled.
In ∆POR, ∠O = 90°
PR² = PO² + OR² = (6)² + (8)² = 36 + 64 = 100 = (10)²
PR = 10
Greatest side QR is 26 cm
QR² = (26)² = 676
and PQ² + PR² = (24)² + (10)² = 576 + 100 = 676
676 = 676
QR² = PQ² + PR²
∆PQR is a right angled triangle and right angle at P.

Question 9.
Solution:
In isosceles ∆ABC, AB = AC = 13 cm
AL is altitude from A to BC
and AL = 5 cm

Now, in right ∆ALB
AB² = AL² + BL²
(13)² = (5)² + BL²
⇒ 169 = 25 + BL²
⇒ BL² = 169 – 25 = 144 = (12)²
BL = 12 cm
L is mid point of BC
BC = 2 x BC = 2 x 12 = 24 cm

Question 10.
Solution:
In an isosceles ∆ABC in which
AB = AC = 2a units, BC = a units

Question 11.
Solution:
∆ABC is an equilateral triangle
and AB = BC = CA = 2a

AD ⊥ BC
D is mid point of BC
BD = DC = \(\frac { 1 }{ 2 }\) BC
= \(\frac { 1 }{ 2 }\) x 2a = a
Now, in right ∆ADB,
AB² = AD² + BD² (Pythagoras Theorem)
(2a)² = AD² + a²
⇒ 4a² – a² = AD²
⇒ AD² = 3a² = (√3 a)²
AD = √3 a = a√3 units

Question 12.
Solution:
∆ABC is an equilateral triangle in which
AB = BC = CA = 12 cm

AD ⊥ BC which bisects BC at D
BD = DC = \(\frac { 1 }{ 2 }\) BC = \(\frac { 1 }{ 2 }\) x 12 = 6cm
Now, in right ∆ADB,
AB² = AD² + BD²
⇒ (12)² = AD² + (6)²
⇒ 144 = AD² + 36
AD² = 144 – 36 = 108
AD = √108 = √(36 x 3) = 6√3 cm

Question 13.
Solution:
Let ABCD is a rectangle in which adjacent sides.
AB = 30 cm and BC = 16 cm

AC is its diagonal.
In right ∆ABC,
AC² = AB² + BC² (Pythagoras Theorem)
= (30)² + (16)² = 900 + 256 = 1156 = (34)²
Diagonal AC = 34 cm

Question 14.
Solution:
ABCD is a rhombus
Its diagonals AC and BD bisect each other at O.

AO = OC = \(\frac { 1 }{ 2 }\) AC.
and BO = OD = \(\frac { 1 }{ 2 }\) BD
BD = 24 cm and AC = 10 cm
BO = \(\frac { 1 }{ 2 }\) x BD = \(\frac { 1 }{ 2 }\) x 24 = 12 cm
AO = \(\frac { 1 }{ 2 }\) x AC = \(\frac { 1 }{ 2 }\) x 10 = 5 cm
Now, in right ∆AOB,
AB² = AO² + BO² = (5)² + (12)² = 144 + 25 = 169 = (13)²
AB = 13
Hence, each side of rhombus = 13 cm

Question 15.
Solution:
Given : In ∆ABC, AC > AB.
D is the mid point of BC and AE ⊥ BC.
AD is joined.

To prove: AB² = AD² – BC x DE + \(\frac { 1 }{ 4 }\) BC2
Proof: In ∆AEB, ∠E = 90°
AB² = AE² + BE² …..(i) (Pythagoras Theorem)
In ∆AED, ∠E = 90°
AD² = AE² + DE²
⇒ AE² = AD² – DE² …..(ii)
Now, substitute eq. (ii) in eq. (i)
AB² = AE² + BE²
AB² = AD² – DE² + BE² [from (ii)]
AB² = (AD² – DE²) + (BD – DE)² [BE = BD – DE²]

Question 16.
Solution:

Question 17.
Solution:
Given : In ∆ABC, D is the mid point of BC, AE ⊥ BC,
BC = a, AC = b, AB = c, ED = x, AD =p and AE =
AD is joined.
To prove :

Question 18.
Solution:
Given : In ∆ABC, AB =AC
BC is produced to D and AD is joined.
To prove : (AD² – AC²) = BD x CD
Construction : Draw AE ⊥ BC.

Proof: In ∆ABC,
AB = AC and AE ⊥ BC
BE = EC
Now, in right ∆AED, ∠E = 90°
AD² = AE² + ED² …..(i)
and in right ∆AEC, ∠E = 90°
AC² = AE² + EC² …..(ii)
Now, subtracting (i) and (ii),
AD² – AC² = (AE² + ED²) – (AE² + EC²)
= AE² + ED² – AE² – EC²
= ED² – EC²
= (ED + EC) (ED – EC) (BE = EC proved above)
= BD x CD = BD x CD
AD² – AC² = BD x CD
Hence proved.

Question 19.
Solution:
Given : In ∆ABC, AB = BC and ∠ABC = 90°
∆ACD and ∆ABE are similar to each other.

To prove : Ratio between area ∆ABE and area ∆ACD.
Proof: Let AB = BC = x
Now, in right ∆ABC,
⇒ AC² = AB² + BC² = AB² + AB² = 2AB² = 2x²
∆ABE and ∆ACD are similar

Ratio between the areas of ∆ABE and ∆ACD = 1 : 2

Question 20.
Solution:
An aeroplane flies from airport to north at the speed of 1000 km/hr.
Another aeroplane flies from the airport to west at the speed of 1200 km/hr.
Period = 1\(\frac { 1 }{ 2 }\) hours
Distance covered by the first plane in 1\(\frac { 1 }{ 2 }\) hours = 1000 x \(\frac { 3 }{ 2 }\) km = 1500 km
and distance covered by another plane in 1\(\frac { 1 }{ 2 }\) hours = 1200 x \(\frac { 3 }{ 2 }\) km = 1800 km
At present, the distance between them
AB² = (BO)² + (AO)²
= (1800)² + (1500)²
= 3240000 + 2250000
= 5490000

Question 21.
Solution:
Given : In ∆ABC,
D is the mid point of BC and AL ⊥ BC
AD is joined.
To prove:

Question 22.
Solution:
AM is rod and BC is string out of rod.
In ∆BMC,
BC² = BM² + CM² = (1.8)² + (2.4)²

Hope given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 4 Triangles MCQS

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 4 Triangles MCQS.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4A
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4B
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4C
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4D
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4E
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles MCQS
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Test Yourself

Choose the correct answer in each of the following questions.
Question 1.
Solution:
(c) A man goes from O to 24 m due west at A and then 10 m due north at B.

Now, AB² = OA² + OB²
= (24)² + (10)² = 576 + 100 = 676 = (26)²
AB = 26 m

Question 2.
Solution:
(b) Two poles AB and CD are standing on the plane ground 8 m apart.
AB = 13 m and CD = 7 m, CE || DB

In right ∆ACE,
AC² = CE² + AE²
= (8)² + (6)² = 64 + 36 = 100 = (10)²
AC = 10 m
Distance between the tops of poles = 10 m

Question 3.
Solution:
(c) A vertical stick AB = 1.8 m
and its shadow = 45 cm = 0.45 m

At the same time, let x cm be the shadow of 6 m long pole.
∆ABC ~ ∆DEF

Question 4.
Solution:
(d) Shadow of a vertical pole 6 m long is 3.6 m on the ground and shadow of a tower at the same, is 18 m.

Question 5.
Solution:
(d) Shadow of 5 m long stick = 2 m
Let shadow of 12.5 m high tree at the same time = x
∆ABC ~ ∆DEF

Question 6.
Solution:
(a) Length of ladder AB = 25 m .
Height above the ground = 24 m

Let its foot is x m away from the foot of building.
In right ∆ABC,
AB² = AC² + BC² (Pythagoras Theorem)
(25)² = (24)² + x²
⇒ 625 = 576 + x²
⇒ x² = 625 – 576 = 49 = (7)²
x = 7
Distance = 7 m

Question 7.
Solution:
(b) O is a point inside ∆MNP such that
MOP = 90°, OM = 16 cm, OP = 12 cm.
If MN = 21 cm ∠NMP = 90°, then NP = ?
Let MP = x Now, in right ∆MOP,
∠O = 90°
MP² = OM² + OP² (Pythagoras Theorem)
= (16)² + (12)² = 256 + 144 = 400 = (20)²
MP = 20 cm
Now, in right ∆MNP, ∠M = 90°
NP² = MN² + MP²
= (21)² + (20)² = 441 + 400 = 841 = (29)²
NP = 29 cm

Question 8.
Solution:
(b) Let ∆ABC is a right angled triangle with ∠B = 90°
AC = 25 cm
Let one side AB of the other two sides = x cm
then second side BC = (x + 5) cm
According to the Pythagoras Theorem,
AC² = AB² + BC²
(25)² = x² + (x + 5)²
625 = x² + x² + 10x + 25
⇒ 2x² + 10x + 25 – 625 = 0
⇒ 2x² + 10x – 600 = 0
⇒ x² + 5x – 300 = 0
⇒ x² + 20x – 15x – 300 = 0
⇒ x (x + 20) – 15 (x + 20) = 0
⇒ (x + 20)(x – 15) = 0
Either x + 20 = 0, then x = -20 which is not possible being negative,
or x – 15 = 0, then x = 15
First side = 15 cm
and second side = 15 + 5 = 20 cm

Question 9.
Solution:
(b) Side of an equilateral triangle = 12 cm

Question 10.
Solution:
(d) In isosceles ∆ABC,
AB = AC = 13 cm
Length of altitude AB, (from A to BC) = 5 cm

Question 11.
Solution:
(a) In the given figure,
AB = 6 cm, AC = 8 cm
AD is the bisector of ∠A which meets BC at D.

Question 12.
Solution:
(d) In the given figure,
AD is the internal bisector of ∠A
BD = 4 cm, DC = 5 cm, AB = 6 cm
Let AC = x cm

Question 13.
Solution:
(b) In the given figure,
AD is the bisector of ∠A of ∆ABC.
AB = 10 cm, AC = 14 cm and BC = 6 cm
Let CD = x cm
Then BD = (6 – x) cm
Now, AD is the bisector of ∠A

Question 14.
Solution:
(b) In a ∆ABC, AD ⊥ BC and BD = DC

In a ∆ABC, AD = \(\frac { 1 }{ 2 }\) BC and BD = DC.
In right ∆ABD and ∆ACD
AD = AD (common)
∠ABD = ∠ADC (each 90°)
BD = DC (given)
∆ABD = ∆ACD (SAS axiom)
AB = AC
∆ABC is an isosceles triangle.

Question 15.
Solution:
(c) In equilateral ∆ABC, AD ⊥ BC
Then BD = DC = \(\frac { 1 }{ 2 }\) BC
Now, in right ∆ABD,
AB² = BD² + AD² (Pythagoras Theorem)

Question 16.
Solution:
(c) In a rhombus, each side = 10 cm and one diagonal = 12 cm
AB = BC = CD = DA = 10 cm BD = 12 cm

The diagonals of a rhombus bisect each other at right angles.
In ∆AOB,
AB² = AO² + BO²
⇒ (10)² = AO² + (6)²
⇒ AO² = (10)² – (6)² = 100 – 36 = 64 = 8²
AO = 8 cm
Diagonals AC = 2 x AO = 2 x 8 = 16 cm

Question 17.
Solution:
(b) Length of diagonals of a rhombus are 24 cm and 10 cm.
The diagonals of a rhombus bisect each other at right angles.

In rhombus ABCD
AO = OC, BO = OD
Let AO = OC = \(\frac { 24 }{ 2 }\) = 12 cm
BO = OD = \(\frac { 10 }{ 2 }\) = 5 cm
Now, in right ∆AOB,
AB² = AO² + BO² (Pythagoras Theorem)
= (12)² + (5)² = 144 + 25 = 169 = (13)²
AB = 13
Each side of rhombus = 13 cm

Question 18.
Solution:
(b) Diagonals of e. quadrilateral divides each other proportionally, then it is

In quadrilateral ABCD, diagonals AC and BD intersect each-other at O and \(\frac { AO }{ OC }\) = \(\frac { BO }{ OD }\)
Then, quadrilateral ABCD is a trapezium.

Question 19.
Solution:
(a) In the given figure,
ABCD is a trape∠ium and its diagonals AC
and BD intersect at O.
and OA = (3x – 1) cm OB = (2x + 1) cm, OC and OD = (6x – 5) cm

Question 20.
Solution:
(a) The line segments joining the midpoints of the adjacent sides of a quadrilateral form a parallelogram

Question 21.
Solution:
(c) If the bisector of angle of a triangle bisects the opposite side of a triangle.

Question 22.
Solution:
(a) In ∆ABC,

∠B = 70° and ∠C = 50°
But ∠A + ∠B + ∠C = 180° (Angles of a triangle)
∠A = 180° – (∠B + ∠C)
= 180° – (70° + 50°)
= 180° – 120° = 60°
\(\frac { AB }{ AC }\) = \(\frac { BD }{ DC }\)
AD is the bisector of ∠A
∠BAD = \(\frac { 60 }{ 2 }\) = 30°

Question 23.
Solution:
(b) In ∆ABC, DE || BC
AD = 2.4 cm, AE = 3.2 cm, EC = 4.8 cm
Let AD = x cm
DE || BC

Question 24.
Solution:
(b) In ∆ABC, DE || BC
AB = 7.2 cm, AC = 6.4 cm, AD = 4.5 cm
Let AE = x cm
DE || BC
∆ADE ~ ∆ABC

Question 25.
Solution:
(c) In ∆ABC, DE || BC
AD = (7x – 4) cm, AE = (5x – 2) cm DB = (3x + 4) cm and EC = 3x cm
In ∆ABC, DE || BC

Question 26.
Solution:
(d) In ∆ABC, DE || BC

Question 27.
Solution:
(b) ∆ABC ~ ∆DEF

Question 28.
Solution:
(a) ∆ABC ~ ∆DEF

Question 29.
Solution:
(d) ∆DEF ~ ∆ABC

Perimeter of ∆DEF = DE + EF + DF
= 12 + 8 + 10 = 30 cm

Question 30.
Solution:
(d) ABC and BDE are two equilateral triangles such that D is the midpoint of BC.

Question 31.
Solution:
(b) ∆ABC ~ ∆DFE.
∠A = 30°, ∠C = 50°, AB = 5cm, AC = 8 cm and DF = 7.5 cm

Question 32.
Solution:
(c) In ∆ABC, ∠A = 90°
AD ⊥ BC
In ∆ABD and ∆ADC

Question 33.
Solution:
(c) In ∆ABC, AB = 6 cm, AC = 12 cm and BC = 6 cm.

Longest side (AC)2 = (12)2 = 144
AB2 + BC2 = (6√3)2 + (6)2 = 108 + 36 = 144
AC2 = AB2 + BC2 (Converse of Pythagoras Theorem)
∠B = 90°

Question 34.
Solution:
(c) In ∆ABC and ∆DEF, \(\frac { AB }{ DE }\) = \(\frac { BC }{ FD }\)

For similarity,
Here, included angles must be equal and these
are ∠B = ∠D.

Question 35.
Solution:
(b) In ∆DEF and ∆PQR,
∠D = ∠Q and ∠R = ∠E

Question 36.
Solution:
(c) ∆ABC ~ ∆EDF
∠A = ∠E, ∠B = ∠D, ∠C = ∠F

Question 37.
Solution:
(b) In ∆ABC and ∆DEF,
∠B = ∠E, ∠F = ∠C and AB = 3DE
The triangles are similar as two angles are equal but including sides are not proportional.

Question 38.
Solution:
(a)

Question 39.
Solution:
(d) In the given figure, two line segments AC and BD intersect each other at P such that
PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°
In ∆ABP and ∆CPD,

Question 40.
Solution:
(d) Corresponding sides of two similar triangles = 4:9
The areas of there triangle will be in the ratio

Question 41.
Solution:
(d)

Question 42.
Solution:
(b) In the given figure,
∆ABC is an equilateral triangle.
D is midpoint of AB and E is the midpoint of AC.

Question 43.
Solution:
(b)

Question 44.
Solution:
(b) ∆ABC ~ ∆DEF
ar (∆ABC) = 36 cm² and ar (∆DEF) = 49 cm²
i.e. areas are in the ratio 36 : 49
Ratio in their corresponding sides = √36 : √49 = 6 : 7

Question 45.
Solution:
(c) Two isosceles triangles have their corresponding angles equal and ratio in their areas is 25 : 36.
The ratio in their corresponding altitude
(heights) = √25 : √36 = 5 : 6 (∆s are similar)

Question 46.
Solution:
(b) The line segments joining the midpoints of a triangle form 4 triangles which are similar to the given (original) triangle.

Question 47.
Solution:
(b) ∆ABC ~ ∆QRP

Question 48.
Solution:
(c) In the given figure, O is the point of intersection of two chords AB and CD.
OB = OD and ∠AOC = 45°
∠B = ∠D (Angles opposite to equal sides)
∠A = ∠D, ∠C = ∠B (Angles in the same segment)
and ∠AOC = ∠BOD = 45° each
∆OAC ~ ∆ODB (AAA axiom)
OA = OC (Sides opposite to equal angles)
∆OAC and ∆ODB are isosceles and similar.

Question 49.
Solution:
(d) In an isosceles ∆ABC,
AC = BC
⇒ AB² = 2 AC²
⇒ AB² = AC² + AC²
⇒ AB² = AC² + BC² (AC = BC)

Converse of the Pythagoras Theorem,
∆ABC is a right triangle and angle opposite to AB = 90°
∠C = 90°

Question 50.
Solution:
(b) In ∆ABC,
AB = 16 cm, BC = 12 cm and AC = 20 cm
(Longest side)2 = 20² = 400
Sum of square on other sides = AB² + BC²
= 162 + 122 = 256 + 144 = 400
AC² = AB² + BC²
∆ABC is a right triangle.

True/False type
Question 51.
Solution:
(c) (a) False. Not always congruent.
(b) False. Two similar figures are similar if they have same shape, not size in every case.
(c) True.
(d) False. Not in each case.

Question 52.
Solution:
(a) True
(b) False, as ratio of the areas of the two similar triangles is equal to the ratio of the square of their corresponding sides.
(c) True
(d) True

Question 53.
Matching of columns : (2 marks)
Solution:

Question 54.
Solution:


correct answer is
(a) → (r)
(b) → (q)
(c) → (p)
(d) → (s)

Hope given RS Aggarwal Solutions Class 10 Chapter 4 Triangles MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4A

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4A.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4A
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4B
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4C
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4D
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4E
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles MCQS
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Test Yourself

Question 1.
Solution:
In ∆ABC, points D and E are on the sides AB and AC respectively such that DE || BC.



⇒ 7x = 28 ⇒ x = 4

Question 2.
Solution:
D and E are the points on the sides AB and AC of ∆ABC respectively and DE || BC,


By cross multiplication,
⇒ (7x – 4) (3x) = (5x – 2) (3x + 4)
⇒ 21x² – 12x = 15x² + 20x – 6x – 8
⇒ 21x² – 12x – 15x² – 20x + 6x = -8
⇒ 6x² – 26x + 8 = 0
⇒ 3x² – 13x + 4 = 0
⇒ 3x² – 12x – x + 4 = 0
⇒ 3x (x – 4) – 1 (x – 4) = 0
⇒ (x – 4) (3x – 1) = 0
Either x – 4 = 0, then x = 4
or 3x – 1 = 0 then 3x = 1 ⇒ x = \(\frac { 1 }{ 3 }\) which is not possible
x = 4

Question 3.
Solution:
D and E are the points on the sides AB and AC of ∆ABC
(i) AD = 5.7 cm, DB = 9.5 cm, AE = 4.8 cm and EC = 8 cm

Question 4.
Solution:
In ∆ABC, AD is the bisector of ∠A

Question 5.
Solution:
Given : M is a point on the side BC of a parallelogram ABCD.
DM when produced meets AB produced at N.

Question 6.
Solution:
Given : In trapezium AB || DC.
M and N are the mid points of sides AD and BC respectively.
MN is joined.
To prove : MN || AB or DC.
Construction: Produce AD and BC to meet at P.

Question 7.
Solution:
ABCD is a trapezium and its diagonals AC and BD intersect each other at O.

Question 8.
Solution:
Given : In ∆ABC, M and N are points on the sides AB and AC respectively such that
BM = CN and if ∠B = ∠C.

Question 9.
Solution:
Given : ∆ABC and ∆DBC are on the same side of BC.
P is any point on BC.
PQ || AB and PR || BD are drawn, which meet AC at Q and CD at R.
AD is joined.
To prove : QR || AD.
Proof:
In ∆ABC, PQ||AB


Hence proved.

Question 10.
Solution:
Given : In the given figure, D is the mid point of BC. AD is joined. O is any point on AD. BO and CO are produced to meet AC at F and AB at E respectively. AD is produced to X such that D is the mid point of OX.
To prove: AO : AX = AF : AB and EF || BC
Construction. Join BX and CX.

D is the midpoint of BC.
Proof: BD = DC and OD = DX. (given)
OBXC is a parallelogram. (Diagonals of a ||gm bisect each other)

Question 11.
Solution:
Given : In ||gm, ABCD, P is mid point of DC and Q is the mid point of AC. Such that
CQ = \(\frac { 1 }{ 4 }\) AC.
PQ is produced to meet BC at R.
To prove : R is the mid point of BC.
Construction : Join BD which intersects AC at O.

Proof: Diagonals of a parallelogram bisect each other
CO = \(\frac { 1 }{ 2 }\) AC.
But CQ = \(\frac { 1 }{ 2 }\) CO (given)
Q is the mid point of CO.
PQ || DO
⇒ PR || DB and P is mid point of CD
R is the midpoint BC.
Hence proved.

Question 12.
Solution:
Given : In ∆ABC, AB = AC
D and E are the points on AB and AC such that
AD = AE
To prove : BCED is a cyclic quadrilateral.
Proof: In ∆ABC,
AB = AC,
D and E are the mid points of AB and AC respectively.

But these are opposite angles of quad. BCED
BCED is a cyclic quadrilateral
Hence, B, C, E and D are concyclic.

Question 13.
Solution:
Given : In ∆ABC, BD is the bisector of AB which meets AC at D.
A line PQ || AC which meets AB, BC, BD at P, Q, R respectively.
To prove : PR x BQ = QR x BP
Proof: In ∆ABC, PQ || AC
and BD is the bisector of ∠B

Hope given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4B

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4B.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4A
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4B
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4C
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4D
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4E
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles MCQS
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Test Yourself

Question 1.
Solution:
We know that two triangles are similarity of their corresponding angles are equal and corresponding sides are proportional.
(i) In ∆ABC and ∆PQR
∠A = ∠Q = 50°
∠B = ∠P = 60° and ∠C = ∠R = 70°
∆ABC ~ ∆QPR (AAA axiom)
(ii) In ∆ABC and ∆DEF
In ∆ABC,
AB = 3 cm, BC = 4.5
and in ∆DEF
DF = 6 cm, DE = 9 cm
∆ABC is not similar to ∆DEF
As in ∆ABC, ∠A is not included of two sides AB and BC.
(iii) In ∆ABC and ∆PQR
In ∆ABC,
AC = 8 cm BC = 6 cm
Included ∠C = 80°
In ∆PQR,
PQ = 4.5 cm, QR = 6 cm
and included ∠Q = 80°

(v) In ∆ABC,
∠A = 80°, ∠C = 70°
and third angle
∠B = 180° – (80° + 70°)
⇒ ∠B = 180° – 150° = 30°
In ∆MNR,
∠M = 80°, ∠N = 30°, and ∠R = [180° – (80° + 30°)]
∠R = 180° – 110° = 70°
Now, in ∆ABC
∠A = ∠M – 80°, ∠B = ∠N = 30°
and ∠C = ∠R = 70°
∆ABC ~ ∆MNR (AAA or AA axiom)

Question 2.
Solution:
In the given figure, ∆ODC ~ ∆OBA and ∠BOC =115°, ∠CDO = 70°

To find :
(i) ∠DOC
(ii) ∠DCO
(iii) ∠OAB
(iv) ∠OBA
∆ODC ~ ∆OBA
∠D = ∠B = 70°
∠C = ∠A
∠COD = ∠AOB
(i) But ∠DOC + ∠BOC = 180° (Linear pair)
⇒ ∠DOC + 115°= 180°
⇒ ∠DOC = 180° – 115° = 65°
(ii) ∠DOC + ∠CDO + ∠DCO = 180° (Angles of a triangle)
⇒ 65° + 70° + ∠DCO = 180°
⇒ 135° + ∠DCO = 180°
⇒ ∠DCO = 180° – 135°
∠DCO = 45°
(iii) ∠AOB = ∠DOC = 65° (vertically opposite angles)
∠OAB = ∠DCO = 45° (∆ODC ~ ∆OBA)
(iv) ∠OBA = ∠CDO = 70° (∆ODC ~ ∆OBA)

Question 3.
Solution:
In the given figure, ∆OAB ~ ∆OCD
AB = 8 cm, BO = 6.4 cm OC = 3.5 cm, CD = 5 cm

Question 4.
Solution:
Given : In the given figure,
∠ADE = ∠B
To prove:
(i) ∆ADE ~ ∆ABC
(ii) If AD = 3.8 cm, AE = 3.6 cm, BE = 2.1 cm and BC = 4.2 cm, find DE
Proof: (i) In ∆ADE and ∆ABC
∠ADE = ∠B (given)
∠A = ∠A (common)
∆ADE ~ ∆ABC (AA axiom)

Question 5.
Solution:
∆ABC ~ ∆PQR,
PQ = 12 cm
To find AB.
Perimeter of ∆ABC = AB + BC + CA = 32 cm
Perimeter of ∆PQR = PQ + QR + RP = 24 cm
Now,
∆ABC ~ ∆PQR

Question 6.
Solution:
∆ABC ~ ∆DEF
BC = 9.1 cm, EF = 6.5 cm
Perimeter of ∆DEF = 25 cm

Question 7.
Solution:
Given : In the given figure,
∠CAB = 90° and AD ⊥ BC
To prove : ∆BDA ~ ∆BAC
If AC = 75 cm, AB = 1 m or 100 cm,
BC = 1.25 m or 125 cm
Find AD.
∆BDA ~ ∆BAC (corresponding sides and proportional)

Question 8.
Solution:
In the given figure,
∠ABC = 90°, BD ⊥ AC.
AB = 5.7 cm, BD = 3.8 cm, CD = 5.4 cm
To find BC,
In ∆ABC and ∆BDC,
∠ABC = ∠BDC (each 90°)
∠BCA = ∠BCD (common)
∆ABC ~ ∆BDC (AA axiom)
Corresponding sides are proportional

Question 9.
Solution:
In the given figure, ”
∠ABC = 90°, BD ⊥ AC
BD = 8 cm, AD = 4cm
To find CD,
Let CD = x
Now in ∆DBC and ∆BDA
∠BDC = ∠BDA (each 90°)
∠C = ∠ABD
∆DBC ~ ∆BDA
Sides are proportional

Question 10.
Solution:
In ∆ABC, P and Q are points on the sides AB and AC respectively such that
AP = 2 cm, PB = 4 cm, AQ = 3 cm and QC = 6 cm.
To prove : BC = 3 PQ

BC = 3 PQ
Hence proved.

Question 11.
Solution:
Given: ABCD is a parallelogram.
E is a point on BC and diagonal BD intersects AE at F.

To prove : AF x FB = EF x FD
Proof: In ∆AFD and ∆BFE
∠AFD = ∠BFE (vertically opposite angles)
∠ADF = ∠FBE (alternate angles)
∆AFD ~ ∆BFE (AA axiom)
\(\frac { AF }{ EF }\) = \(\frac { FD }{ FB }\)
By cross multiplication,
⇒ AF x FB = EF x FD
Hence proved.

Question 12.
Solution:
Given : In the given figure,
DB ⊥ BC, DE ⊥ AB and AC ⊥ BC

Question 13.
Solution:
In ∆ABC and ∆DEF
AC is stick and BC is its shadow.
DF is the tower and EF is its shadow
AC = 7.5 m, BC = 5 m EF = 24 m,
let DF = x m

Question 14.
Solution:
Given : In isosceles ∆ABC,
CA = CB, base AB and BA are produced in P and Q such that
AP x BQ = AC²
To prove : ∆ACP ~ ∆BCQ
Proof: In ∆ABC,
CA = CB
∠CAB = ∠CBA (Angles opposite to equal sides)
⇒ 180° – ∠CAB = 180° – ∠CBA (Subtracting each from 180°)
⇒ ∠CAP = ∠CBQ
AP x BQ = AC² (given)

Question 15.
Solution:
Given : In the given figure, ∠1 = ∠2

Question 16.
Solution:
Given : In quadrilateral ABCD,
AD = BC
P, Q, R and S are midpoints of AB, AC, CD and BD respectively.

To proof : PQRS is a rhombus.
Proof: In ∆ABC,
P and Q are the midpoints of sides AB and AC respectively.
PQ || BC ……(i)

Question 17.
Solution:
In the given circle, two chords AB and CD intersect each other at P inside the circle.
To prove :
(a) ∆PAC ~ ∆PDB
(b) PA . PB = PC . PD
Proof:
(a) In ∆PAC and ∆PDB
∠APC = ∠BPD (Vertically opposite angles)
∠A = ∠D (Angles in the same segment)
∆PAC ~ ∆PDB (AA axiom)
\(\frac { PA }{ PD }\) = \(\frac { PC }{ PB }\)
⇒ PA x PB = PC x PD
Hence proved.

Question 18.
Solution:
In a circle, two chords AB and CD intersect each other at the point P outside the circle.
AC and BD are joined.

To prove :
(a) ∆PAC ~ ∆PDB
(b) PA . PB = PC . PD
Proof: In the circle, quadrilateral ABDC is a cyclic.
Ext. ∠PAC = ∠D
Now, in ∆PDB and ∆PAC
∠P = ∠P (common)
∠PAC = ∠D (proved)
∆PDB ~ ∆PAC (AA axiom)
or ∆PAC ~ ∆PBD
\(\frac { PA }{ PD }\) = \(\frac { PC }{ PB }\)
⇒ PA . PB = PC . PD
Hence proved

Question 19.
Solution:
Given : In right ∆ABC, ∠B = 90°
D is a point on hypotenuse AC such that
BD ⊥ AC and DP ⊥ AB and DQ ⊥ BC.

To prove :
(a) DQ² = DP . QC
(b) DP² = DQ . AP
Proof: AB ⊥ BC and DQ ⊥ BC
AB || DQ
DP ⊥ AB
DP || BC
Now, AB or PB || DQ and BC or BQ || DP BQDP is a rectangle
BQ = DP and BP = DQ
Now, in right ∆BQD
∠1 + ∠2 = 90° …..(i)
Similarly in rt. ∆DQC,
∠3 + ∠4 = 90° (DQ ⊥ BC) …(ii)
and in right ∆BDC,
∠2 + ∠3 = 90° …(iii)
∠BDC = 90° (BD ⊥ AC)
From (i) and (ii),
∠1 = ∠3
and from (ii) and (iii),
∠2 = ∠4
Now, in ∆BQD and ∆DQC
∠1 = ∠3
∠2 = ∠4 (proved)
∆BQD ~ ∆DQC (AA axiom)
\(\frac { BQ }{ DQ }\) = \(\frac { DQ }{ QC }\)
⇒ DQ² = BQ x QC
⇒ DQ² = DP x QC
(b) Similarly, we can prove that
∆PDA ~ ∆PBD
\(\frac { PD }{ PB }\) = \(\frac { AP }{ DP }\)
⇒ DP² = BP x AP
⇒ DP² = DQ . AP (BP = DQ)
Hence proved.

Hope given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 4 Triangles Test Yourself

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Test Yourself.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4A
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4B
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4C
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4D
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4E
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles MCQS
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Test Yourself

MCQ
Question 1.
Solution:
(b) ∆ABC ~ ∆DEF

Question 2.
Solution:
(a) In the given figure,

Question 3.
Solution:
(b) Length of pole AB = 6 m
and CD = 11 m
and distance between the BD = 12 m
Draw AE || BD, then
ED = AB = 6 m, AE = BD = 12 m
CE = CD – ED = 11 – 6 = 5 m

Now, in right ∆ACE,
AC² = AE² + CE² (Pythagoras Theorem)
= (12)² + (5)² = 144 + 25 = 169 = 13²
AC = 13
Distance between their tops = 13 m

Question 4.
Solution:
(c) Area of two similar triangles ABC and DEF are 25 cm² and 36 cm².
Altitude of first ∆ABC is AL = 3.5 m.
Let DM be the altitude of second triangle.

Short-Answer Questions
Question 5.
Solution:
∆ABC ~ ∆DEF
and 2AB = DE

Question 6.
Solution:
In the given figure,

DE || BC, AL ⊥ BC
AD = x cm,
DB = (3x + 4) cm AE = (x + 3) cm, EC = (3x + 19) cm
In ∆ABC, DE || BC

Question 7.
Solution:
Let AB be the ladder, and A is the window.
Length of ladder AB = 10 m and AC = 8 m
Distance between the foot of the ladder from the house = x m

In right ∆ABC,
AB² = AC² + BC²
⇒ (10)² = (8)² + (x)²
⇒x² = (10)² – (8)²
⇒ x² = 100 – 64 = 36
⇒ x² = (6)²
⇒ x = 6
Distance between the foot of ladder and foot of the house = 6m.

Question 8.
Solution:
In ∆ABC, AB = BC = CA = 2a cm
AD ⊥ BC which bisects the base BC at D

BD = DC = \(\frac { 2a }{ 2 }\) = a cm
Now, in right ∆ABD
AB² = AD² + BD²
(2a)² = AD² + a²
⇒ AD² = 4a² – a² = 3a²
AD = √3a² = √3 a
Height of altitude = √3 a cm

Question 9.
Solution:
Let EF = x cm
∆ABC ~ ∆DEF

Question 10.
Solution:
ABCD is a trape∠ium in which AB || DC
AB = 2CD
Diagonals AC and BD intersect each other at O.

Question 11.
Solution:
Let corresponding sides of two similar triangles ABC and DEF are in the ratio 2 : 3.

Question 12.
Solution:
In the given figure,

Question 13.
Solution:
Given : In ∆ABC, AD is the bisector of ∠A which meets BC at D.

Construction : Produce BA and draw CE || DA meeting BA produced at E.
DA || CE
∠3 = ∠1 (corresponding angles)
∠4 = ∠2 (alternate angles)
But ∠3 = ∠4 (AD is the bisector of ∠A)
∠1 = ∠2
AC = AE (Sides opposite to equal angles)
Now, in ∆AEC,
AD || EC

Question 14.
Solution:
Given : In ∆ABC,
AB = BC = CA = a cm

Question 15.
Solution:
In rhombus ABCD, diagonals AC = 24 cm and BD = 10 cm.

The diagonals of a rhombus bisect each other at right angles.
AO = OC = \(\frac { 24 }{ 2 }\) = 12 cm
and BO = OD = \(\frac { 10 }{ 2 }\) = 5 cm
Now, in right ∆AOB,
AB² = AO² + BO² = 12² + 5² = 144 + 25 = 169 = (13)²
AB = 13
Each side of a rhombus = 13 cm

Question 16.
Solution:
Given : ∆ABC ~ ∆DEF

Long-Answer Questions
Question 17.
Solution:
Given: In the given figure, ∆ABC and ∆DBC are on the same base BC but in opposite sides.
AD and BC intersect at O.

Question 18.
Solution:
In the given figure,
XY || AC and XY divides
∆ABC into two regions equal in area

Question 19.
Solution:
In the given figure, ∆ABC is an obtuse triangle, obtuse angle at B.
AD ⊥ CB produced.

To prove : AC² = AB² + BC² + 2BC x BD
Proof: In ∆ADB, ∠D = 90°
AB² = AD² + DB² (Pythagoras Theorem)
⇒ AD² = AB² – DB² ……(i)
Similarly, in right ∆ADC,
AC² = AD² + DC²
= AB² – DB² + (DB + BC)² [From (i)]
= AB² – DB² + DB² + BC² + 2BC x BD
= AB² + BC² + 2 BC x BD

Question 20.
Solution:
In the given figure,
PA, QB and RC is perpendicular to AC.
AP = x, QB = z, RC =y, AB = a and BC = b.

Hope given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Test Yourself are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.