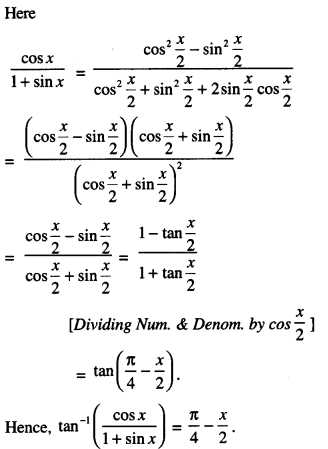
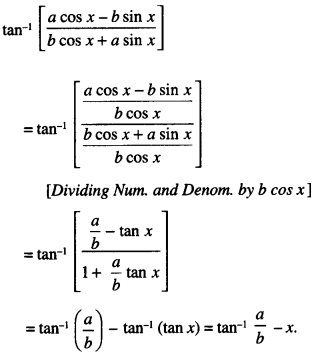
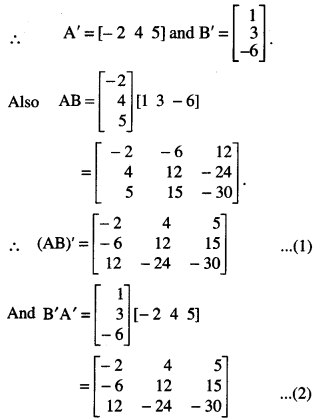
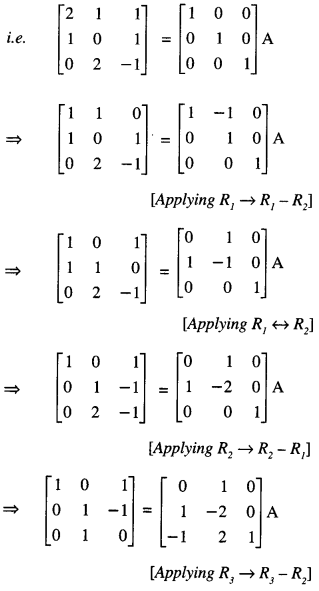
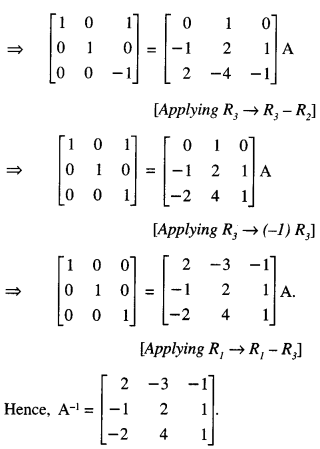
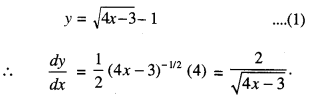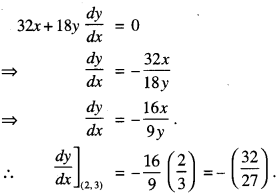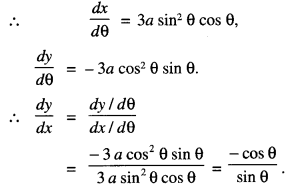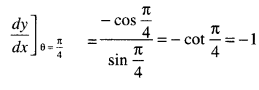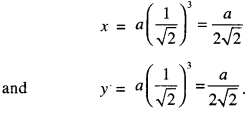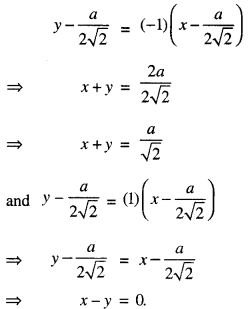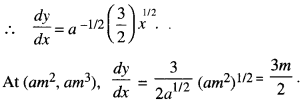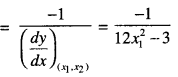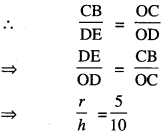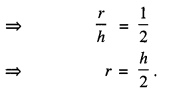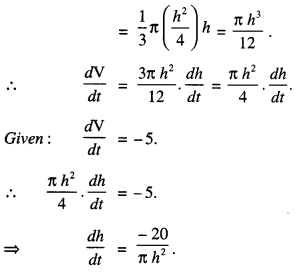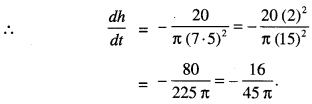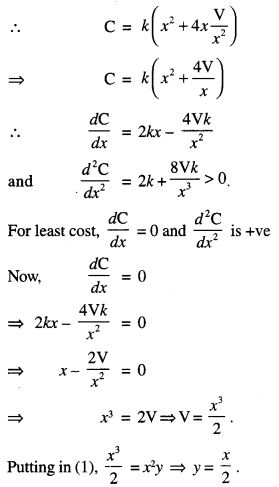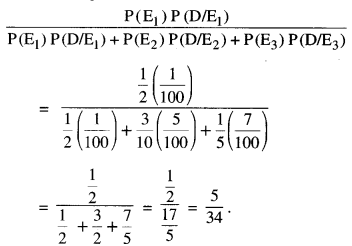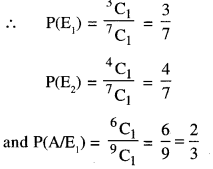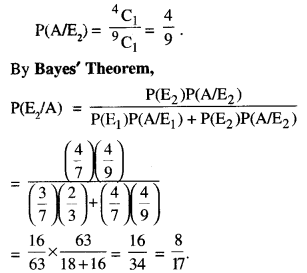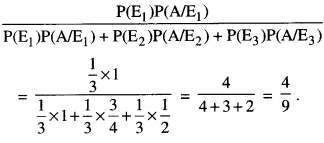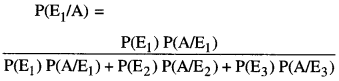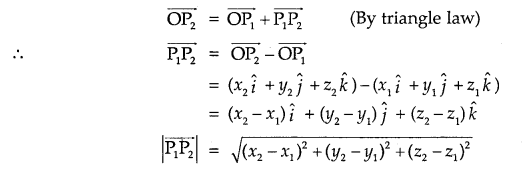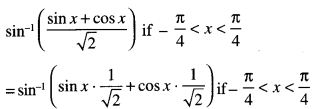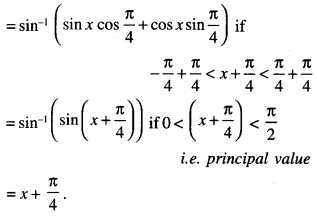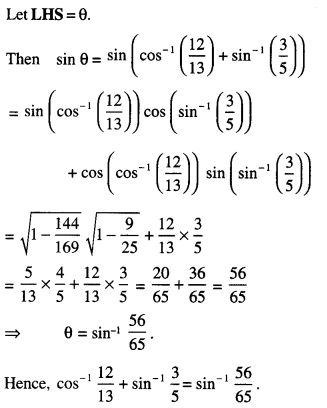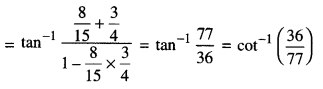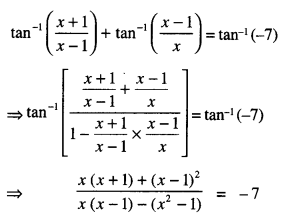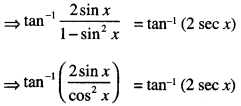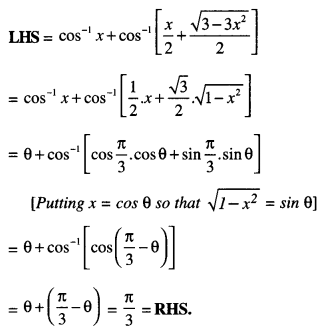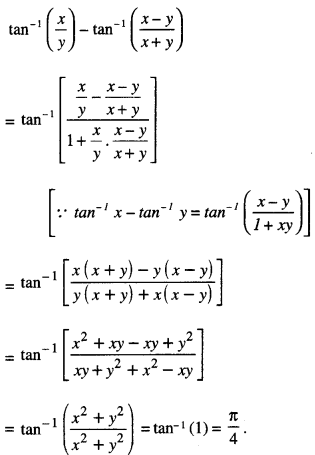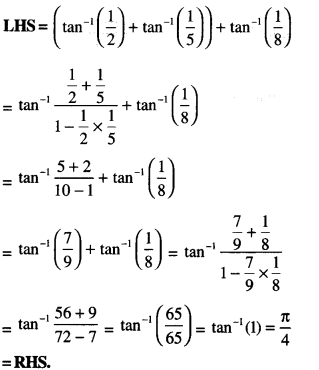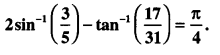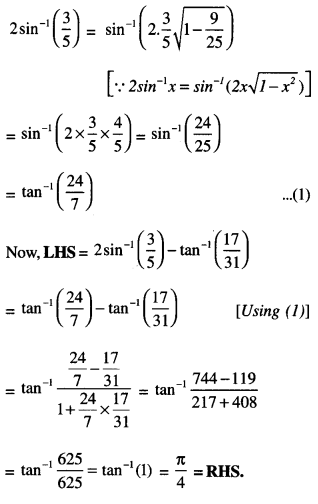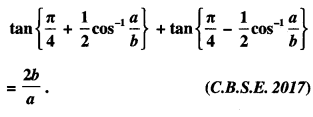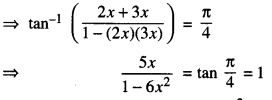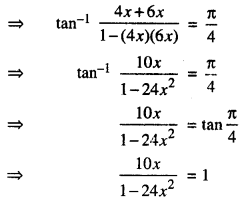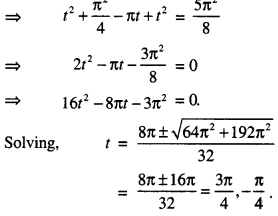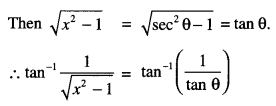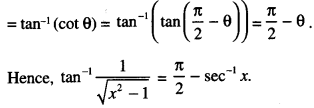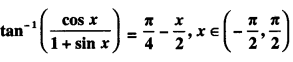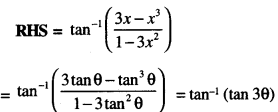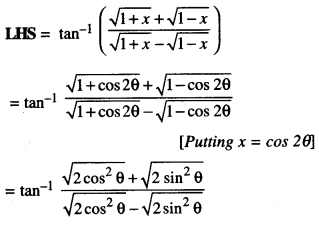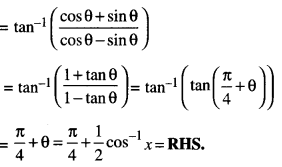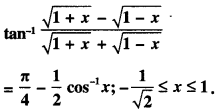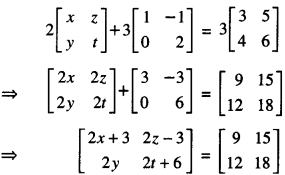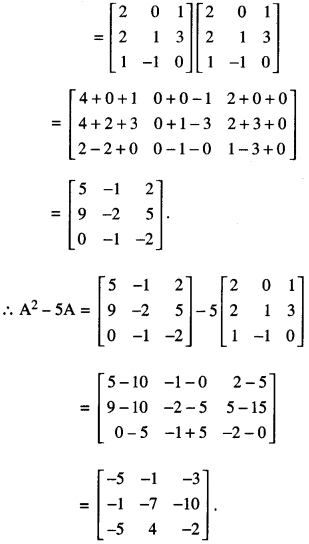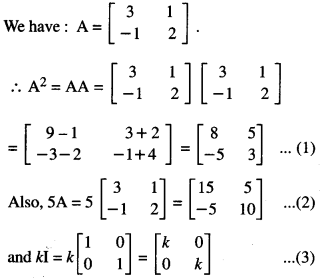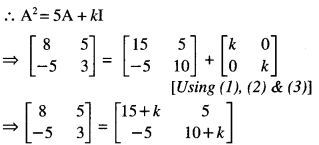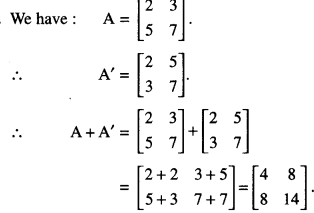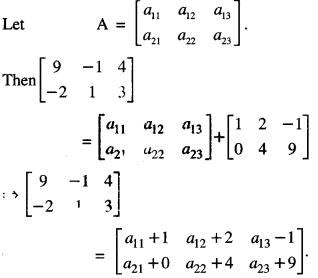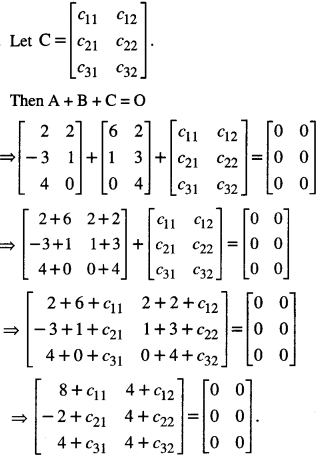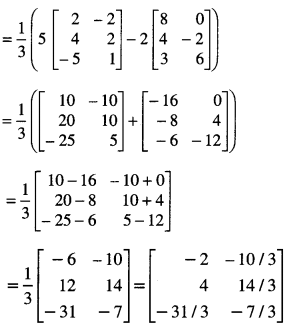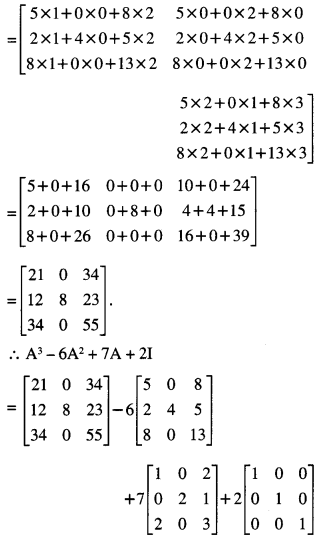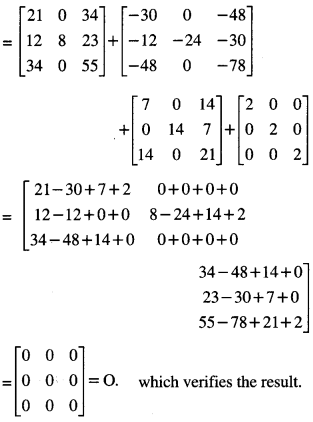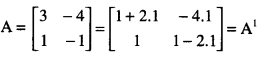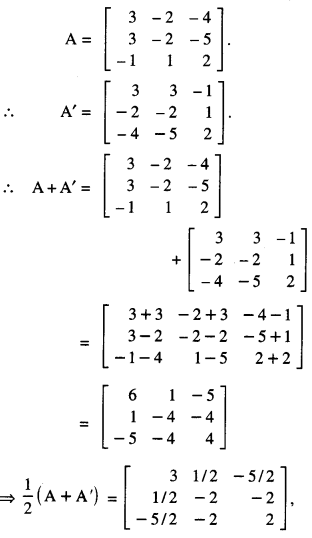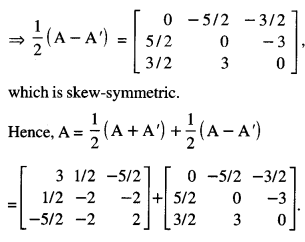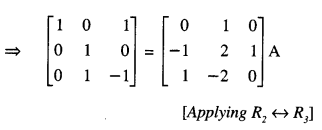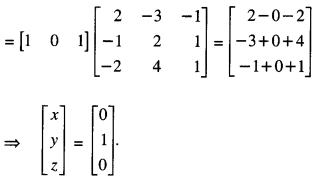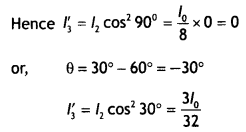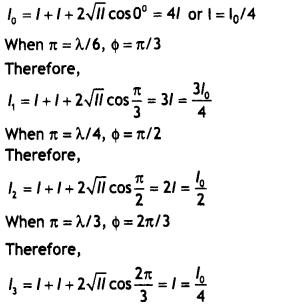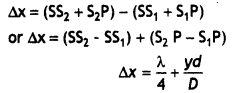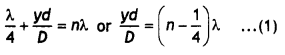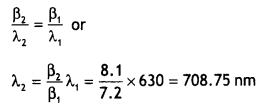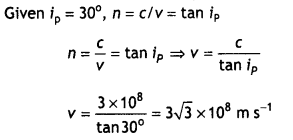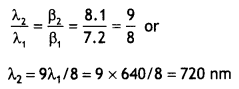Here we are providing 1 Mark Questions for Accountancy Class 12 Chapter 4 Reconstitution of Partnership Firm: Retirement/Death of a Partner are the best resource for students which helps in class 12 board exams.
One Mark Questions for Class 12 Accountancy Chapter 4 Reconstitution of Partnership Firm: Retirement/Death of a Partner
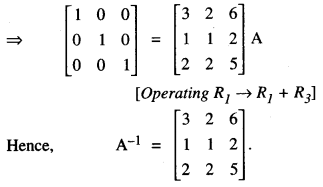
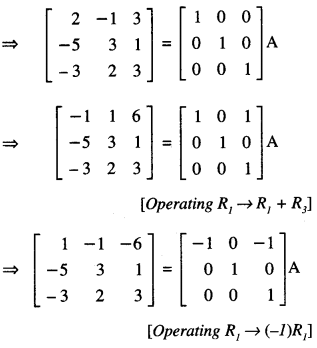
Question 1.
What is meant by ‘Gaining Ratio’ on retirement of a partner?
Or
P, Q and R were partners in a firm. On 31st March, 2018 R retired. The amount payable to R ₹ 2,17,000 was transferred to his loan account. R agreed to receive interest on this amount as per the provisions of Partnership Act, 1932. State the rate at which interest will be paid to R. (CBSE Delhi 2019)
Answer:
The ratio in which retiring Partner’s Share is distributed between remaining Partner is called gaining ratio.
Or
Rate of interest will be 6% p.a.
Question 2.
Aman, Bimal and Deepak are partners sharing profits in the ratio of 2 : 3 : 5. The goodwill of the firm has been valued at ₹ 37,500. Aman retired. Bimal and Deepak decided to share profits equally in future. Calculate gain/sacrifice of Bimal and Deepak on Aman’s retirement and also pass necessary journal entry for the treatment of goodwill. (CBSE Outside Delhi 2019)
Answer:
Old Ratio = 2:3:5
New Ratio =1:1 (on Aman’s Retirement)
Bimal’s Gain = 1/2 – 3/10 = 2/10
Deepak’s Gain = 1/2 – 5/10 = nil
Firm’s Goodwill = 37,500 .
A man’s share = 2/10 x 37,500 = 7,500

Question 3.
Riyansh, Garv and Kavleen were partners in a firm sharing profit and loss in the ratio of 8 : 7 : 5. On 2nd November 2018, Kavleen died. Kalveen’s share of profits till the date of her death was calculated at ₹ 9,375. Pass the necessary journal entry. (CBSE Sample Paper 2019-20)
Answer:

Question 4.
At the time of retirement how is the new profit sharing ratio among the remaining partners calculated₹ (CBSE Compt. 2019)
Answer:
The new share of each of the remaining partner is calculated as his/her own share in the firm plus the share acquired from the retiring partner.
Question 5.
In which ratio do the remaining partners acquire the share of profit of the retiring partner? (CBSE Compt. 2017)
Answer:
Gaining ratio.
Question 6.
At the time of retirement of a partner, state the condition when there is no need to compute gaining ratio. (CBSE 2013 Compartment OD)
Answer:
When the remaining partners share profits in old ratio.
Question 7.
On the retirement of a partner, how is the profit sharing ratio of the remaining partners decided?
Answer:
On the basis of old profit sharing ratio.
Question 8.
Why is gaining ratio of the remaining partners calculated at the time of retirement/death of a partner?
Answer:
Gaining ratio of the remaining partners is calculated to determine amount of goodwill payable by them to retired/deceased partner.
Question 9.
State the ratio in which share of goodwill of the retiring partner is debited to Capital Accounts of the remaining partners.
Answer:
In their gaining ratio.
Question 10.
Abha and Beena were partners sharing profits and losses in the ratio of 3 : 2 on April 1st 2013, they decided to admit Chanda for 1/5th share in the profits. They had a reserve of ₹ 25,000 which they wanted to show in their new balance sheet. Chanda agreed and the necessary adjustments were made in the books. On October 1st 2013, Abha met with an accident and died. Beena and Chanda decided to admit Abha’s daughter Fiza in their partnership, who agreed to bring ₹ 2,00,000 as capital. Calculate Abha’s share in the reserve on the date of her death. (CBSE Sample Paper 2015)
Answer:
₹ 12,000
Question 11.
X, Y and Z were partners sharing profits and losses in the ratio of 3:2:2. Z retired and the amount due to him was ₹ 85,000. He was paid ₹ 5,000 immediately. The balance was payable in three equal annual installments carrying interest @ 6% p.a. Pass necessary journal entry for recording the same on the date of Z’s retirement.
(Compt. Delhi 2017)
Answer:

Question 12.
Ram, Mohan and Sohan were partners in a firm sharing profits in the ratio of 4 : 3 : 1. Mohan retired. His share was taken over equally by Ram and Sohan. In which ratio will the profit and loss on revaluation of assets and liabilities on the retirement of Mohan be transferred to capital accounts of the partners?
(CBSE 2010 Compartment Delhi)
Answer:
In old profit sharing ratio.