Category: CBSE Notes

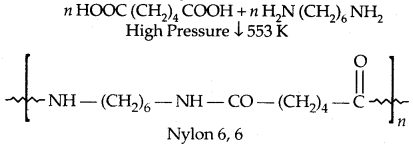
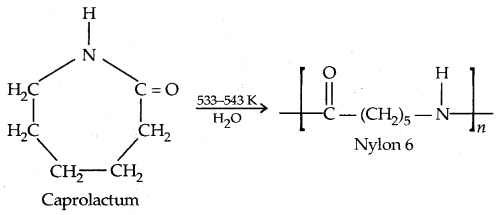
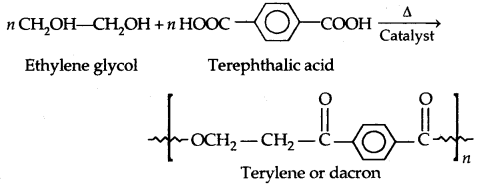
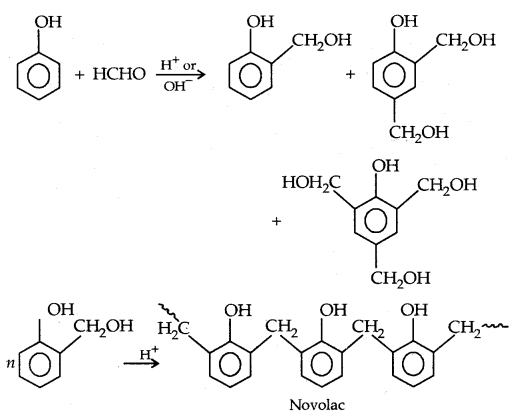
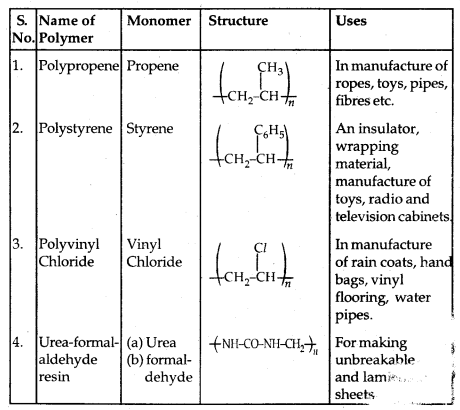
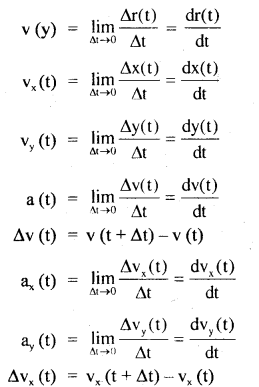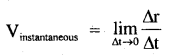By going through these CBSE Class 11 Physics Notes Chapter 7 Systems of Particles and Rotational Motion, students can recall all the concepts quickly.

Systems of Particles and Rotational Motion Notes Class 11 Physics Chapter 7

→ C.M. of a body or a system may or may not lie inside the body.

→ The momentum of the C.M. of the system remains constant if the external force acting on it is zero.

→ C.M. of the system moves with a constant velocity if the external force on the system is zero.

→ Only the angular component of the force gives rise to torque.

→ Both angular momentum and torque are vector quantities.

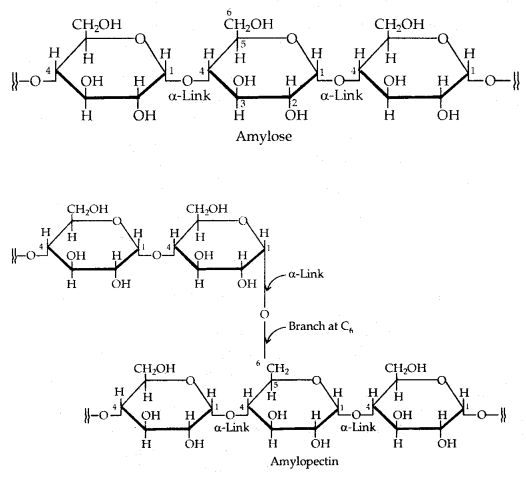
→ The rotatory cum translatory motion of a ring, disc, cylinder, spherical shell, or solid sphere on a surface is called rolling.

→ The axis of rotation of the rolling body is parallel to the plane on which it rolls.

→ When the angular speed of all the particles of the rolling body is the same, it is called rolling without slipping.

→ The linear speed of different particles is different, although the angular speed is the same for all the particles.

→ K.E. is the same for all bodies having the same m, R, and ω.

→ Total energy and rotational kinetic energy are maximum for the ring and minimum for the solid sphere.

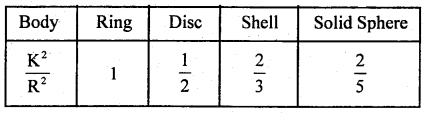
→ For ring K_r = K_t, K_r = \(\frac{1}{2}\) K_t for disc, K_r = 66%Kt for spherical shell and for solid sphere K_r = 40% of K_t.

→ The body rolls down the inclined plane without slipping only when the coefficient of limiting friction (p) bears the following relation:
µ ≥ (\(\frac{\mathrm{K}^{2}}{\mathrm{~K}^{2}+\mathrm{R}^{2}}\)) tan θ

→ The relative values of p for rolling without slipping down the inclined plane are as follows :
μ_ring > μ_shell > μ_disc > μ_{solid sphere}

→ When a body roll Is without slipping, no work is done against friction.

→ A body may roll with slipping if friction is less than a particular value and it may roll without slipping if the friction is sufficient.

→ M.I. is not a scalar quantity because for the same body its values are different for different orientations of the axis of rotation.

→ M.I. is defined w.r.t. the axis of rotation.

→ M.I. is not a vector quantity because the clockwise or anticlockwise direction is not associated with it.

→ The radius of gyration depends on the mass and the position of the axes of rotation.

→ M.I. depends on the position of the axis of rotation.

→ The theorem of ⊥ar axes is applicable to thin laminae like a sheet, disc, ring, etc.

→ The theorem of || axes is applicable to all types of bodies.

→ M.I. about the axis in a particular direction is least when the axis of rotation passes through the C.M.

→ A pair of equal and opposite forces with different lines of action is known as a couple.

→ A body may be in partial equilibrium i.e. it may be in translational. equilibrium and not in rotational equilibrium or vice-versa.

→ If the sum of forces is zero, it is said to be in translational equilibrium. 0 If the sum of moments of forces about C.G. is zero then it is said to be in rotational equilibrium.

Important Formulae:
→ Position vector of C.M. of a system of two particles is
R_cm = \(\frac{\mathrm{m}_{1} \mathbf{r}_{1}+\mathrm{m}_{2} \mathbf{r}_{2}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}\)

→ Position vector of C.M of a system of two particles of equal masses is
R_cm = \(\frac{\mathbf{r}_{1}+\mathbf{r}_{2}}{2}\)

→ Torque acting on a particle is given by
τ = r × p

→ Angular momentum is given by
L = r × p
or
L = mv r = Iω = mr² ω

→ τ = \(\frac{\mathrm{dL}}{\mathrm{dt}}\)

→ τ = Iα

→ I₁ω₁ = I₂ω₂
or
\(\frac{I_{1}}{T_{1}}=\frac{I_{2}}{T_{2}}\)

→ K.E. of rotation, K_t = \(\frac{1}{2}\)Iω²

→ Power in rotational motion, P = τω

→ According to theorem of perpendicular axes,
I_z = I_x + I_y

→ According to theorem of || axes, 1 = I_c + mh²

→ K.E. of a body rolling down an inclined plane is given by
E = \(\frac{1}{2}\)mv² + \(\frac{1}{2}\) Iω² = K_t + K_r

→ \(\frac{K_{r}}{K_{t}}=\frac{\frac{1}{2} I \omega^{2}}{\frac{1}{2} m v^{2}}=\frac{\frac{1}{2} m K^{2} \omega^{2}}{\frac{1}{2} m v^{2}}\)

= \(\frac{\mathrm{K}^{2} \omega^{2}}{\mathrm{R}^{2} \omega^{2}}=\frac{K^{2}}{\mathrm{R}^{2}}\)

→ \(\frac{\mathrm{K}_{\mathrm{r}}}{\mathrm{E}}=\frac{\frac{1}{2} \mathrm{mK}^{2} \omega^{2}}{\frac{1}{2} \mathrm{~m}\left(\mathrm{R}^{2}+\mathrm{K}^{2}\right) \omega^{2}}=\frac{\mathrm{K}^{2}}{\mathrm{~K}^{2}+\mathrm{R}^{2}}\)

→ \(\frac{K_{t}}{E}=\frac{R^{2}}{R^{2}+K^{2}}\)

→ If inclined plane is smooth, then the body will slide down and on reaching the bottom, its sliding velocity (V_s) is given by
V_s = \(\sqrt{2 \mathrm{gh}}\) and acceleration is a_s = g sin θ.

→ For rough inclined plane :
V_r = \(\frac{\sqrt{2 \mathrm{gh}}}{\sqrt{1+\frac{\mathrm{K}^{2}}{\mathrm{R}^{2}}}}\)

→ The acceleration of the body rolling down the inclined plane is
a_r = \(\frac{g \sin \theta}{\sqrt{1+\frac{K^{2}}{R^{2}}}}\)

→ Time taken to reach the bottom is t_s = \(\sqrt{\frac{2 l}{a_{s}}}\) and t_r = \(\sqrt{\frac{2 l}{a_{r}}}\)

→ If a particle of mass m is moving along a circular path of radius r with acceleration ‘a’, then
τ = mr² α
Where α = \(\frac{a}{r}\)

→ The value of \(\frac{\mathrm{K}^{2}}{\mathrm{R}^{2}}\) for different bodies are as follows:

By going through these CBSE Class 11 Physics Notes Chapter 6 Work, Energy and Power, students can recall all the concepts quickly.

Work, Energy and Power Notes Class 11 Physics Chapter 6

→ The total work done in the uniform speed of a body is zero i.e. if work is done is zero then the speed of the body is uniform.

→ In doing work in stretching or compressing a spring and by a falling body, the variable forces involved are restoring force and force of gravitation.

→ Work is done by a force on a body over a certain displacement.

→ The change in kinetic energy of an object is equal to the work done on it by the net force.

→ No work is done by the force if it acts perpendicular to the displacement of the body.

→ The total mechanical energy of a system is conserved if the forces doing work on it are conservative.

→ Energy can exist in various forms such as mechanical energy, heat energy, light energy, sound energy, etc.

→ The motion of a simple pendulum is an example of the conversion of P.E. into K.E. and vice-versa.

→ A body possesses chemical energy due to the chemical bonding of its atoms.

→ A body possesses heat energy due to the disorderly motion of its molecules.

→ The mass-energy equivalence formula describes energies to all masses (E = mc²) and masses to all energies (\(\frac{\mathrm{E}}{\mathrm{c}^{2}}\) = m)

→ The P.E. which an elevator loses in coming down from an upper story of the building to stop at the ground floor is used up to lift up the counter-poise weight.

→ When a very light body in motion collides with a heavy stationary body in an elastic collision, the lighter one rebounds back with the same speed without the heavy body being displaced.

→ When a body moving with some velocity undergoes elastic collision with another similar body at rest, then there is an exchange of their velocities after collision i.e. first one comes to rest and the second starts moving with the velocity of the first one.

→ 1 J = 10⁷ erg.

→ Joule (J) and erg are the S.I. and C.G.S. units of work and energy. Energy is the capacity of the body to do the work.

→ The area under the force-displacement graph is equal to the work done.

→ Work done by the gravitational or electric force does not depend on the nature of the path followed.

→ It depends only on the initial and final positions of the path of the body.

→ Power is measured in horsepower (h.p.). It is the fps unit of power used in engineering.

→ 1 h.p. = 746 W.

→ Watt (W) is the S.I. unit of power.

→ The area under the force-velocity graph is equal to the power dissipated. Body or external agency dissipates power against friction.

→ If the rails are on a plane surface and there is no friction, the power dissipated by the engine is zero.

→ When a body moves along a circular path with constant speed, its kinetic energy remains constant.

→ K.E. of a body can’t change if the force acting on a body is perpendicular to the instantaneous velocity. ,

→ K.E. is always positive.

→ If a machine gun fires n bullets per second with kinetic energy K, then the power of the machine gun is P = nK.

→ The force required to hold the machine gun in the above case is
F = nv = n \(\sqrt{2 \mathrm{mK}}\)

→ When work is done on a body, it’s K.E. or P.E. increases.

→ When work is done by a body, its P.E. or K.E. decreases.

→ Mass and energy are interconvertible.

→ K.E. can change into P.E. and vice-versa.

→ One form of energy can be changed into other forms according to the law of conservation of energy.

→ When a body falls, its P.E. is converted into its K.E.

→ The collision generally occurs for every small interval of time.

→ Physical contact between the colliding bodies is not essential for the collision.

→ The mutual forces between the colliding bodies are action and reaction pair.

→ Momentum and total energy are conserved during elastic collisions.

→ The collision is said to be elastic when the K.E. is conserved.

→ Inelastic collisions the forces involved are conservative.

→ Elastic collisions, the K.E. or mechanical energy is not converted into any other form of energy.

→ Elastic collisions produce no sound or heat.

→ There is no difference between the elastic and perfectly elastic collisions.

→ In the elastic collisions, the relative velocity before the collision is equal to the relative velocity after collision i.e. u₁ – u₂ = v₂ – v_1.

→ The collision is said to be inelastic when the K.E. is not conserved.

→ Head-on collisions are called one-dimensional collisions.

→ When the momentum of a body increases by a factor n, then its K.E. is increased by a factor n².

→ If the speed of a vehicle is made n-times then its stopping distance becomes n² times.

→ Work: Work is said to be done if a force acting on a body displaces it by some distance along the line of action of the force.

→ Energy: It is defined as the capacity of a body to do work.

→ K.E.: It is defined as the energy possessed by a body due to its motion.

→ P.E.: It is defined as the energy possessed by a body due to its position or configuration.

→ Gravitational P.E.: It is defined as the energy possessed by a body due to its position above the surface of death.

→ Power: It is defined as the time rate of doing work.

→ Work-energy theorem: It states that the work is done by a force acting on a body is equal to the change in its K.E.

→ Law of conservation of energy: Total energy of the universe always remains constant.

→ Instantaneous Power: It is the limiting value of the average power of an agent in a small time interval tending to zero.

→ Mass-energy Equivalence: E = mc².

→ Elastic collision: The collision is said to be elastic if both momentum and the K.E. of the system remain conserved.

→ Elastic collision in one dimension: The collision is said to be one-dimensional if the colliding bodies move along the same straight line after the collision.

→ In-elastic collision: It is defined as the collision in which K.E. does not remain conserved.

→ Transformation of energy: It is defined as the phenomena of change of energy from one form to the other.

→ Coefficient of restitution: It is defined as the ratio of the velocity of separation to the velocity of approach i.e.
e = \(\frac{v_{2}-v_{1}}{u_{1}-u_{2}}\)

→ Moderator: It is defined as a substance used in atomic reactors to slow down fast-moving neutrons to make them thermal neutrons. e.g. graphite and heavy water are moderators

→ 1 eV: It is defined as the energy acquired by an electron when a potential difference of 1 volt is applied
i. e. 1 eV = 1.6 × 10^-19 c × 1 V
= 1.6 × 10^-19 J

Important Formulae:
→ Work done by F in moving a body by S is
W = F . S = FS cos θ

→ P = \(\frac{W}{t}\)

→ Instantaneous power is P = F.v

→ K.E. = \(\frac{1}{2}\)mv².

→ P.E. = mgh.

→ P.E. of a spring is given by = \(\frac{1}{2}\)kx².
where k = force constant, x = displacement i.e. extension or compression produced in the spring. .

→ E = mc².

→ Velocities of the two bodies after collisions are given by
v₁ = \(\frac{m_{1}-\dot{m}_{2}}{m_{1}+m_{2}}\)u₁ + \(\frac{2 m_{2}}{m_{1}+m_{2}}\)u₂
and
v₂ = \(\frac{m_{2}-\dot{m}_{1}}{m_{1}+m_{2}}\)u₂ + \(\frac{2 m_{2}}{m_{1}+m_{2}}\)u₁

→ Power of an engine pulling a train on rails having coefficient of friction p is given by:
P = μ mg v.
where μ = coefficient of friction.
m = mass of train,
v = velocity of train.

→ Power of engine on an inclined plane pulling the train up is
P = (μ cos θ + sin θ)mg v

→ And pulling down the inclined plane is
P = (μ cos θ – sin θ)mg v

→ Work against friction in above cases when the body moves down the inclined plane is W = m.g.(sin θ – μ cos θ)S

→ When body moves up the incline,
W = mg(μ cos θ + sin θ)S

→ % efficiency (n%) = \(\frac{\text { Poweroutput }}{\text { Powerinput }}\) × 100
= \(\frac{\text { Output energy }}{\text { Input energy }}\) × 100

By going through these CBSE Class 11 Physics Notes Chapter 5 Law of Motion, students can recall all the concepts quickly.

Law of Motion Notes Class 11 Physics Chapter 5

→ Inertia is proportional to the mass of the body.

→ The force causes acceleration.

→ In the absence of force, a body moves along a straight-line path.

→ If the net external force on a body is zero, its acceleration is zero. Acceleration can be non-zero only if there is a net external force on the body.

→ If a body moves along a curved path, then it is certainly acted upon by a force.

→ C.G.S. and S.I. absolute units of force are dyne and newton (N) respectively and 1 N = 10⁵ dynes.

→ C.G.S. and S.I. gravitational units of force are gm wt. and kg wt. (i.e. kilogram weight) respectively and 1 kg wt = kgf.

→ 1 gm wt = 1 gmf, 1 kg f = 10³ gm f.

→ 1 kg f = 9.8 N.

→ 1 gm f = 1 gm wt = 980 dyne.

→ Impulse = change in momentum.

→ Four types of forces exist in nature, they are gravitational force (F_g), electromagnetic force (F_em), weak force (F_w), and nuclear force (F_n).

→ F_g: F_em: F_w: F_n:: 1: 1025: 1036: 1038.

→ Rocket works on the principle of conservation of linear momentum.

→ Rocket ejects gases backward and as a result, acquires a forward momentum.

→ If Δm is the mass of the gas ejected backward in time At with speed u, then the force acting on the rocket will be:
F = u \(\frac{\Delta m}{\Delta t}\)

→ When a force acting on a particle is always perpendicular to its velocity, then the path followed by the particle is a circle.

→ In a uniform circular motion, the magnitude of velocity always remains constant and only its direction changes continuously.

→ If a body moves with a vertical acceleration a, then its apparent weight is given by:
R = m (g – a)

→ The weight of a body measured by the spring balance in a lift is equal to the apparent weight.

→ The apparent weight of a body falling freely is zero because for it, a = g. It is the case of weightlessness.

→ If the lift falls with a < g, the apparent weight of the body decreases.

→ If the lift accelerates upwards, the apparent weight of the body increases.

→ The true weight of the body = mg.

→ If the lift rises or falls with constant speed, then apparent weight = true weight

→ If the person climbs up along the rope with acceleration ‘a’, then tension in the rope will be T = m (g + a).

→ If the person climbs down along the rope with acceleration ‘a’, then tension in the rope will be T = m (g – a).

→ If the person climbs up or down the rope with uniform velocity, then tension in the string, T = mg.

→ If a body starting from rest moves along a smooth inclined plane of length l, height h and having an angle of inclination 0, then:
1. Its acceleration down the plane is g sin θ.

2. Its velocity at the bottom of the inclined plane will be
\(\sqrt{2 \mathrm{gh}}=\sqrt{2 \mathrm{~g} l \sin \theta}\)

3. Time taken to reach the bottom will be:
t = \(\sqrt{\frac{2 l}{g \sin \theta}}=\left(\frac{2 l^{2}}{g h}\right)^{\frac{1}{2}}\)

= \(\left(\frac{2 \mathrm{~h}}{\mathrm{~g} \sin \theta}\right)^{\frac{1}{2}}=\frac{1}{\sin \theta}\left(\frac{2 \mathrm{~h}}{\mathrm{~g}}\right)^{\frac{1}{2}}\)

4. If the angle of inclination is changed keeping the length constant, then:
\(\frac{\mathrm{t}_{1}}{\mathrm{t}_{2}}=\left(\frac{\sin \theta_{2}}{\sin \theta_{1}}\right)^{\frac{1}{2}}\)

5. If the angle of inclination is changed keeping the height constant, then
\(\frac{\mathrm{t}_{1}}{\mathrm{t}_{2}}=\frac{\sin \theta_{2}}{\sin \theta_{1}}\)

→ A system or a body is said to be in equilibrium when the net force acting on it is zero.

→ If the vector sum of a number of forces acting on a body is zero, then it is said to be in equilibrium.

→ Friction acts opposite to the direction of motion of the body and parallel to the surfaces in contact.

→ Friction depends on the nature of surfaces in contact.

→ Friction is more when the surfaces in contact are rough.

→ Friction is a necessary evil it causes the dissipation of energy. But we need.

→ Friction is of different types such as static friction, kinetic (sliding or rolling) friction, dry friction, wet friction.

→ Static friction is a variable force.

→ The maximum value of static friction is called limiting friction.

→ Static friction is equal and opposite to the force applied to the body.

→ When the applied force is equal to the limiting friction, the body begins to slide.

→ The kinetic friction is less than the limiting friction.

→ The friction on a rolling body is called rolling friction.

→ The rolling friction is less than sliding friction.

→ Friction is a self-adjusting force.

→ The limiting friction is directly proportional to the normal reaction i. e. F ∝ R.

→ The net reactive force acting perpendicular to the surface is called normal reaction (R) and is equal to the force with which the two bodies are pressed against each other.

→ The ratio of limiting friction (F) to the normal reaction (R) is called the coefficient of limiting friction (μ_l) i.e. μ_l = F/R.

→ The limiting friction is independent of the shape or area of surfaces in contact if R = constant.

→ μ_l is a dimensionless constant. It depends on the nature of the surfaces in contact. It is independent of the normal reaction.

→ No work is done against static friction.

→ The kinetic friction opposes the motion of the body.

→ Static friction is the frictional force that comes into play when a body tends to move on the surface of another body.

→ Static friction is due to the interlocking of microscopic projections on the surface of the body.

→ The change from static to kinetic friction is by a stick and slip process. The slip is a break away from the static condition.

→ Sticking is caused by the second interlocking.

→ Kinetic friction is a constant force.

→ It is independent of the applied force.

→ The coefficient of kinetic friction is equal to the ratio of kinetic friction (F_k) to the normal reaction (R) i.e. μ_k = F_k/R.

→ F_k is independent of the area of contact between two bodies.

→ Work is done against kinetic friction.

→ Coefficient of rolling friction (μ_r) = \(\frac{\mathrm{F}_{\mathrm{r}}}{\mathrm{R}}=\frac{\text { rolling friction }}{\text { normal reaction }}\)

→ μ_r < μ_k < μ_s.

→ The friction between two solid surfaces is called dry friction.

→ The friction between a solid surface and a liquid surface is called wet friction.

→ The dry friction causes squeaking of the surfaces trying to move over each other.

→ The dry friction can also cause pleasant sound e.g. the bow under-going stick and slip motion on the string of violin causes pleasant sound.

→ Friction can be decreased by converting dry friction to wet friction.

→ Friction may increase if the surfaces are highly polished. This happens due to cold welding together of the polished surfaces.

→ The angle between the normal reaction and the resultant force of friction and the normal reaction is called the angle of friction (θ).

→ µ = tan θ i.e. coefficient of friction = tan θ.

→ The angle of the inclined plane at which the body placed on it just begins to slide down is called the angle of repose (α) or angle of sliding.

→ µ = tan α.

→ Also α = θ.

→ When a body rotates, all its particles describe circular paths about a line called the axis of rotation.

→ The centers of circles described by the different particles of the rotating body lie on the axis of rotation.

→ The Axis of rotation is perpendicular to the plane of rotation.

→ For uniform circular motion, we have

1. a_c = v²/r = rω²
2. v = rω
3. a ∝ r

where α = angular acceleration.

→ When a body rotates with uniform velocity, its different particles have centripetal acceleration directly proportional to the radius i.e. a_c ∝ r.

→ There can be no circular motion without centripetal force.

→ Centripetal force can be a mechanical, electrical, or magnetic force.

→ In a uniform circular motion, the magnitude of momentum, velocity, and kinetic energy remains constant.

→ Centrifugal force is the pseudo force that is equal and opposite to the centripetal force. It is directed away from the center along the radius.

→ The centrifugal force appears to act on the agency which exerts the centripetal force.

→ The centrifugal force cannot balance the centripetal force because they act on different bodies.

→ The railway tracks and roads are banked for safe turning. The banking angle θ for safe turning is tan θ = \(\frac{\mathbf{v}^{2}}{r g}\) . Also tan θ = \(\frac{\mathrm{h}}{\mathrm{d}}\)
where d = width of road
h = height of the outer edge of the road above the inner edge

→ Maximum speed of the car without overturning when it moves on a circular banked road of radius r is
u_max = \(\sqrt{\frac{\mathrm{grd}}{\mathrm{h}}}\)
when d = \(\frac{1}{2}\) of the distance between two wheels of the car.

→ When a particle of mass m, tied to a string of length is rotated in a horizontal plane with a speed ‘y’, the tension is given by
T = \(\frac{m v^{2}}{r}\)

→ When the string breaks, the particle moves away from the center but tangentially.

→ K.E. of a body rotating in a vertical plane is different at different points.

→ The angle through which the outer edge of the road track is raised above the inner edge is called the angle of banking of roads/ tracks.

→ For safe going of the vehicle round the circular level road, the required condition is:
μ ≤ \(\frac{\mathrm{v}^{2}}{\mathrm{rg}}\)

→ A simple pendulum oscillates in a vertical plane. It will oscillate only if its motion is in the lower semi-circle.

→ For oscillation, the velocity at the lowest point L must be such that the velocity reduces to zero at points M₁ and M₂.

Thus, \(\frac{1}{2}\)mv_e² = mgr
or
v_e = \(\sqrt{2 \mathrm{gr}}\)
i.e v_e ≤ \(\sqrt{2 \mathrm{gr}}\)

→ If v_e > \(\sqrt{2 \mathrm{gr}}\) it will not then oscillate in the lower semi-circle.

→ Minimum velocity that a body should have at the lowest point (L) and highest point (H) of a vertical circle for looping it are
v₁ = \(\sqrt{5 \mathrm{gr}}\) and v₂ = \(\sqrt{\mathrm{gr}}\)
where v₁ and v₂ are velocities at L and H points respectively. Maximum speed with which a vehicle can take a safe turn on a level road is v = \(\sqrt{\mu \mathrm{gr}}\).

→ Maximum speed of the vehicle with which it can take a safe turn on a banked road is given by
v = \(\sqrt{rgθ}\)

→ Sufficient force of friction is there between the tyres of the vehicle and the banked road, then the maximum speed of the vehicle for taking a safe turn is given by

v_max = \(\left(rg\frac{\mu_{\mathrm{s}}+\tan \theta}{1-\mu_{\mathrm{s}} \tan \theta}\right)^{\frac{1}{2}}\)

→ The first law is also called the law of inertia according to which the state of rest or uniform motion of a body remains the same unless acted upon by an external force.

→ The action and reaction always occur in pairs.

→ The position of an event or particle is measured by using a system of coordinates called a frame of reference.

→ There are two types of frame of reference

1. inertial and
2. non-inertial (or accelerated frame of reference).

→ A frame of reference with uniform motion with respect to another inertial frame of reference is also the inertial frame of reference in which the body is situated and obey’s Newton’s law of motion.

→ Inertia: A body at rest or in uniform motion continues in its state unless acted upon by an external force.

→ Force: Force is the action that changes or tends to change the state of rest or uniform motion of a rigid body along a straight line.

→ Rigid body: A body whose various particles move through the same distance parallel to each other under the action of external force i.e. there is no relative motion amongst the various particles of the body under the action of an external force is called a rigid body.

→ Linear momentum (p).: The quantity of motion possessed by a body is called its momentum Mathematically the linear momentum of the body is equal to the product of its mass and velocity i.e.
p = mv

→ Retardation: The quantity of hindrance in the motion of a body is called retardation and the force which retards the body is called retarding force.

→ Newton’s first law of motion: A body continues in its state of rest or uniform motion along a straight line in the absence of external force.

This is called Newton’s first law of motion.
\(\overrightarrow{\mathrm{F}}\) ∞ \(\frac{\mathrm{d}(\overrightarrow{\mathrm{p}})}{\mathrm{dt}}\)
or
\(\overrightarrow{\mathrm{F}}\) = k m\(\overrightarrow{\mathrm{a}}\)

In non-relativistic dynamics \(\frac{\Delta \overrightarrow{\mathrm{v}}}{\Delta \mathrm{t}}=\overrightarrow{\mathrm{a}}\), the acceleration of the body or particle.

When force F, mass m and acceleration arc measured in Newton, kilogram and meter per second respectively. i.e. in S.L units. so that
\(\overrightarrow{\mathrm{F}}\) = m \(\overrightarrow{\mathrm{a}}\)

Its scalar from is F = ma

→ Newton (N): It is the SI unit of measurement of force. One newton is that force that causes an acceleration of 1 ms 2 in a rigid body of mass 1 kg.
∴ 1 N = 1 kg × 1 ms^-2

→ Impulse: The impact of force is called impulse. Mathematically impulse = F × Δt = force × time. So impulse = m(Δv).

→ The inertia of rest: The property of a body to be unable to change its state of rest itself is called the inertia of rest,

→ The inertia of motion: The property of a body by virtue of which it cannot change by itself its state of uniform motion is called inertia of motion.

→ The inertia of direction: The property of a body by virtue of which it cannot change its own direction of motion is called the direction of inertia.

→ Newton’s third law of motion: States that “To every action, there is an equal and opposite reaction.”
F_BA = – F_AB
where F_AB = force exerted on body 8 by body A, and F_BA = force exerted on body A by body B.

→ Law of conservation of linear momentum: The linear momentum of an isolated system of bodies or particles is always conserved, that is it remains constant.

→ Static equilibrium: A body is said to be in static equilibrium if the vector sum of all the forces acting on it is zero. This is a necessary and sufficient condition for a point object only.

→ Lubricants: The substances which are applied to the surfaces to reduce friction are called lubricants.

Important Formulae:
→ Linear momentum of a body of mass m and moving with a velocity v is: p = mv

→ Change in momentum, Δp = m Δ v

→ If two objects of masses M and m have same momentum, then
\(\frac{M}{m}=\frac{v}{V}\)

→ F = ma

→ Resultant of two forces F, and F2 acting simultaneously at angle θ is given by F = F₁ + F₂
The magnitude of F is given by parallelogram law of vectors
F = \(\sqrt{F_{1}^{2}+F_{2}^{2}+2 F_{1} F_{2} \cos \theta}\)

→ The orthogonal components of F and a are:
F = F_xi + F_yj + F_zk
and a = a_xi + a_yj + a_zk

→ Inertial mass, m₁ = \(\frac{\mathrm{F}}{\mathrm{a}}\)

→ Gravitational mass, mg = \(\frac{\mathrm{F}}{\mathrm{g}}\)

→ Impulse I = FΔt = mΔv

→ Newton’s third law of motion:
F₁₂ = – F₂₁
or
m₁a₁ = – m₂a₂

→ Equilibrium of body under three concurrent forces:
F₁ + F₂ + F₃ = 0
Or
F₃ = – (F₁ +F₂)

→ Simple pulley: a = acceleration of masses m₁ and m₂
= \(\left(\frac{m_{2}-m_{1}}{m_{1}+m_{2}}\right)\)
If m₂ > m₁

Tension in the string connecting the two masses and passing over the pulley is given by
T = \(\left(\frac{2 m_{1} m_{2}}{m_{1}+m_{2}}\right)\)g

→ Solving problems using Free Body Diagram Technique:

1. Draw a simple neat diagram of the system as per the given problem.
2. Isolate the object of interest. This is now called a free body.
3. Consider all the external forces acting on the free body and mark them by arrows touching the free body with their line of action clearly represented.
4. Now apply Newton’s second law of motion.
5. In a non-inertial frame consider the pseudo forces like real forces acting on the object in addition to other external forces. The direction of such a force will be opposite to the direction of acceleration of the frame of reference.

By going through these CBSE Class 11 Physics Notes Chapter 4 Motion in a Plane, students can recall all the concepts quickly.

Motion in a Plane Notes Class 11 Physics Chapter 4

→ All physical quantities having direction are not vectors.

→ The following quantities are neither scalars nor vectors: Relative density, density, frequency, stress, strain, pressure, viscosity, modulus of elasticity, Poisson’s ratio, specific heat, latent leat, a moment of Inertia, loudness, spring constant, Boltzman constant, Stefan’s constant, Gas constant, Gravitational constant, Plank’s constant, Rydberg’s constant etc.

→ A vector can have only two rectangular components in a plane and only three rectangular components in space.

→ Vectors cannot be added or subtracted or divided algebraically.

→ Division of two vectors is not allowed.

→ A vector can have any number of components (even infinite in number but a minimum of two components).

→ Two vectors can be added graphically by using head to tail method or by using the parallelogram or triangle law method.

→ A vector multiplied by a real number gives another vector having a magnitude equal to real number times the magnitude of the given vector and having direction same or opposite depending upon whether the number is positive or negative.

→ Multiplication of a vector by -1 reverses its direction.

→ If A + B = C or A + B + C = 0, then A, B and C are in one place.

→ Vector addition obeys commutative law
i.e. A + B = B + A

→ Vector addition obeys associative law
i.e. (A + B) + C = A + (B + C)

→ Subtraction of B from A is defined as the sum of
– B + A i.e. A – B = A + (-B)

→ The angle between two equal vectors is zero.

→ The angle between -ve vectors is 180°.

→ Unit vector  = \(\frac{\mathbf{A}}{|\mathbf{A}|}\) .

→ The magnitude of  = 1.

→ The direction of A is the same as that of the given vector along which it acts.

→ The resultant of two vectors of unequal magnitudes can never be a null vector.

→ î, ĵ, k̂ are the unit vectors acting mutually perpendicular to each other along X, Y and Z axes respectively and are called orthogonal unit vectors.

→ î.î = ĵ.ĵ = k̂.k̂ = 1

→ î.ĵ = ĵ.k̂ = k̂.î = 0

→ î × î = ĵ × ĵ = k̂ × k̂-= 0

→ î × ĵ = k̂, ĵ × k̂ = î, k̂ × î = ĵ

→ A × A = 0 , Also A – A = 0
But A × A ≠ A – A as A × A ⊥ A and A – A is collinear with A.

→ The cross product:

1. Is not commutative (i.e. don’t obey commutative law):
   i. e. A × B ≠ B × A
   = B × A (anticommutative law)
2. obeys distributive law i.e.
   A × (B + C) = A × B + A × C

→ Vectors lying in the same plane are called co-planer vectors.

→ Vectors are added according to triangle law, parallelogram law, and polygram law of vector addition.

→ The maximum resultant of two vectors A and B is
|R_max| = |A| + |B|

→ The minimum resultant of two vectors A and B is
|R_max| = |A| – |B|

→ The minimum number of vectors lying in the same plane whose results can be zero is 3.

→ The minimum number of vectors that are not co-planar and their results can be zero is 4.

→ A minimum number of collinear vectors whose resultant can be zero is 2.

→ A vector in component form is A = A_xî + A_yĵ +A_zk̂

→ Magnitude of A is = \(\sqrt{A_{x}^{2}+A_{y}^{2}+A_{z}^{2}}\).

→ A projectile is any object thrown with some initial velocity and then it moves under the effect of gravity alone.

→ The trajectory is the path followed by the projectile during its flight.

→ Its trajectory is always parabolic in nature.

→ Two-dimensional motion: The motion of an object in a plane is a two-dimensional motion such as the motion of an arrow shot at some angle and then moving under gravity.

→ Three-dimensional motion: The motion of an object in space is called a three-dimensional motion, for example, the motion of a free gas molecule.

→ Scalar quantities: The quantities which do not need direction for their description are called scalar quantities. Only the magnitude of the quantity is needed to express them correctly. Such quantities are distance, mass, density, energy, temperature etc.

→ Vector quantities: The quantities which need both magnitude and direction for their correct description are called vector quantities. They also obey the law of the addition of vectors. For example displacement, velocity, acceleration, force, momentum etc. are vector quantities.

→ Triangle law of vector addition: If the two vectors are represented by the two adjacent sides of a triangle taken in order, their resultant is given in magnitude and direction by the third side of the triangle taken in the opposite order.

→ Parallelogram law of vector addition: If two vectors acting simultaneously at a point are represented by the two adjacent sides of a parallelogram, then their resultant is completely given in magnitude and direction by the diagonal of the parallelogram passing through that point.

→ Unit vector: A unit vector is a vector in the direction of a given vector whose magnitude is unity. It is represented by a cap or a hat over letter e.g. n̂, î, ĵ, k̂, x̂, ŷ, ẑ etc. The unit vectors in the cartesian coordinate system along the three axes are generally written as î, ĵ and k̂ such that |î| = |ĵ| = |k̂| = 1.

→ Uniform velocity: The uniform or constant velocity is the one in which the moving object undergoes equal displacements in equal intervals of time.

→ Speed: The magnitude of velocity is known as speed. It is the distance travelled divided by the time taken.

→ Uniform acceleration: When the velocity of an object changes by equal amounts in equal intervals of time, the object is said to be having uniform acceleration.

→ Projectile: Projectile is a particle or an object projected with some initial velocity and then left to move under gravity alone.

→ The uniform circular motion: The motion of an object in a circular path with constant speed and constant acceleration (magnitude) is called a uniform circular motion.

→ Equal vectors: Two vectors are said to be equal if they have the same magnitude and act in the same direction.

→ Negative vector: A vector having the same magnitude as the given vector but acting in exactly the opposite direction is called a negative vector.

→ Co-initial vectors: Vectors starting from the same initial point are called co-initial vectors.

→ Zero vector or Null vector: The vector whose magnitude is zero but the direction is uncertain (or arbitrary) is called a zero or null vector. It is represented by 0.

→ Collinear vectors: Two vectors acting along the same or parallel lines in the same or opposite directions are called collinear vectors.

→ Fixed vector: A vector whose tail point or initial point is fixed is called a fixed vector.

→ Free vector: A vector whose initial point or tail is not fixed is called a free vector.

→ Polygon law of addition of vectors: It states that if a number of vectors are represented by the sides of a polygon taken in the same order, then their resultant is given completely by the closing side of the polygon taken in the opposite order.

→ Rectangular components of a vector in a plane: The resolution of a vector into two mutually perpendicular components in a plane is called rectangular resolution and each component is called a rectangular component.

→ Rectangular components in a plane: The components of a vector along three mutually perpendicular axes are called the rectangular component of a vector in space.

→ Scalar product of vectors: If the multiplication of two vectors yields a scalar quantity, the multiplication is called a scalar or dot product. This is because of the fact that multiplication is denoted by a dot (.) between the multiplying vectors e.g. A.B = AB cos θ, where θ is the angle between the two vectors.

→ Cross or vector product: When the multiplication of two vectors is shown by a cross (×) between them, it is called a cross product. The resultant is also a vector quantity e.g. A × B = C. This multiplication is, therefore, also known as the vector product.

Important Formulae:
→ Uniform circular motion: Time period T second, frequency
v = \(\frac{1}{T}\)
Angular velocity ω = \(\frac{θ}{T}\),
ω = \(\frac{2 \pi}{\mathrm{T}}\) = 2πv,
v = \(\frac{1}{T}\),
θ = \(\frac{l}{r}\)
or
l = rθ.

→ Angular acceleration: α = \(\frac{\omega_{2}-\omega_{1}}{t_{2}-t_{1}}=\frac{d \omega}{d t}\)
average acceleration, a_av = \(\frac{v_{2}-v_{1}}{t_{2}-t_{1}}\)
Average angular acceleration,

→ Time for maximum height: t = \(\frac{\mathrm{u} \sin \theta}{\mathrm{g}}\)

→ Angle of projection of maximum horizontal range:
θ = \(\frac{π}{4}\) or 45°.

→ Angles for same range θ, (\(\frac{π}{2}\) – θ)

→ General position – velocity – acceleration relations:
Δr (t) = r(t + Δt) – r(t)
v(t) = \(\frac{\Delta \mathrm{x}(\mathrm{t})}{\Delta \mathrm{t}}\);

vx(t) = \(\frac{\Delta \mathrm{x}(\mathrm{t})}{\Delta \mathrm{t}}\),

vy(t) = \(\frac{\Delta \mathrm{y}(\mathrm{t})}{\Delta \mathrm{t}}\)

Δx(t) = x(t + Δt) – x(t)
Δy(t) = y(t + Δt) – y(t)

→ Since: A.A = A², so

• î.î =1,
• ĵ.ĵ =1,
• k̂.k̂ =1

As î, ĵ and k̂ are mutually perpendicular so
î.ĵ = ĵ.k̂ =0,
k̂.î = 0

→ A.(B + C) = A.B. +A.C

→ Vector product:
A × B = C = |A| |B|sin θ n̂
In cartesian coordinates,
A × B = (A_xî + A_yĵ + A_zk̂) × (B_xî + B_yĵ + B_zk̂)
= (A_yB_z – A_zB_y) î + (A_zB_x – A_xB_z)ĵ + (A_xB_y – A_yB_x)k̂
= \(\left|\begin{array}{ccc}
\hat{\mathrm{i}} & \hat{\mathbf{j}} & \hat{\mathbf{k}} \\
\mathrm{A}_{\mathrm{x}} & \mathrm{A}_{\mathrm{y}} & \mathrm{A} \\
\mathrm{B}_{\mathrm{x}} & \mathrm{B}_{\mathrm{y}} & \mathrm{B}
\end{array}\right|\)

→ A × B ≠ B × A
= -B × A

→ |A × B|² + |A . B|² = 2|\(\overrightarrow{\mathrm{A}}\)|²|\(\overrightarrow{\mathrm{B}}\)|²

→ Direction cosines:
cos α = \(\frac{A_{x}}{A}\) = l,
cos β = \(\frac{A_{y}}{A}\) = m, and
cos γ = \(\frac{A_{z}}{A}\) = n

→ l² + m² + n² = 1

→ Velocity: v = vxi + vyj

→ Speed: v = |v| = (v_x² + v_y²)^1/2 .

→ Distance travelled in time t:
x(t)î + y(t)ĵ = x(0)î + y(0)ĵ + (v_xî + v_yĵ)t

→ x (t) = x (0) + v_xt

→ y (t) = y (0) + v_yt

→ Average velocity:
V_average = \(\frac{\left|r\left(t^{\prime}\right)-r(t)\right|}{t^{\prime}-t}=\frac{r_{12}}{\left(t_{2}-t_{1}\right)}=\frac{\Delta r}{\Delta t}\)

→ Instantaneous velocity:

→ Scalar product of A and B is
A . B = AB cos θ, where θ = angle between A and B.

→ Scalar (or Dot) product always gives a scalar quantity.

→ When A. B = 0 then A and B are perpendicular to each other.

→ A . B in component form is
A.B = A_xB_x + A_yB_y + A_zB_z.

→ Cross product of A and B is
A × B = (AB sin θ) n̂ = C
where n̂ = unit vector ⊥ to the plane containing A and B i.e. n̂ acts along C.

→ If we move anticlockwise, n is vertically upward i.e. +ve.

→ If we move clockwise, n vertically downward i.e. -ve.

→ Maximum height attained by the projectile fired at an angle 0 with the horizontal with velocity u is
H = \(\frac{\mathbf{u}^{2} \sin ^{2} \theta}{2 \mathrm{~g}}\)

→ Time of flight = T = \(\frac{2 u \sin \theta}{g}\)

→ Time of maximum height attained = Time of ascent = Time of descent = \(\frac{u \sin \theta}{g}\)

→ Horizontal range of the projectile is R = \(\frac{\mathrm{u}^{2} \sin 2 \theta}{\mathrm{g}}\)

→The range of projectile is maximum if θ = 45°.

→ Rmax = \(\frac{\mathrm{u}^{2}}{\mathrm{~g}}\)

→ When the range is maximum, the maximum height attained by the projectile (Hm) is
H_m = \(\frac{u^{2}}{4 g}=\frac{R_{\max }}{4}\)

→ For R_max , T_max = \(\frac{\mathrm{u}}{\sqrt{2} \mathrm{~g}}\)

→ When θ = 90, H_max = \(\frac{u^{2}}{2 g}\) and is twice the maximum height attained by the projectile when range is maximum.

→ For θ = 90°, Time of flight is Maximum = \(\frac{2 \mathrm{u}}{\mathrm{g}}\)

→ Horizontal range is same for two angles of projections i.e. θ and 90 – θ with the horizontal.

→ If an object is moving in a plane with constant acceleration a, then a = \(\sqrt{\mathrm{a}_{\mathrm{x}}^{2}+\mathrm{a}_{\mathrm{y}}^{2}}\)

→ If r0 be the position vector of a particle moving in a plane at time t = 0, then at any other time t, its position vector will be
r = r_o + v_ot + \(\frac{1}{2}\) at²
where v0 = its velocity at t = 0.

→ Its velocity at time t will be v = v_o + at.

→ When the object moves in a circular path at constant speed, then its motion is called uniform circular motion. The angle described by the rotating particle is called angular displacement.

→ Angular displacement, Δθ = \(\frac{\Delta l}{\mathrm{r}}\) .

→ Angular velocity, ω = \(\frac{\Delta \theta}{\Delta \mathrm{t}}\)

Instantaneous angular velocity, ω = \(\frac{\mathrm{d} \theta}{\mathrm{dt}}\)

ω = \(\frac{2 \pi}{\mathrm{T}}\) = 2πv (∵ v = \(\frac{1}{T}\))

Angular velocity (ω) of a rigid body rotating about a given axis is constant, so v is different for different particles of the body.

Angular acceleration α = \(\frac{\mathrm{d} \omega}{\mathrm{dt}}=\frac{\mathrm{d}^{2} \theta}{\mathrm{dt}^{2}}\)

Tangential acceleration is a₁ = α × r and a_t is directed along the tangent to the circular path.

→ Centripetal acceleration (a_c) is given by a_c = \(\vec{\omega}\) × v and it is directed towards the centre of the circular path. Thus acceleration of the particle is
a = a_t + a_c
then a_t ⊥ a_c
∴ |a| = \(\sqrt{a_{1}^{2}+a_{c}^{2}}\)

→ Also \(\vec{\omega}\) ⊥v as to and a are parallel to Δθ. i.e. they are directed along the axis of rotation
Hence a_c = ω v sin 90
ac = ω v = ω . rω = rω²
= \(\frac{v^{2}}{r}\)

→ Centripetal force, F_c = ma_c = \(\frac{m v^{2}}{r}\) = mrω².

→ Fc is always directed towards the centre of the circular path.

→ The Axis of rotation is perpendicular to the plane of rotation.

→ There can be no circular motion without centripetal force. Centripetal force can be a mechanical, electrical or magnetic force in nature.

→ Fc is always ⊥ to the velocity of the particle.

→ θ, ω, α are called axial vectors or pseudo vectors.

→ Tangential acceleration is equal to the product of angular acceleration and the radius of the circular path i.e. at = rα.

By going through these CBSE Class 11 Physics Notes Chapter 3 Motion in a Straight Line, students can recall all the concepts quickly.

Motion in a Straight Line Notes Class 11 Physics Chapter 3

→ Mechanics is divided into three main branches: Statics, Kinematics and Dynamics.

→ Distance is a scalar quantity.

→ Displacement is a vector quantity.

→ An object is said to be in motion if it changes its position w.r.t. its surroundings as time passes.

→ An object is said to be at rest or it does not change its position w.r.t. its surroundings as time passes.

→ Both rest and motion are relative terms.

→ Distance travelled by a moving body can never be zero or negative i.e. it is always positive.

→ Displacement can be positive, negative or zero.

→ The magnitude of displacement = distance only if a body moves in a straight line without a change in direction.

→ The magnitude of the displacement of a body is the minimum possible distance, so distance ≥ displacement.

→ Speed is a scalar quantity.

→ Velocity is a vector quantity.

→ When a body moves with variable speed, then the average speed of the body is calculated as:
Average speed = \(\frac{\text { Total distance travelled by the body }}{\text { Total time taken }}\)

→ When a body moves with variable velocity, then the average velocity of the body is calculated as:
Average velocity = \(\frac{\text { Total displacement }}{\text { Total time taken }}\)

→ Distance travelled by an object in a given time interval is equal to the area under the velocity-time graph.

→ The direction of velocity and acceleration may not necessarily be the same.

→ The velocity and acceleration of a body may not be zero simultaneously. When the body is in equilibrium, its acceleration is zero.

→ In one, two and three dimensional motions, the object changes its position w.r.t. one, two and three coordinate axes respectively.

→ At a particular instant of time, any point may be chosen as a reference or zero points.

→ The events taking place before the zero time are assigned negative number and events after zero are assigned +ve number.

→ A suitable unit of time say, second, minute or hour may be chosen. In fact, zero points of time and unit of time are chosen according to one’s convenience.

→ The position is also measured with respect to a chosen zero position or origin on the path line.

→ Positions to the right of origin are represented by a positive number and a unit.

→ The position to the left of the origin is represented by a negative number and the unit.

→ For motion in the vertical direction, we can use ‘up’ or ‘down’ instead of ‘right’ and ‘left’.

→ The position is always stated with respect to time,

→ x (t) shows that x is a function of time t.

→ The shift in position x (t’) – x (t) is called the displacement.

→ The rate of change, of displacement, is called velocity.

→ The motion in which an object covers equal distances in equal intervals of time is called uniform motion.

→ Uniform motion may be represented by a straight line parallel to the time axis in a velocity-time graph.

→ It is also represented by a straight line inclined at some angle. The magnitude of velocity is speed.

→ The velocity of a body w.r.t. another body is called its relative velocity.

→ The x-t graph is a straight line parallel to the time axis for a stationary object.

→ Uniformly accelerated motion is a non-uniform motion.

→ When the velocity of the body decreases with time it is said to be decelerated or retarded.

→ When a particle returns to the starting point, its average velocity is zero but the average speed is not zero.

→ For one dimensional motion, the angle between acceleration and velocity is either zero or 180°. It may also change with time.

→ For two dimensional motion, the angle between acceleration and velocity is other than 0° or 180°. It may also change with time.

→ If the angle between a and v is 90°, the path of motion is a circle.

→ If the angle between a and v is other than 0° or 180°, the path of the particle is a curve.

→ For motion with constant acceleration, the graph between x and t is a parabola.

→ For uniform motion, the average velocity is equal to the instantaneous velocity.

→ Statics: It deals with the law of composition of forces and with the conditions of equilibrium of solid, liquid and gaseous states of the objects.

→ Kinematics: It is the branch of mechanics that deals with the study of the motion of objects without knowing the cause of their motion.

→ Dynamics: It is the branch of mechanics that deals with the study of the motion of objects by taking into account the cause of their motion.

→ Point object: It is defined as an object having its dimensions much smaller as compared to the distance covered by it.

→ Acceleration: It is defined as the change in velocity with time i. e.

→ Speed: Theatre of covering distance with time is called speed i.e.
speed = \(\frac{\text { Distance }}{\text { Time }}\)

→ Average speed: It is the ratio of total path length traversed and the corresponding time interval.

→ Velocity: The rate of change of displacement is called velocity.

→ Average velocity: When an object travels with different velocities, its rate of motion is measured by its average velocity.
Average velocity = \(\frac{x_{2}-x_{1}}{t_{2}-t_{1}}=\frac{\Delta x}{\Delta t}\)

→ Instantaneous velocity: The velocity of the object at any particular instant of time is known as instantaneous velocity.

→ V_inst = \(\frac{\mathrm{dx}}{\mathrm{dt}}\)

→ Uniform velocity: A motion in which the velocity of the moving object is constant is called uniform and the velocity is called the uniform velocity. In uniform motion, the object covers equal distances in equal intervals of time along a straight line.

→ Relative velocity: The rate of change in the relative position of an object with respect to the other object is known as the relative velocity of that object.

→ Acceleration: The time rate of change of velocity is known as acceleration.

→ Average acceleration: It is defined as the change in velocity divided by the time interval.
a_av = \(\frac{\text { Final velocity – Initial velocity }}{\text { Change in time }}=\frac{v_{2}-v_{1}}{t_{2}-t_{1}}=\frac{\Delta v}{\Delta t}\)

→ Instantaneous acceleration: The acceleration of an object at any instant of time is called instantaneous acceleration. It is also the limiting value of average acceleration.

→ Retardation: The negative acceleration due to which the body slows down is known as deacceleration or retardation.

→ Non-uniform motion: An object is said to have non-uniform motion when its velocity changes with time even though it has a constant acceleration.

Important Formulae:
→ Displacement in time from t to t’ = x(t’) – x (t)

→ Average velocity, vav = \(\frac{\mathrm{x}\left(\mathrm{t}^{\prime}\right)-\mathrm{x}(\mathrm{t})}{\mathrm{t}-\mathrm{t}}=\frac{\Delta \mathrm{x}}{\Delta \mathrm{t}}\)

→ The relative velocity of a body A w.r.t. another body B when they are moving along two parallel straight paths in the same direction is V_AB = V_A – V_B and if they are movinig in opposite direction, then V_AB = V_A – (-V_B) = V_A + V_B.

Average Speed V_av = \(\frac{\mathrm{S}_{1}+\mathrm{S}_{2}}{\left(\frac{\mathrm{S}_{1}}{\mathrm{v}_{1}}+\frac{\mathrm{S}_{2}}{\mathrm{v}_{2}}\right)}\)
Where S₁ is the distance travelled with velocity v₁ and S₂ is the distant travelled with velocity v₂.

→ If S₁ = S₂, then vav = \(\frac{2 v_{i} v_{2}}{v_{1}+v_{2}}=\frac{2}{\frac{1}{v_{1}}+\frac{1}{v_{2}}}\)

→ Average speed of a body when it travels with speeds v₁, v₂, v₃…..v_n in time intervals t₁, t₂, t₃,… t_n, respectively is given by
V_av = \(\frac{v_{1} t_{1}+v_{2} t_{2}+v_{3} t_{3}+\ldots .+v_{n} t_{n}}{t_{1}+t_{2}+t_{3}+\ldots+t_{n}}=\frac{\sum_{i=1}^{n} v_{i} t_{i}}{\sum_{i=1}^{n} t_{i}}\)

→ Distance travelled by a body moving with uniform velocity is S = ut.

→ Velocity of an object after a time t in uniformly accelerated motion is, v = u + at.

→ Distance covered by an object after a time t in accelerated motion is, S = ut + \(\frac{1}{2}\)at².

→ Velocity of an object after covering a distance S in uniformly accelerated motion is, v² – u² = 2aS.

→ Distance covered in nth second by a uniformly accelerated object
Snth = u + \(\frac{a}{2}\)(2n – 1)

→ Total time a flight = Time of Ascent + Time of descent.

→ Time of Ascent = Time of descent.

By going through these CBSE Class 11 Physics Notes Chapter 2 Units and Measurement, students can recall all the concepts quickly.

Units and Measurement Notes Class 11 Physics Chapter 2

→ Physical Quantity = numerical value × unit = nu

→ Numerical value (n) ∝ \(\frac{1}{\text { size of unit(u) }}\)

→ Physical quantities which are independent of each other are called fundamental quantities.

→ Units of fundamental quantities are called fundamental units.

→ There are four systems of units namely FPS, CGS, MKS, and S.I. system.

→ 1 a. m.u.= 1.66 × 10^-27kg.

→ The product of n and u is called the magnitude of the physical quantity.

→ Force, thrust, and weight have the same SI unit, i.e. Newton.

→ Pressure, stress, and coefficient of elasticity have the same SI unit, i.e. Pascal.

→ The standard unit must not change with time and space. That is why the atomic standards for length and time have been defined.

→ The dimensions of many physical quantities especially those of heat, electricity, thermodynamics, and magnetism in terms of mass, length, and time alone become irrational, so SI is adopted which uses 7 basic units and two supplementary units.

→ The first conference on weights and measures was held in 1889.

→ Sevres near Paris is the headquarter of the International Bureau of Weights and Measures.

→ SI system was first adopted in the 11th general Conference of Weights and Measures in 1960.

→ S.I. system is also known as the rationalized M.K.S. system.

→ The various units of the S.I. system are rational in nature.

→ The various units of the S.I. system are coherent in nature.

→ It is wrong to say that the dimensions of force are [MLT^-2]. On the other hand, we should say that the dimensional formula for force is [MLT^-2].

→ The dimensional formula for the dimensionless physical quantity is written as [M°L°T°].

→ The dimensions of a physical quantity don’t depend on the system of units.

→ The dimensional formula is very helpful in writing the unit of a physical quantity in terms of the basic units.

→ The pure numbers are dimensionless.

→ Physical quantities defined as the ratio of two similar quantities are dimensionless.

→ The physical relations involving logarithm, exponential, trigonometric ratios, numerical factors, etc. cannot be derived by the method of dimensional analysis.

→ Physical relations involving addition or subtraction sign cannot be derived by the method of dimensional analysis.

→ If units or dimensions of two physical quantities are the same, these need not represent the same physical characteristics.

→ Torque and work have the same dimensions but have different physical characteristics.

→ Measurement is most accurate if its observed value is very close to the true value.

→ Significant figures are the number of digits up to which we are sure about their accuracy.

→ Significant figures don’t change if we measure a physical quantity in different units.

→ Significant figures retained after the mathematical operation (like addition, subtraction, multiplication, or division) should be equal to the minimum significant figures involved in any physical quantity in the given operation.

→ Error = Actual value: Observed value.

→ Absolute error: Δx_i = \(\overline{\mathrm{x}}\) – x_i

→ The absolute error in each measurement is equal to the least count of the measuring instrument.

→ Mean absolute error
Δx = \(\frac{1}{x} \sum_{i=1}^{n}\)(Δx₁)

→ When we add or subtract two measured quantities, the absolute error in the final result is equal to the sum of the absolute errors in the measured quantities.

→ When multiply or divide two measured quantities, the relative error in the final result is equal to the sum of the relative errors in the measured quantities.

→ For greater accuracy, the quantity with higher power should have the least error.

→ Smaller is the least count higher is the accuracy of measurement.

→ The relative error is a dimensionless quantity.

→ The unit and dimensions of the error are the same as that of the quantity itself.

→ The larger the number of significant digits after the decimal point in measurement, the higher is the accuracy of measurement.

→ Physical quantities: Physical quantities may be defined as the quantities in terms of which physical laws can be expressed and which can be measured directly or indirectly.

→ Subjective methods: The methods of measurement which depend on our senses are called subjective methods.

→ Objective methods: The methods of measurement which make use of scientific instruments are called objective methods.

→ Fundamental quantities: The quantities which are independent of each other and which are not generally defined in terms of other physical quantities are known as fundamental or basic quantities.

→ Derived quantities: The quantities whose defining operations are based on the fundamental physical quantities are called derived quantities.

→ Unit: A unit is defined as the reference standard of measurement.

→ If a number is without a decimal point and ends in one or more zeros, then all the zeros at the end of the number may not be significant.

→ To make the number, of Significant digits clear, it is suggested that the number may be written in exponential form.

→ For example, 20300 may be expressed as 203.00 × 10², to suggest that all the zeros at the end of 20300 are significant.

→ Fundamental or basic units: The basic units are those which can neither be derived from one another nor can be resolved into further units! For example units of length, mass and time, etc. These are 7 in number.

→ Derived units: The units of all those physical quantities which can be expressed in terms of fundamental units are called derived units. For example, units of velocity, force, and energy, etc.

→ Size of a physical quantity: The size of a physical quantity is determined by a unit and the number of times that unit is to be repeated to represent the complete quantity.
Size of a physical quantity = nu;
n = number of times the chosen unit is contained in the physical quantity,
u = size of the unit.

→ System of units: Complete set of units both for fundamental and derived quantities is known as a system of units.

→ S.I. Units: Systeme international of units, in short, is called S.I. units.
It has seven fundamental units namely

1. unit of length is meter (m),
2. kilogram (kg) unit of mass,
3. second (s) unit of time,
4. ampere (A) unit of current,
5. Kelvin (K) unit of temperature,
6. Candela (cd) unit of light intensity and
7. mol (mole) for a unit of amount of substance.

→ There are two supplementary units for measuring: (a) plane angle and solid angle. These are radian (rad) and steradian (sr) respectively.

→ θ(rad) = \(\frac{\text { arc }}{\text { radius }}=\frac{l}{r}\)

→ Ω(sr) = \(\frac{\text { surface area }}{(\text { radius })^{2}}=\frac{\Delta \mathrm{A}}{\mathrm{r}^{2}}\)

→ Length: It is defined as a measure of separation between two points in space.

→ Mass: It is the amount of substance contained in the body. Inertial mass: It is the mass of the body which is a measure of inertia F
∴ m = \(\frac{F}{a}\)

→ Gravitational mass: It is the mass of the body that determines the gravitational pull due to the earth acting on the body.
∴ m = \(\frac{W}{g}\)

→ Fermi (F): It is a unit of extremely small distances:
1 F = 10^-15 m.

→ Angstrom (A): It is the unit of length at the atomic level:
1 A = 10^-10 m ,

→ Astronomical unit (AU): It is the unit of length at a large scale:
1 A.U. = 1.496 × 10¹¹ m= 1.5 × 10¹¹ m.

→ Light year- It is defined as the distance traveled by light in one year
1 L.Y. = 9.46 × 10¹⁵ m.

→ Meter (m): Metre is the unit of length and is defined as the space occupied by 1,650,763.73 wavelengths of orange-red light emitted by krypton: 86 kept “at the triple point of nitrogen (radiation emitted due to transition between the levels 2P₁₀ and 5d₅).

→ Kilogram (kg): Kilogram is the unit of measurement of mass. It is the mass of international prototype platinum-iridium cylinders kept in the International Bureau of Weights and Measures at Sevres, France.

→ Second(s): It is the unit of time. A second is the duration of time corresponding to 9,192,631,770 vibrations corresponding to the transition between two hyperfine levels of cesium-133 atom in the ground state.

→ Ampere(A): An ampere of current is defined as the constant current, which when flowing through two straight parallel conductors of infinite length and negligible area of cross-section placed lm apart in air produces a force of 2 × 10^-7 Nm^-1.

→ Parsec: This unit is used to measure very large distances i.e., the distance between stars or galaxies.
1 Parsec = 3.08 × 10¹⁶m

→ Atomic mass unit (AMU): It is the unit of mass at the atomic and subatomic levels.
1 amu = \(\frac{\left(\text { mass of }_{6} C^{12} \text { atom }\right)}{12}\)

→ Dimensions: The dimensions of a physical quantity are the powers to which the fundamental units of length, mass and time have to be raised to obtain its units, e.g., dimensions of force [MLT^-2] are 1 in mass 1 in length and -2 in time.

→ Dimensional formula: Dimensional formula of a physical quantity is defined as the expression that indicates which of the fundamental units of mass, length, and time appear into the derived unit of that physical quantity and with what powers.

→ Dimensional equation: The equation obtained by equating the physical quantity to its dimensional formula is called the dimensional equation of that physical quantity.

→ Dimensional variables: The variable quantities which have dimensions are called dimensional variables! For example, velocity, force, momentum, etc.

→ Dimensionless variables: These are variable physical quantities that do not have dimensions. For example, relative density, specific heat, strain, etc.

→ Dimensional constants: Those constants which have dimensions are called dimensional constants. For example, gravitational constant, Planck’s constant.

→ Dimensionless constants: Those constants which do not have, dimensions are dimensionless constants. For example, all trigonometric functions, natural numbers 1, 2, 3…. π, e.

→ Significant figure: The significant figures are a measure of the accuracy of a particular measurement of a physical quantity. Significant figures in measurement are those digits in a physical quantity that are known reliably plus the one-digit which is uncertain.

→ Error: It is the difference between a true and measured value of a physical quantity.

→ Discrepancy: The difference between the two measured values of a physical quantity is known as a discrepancy.

→ Constant error: It is an error in measurements. It arises due to some constant causes such as faulty calibration on the instrument. This error remains constant in all observations.

→ Systematic error: This error is also a measurement error. The error is one that always produces an error of the same sign. This error may be due to imperfect technique, due to alteration of the quantity being measured, or due to carelessness and mistakes on the part of the observer.

→ Instrumental error: This is a constant type of error. These are errors of an apparatus and that of the measuring instruments used e.g., zero error in vernier calipers or screw gauge.

→ Error due to least count: This also is another type of constant error. The error due to the limitations imposed by the least counts of the measuring instruments comes under this heading.

→ Observational or Personal Error: This is a subheading of systematic error. This error is due to the experimental arrangement or due to the habits of the observer.

→ Error due to physical conditions: These errors are due to the experimental arrangement or due to the habits of the observer. These are also systematic errors.

→ Error due to unavoidable situations: These errors are due to the imperfectness of the apparatus or of non-availability of ideal conditions.

→ Random errors: The errors due to unknown causes are random errors.

→ Gross error: These types of errors are because of the carelessness of the observer.
These errors may be due to

• negligence towards sources of error due to overlooking of sources of error by the observer;
• the observer, without caring for least count, takes wrong observations;
• wrong recording of the observation.

→ Absolute error: The magnitude of the difference between the true value and the measured value is called absolute error.

→ A relative error: It is defined as the ratio of the mean absolute error to the true value.

→ Percentage error: The relative error expressed in percentage is percentage error.

→ Standard error: The error which takes into account all the factors affecting the accuracy of the result is known as the standard error.

→ Standard deviation: The root means the square value of deviations (the deviation of different sets of observations from the arithmetic mean) is known as standard deviation.
Standard deviation σ = \(\sqrt{\frac{\left(\mathrm{x}_{1}-\overline{\mathrm{x}}\right)^{2}+\left(\mathrm{x}_{2}-\overline{\mathrm{x}}\right)^{2}+\left(\mathrm{x}_{\mathrm{n}}-\overline{\mathrm{x}}\right)^{2}}{\mathrm{n}}}=\sqrt{\frac{\mathrm{S}}{\mathrm{n}}}\)

→ Probable error: The error calculated by using the principle of probability are probable errors. According to Bessels formula

→ Probable error e = ± 0.6745\(\sqrt{\frac{S}{n(n-1)}}\)

→ Standard error = \(\sqrt{\frac{\mathrm{S}}{n(n-1)}}\)

Important Formulae:
→ t = Size of oleic acid molecule = thickness of film of oleic acid
= \(\frac{\text { Volume of film }}{\text { Area of film }}\)

→ Inertial mass determination:
\(\frac{m_{1 i}}{m_{2 i}}=\frac{T_{1}^{2}}{T_{2}^{2}}\) where T₁ and T₂ are of the time of oscillation of inertia balance with inertial masses.

→ Gravitational mass determination:
\(\frac{\mathrm{w}_{1}}{\mathrm{w}_{2}}=\frac{\mathrm{m}_{\mathrm{g}_{1}}}{\mathrm{~m}_{\mathrm{g}_{2}}}\)
where m_g1 and m_g2 are gravitational masses.

→ Height by triangulation method:

1. The height of an accessible object, h = x tanθ, where θ = angle of elevation of the object at the point of observation at a distance x from it.
2. The height of the inaccessible object is:
   h = \(\frac{x}{\cot \theta_{2}-\cot \theta_{1}}\)
   where θ₁ and θ₂ are the angles made at two points of observation at distance x from each other.

→ Distance of stars (parallax method):
S = \(\frac{\mathrm{b}}{\theta}\), θ = Φ₁, + Φ₂, where Φ₁, and Φ₂, are the angles subtended by star on observer on Earth with an interval of 6 months.
θ = angle of parallax.
b = basis = distance between two points on the surface of earth.

→ n₂ = n₁ \(\left[\frac{\mathrm{m}_{1}}{\mathrm{~m}_{2}}\right]^{a}\left[\frac{\mathrm{L}_{1}}{\mathrm{~L}_{2}}\right]^{b}\left[\frac{\mathrm{T}_{1}}{\mathrm{~T}_{2}}\right]^{\mathrm{c}}\)

→ Distance by reflection method (Radar) is given by
d = \(\frac{c \times t}{2}\) where
c = velocity of light in vacuum
t = time in which it is covered twice.

→ d = \(\frac{\mathrm{ut}}{2}\) for Sonar, where u = velocity of sound waves.

→ Diameter of moon is D = Sθ, where θ is the angle made by the diameter of moon at the observer, S = distance of observer from the moon, D = diameter of moon or an astronomical object.

→ Radius of atom is r = \(\left(\frac{M}{2 \pi N \rho}\right)^{1 / 3}\)
Where N = Avogadro’s number
M = molecular weight of the substance
ρ = density of substance.

→ Relative error = \(\frac{\Delta \mathrm{x}}{\mathrm{x}}\)

→ % error = \(\frac{\Delta \mathrm{x}}{\mathrm{x}}\) × 100

→ Error in sum or difference form, ± Δz = ± Δp ± Δq

→ Maximum error in product or quotient form, \(\frac{\Delta z}{z}=\frac{\Delta p}{p}+\frac{\Delta q}{q}\)

→ % Error in power form,\(\frac{\Delta \mathrm{z}}{\mathrm{z}}\) × 100 = n\(\frac{\Delta \mathrm{p}}{\mathrm{p}}\) × 100

By going through these CBSE Class 11 Physics Notes Chapter 1 Physical World, students can recall all the concepts quickly.

Physical World Notes Class 11 Physics Chapter 1

→ Physics deals with nature and natural phenomenon.

→ Science is the knowledge acquired by man in an organised way.

→ The various steps involved in acquiring knowledge are:

1. systematic observations
2. reasoning
3. model making
4. a theoretical prediction.

→ The theory is the explanation of the behaviour of a physical system using a limited number of laws.

→ A theory is valid if it is able to explain satisfactorily most of the relevant measurements.

→ There is a certain amount of overlapping between Physics, Chemistry and Biology.

→ Advances in Physics are directly related to the advances in experimental observations.

→ Advances in Physics lead to the development of concepts.

→ A wide diversity in the physical world can be understood on the basis of a few concepts.

It is due to three reasons:
(a) Strict regularities and laws help in quantitative measurements.
(b) There is a small number of common and basic principles covering enormous diversities of scales of the phenomenon.
(c) It is easier to understand a phenomenon by separating important features from unimportant features.

→ The technological development of any society is very closely related to the application of Physics and other branches of science.

→ Measurements are the heart of Physics. In fact, Physics is also defined as the science of measurements.

→ Motion, energy, gravitation, properties of matter in bulk and their atomic origin, study of details of mechanical oscillations and waves, description of matter with a microscope all form a systematic study.

→ Science: An organised attempt of man to know and the knowledge he acquires is science.

→ Physics: It is the subject which deals with nature and natural phenomenon and their quantitative measurements.

→ Scientific method: Scientific method involves systematic observation, reasoning, model making and theoretical prediction altogether.

→ Theory: A scientific theory is the explanation of the natural phenomenon in terms of a limited number of laws.

→ Geocentric theory: It is a theory in which the earth is assumed to be at the centre of the universe.

→ Heliocentric theory: The sun is at the centre of the world consisting of Earth and other planets.

→ Corpuscular theory of light: Newton assumed light to be made up of corpuscles or particles.

→ Hydroelectric energy: Conversion of gravitational energy into ‘ electric energy through water.

→ Thermal power: Conversion of chemical energy of coal by burning it into electric energy.

→ Geothermal energy: It is the heat in the depth of the Earth.

→ Gravitational force: The force is an attraction between two masses is called the gravitational force. This force of attraction between the two bodies is directly proportional to the product of their masses and inversely proportional to the square of the distance between them. The constant of proportionality is called the Gravitational constant or constant of gravitation G.
F = G\(\frac{m_{1} m_{2}}{r^{3}}\)r̂
Its scalar form is F = G\(\frac{m_{1} m_{2}}{r^{2}}\)

→ Constant of gravitation ‘G’: It is equal to the force of attraction acting between two masses each of 1 kg placed 1 m apart in the air.

→ Electromagnetic force: The combined electrostatic and magnetic force between charged particles and magnetic poles is called electromagnetic force.

→ Nuclear or strong forces: The strong attractive forces between particles in a nucleus are called nuclear forces. This force can act within a distance of 10-15m. These forces are charge independent
i. e. even a proton attracts another proton.

→ Weak forces: The forces of interaction between elementary particles are weaker than the strong forces and these activities within a distance of about 10^-12 m.

Studying from CBSE Class 11th Physics Revision Notes helps students to prepare for the exam in a well-structured and organised way. Making Class 11 Physics NCERT Notes saves students time during revision as they don’t have to go through the entire textbook. In CBSE Notes, students find the summary of the complete chapters in a short and concise way. Students can refer to the NCERT Solutions for Class 11 Physics, to get the answers to the exercise questions.

Physics Class 11 NCERT Notes | Notes of Physics Class 11

Notes of Physics Class 11 | NCERT Notes for Class 11 Physics

1. Physical World Class 11 Notes
2. Units and Measurement Class 11 Notes
3. Motion in a Straight Line Class 11 Notes
4. Motion in a Plane Class 11 Notes
5. Law of Motion Class 11 Notes
6. Work, Energy and Power Class 11 Notes
7. Systems of Particles and Rotational Motion Class 11 Notes
8. Gravitation Class 11 Notes
9. Mechanical Properties of Solids Class 11 Notes
10. Mechanical Properties of Fluids Class 11 Notes
11. Thermal Properties of Matter Class 11 Notes
12. Thermodynamics Class 11 Notes
13. Kinetic Theory Class 11 Notes
14. Oscillations Class 11 Notes
15. Waves Class 11 Notes

We hope students have found these 11th Class Physics Notes Pdf Download useful for their studies. If you have any queries related to Physics Notes for Class 11 Pdf, drop your questions below in the comment box.

By going through these CBSE Class 12 Chemistry Notes Chapter 16 Chemistry in Everyday Life, students can recall all the concepts quickly.

Chemistry in Everyday Life Notes Class 12 Chemistry Chapter 16

Medicines: Medical chemistry deals with the design and synthesis of drugs based on an undertaking of how these work in our body.

Drugs are chemicals of low molecular mass (~ 100-500 μ). They interact with macromolecular targets and produce a biological response. When the biological response is effective and useful, these chemicals are called medicines and are used in the treatment, diagnosis, and prevention of diseases. In larger doses than recommended, they are potential poisons. The use of chemicals for therapeutic effect is called Chemotherapy.

Designing of a Drug: Two considerations arise

1. Drug target,
2. drug metabolism.

1. Drug target: The biological macromolecules such as carbohydrates lipids, proteins, nucleic acids with which drugs interact are called targets. The correct choice of the molecular target for a drug is important to obtain a desired therapeutic effect.

2. Drug metabolism: A drug travels through the body in order to reach the target. So its design should be such that it reaches the target without being metabolized in between. Also, after its action, it should be excreted without causing harm to the body.

Compounds from which drugs are designed are called lead compounds. These lead compounds may be obtained from natural sources such as plants, trees, bushes, venoms, and metabolites of microorganisms or they may be synthesized in order to improve drug activity and to have minimum side effects, mechanisms of drug action in the biological systems are also considered while drug designing.

Classification of Drugs:
1. On the basis of Pharmacological effect: It is useful for doctors. For example, analgesics have a pain-killing effect, antiseptics kill or arrest the growth of microorganisms.

2. On the basis of action on a particular biochemical process: All antihistamines inhibit the action of the compound histamine, which causes inflammation in the body.

3. On the basis of chemical structure: Drugs classified in this way share common structural features and often have similar pharmacological activity. For example, sulphonamides have common structural features given below and are mostly antibacterial.

(Sfructuralfratures of Suiphona mides)

4. On the basis of molecular targets: This classification is most useful for medicinal chemists. Various enzymes and receptors in the cell are some of the common drug targets.

Interaction of drugs with targets: Proteins that perform the role of biological catalysts in the body are called enzymes. Proteins that are important to a communication system in the body are called receptors. Tires enzymes and receptors serve as drug targets among others.

Enzymes as Drug Targets:
(a) Catalytical activity of enzymes: Enzymes perform two major functions:
1. The first function of an enzyme is to hold the substrate for a chemical reaction. Active sites of enzymes hold the substrate molecule in a suitable position so that it can be attacked by the reagent effectively.

Substrates bind to the amino acid residues of the protein present on the active site of the enzyme through a variety of interactions such as ionic bonding, hydrogen bonding, van der Waals interaction of dipole-dipole interaction (Fig.).

These binding interactions should be strong enough to hold the substrate long enough so that the enzyme can catalyze the reaction, but weak enough to allow the products to depart after their formation.

(a) Active site of an enzyme,
(b) substrate
(c) Substrate held in the active site of the enzyme

(a) The second function of the enzyme is to provide functional groups that will attack the substrate and carry out a chemical reaction. This function is carried out by some other amino acid residues of protein present on the active site of the enzyme.

These provide free functional groups to attack the substrate and bring about chemical reactions. For example, if amino acid, serine is present nearby the substrate held on the active site, then its – OH group is free to act as a nucleophile in the enzyme-catalyzed reaction.

(b) Interaction of drugs with enzymes: Drugs inhibit the activity of the enzymes and so are called Enzyme Inhibitors. Enzyme inhibitors can block the binding site and prevent the binding of substrate or these can inhibit the catalytical activity of the enzyme.

(c) Prevention of attachment of natural substrate in the active site by drugs: Drugs inhibit the attachment of substrate on the active site of enzymes in two different ways explained below:

Drugs compete with the natural substrate for the active sites. Such drugs are called competitive inhibitors.

(Drug and substrate competing for the active site)

2. On the other hand, some drugs do not bind to the active site. These bind to a different site of enzyme which is called the allosteric site. This binding of inhibitors at the allosteric sites changes the shape of the active site in such a way that the substrate cannot recognize it.

[Noncompetitive inhibitor changes the active site of the enzyme after binding at the allosteric site]

If the bond formed between enzyme and inhibitor is a strong covalent bond and cannot be broken easily then the enzyme is blocked permanently. The body then degrades the enzyme inhibitors complex and synthesizes new enzymes.

Receptors as Drug Targets:
→ Location of receptor in the animal cell: Receptors are proteins that are crucial to the body’s communication process. The majority of these are embedded in cell membranes.

Receptor proteins are embedded in the cell membrane in such a way that their small part possessing active site projects out of the surface of the membrane and opens on the outer region of the cell membrane.

→ Transfer of message into the cell by receptors: Neurotransmitters communicate messages in the body between the 3 neurons and that between neurons to muscles. These chemical messengers are received at the binding site of the receptor protein. To accommodate messenger, the shape of the receptor changes. This brings about the transfer of the message into the cell. Thus, chemical messenger gives a message to the cell without entering the cell.

Two types of chemical messengers are involved in the message transfer:

1. Hormones
2. neurotransmitters

1. Hormones: Adrenaline (epinephrine) is an example of hormone. It is released from the adrenal medulla in situations of stress or danger.

2. Neurotransmitters are small molecules such as acetylcholine, dopamine, and serotonin.


→ Interaction of Drugs: Receptors that interact with one specific chemical messenger may differ slightly in their binding sites.

For example, there are two types of adrenergic receptors named a-adrenergic receptors and β-adrenergic receptors. These differ slightly in the structure of their binding sites, but both of these receptors can bind epinephrine.

Drugs that bind to the receptor site and inhibit its natural function are called antagonists. There are other types of drugs that mimic the natural messenger by switching on the receptor. They are called agonists.

→ Side-effects caused by drugs: Side effects are caused when a drug binds to more than one type of receptor, e.g., the serotonin receptor is a target for some anti-depressant drugs. Side effects can arise if the drug interacts with histamine or acetylcholine.

Types erf Drugs:
1. Antacids: If acid is produced in excess in the stomach, it causes irritation and pain and in severe cases, ulcers are produced. Histamine stimulates the secretion of pepsin and hydrochloric acid. A drug like cimetidine (Tagamet) and ranitidine (Zantac) was designed to prevent the interaction of histamine with the receptors present in the stomach wall. This resulted in the release of a lesser amount of acid.

2. Antihistammines: Histamine is a potent vasodilator. It has various functions. It contracts the smooth muscles in the bronchi and gut and relaxes other muscles. It is also responsible for the nasal congestion associated with common colds and allergic response to pollen. Synthetic drugs brompheniramine (Dimetapp) and terfenadine (Seldane) act as antihistamines.

The above-mentioned antihistamines do not affect the secretion of acid in the stomach. It is because that antiallergic and antacid drugs work on different receptors.

3. Neurologically Active Drugs: Tranquilizers and analgesics are neurologically active drugs.

These affect the message transfer mechanism from the nerve to the receptor.
(a) Tranquilizers are a class of compounds used for the treatment of stress, mild and severe mental diseases. They relieve stress, anxiety irritability, and excitement by inducing a sense of well-being.

→ They act on the central nervous system (CNS): Noradrenaline is one of the neurotransmitters that plays role in mood changes. If its level is low for some reason, the signal sending activity becomes low and the person suffers from depression.

Antidepressant drugs, in such cases, inhibit the enzymes which catalyze the degradation of noradrenaline. If the enzyme is inhibited, this important neurotransmitter is slowly metabolized and can activate its receptor for longer periods of time, thus countering the effect of depression. Iproniazid and phenelzine are two such drugs.

Some tranquilizers namely, Chlorodiazepoxide and Meprobamate are relatively mild tranquilizers suitable for relieving tension. Equanil is used in controlling depression and hypertension.


→ Barbiturates: The derivatives of barbituric acid are hypnotic- sleep-producing agents. Some of them are Veronal, Valium and Serotonium.

(b) Analgesics: are the drugs that reduce or abolish pain without causing impairment of consciousness, mental confusion, or some other disturbance of the nervous system.

They are of two types:
1. Non-narcotic (non-addictive) drugs: Aspirin and paracetamol belong to the class of non-addictive analgesics. These drugs have many other effects such as reducing fever (antipyretic) and preventing platelet coagulation. Aspirin is helpful to prevent heart attacks,

2. Narcotic analgesics: like morphine, heroin, codeine relieve pain and produce sleep in medicinal doses, and in excess are fatal. These analgesics are chiefly used for the relief of post-operative pain, cardiac pain, and pains of terminal cancer and in childbirth.

4. Antimicrobials: Disease may be caused by bacteria, viruses, etc. P. Ehrlich who developed the medicine Salvarsan for the treatment of syphilis found that the -As = As – linkage present in arsphenamine (salvarsan) resembles the -N = N- linkage present in azo-dyes in the sense that N atom is present in place of As. He was successful in 1932 in preparing the first effective antibacterial agent Prontosil which resembles the structure of the compound salvarsan.

[The structures of salvarsan and prontosil and azo dye showing structural similarity]

This led to the study of the relation between structure and activity. It was found that part of the proposal molecule (shown in the box) in the form of p-amino benzene sulphonamide (Sulphanilamide) has antibacterial activity. The led to the discovery of Sulpha drugs.

Antimicrobials control microbial diseases in three ways:
(a) a drug that kills the organism in the body (bactericidal).
(b) a drug that inhibits or arrests the growth of organisms (bacteriostatic) and
(c) increasing immunity and resistance to infection in the body,

5. Antibiotics: It is a substance (produced wholly or partly by chemical synthesis) that in low concentration inhibits the growth or destroys microorganisms by intervening in their metabolic processes.

The first antibiotic discovered by Alexander Fleming’s Penicillin from the mold Penicillium Notatum.

The antibiotics can be either bactericidal or bacteriostatic.

Bactericidal	Bacteriostatic
Penicillin	Erythromycin
Aminoglycosides	Tetracycline
Ofloxacin	Chloramphenicol

Broad Spectrum antibiotics are medicines effective against several types of harmful microorganisms, e.g., tetracycline, chloramphenicol.

6. Antiseptics and disinfectants: Antiseptics and disinfectants are also the chemicals which either kill or prevent the growth of microorganism.

Antiseptics are applied to living tissues such as wounds, cuts, ulcers, and diseased skin surfaces. Examples are Furacine, Soframicine, etc. Dettol is a mixture of Chloroxylenol and terpineol. Bithinol is added to soaps to impart antiseptic properties. Iodine is a powerful antiseptic. Its 2-3% solution in alcohol-water solution is known as tincture of iodine. It is applied to wounds. Iodoform is also used as an antiseptic for wounds. Boric acid (H3P03) in dilute solution (aqueous) is a weak antiseptic for the eyes.

Disinfectants are applied to inanimate objects such as floors, drainage systems, instruments, etc. The same substance can act as an antiseptic as well as a disinfectant by varying the concentration. For example, 0.2 percent situation of phenol is an antiseptic while it’s one percent solution is disinfectant.

Chlorine in the concentration of 0.2 to 0.4 ppm and S02 in very low concentration are disinfectants.

7. Antifertility Drugs: Norethindrone is an example of synthetic progesterone (a type of hormone) derivative most widely used as an antifertility drug for birth control. The estrogen derivative is used in combination with progesterone derivative is ethynylestradiol (Novestrol).

→ Chemicals in Food: To enhance the shelf life of food to make it more appealing and sometimes more nutritive, chemicals are added to it.

They are:

1. Food colors,
2. Flavors and sweeteners,
3. Fat emulsifiers and stabilizing agents,
4. Flour improvers antistaling agents and bleaches,
5. Antioxidants,
6. Preservatives,
7. Nutritional supplements such as minerals, vitamins, and amino acids.

Except for category (7), none of the chemical additives have any nutritive value.

→ Artificial Sweetening agents: Ortho-Sulphobenzimide (saccharine)

is an artificial sweetener and mass/mass, it is 550 times as sweet as cane sugar. It is excreted from the body in the urine unchanged and appears to be entirely harmless and inert and so is of great value to diabetic persons and people who need to control the intake of calories.

Other artificial sweeteners are aspartame (100 times sweet as sugar), sucralose (600 times) alitame (2000 times as sweet as sugar).

→ Preservatives: In addition to class I preservatives like salts, sugar, and vegetable oils, the most common class II preservative is sodium benzoate

which is used in limited quantities and is metabolized in the body.

→ Chemistry of Cleansing Agents:
1. Soaps: Soaps are sodium or potassium salts of long-chain fatty acids, e.g., stearic acid, oleic acid, and palmitic acid. Soaps are obtained by the saponification of triglycerides of fatty acids.

Potassium soaps are softer than sodium soaps.

Types of Soaps: Toilet Soaps are prepared by using better grades of fats and oils and excess alkali is removed. Colour and perfumes are added. Transparent Soap is made by dissolving the soap in ethanol and then evaporating the excess solvent.

In medicated soaps, substances of medicinal value are added. ! Shaving soaps contain glycerol to prevent rapid drying. Laundry soaps t contain fillers like sodium proximate, sodium silicate borax, and sodium \ carbonate.

Soaps do not work in hard water as soaps react with Ca²⁺ and Mg²⁺ ions present in hard water to produce curdy precipitate or scum,

2. Soapless detergents: Soapless detergents are cleansing agents; which have all the properties of soaps, but they actually do not contain; soap. They are useful in hard water also.

Synthetic detergents are mainly of three types:

1. Anionic detergents
2. Cationic detergents
3. Non-ionic detergents

1. Anionic Detergents are sodium salts of sulfonated long-chain alcohols.

In anionic detergents, the anionic part of the molecule is involved in the cleansing action.

2. Cationic Detergents: Cationic detergents are acetates, chlorides, or bromides of quaternary ammonium salts. An example is cetyltrimethylammonium bromide:

Cationic detergents are expensive and due to their germicidal properties, they are used as hair conditioners.

3. Non-ionic Detergents: Stearic acid reacts with polyethylene glycol to form non-ionic detergents.

Liquid dishwashing detergents are non-ionic types. Detergents containing highly branched hydrocarbon chains are not easily biodegradable.

By going through these CBSE Class 12 Chemistry Notes Chapter 15 Polymers, students can recall all the concepts quickly.

Polymers Notes Class 12 Chemistry Chapter 15

Polymers are macromolecules having high molecular mass [10³ – 10⁷ p]. They are formed by joining repeating structural units on a large scale. The repeating structural units are derived from some simple and reactive molecules known as monomers and are linked to each other by covalent bonds. The process of the formation of polymers from respective monomers is called polymerisation.

Classification of Polymers:
A. Based on the source.

1. Natural Polymers: These are found in plants and animals. Examples are proteins, cellulose, starch, resins and rubber.
2. Semi-synthetic Polymers: Cellulose acetate (rayon) and cellulose nitrate are examples of this category.
3. Synthetic Polymers: Polyethene; nylon 6, 6; Buna-S are examples of man-made polymers.

B. Based on the structure of Polymers:
1. Linear Polymers: These polymers Consist of long and straight-chain repeating units derived from the monomers. The examples are high-density polyethene, polyvinyl chloride (PVC) etc. These are schematically represented as

2. Branched Chain Polymers: These polymers contain linear chains having some branches, e.g., low-density polyethene.

3. Cross-linked or Network Polymers: These are usually formed from bifunctional and trifunctional monomers, e.g., bakelite, melamine etc.

C. Classification Based on mode of Polymerisation:
1. Addition Polymers: The addition polymers are formed by the repeated addition of monomer molecules possessing double or triple bonds, e..g, the formation of polyethene from ethene and polypropene from propene. In addition, polymers obtained from the same monomer are called Homopolymers, e.g., Polyethene.

If two different units of monomers get added, they are called copolymers, e.g., Buna-S, Buna-N,

2. Condensation Polymers: The condensation polymers are formed by repeated condensation reaction between two monomeric units having different bifunctional and trifunctional groups with the elimination of small molecules like water, alcohol, hydrogen chloride etc. The formation of Nylon 6,6 is an example.

D. Classification based upon molecular forces:
1. Elastomers: These are rubber-like solids with elastic properties. The polymer chains are held together by weak intermolecular forces. They can be easily stretched. Examples are Buna-S, Buna-N, Neoprene etc.

2. Fibres: The intermolecular forces between the chains are strong hydrogen bonds. They have large tensile strength and are used to form thread forming crystalline solids. The examples are Nylon 6, 6 and polyesters.

3. Thermoplastic Polymers: In these polymers, the intermolecular forces are intermediate between those of elastomers and fibres. In these polymers, there is cross-linking between the chains. They soften on heating and harden on cooling. Common examples are polyethene, polystyrene polyvinyls etc.

4. Thermosetting Polymers: These polymers are cross-linked or heavily branched molecules, which on heating undergo expensive cross-linking in moulds and become infusible. They cannot be reused again. Common examples are bakelite and urea-formaldehyde resins etc.

E. Classification based on Growth Polymerisation: The addition and condensation polymers are nowadays also referred to as chain-growth polymers and step-growth polymers depending upon the type of polymerisation mechanism they undergo during their formation.

Types of Polymerization:
1. Addition Polymerization or Chain growth Polymerization: Here molecules of the same or different monomers add together on a large scale to form a polymer. It can proceed through the formation of free radicals or ionic species.
(a) Free Radical Mechanism: A variety of alkenes or dienes and their derivatives are polymerised in the presence of a free radical generating initiator (catalyst) like benzoyl chloride.

It consists up of the following three steps.
1. Chain-initiation Step:

2. Chain propagating step:

3. Chain terminating step:

(b) Preparation of some important Addition Polymers:
1. Polyethene: There are two types of polyethenes as given below:
1. Low-Density Polyethene (LDPE]:

It is chemically inert and tough, but flexible and a poor conductor of electricity. It is used in the insulation of electric wires and the manufacture of squeeze bottles, toys and flexible pipes.

2. High-Density Polyethene (HDPE):

It has a high density. It is also chemically inert and tougher and harder. It is used for making buckets, dustbins, bottles and pipes.

2. Polytetrafluoroethene (Teflon):

Chemically inert, it is resistant to attack by corrosive reagents. Used for making oil seals, gaskets and non-stick surface coated utensils.

3. Polyacrylonitrile:

It is used as a substitute for wool in making fibres like Orlon or Acrilan.

→ Condensation Polymerization or Step-Growth polymerization: It involves a repetitive condensation reaction between two bifunctional monomers. It may result in the loss of simple molecules as H₂O, alcohol etc.

1. Polyamides: Preparation of Nylons
1. Nylon 6,6:

It is used in making sheets, bristles for brushes and in the textile industry.

2. Nylon 6: It is obtained by heating caprolactam with water at high temperature.

Nylon 6 is used for the manufacture of tyre cords, fabrics and ropes.

2. Polyesters: These are the polycondensation products of dicarboxylic acids and diols. The formation of terylene or dacron by the reaction between ethylene glycol and terephthalic acid is an example.

Dacron fibre (terylene) is crease-resistant and is used in blending with cotton and wool fibres and also as glass reinforcing materials in safety helmets etc.

3. Phenols formaldehyde polymer (Bakelite and related polymers): Phenol reacts with formaldehyde in the presence of dil. acid or base.

Novolac (used in paints) on heating with HCHO undergoes cross-linking to form an infusible solid mass called bakelite

It is used for making combs, photograph records, electrical switches and handles of various utensils.

4. melamine-formaldehyde polymers: It is obtained by the condensation polymerisation of melamine and formaldehyde.

It is used in the manufacture of unbreakable cups and plates.

Copolymerization: A mixture of 1,3-butadiene and styrene form a copolymer: Butadiene-Styrene copolymer.

1. Natural rubber: It possesses elastic properties. It is a linear polymer of isoprene (2-methyl-l, 3-butadiene).

It is also called cis-1, 4-polyisoprene. It consists of various chains held together by weak van der Waals forces and has a coiled structure.

→ Vulcanisation of Rubber: To improve upon the physical properties of natural rubber, its vulcanisation is carried out. It consists of heating a mixture of raw rubber with sulphur and an appropriate additive at a temperature range between 373-415 K. On vulcanization sulphur forms cross-links at the reactive sites of double bonds and the rubber gets Stiffened. The probable structure of vulcanised rubber is:

→ Synthetic Rubber: Synthetic rubbers are either homopolymers of 1, 3-butadiene derivatives or are copolymers of 1, 3-hutadíene or its derivatives with another unusual rated monomer.

1. Neoprene: It has superior qualities to natural rubber. It has better resistance to vegetable and mineral oils. It is used for the manufacture of conveyor belts, gaskets and hoses.

2. Buna-N: It is a copolymer of 1,3-butadiene and acrylonitrile in the presence of a peroxide catalyst.

It is resistant to the action of petrol, lubricating oil and organic St .h ents. It is used is making oil seals tank living etc.

→ Molecular Mass of Polymers: Polymer properties are closely related to their molecular mass, size and structure. Its molecular mass is always expressed as an average.

It can be determined by chemical and physical methods.

1. Weight-average molecular mass
2. Number-average molecular mass.

→ Biodegradable Polymers: A large number of polymers are non-biodegradable and are the reuse for environmental pollution. Nowadays, certain new biodegradable synthetic polymers have been designed and developed. Aliphatic polyesters are one of the important class of biodegradable polymers, e.g.,

→ Poly β-hydroxybutyrate-co-β-hydroxy valerate (PHBV): It is obtained by the copolymerisation of 3-hydroxybutyric acid and 3-hydroxy pentanoic acid.

PHBV undergosbateria1 degradation in the environment.

→ Nylon-2-Nylon 6: It is an alternating polyamide copolymer of glycine (H₂N—CH₂—COOH) and aminocaproic acid. (H₂N (CH₂)₅ COOH) and is biodegradable.

Some other commercially important Polymers along with their structures and uses are given below in the table:

By going through these CBSE Class 12 Chemistry Notes Chapter 14 Biomolecules, students can recall all the concepts quickly.

Biomolecules Notes Class 12 Chemistry Chapter 14

Carbohydrates: Most common examples of carbohydrates are glucose, fructose, cane sugar, starch etc. Most of them have a general formula C_x (H₂O)_y. Earlier they were considered hydrates of carbon. For example, glucose C₆H₁₂O₆ fits into this general formula C₆(H₂O)₆ But even acetic acid (CH₃COOH) fits into this general formula C₂(H₂O) and it is not a carbohydrate. Similarly, rhamnose, C₆H₁₂O₅ is a carbohydrate but does not fit into this definition.

Chemically, the carbohydrates may be defined as optically active polyhydroxy aldehydes or ketones or the compounds which produce such units on hydrolysis.

They are classified as:

1. Sugars: They are sweet in taste and water-soluble, e.g. glucose, fructose, sucrose.
2. Non-sugars: They are tasteless and water-insoluble, e.g., starch, cellulose. Carbohydrates are systemically classified as:

1. Monosaccharides: A carbohydrate that cannot be hydrolysed further to give simpler units of polyhydroxy aldehydes or ketones is called monosaccharides. Glucose (C6H1206) is an aldohexose and fructose (C6H1206) is a ketohexose.

2. Oligosaccharides: Carbohydrates that yield two to ten monosaccharides on hydrolysis are called oligosaccharides.
(a) Disaccharides: They hydrolyse to give two units of monosaccharides. They include sucrose, maltose, lactose.

(b) Trisaccharides: They yield three units of monosaccharides on hydrolysis, e.g. C₁₈H₃₂O₁₆ (raffinose).
(c) Tetrasaccharides: Yields four units of monosaccharides on hydrolysis, e.g. stachyose C₂₄H₄₂O₂₁

2. Polysaccharides: They yield a large number of monosaccharide units on hydrolysis: Common examples are starch, cellulose. They are not sweet in taste.

Reducing sugars are those which reduce Fehling’s solution and Tollen’s reagent. All monosaccharides whether aldoses and ketoses are reducing sugars.

Sugars that do not reduce Fehling solution or Tollen’s reagent are termed as non-reducing e.g., sucrose.

→ Monosaccharides: They contain three to seven carbon atoms. If they contain an aldehyde group (- CHO), they are termed aldoses. If they contain a keto group (C = O), they are termed ketoses.

Different Types of Monosaccharides:

1. Glucose:
Preparation:
(a) From Sucrose (Cane Sugar)

(b) From Starch:

→ Structure of Glucose: It is an aldohexose and is also known as dextrose. Its structure (open chain) is

Evidence in favour of the above structure:

1. Its molecular formula was determined to be C₆H₁₂O₆.
2. On heating (prolonged) with HI, it formed an n-hexane suggesting that all the 6 carbon atoms are in a straight chain.
   
3. It reacts with hydroxylamine to form an oxime and adds a molecule of hydrogen cyanide (HCN) to give cyanohydrin showing the presence of a carbonyl group in it,
   
4. Glucose is oxidised to gluconic acid by mild Oxidizing agent Br. water, confirming that a carbonyl group is an aldehyde group.
   
5. Acetylation with acetic anhydride gives glucose pentaacetate which confirms the presence of five – OH groups attached to 5 different C atoms.
   
6. on oxidation with nitric acid, glucose well as gluconic acid both yield a dicarboxylic acid, saccharic acid indicating the presence of -CH₂OH group in it in addition to an aldehyde.
   

The exact spatial arrangement of different – OH groups was given by Fischer. Its exact configuration is correctly represented by I. Gluconic acid is II and Saccharic acid is III.

Glucose is correctly named as D (+) glucose. ‘D’ represents the configuration whereas (+) represents the dextro-rotatory nature of it. The meaning of D- and L- notations is given as follows:

[Note: It may be remembered that ‘D’ and ‘L’ notations have nothing to do with the optical activity of the compound.]

The letters ‘D’ or ‘L’ before the name of any compound indicate the relative configuration of a particular stereoisomer. This refers to their relationship with a particular isomer of glyceraldehyde. Glyceraldehyde contains one asymmetric carbon atom and exists in two enantiomeric forms as shown below.

All those compounds which can be chemically correlated to (+) isomer of glyceraldehyde are said to have D-configuration whereas those which can be correlated to (-) isomer of glyceraldehyde are said to have L—configuration.

For assigning the configuration of monosaccharides, it is the lowest asymmetric carbon atom (as shown below) which is compared. As in (+) glucose, —OH on the lowest asymmetric carbon is on the right side which is comparable to (+) glyceraldehyde, so it is assigned D-configuration. For this comparison, the structure is written in a way that most oxidised carbon is at the top.

Cyclic Structure of Glucose

The structure (I) of glucose explained most of its properties but the following reactions and facts could not be explained by this structure.

1. Despite having the aldehyde group, glucose does not give 2,4- DNP test, Schiff’s test and it does not form the hydrogen sulphite addition product with NaHSO₃.
2. The pentaacetate of glucose does not react with hydroxylamine indicating the absence of the free -CHO group.
3. Glucose is found to exist in two different crystalline forms which are named a and b. The a-form of glucose (m.p. 419 K) is obtained by crystallization from a concentrated solution of glucose at 303 K while the (i-form (m.p. 423 K) is obtained by crystallisation from hot and saturated aqueous solution at 371 K,

This behaviour could not be explained by the open-chain structure (I) for glucose. It was proposed that one of the -OH groups may add to the -CHO group and form a cyclic hemiacetal structure. It was found that glucose forms a six-membered ring in which -OH at C-5 is involved in a ring formation. This explains the absence of -CHO group and also the existence of glucose in two forms as shown below. These two cyclic forms exist in equilibrium with an open-chain structure.

The two cyclic hemiacetal forms of glucose differ only in the configuration of the hydroxyl group at Cl, called anomeric carbon (the aldehyde carbon before cyclization). Such isomers, i.e., a-form and b-form, are called anomers.

The six-membered cyclic structure of glucose is called the pyranose structure (α- or β-), in analogy with pyran. Pyran is a cyclic organic compound with one oxygen atom and five carbon atoms in the ring. The cyclic structure of glucose is more correctly represented by Haworth structure as given below:

II. Fructose
Fructose is an important ketohexose. It is obtained along with glucose by the hydrolysis of disaccharide, sucrose. It has a ketonic group at C – 2. It belongs to D-series and is a laevorotatory compound. Therefore, it is written as D – (-) fructose. Its open-chain structures are given below:

→ It differs from glucose only at C – 1 and C – 2. Its furanose form (cyclic) is:

→ The cyclic structures of two anomers of fructose as represented by Haworth are given below:

Disaccharides:
1. Sucrose: Sucrose on hydrolysis gives an equimolar mixture of D – (+) – glucose and D – (-) fructose.

Sucrose is a non-reducing sugar. Therefore, it has a glucoside linkage between C₁ of α-glucose and C₂ of β-fructose.

or

Sucrose is dextrorotatory but after hydrolysis gives dextrorotatory glucose and laevorotatory fructose. Since the laevorotation of fructose (- 92.4°) is more than the dextrorotation of glucose (+ 52.5°), the mixture is laevorotatory. Thus hydrolysis of sucrose brings about a change in the sign of rotation, from Dextro (+) to leave (-) and the product is named as invert sugar.

II. Maltose: Another disaccharide, maltose is composed of two α-D-glucose units in which C₄ of one glucose (I) is linked to C₄ of another glucose unit (II). Hie free aldehyde group can be produced at C₁ of second glucose in solution and it shows reducing properties, so it is a reducing sugar.

II. Lactose: It is more commonly known as milk sugar since this disaccharide is found in milk. It is composed of (β-D-galactose and β-D- glucose. The linkage is between C₄ of galactose and C₄ of glucose. Hence it is also a reducing sugar.

Polysaccharides: Polysaccharides contain a large number of monosaccharide units joined together by glycosidic linkages.
I. Starch: Starch is the main storage polysaccharide of plants. It is a polymer of a-glucose and consists of two components 15-20% of water-soluble Amylose and Amylopectin which is water-insoluble and constitutes about 80-85% of starch. Their structures have been given below:

II. Cellulose: Cellulose occurs exclusively in plants. It is a predominant constituent of the cell walls of plant cells. Cellulose is a straight-chain polysaccharide composed of only β-D-glucose units which are joined by the glycosidic linkage between C₁ of one glucose unit and C₄ of the next glucose unit.

III. Glycogen: The carbohydrates are stored in the animal body as glycogen. It is also known as animal starch because its structure is similar to amylopectin and is more highly branched.

→ Proteins: Proteins are the most abundant biomolecules of the living system. Chief sources of proteins are milk, cheese, pulses, peanuts, fish and meat etc. They are required for the growth and maintenance of the body. All proteins are polymers of a-amino acids.

→ Amino acids: Amino acids contain an amino (- NH₂) and carboxyl (- COOH) functional groups.

→ Classification of Amino acids: Amino acids are classified as acidic, basic or neutral depending upon the relative number of amino and carboxyl groups in their molecule. An equal number of amino and carboxyl groups makes it neutral; more amino than carboxyl groups makes it basic and more carboxyl groups as compared to amino groups makes it acidic.

The amino acids, which can be synthesized in the body, are known as non-essential amino acids. On the other hand, which cannot be synthesized in the boxy and must be obtained through diet, are known as essential amino acids (marked with an asterisk in Table below).

Amino acids are usually colourless, crystalline solids. These are water-soluble, high melting solids and behave like salts rather than simple amines or carboxylic acids. This behaviour is due to the presence of both an acidic (carboxyl group) and a basic (amino group) group in the same molecule. In an aqueous solution, the carboxyl group can lose a proton and the amino group can accept a proton, giving rise to a dipolar ion known as a zwitterion. This is neutral but contains both positive and negative charges.

In zwitterionic form, amino acids show amphoteric behaviour as they react both with acids and bases.

Except for glycine, all other naturally occurring a-amino acids are optically active. These exist both in D and L forms. Most naturally occurring amino acids have L-configuration. L-Amino acids are represented by writing the – NH₂ group on the left hand.

Table: Natural Amino Acids,



→ Structures of Proteins: Proteins are the polymers of a-amino adds linked through peptide bond or peptide linkage.

If a third amino acid combines with a dipeptide, the product is called a tripeptide. When the number of such amino acids is more than 10, then the products are called polypeptides. A polypeptide with more than 100 units of amino acid residues, having a molecular mass higher than 10,000 u is called a protein.

Proteins can be classified into two types:
(a) Fibrous proteins: When the polypeptide chains run parallel and held together by hydrogen and disulphide bonds, then a fibre-like structure is formed. Such proteins are generally insoluble in water.

(b) Globular proteins: This structure results when the chains of polypeptides coil around to give a spherical shape. These are usually soluble in water.

Insulin and albumins are common examples.
1. Primary structure of Proteins: Proteins may have one or more polypeptide chains. Each polypeptide is a protein that has amino acids linked with each other in a specific sequence and it is this sequence of amino acids that are said to be the primary structure of that protein.

2. Secondary structure of Proteins: The secondary structure of a protein refers to the shape in which a long polypeptide chain can exist. They are found to exist in two different types of structures, viz., a-helix and P-pleated sheet structure.

3. The tertiary structure of protein represents overall folding of the polypeptide chains i.e., further folding of the secondary structure. It gives rise to two major molecular shapes viz. fibrous and globular. The main forces which stabilise the 2° and 3° structures of proteins are hydrogen bonds, disulphide linkages, van der Waals and electrostatic forces of attraction.

4. Quaternary Structure of Proteins: Some of the proteins are composed of two or more polypeptide chains referred to as sub-units. The spatial arrangement of these subunits with respect to each other is known as a quaternary structure.

A diagrammatic representation of all these four structures is given in the figure below:

→ Denaturation of Proteins: When a protein in its native form is subjected to physical change like change in temperature or chemical change like change in pH, the hydrogen bonds are disturbed. The protein loses its biological activity. This is called denaturing of proteins, 2° and 3° structures are destroyed, but 1° structure remains intact. The coagulation of egg white on boiling is a common example.

→ Enzymes: The enzymes are biological catalysts produced by living cells that catalyse biochemical reactions. The enzymes differ from other types of catalysts in being highly specific and selective.

→ Mechanism of Enzyme Action: Enzymes, like catalysts, are needed only in small quantities and reduce the magnitude of activation energy of the activated complex. For example, the activation energy for acid hydrolysis of sucrose is 6.22 kJ mol^-1 which is reduced to 2.15 kJ mol^-1 when hydrolysed by the enzyme sucrase.

→ Vitamins: Certain organic compounds are required in small amounts in our diet but their deficiency in the body causes specific diseases. These compounds are called vitamins. In small quantities in the diet perform specific biological functions for normal maintenance of optimum growth and health of the organism.

Classification of Vitamins:

1. Fat-soluble Vitamins: Vitamins like A, D, E and K are fat or oil-soluble, but insoluble in water. They are stored in the liver and adipose tissues.
2. Water-soluble Vitamins: B group Vitamins and Vitamin C are soluble in water. They (except vitamin B12) cannot be stored in a body.

→ Nucleic acids: The particles in the nucleus of the cell, responsible for heredity, are called chromosomes which are made up of proteins and another type of biomolecules called nucleic acids. They are mainly of two types, deoxyribonucleic acid (DNA) and ribonucleic acid (RNA). Since nucleic acids are long-chain polymers of nucleotides, so they are also called polynucleotides.

→ Chemical composition of Nucleic acids: Complete hydrolysis of DNA (or RNA) yields a pentose sugar, phosphoric acid and nitrogen

Table: Vitamins, their sources and their deficiency diseases:

containing heterocyclic compounds called bases. In DNA molecules, the sugar part is β-D-2-deoxyribose whereas, in the RNA molecule, it is β-D- ribose.

DNA contains four bases viz. adenine (A), guanine (G), cytosine (C) and thymine (T). RNA also contains four bases, the first three bases are A, G and C (as in DNA), but the fourth base is Uracil (U).

→ Structure of.Nucleic acids: A unit formed by the attachment of a base to the 1′ position of sugar is known as a nucleoside. In nucleosides, the sugar carbons are numbered as 1′, 2′, 3′ etc in order to distinguish these from the bases (Fig. (a) below). When nucleoside is linked to phosphoric acid at 5′-position of sugar moiety we get a nucleotide (Fig. (b) below)

(a) Structure of a nucleoside
(b) Structure of a nucleotide.

Nucleotides are joined together by phosphodiester linkage between 5′ and 3′ carbon atoms of the pentose sugar. The formation of a typical dinucleotide is:

(Formation of a dinucleotide)

A simplified version of the nucleic acid chain is shown below:

RNA molecules are of three types and they perform different functions. They are named messenger RN A (m-RNA), ribosomal RNA (rRNA) transfer RNA (f-RNA).

DNA Fingerprinting is now used:

• in forensic laboratories for the identification of criminals.
• to determine the paternity of an individual.
• to identify the dead bodies in an accident by comparing the DNAs of parents or children.
• to identify racial groups to rewrite biological evolution.

Biological Functions of Nucleic Acids: DNA is the chemical basis of heredity and may be regarded as the reserve of genetic information. DNA is exclusively responsible for maintaining the identity of different species of organisms over millions of years. A DNA molecule is capable of self-duplication during cell division, and identical DNA strands are transferred to daughter cells.

Another important function of nucleic acids is the protein synthesis in the cell. Actually, the proteins are synthesised by various RNA molecules in the cell but the message is if the synthesis of a particular protein is present in DNA.

The first one is called Replication and the second one is called protein synthesis.

1. Replication: The process by which a single DNA molecule produces two identical copies of itself is called cell division or replication. Replication of DNA is an enzyme catalysed process.
2. Synthesis of Proteins: Another important function of DNA is the synthesis of proteins. In fact, DNA may be regarded as the instrument manual for the synthesis of all the proteins present in a cell.

The DNA directed synthesis of proteins occurs in the following two steps:

1. Transcription,
2. Translation

1. Transcription: It involves copying of DNA base sequence into an RNA molecule called the messenger RNA (m RNA).

2. Translation: The mRNA directs protein synthesis in the cytoplasm of the cell with the help of r RNA and t RNA. The process is called translation.