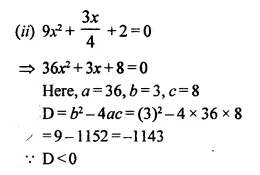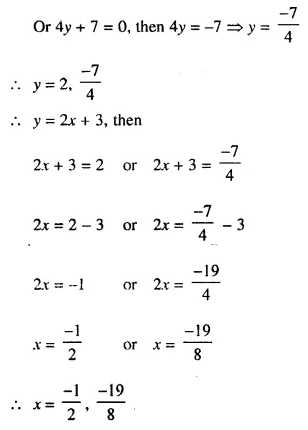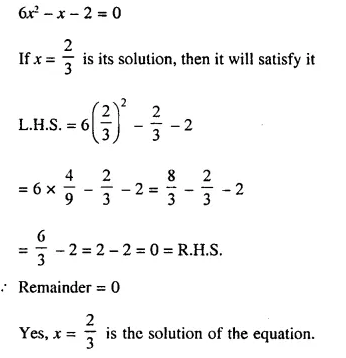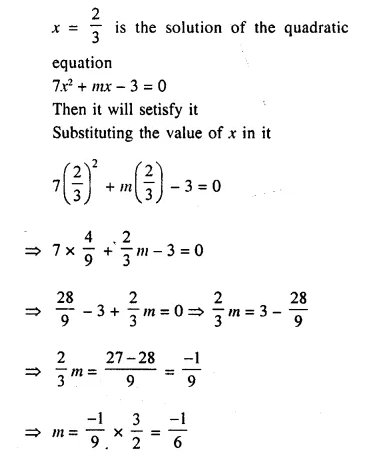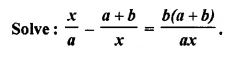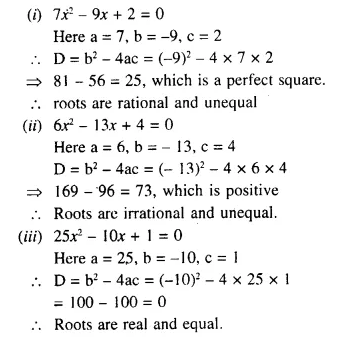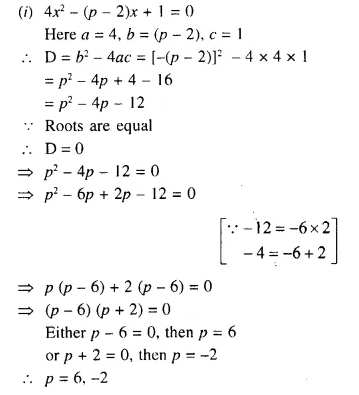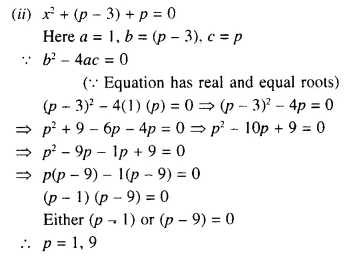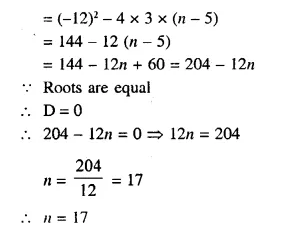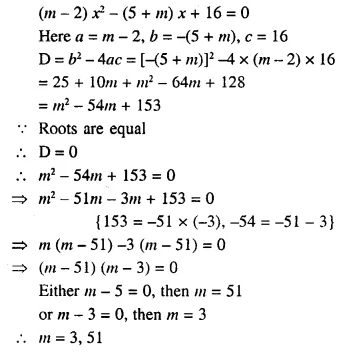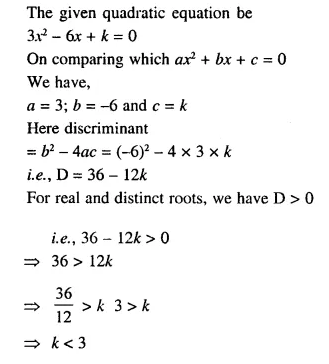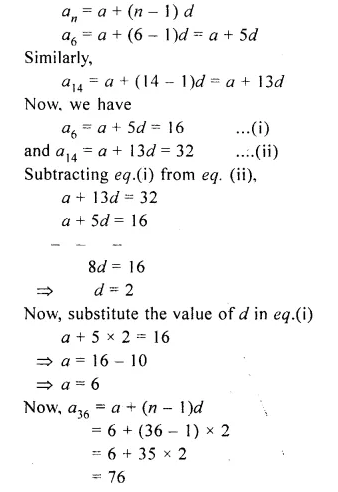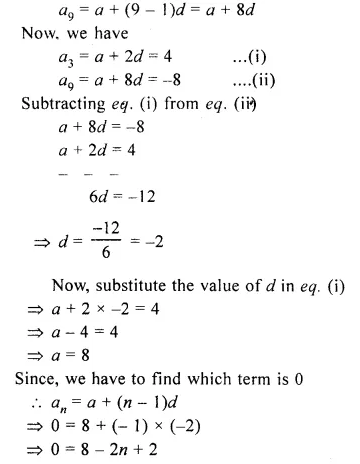Category: ICSE Class 10

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 16 Loci (Locus and Its Constructions) Ex 16B

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 16 Loci (Locus and Its Constructions) Ex 16B

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 16 Loci (Locus and Its Constructions) Ex 16A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 16 Loci (Locus and Its Constructions) Ex 16B

Question 1.
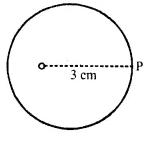
Describe the locus for questions 1 to 13 given below: 1. The locus of a point at a distance 3 cm from a fixed point.

Solution:
The locus of a point which is 3 cm away from a fixed point is circumference of a circle whose radius is 3 cm and the fixed point is called the centre of the circle.

Question 2.
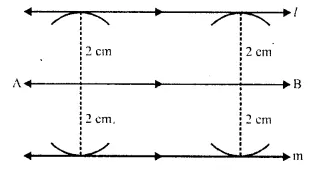
The locus of points at a distance 2 cm from a fixed line.
Solution:
A pair of straight lines 1 and m which are parallel to the given line at a distance of 2 cm, from it is the locus.

Question 3.
The locus of the centre of a wheel of a bicycle going straight along a level road.
Solution:

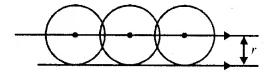
The locus of the centre of a wheel which is going straight along a level road will be a straight line parallel to the road at a distance equal to the radius of the wheel.

Question 4.
The locus of the moving end of the minute hand of a clock.
Solution:

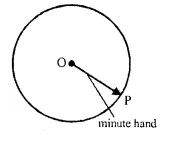
The locus of the moving end of the minute hand of the clock will be a circle where radius will be of the length of the minute hand.

Question 5.
The locus of a stone dropped from the top of a tower.
Solution:

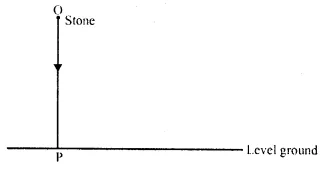
The locus of stone which is dropped from the top of the tower will be a vertical line through the point from which the stone is dropped.

Question 6.
The locus of a runner running around a circular track and always keeping a distance of 1.5 m from the inner edge.
Solution:

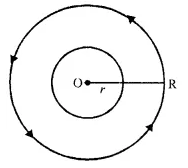
The locus of the runner running round a circular track at a distance of 1.5 m from the inner edge will be the circum¬ference of a circle whose radius is equal to the radius of the inner circular track plus 1.5 m

Question 7.
The locus of the door-handle as the door opens.
Solution:

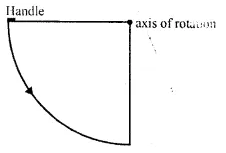
The locus of the door handle will be the circumfer-ence of a circle with centre at the axis of rotation of the door and radius equal to the distance between the door handle and the axis of rotation of the door.

Question 8.
The locus of points inside a circle and equidistant from two fixed points on the circumference of the circle.
Solution:

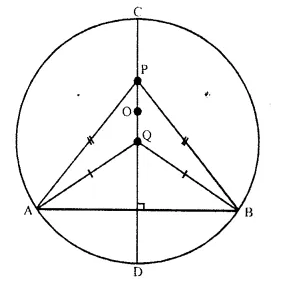
The locus of the points inside the circle which are equidistant from the fixed points on the circumference of the circle will be the diameter which is perpendicular bisector of the line joining the two fixed points on the circle.

Question 9.
The locus of the centres of all circles passing through two fixed points.
Solution:

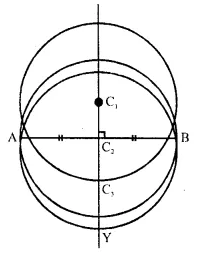
The locus of the centre of all the circles which pass through two fixed points will be the perpendicular bisector of the line segment joining the two fixed points which are given.

Question 10.
The locus of vertices of all isosceles triangles having a common base.
Solution:

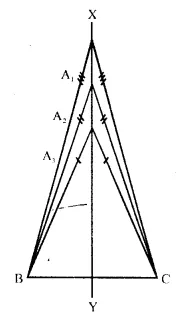
The locus of vertices of all isosceles triangles have a common base will be the perpendicular bisector of the common base of the triangles.

Question 11.
The locus of a point in space, which is always at a distance of 4 cm from a fixed point.
Solution:
The locus of a point in space is the surface of the sphere whose centre is the fixed point and radius equal to 4 cm.

Question 12.
The locus of a point P, so that:
AB² = AP²+ BP², where A and B are two fixed points.
Solution:


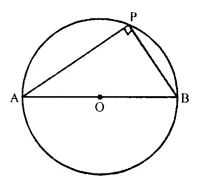
The locus of the point P is the circumference of a circle with AB as diameter and satisfies the condition AB² = AP²+ BP².

Question 13.
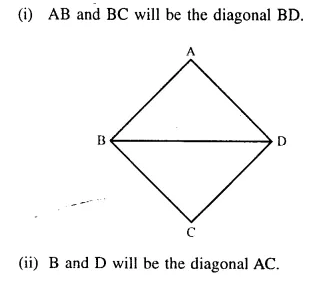
The locus of a point in rhombus ABCD, so that it is equidistant from
(i) AB and BC ; (ii) B and D.
Solution:
Locus of the point in a rhombus ABCD which is equidistant from.

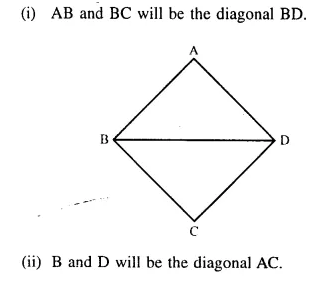
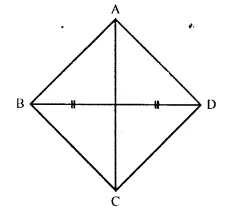
Question 14.
The speed of sound is 332 metres per second. A gun is fired. Describe the locus of all the people on the earth’s surface, who hear the sound exactly after one second.
Solution:
The locus of all the people on earth’s surface is the circumference of a circle whose radius is 332 m and centre is the point where the gun is fired.

Question 15.
Describe:
(i) The locus of points at distances less than 3 cm from a given point.
(ii) The locus of points at distances greater than 4 cm from a given point.
(iii) The locus of points at distances less than or equal to 2.5 cm from a given point.
(iv) The locus of points at distances greater than or equal to 35 mm from a given point.
(v) The locus of the centre of a given circle which rolls around the outside of a second circle and is always touching it.
(vi) The locus of the centres of all circles that are tangent to both the arms of a given angle.
(vii) The locus of the mid-points of all chords par-allel to a given chord of a circle.
(viii) The locus of points within a circle that are equidistant from the end points of a given chord.
Solution:
(i) The space inside of the circle whose radius is 3 cm and centre is the fixed point which is given.
(ii) The space outside of the circle whose radius is 4 cm and centre is the fixed point which is given.
(iii) The space inside and circumference of the circle with a raduis of 2.5 cm and centre is the given fixed point.
(iv) The space outside and the circumference of a circle with a radius of 35 mm and centre is the given fixed point.
(v) Circumference of the circle concentric with

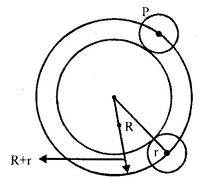
the second circle whose radius is equal to the sum of the radii of the two given circles.
(vi) The locus of the centre of all circle whose tan-gents are the arms of a given angle is the bisector of that angle.

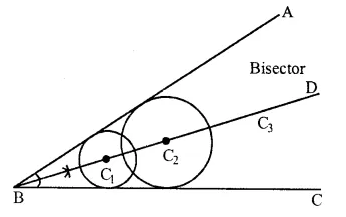
(vii) The locus of the mid-points of the chords which are parallel to a given chords is the diameter perpendicular to the given circle.


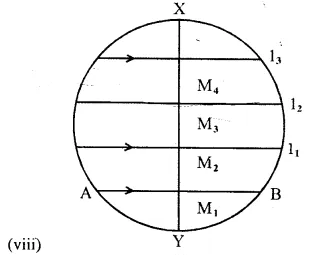
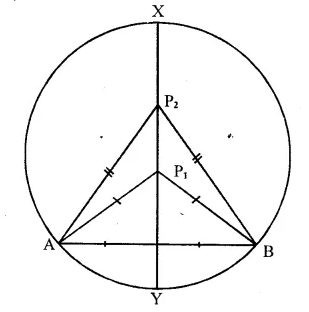
The locus of points within a circle that are equidistant from the end points of a given chord is a diameter which is perpendicular bisector of the given chord.

Question 16.
Sketch and describe the locus of the vertices of all triangles with a given base and a given altitude.
Solution:
Steps of Construction:

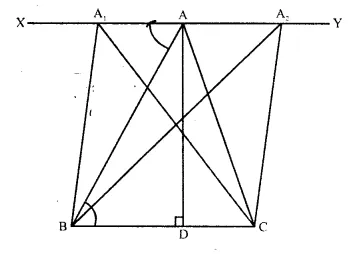
Draw a line XY parallel to the base BC from the vertex A.
This line is the locus of vertex A. All the tri-angles which have the base BC and altitude (length) equal to AD.

Question 17.
In the given figure, obtain all the points equidistant from lines m and n ; and 2.5 cm from O.

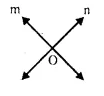
Solution:

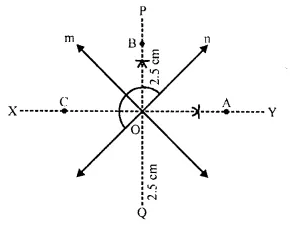
Draw angle bisector PQ and XY of angles formed by the lines m and n. From O, draw arcs with radius 2.5 cm, which intersects the angle bisectors at A, B, C and D respectively.
Hence A, B, C and D are the required points.
P.Q.
By actual drawing obtain the points equidistant from lines m and n ; and 6 cm from a point P, where P is 2 cm above m, m is parallel to – n and m is 6cm above n
Solution:
Steps of construction:

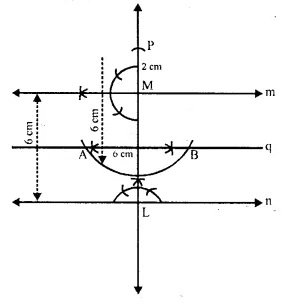
(i) Draw a line n.
(ii) Take a point P on n and draw a perpendicular to n. ,
(iii) Cut off LM = 6 cm and draw a line q, the per pendicu lar bisector of LM
(iv) At M, draw a line n making an angle of 900 at.
(v) Produce LM and take a point P such that PM =2 cm.
(vi) From P, draw are an with 6 cm radius which intersects the line q, (he perpendicular bisector cf LM, atA and B.
A and B are the required points which are equidisant from rn and n and is at a distance of 6 cm from P

Question 18.
A straight line AB is 8 cm long. Draw and describe the locus of a point which is :
(i) always 4 cm from the line AB.
(ii) equidistant from A and B.
Mark the two points X and Y, which are 4 cm from AB and equidistant from A and B. Describe the figure AXBY.
Solution:
Steps of Construction:

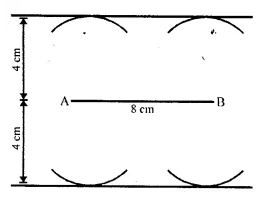
(i) Draw a line segment AB equal to 8 cm.
(ii) Draw two parallel lines  ℓ and m to AB at a distance of 4cm

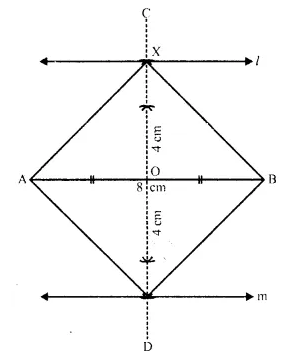
(iii) Draw the perpendicular bisector of AB which intersects the parallel lines  ℓ and m at X and Y respectively then X and Y are the required points.
(iv) Join AX.AY, BX and BY.
The figure so formed is a square as its diago¬nals are equal and intersect at 90°.

Question 19.
Angle ABC = 60° and BA = BC = 8 cm. The mid-points of BA and BC are M and N respec¬tively. Draw and describe the locus of a point which is :
(i) equidistant from BA and BC.
(ii) 4 cm from M.
(iii) 4 cm from N.
Mark the point P, which is 4 cm from both M and N, and equidistant from BA and BC. Join MP and NP, and describe the figure BMPN.
Solution:
(i) Draw an angle of 60° with AB = BC = 8 cm.
(ii) Draw the angle bisector BX of ∠ABC.

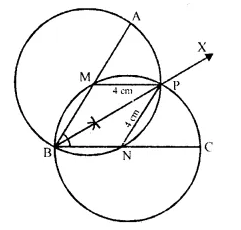
(iii) With centre M and N, draw circles of radius equal to 4 cm, which intersect each other at P. P is the required point.
(iv) Join MP, NP.
BMPN is a rhombus.
∵ MP = PM = BN = PN = 4 cm.

Question 20.
Draw a triangle ABC in which AB = 6 cm, BC = 4.5 cm and AC = 5 cm. Draw and label :
(i) the locus of the centres of all circles which touch AB and AC ;
(ii) the locus of the centres of all the circles of radius 2 cm which touch AB.
Hence, construct the circle of radius 2 cm which touches AB and AC.
Solution:

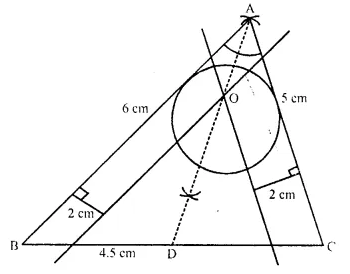
(i) Draw a line segment BC = 4.5 cm
(ii) With centre B and radius 6 cm and with centre C and radius 5 cm, draw arcs which intersects each other at point A
(iii) Join AB and AC.
ABC is a required triangle.
(iv) Draw the angle bisector of ∠BAC.
(v) Draw a lines parallel to AC and AB at a distance of 2 cm. which intersects each other AD at O.
(vi) With centre O and radius 2 cm, draw a circle which touches AB and AC.

Question 21.
Construct a triangle ABC, having given AB = 4.8 cm. AC = 4 cm and ∠A = 75°. Find a point P.
(i) inside the triangle ABC.
(ii) outside the triangle ABC.
equidistant from B and C; and at a distance of 1.2 cm from BC.
Solution:

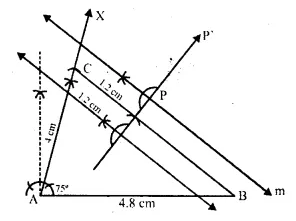
(i) Draw a line segment AB = 4.8 cm.
(ii) At, A draw a ray AX making an angle of 75°.
(iii) Cut off AC = 4 cm from AX.
(iv) Join BC.
(v) Draw two lines  ℓ and m parallel to BC at a distance of 1.2 cm.
(vi) Draw the perpendicular bisector of BC which intersect  ℓ and m at P and P .
P and P1 are the required points which are in¬side and outside the given triangle ABC.

P.Q.
O is a fixed point. Point P moves along a fixed line AB. Q is a point on OP produced such that OP = PQ. Prove that the locus of point Q is a line parallel to AB.
Solution:
O is fixed point. P moves along AB; a fixed line. OP is joined and produced it to Q such that OP = PQ, Now we have to prove that locus of P is a line parallel to AB.

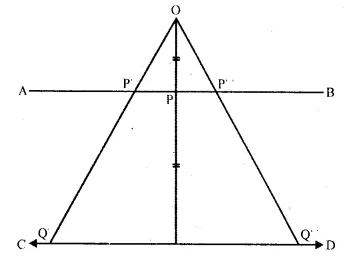
Proof:
∵ P moves along AB, and Q moves in such a way that PQ is always equal to OP.
P is the mid-point of OQ.
Now is A OQQ’
P and P’ are the mid-point of OQ and OQ’
AB || OQ’
Locus of Q is a line CD, which is parallel to AB.

Question 22.
Draw an angle ABC = 75°. Find a point P such that P is at a distance of 2 cm from AB and 1.5 cm from BC.
Solution:

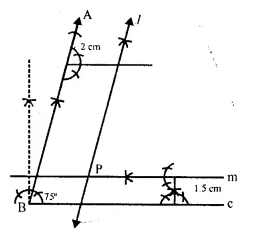
Steps of Construction:
(i) Draw a ray BC.
(ii) At B, draw a ray BA making an angle of 75° with BC.
(iii) Draw a line  ℓ parallel to AB at a distance of 2 cm.
(iv) Draw another line m parallel to BC at a distance of 1.5 cm. which intersects m at P.
∴ P is the required point.

Question 23.
Construct a triangle ABC, with AB = 5.6 cm, AC = BC = 9.2 cm. Find the points equidistant from AB and AC; and also 2 cm from BC. Measure the distance between the two points obtained.
Solution:

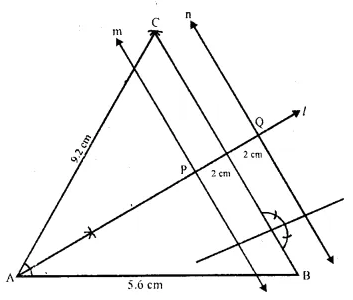
(i) Draw a line segment AB = 5.6 cm.
(ii) From A and B, as centres and radius 9.2 cm, draw the arcs which intersect each other at C.
(iii) Join CA and CB.
(iv) Draw two lines m and n parallel to BC at a distance of 2 cm each.
(v) Draw the angle bisector of ∠CAB which inter-sects the parallel lines m and n at P and Q respectively.
P and Q are the required points which are equi-distant from AB and AC.
On measuring the distance between P and Q is 4.3 cm.

Question 24.
Construct a triangle ABC, with AB = 6 cm, AC = BC = 9 cm. Find a point 4 cm from A and equidistant from B and C.
Solution:

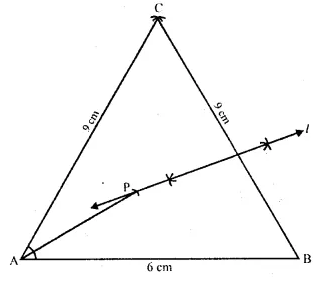
(iii) Join CA and CB.
(iv) Draw the perpendicular bisector of BC.
(v) A as centre and radius 4 cm, draw an arc which intersect the perpendicular bisector of BC, at P.
P is the required point which is equidistant from B and C and at a distance of 4 cm from A.

Question 25.
thythtyhRuler and compasses may be used in this question. All construction lines and arcs must be clearly shown and be of sufficient length and clarity to permit assessment.
(i) Construct a triangle ABC, in which BC = 6 cm, AB = 9 cm and angle ABC = 60°.
(ii) Construct the locus of all points inside triangle ABC, which are equidistant from B and C.
(iii) Construct the locus of the vertices of the triangles with BC as base and which are equal in area to triangle ABC.
(iv) Mark the point Q, in your construction, which would make A QBC equal in area to A ABC, and isosceles.
(v) Measure and record the length of CQ. [1998]
Solution:
(i) Draw a line segument BC = 6 cm.
(ii) At B, draw a ray BX making an angle of 60H and cut off BA = 9 cm.
(iii) Join AC, then A ABC is the given triangle. ..(i)
(iv) Draw perpendicular bisector of BC which
intersects BA in M, then any point on LM, is the equidistant from B and C. ….(ii)

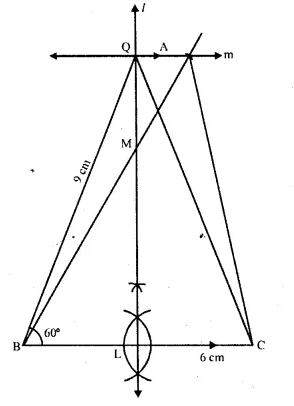
(v) Though A, draw a line m II BC.
(vi) The perpendicular bisector of BC and the par-allel line intersect each other at Q.
(vii) Join QB and QC.
Then A QBC is equal in the area of A ABC and through any point on line m, and bace BC, every triangle is equal in area to the given triangle ABC. Length of CQ, on measuring.

Question 26.
State the locus of a point in a rhombus ABCD, wi.r’ch is equidistant
(i) from AB and AD; (ii) from the vertices A and C.
[1998]
Solution:
In rhombus ABCD, draw the angle bisector of ∠A which meets in C
∴ Join BD, which intersects AC at O.
O is the required locus.
From O, draw OL ⊥ AB and OM ⊥ AD.
In Δ AOL and Δ AOM

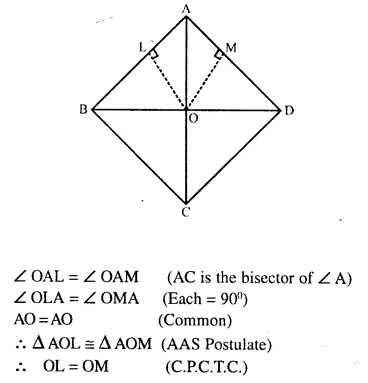
∴ O is equidistant from AB and AD.
∵ Diagonal AC and BD bisect each other at O at right angles.
∴ AO = OC
O is equidistant from A and C.

Question 27.
Use graph paper for this question. Take 2 cm = 1 unit on both the axes.
(i) Plot the points A (1,1), B (5,3) and C (2.7).
(ii) Construct the locus of points equidistant from A and B.
(iii) Construct the locus of points equidistant from ABandAC.
(iv) Locate the point P such that PA = PB and P is equidistant from AB and AC.
(v) Measure and record the length PA in cm.
[1999]
Solution:

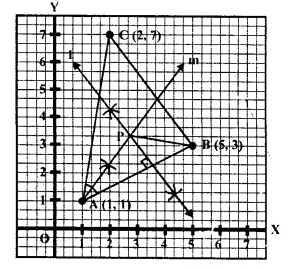
Plot the points A (1, 1), B (5, 3) and C (2, 7) on the graph and join AB, BC and CA.
Draw the perpendicular bisector of AB and angle bisector of ∠A which intersect each other at P. P is the required point,
∵ P lies on the perpendicular bisector of AB.
∴P is equidistant from A and B.
Again,
∵ P lies on the angle bisector of ∠A
∴ P is equidistant’from AB and AC
Now, on measuring the length of PA, it is 5.2 cm
(Approx.)

Question 28.
Construct an isosceles triangle ABC such that AB = 6 cm, BC = AC = 4 cm. Biscet ∠C internally and mark a point P on this bisector such that CP = 5 cm. Find the points Q and R which are 5 cm from P and also 5 cm from the line AB. [2001]
Solution:
(i) Draw a line segment AB = 6 cm.
(ii) With centres A and B and radius 4 cm, draw two arcs which intersect each other at C.

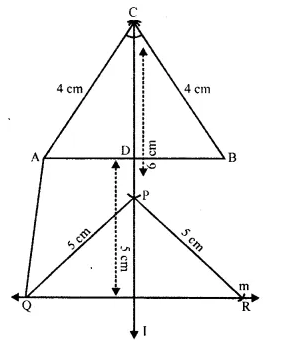
(iii) Join CA and CB.
(iv) Draw the angle bisector of ∠C and cut off CP – 5 cm.
(v) A line m is drawn parallel to AB at a distance of 5 cm.
(vi) P as centre and radius 5 cm, draw arcs which
intersect the line m at Q and R.
(vii) Join PQ, PR and AQ.
Q and R are the required points.
P.Q
Use ruler and compasses only for this question. Draw a circle of radius 4 cm and mark two chords AB and AC of the circle of lengths 6 cm and 5 cm respectively.
(i) Construct the locus of points, inside the circle, that are equidistant from A and C. Prove your construction.
(ii) Construct the locus of points, inside the circle, that are equidistant from AB and AC. [1995]
Solution:

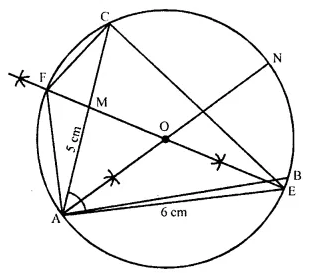
(i) Draw a circle with radius = 4 cm and O is the centre.
(ii) Take a point A on it.
(iii) A as centre and radius 6 cm draw an arc which intersects the circle at B.
(iv) Again A as centre and radius 5 cm, draw another arc which intersects the circle at C.
(v) Join AB and AC.
(vi) Draw the perpendicular bisector of AC, which intersects AC at M and meets the circle at E and F. EF is the locus of the points inside the circle which are equidistant from A and C.
(vii) Join AE, AF, CE and CF.
Proof:

Similarly, we can prove that CF = AF Hence EF is the locus of points which are equidistant from A and C.
(ii) Again draw the bisector of ∠A which meets the circle at N.
∴ Locus of points inside the circle which are equidistant from AB and AC is the perpendicular bisector of ∠A.

Question 29.
Plot the points A (2,9), B (-1,3) and C (6,3) on a graph paper. On the same graph paper, draw the locus of point A so that the area of ΔABC remains the same as A moves.
Solution:

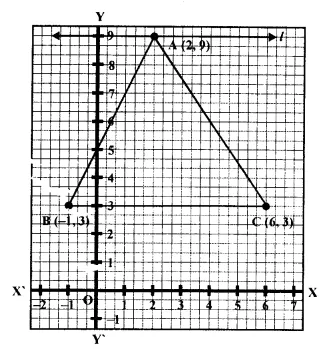
Draw axis XOX’ and YOY’ on the graph paper. Plot the points A (2, 9), B (-1,3) and C (6, 3) Join AB, BC and CA which form a ΔABC. From A, draw a line l parallel to BC on x-axis The locus of point A is the line l.
∵ l || BC and triangles on the same base BC and between the same parallel are equal in area.
∴ l is the required locus of point A.

Question 30.
Construct a triangle BCP given BC = 5 cm, BP = 4 cm and ∠PBC = 45°.
(i) Complete the rectangle ABCD such that:
(a) P is equidistant from A B and BC.
(b) P is equidistant from C and D.
(ii) Measure and record the length of AB.
(2007)
Solution:
(i) Draw a line segment BC = 5 cm.
(ii) At B, draw a ray making an angle of 45° and cut off BP = 4 cm.
(iii) Join PC.
(iv) v P is equidistant from AB and BC.
∴ P lies on the bisector of ∠ABC.
Now draw a ray BY making an angle of 90°.
P is equidistant from C and D P lies on the perpendicular bisector of CD.

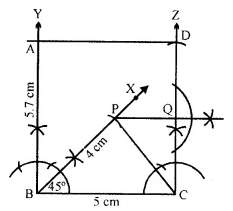
(v) From C, draw CZ ⊥ BC which intersect the perpendicular bisector at Q.
(vi) Cut off QD = CQ and from BP, cut off BA = CD.
(vii) Join AD.
Then ABCD is the required rectangle. Measuring the length of AB, it is 5.7 cm approximately.

Question 31.
Use ruler and compasses only for the following questions. All constructions lines and arcs must be clearly shown.
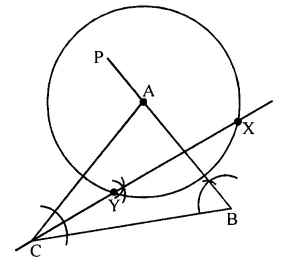
(i) Construct a ΔABC in which BC = 6.5 cm, ∠ABC = 60°, AB = 5 cm.
(ii) Construct the locus of points at a distance of 3.5 cm from A.
(iii) Construct the locus of points equidistant from AC and BC.
(iv) Mark 2 points X and Y which are at
distance of 3.5 cm from A and also equidistant from AC and BC. Measure XY. (2016)
Solution:
(i) Steps of construction :
(1) Draw BC = 6.5 cm using a ruler.
(2) At B, draw ∠CBP = 60°
From BP, cut off BA = 5 cm.
(3) Join AC to get the required triangle.
(4) With A as a centre and radius equal to 3.5 cm, draw a circle. This circle is the required
locus of points at a distance of 3.5 cm from A.
(5) Draw the bisector of ∠ACB. This bisector is the locus of points equidistant from AC and BC.
(6) The angle bisector drawn above cuts the circle at X and Y. These are the points which are at a distance of 3.5 cm from A and also equidistant from AC and BC. On measuring, the length of XY comes out to be 5.2 cm.

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 16 Loci (Locus and Its Constructions) Ex 16B Heights and Distances Ex 22C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5B

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5B.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5D

Solve equations, number 1 to number 20, given below, using factorisation method :
Question 1.
x² – 10x – 24 = 0
Solution:
x² – 12x + 2x – 24 = 0
⇒ x (x – 12) + 2 (x – 12) = 0
⇒ (x – 12) (x + 2) = 0
Either x – 12 = 0, then x = 12
or x + 2 = 0, then x = – 2
x = 12, – 2

Question 2.
x² – 16 = 0
Solution:
⇒ x² – (4)² = 0
⇒ (x + 4) (x – 4) = 0
Either x + 4 = 0, then x = – 4
or x – 4 = 0, then x = 4
x = 4, – 4

Question 3.
2x² – \(\frac { 1 }{ 2 }\) x = 0
Solution:
⇒ 4x² – x = 0
⇒ x (4x – 1) = 0
Either x = 0,
or 4x – 1 = 0, then 4x = 1 ⇒ x = \(\frac { 1 }{ 4 }\)
x = 0, \(\frac { 1 }{ 4 }\)

Question 4.
x (x – 5) = 24
Solution:
⇒ x² – 5x – 24 = 0
⇒ x² – 8x + 3x – 24 = 0
⇒ x (x – 8) + 3 (x – 8) = 0
⇒ (x – 8) (x + 3) = 0
Either x – 8 = 0, then x = 8
or x + 3 = 0, then x = – 3
x = 8, – 3

Question 5.
\(\frac { 9 }{ 2 }\) x = 5 + x²
Solution:
⇒ 9x = 10 + 2x²
⇒ 2x² – 9x + 10 = 0
⇒ 2x² – 4x – 5x + 10 = 0
⇒ 2x (x – 2) – 5 (x – 2) = 0
⇒ (x – 2) (2x – 5) = 0
Either x – 2 = 0, then x = 2
or 2x – 5 = 0, then 2x = 5 ⇒ x = \(\frac { 5 }{ 2 }\)
x = 2, \(\frac { 5 }{ 2 }\)

Question 6.
\(\frac { 6 }{ x }\) = 1 + x
Solution:
⇒ 6 = x + x²
⇒ x² + x – 6 = 0
⇒ x² + 3x – 2x – 6 = 0
⇒ x (x + 3) – 2 (x + 3) = 0
⇒ (x + 3) (x – 2) = 0
Either x + 3 = 0, then x = – 3
or x – 2 = 0, then x = 2
x = 2, – 3

Question 7.
x = \(\frac { 3x + 1 }{ 4x }\)
Solution:
⇒ 4x² = 3x + 1
⇒ 4x² – 3x – 1 = 0
⇒ 4x² – 4x + x – 1 = 0
⇒ 4x (x – 1) + 1 (x – 1) = 0
⇒ (x – 1) (4x + 1) = 0
Either x – 1 = 0, then x = 1
or 4x + 1 = 0, then 4x = -1 ⇒ x = \(\frac { -1 }{ 4 }\)
x = 1, \(\frac { -1 }{ 4 }\)

Question 8.
x + \(\frac { 1 }{ x }\) = 2.5
Solution:

Question 9.
(2x – 3)² = 49
Solution:
⇒ 4x² – 12x + 9 = 49
⇒ 4x² – 12x + 9 – 49 = 0
⇒ 4x² – 12x – 40 = 0
⇒ x² – 3x – 10 = 0 (Dividing by 4)
⇒ x² – 5x + 2x – 10 = 0
⇒ x (x – 5) + 2 (x – 5) = 0
⇒ (x – 5) (x + 2) = 0
Either x – 5 = 0, then x = 5
or x + 2 = 0, then x = – 2
x = 5, – 2

Question 10.
2 (x² – 6) = 3 (x – 4)
Solution:
⇒ 2x² – 12 = 3x- 12
⇒ 2x² – 3x – 12 + 12 = 0
⇒ 2x² – 3x = 0
⇒ x (2x – 3) = 0
Either A = 0,
or 2x – 3 = 0, then 2x = 3 ⇒ x = \(\frac { 3 }{ 2 }\)
x = 0, \(\frac { 3 }{ 2 }\)

Question 11.
(x + 1) (2x + 8) = (x + 7) (x + 3)
Solution:

Question 12.
x² – (a + b) x + ab = 0
Solution:
⇒ x² – ax – bx + ab = 0
⇒ x (x – a) – b (x – a) = 0
⇒ (x – a) (x – b) = 0
Either x – a = 0, then x = a
or x – b = 0, then x = b
x = a, b

Question 13.
(x + 3)² – 4 (x + 3) – 5 = 0
Solution:
Let x + 3 = y, then
⇒ y² – 4y – 5 = 0
⇒y² – 5y + y – 5 = 0
⇒ y (y – 5) + 1 (y – 5) = 0
⇒ (y – 5) (y + 1) = 0
Substituting the value of y,
⇒ (x + 3 – 5) (x + 3 + 1) = 0
⇒ (x – 2) (x + 4) = 0
Either x – 2 = 0, then x = 2
or x + 4 = 0, then x = – 4
x = 2, -4

Question 14.
4 (2x – 3)² – (2x – 3) – 14 = 0
Solution:
Let 2x – 3 = y, then
⇒ 4y² – y – 14 = 0
⇒ 4y² – 8y + 7y – 14 = 0
⇒ 4y (y – 2) + 7 (y – 2) = 0
⇒ (y – 2) (4y + 7) = 0
Substituting the value of y,
⇒ (2x – 3 – 2) (8x – 12 + 7) = 0
⇒ (2x – 5) (8x – 5) = 0
Either 2x – 5 = 0, then 2x = 5 ⇒ x = \(\frac { 5 }{ 2 }\)
or 8x – 5 = 0, then 8x = 5 ⇒ x = \(\frac { 5 }{ 8 }\)
x = \(\frac { 5 }{ 2 }\) , \(\frac { 5 }{ 8 }\)

Question 15.

Solution:
⇒ (3x – 2) (x + 4) = (3x – 8) (2x – 3)
⇒ 3x² + 12x – 2x – 8 = 6x² – 9x – 16x + 24
⇒ 3x² + 12x – 2x – 8 – 6x² + 9x + 16x – 24 = 0
⇒ – 3x² + 35x – 32 = 0
⇒ 3x² – 35x + 32 = 0
⇒ 3x² – 3x – 32x + 32 = 0
⇒ 3x (x – 1) – 32 (x – 1) = 0
⇒ (x – 1) (3x – 32) = 0
⇒ 3x (x – 1) – 32 (x – 1) = 0
⇒ (x – 1) (3x – 32) – 0
Either x – 1 = 0, then x = 1
or 3x – 32 = 0, then 3x = 32 ⇒ x = \(\frac { 32 }{ 3 }\)
x = 1, \(\frac { 32 }{ 3 }\) or 1, 10\(\frac { 2 }{ 3 }\)

Question 16.
2x² – 9x + 10 = 0, when :
(i) x ∈ N
(ii) x ∈ Q.
Solution:
2x² – 9x + 10 = 0
⇒ 2x² – 4x – 5x + 10 = 0
⇒ 2x (x – 2) – 5 (x – 2) = 0
⇒ (x – 2) (2 – 5) = 0
Either x – 2 = 0, then x = 2
or 2x – 5 = 0, then 2x = 5 ⇒ x = \(\frac { 5 }{ 2 }\)
(i) When x ∈ N, then x = 2
(ii) When x ∈ Q, then x = 2 , \(\frac { 5 }{ 2 }\)

Question 17.

Solution:

Question 18.

Solution:

Question 19.

Solution:

Question 20.

Solution:

Question 21.
Find the quadratic equation, whose solution set is :
(i) {3, 5}
(ii) {-2, 3}
Solution:
(i) Solution set is {3, 5} or x = 3 and x = 5
Equation will be
(x – 3) (x – 5) = 0
⇒ x² – 5x – 3x + 15 = 0
⇒ x² – 8x + 15 = 0
(ii) Solution set is {-2, 3} or x = -2, x = 3
Equation will be
(x + 2) (x – 3) = 0
⇒ x² – 3x + 2x – 6 = 0
⇒ x² – x – 6 = 0

Question 22.

Solution:


Roots are not real.
Hence there is no possible real value of x.

Question 23.
Find the value of x, if a + 1 = 0 and x² + ax – 6 = 0.
Solution:
a + 1 = 0 ⇒ a = -1
Now the equation x² + ax – 6 = 0 will be x² + (-1) x – 6 = 0
⇒ x² – x – 6 = 0
⇒ x² – 3x + 2x – 6 = 0
⇒ x (x – 3) + 2 (x – 3) = 0
Either x – 3 = 0, then x = 3
or x + 2 = 0, then x = – 2
x = 3, – 2

Question 24.
Find the value of x, if a + 7 = 0; b + 10 = 0 and 12x² = ax – b.
Solution:
a + 7 = 0, then a = -7
and b + 10 = 0, then b = -10
Now, substituting the value of a and b in
12x² = ax – b
⇒ 12x² = – 7x – (-10)
⇒ 12x² = – 7x + 10
⇒ 12x² + 7x – 10 = 0
⇒ 12x² + 15x – 8x – 10 = 0
⇒ 3x (4x + 5) – 2 (4x + 5) = 0
⇒ (4x + 5) (3x – 2) = 0
Either 4x + 5 = 0, then 4x = -5 ⇒ x = \(\frac { 5 }{ 4 }\)
or 3x – 2 = 0, then 3x = 2 ⇒ x = \(\frac { 2 }{ 3 }\)
x = \(\frac { 5 }{ 4 }\), \(\frac { 2 }{ 3 }\)

Question 25.
Use the substitution y = 2x + 3 to solve for x, if 4 (2x + 3)² – (2x + 3) – 14 = 0.
Solution:
y = 2x + 3, then equation
4 (2x + 3)² – (2x + 3) – 14 = 0 will be 4y² – y – 14 = 0
⇒ 4y² – 8y + 7y – 14 = 0
⇒ 4y (y – 2) + 7 (y – 2) = 0
⇒ (y – 2) (4y + 7) = 0
Either y – 2 = 0, then y = 2

Question 26.
Without solving the quadratic equation 6x² – x – 2 = 0, find whether x = \(\frac { 2 }{ 3 }\) is a solution of this equation or not.
Solution:

Question 27.
Determine whether x = -1 is a root of the equation x² – 3x + 2 = 0 or not.
Solution:
x² – 3x + 2 = 0
x = -1
Substituting the value of x = -1, in the quadratic equation
L.H.S. = x² – 3x + 2 = (-1)² – 3(-1) + 2 = 1 + 3 + 2 = 6 ≠ 0
Remainder is not equal to zero
x = -1 is not its root.

Question 28.
If x = \(\frac { 2 }{ 3 }\) is a solution of the quadratic equation 7x² + mx – 3 = 0; find the value of m.
Solution:

Question 29.
If x = -3 and x = \(\frac { 2 }{ 3 }\) are solutions of quadratic equation mx² + 7x + n = 0, find the values of m and n.
Solution:
x = -3, x = \(\frac { 2 }{ 3 }\) are the solution of the quadratic equation, mx² + 7x + n = 0
Then these values of x will satisfy it
(i) If x = -3, then mx² + 7x + n = 0
⇒ m(-3)² + 7(-3) + n = 0
⇒ 9m – 21 + n = 0
⇒ n = 21 – 9m ……(i)

Question 30.
If quadratic equation x² – (m + 1) x + 6 = 0 has one root as x = 3; find the value of m and the other root of the equation.
Solution:
In equation, x² – (m + 1) x + 6 = 0
x = 3 is its root, then it will satisfy it
⇒ (3)² – (m + 1) x 3 + 6 = 0
⇒ 9 – 3m – 3 + 6 = 0
⇒ -3m + 12 = 0

Question 31.
Give that 2 is a root of the equation 3x² – p (x + 1) = 0 and that the equation px² – qx + 9 = 0 has equal roots, find the values of p and q.
Solution:
3x² – p (x + 1) = 0
⇒ 3x² – px – p = 0
2 is a root of the equal It will satisfy it
3(2)² – p(2) – p = 0
⇒ 3 x 4 – 2p – p = 0
⇒ 12 – 3p = 0
⇒ 3p = 12
⇒ p = 4
px² – qx + 9 = 0
Here, a = p, b = -q, c = 9
D = b² – 4ac = (-q)² – 4 x p x 9 = q² – 36p
Roots are equal.
D = 0
⇒ q² – 36p = 0
⇒ q² – 36 x 4 = 0
⇒ q² = 144
⇒ q² = (±12)²
⇒ q = ± 12
Hence, p = 4 and q = ±12

Question 32.

Solution:

Question 33.
Solve: ( \(\frac { 1200 }{ x }\) + 2 ) (x – 10) – 1200 = 60
Solution:

By cross multiplication,
⇒ 1200x – 12000 + 2x² – 20x – 1260x = 0
⇒ 2x² + 1200x – 20x – 1260x – 12000 = 0
⇒ 2x² – 80x – 12000 = 0
⇒ x² – 40x – 6000 = 0
⇒ x² – 100x + 60x – 6000 = 0
⇒ x (x – 100) + 60 (x – 100) = 0
⇒ (x – 100) (x + 60) = 0
Either x – 100 = 0, then x = 100
or x + 60 = 0, then x = -60
x = 100, -60

Question 34.
If -1 and 3 are the roots of x² + px + q = 0, find the values of p and q.
Solution:
-1 and 3 are the roots of the equation
x² + px + q = 0
Substituting the value of x = -1 and also x = 3, then
(-1 )² + p(-1) + q = 0
⇒ 1 – p + q = 0
⇒ p – q = 1
⇒ p = 1 + q …(i)
and (3)² + p x 3 + q = 0
⇒ 9 + 3p + q = 0
⇒ 9 + 3 (1 + q) + q = 0 [From(i)]
⇒ 9 + 3 + 3q + q = 0
⇒ 12 + 4q = 0
⇒ 4q = -12
⇒ q = -3
p = 1 + q = 1 – 3 = -2
Hence, p = -2, q = -3

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5A

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5A.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5D

Question 1.
Without solving, comment upon the nature of roots of each of the following equations:
(i) 7x² – 9x + 2 = 0
(ii) 6x² – 13x + 4 = 0
(iii) 25x² – 10x + 1 = 0
(iv) x² + 2√3 x – 9 = 0
(v) x² – ax – b² = 0
(vi) 2x² + 8x + 9 = 0
Solution:

Question 2.
Find the value of ‘p’, if the following quadratic equations have equal roots :
(i) 4x² – (p – 2) x + 1 = 0
(ii) x² + (p – 3) x + p = 0
Solution:

Question 3.
The equation 3x² – 12x + (n – 5) = 0 has equal roots. Find the value of n.
Solution:
3x² – 12x + (n – 5) = 0
Here a = 3, b = -12, c = (n – 5)
D = b² – 4ac

Question 4.
Find the value of ‘m’, if the following equation has equal roots :
(m – 2) x² – (5 + m) x + 16 = 0
Solution:

Question 5.
Find the value of k for the which the equation 3x² – 6x + k = 0 has distinct and real root.
Solution:

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 25 Probability Ex 25B

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Chapter 25 Probability Ex 25B.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 25 Probability Ex 25A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 25 Probability Ex 25B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 25 Probability Ex 25C

Question 1.
Nine cards (identical in all respects) are numbered 2 to 10. A card is selected from them at random. Find the probability that the card selected will be :
(i) an even number.
(ii) a multiple of 3 ,
(iii) an even number and a multiple of 3.
(iv) an even number or a multiple of 3.
Solution:
No. of cards = 9
Having numbers marked on it = 2 to 10
∴ Number of possible outcomes = 9
(i) An even number i.e. 2, 4, 6, 8, 10 = 5
∴ Number of even numbers = 5

(ii) A multiple of 3 are 3, 6, 9
Number of multiple of 3 = 3

(iii) An even number and a multiple of 3 are 6
which is one in number

(iv) An even number or a multiple of 3 are 2, 3, 4, 6, 8, 9, 10
which are 7 in numbers

Question 2.
Hundred identical cards are numbered from 1 to 100. The cards are well shuffled and then a card is drawn. Find the probability that the number on the card drawn is :
(i) a multiple of 5.
(ii) a multiple of 6.
(iii) between 40 and 60.
(iv) greater than 85.
(v) less than 48.
Solution:
Number of cards = 100
Marked with numbers from 1 to 100
∴ Number of possible outcome = 100
(i) A multiple of 5 are 5, 10, 15 95, 100
which are 20 in numbers.
∴ Number of favourable outcome = 20

(ii) A multiple of 6 are 6, 12, 18, 24, 90, 96
which are 16 in numbers.
∴ Number of favourable outcome =16

(iii) Between 40 and 60 are 41, 42, ……. , 58, 59,
which are 19

(iv) Greater than 85 are 86 to 100 which are 15 in numbers.

(v) Less than 48 are 1 to 47 which are 47 in numbers

Question 3.
From 25 identical cards, numbered, 1, 2, 3, 4, 5 ,…………, 24, 25 ; one card is drawn at random.
Find the probability that the number on the card drawn is a multiple of :
(i) 3
(ii) 5
(iii) 3 and 5
(iv) 3 or 5
Solution:
Number of identical cards = 25
Numbers marked on their are 1 to 25 i.e.
1, 2, 3, 4, 5, …. 21, 22, 23, 24, 25
∴ Number of possible outcome = 25
(i) Multiple of 3 are 3, 6, 9, 12, 15, 18, 21, 24
Which are 8 in numbers.

(ii) Multiple of 5 are 5, 10, 15, 20, 25
which are 5 in numbers

(iii) Multiple of 3 and 5 are = 15
which is 1 in number

(iv) Multiple of 3 or 5 are 3, 5, 6, 9, 10, 12, 15, 18, 20, 21, 24, 25
which are 12 in numbers

Question 4.
A die is thrown once. Find the probability of getting a number :
(i) less than 3.
(ii) greater than or equal to 4.
(iii) less than 8
(iv) greater than 6.
Solution:
A die has 6 numbers i.e., 1, 2, 3, 4, 5, 6
∴ Number of possible outcome = 6
(i) Less than 3 are 1, 2 which are 2 in numbers

(ii) Greater than or equal to 4 are 4, 5, 6
which are 3 in number.

(iii) Less than 8 are 1, 2, 3, 4, 5, 6
which are 6 in numbers

(iv) Greater than 6 is nothing on the die

Question 5.
A book contains 85 pages. A page is chosen at random. What is the probability that the sum of the digits on the page is 8 ?
Solution:
Number of pages of the book = 85
which are from 1 to 85
Number of possible outcome = 85
∴ Number of pages whose sum of its page is 8 are : 17, 26, 35, 44, 53, 62, 71, 80 and 8

Question 6.
A pair of dice is thrown. Find the probability of getting a sum of 10 or more if 5 appears on the first die.
Solution:
Numbers marked on each die = 6
∴ Total number of cases = 6 x 6 = 36
∵ Favourable come are (5, 5), (5, 6) as 5 appears on the first, which are 2 in number

Question 7.
If two coins are tossed once, what is the probability of getting :
(i) 2 heads
(ii) at least one head
(iii) both heads or both tails.
Solution:
∵ A coins has two faces Head and Jail or H, T
∴ Two coins are tossed
∴ Number of coins = 2 x 2 = 4
which are HH, HT, TH, TT
(i) When both are Head, then
∴ Number of outcome = 1

(ii) At least one head, then
Number of outcomes = 3

(iii) When both head or both tails, then 1
Number of outcomes = 2

Question 8.
Two dice are rolled together. Find the probability of getting :
(i) a total of at least 10.
(ii) a multiple of 2 on one die and an odd number on the other die.
Solution:
∵ A die has 6 faces which are 1, 2, 3, 4, 5,6
∴ On rolling two dice at a time, number of comes = 6 x 6 = 36
∴ Number of possible outcome = 36
(i) a total of atleast 10, the favourable can be (4,6), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6) which are 6 in number

(ii) A multiple of 2 on one die and an odd number on the other
∴ Outcome can be (2, 1), (2, 3), (g, 5), (4, 1), (4,3) , (4, 5), (6, 1), (6, 3), (6, 5), (1, 2), (3, 2), (5, 2), (1, 4), (3, 4), (5, 4), (1, 6), (3, 6), 5, 6) which are 18 in numbers.
Number of favourable outcome

Question 9.
A card is drawn from a well-shuffled pack of 52 cards. Find the probability that the card drawn is :
(i) a spade.
(ii) a red card.
(iii) a face card.
(iv) 5 of heart or diamond.
(v) Jack or queen.
(vi) ace and king.
(vii) a red and a king.
(viii) a red or a king.
Solution:
A pack of playing card has 52 cards
∴ Number of possible outcome = 52
(i) A spade
∵ there are 13 cards of spade
∴ Number of favourable outcome = 13

(ii) A red card.
∵ There are 13 + 13 = 26 red card

(iii) A face card.
∵ There are 3 x 4 = 12 faces which are red.

(iv) 5 of heart or diamond.
∴ Number of cards =1 + 1=2

(v) Jack or queen
There are 4 + 4 = 8 such cards

(vi) ace and king.
There is no such card which is ace and king both
∴ P(E) = 0.
(vii) a red and a king
There are 2 such cards which are red kings

(viii) a red or a king
There are 26 cards which are red in which 2 kings are red and 2 more kings which are black = 26 + 2 = 28

Question 10.
A bag contains 16 coloured balls. Six are green, 7 are red and 3 are white. A ball is chosen, without looking into the bag. Find the probability that the ball chosen is :
(i) red
(ii) not red
(iii) white
(iv) not white
(v) green or red
(vi) white or green
(vii) green or red or white.
Solution:
Number of balls in a bag = 16
Green balls = 6
White balls = 3
Red balls = 7
∴ Total possible outcome =16
(i) Red balls = 7

(ii) Not red balls = 16-7 = 9

(iii) White balls = 3

(iv) Not white balls = 16 – 3= 13

(v) Green or red balls = 6 + 7 = 13

(vi) White or green balls = 3 + 6 = 9

(vii) Green or red or white balls =16

Question 11.
A ball is drawn at random from a box .ontammg 12 white. 16 red and 20 green balls. Determine the probability that the ball drawn is:
(i) white
(ii) red
(iii) not green
(iv) red or white.
Solution:
Number of balls in a box
White = 12
Red = 16
Green = 20
Total balls = 12 + 16 +20 = 48
∴ Total possible outcome = 48
(i) White balls = 12
∴ Number of favourable outcome =12

(ii) Red balls = 16
∴ Number of favourable outcome =16

(iii) Not green
Number of balls =12 + 16 = 28
∴ Number of favourable outcome = 28

(iv) Red or white balls =12 + 16 = 28
∴ Number of favourable outcome = 28

Question 12.
A card is drawn from a pack of 52 cards. Find the probability that the card drawn is :
(i) a red card
(ii) a black card
(iii) a spade
(iv) an ace
(v) a black ace
(vi) ace of diamonds
(vii) not a club
(viii) a queen or a jack
Solution:
Number of cards in playing card deck = 52
∴ Number of possible outcome = 52
(i) A red card
There are 13 + 13 = 26 red cards in the deck
∴ Number of favourable outcome = 26

(ii) A black card
There are 13 + 13 = 26 black cards
∴ Number of favourable outcome = 26

(iii) A spade
There are 13 spade cards in the deck
∴ Number of favourable outcome = 13

(iv) An Ace
There use 4 aces in the deck
Number of favourable outcome = 4

(v) A black ace
There are two black aces in a deck
∴ Number of favourable outcome = 2
Number of cards in playing card deck = 52

(vi) Ace of diamonds
∴ There are only one ace of diamonds
∴ Number of favourable of outcome = 1

(vii) Not a club
There are 13 x 3 = 39 cards which are not a club
∴ Number of favourable outcome = 39

(viii) A queen or a Jack
There are 4 queen cards and 4 Jack cards
∴ Number of favourable outcome = 4 + 4 = 8

Question 13.
Thirty identical cards are marked with numbers 1 to 30. If one card is drawn at random, find the probability that it is :
(i) a multiple of 4 or 6.
(ii) a multiple of 3 and 5
(iii) a multiple of 3 or 5
Solution:
There are 30 cards which are marks with numbers 1 to 30 and one card is drawn
(i) A multiple of 4 or 6.
∴ There are multiple of 4 or 6 = 4,6, 8, 12, 16, 18, 20, 24, 28, 30 which are 10
∴ Number of favourable outcome = 10

(ii) A multiple of 3 and 5 are 15, 30 which are 2
∴ Number of favourable outcome = 2

(iii) A multiple of 3 or 5
which are 3, 5, 6, 9, 10, 12, 15, 18, 20, 21, 24, 25, 27, 30 which are 14
∴ Number of favourable outcome = 14

Question 14.
In a single throw of two dice, find the probability of :
(i) a doublet
(ii) a number less than 3 on each dice.
(iii) an odd number as a sum.
(iv) a total of at most 10.
(v) an odd number on one dice and a number less than or equal to 4 on the other dice.
Solution:
Number of dice thrown = 2
Each die has 1 to 6 numbers on its faces Number of possible outcomes = 6 X 6 = 36
(i) A doublet : These can be (1, 1), (2, 2),(3, 3), (4, 4), (5, 5) and (6, 6) which are 6
∴ Number of favourable outcome = 6

(ii) A number less than 3 on each die which can be (1, 1), (1, 2), (2, 1), (2, 2) which are 4 in numbers
∴ Number of favourable outcome = 4

(iii) An odd number as a sum which can be (1, 1), (1,3), (1,5), (2, 1), (2,3), (2,5), (3, 1), (3,3), (3,5), (4, 1), (4,3), (4, 5), (5,1),(5,3), (5,5), (6, 1), (6, 3), (6, 5) which are 18 in numbers.
∴ Number of favourable outcome = 18

(iv) Total of at most 10
Which can be = 36 – 3 (which can be (5, 6), (6, 6), (6, 5) = 33
∴ Number of favourable outcome = 33

(v) An odd number on one die and a number less than or equal to 4 on the other die
(1, 1), (1,2), (1,3), (1,4), (3,1), (3,2), (3, 3), (3,4) , (5, 1), (5, 2), (5, 3), (5, 4), (2, 1), (3, 1), (4, 1),(1, 3), (2, 3), (2, 5), (3, 1), (3, 5), (4, 1), (4, 3), (4,5) which are 23 in numbers
∴ Number of favourable outcome = 23

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 25 Probability Ex 25B  are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.