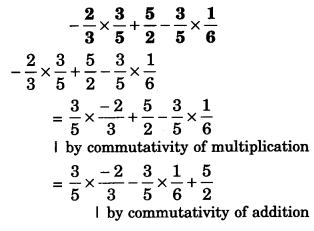Tag: NCERT Solutions for Class 8 Maths

NCERT Solutions for Class 8 Maths Chapter 1 Rational Numbers Ex 1.2 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 1 Rational Numbers Ex 1.2.

• Rational Numbers Class 8 Ex 1.1

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 1
Chapter Name	Rational Numbers
Exercise	Ex 1.2
Number of Questions Solved	7
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 1 Rational Numbers Ex 1.2

Question 1.
Represent these numbers on the number line.
(i) \(\frac { 7 }{ 4 } \)
(ii) \(\frac { -5 }{ 6 } \)
Solution.
(i) \(\frac { 7 }{ 4 } \)
We make 7 markings of distance \(\frac { 1 }{ 4 } \) each on the right of 0 and starting from 0. The seventh marking represents \(\frac { 7 }{ 4 } \)

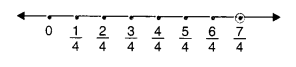
(ii) \(\frac { -5 }{ 6 } \)
We make 5 markings of distance \(\frac { 1 }{ 6 } \) each on the right of 0 and starting from 0. The seventh marking represents \(\frac { -5 }{ 6 } \)

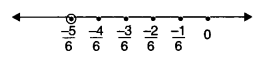
Question 2.
Represent \(\frac { -2 }{ 11 } ,\frac { -5 }{ 11 } ,\frac { -9 }{ 11 } \) on the number line.
Solution.
We make 9 markings of distance \(\frac { 1 }{ 11 } \) each on the left of 0 and starting from 0.
The second marking represents \(-\frac { 2 }{ 11 } \) the fifth marking represents \(-\frac { 5 }{ 11 } \) and the ninth marking represents \(-\frac { 9 }{ 11 } \)

Question 3.
Write five rational numbers which are smaller than 2.
Solution.
Five rational numbers which are smaller than 2 are 1, \(\frac { 1 }{ 2 } \),0, -1, \(-\frac { 1 }{ 2 } \)

Question 4.
Find ten rational numbers between \(-\frac { 2 }{ 5 } \) and \(\frac { 1 }{ 2 } \)
Solution.

Question 5.
Find five rational numbers between:

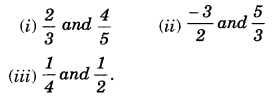
Solution.

Question 6.
Write five rational numbers greater than -2.
Solution.
Five rational numbers greater than -2 are:
\(\frac { -3 }{ 2 } \), -1, \(\frac { -1 }{ 2 } \), 0, \(\frac { 1 }{ 2 } \)
There can be many more such rational numbers

Question 7.
Find ten rational numbers between \(\frac { 3 }{ 5 } \) and \(\frac { 3 }{ 4 } \)
Solution.

We hope the NCERT Solutions for Class 8 Maths Chapter 1 Rational Numbers Ex 1.2 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 1 Rational Numbers Ex 1.2, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities Ex 8.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities Ex 8.1.

• Comparing Quantities Class 8 Ex 8.2
• Comparing Quantities Class 8 Ex 8.3

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 8
Chapter Name	Comparing Quantities
Exercise	Ex 8.1
Number of Questions Solved	6
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities Ex 8.1

Question 1.
Find ratio of the following:
(a) Speed of a cycle 15 km per hour to the speed of scooter 30 km per hour.
(b) 5 m to 10 km
(c) 50 paise ₹ 5
Solution.
(a)
Speed of a cycle 15 km per hour to the speed of scooter 30 km per hour
Ratio of the speed of cycle which is 15 km per hour to the speed of scooter which is 30 km per hour
= 15 km per hour : 30 km per hour = 15 : 30
= \(\frac { 15 }{ 30 } =\frac { 1 }{ 2 } \) or 1 : 2

(b)
5 m to 10 km
10 km = 10 x 1000 m = 10000 m
∴ Ratio of 5 m to 10 km
= 5 m : 10 km
= 5 m : 10000 m
= 5 : 10000
= \(\frac { 5 }{ 10000 } =\frac { 1 }{ 2000 } \) or 1 : 2000

(c)
50 paise to ₹ 5
₹ 5 = 5 x 100 = 500 paise
∴ Ratio of 50 paise to ₹ 5
= 50 paise : ₹ 5
= 50 paise : 500 paise
= 50 : 500
= \(\frac { 50 }{ 500 } =\frac { 1 }{ 10 } \) or 1 : 10

Question 2.
Convert the following ratios to percentages:
(a) 3: 4
(b) 2 : 3
Solution.
(a) 3: 4

(b) 2 : 3

Question 3.
72% of 25 students are good in mathematics. How many are not good in Mathematics?
Solution.
Total number of students = 25
Students good in mathematics = 72%
∴ Students who are not good in mathematics
= (100 – 72)% = 28%
∴ Number of those students who are not good in mathematics
= 28% of 25
= \(\frac { 28 }{ 100 } \times 25=7\)
Hence, 7 students are not good in mathematics.

Question 4.
A football team won 10 matches out of the total number of matches they played. If their win percentage was 40, then how many matches did they play in all?
Solution.
∵ If 40 matches were won, then the total number of matches played = 100
∴ If 1 match was won, then the total number of matches played = \(\frac { 100 }{ 40 } \)
∴ If 10 matches were won, then the total number of matches played = \(\frac { 100 }{ 40 } \times 10=25\)
Hence, they played 25 matches in all.
Aliter: According to the question, 40% of (total number of matches) = 10
⇒ \(\frac { 40 }{ 100 } \) x (total number of matches) = 10
⇒ Total number of matches = \(\frac { 10\times 100 }{ 40 } \) = 25
Hence, they played 25 matches in all.

Question 5.
If Chameli had ₹ 600 left after spending 75% of her money, how much did she have in the beginning?
Solution.
Percentage of money left = (100 – 75)% = 25%
∵ If Chameli had ₹ 25 left, then the money she had in the beginning = 100
∴ If Chameli had ₹ 1 left, then the money she had in the beginning = \(\frac { 100 }{ 25 } \)
∴ If Chameli has ₹ 600 left, then the money she had in the beginning = \(\frac { 100 }{ 25 } \times 600=2400\)
Hence, the money she had in the beginning was ₹ 2400.
Aliter:
According to the question, 25% of total money = ₹ 600
⇒ \(\frac { 25 }{ 100 } \) x total money = ₹ 600
⇒ Total money = ₹ \(\frac { 600\times 100 }{ 25 } \) = ₹ 2400
Hence, the money she had in the beginning was ₹ 2400

Question 6.
If 60% of people in a city like a cricket, 30% like football and the remaining like other games then what percent of the people like other games? If the total number of people are 50 lakh, find the exact number who like each type of game.
Solution.
People who like other games = [100 – (60 + 30)]%
= (100 – 90)% = 10%.
Total number of people = 50 lakh
= 5000000
∴ Number of people who like cricket = 60% of 5000000
= 5000000 x \(\frac { 60 }{ 100 } \)
= 3000000 = 30 lakh
Number of people who like football = 30% of 5000000
= 5000000 x \(\frac { 30 }{ 100 } \)
= 1500000 = 15 lakh
Number of people who like the other games
= 10% of 5000000
= 5000000 x \(\frac { 10 }{ 100 } \)
= 5,00,000 = 5 lakh

 

We hope the NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities Ex 8.1 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities Ex 8.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.1.

• Mensuration Class 8 Ex 11.2
• Mensuration Class 8 Ex 11.3
• Mensuration Class 8 Ex 11.4

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 11
Chapter Name	Mensuration
Exercise	Ex 11.1, Ex 11.2, Ex 11.3, Ex 11.4
Number of Questions Solved	5
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.1

Question 1.
A square and a rectangular field with measurements as given in the figure have the same perimeter. Which field has a larger area?


Solution.
Area of the square field = a x a
= 60 m x 60 m = 3,600 \({ m }^{ 2 }\)
Perimeter of the square field = 4a
= 4 x 60 m = 240 m
∴ Perimeter of rectangular field = 240 m
⇒ 2(l + b) = 240
⇒ 2(80 + b) = 240
where b m is the breadth of the rectangular field
⇒ 80 + b = \(\frac { 240 }{ 2 } \) ⇒ 80 + bx = 120
⇒ b = 120 – 80 = 40
∴ Breadth = 40 m
∴ Area of rectangular field
= l x b = 80 m x 40 m = 3,200 \({ m }^{ 2 }\)
So, the square field (a) has a larger area

Question 2.
Mrs. Kaushik has a square plot ‘ with the measurement as shown in the figure. She wants to construct a house in the middle of the plot. A garden is developed around the house. Find the total cost of developing a: garden around the house at the rate of ₹ 55 per \({ m }^{ 2 }\).
Solution.
Area of the square plot = a x a
= 25 x 25 \({ m }^{ 2 }\) = 625 \({ m }^{ 2 }\)
Area of the house = a x b
= 20 x 15 \({ m }^{ 2 }\) = 300 \({ m }^{ 2 }\)
∴ Area of the garden
= Area of the square plot – Area of the house
= 625 \({ m }^{ 2 }\) – 300 \({ m }^{ 2 }\)
= 325 \({ m }^{ 2 }\)
∵ The cost of developing the garden per square metre = ₹ 55.
∴ Total cost of developing the garden
= ₹ 325 x 55
= ₹ 17,875.

Question 3.
The shape of a garden is rectangular in the middle and semicircular at the ends as shown in the diagram. Find the area and the perimeter of this garden.

Solution.

Question 4.
A flooring tile has the shape of a parallelogram whose base is 24 cm and the cor-responding height is 10 cm. How many such tiles are required to cover a floor of area 1080 m2? (If required you can split the tiles in whatever way you want to fill up the corners).
Solution.
Area of a flooring tile = bh
= 24 x 10 \({ cm }^{ 2 }\)
= 240 \({ cm }^{ 2 }\)
Area of the floor
= 1080 \({ m }^{ 2 }\)
= 1080 x 100 x 100 \({ cm }^{ 2 }\)
∵ m2 = 100 x 100 \({ cm }^{ 2 }\)

∴ Number of tiles required to cover the floor
=\(\frac { Area\quad of\quad the\quad floor\quad }{ Area\quad of\quad a\quad flooring\quad tile } \)
= \(\frac { 1080\times 100\times 100\quad }{ 240 } \)
= 45000.

Question 5.
An ant is moving around a few food pieces of different shapes scattered on the floor. For which food-piece would the ant have to take a longer round? Remember, the circumference of a circle can be obtained by using the expression c = 2πr, where r is the radius of the circle.


Solution.

 

We hope the NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.1 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 4 Practical Geometry Ex 4.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 4 Practical Geometry Ex 4.1.

• Practical Geometry Class 8 Ex 4.2
• Practical Geometry Class 8 Ex 4.3
• Practical Geometry Class 8 Ex 4.4
• Practical Geometry Class 8 Ex 4.5

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 4
Chapter Name	Practical Geometry
Exercise	Ex 4.1
Number of Questions Solved	1
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 4 Practical Geometry Ex 4.1

Question 1.
Construct the following quadrilaterals:
(i) Quadrilateral ABCD
AB = 4.5 cm
BC = 5.5 cm
CD = 4 cm
AD = 6 cm
AC = 7 cm

(ii) Quadrilateral JUMP
JU = 3.5 cm
UM = 4 cm
MP = 5 cm
PJ = 4.5 cm
PU 6.5 cm

(iii) Parallelogram MORE
OR = 6 cm
RE = 4.5 cm
EO = 7.5 cm

(iv) Rhombus BEST
BE = 4.5 cm
ET = 6 cm
Solution.
(i) Steps of Construction

1. Draw AB 4.5 cm
2. With A as centre and radius AC = 7 cm, draw an arc.
   
3. With B as center and radius BC = 5.5 cm, draw another arc to intersect the arc drawn in step (2) at C.
4. With A as center and radius AD = 6 cm, draw an arc on the side of AC, opposite to that of B.
5. With C as center and radius CD = 4 cm, draw another arc to intersect the arc drawn in step (4) at D.
6. Join BC, CD, DA, and AC.

Then, ABCD is the required quadrilateral.

(ii) Steps of Construction

1. Draw JU = 3.5 cm
2. With J as center and radius JP = 4.5 cm, draw an arc.
3. With U as center and radius UP = 6.5 cm, draw another arc to intersect the arc drawn in step 2 at P.
   
4. With U as center and radius UM = 4 cm, draw an arc on the side of PU opposite to that of J.
5. With P as center and radius PM = 5 cm, draw another arc to intersect the arc drawn in step 4 at M.
6. Join UM, MP, PJ, and UP.

Then, JUMP is the required quadrilateral.

(iii) Steps of Construction
[We know that in a parallelogram, opposite sides are equal in length.
∴ MO = ER = 4.5 cm and ME – OR = 6 cm]

1. Draw MO = 4.5 cm
2. With M as center and radius ME = 6 cm, draw an arc.
   
3. With O as center and radius OE = 7.5 cm, draw an arc to intersect the arc drawn in step 2 at E.
4. With O as center and radius OR = 6 cm, draw an arc on the side of OE opposite to that of M.
5. With E as center and radius ER = 4.5 cm, draw another arc to intersect the arc drawn in step 4 at R.
6. Join OR, RE, EM, and EO.

Then, MORE is the required parallelogram.

(iv) Steps of Construction
[We know that in a rhombus, all the sides are equal in length.
∴ BE = ES = ST = TB = 4.5 cm]

1. Draw BE = 4.5 cm
2. With B as centre and radius BT = 4.5 cm, draw an arc.
   
3. With E as center and radius
   ET = 6 cm, draw another arc to intersect the arc drawn in step 2 at T.
4. With E as center and radius
   ES = 4.5 cm, draw an arc on the side of ET opposite to that of B.
5. With T as center and radius
   TS = 4.5 cm, draw another arc to
   intersect the arc drawn in step 4 at S.
6. Join ES, ST, TB, and TE.

Then, BEST is the required rhombus.

 

We hope the NCERT Solutions for Class 8 Maths Chapter 4 Practical Geometry Ex 4.1 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 4 Practical Geometry Ex 4.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 1 Rational Numbers Ex 1.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 1 Rational Numbers Ex 1.1.

• Rational Numbers Class 8 Ex 1.2

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 1
Chapter Name	Rational Numbers
Exercise	Ex 1.1
Number of Questions Solved	11
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 1 Rational Numbers Ex 1.1

Question 1.
Using appropriate properties find:
(i) \(-\frac { 2 }{ 5 } \times \frac { 3 }{ 5 } +\frac { 5 }{ 2 } -\frac { 3 }{ 5 } \times \frac { 1 }{ 6 } \)
(ii) \(\frac { 2 }{ 5 } \times \left( -\frac { 3 }{ 7 } \right) -\frac { 1 }{ 6 } \times \frac { 3 }{ 2 } +\frac { 1 }{ 14 } \times \frac { 2 }{ 5 } \)
Solution.

Question 2.
Write the additive inverse of each of the following:

Solution.
(i) \(\frac { 2 }{ 8 } \)
Additive inverse of \(\frac { 2 }{ 8 } \) is \(\frac { 2 }{ 8 } \)

(ii) \(-\frac { 5 }{ 9 } \)
\(\frac { -6 }{ -5 } =\frac { 6 }{ 5 } \)
Additive inverse of \(\frac { -6 }{ -5 } \) is \(\frac { -6 }{ 5 } \)

(iii) \(\frac { -6 }{ -5 } \)
\(\frac { -6 }{ -5 } \)=\(\frac { 6 }{ 5 } \)
Additive inverse of \(\frac { -6 }{ -5 } \) is \(\frac { -6 }{ 5 } \)

(iv) \(\frac { 2 }{ -9 } \)
Additive inverse of \(\frac { 2 }{ -9 } \) is \(\frac { 2 }{ 9 }\)

(v) \(\frac { 19 }{ -6 } \)
Additive inverse of  \(\frac { 19 }{ -6 } \) is \(\frac { 19 }{ 6 }\)

Question 3.
Verify that – (-x) = x for :
(i) \(x=\frac { 11 }{ 15 } \)
(ii) \(x=-\frac { 13 }{ 17 } \)
Solution.

Question 4.
Find the multiplicative inverse of the following:

Solution.

Question 5.
Name the property under multiplication used in each of the following:
(i) \(\frac { -4 }{ 5 } \times \left( 1 \right) =1\times \frac { -4 }{ 5 } =-\frac { 4 }{ 5 } \)
(ii) \(-\frac { 13 }{ 17 } \times \frac { -2 }{ 7 } =\frac { -2 }{ 7 } \times \frac { -13 }{ 17 } \)
(iii) \(\frac { -19 }{ 29 } \times \frac { 29 }{ -19 } =1\)
Solution.
(i) 1 is the multiplicative identity
(ii) Commutativity of multiplication
(iii) Multiplicative inverse.

Question 6.
Multiply \(\frac { 6 }{ 13 } \) by the reciprocal of \(\frac { -7 }{ 16 } \)
Solution.
Reciprocal of \(\frac { -7 }{ 16 } \) is \(\frac { -16 }{ 7 } \)
Now,
\(\frac { 6 }{ 13 } \times \frac { -16 }{ 7 } =\frac { 6\times \left( -16 \right) }{ 13\times 7 } =\frac { -96 }{ 91 } \)

Question 7.
Tell what property allows you to compute : \(\frac { 1 }{ 3 } \times \left( 6\times \frac { 4 }{ 3 } \right) \) as \(\left( \frac { 1 }{ 3 } \times 6 \right) \times \frac { 4 }{ 3 } \)
Solution.
Associativity.

Question 8.
Is the \(\frac { 8 }{ 9 } \) multiplicative inverse of \(-1\frac { 1 }{ 8 } \) ? Why or why not?
Solution.
\(-1\frac { 1 }{ 8 } =-\frac { 9 }{ 8 } \)
Now, \(\frac { 8 }{ 9 } \times \frac { -9 }{ 8 } =-1\neq 1\)
So, No ; \(\frac { 8 }{ 9 } \) is not the multiplicative inverse of \(-1\frac { 1 }{ 8 } \left( =-\frac { 9 }{ 8 } \right) \) because the product of \(\frac { 8 }{ 9 } \) and -13(-) and \(-1\frac { 1 }{ 8 } \left( =-\frac { 9 }{ 8 } \right) \) is not 1.

Question 9.
Is 0.3 the multiplicative inverse of \(3\frac { 1 }{ 3 }\) ? Why or why not?
Solution.
Yes ; 0.3 is the multiplicative inverse of \(\frac { 10 }{ 3 } \) because
\(\frac { 3 }{ 10 } \times \frac { 10 }{ 3 } =\frac { 3\times 10 }{ 10\times 3 } =\frac { 30 }{ 30 } =1\)

Question 10.
Write :
(i) The rational number that does not have a reciprocal.
(ii) The rational numbers that are equal to their reciprocals.
(iii) The rational number that is equal to its negative.
Solution.
(i) The rational number ‘0′ does not have a reciprocal.
(ii) The rational numbers 1 and (-1) are equal to their own reciprocals.
(iii) The rational number 0 is equal to its negative.

Question 11.
Fill in the blanks :
(i) Zero has……….reciprocal.
(ii) The numbers……….and………are their own reciprocals.
(iii) The reciprocal of – 5 is.………….
(iv) Reciprocal of \(\frac { 1 }{ x } \), where \(x\neq 0\)
(v) The product of two rational numbers is always a.………
(vi) The reciprocal of a positive rational number is……….
Solution.
(i) Zero has no reciprocal.
(ii) The numbers 1 and -1 are their own reciprocals.
(iii) The reciprocal of – 5 is \(-\frac { 1 }{ 5 } \)
(iv) Reciprocal of \(\frac { 1 }{ x } \), where \(x\neq 0\) is x.
(v) The product of two rational numbers is always a rational number.
(vi) The reciprocal of a positive rational number is positive.

We hope the NCERT Solutions for Class 8 Maths Chapter 1 Rational Numbers Ex 1.1 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 1 Rational Numbers Ex 1.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 7 Cubes and Cube Roots Ex 7.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 7 Cubes and Cube Roots Ex 7.1.

• Cubes and Cube Roots Class 8 Ex 7.2

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 7
Chapter Name	Cubes and Cube Roots
Exercise	Ex 7.1
Number of Questions Solved	4
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 7 Cubes and Cube Roots Ex 7.1

Question 1.
Which of the following numbers are not perfect cubes?
(i) 216
(ii) 128
(iii) 1000
(iv) 100
(v) 46656
Solution.
(i) 216

(ii) 128

(iii) 1000

(iv) 100

(v) 46656

Question 2.
Find the smallest number by which each of the following numbers must be multiplied to obtain a perfect cube.
(i) 243
(ii) 256
(iii) 72
(iv) 675
(v) 100
Solution.
(i) 243

(ii) 256

(iii) 72

(iv) 675

(v) 100

Question 3.
Find the smallest number by which each of the following numbers must be divided to obtain a perfect cube.
(i) 81
(ii) 128
(iii) 135
(iv) 192
(v) 704
Solution.
(i) 81

(ii) 128

(iii) 135

(iv) 192

(v) 704

Question 4.
Parikshit makes a cuboid of plasticine of sides 5 cm, 2 cm, 5 cm. How many such cuboids will he need to form a cube?
Solution.
Volume of a cuboid = 5 x 2 x 5 \({ cm }^{ 3 }\).
Since there is only one 2 and only two 5’s in the prime factorization, so, we need 2 x 2 x 5, i.e., 20 to make a perfect cube. Therefore, we need 20 such cuboids to make a cube.

 

We hope the NCERT Solutions for Class 8 Maths Chapter 7 Cubes and Cube Roots Ex 7.1 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 7 Cubes and Cube Roots Ex 7.1, drop a comment below and we will get back to you at the earliest.

 

NCERT Solutions for Class 8 Maths Chapter 10 Visualising Solid Shapes Ex 10.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 10 Visualising Solid Shapes Ex 10.1.

• Visualising Solid Shapes Class 8 Ex 10.2
• Visualising Solid Shapes Class 8 Ex 10.3

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 10
Chapter Name	Visualising Solid Shapes
Exercise	Ex 10.1
Number of Questions Solved	4
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 10 Visualising Solid Shapes Ex 10.1

Question 1.
For each of the given solid, the two views are given. Match for each solid the corresponding top and front views. The first one is done for you.

Solution.

Question 2.
For each of the given solid, the three views are given. Identify for each solid the corresponding top, front and side views.

Solution.

Question 3.
For each given solid, identify the top view, front view, and side view.

Solution.

Question 4.
Draw the front view, side view and top view of the given objects,

Solution.

 

We hope the NCERT Solutions for Class 8 Maths Chapter 10 Visualising Solid Shapes Ex 10.1 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 10 Visualising Solid Shapes Ex 10.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Ex 3.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Ex 3.1.

• Understanding Quadrilaterals Class 8 Ex 3.2
• Understanding Quadrilaterals Class 8 Ex 3.3
• Understanding Quadrilaterals Class 8 Ex 3.4

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 3
Chapter Name	Understanding Quadrilaterals
Exercise	Ex 3.1
Number of Questions Solved	7
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Ex 3.1

Question 1.
Given here are some figures :

Classify each of them on the basis of the following :
(a) Simple curve
(b) Simple closed curve
(c) Polygon
(d) Convex polygon
(e) Concave polygon
Solution.
(a) ⟷ 1, 2, 5, 6, 7
(b) ⟷ 1, 2, 5, 6, 7

Question 2.
How many diagonals does each of the following have?
(a) A convex quadrilateral
(b) A regular hexagon
(c) A triangle.
Solution.
(a) → 2
(b) → 9
(c) → 0

Question 3.
What is the sum of the measures of the angles of a convex quadrilateral? Will this property hold if the quadrilateral is not convex? (Make a non-convex quadrilateral and j try!)
Solution.
The sum of the measures of the angles of a convex quadrilateral is 360°.
Yes! this property will hold if the; quadrilateral is not convex.
If the quadrilateral is not convex, then it will be concave.
Split the concave quadrilateral ABCD into two triangles ABD and CBD by joining BD.

Question 4.
Examine the table. (Each figure is divided into triangles and the sum of the angles deduced from that.)

What can you say about the angle sum of a convex polygon with number of sides ?
(a) 7
(b) 8
(c) 10
(d) n
Solution.
(a) 7
Angle sum = \(\left( 7-2 \right) \times { 180 }^{ \circ }\)
= \(5\times { 180 }^{ \circ }={ 900 }^{ \circ }\)

(b) 8
Angle sum = \(\left( 8-2 \right) \times { 180 }^{ \circ }\)
= \(6\times { 180 }^{ \circ }={ 1080 }^{ \circ }\)

(c) 10
Angle sum = \(\left( 10-2 \right) \times { 180 }^{ \circ }\)
= \(8\times { 180 }^{ \circ }={ 1440 }^{ \circ }\)

(d) n
Angle sum = \(\left( n-2 \right) \times { 180 }^{ \circ }\)

Question 5.
What is a regular polygon? State the name of a regular polygon of
(i) 3 slides
(ii) 4 slides
(iii) 6 slides
Solution.
A polygon, which is both ‘equilateral’ and ‘equiangular’, is called a regular polygon.
(i) 3 slides
The name of the regular polygon of 3 slides is an equilateral triangle.
(ii) 4 slides
The name of the regular polygon of 4 slides is square
(iii) 6 slides
The name of the regular polygon of 6 slides is a regular hexagon

Question 6.
Find the angle measure x in the following figures.

Solution.

Question 7.

(a) Find x+y+z

(b) Find x+y+z+w.
Solution.

 

We hope the NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Ex 3.1 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Ex 3.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 16 Playing with Numbers Ex 16.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 16 Playing with Numbers Ex 16.1.

• Playing with Numbers Class 8 Ex 16.2

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 16
Chapter Name	Playing with Numbers
Exercise	Ex 16.1
Number of Questions Solved	1
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 16 Playing with Numbers Ex 16.1

Question 1.
Find the values of the letters in each of the following and give reasons for the steps involved.

Solution.
1.
Here, there are two letters A and B whose values are to be found out.
Let us see the sum in unit’s column. It is A + 5 and we get 2 from this. So,

2.
Here, there are three letters A, B and C whose values are to be found out.
Let us see the sum in unit’s column. It is A + 8 and we get 3 from this. So A has to be 5

That is, A = 5, B = 4 and C = 1.

4.
Here, there are two letters A and B whose values are to be found out.

5.
Here, there are three letters A, B and C whose values are to be found out.

∴ A = 5, B = 0 and C = 1

6.
Here, there are three letters A, B and C, whose values are to be found out.

7.
Here, there are two letters A and B whose values are to be found out. We have

8.
Here, there are two letters A and B whose values are to be found out.

10.
We are to find out values of A and B

We hope the NCERT Solutions for Class 8 Maths Chapter 16 Playing with Numbers Ex 16.1 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 16 Playing with Numbers Ex 16.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 15 Introduction to Graphs Ex 15.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 15 Introduction to Graphs Ex 15.1.

• Introduction to Graphs Class 8 Ex 15.2
• Introduction to Graphs Class 8 Ex 15.3

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 15
Chapter Name	Introduction to Graphs
Exercise	Ex 15.1
Number of Questions Solved	7
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 15 Introduction to Graphs Ex 15.1

Question 1.
The following graph shows the temperature of a patient in a hospital, recorded every hour.
(a) What was the patient’s temperature at 1 p.m.?
(b) When was the patient’s temperature 38.5°C?
(c) The patient’s temperature was the same two times during the period given. What were these two times?
(d) What was the temperature at 1.30 p.m.? How did you arrive at your answer?
(e) During which periods did the patient’s temperature showed an upward trend?

Solution.
(а) The patient’s temperature at 1 p.m. was 36.5°C.
(b) The patient’s temperature was 38.5°C at 10.50 a.m. and 12 noon.
(c) The two times when the patient’s temperature was the same were 1 p.m. and 2 p.m.
(d) The temperature at 1.30 p.m. was 36.5°C.
From the graph, we see that the temperature was constant from 1 p.m. to 2 p.m. Since 1.30 p.m. comes in between 1 p.m. and 2 p.m., therefore we arrived at our answer.
(e) The patient’s temperature showed an upward trend during the periods 9 a.m. to 10 a.m., 10 a.m. to 11 a.m. and 2 p.m. to 3 p.m.

Question 2.
The following line graph shows the yearly sales figures for a manufacturing company.
(a) What were the sales in
(i) 2002
(ii) 2006?

(b) What were the sales in
(i) 2003
(ii) 2005?

(c) Compute the difference between sales in 2002 and 2006.
(d) In which year was there the greatest difference between the sales as compared to its previous year?

Solution.
(а) The sales in
(i) 2002 were ₹ 4 crores and in
(ii) 2006 were ₹ 8 crores.

(b) The sales in
(i) 2003 were ₹ 7 crores and in
(ii) 2005 were ₹ 10 crores.

(c) The difference between the sales in 2002 and 2006
= ₹ 8 crores – ₹ 4 crores = ₹ 4 crores

(d) The difference between sales in 2002 and 2003
= ₹ 7 crores – ₹ 4 crores = ₹ 3 crores
The difference between sales in 2003 and 2004
= ₹ 7 crores – ₹ 6 crores = ₹ 1 crore
The difference between the sales in 2004 and 2005
= ₹ 10 crores – ₹ 6 crores = ₹ 4 crores
The difference between sales in 2005 and 2006
= ₹ 10 crores – ₹ 8 crores = ₹ 2 crores
Therefore, in year 2005 the difference between the sales as compared to its previous year was the greatest.

Question 3.
For an experiment in Botany, two different plants, plant A and plant B were grown under similar laboratory conditions. Their heights were measured at the end of each week for 3 weeks. The results are shown by the following graph.

(a) How high was Plant A after
(i) 2 weeks
(ii) 3 weeks?

(b) How high was Plant B after
(i) 2 weeks
(ii) 3 weeks?

(c) How much did Plant A grow during
(d) How much did Plant B grow from the end of the 2nd week to the end of the 3rd week?
(e) During which week did Plant A grow most?
(f) During which week did Plant B grow least?
(g) Were the two plants of the same height during any week shown here? Specify.
Solution.
(а) The Plant A
after (i) 2 weeks was 7 cm high and
after (ii) 3 weeks was 9 cm high.

(b) The Plant B
after (i) 2 weeks was 7 cm high and
after (ii) 3 weeks was 10 cm high.

(c) The Plant A grew 9 cm – 7 cm = 2 cm during the 3rd week.

(d) From the end of the 2nd week to the end of the 3rd week, Plant B grew
= 10 cm – 7 cm = 3 cm.

(e) The Plant A grew in 1st week
= 2 cm – 0 cm = 2 cm
The Plant A grew in 2nd week
= 7 cm – 2 cm = 5 cm
The Plant A grew in 3rd week
= 9 cm – 7 cm = 2 cm
Therefore, Plant A grew mostly in the second week.

(f) Plant B grew in 1st week
= 1 cm – 0 cm = 1 cm
Plant B grew in 2nd week
= 7 cm – 1 cm = 6 cm
Plant B grew in 3rd week
= 10 cm – 7 cm = 3 cm
Therefore, Plant B grew least in the first week.

(g) At the end of 2nd week, the two plants shown here were of the same height.

Question 4.
The following graph shows the temperature forecast and the actual temperature for each day of a week:

(a) On which days was the forecast temperature the same as the actual temperature?
(b) What was the maximum forecast temperature during the week?
(c) What was the minimum actual temperature during the week?
(d) On which day did the actual temperature differ the most from the forecast temperature?
Solution.
(a) The forecast temperature was the same as the actual temperature on Tuesday, Friday and Sunday.
(b) The maximum forecast temperature during the week was 35°C.
(c) The minimum actual temperature during the week was 15°C.
(d)

Therefore, the actual temperature differed the most from the forecast temperature on Thursday.

Question 5.
Use the tables below to draw linear graphs.
(a) The number of days a hill side city received snow in different years.

(b) Population (in thousands) of men and women in a village in different years.

Solution.
(a)

(b)

Question 6.
Courier-person cycles from a town to a neighboring suburban area to deliver a parcel to a merchant. His distance from the town at different times is shown by the following graph.
(a) What is the scale taken for the time axis?
(b) How much time did the person take for the travel?
(c) How far is the place of the merchant from the town?
(d) Did the person stop on his way? Explain.
(e) During which period did he ride fastest?

Solution.
(a) The scale taken for the time axis is 4 units = 1 hour.
(b) The time taken by the person for the travel 8 a.m. to 11.30 a.m. = \(3\frac { 1 }{ 2 } \) hours.
(c) The place of the merchant from the town in 22 km.
(d) Yes. This is indicated by the hori¬zontal part of the graph (10 a.m. – 10.30 a.m.)
(e) He rides fastest between 8 a.m. and 9 a.m. (As line is more steep in this period).

Question 7.
Can there be a time-temperature graph as follows ? Justify your answer.


Solution.
(i) Yes; it can be
It shows a time-temperature graph. It shows an increase in temperature with an increase in time.
(ii) Yes; it can be
It shows a time-temperature graph.
It shows a decrease in temperature with increase in time.
(iii) It cannot be a time-temperature graph because it shows infinitely many different temperatures at one particular time which is not possible.
(iv) Yes; it can be
It shows a time-temperature graph,
It shows a fixed temperature at different times.

 

We hope the NCERT Solutions for Class 8 Maths Chapter 15 Introduction to Graphs Ex 15.1 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 15 Introduction to Graphs Ex 15.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.1.

• Algebraic Expressions and Identities Class 8 Ex 9.2
• Algebraic Expressions and Identities Class 8 Ex 9.3
• Algebraic Expressions and Identities Class 8 Ex 9.4
• Algebraic Expressions and Identities Class 8 Ex 9.5

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 9
Chapter Name	Algebraic Expressions and Identities
Exercise	Ex 9.1
Number of Questions Solved	4
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.1

Question 1.
Identify the terms, their coefficients for each of the following expressions:
(i) \({ 5xyz }^{ 2 }-3zy\)
(ii) \(1+x+{ x }^{ 2 }\)
(iii) \(4{ x }^{ 2 }{ y }^{ 2 }-4{ x }^{ 2 }{ y }^{ 2 }{ z }^{ 2 }+{ z }^{ 2 }\)
(iv) 3 – pq + qr – rp
(v) \(\frac { x }{ 2 } +\frac { y }{ 2 } -xy\)
(vi) 0.3a – 0.6ab + 0.5b.
Solution.
(i) \({ 5xyz }^{ 2 }-3zy\)

(ii) \(1+x+{ x }^{ 2 }\)

(iii) \(4{ x }^{ 2 }{ y }^{ 2 }-4{ x }^{ 2 }{ y }^{ 2 }{ z }^{ 2 }+{ z }^{ 2 }\)

(iv) 3 – pq + qr – rp

(v) \(\frac { x }{ 2 } +\frac { y }{ 2 } -xy\)

(vi)0.3a – 0.6ab + 0.5b.

Question 2.
Classify the following polynomials as monomials, binomials, trinomials. Which polynomials do not fit in any of these three categories?

Solution.

Question 3.
Add the following.
(i) ab – be, be – ca, ca – ab
(ii) a -b + ab, b – c + be, c – a + ac
(iii) \(2{ p }^{ 2 }{ q }^{ 2 }-3pq+4,\quad 5+7pq-3{ p }^{ 2 }{ q }^{ 2 }\)
(iv) \({ l }^{ 2 }+{ m }^{ 2 },\quad { m }^{ 2 }+{ n }^{ 2 },\quad { n }^{ 2 }+{ l }^{ 2 }\), 2lm + 2mn + 2nl.
Solution.
(i) ab – be, be – ca, ca – ab

(ii) a -b + ab, b – c + be, c – a + ac

(iii) \(2{ p }^{ 2 }{ q }^{ 2 }-3pq+4,\quad 5+7pq-3{ p }^{ 2 }{ q }^{ 2 }\)

(iv) \({ l }^{ 2 }+{ m }^{ 2 },\quad { m }^{ 2 }+{ n }^{ 2 },\quad { n }^{ 2 }+{ l }^{ 2 }\), 2lm + 2mn + 2nl.

Question 4.
(a) Subtract 4a – 7ab + 3b + 12 from 12a – 9ab + 56 – 3
(b) Subtract 3xy + 5yz – 7zx from 5xy – 2yz – 2zx + 10xyz
(c) Subtract \(4{ p }^{ 2 }q-3pq+5p{ q }^{ 2 }-8p+7q-10\) from \(18-3p-11q+5pq-2p{ q }^{ 2 }+5{ p }^{ 2 }q\)
Solution.

 

We hope the NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.1 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.1, drop a comment below and we will get back to you at the earliest.