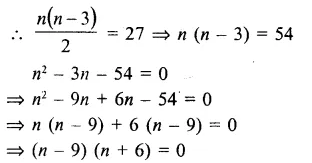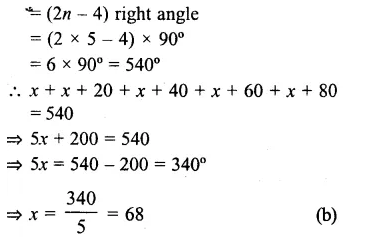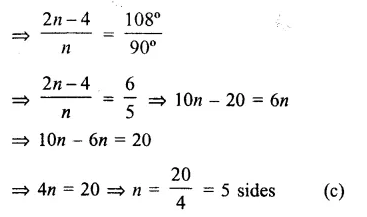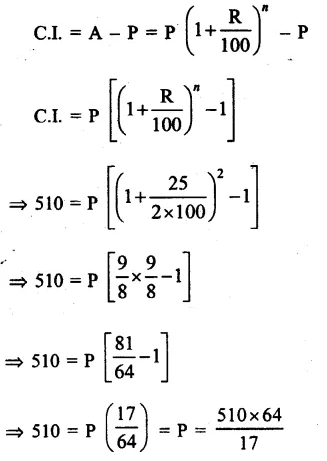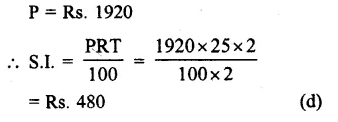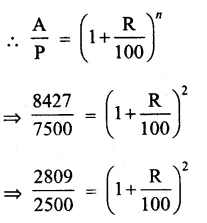Tag: RS Aggarwal Maths Solutions Class 8

RS Aggarwal Class 8 Solutions Chapter 16 Parallelograms Ex 16B

These Solutions are part of RS Aggarwal Solutions Class 8. RS Aggarwal Solutions Class 8 Chapter 16 Parallelograms Ex 16B.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 16 Parallelograms Ex 16A
• RS Aggarwal Solutions Class 8 Chapter 16 Parallelograms Ex 16B

Questions Tick the correct answer in each of the following.

Question 1.
Solution:
Answer = (c)
The diagonals of a rhombus are not necessarily equal but the diagonals in rectangle, square and isosceles trapezium are always equal.

Question 2.
Solution:
Answer = (c)
Each side of a rhombus

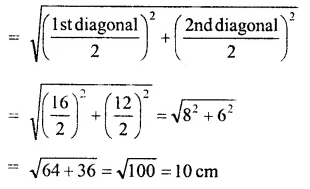
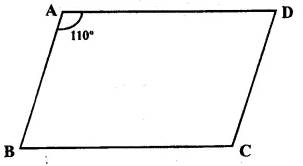
Question 3.
Solution:
Answer = (b)
The sum of adjacent angles of a || gm = 180°
2x + 25° + 3x – 5° = 180°
=> 5x + 20° = 180°
=> 5x = 180° – 20° = 160°
=> x = \(\\ \frac { 160 }{ 5 } \)
= 32°

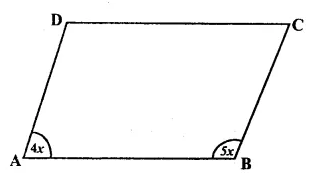
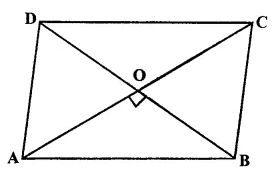
Question 4.
Solution:
Answer = (a)
The diagonals in rhombus, kite intersect each other at right angles.
But the diagonals of parallelogram do not necessarily intersect at right angles.

Question 5.
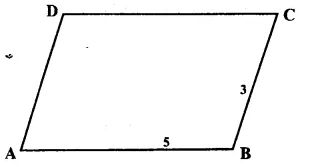
Solution:
Answer = (c)
Let l = 4x, b = 3x,
Then (diagonal)² = l² + b²
=> (25)² = 16x² + 9x²
=> 25x² = 625
=> x² = 25
=> x = 5
=> l = 4x = 4 x 5 = 20cm
b = 3x = 3 x 5 = 15cm
Perimeter = 2(l + b) = 2 (20 + 15)
= 2 x 35 = 70 cm

Question 6.
Solution:
Answer = (d)
AP and BP are the bisector of ∠A and ∠B
Sum of two adjacent angles of a ||gm = 180°
or ∠A + ∠B = 180°

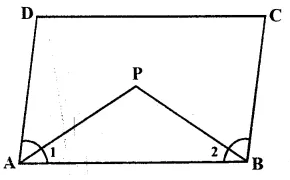
But ∠1 = \(\\ \frac { 1 }{ 2 } \) ∠A and ∠2 =\(\\ \frac { 1 }{ 2 } \) ∠B
∠1 + ∠2 = \(\\ \frac { 1 }{ 2 } \) ∠A + \(\\ \frac { 1 }{ 2 } \) ∠B
= \(\\ \frac { 1 }{ 2 } \) (∠A + ∠B)
= 180° x \(\\ \frac { 1 }{ 2 } \) = 90°
∠P = 180° – (∠1 + ∠2)
= 180° – 90° = 90°

Question 7.
Solution:
Answer = (b)
Let one adjacent angle = x
Then second angle (smallest) = \(\frac { 2 }{ 3 } x \)
x + \(\frac { 2 }{ 3 } x \) = 180°
= \(\frac { 5 }{ 3 } x \) = 180°
=> x = 180° x \(\\ \frac { 3 }{ 5 }\) = 108°
=> Smallest angle = 108° x \(\\ \frac { 2 }{ 3 }\) = 72°

Question 8.
Solution:
Answer = (a)
The diagonals of square, rhombus bisect the interior angle but the diagonals of a rectangle do not.

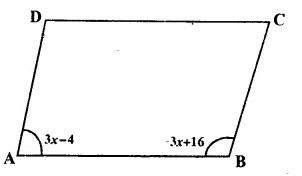
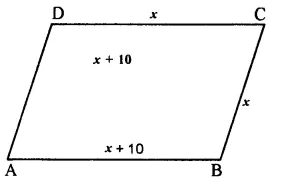
Question 9.
Solution:
Answer = (d)
Sides of a square are equal
2x + 3 = 3x – 5
=> 3x – 2x = 3 + 5
=> x = 8

Question 10.
Solution:
Answer = (c)
Let smallest angle = x
then largest angle = 2x – 24°
But x + 2x – 24° = 180°
=> 3x – 24° = 180°
=> 3x = 180° + 24 = 204°
=> x = \(\\ \frac { 204 }{ 3 }\) = 68°
largest angle = 180° – 68° = 112°

Hope given RS Aggarwal Solutions Class 8 Chapter 16 Parallelograms Ex 16B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 16 Parallelograms Ex 16A

These Solutions are part of RS Aggarwal Solutions Class 8. RS Aggarwal Solutions Class 8 Chapter 16 Parallelograms Ex 16A.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 16 Parallelograms Ex 16A
• RS Aggarwal Solutions Class 8 Chapter 16 Parallelograms Ex 16B

Question 1.
Solution:
In ||gm ABCD,
∠A = 110°
But ∠ C = ∠ A {Opposite angles of a ||gm are equal}

∴ ∠C = 110°
But ∠A + ∠B = 180°
(Sum of adjacent angles)
=> 110° + ∠B = 180°
=> ∠B – 180° – 110° = 70°
But ∠ D = ∠ B (opposite angles)
∴ ∠ D = 70°
Hence ∠B = 70°, ∠C = 110° and ∠D = 70° Ans.

Question 2.
Solution:
In a parallelogram, sum of two adjacent angles is 180°
But these are equal to each other
∴ Each angle will be \(\frac { 180^{ o } }{ 2 } \)
= 90° Ans.

Question 3.
Solution:
The ratio between two adjacent angles of a ||gm ABCD are in the ratio 4 : 5

Let ∠ A = 4x and ∠ B = 5x
But ∠A + ∠B = 180°
=> 4x + 5x = 180°
=> 9x = 180°
∴ x = \(\frac { 180^{ o } }{ 9 } \)
= 20°
∴ ∠A = Ax = 4 x 20° = 80°
∠B = 5x = 5 x 20 = 100° Ans.

Question 4.
Solution:
In || gm ABCD, ∠ A and ∠ B are two adjacent angles
Let ∠ A = (3x – 4)° and ∠ B = (3x + 16)°
But ∠A + ∠B = 180°

=> (3x – 4)° + (3x + 16) = 180°
=> 3x – 4° + 3x + 16° = 180°
=> 6x + 12° = 180°
=> 6x= 180° – 12°
=> 6x = 168
=> x = \(\\ \frac { 168 }{ 6 } \) = 28°
∴ x = 28°
Now ∠A = 3x – 4 = 3 x 28° – 4° = 84° – 4° = 80°
∠B = 3x + 16
= 3 x 28 + 16
= 84°+ 16° = 100°
But ∠C = ∠A (opposite angles of ||gm)
∴ ∠ C = 80°
Similarly ∠ D = ∠ B = 100°
Hence ∠A = 80°, ∠B = 100°, ∠C = 80° and ∠D= 100° Ans.

Question 5.
Solution:
In ||gm ABCD, ∠A and ∠C are opposite angles.
∴ ∠A = ∠C= 130°

But ∠A = ∠C (opposite angles)
∴ ∠A = ∠C
= \(\frac { 130^{ o } }{ 2 } \)
= 65°
But ∠A + ∠B = 180°
(sum of adjacent angles)
=> 65° + ∠B = 180°
=> ∠B = 180° – 65° = 115°
But ∠ D = ∠ B (opposite angles)
∴ ∠D = 115°
Hence ∠A = 65°, ∠B = 115°, ∠C = 65° and ∠ D = 115° Ans.

Question 6.
Solution:
Let ABCD is a parallelogram in which AB : BC = 5:3
Let AB = 5x: and BC = 3x.

But perimeter = 64 cm.
∴ 2(5x + 3x) = 64
=> 2 x 8x = 64
=> 16x = 64
x = \(\\ \frac { 64 }{ 16 } \)
= 4
∴ AB = 5x = 5 x 4 = 20 cm
BC = 3x = 3 x 4=12 cm
But CD = AB and AD = BC
(opposite sides of ||gm)
∴ CD = 20 cm and AD = 12 cm Ans.

Question 7.
Solution:
Perimeter of parallelogram ABCD = 140 cm.
=> ∴ 2 (AB + BC) = 140 cm.
=> AB + BC = \(\\ \frac { 140 }{ 2 } \) = 70 cm.
Let BC = x

then AB = x + 10
∴ x + x + 10 = 70
=> 2x + 10 = 70
=> 2x = 70 – 10 = 60
=>x = \(\\ \frac { 60 }{ 2 } \) = 30
∴ BC = 30 cm. and
AB = 30 + 10 = 40 cm.
But AD = BC and CD = AB
(Opposite sides of parallelogram)
∴ AD = 30 cm. and CD = 40 cm.

Question 8.
Solution:
In rectangle ABCD, AC is diagonal BM ⊥ AC and DN ⊥ AC.
Now, we have to prove that
∆BMC ≅ ∆DNA
In ∆BMC and ∆DNA,
BC = AD (opposite sides of the rectangle)
∠M = ∠N (each = 90°)
∠BCM = ∠D AN (Alternate angles)
∴ ∆BMC ≅ ∆DNA
(S.A.A. axiom of congruency)
∴ BM = DN (c.p .c.t.)

Question 9.
Solution:
ABCD is a parallelogram.
AE and CF are the bisectors of ∠A and ∠C respectively.
In ∆ADE and ∆CBF,
AD = BC
(Opposite sides of the parallelogram)
∠D = ∠B
(Opposite angles of the parallelogram)
∠DAE = ∠FCB (\(\\ \frac { 1 }{ 2 } \) of equal angles)
∴ ∆ADE ≅ ∆CBF
(S.A.A. axiom of congruency)
∴ DE = BF (c.p.c.t.)
But CD = AB
(Opposite sides of the parallelogram)
∴ CD – DE = AB – BF
=> EC = AF
and AB || CD
∴ AFCE is a parallelogram
∴ AE || CF.

Question 10.
Solution:
Let ABCD is a rhombus AC and BD are its diagonals which bisect each other at right angles at O.
AC = 16cm and BD = 12cm
∴ AO = \(\\ \frac { 16 }{ 2 } \) = 8cm

BO = \(\\ \frac { 12 }{ 2 } \) = 6 cm
Now, in right ∆AOB
AB² = AO² + BO²
(Pythagorus Theorem)
= (8)² + (6)²
= 64 + 36 = 100 = (10)²
∴ AB = 10 cm
But all the sides of a rhombus are equal
∴ Each side will be 10 cm Ans.

Question 11.
Solution:
In square ABCD, AC is its diagonal
∴ Diagonals of a square bisect each angle at the vertex
∴ ∠ CAD = ∠ CAB
But ∠ DAB = 90° (Angle of a square)
∴ ∠ CAD = ∠ CAB = \(\\ \frac { 1 }{ 2 } \) ∠ DAB
= \(\\ \frac { 1 }{ 2 } \) x 90° = 45°
Hence ∠ CAD = 45° Ans.

Question 12.
Solution:
Let ABCD is a rectangle
AB : BC = 5 : 4
Let AB = 5x and BC = 4x.
But perimeter = 90cm

2(AB + BC) = 90
=> 2(5x + 4x) = 90
=> 2 x 9x = 90
=> 18x = 90
x = \(\\ \frac { 90 }{ 18 } \) = 5
∴ Length (AB) = 5x = 5 x 5 = 25 cm
Breadth (BC) = 4x = 4 x 5 = 20 cm Ans.

Question 13.
Solution:
(i) It is a rectangle
(ii) Square
(iii) rhombus
(iv) rhombus
(v) square
(vi) rectangle.

Question 14.
Solution:
(i) False
(ii) False
(iii) False
(iv) False
(v) False
(vi) True
(vii) True
(viii) True
(ix) False
(x) True

 

Hope given RS Aggarwal Solutions Class 8 Chapter 16 Parallelograms Ex 16A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 15 Quadrilaterals Ex 15

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Class 8 Solutions Chapter 15 Quadrilaterals Ex 15.

Question 1.
Solution:
(i) Four
(ii) Four
(iii) 4, collinear
(iv) two
(v) opposite
(vi) 360°

Question 2.
Solution:
(i) There are four pairs of adjacent sides which are (AB, BC), (BC, CD), (CD, DA) and (DA, AB)
(ii) There are two pairs of opposite sides which are (AB, CD) and (BC, AD)
(iii) There are four pairs of adjacent angles which are (∠ A, ∠ B), (∠ B, ∠ C), (∠ C, ∠ D) and (∠ D, ∠ A)
(iv) There are two pairs of opposite angles which are (∠A, ∠C) and (∠B, ∠D)
(v) There are two diagonals which are AC and BD.

Question 3.
Solution:
Given : ABCD is a quadrilateral

To prove : ∠A + ∠B + ∠C + ∠D = 360°
Construction : Join BD
Proof : In ∆ ABD,
∠ A + ∠1 + ∠ 4 = 180° (sum of angles of a triangle)
Similarly ∠2 + ∠C + ∠ 3 = 180° Adding we get,
∠ A + ∠1 + ∠4 + ∠2 + ∠C + ∠ 3
= 180° + 180°
=> ∠A + ∠1 + ∠2 + ∠C + ∠3 + ∠4 = 360°
=> ∠A + ∠B + ∠C + ∠D = 360° Hence proved.

Question 4.
Solution:
We know that
Sum of 4 angles of a quadrilateral = 360°
But sum of 3 angles = 76° + 54° + 108°
= 238°
4th angle = 360 – 238°
= 122°
Hence, measure of fourth angle = 122° Ans

Question 5.
Solution:
Ratio of four angles of a quadrilateral = 3 : 5 : 7 : 9
Let these angles be 3x, 5x, 7x and 9x
then 3x + 5x + 7x + 9x = 360° (sum of angles)
=> 24x = 360°
First angle = 3x = 3 x 15° = 45°
Second angle = 5x = 5 x 15° = 75°
Third angle = 7x = 7 x 15° = 105°
Fourth angle = 9x = 9 x 15° = 135° Ans.

Question 6.
Solution:
Three acute angles of a quadrilateral are 75° each
Sum of three angles = 3 x 75° = 225°
But sum of 4 angles = 360°
Fourth angle = 360° – 225°
= 135° Ans.

Question 7.
Solution:
Sum of 4 angles of a quadrilateral 360°
One angles = 120°
Sum of other three angles = 360° – 120° = 240°
But each of these 3 angles are equal
Each of equal angles = \(\frac { 240^{ o } }{ 3 } \)
= 80°

Question 8.
Solution:
Sum of 4 angles of a quadrilateral = 360°
Sum of two angles = 85° + 75° = 160°
Sum of other two angles = 360° – 160° = 200°
But each of these two angles are equal
Measure of each equal angle = \(\frac { 200^{ o } }{ 2 } \)
= 100° Ans.

Question 9.
Solution:
In quadrilateral ABCD
∠C = 100°, ∠D = 60°
and ∠A + ∠B + ∠C + ∠D = 360°
(sum of angles of a quadrilateral)
∴ ∠ A + ∠ B = 360° – (100° + 60°)
= 360° – 160° = 200°
But AP and BP are the bisectors of ∠ A and ∠ B
∴ \(\\ \frac { 1 }{ 2 } \) – (∠ A + ∠B) = 200° x \(\\ \frac { 1 }{ 2 } \) = 100°
i.e. ∠ 1 + ∠2 = 100°
But in ∆ APB,
∠1 + ∠2 + ∠P = 180°
=> 100° + ∠P = 180°
=> ∠P = 180° – 100° = 80°
or ∠APB = 80° Ans.

 

Hope given RS Aggarwal Class 8 Solutions Chapter 15 Quadrilaterals Ex 15 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for yo

RS Aggarwal Class 8 Solutions Chapter 14 Polygons Ex 14B

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 14 Polygons Ex 14B.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 14 Polygons Ex 14A
• RS Aggarwal Solutions Class 8 Chapter 14 Polygons Ex 14B

Question 1.
Solution:
In a pentagon, no. of diagonals
\(=\frac { n\left( n-3 \right) }{ 2 }\)
\(=\frac { 5\left( 5-3 \right) }{ 2 }\)
\( =\frac { 5\times 2 }{ 2 } \)
= 5 (a)

Question 2.
Solution:
In a hexagon, no. of diagonals
\(=\frac { n\left( n-3 \right) }{ 2 }\)
\(=\frac { 6\left( 6-3 \right) }{ 2 }\)
\( =\frac { 6\times 3 }{ 2 } \)
= 9 (c)

Question 3.
Solution:
In an octagon, no. of diagonals
\(=\frac { n\left( n-3 \right) }{ 2 }\)
\(=\frac { 8\left( 8-3 \right) }{ 2 }\)
\( =\frac { 8\times 5 }{ 2 } \)
= 20 (d)

Question 4.
Solution:
In a polygon of 12 sides, no. of diagonals
\(=\frac { n\left( n-3 \right) }{ 2 }\)
\(=\frac { 12\left( 12-3 \right) }{ 2 }\)
\( =\frac { 12\times 9 }{ 2 } \)
= 54 (c)

Question 5.
Solution:
A polygon has 27 diagonal

Either n – 9 = 0, then n = 9
or n + 6 = 0, then n = – 6 but it is not possible being negative
No. of sides = 9 (c)

Question 6.
Solution:
Angles of a pentagon are x°, (x + 20)°, (x + 40)°, (x + 60°) and (x + 80)°
But sum of angle of a pentagon

Question 7.
Solution:
Measure of each exterior angle = 40°
No. of sides = \(\frac { { 360 }^{ o } }{ 40 }\)9 sides (b)

Question 8.
Solution:
Each interior angle of a polygon = 108°

Question 9.
Solution:
Each interior angle = 135°

Question 10.
Solution:
Let each exterior angle = x, then
Each interior angles = 3n
But sum of angle = 180°
x + 3x = 180°
=>4x = 180°
=> x = 45°
No. of sides = \(\frac { { 360 }^{ o } }{ 45 } \)
= 8 sides (b)

Question 11.
Solution:
Each interior angles of decagon

Question 12.
Solution:
Sum of all interior angles of a hexagon
= (2n – 4) x right angle
= (2 x 6 – 4) right angle
= 8 right angles (b)

Question 13.
Solution:
Sum of all interior angles of polygon = 1080°
Let n be the number of sides, then
(2n – 4) x 90°= 1080°

Question 14.
Solution:
Difference between each interior and exterior angle = 108°
Then each interior angle = x + 108°
x + x + 108°= 180°
(Sum of both angles = 180°)
=> 2x = 180° – 108° = 72°
x = \(\\ \frac { 72 }{ 2 } \)
= 36°
No. of sides = \( \frac { { 360 }^{ o } }{ { 36 }^{ o } } \)
= 10 (d)

Hope given RS Aggarwal Solutions Class 8 Chapter 14 Polygons Ex 14B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 14 Polygons Ex 14A

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 14 Polygons Ex 14A.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 14 Polygons Ex 14A
• RS Aggarwal Solutions Class 8 Chapter 14 Polygons Ex 14B

Question 1.
Solution:
We know that sum of exterior angles of a polygon is 360°
Then,
(i) Pentagon’s exterior angle = \(\frac { { 360 }^{ o } }{ 5 } \)
= 72°

Question 2.
Solution:
Each exterior angle a n sided polygon = 50°
No of sides = \(\frac { { 360 }^{ o } }{ 50 } \)
= \(7\frac { 1 }{ 5 } \)
Which is not possible to have \(7\frac { 1 }{ 5 } \) sides
Which is not a whole number

You can also Download NCERT Solutions for Class 8 English to help you to revise complete Syllabus and score more marks in your examinations.

Question 3.
Solution:
We know that each interior angle of a regular polygon of n sides = \(\\ \frac { 2n-4 }{ n } \) right angle
(i) Polygon having 10 sides, each interior

Question 4.
Solution:
Let interior angle of a polygon having n sides = 100°
\(\\ \frac { 2n-4 }{ n } \) x 90° = 100°
=>\(\\ \frac { 2n-4 }{ n } \)
= \(\\ \frac { 100 }{ 90 } \)
= \(\\ \frac { 10 }{ 9 } \)

Question 5.
Solution:
We know that sum of all interior angles = 2n – 4 right angles
(i) Pentagon
Sum of its angles = (2 x 5 – 4) x 90°
= 6 x 90° = 540°

Question 6.
Solution:
We know that number of diagonal of polygon having n sides = \(\frac { n\left( n-3 \right) }{ 2 } \)
(i) In heptagon, no of diagonals = \(\frac { 7\left( 7-3 \right) }{ 2 } \)

Question 7.
Solution:
We know that each exterior angle
= \( \frac { { 360 }^{ o } }{ n } \)
Where n sides are of polygon
(i) Each exterior angle = 40°

Question 8.
Solution:
We know that sum of all exterior angle of a polygon – 360°
Exterior ∠A + ∠B + ∠C + ∠D = 360°
=> 115° + x + 90° + 50° = 360°
=> 255° + x + 360°
=> x = 360° – 255°
=> x = 105°

Question 9.
Solution:
In the given figure polygon is of 5 sides and each interior angle is x
\(x=\frac { 2x-4 }{ n } \times { 90 }^{ o }=\frac { 2\times 5-4 }{ 5 } \times { 90 }^{ o } \)
= \(=\frac { 6 }{ 5 } \times { 90 }^{ o } \)
= 108°

 

Hope given RS Aggarwal Solutions Class 8 Chapter 14 Polygons Ex 14A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 13 Time and Work Ex 13B

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 13 Time and Work Ex 13B.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 13 Time and Work Ex 13A
• RS Aggarwal Solutions Class 8 Chapter 13 Time and Work Ex 13B

Question 1.
Solution:
A’s 1 day’s work = \(\\ \frac { 1 }{ 10 } \)
B’s 1 day’s work = \(\\ \frac { 1 }{ 15 } \)

Question 2.
Solution:
A man’s 1 day work = \(\\ \frac { 1 }{ 5 } \)
Man and his son’s 1 days work = \(\\ \frac { 1 }{ 3 } \)

Question 3.
Solution:
A’s 1 day’s work = \(\\ \frac { 1 }{ 16 } \)
B’s 1 day’s work = \(\\ \frac { 1 }{ 12 } \)

Question 4.
Solution:
Let B can do a work in = x days
Then A can do the work

Question 5.
Solution:
Let B’s 1 day’s work = x
Then A’s 1 day’s work = 2x

Question 6.
Solution:
Total wages = Rs. 3000
A’s 1 day’s work = \(\\ \frac { 1 }{ 10 } \)
B’s 1 day’s work = \(\\ \frac { 1 }{ 15 } \)

Question 7.
Solution:
Ratio in the rates of working of A and B = 3:4
Ratio in time = \(\\ \frac { 1 }{ 3 } \) : \(\\ \frac { 1 }{ 4 } \)
= \(\\ \frac { 4:3 }{ 12 } \)
= 4 : 3 (c)

Question 8.
Solution:
A and B’s 1 day’s wok = \(\\ \frac { 1 }{ 12 } \)
B and C’s 1 day’s work = \(\\ \frac { 1 }{ 20 } \)
C and A’s 1 day’s work = \(\\ \frac { 1 }{ 15 } \)

Question 9.
Solution:
3 men = 5 women
1 man = \(\\ \frac { 5 }{ 3 } \) women 5
6 men = \(\\ \frac { 5 }{ 3 } \) x 6 = 10 women

Question 10.
Solution:
A’s 1 day’s work = \(\\ \frac { 1 }{ 15 } \)
Then B’s 1 day’s work = \(\\ \frac { 1 }{ 10 } \) x \(\\ \frac { 100+50 }{ 100 } \)
= \(\\ \frac { 1 }{ 15 } \) x \(\\ \frac { 150 }{ 100 } \)
= \(\\ \frac { 1 }{ 10 } \)
B will finish the work in = 10 days (a)

Question 11.
Solution:
A’s 1 hour’s work = \(\\ \frac { 2 }{ 15 } \)
A and B’s ratio in work = \(\\ \frac { 100-20 }{ 100 } \) : 1
= \(\\ \frac { 80 }{ 100 } \) : 1
= \(\\ \frac { 4 }{ 5 } \) : 1

Question 12.
Solution:
A’s 1 day’s work = \(\\ \frac { 1 }{ 20 } \)
B’s 1 day’s work = \(\\ \frac { 1 }{ 12 } \)

Question 13.
Solution:
A’s 1 days work = \(\\ \frac { 1 }{ 25 } \)
B’s 1 days work = \(\\ \frac { 1 }{ 20 } \)

Question 14.
Solution:
First pipe 1 minutes work = \(\\ \frac { 1 }{ 20 } \)
Second pipe 1 minutes work = \(\\ \frac { 1 }{ 30 } \)

Question 15.
Solution:
First tap’s 1 hours work to fill = \(\\ \frac { 1 }{ 8 } \)
Second tap’s 1 hours work to empty = \(\\ \frac { 1 }{ 16 } \)
Both 1 hour can fill the cistern

Question 16.
Solution:
First pump’s 1 hr work to fill = \(\\ \frac { 1 }{ 2 } \)
Due to leakage, tank is filled in \(2\frac { 1 }{ 3 } \) hour

Question 17.
Solution:
Answer = (b)
First inlet pipe’s 1 hour work = \(\\ \frac { 1 }{ 10 } \)
Second inlet pipe’s 1 hour work = \(\\ \frac { 1 }{ 12 } \)

Hope given RS Aggarwal Solutions Class 8 Chapter 13 Time and Work Ex 13B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 13 Time and Work Ex 13A

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 13 Time and Work Ex 13A.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 13 Time and Work Ex 13A
• RS Aggarwal Solutions Class 8 Chapter 13 Time and Work Ex 13B

Question 1.
Solution:
Rajan’s one day’s work = \(\\ \frac { 1 }{ 24 } \)
Amit’s one day’s work = \(\\ \frac { 1 }{ 30 } \)

Question 2.
Solution:
Ravi’s one hours = \(\\ \frac { 1 }{ 15 } \)
Both’s one day’s work = \(\\ \frac { 1 }{ 12 } \)

or 6 hours, 40 minutes.

Question 3.
Solution:
A and B both’s one day’s work = \(\\ \frac { 1 }{ 6 } \)
A’s alone’s one day’s work = \(\\ \frac { 1 }{ 9 } \)

Question 4.
Solution:
Raju and Siraj’s 1 hour work = \(\\ \frac { 1 }{ 6 } \)
Raju’s alone 1 hour work = \(\\ \frac { 1 }{ 15 } \)

Question 5.
Solution:
A’s one day’s work = \(\\ \frac { 1}{ 10 } \)
B’s one day’s work = \(\\ \frac { 1 }{ 12 } \)

Question 6.
Solution:
A’s 1 hour work = \(\\ \frac { 1 }{ 24 } \)
B’s 1 hour work = \(\\ \frac { 1 }{ 16 } \)

Question 7.
Solution:
A,B and C’s 1 hr work = \(\\ \frac { 1 }{ 8 } \)
A’s 1 hour work = \(\\ \frac { 1 }{ 20 } \)
B’s 1 hour work = \(\\ \frac { 1 }{ 24 } \)

Question 8.
Solution:
A’s one day’s work = \(\\ \frac { 1 }{ 16 } \)
B’s one days work = \(\\ \frac { 1 }{ 12 } \)

Question 9.
Solution:
A’s 1 day’s work = \(\\ \frac { 1 }{ 14 } \)
B’s 1 day’s work = \(\\ \frac { 1 }{ 21 } \)

Question 10.
Solution:
A can do \(\\ \frac { 2 }{ 3 } \) work in = 16 days
A’s 1 days work = \(\\ \frac { 2 }{ 3 } \) x \(\\ \frac { 1 }{ 16 } \) = \(\\ \frac { 1 }{ 24 } \)

Question 11.
Solution:
A’s one day’s work = \(\\ \frac { 1 }{ 15 } \)
B’s one day’s work = \(\\ \frac { 1 }{ 12 } \)

Question 12.
Solution:
A and B’s one day’s work = \(\\ \frac { 1 }{ 18 } \)
B and C’s one day’s work = \(\\ \frac { 1 }{ 24 } \)

A, B and C’s one days work = \(\frac { 1 }{ 2\times 2 } \)
= \(\\ \frac { 1 }{ 16 } \)
A, B and C can do the work in 16 days.

Question 13.
Solution:
A and B’s one days work = \(\\ \frac { 1 }{ 12 } \)
B and C’s one day’s work = \(\\ \frac { 1 }{ 15 } \)

Question 14.
Solution:
A’s one hr work =\(\\ \frac { 1 }{ 10 } \)
B’s one hr work = \(\\ \frac { 1 }{ 15 } \)

Question 15.
Solution:
Pipe A’s one hour’s work for filling the tank = \(\\ \frac { 1 }{ 5 } \)
Pipe B’s one hour’s work for emptying = \(\\ \frac { 1 }{ 6 } \)

Question 16.
Solution:
Tap A’s one hour’s work = \(\\ \frac { 1 }{ 6 } \)
Tap B’s one hour’s work = \(\\ \frac { 1 }{ 8 } \)
Tap C’s one hour’s work = \(\\ \frac { 1 }{ 12 } \)
A, B and C’s together one hour’s work

Question 17.
Solution:
Inlet A’s 1 minutes work = \(\\ \frac { 1 }{ 12 } \)
Inlet B’s 1 minutes work = \(\\ \frac { 1 }{ 15 } \)

Question 18.
Solution:
The inlet pipe’s 1 hour’s work = \(\\ \frac { 1 }{ 9 } \)
The leak and inlet’s 1 hours work = \(\\ \frac { 1 }{ 10 } \)
Leak’s 1 hour work = \(\frac { 1 }{ 9 } -\frac { 1 }{ 10 } \)
= \(\\ \frac { 10-9 }{ 90 } \)
= \(\\ \frac { 1 }{ 90 } \)
The leak can empty the cistern in = 90 hours Ans.

Question 19.
Solution:
Inlet pipe A’s one hour’s work = \(\\ \frac { 1 }{ 6 } \)
Inlet pipe B’s one hour’s work = \(\\ \frac { 1 }{ 8 } \)

 

Hope given RS Aggarwal Solutions Class 8 Chapter 13 Time and Work Ex 13A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12C

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 12 Direct and Inverse Proportions Ex 12C.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 12 Direct and Inverse Proportions Ex 12A
• RS Aggarwal Solutions Class 8 Chapter 12 Direct and Inverse Proportions Ex 12B
• RS Aggarwal Solutions Class 8 Chapter 12 Direct and Inverse Proportions Ex 12C

OBJECTIVE QUESTIONS :
Tick the correct answer in each of the following :

Question 1.
Solution:
Answer = (d)
Cost of 14 kg of pulses = Rs 882
Cost of 1 kg of pulses Rs \(\\ \frac { 882 }{ 14 } \)
Cost of 22 kg of pulses = Rs \(\frac { 882\times 22 }{ 14 } \)
= 63 x 22
= Rs 1386

Question 2.
Solution:
Let x be oranges which can be bought for Rs. 33.80
8 : x : : 10.40 : 33.80
=> x × 10.40 = 8 x 33.80
=> \(\frac { 8\times 33.80 }{ 10.40 } \)
=> \(\frac { 8\times 3380 }{ 1040 } \)
= 26
∴ No. of oranges = 26 Ans. (c)

Question 3.
Solution:
No. of bottles 420 x
Time 3 5
More time, more bottles
By direct proportion
420 : x :: 3 : 5
x = \(\frac { 420\times 5 }{ 3 } \)
= 700
∴ No. of bottle will be 700 (b)

Question 4.
Solution:
Distance covered 75 km x
Time taken 60 min. 20 min.
Less time, less distance By direct proportion,
75 : x :: 60 : 20
x = \(\frac { 75\times 20 }{ 60 } \)
= 25
∴ Distance covered = 25 km (a)

Question 5.
Solution:
No. of sheets 12 : x
Weight 40 g : 1000 g
More weight, more sheets
By direct proportion 12 : x :: 40 : 1000
x = \(\frac { 12\times 1000 }{ 40 } \)
= 300
∴ No. of sheets = 300 (c)

Question 6.
Solution:
Let x be the height of tree
Height of pole 14 m : x m
Length of shadow 10 m : 7 m
Less shadow, less height
By direct proportion 14 : x :: 10 : 7
x = \(\frac { 14\times 7 }{ 10 } \)
= \(\\ \frac { 98 }{ 10 } \)
= 9.8 m
∴ Height of the = 9.8 m (b)

Question 7.
Solution:
Let actual length of bacteria = x cm
Enlarged (times) 50000
Length 5 cm
Then actual length (x)
Then \(\frac { x\times 50000 }{ -4 } \)
= 5
=> x = \(\\ \frac { 5 }{ 50000 } \)
= \(\\ \frac { 1 }{ 10000 } \)
= 10 cm (c)

Question 8.
Solution:
No. of pipes 6 : 5
Time taken to 120 min : x min
fill the tank
Less pipes, more time
By inverse proportion 6 : 5 :: x : 120
x = \(\frac { 6\times 120 }{ 5 } \)
= 144 (b)
∴ Time taken = 144 minutes

Question 9.
Solution:
Let number of days = x, then
Persons 3 : 4
(Time taken to build a wall) 4 : x
More person, less time take
By inverse proportion,
3 : 4 :: x : 4
x = \(\frac { 4\times 3 }{ 4 } \)
= 3 (b)
∴ Time taken to build the wall = 3 days

Question 10.
Solution:
Let time taken will be x hrs
Speed 60 km/h : 80 km/h
Time taken to 2hr : x
reach
(More speed, less time)
By inverse proportion 60 : 80 :: x : 2
x = \(\frac { 60\times 2 }{ 80 } \)
= \(\\ \frac { 3 }{ 2 } \)
∴ Time take \(\\ \frac { 3 }{ 2 } \) hours or 1 hr. 30 m in. (a)

Hope given RS Aggarwal Solutions Class 8 Chapter 12 Direct and Inverse Proportions Ex 12C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12B

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 12 Direct and Inverse Proportions Ex 12B.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 12 Direct and Inverse Proportions Ex 12A
• RS Aggarwal Solutions Class 8 Chapter 12 Direct and Inverse Proportions Ex 12B
• RS Aggarwal Solutions Class 8 Chapter 12 Direct and Inverse Proportions Ex 12C

Question 1.
Solution:
∵ x and y are inversely proportional
Then xy are equal
(i) xy = 6 x 9 = 54
= 10 x 15 = 150
= 14 x 21 = 294
= 16 x 24 = 384
∵ xy in each case is not equal
So, x and y are not inversely proportional
(ii) xy = 5 x 18 = 90
= 9 x 10 = 90
= 15 x 6 = 90
= 3 x 30 = 90
= 45 x 2 = 90
∵ xy in each case is equal
x and y are inversely proportional
(iii) xy = 9 x 4 = 36
= 3 x 12 = 36
= 6 x 9 = 54
= 36 x 1 = 36
∵ xy in each is not equal
x and y are not inversely proportional

You can also Download NCERT Solutions for Class 8 English to help you to revise complete Syllabus and score more marks in your examinations.

Question 2.
Solution:
x and y are inversely proportional
xy is equal
Now,

Question 3.
Solution:
Let required number of days = x

Question 4.
Solution:
A pond is! dug in 8 days by = 12 men
It can be dug in 1 day by = 12 x 8 men (Less days, more men)
and it can be dug in 6 days by = \(\\ \frac { 12X8 }{ 6 } \)
= 16 men Ans. (more days, less men)

Question 5.
Solution:
Let 14 cows can graze in x days

Question 6.
Solution:
Let required time take = x hour

By inverse proportion
60 : x :: 75 : 5
x = \(\\ \frac { 50X5 }{ 75 } \)
Time required = 4 hours

Question 7.
Solution:
Let machines required = x

Question 8.
Solution:
Let 8 taken will fill in tank in x hour

Question 9.
Solution:
8 taps can fill tank in = 27 minutes
1 tap can fill that tank in = 27 x 8 minutes (less tap, more time)
8 – 2 = 6 taps can fill that tank in
= \(\\ \frac { 27X8 }{ 6 } \) minutes
= 36 minutes

Question 10.
Solution:
Let total animals can be feed with food in x days

Question 11.
Solution:
Let for x day, the food provision is sufficient for 900 + 500 = 1400 men

Question 12.
Solution:
Let the food will be for x days

Question 13.
Solution:
Let each period will be of x minutes

Question 14.
Solution:
x and y are inversely
and x = 15, y = 6
Then xy = 15 x 6 = 90
Now if x = 9, then y = \(\\ \frac { 90 }{ 9 } \)
= 10

Question 15.
Solution:
x and y are inversely and x = 18, y = 8
xy = 18 x 8 = 144
Now if y = 16,
then x = \(\\ \frac { 144 }{ 16 } \)
= 9

Hope given RS Aggarwal Solutions Class 8 Chapter 12 Direct and Inverse Proportions Ex 12B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 12 Direct and Inverse Proportions Ex 12A

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 12 Direct and Inverse Proportions Ex 12A.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 12 Direct and Inverse Proportions Ex 12A
• RS Aggarwal Solutions Class 8 Chapter 12 Direct and Inverse Proportions Ex 12B
• RS Aggarwal Solutions Class 8 Chapter 12 Direct and Inverse Proportions Ex 12C

Question 1.
Solution:
(i) \(\\ \frac { x }{ y } \) = \(\\ \frac { 3 }{ 9 } \) = \(\\ \frac { 1 }{ 3 } \)

Question 2.
Solution:
x and y are directly proportional
\(\\ \frac { x }{ y } \) = \(\\ \frac { 3 }{ 72 } \) = \(\\ \frac { 1 }{ 24 } \)

Question 3.
Solution:

Question 4.
Solution:

Question 5.
Solution:
Let distance covered = x then

Question 6.
Solution:
Let no. of dolls = x, then

Question 7.
Solution:
Let x kg of sugar will be bought

Question 8.
Solution:
Let cloth bought = x m

Question 9.
Solution:
Let length of model ship = x m

Question 10.
Solution:
Let x kg dust will be picked up

Question 11.
Solution:
A speed of car = 50 km/hr
Distance travelled in 1 hr. = 5 m
Let required distance travelled in 1 hr. 12 min.

Question 12.
Solution:
Let required distance covered = x km
Speed of man = 5 km/hr

Question 13.
Solution:
Let required thickness = x mm

Question 14.
Solution:
Let men required = x

Question 15.
Solution:
Let no. of words type in 8 minutes = x

 

Hope given RS Aggarwal Solutions Class 8 Chapter 12 Direct and Inverse Proportions Ex 12A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 11 Compound Interest Ex 11D

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 11 Compound Interest Ex 11D.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 11 Compound Interest Ex 11A
• RS Aggarwal Solutions Class 8 Chapter 11 Compound Interest Ex 11B
• RS Aggarwal Solutions Class 8 Chapter 11 Compound Interest Ex 11C
• RS Aggarwal Solutions Class 8 Chapter 11 Compound Interest Ex 11D

Tick the correct answer in each of the following

Question 1.
Solution:
Principal (P) = Rs. 5000
Rate (R) = 8% p.a.
Period (n) = 2 years

Question 2.
Solution:
Principal (P) = Rs. 10000
Rate (R) = 10% p.a.
Period (n) = 3 years

Question 3.
Solution:
Principal (P) = Rs. 10000
Rate (R) = 12% p.a.

Question 4.
Solution:
Principal (P) = Rs. 4000
Rate (R) = 10% p.a.
Period (a) = 2 years 3 months

Question 5.
Solution:
Principal (P) = Rs. 25000
Rate (R1) = 5% for the first year
R2 = 6% for the second year
R3 = 8% for the third year

Question 6.
Solution:
Principal (P) = Rs. 6250
Rate (R) = 8% p.a. or 4% half yearly
Period (n) = 1 year or 2 half years

Question 7.
Solution:
Principal (P) = Rs. 40000
Rate (R) = 6% p.a. \(\\ \frac { 6 }{ 4 } \) = \(\\ \frac { 3 }{ 2 } \) % quarterly
Period (n) = 6 months = 2 quarters

Question 8.
Solution:
Present population (P) = 24000
Rate of increase (R) = 5% p.a.
Period (n) = 2 years

Question 9.
Solution:
3 years ago, the value of machine = Rs. 60000
Rate of depreciation (R) = 10%
Period (n) = 3 years

Question 10.
Solution:
Present value = Rs. 40000
Rate of depreciation (R) = 20% p.a.
Value of machine 2 years ago

Question 11.
Solution:
Rate of growth in population (R) = 10%
Present population = 33275
Population 3 years ago = A

Question 12.
Solution:
S.I. = Rs. 1200
Rate (R) = 5%
Period (T) = 3 years

Question 13.
Solution:
C.I. on a sum = Rs. 510
Rate (R) = \(12\frac { 1 }{ 2 } \) % = \(\\ \frac { 25 }{ 2 } \) % p.a.
Period (n) = 2 years

Question 14.
Solution:
Amount = Rs. 4913
Rate (R) = \(6\frac { 1 }{ 4 } \) = \(\\ \frac { 25 }{ 4 } \) %
Period (n) = 3 years

Question 15.
Solution:
Sum (P) = Rs. 7500
Amount (A) = 8427
Period = 2 years
Let R be the rate of p.a., then

Hope given RS Aggarwal Solutions Class 8 Chapter 11 Compound Interest Ex 11D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.