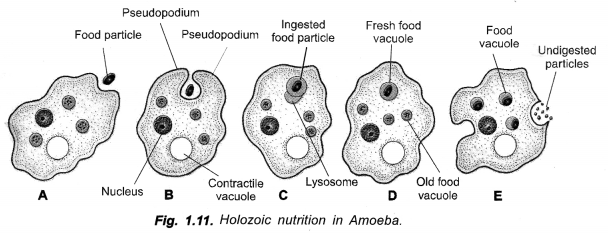
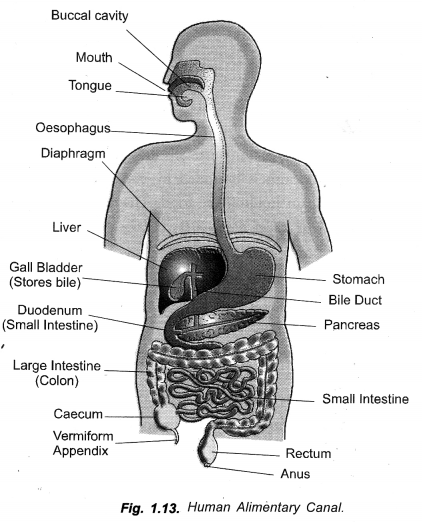
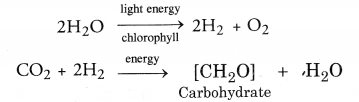
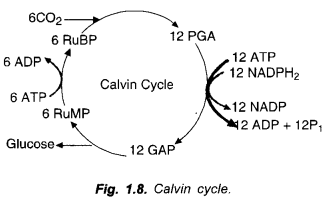
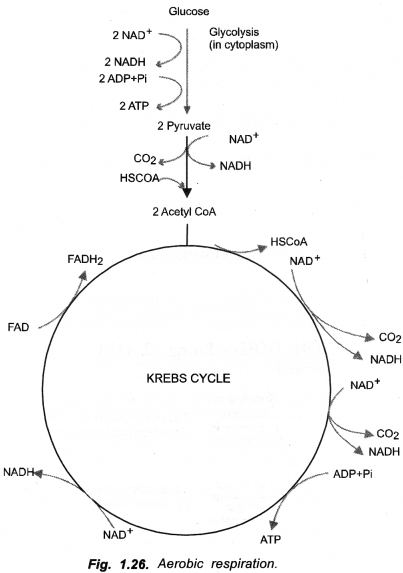
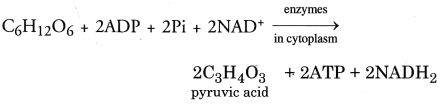
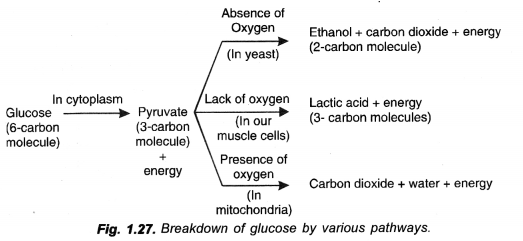
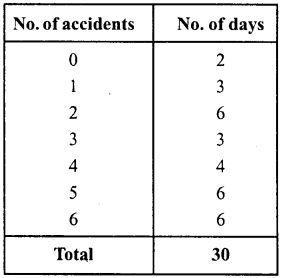
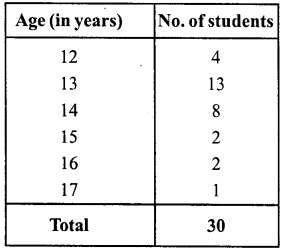
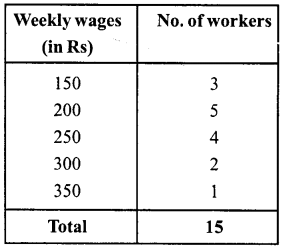
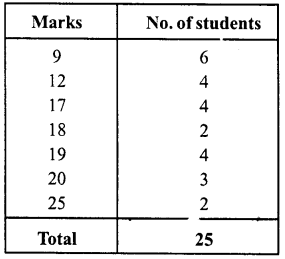
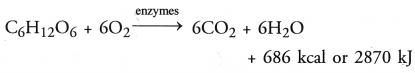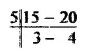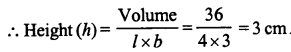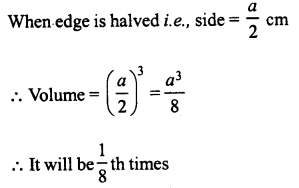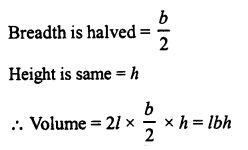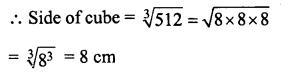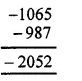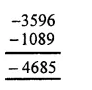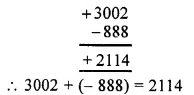RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3A

RS Aggarwal Class 6 Solutions Chapter 3 Whole Numbers Ex 3A

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 3 Whole Numbers Ex 3A.

Other Exercises

Question 1.
Solution:
After 30999, three whole numbers will be
30999 + 1 = 31000
31000 + 1 = 31001
31001 + 1 = 31002
i.e., 31000, 31001 and 31002

Question 2.
Solution:
Before 10001, three whole numbers will be 10001 – 1 = 10000
10000 – 1 = 9999
9999 – 1 = 9998
i.e., 10000, 9999, 9998

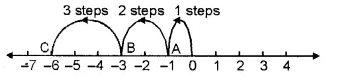
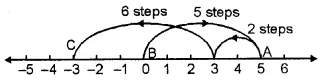
Question 3.
Solution:
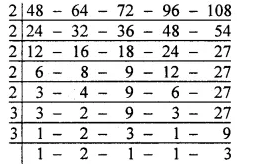
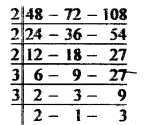
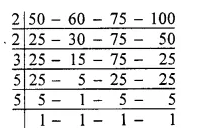
Between 1032 and 1209, whole number are 1209 – 1031
= 178

Question 4.
Solution:
The smallest whole number is 0

Question 5.
Solution:
The successor of
(i) 2540801 is 2540801 + 1 = 2540802
(ii) 9999 is 9999 + 1 = 10000
(iii) 50904 is 50904 + 1 = 50905
(iv) 61639 is 61639 + 1 = 61640
(v) 687890 is 687890 + 1 = 687891
(vi) 5386700 is 5386700 + 1 = 5386701
(vii) 6475999 is 6475999 + 1 = 6476000
(viii) 9999999 is 9999999 + 1 = 10000000

Question 6.
Solution:
Predecessor of
(i) 97 is 97 – 1 = 96
(ii) 10000 is 10000 – 1 = 9999
(iii) 36900 is 36900 – 1 = 36899
(iv) 7684320 is 7684320 – 1 = 7684319
(v) 1566391 is 1566391 – 1 = 1566390
(vi) 2456800 is 2456800 – 1 = 2456799
(vii) 100000 is 100000 – 1 = 99999
(viii) 1000000 is 1000000 – 1 = 999999

Question 7.
Solution:
Three consecutive whole numbers just preceding 7510001 are (7510001 – 1), (7510001 – 2), (7510001 – 3)
i.e. 7510000, 7509999, 7509998.

Question 8.
Solution:
(i) Zero is not a natural number. (F)
(ii) Zero is the smallest whole number (T)
(iii) No, it is false, as zero is not a natural number but it is a whole number.
(iv) Yes, it is true, as set of natural numbers is a subset of whole numbers.
(v) False, zero is the smallest whole number.
(vi) The natural number 1 has no predecessor as 0 is the predecessor of 1 (T)
Which is not a natural number
(vii) The whole number 1 has no predecessor (F)
Predecessor of 1 is 0 which is a whole number
(viii) The whole number 0 has no predecessor (T)
(ix) The predecessor of a two-digit number is never a single-digit number (F)
As predecessor of two digit number say 99 is 99 – 1 = 98
Which is also a two-digit number and of 10 is 10 – 1 = 9
which is single-digit number
(x) The successor of a two-digit number is always a two-digit number (F)
The successor of a two-digit number 99 is 99 + 1 = 100 which is a three digit number
(xi) 500 is the predecessor of 499 (F)
As predecessor of 499 is 499 – 1 = 498 not 500 as 500 is the successor of 499
(xii) 7000 is the successor of 6999 (T)

 

Hope given RS Aggarwal Solutions Class 6 Chapter 3 Whole Numbers Ex 3A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2F

RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2F

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 2 Factors and Multiples Ex 2F.

Other Exercises

Objective Questions
Tick the correct answer in each of the following :

Question 1.
Solution:
(c) Because sum of its digits is 8 + 3 + 4 + 7 + 9 + 5 + 6 + 0 = 42 which is divisible by 3.

Question 2.
Solution:
(a) Because sum of its digits is 8 + 5 + 7 + 6 + 9 + 0 + 1 = 36 which is divisible by 9.

Question 3.
Solution:
(d) Because the number formed by tens and ones digits is divisible by 4 i.e. 32 ÷ 4 = 8.

Question 4.
Solution:
(b) Because the number formed by hundred, tens and ones digits is divisible by 8 i.e. 176 ÷ 8 = 22.

Question 5.
Solution:
(a) Because its one digit is divisible by 2 and sum of its digits is 8 + 7 + 9 + 0 + 4 + 3 + 2 = 33,
which is divisible by 3. Hence it is divisible by 6.

Question 6.
Solution:
(c) Because the difference of the sums of its odd places digits and of its even places digits is (2 + 2 + 2 + 2) – (2 + 2 + 2 + 2) i.e. 8 – 8 = 0, which is zero and is divisible by 11.

Question 7.
Solution:
(d) Because 97 has no factors other than 1 and itself.

Question 8.
Solution:
(c) Because 179 has no factors other than 1 and itself.

Question 9.
Solution:
(c) Because 263 has no factors other than 1 and itself.

Question 10.
Solution:
(a), (b) Because the common factors of 9 and 10 are none but 1.

Question 11.
Solution:
(c) Because 32 has factors which are 2, 2, 2, 2, 2.

Question 12.
Solution:
(d) Because 18 is the highest common factor of 144 and 198.

Question 13.
Solution:
(a) Because 12 is the highest common factors of these numbers 144, 180 and 192.

Question 14.
Solution:
(b) Because 161 and 192 have no common factor other than 1, i.e., HCF of 161 and 192 is 1.

Question 15.
Solution:
(d) Because HCF of 289 and 391 is 289
and \(\frac { 289\div 17 }{ 391\div 17 } \) = \(\\ \frac { 17 }{ 23 } \)

Question 16.
Solution:
(d) Because dividing 134 and 167 by 33 remainder is 2 in each case.

Question 17.
Solution:
(c) Because 360 is the least multiple of 24, 36 and 40.

Question 18.
Solution:
(d) Because 540 is the least multiple of 12, 15, 20 and 27

Question 19.
Solution:
(c) Because 1263 – 3 = 1260 is divisible by 14, 28, 36 and 45.

Question 20.
Solution:
(c) Because HCF of two co-prime number is always 1.

Question 21.
Solution:
(c) Because HCF of a and b, two co-primes is 1.
LCM = a x b = ab.

Question 22.
Solution:
(c) Because LCM of two numbers = Product of these number ÷ their HCF i.e 2160 ÷ 12 = 180.

Question 23.
Solution:
(b) Because second number
= \( \frac { LCM\times HCF }{ 1st\quad number } \)
i.e., \(\\ \frac { 145\times 2175 }{ 725 } \)
= 435

Question 24.
Solution:
(c) Because LCM of 15, 20, 24. 32 and 36 = 1440.

Question 25.
Solution:
(d) Because LCM of 9, 12, 15 is 180. 180
180 minutes = \(\\ \frac { 180 }{ 60 } \)
= 3 hours.

Hope given RS Aggarwal Solutions Class 6 Chapter 2 Factors and Multiples Ex 2F are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.2

RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.2

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.2

Other Exercises

Question 1.
The marks obtained by 40 students of class VIII in an examination are given below :
16, 17, 18, 3, 7, 23, 18, 13, 10, 21, 7, 1, 13,
21, 13, 15, 19, 24, 16, 3, 23, 5, 12, 18, 8, 12, 6,
8, 16, 5, 3, 5, 0, 7, 9, 12, 20, 10, 2, 23.
Divide the data into five groups, namely 0-5,5-10,10-15,15-20 and 20-25 and prepare a grouped frequency table.
Solution:
Frequency distribution table
RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.2 1

Question 2.
The marks scored by 20 students in a test are given below :
54, 42, 68, 56, 62, 71, 78, 51, 72, 53, 44, 58, 47, 64, 41, 57, 89, 53, 84, 57.
Complete the following frequency table :
RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.2 2
What is the class interval in which the greatest frequency occurs ?
Solution:
RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.2 3
The class in which the greatest frequency is 50-60

Question 3.
The following is the distribution of weights (in kg) of 52 persons :
RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.2 4
RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.2 5
(i) What is the lower limit of class 50-60 ?
(ii) Find the class marks of the classes 40-50, 50-60.
(iii) What is the class size ?
Solution:
(i) Lower limit of class 50-60 = 50
(ii) Class marks of 40-50 = \(\frac { 40+50 }{ 2 }\) = \(\frac { 90 }{ 2 }\)
= 45 and of 50-60 = \(\frac { 50+60 }{ 2 }\) = \(\frac { 110 }{ 2 }\) =55
(iii) Class size is 10

Question 4.
Construct a frequency table for the following weights (in gm) of 35 mangoes using the equal class intervals, one of them is 40-45 (45 not included):
30,40,45,32,43,50,55,62,70,70,61,62, 53,52, 50,42,35,37,53,55,65,70, 73, 74,45, 46, 58, 59, 60, 62, 74, 34, 35, 70 ,68.
(i) What is the class mark of the class interval 40-45 ?
(ii) What is the range of the above weights ?
(iii) How many classes are there ?
Solution:
Smallest observation = 30
Greatest observation = 74
Range = 74 – 30 = 44
Now forming the distribution table
RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.2 6
(i) Class mark of 40-45
= \(\frac { 40+45 }{ 2 }\) = \(\frac { 85 }{ 2 }\) = 42.5
(ii) Range = 74 – 30 = 44
(iii) Number of classes are 9

Question 5.
Construct a frequency table with class-intervals 0-5 (5 not included) of the following marks obtained by a group of 30 students in an examination :
0, 5, 7,10, 12,15, 20, 22, 25, 27, 8, 11, 17,3, 6, 9,17,19, 21, 29, 31,35,37,40,42, 45, 49, 4, 50, 16.
Solution:
Frequency distribution table.
RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.2 7

Question 6.
The marks scored by 40 students of class VIII in mathematics are given below:
81,55, 68, 79,85,43,29,68,54,73,47, 35, 72,64,95,44,50, 77,64,35,79, 52, 45,54,70,83, 62′, 64,72,92,84,76,63, 43, 54, 38, 73, 68, 52, 54.
Prepare a frequency distribution with class size of 10 marks.
Solution:
Largest marks = 95
Lowest marks = 29
Range = 95 – 29 = 66
Frequency distribution table
RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.2 8

Question 7.
The heights (in cm) of 30 students of class VIII are given below :
155.158.154.158.160.148.149.150.153, 159,161,148,157,153,157,162,159,151, 154,156,152,156,160,152,147,155,163,155,157,153.
Prepare a frequency distribution table with 160-164 as one of the class intervals.
Solution:
Largest height =163
Lowest height =147
Range = 163- 147 = 16
RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.2 9

Question 8.
The monthly wages of 30 workers in a factory are given below :
830,835,890,810,835,836,869,845,898, 890, 820, 860, 832, 833, 855, 845, 804, 808, 812, 840, 885, 835, 836, 878, 840, 868, 890, 806, 840, 890.
Represent the data in the form of a frequency distribution with class size 10.
Solution:
Highest wage = 898
Lowest wage = 804
Range = 898 – 804 = 94
Frequency distribution table
RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.2 10

Question 9.
Construct a frequency table with equal class intervals from the following data on the monthly wages (in rupees) at 28 labourers working in a factory, taking one of the class intervals as 210-230 (230 not included):
220, 268, 258, 242, 210, 268, 272,242, 311, 290, 300, 320,319,304,302,318,306,292, 254, 278, 210,240, 280,316,306, 215, 256, 236.
Solution:
Highest wages = 320
Lowest wages = 210
Range = 320-210= 110
Frequency distribution table
RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.2 11

Question 10.
The daily minimum temperatures in degrees Celsius recorded in a certain Arctic region are as follows :
-12.5, -10.8, -18.6, -8.4, -10.8, -4.2, -4.8, -6.7, -13.2, -11.8, -2.3,1.2, 2.6, 0, -2.4, 0, 3.2, 2.7,3.4,0, -2.4, -2.4, 0,3.2, 2.7,3.4, 0,2.4, -5.8, -8.9, -14.6, -12.3, -11.5, -7.8, – 2.9
Represent them as frequency distribution table taking -19.9 to -15 as the first class interval.
Solution:
Lowest temperature = -19.9
Highest temperature = 3.4
Frequency distribution table
RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.2 12

Hope given RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4D

RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4D

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4D.

Other Exercises

Question 1.
Solution:
(i) 15 by 9 = 15 x 9 = 135
(ii) 18 by – 7 = 18 x ( – 7) = – 126
(iii) 29 by – 11 = 29 x ( – 11) = – 319
(iv) – 18 by 13 = ( – 18) x 13 = – 234
(v) – 56 by 16 = ( – 56) x 16 = – 896
(vi) 32 by – 21 = 32 x ( – 21) = – 672
(vii) – 57 x 0 = ( – 57) x 0 = 0
(viii) 0 by – 31 = 0 x ( – 31) = 0
(ix) – 12 by – 9 = ( – 12) x ( – 9) = 108
(x) – 746 by – 8 = ( – 746) x ( – 8) = 5968
(xi) 118 by – 7 = 118 x ( – 7) = – 826
(xii) – 238 by – 143 = ( – 238) x ( – 143) = 238 x 143 = 34034
RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4D 1.1

Question 2.
Solution:
(i) ( – 2) x 3 x ( – 4) = [( – 2) x 3] x ( – 4) = ( – 6) x ( – 4) = 24
(ii) 2 x ( – 5) x ( – 6) = 2 x [( – 5) x ( – 6)] = 2 x 30 = 60
(iii) ( – 8) x 3 x 5 = ( – 8) x (3 x 5) = ( – 8) x 15 = – 120
(iv) 8 x 7 x ( – 10) = (8 x 7) x ( – 10) = 56 x ( – 10) = – 560
(v) ( – 3) x ( – 7) x ( – 6) = [( – 3) x ( – 7)] x ( – 6) = 21 x ( – 6) = – 126
(vi) ( – 8) x ( – 3) x ( – 9) = ( – 8) x [( – 3) x ( – 9)] = ( – 8) x 27 = – 216

Question 3.
Solution:
(i) 18 x ( – 27) x 30 = 18 x [( – 27) x 30] = 18 x ( – 810) = – 14580
(ii) ( – 8) x ( – 63) x 9 = [( – 8) x ( – 63)] x 9 = 504 x 9 = 4536
(iii) ( – 17) x ( – 23) x 41 = [( – 17) x ( – 23)] x 41 = 391 x 41 = 16031
RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4D 3.1
(iv) ( – 51) x ( – 47) x ( – 19) = [( – 51) x ( – 47)] x ( – 19) = 2397 x ( – 19) = – 45543
RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4D 3.2

Question 4.
Solution:
(i) We have :
18 x [9 + ( – 7)] = 18 x 2 = 36
18 x 9 + 18 x ( – 7)
= (18 x 9) + [18 x ( – 7)]
= 162 – 126
= 36
18 x [9 x ( – 7)] = 18 x 9 + 18 x ( – 7) is verified.
(ii) We have :
( – 13) x [( – 6) x ( – 19)]
= ( – 13) x ( – 25) = 325
( – 13) x ( – 6) + ( – 13) x – 9
= [( – 13) x ( – 6)] + [( – 13) x ( – 19)]
= 78 + 247 = 325
( – 13) x [( – 6) + ( – 19)]
= ( – 13) x ( – 6) + ( – 13) x ( – 19) is verified.

Question 5.
Solution:
The complete multiplication table is given below
RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4D 5.1

Question 6.
Solution:
(i) True
(ii) False
(iii) True
(iv) True

Question 7.
Solution:
(i) ( – 9) x 6 + ( – 9) x 4
= ( – 9) x (6 + 4)
(By distributive law)
= ( – 9) x 10
= – 90
(ii) 8 x ( – 12) + 7 x ( – 12)
= ( 8 + 7) x ( – 12)
(By distributive law)
= 15 x ( – 12)
= – 180
(iii) 30 x ( – 22) + 30 x (14)
= 30 x [( – 22) + 14]
(By distributive law)
= 30 x ( – 8)
= – 240
(iv) ( – 15) x ( – 14) + ( – 15) x ( – 6)
= ( – 15) x [( – 14) + ( – 6)]
(By distributive law)
= ( – 15) x ( – 20)
= 300
(v) 43 x ( – 33) + 43 x ( – 17)
= 43 x [( – 33) + ( – 17)]
(By distributive law)
= 43 x ( – 50) = – 2150
(vi) ( – 36) x 72 + ( – 36) x 28
= ( – 36) x (72 + 28)
(By distributive law)
= ( – 36) x 100
= – 3600
(vii)( – 27) x ( – 16) + ( – 27) x ( – 14)
= ( – 27) x [( – 16) + ( – 14)]
(By distributive law)
= ( – 27) x ( – 30)
= 810

Hope given RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

NCERT Exemplar Solutions for Class 10 Science Chapter 6 Life Processes

NCERT Exemplar Solutions for Class 10 Science Chapter 6 Life Processes

These Solutions are part of NCERT Exemplar Solutions for Class 10 Science. Here we have given NCERT Exemplar Solutions for Class 10 Science Chapter 6 Life Processes

NCERT Exemplar Solutions for Class 10 Science Chapter 6 Short Answer Questions

Question 1.
Name the following :

    1. The process in plants that links light energy with chemical energy.
  1. Organisms that can prepare their own food.
  2. Cells that surround a stomatal pore.
  3. The cell organelle where photosynthesis occurs.
  4. Organisms that cannot prepare their own food.
  5. An enzyme secreted by gastric glands in stomach that acts on proteins.

Answer:

  1. Photosynthesis
  2. Autotrophs
  3. Guard cells
  4. Chloroplast
  5. Heterotrophs
  6. Pepsin.

More Resources

Question 2.
“All plants give out oxygen during day and carbon dioxide during night.” Do you agree with the statement ? Give reason.
(CCE 2010)
Answer:
Yes. Respiration is going on throughout day and night. Photosynthesis occurs only during the day. Rate of photosynthesis is several times the rate of respiration. All the CO2 produced in respiration is also consumed in photosynthesis during the day time. Therefore, during day time, plants give out oxygen, which is a product of photosynthesis. However, during night when there is no photosynthesis, plants liberate carbon dioxide.

Question 3.
How do the guard cells regulate opening and closing of stomatal pores ? (CCE 2010, 2012)
Answer:
Opening and closing of stomata is regulated by gain or loss of turgidity of their guard cells. During opening of stomata, guard cells withdraw K+ ions from surrounding epidermal cells, followed by absorption of water from them. As a result, guard cells swell up and become turgid. Their outer thin and elastic walls bend outwardly followed by outward movement of thicker inner walls. The latter creates a pore in between the two guard cells.
During closure movement of stomata, guard cells send out K+ ions. Water also passes out. Guard cells become flaccid. Their inner thick walls come to touch each other. The stomatal pore gets closed.

Question 4.
Two green plants are kept separately in oxygen free containers, one in dark and the other in continuous light. Which one will live longer ? Give reasons. (CCE 2010)
Answer:
Plant kept in continuous light will live longer due to

  1. Manufacture of food and hence its availability to the plant for maintenance and growth,
  2. Production of oxygen in photosynthesis and its availability for respiration of the plant. Plant kept in oxygen free container kept in dark will die within a few days due to non-availability of food and oxygen.

Question 5.
If a plant is releasing carbon dioxide and taking in oxygen during the day, does it mean that there is no photosynthesis occurring ? Justify your answer.
Answer:
A plant releases carbon dioxide and takes in oxygen only when photosynthesis is either absent or too small as not to compensate for respiration.
(In photosynthesis, plants absorb CO2 and release O2. The normal rate of photosynthesis is many times the rate of respiration. As a result, CO2 produced during respiration is consumed and a lot of more is absorbed from outside. Oxygen produced during photosynthesis is much more than required for respiration. Therefore, oxygen passes out.)

Question 6.
Why do fishes die when taken out of water ?
Answer:
Fish taken out of water die due to

  1. Inability to obtain oxygen from air
  2. Collapsing of gill lamellae so that no space is left for gaseous exchange.

Question 7.
Differentiate between an autotroph and a heterotroph.
Answer:

Autotroph Heterotroph
1. Food: It manufactures its own food. It obtains its food from outside sources.
2. Chlorophyll: It has chlorophyll for performing photosynthesis. Chlorophyll is absent.
3. Energy: It is obtained from sunlight and changed into chemical energy. It does not require an external source of energy as the same is present in food obtained from outside.
4. Digestion: It is absent. Food obtained from outside is digested before being absorbed and assimilated.

Question 8.
Is nutrition a necessity for an organism ? Discuss.
Answer:
Yes, nutrition is a must for an organism because of the following reasons :
Importance of Nutrition/Food

  1. Food provides energy: Energy is required by the body all the time, whether asleep, taking rest or doing work. When the body is not doing any apparent work, energy is still being consumed in maintaining order. Further, biosynthetic activities continue for replacing materials being consumed or degraded. A number of other activities are going on all the time. Heart is always beating. Breathing movements never stop. Food eaten by a person has to be digested and absorbed. Excretory products are being produced.
  2. Body Structure: All body components are built up of materials obtained from food.
  3. Food is used in building protoplasm. More protoplasm is required for formation and enlargement of cells that take part in growth of the organism.
  4. Food provides materials for replacement and repair of worn out or damaged structures.
  5. Hormones and enzymes are formed from ingredients of food. They regulate metabolism and body functions.                                                                ‘
  6. Defence system of the body is formed from raw materials got- from food.
  7. Food provides materials to form reproductive structures.

Question 9.
What would happen if green plants disappear from earth ?
Answer:
Herbivores will die of starvation followed by carnivores and then decomposers.

Question 10.
Leaves of a healthy plant were coated with vaseline. Will this plant remain healthy for long ? Give reasons for your answer.
Answer:
The plant will not remain healthy for long. Vaseline covers the cuticle and blocks the stomata. As a result

  1. It is unable to obtain oxygen from air for respiration,
  2. It is unable to perform photosynthesis as no carbon dioxide diffuses from air.
  3. In the absence of transpiration, the leaves get heated up and injured.

Question 11.
How does aerobic respiration differ from anaerobic respiration ?
Answer:

Aerobic Respiration Anaerobic Respiration
1. Method: It is the common method of respiration. It occurs permanently only in a few organisms. In others it may occur as a temporary measure to overcome shortage of oxygen.
2. Steps: It is completed in 3 steps—glycolysis, Krebs cycle and terminal oxidation. There are two steps— glycolysis and anaerobic breakdown of pyruvic acid.
3. Oxygen: It requires oxygen. Oxygen is not required.

Question 12.
Match the words of column A with those of column B

A B

(a)  Phloem

(b)   Nephron

(c)  Veins

(d)  Platelets

(i)   Excretion

(ii)  Translocation of food.

(iii)   Clotting of blood

(iv)   Deoxygenated blood.

Answer:
a — ii,
b — i,
c —iv,
d —iii.

Question 13.
Differentiate between an artery and a vein. (CCE 2013)
Answer:

Artery Vein
1. Direction of Flow: It carries blood from heart to an organ. It brings blood from an organ towards the heart.
2. Speed: Blood flow is rapid in artery. Blood flow is slow in vein.
3. Jerks: Blood flows with jerks. Blood flows smoothly.
4. Pressure: Blood flows under pressure There is little pressure.
5. Internal Valves: They are absent. Internal valves are present to prevent back flow.
6. Wall: It is thick and elastic. It is comparatively thinner and little elastic.
7. Lumen: Narrow. Wide.
8. Type of Blood: Artery carries oxygenated blood except pulmonary arteries. Vein carries deoxygenated blood except pulmonary veins.
9. Occurrence: It is deep seated. It is superficial.
10. Collapsibility: Artery is not collapsible. Vein is collapsible.
11. Blood After Death: It does not contain blood after death. Vein is full of blood even after death.

Question 14.
What are the adaptations of leaf for photosynthesis ?
Answer:

  1. Large Surface Area : Leaf has a large surface area to absorb maximum amount of lift.
  2. Leaf Orientation: It is such as to absorb the optimum amount of light.
  3. Veins: A number of veins occur in a leaf. They provide mechanical strength to the otherwise soft leaf. Veins also take part in quick transport of substances to and from the mesophyll cells.
  4. Transpiration: Leaf is the seat of transpiration. Transpiration cools the surface of leaf for optimum photosynthesis.
  5. Gaseous Exchange: A leaf has a large number of stomata for gaseous exchange, required for photosynthesis.
  6. Chloroplasts: A very large number of chloroplasts occur in the mesophyll of a leaf for efficient photosynthesis.

Question 15.
Why is small intestine in herbivore longer than in carnivores ? (CCE 2013)
Answer:
Herbivorous diet has a large bulk. It is rich in cellulose. However, cellulose digesting enzymes are absent in them. For digestion
of cellulose, herbivores depend upon bacteria. The food has to be kept for longer period in the intestine for complete digestion of cellulose. Therefore, small intestine where bacterial digestion of cellulose occurs has to be long. There is no such requirement in carnivores as their diet has a smaller bulk which does not contain cellulose. They have a shorter intestine.

Question 16.
What will happen if mucus is not secreted by gastric glands ?
Answer:
Mucus protects the stomach from corrosion by HCl and pepsin of gastric juice. In the absence of mucus, the lining layer of stomach wall will be corroded forming gastric ulcers. There will be excessive acidity and extreme discomfort.

Question 17.
What is the significance of emulsification of fats ?
Answer:
Emulsification of fat is the conversion of large fat pieces into very fine fat globules which can be efficiently acted upon by lipase.

Question 18.
What causes movement of food inside the alimentary canal ?
Answer:
Involuntary movement consisting of rhythmic contraction and expansion of the alimentary canal called peristalsis.

Question 19.
Why does absorption of digested food occur mainly in the small intestine ?
Answer:

  1. Digestion of food is completed only in small intestine.
  2. Wall of the intestine bears a number of finger-like projections called villi. Villi provide a large surface area to the lining layer for absorption.
  3. The epithelium, lining the villi, is made of cells having a number of very fine projections known as microvilli. Microvilli are specialised for absorption.
  4. Wall of the intestine, especially the interior of villi, has lymph and blood vessels for carrying the absorbed food to different parts of the body.

Question 20.
Match the articles of columns A and B :

A B

(a)  Autotrophic nutrition

(b)  Heterotrophic nutrition

(c) Parasitic nutrition

(d)  Digestion in food vacuoles

 (i) Leech

(ii) Paramoecium

(iii)   Deer

(iv)    Green plant.

Answer:
a — iv,
b — iii,
c—i,
d — ii.

Question 21.
Why is the rate of breathing in aquatic organisms much faster than in terrestrial organisms ? (CCE 2011, 2012)
Answer:
Most of the aquatic organisms obtain oxygen from water. The amount of dissolved oxygen is quite small as compared to the amount of oxygen in air. Therefore, in order to obtain required oxygen from water, the aquatic animals like fishes have to breathe much faster as compared to the terrestrial organisms.

Question 22.
Why is blood circulation in human heart called double circulation ? (CCE 2011)
Answer:
Blood circulation in human heart is called double circulation as blood passes twice through the heart in order to complete one cycle—once through right side as deoxygenated blood and once through left side as oxygenated blood. Deoxygenated blood passes to lungs. It returns to left side as oxygenated blood. Oxygenated blood is supplied to different parts of the body. It returns to right side of the heart as deoxygenated blood.

Question 23.
What is the advantage of having four chambered heart ? (CCE 2010)
Four chambered heart ensures complete separation of oxygenated and deoxygenated bloods. Only oxygenated blood is pumped out to supply all parts of the body. It is received by left auricle from lungs and pumped out by left ventricle. The blood returns to heart after deoxygenation. It is received by right auricle and pumped out by right ventricle to lungs for oxygenation. The mechanism is useful to animals with high energy needs (due to thermoregulation and higher activity) such as birds mammals.

Question 24.
Mention the major events during photosynthesis. (CCE 2011, 2012)
Answer:

  1. Photolysis: With the help of light energy, oxygen evolving Z-complex splits up water into its components —- protons (H+), electrons (e–) and oxygen.
    NCERT Exemplar Solutions for Class 10 Science Chapter 6 Life Processes image - 1
  2. Absorption of Light Energy: Chlorophyll absorbs light energy.
  3. Primary Reaction: Chlorophyll converts the absorbed light energy into chemical energy. It is called primary reaction of photosynthesis. It builds up ATP with the help of excited electrons.
  4. Formation of Reducing Power: Coenzyme NADP+ is changed to reduced form of NADPH.
    NCERT Exemplar Solutions for Class 10 Science Chapter 6 Life Processes image - 3
  5. Reduction of CO2: Carbon dioxide is reduced enzymatically with the help of NADPH and ATP to form carbohydrates.
    NCERT Exemplar Solutions for Class 10 Science Chapter 6 Life Processes image - 4

Question 25.
In each of the following situations, what happens to the rate of photosynthesis ?
(a) Cloudy days
(b) No rainfall in the area
(c) Good manuring
(d) Stomata get blocked due to dirt.
Answer:
(a) Cloudy Days: Photosynthesis is reduced due to low light intensity.
(b) No Rainfall: Rate of photosynthesis decreases due to wilting of leaves, closure of stomata and reduced availability of hydration.
(c) Good Manuring: Rate of photosynthesis increases as good manuring increases soil fertility by providing more minerals, moisture and aeration.
(d) Blocked Stomata: It decreases the rate of photosynthesis by reducing gaseous exchange and non-cooling of leaves due to reduced transpiration.

Question 26.
Name the energy currency in the living organisms. When and where is it produced ?
Energy Currency. ATP (adenosine triphosphate) is the energy; currency of the living beings.
It is produced both during respiration (in all organisms) and photosynthesis (in plants only).

Question 27.
What is common amongst Cuscuta, Ticks and Leeches ?
Answer:
All are parasites which obtain their nutrition from their hosts direcdy without killing them.

Question 28.
Explain the role of mouth cavity in digestion of food.
Answer:

  1. Moistening of food with saliva,
  2. Tongue helps in thorough mixing of food with saliva.
  3. Crushing of food into smaller pieces by teeth,
  4. Partial digestion of starch by enzyme amylase contained in saliva,
  5. Rolling of crushed, moistened and partially digested food into small ball or bolus by the tongue.

Question 29.
What are the functions of gastric glands present in the wall of stomach ? (CCE 2011)
Answer:
Gastric glands produce the following substances :

  1. Mucus: Moistening the food and protecting the wall of the stomach from corroding action of HCl and pepsin.
  2. HCl: It makes the food soft, sterilised and acidified for pepsin to act upon food.
  3. Gastric Lipase: It is active only in infants. It partially breaks down fat into its components.
  4. Rennin: It is active in infants where it helps in curdling of milk (casein to paracasein) for action of pepsin.
  5. Pepsin: It is secreted in inactive state of pepsinogen. Pepsin hydrolyses proteins into soluble fragments of peptones and proteoses.

Question 30.
Match the items of columns A and B

A B

(a)  Trypsin

(b)  Amylase

(c) Bile

(d)  Pepsin

 (i) Pancreas

(ii) Liver

(iii)   Gastric glands

(iv)     Saliva

Answer:
a — i,
b — iv,
c — ii,
d — iii.

Question 31.
Name the correct substrates for the following enzymes :
(a) Trypsin
(b) Amylase
(c) Pepsin
(d) Lipase.
Answer:
(a) Trypsin: Proteins, peptones and proteoses,
(b) Amylase: Starch, dextrins.
(c) Pepsin: Proteins.
(d) Lipase: Fats.

Question 32.
Why do veins have thin walls as compared to arteries ?
Answer:
In arteries, blood flows under pressure so that their walls are thick and elastic. In veins the blood is Therefore, their walls are thin. Rather, they possess semilunar valves to check back flow of blood.

Question 33.
What will happen if platelets were absent in the blood ?
Answer:
Blood platelets are a source of thromboplastin which is essential for blood clotting at the place of injury. In the absence of blood platelets, blood clotting will be litde resulting in greater loss of blood from the place of injury.

Question 34.
Plants have low energy needs as compared to animals. Explain.
Answer:
Plants are anchored. They do not move about. Most of their body is made of dead cells and cell walls. Therefore, their requirement for energy is quite low as compared to animals which move about fast in search of food, mate and shelter.

Question 35.
Why and how does water enter continuously into root xylem ?
Answer:
Root cells in the absorbing part of root pick up ions actively from soil. Ions pass inwardly increasing osmotic concentration of xylem. Because of it soil water (which has very low osmotic concentration) continuously passes into root xylem.

Question 36.
Why is transpiration important for plants ?
Answer:
Importance

  1. Cooling: Evaporation of water from the aerial parts results in lowering of their temperature which will otherwise rise due to exposure to sun.
  2. Concentration of Minerals: Transpiration helps in increasing concentration of minerals present in rising water.
  3. Transport: It creates a pull that helps in transport of water and minerals.

Question 37.
How does leaves of plants help in excretion ? (CCE 2016)
Answer:
Waste materials produced in plant cells are stored ’in their vacuoles. In leaves, the waste materials are

  1. Stored in vacuoles of mesophyll and epidermal cells,
  2. Oxalic acid is crystallised as calcium oxalate.
  3.  Nitrogenous wastes are changed into alkaloids
  4. Vaste aromatic compounds are changed into tannins. As the old leaves fall, the waste materials are also removed from the plant.

NCERT Exemplar Solutions for Class 10 Science Chapter 6 Long Answer Questions

Question 38.
Explain the process of nutrition in Amoeba.
Answer:

  1. Ingestion: (L. ingestus — taken in). It is taking in of solid food with the help of temporary or permanent mouth. Amoeba can ingest food particles from any point on its surface. Paramoecium (another unicellular organism) has fixed point for the same. Amoeba captures food with the help of temporary finger-like processes called pseudopodia. Paramoecium has small hair-like processes called cilia. Beating of cilia creates current in water that pushes food particle through cytostome or cell mouth. The process of ingestion of solid food particle by a cell or unicellular organism is called phagocytosis.
    As soon as Amoeba comes in contact with a food particle or prey, it throws pseudopodia all around the same. The tips of encircling pseudopodia fuse and the prey comes to lie in a vesicle or phagosome.
    NCERT Exemplar Solutions for Class 10 Science Chapter 6 Life Processes image - 5
  2. Digestion: It is conversion of complex insoluble food ingredients into simple absorbable form. Digestion can be intracellular or intercellular. Intercellular digestion occurs in a digestive tract. Intracellular digestion takes place in the cytoplasm of cells. Here, a lysosome fuses with phagosome to produce a food vacuole, also called gastriole or temporary stomach. Reaction of food vacuole is acidic at first and alkaline later on. Digestion of food occurs with the help of digestive enzymes brought by lysosome. It changes complex insoluble substances of food into simpler absorbable substances.
  3. Absorption: The digested simple and soluble substances pass out of food vacuole into the surrounding cytoplasm.
  4. The absorbed food materials are converted into various constituents of protoplasm including food reserve.
  5. (L. egestus — discharge): It is throwing of undigested components of food out of the body. In Amoeba, the old food vacuole with heavier undigested material reaches the rear end, passes to the surface, fuses with surface membrane and throws out the undigested materials. The process is called egestion. Paramoecium has a definite cytopyge or cell anus.

Question 39.
Describe the alimentary canal of man.
Answer:
Alimentary canal (L. alere-to nourish) is a tubular passage extending from mouth to anus through which food passes during its digestion and absorption. It is about 9 metres in length. Alimentary canal consists of mouth, buccal cavity, oesophagus, stomach, small intestine, large intestine and anus.
NCERT Exemplar Solutions for Class 10 Science Chapter 6 Life Processes image - 6

  1. Mouth: It is a transverse slit like aperture that occurs in between the nose and the chin. Mouth is bounded by two soft, movable sensitive lips, upper and lower. Lips help in holding the food. They also aid in phonation (speech).
  2. Buccal or Oral Cavity (L. bucca-cheek): It is anterior part of alimentary canal that extends from mouth to pharynx and lies between two jaws, upper (fixed) and lower (movable). It has palate on upper side, throat and tongue on the lower side and cheeks on the lateral sides. Both the jaws contain teeth in semicircular rows or arches.
    1. It is a muscular, sensory, movable and protrusible flat structure which is attached posteriorly over the lower jaw. Tongue bears taste buds for tasting the quality of food—sweet anteriorly, salt anterio-laterally, sour postero-laterally and bitter posteriorly. It moves food in ‘the buccal cavity for crushing under teeth, mixing with saliva and pushing the food during swallowing. Tongue cleans the teeth. It also aids in phonation (speech). It functions as a movable spoon during drinking.
    2. They are hard structures which are used for cutting, chewing and crushing the food (physical digestion). They are partially embedded in sockets of jaw bones (thecodont). Teeth are made of ivory like substance called dentine. The exposed parts of teeth or crowns are covered by a shining substance called enamel. Enamel is the hardest substance of the body.
    3. Salivary Glands. Three pairs of salivary glands (saliva secreting glands) open into buccal cavity. They are parotid (below ears), sub-maxillary (at the angles of lower jaw) and sublingual (below tongue). About 1-0-1-5 litres of near neutral saliva is poured into buccal cavity every day. Saliva consists of mucus, water, lysozyme and enzyme ptyalin.

Question 40.
Explain the process of breathing in man.
Answer:
Breathing or the process of taking in fresh air and releasing foul air can be easily observed because thorax shows alternate expansion and contraction. It is involuntary though it can be prevented for a brief period. Rate of breathing is controlled by respiratory centre of brain. Expansion of thorax causes fresh air to be drawn in. Contraction of thorax causes foul air to be expelled. Therefore, breathing consists of two steps, inspiration and expiration.

  1. Inspiration or Inhalation: It is bringing of fresh air into lungs for exchange of gases. During inhalation, thoracic cavity enlarges due to two types of inspiratory muscles, phrenic and external intercostals. Phrenic muscles straighten the diaphragm by moving its curved part downwards. It increases length of thorax. Contraction of external intercostal muscles pushes the rib cage in outward and upward direction. It increases girth of thorax. Being air tight, increase in size of thoracic cavity causes expansion of lungs. It decreases air pressure in the lungs. As a result outside air rushes into lungs through external nostrils, nasal cavities, internal nostrils, pharynx, larynx, trachea, bronchi, bronchioles to alveoli. While passing through respiratory tract, the incoming air is :
    1. Filtered by hair present in anterior part of nasal cavities.
    2. Cleansed of dust and microbes throughout respiratory tract by lysozyme, mucus and cilia.
    3. Air conditioned (bringing temperature of inhaled air to that of body) with the help of blood capillaries present below nasal epithelium.
    4. Moistened by water vapours from wet epithelium.
  2. Exchange of Gases: It occurs in the alveoli. Fresh air has high concentration of oxygen and a very low concentration of carbon dioxide. As a result, oxygen diffuses from alveolar air to blood present in capillaries around the alveoli. Carbon dioxide diffuses from blood into alveolar air.

Question 41.
How do carbohydrates, proteins and fats get digested in human beings ?
Answer:
Carbohydrates:    Glucose.
Proteins:               Amino acids.
Fats:                      Fatty acids and   glycerol.
Hints:

  1. Carbohydrates: In mouth cavity (by saliva), duodenum (by pancreatic juice) and jejunum (by intestinal juice).
  2. Proteins: In stomach (by gastric juice), duodenum (by pancreatic juice) and jejunum (by intestinal juice).
  3. Fats: In duodenum and jejunum (by pancreatic juice aided by bile salts). Also in infants in stomach.

Question 42.
Explain the mechanism of photosynthesis.
Answer:
Mechanism of Photosynthesis:
Photosynthesis is formation of organic food from carbon dioxide and water with the help of sunlight inside chlorophyll containing cells. Oxygen is produced as by-product.
NCERT Exemplar Solutions for Class 10 Science Chapter 6 Life Processes image - 7
Oxygen comes from water. Hydrogen of water is used to reduce carbon dioxide to form carbohydrate.
NCERT Exemplar Solutions for Class 10 Science Chapter 6 Life Processes image - 8
Actually, photosynthesis occurs in two steps, photochemical and biochemical.
1. Photochemical Phase (Light or Hill Reaction): The reactions of this phase are driven by light energy. They are of two types— photolysis of water and formation of assimilatory power.
(a) Photolysis of Water. Light energy splits up water into its components. Mn2+, CL and Ca2+ are required for this.
NCERT Exemplar Solutions for Class 10 Science Chapter 6 Life Processes image - 9
(b) Formation of Assimilatory Power: Light energy absorbed by chlorophyll molecules is used in synthesis of ATP and NADPH.
Both ATP and NADPH2 together form assimilatory power.
NCERT Exemplar Solutions for Class 10 Science Chapter 6 Life Processes image - 10
2. Biosynthetic Phase (Dark or Blackman’s Reaction). It is actually light independent reaction which can occur both in light as well as in dark. It requires the energy and reducing power contained in assimilatory power of light reaction. Common pathway of biosynthetic phase is Calvin cycle. Carbon dioxide combines with ribulose bisphosphate in the presence of enzyme ribulose biphosphate carboxylase or rubisco. It produces two molecules of phosphoglyceric acid (PGA).
NCERT Exemplar Solutions for Class 10 Science Chapter 6 Life Processes image - 11
3. In the presence of ATP, phosphoglyceric acid is reduced by NADPH2 to form glyceraldehyde phosphate (GAP).
NCERT Exemplar Solutions for Class 10 Science Chapter 6 Life Processes image - 12
4. A part of glyceraldehyde phosphate is changed into dihydroxyacetone phosphate. The two condense and form glucose. Ribulose biphosphate is regenerated to combine with carbon dioxide again. Glucose undergoes condensation to form reserve carbohydrate called starch.
5. Other inorganic Raw Materials: Synthesis of carbohydrates during photosynthesis is a mechanism to form food materials for body building and releasing energy.
NCERT Exemplar Solutions for Class 1
Plants also require a number of other inorganic raw materials or minerals from soil for building other, e.g., nitrogen, phosphorus, iron, sulphur, magnesium, etc. Nitrogen and sulphur are required for building proteins. Phosphorus is required for synthesis of nucleotides. Minerals are absorbed in the form of ions, e.g., NO2– and NH4+ for nitrogen. Some bacteria convert atmospheric nitrogen into compounds of nitrogen. Parts of them become available to plants.

Question 43.
Explain the three pathways of breakdown (respiration) in living organisms.
Answer:
(i) Aerobic Respiration:
It is a multistep complete oxidative breakdown of respiratory substrate into carbon dioxide and water with the help of oxygen acting as a terminal oxidant. Aerobic respiration is the usual mode of respiration in all higher organisms and most of the lower organisms. The reason is that it yields maximum amount of energy. The energy is stored in some 38 molecules of ATP.
NCERT Exemplar Solutions for Class 10 Science Chapter 6 Life Processes image - 14
Aerobic respiration occurs in two steps, glycolysis and Krebs cycle.
NCERT Exemplar Solutions for Class 10 Science Chapter 6 Life Processes image - 15
Glycolysis: Glycolysis or EMP (Embden, Meyerhof and Parnas) pathway is the first step of respiration which is common to both aerobic and anaerobic modes of respiration. It occurs in cytoplasm. Respiratory substrate is double phosphorylated before it undergoes lysis to produce 3-carbon compound, glyceraldehyde phosphate. NADH2 and ATP are produced when glyceraldehyde is changed to pyruvate. The net reaction of glycolysis is :
NCERT Exemplar Solutions for Class 10 Science Chapter 6 Life Processes image - 16
Krebs Cycle (Krebs, 1940): It is also known as citric acid cycle or tricarboxylic acid cycle (TCA cycle). Pyruvic acid or pyruvate passes into mitochondria. It undergoes oxidative decarboxylation to produce acetyl CoA, carbon dioxide and NADH2. Acetyl CoA enters Krebs cycle. Here two decarboxylations, four dehydrogenations and one phosphorylation or ATP synthesis occur.
NCERT Exemplar Solutions for Class 10 Science Chapter 6 Life Processes image - 17
NADH2 and FADH2 liberate electrons and hydrogen ions. They are used in building up ATP molecules and activating oxygen molecules to combine with hydrogen for forming water. Synthesis of ATP from ADP and inorganic phosphate with the help of electron generated energy during oxidation of reduced coenzymes (NADH2, FADH2) is called oxidative phosphorylation. Water formed in respiration is called metabolic water. As oxygen is used at the end of Krebs cycle for combining with hydrogen, the process is called terminal oxidation.
The overall equation of aerobic respiration using glucose as substrate is
NCERT Exemplar Solutions for Class 10 Science Chapter 6 Life Processes image - 18
(ii) Anaerobic Respiration Producing Alcohol:
It is a multistep breakdown of respiratory substrate in which atleast one end product is organic and which does not employ oxygen as an oxidant. Anaerobic respiration occurs in many lower organisms, e.g., certain bacteria, yeast. In human body it occurs regularly in red blood cells and during heavy exercise in muscles (striated muscles). Anaerobic respiration occurs entirely in the cytoplasm. It has two steps. The first step is glycolysis. Here, respiratory substrate glucose breaks down into two molecules each of pyruvate, ATP and NADH2. Pyruvate is converted into ethyl alcohol (C2H5OH) in Yeast and certain bacteria. It is changed to lactic acid (CH3CHOH.COOH) in muscle cells when oxygen utilisation is faster than its availability as during vigorous exercise. It creates an oxygen debt in the body. No such debt occurs in blood corpuscles.
NCERT Exemplar Solutions for Class 10 Science Chapter 6 Life Processes image - 19
(iii) Anaerobic Respiration Producing Lactic Acid:
Build up of lactic acid in muscles during prolonged activity causes fatigue and results in cramps.
Fermentation (L. fermentum-froth). It is anaerobic breakdown of carbohydrates by microorganisms producing alcohol, organic acids and a variety of other products alongwith heat and waste gases. Fermentation is used in brewing industry (for producing wine, whisky, beer), baking industry (for making bread spongy), curd and yoghurt formation, synthesis of vinegar, citric acid, lactic acid, softening and aromatisation of Tobacco, Tea and other beverages, cleaning of hides and separating or retting of fibres (e.g., Jute, Hemp).
NCERT Exemplar Solutions for Class 10 Science Chapter 6 Life Processes image - 20

Question 44.
Describe the flow of blood through heart of human beings.
Answer:
It is passage of the same blood twice through the heart first on the right side, then on the left side in order to complete one cycle. Double circulation has two components, pulmonary circulation and systemic circulation.

  1. Pulmonary Circulation: It is movement of blood from heart to the lungs and back. Deoxygenated blood of the body enters the right auricle, passes into right ventricle which pumps it into pulmonary arch. With the help of two separate pulmonary arteries the blood passes into the lungs. Here, it is oxygenated. Oxygenated blood comes back to left auricle of heart through four pulmonary veins, two from each lung.
  2. Systemic Circulation: It is the circulation of blood between heart and different parts of the body except lungs. Oxygenated blood received by left auricle passes into left ventricle. The left ventricle pumps it into aorta for supply to different body parts including walls of the heart by means of arteries. Inside the organs the blood loses oxygen and nutrients. It picks up carbon dioxide and waste products. This deoxygenated blood is drained by veins and sent to the right auricle of heart.

NCERT Exemplar Solutions for Class 10 Science Chapter 6 Life Processes image - 21

Question 45.
Describe the process of urine formation in kidneys.
Answer:
Mechanism of Urine Formation: 
It has four components — glomerular filtration, selective reabsorption, tubular secretion and concentration.

  1. Glomerular Filtration: Blood flows in glomerulus under pressure due to narrowness of efferent arteriole. As a result it undergoes pressure filtration or ultrafiltration. All small volume solutes (e.g., urea, uric acid, amino acids, hormones, glucose, ions, vitamins) and water are filtered out and enter the Bowman’s capsule. The product is called nephric or glomerular filtrate. Its volume is 125 ml/min (180 litres/day).
  2. Reabsorption: Nephric filtrate is also called primary urine. It passes into proximal convoluted tubule. The peritubular capillaries around PCT reabsorb all the useful components of nephric filtrate, e.g, glucose, amino acids, vitamins C, calcium, potassium, sodium, chloride, bicarbonate and water (75%). Selective reabsorption also occurs in the region of distal convoluted tubule. The amount of water absorption depends upon amount of excess water present in the body and the amount of dissolved waste to be excreted.
  3. Tubular Secretion (Augmentation): It occurs mostly in the distal convoluted tubule which is also surrounded by peritubular capillaries. Smaller amount of tubular secretion also takes place in the area of proximal convoluted tubule. Tubular secretion is active secretion of waste products by the blood capillaries into the urinary tubule. It ensures removal of all the waste products from blood, viz.,’ urea, uric acid, creatinine. Extra salts, K+ and H+ are also secreted into urinary tubule to maintain a proper concentration and pH of the urine.
  4. Concentration of the Urine: 75% of water content of nephric filtrate is reabsorbed in the region of proximal convoluted tubule. Some 10% of water passes out of the filtrate through osmosis in the area of loop of Henle. It is because loops of Henle are immersed in hyper-osmotic interstitial fluid, Further concentration takes place in the area of collecting tubes in the presence of hormone called antidiuretic hormone (ADH) or vasopressin. The hormone is secreted only when concentrated urine is to be passed out. It is not secreted when a person drinks a lot of water. Absence of antidiuretic  hormone produces a dilute urine. Hormone action, therefore, maintains osmotic concentration of body fluids. Deficiency of ADH causes excessive, repeated, dilute urination (diabetes insipidus).

Hope given NCERT Exemplar Solutions for Class 10 Science Chapter 6 Life Processes are helpful to complete your science homework.

If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.

RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.1

RD Sharma Class 8 Solutions Chapter 23 Data Handling I (Classification and Tabulation of Data) Ex 23.1

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.1

Other Exercises

Question 1.
Define the following terms :
(i) Observations
(ii) Raw data
(iii) Frequency of an observation
(iv) Frequency distribution
(v) Discrete frequency distribution
(vi) Grouped frequency distribution
(vii) Class-interval
(viii) Class-size
(ix) Class limits
(x) True class limits
Solution:
(i) Observations : Each entry in the given data is called an observation. ‘
(ii) Raw data: A collection of observations by an observer, is called raw data.
(iii) Frequency of an observation : The number of times an observation occurs in the given data is called its frequency.
(iv) Frequency distribution : The presentations of given data in order of magnitude ascending or descending, is called the frequency distribution.
(v) Discrete frequency distribution: When the given data is represented by tally marks after arranging it in an order. This kind of distribution is called discrete frequency distribution.
(vi) Grouped frequency distribution: If the number of data is large, and the difference between the greatest and the smallest observation is large, then we represent then in groups or classes. Such representation of data is called grouped frequency distribution.
(vii) Class intervals: The difference between the upper limit and lower limit of a class is called class interval.
(viii) Class-size : Class intervals are also called the class size. Each size of the same intervals
(ix) Class limits : Every class has two limits : upper limit and lower limit.
(x) True class limits or Exclusive limits : When the upper limit of one is the lower limit of the next interval then these are call true class limits.

Question 2.
The final marks in mathematics of 30 students are as follows :
53, 61, 48, 60, 78, 68, 55, 100, 67, 90, 75, 88,77,37,84,58,60,48,62,56,44,58,52,64, 98, 59, 70, 39, 50, 60
(i) Arrange these marks in the ascending order, 30 to 39 one group, 40 to 49 second group etc.
Now answer the following:
(ii) What is the highest score ?
(iii) What is the lowest score ?
(iv) What is the range ?
(v) If 40 is the pass mark how many have failed ?
(vi) How many have scored 75 or more ?
(vii) Which observations between 50 and 60 have not actually appeared ?
(viii) How many have scored less than 50 ?
Solution:
(i) Arranging the given data in ascending order.
30 to 39 : 37,39
40 to 49 : 44, 48, 48
50 to 59 : 50, 52, 53, 55, 56, 58, 58, 59
60 to 69 : 60, 60, 60, 61, 62, 64, 67, 68
70 to 79 : 70, 75, 77, 78
80 to 89 : 84, 88
90 to 99 : 90, 98
100 to 109 : 100
(ii) Highest score is 100
(iii) Lowest score is 37
(iv) Range is 100 – 37 = 63
(v) If 40 is pass marks then number of failed candidates will be = 2
(vi) Number of students who scored 75 or more = 8
(vii) Between 50 and 60, the observations 51, 54, 57 do not appear.
(viii) Number of students who scored less than 50 = 5

Question 3.
The weights of new born babies (in kg) in a hospital on a particular day are as follows:
2.3, 2.2, 2.1, 2.7, 2.6,3.0, 2.5, 2.9, 2-8,3.1, 2.5, 2.8, 2.7, 2.9, 2.4.
(i) Rearrange the weights in descending order.
(ii) Determine the highest weight:
(iii) Determine the lowest weight.
(iv) Determine the range.
(v) How many babies were born on that day?
(vi) How many babies weigh below 2.5 kg ?
(vii) How many babies weigh more than 2.8 kg ?
(viii) How many babies weigh 2.8 kg ?
Solution:
(i) Arranging the given weights in descending order.
3.1, 3.0, 2.9, 2.9, 2.8, 2.8, 2.7, 2.7, 2.6, 2.5, 2.5, 2.4, 2.3, 2.2, 2.1
(ii) Highest weight = 3.1 kg
(iii) Lowest weight = 2.1 kg
(iv) Range : 3.1 – 2.1 = 1 kg.
(v) Number of babies born on that day = 15
(vi) Number of babies having weight below 2.5 kg = 4
(vii) Number of babies having weight more than 2.8 kg = 4
(viii) Number of babies weigh 2.8 kg = 2

Question 4.
Following data gives the number of children in 41 families:
1,2,6,5,1,5,1,3,2,6,2,3,4,2,0,0,4,4, 3, 2, 2, 0, 0,1, 2, 2, 4,3, 2,1, 0, 5,1, 2,4, 3, 4, 1, 6, 2, 2.
Represent it in the form of a frequency distribution.
Solution:
Frequency distribution table
RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.1 1

Question 5.
Prepare a frequency table of the following scores obtained by 50 students in a test:
42, 51, 21, 42, 37. 37, 42, 49, 38, 52, 7, 33, 17, 44, 39, 7, 14, 27, 39, 42, 42, 62, 37, 39, 67, 51, 53, 53, 59, 41, 29, 38, 27, 31, 54,19, 53, 51, 22, 61, 42, 39, 59, 47, 33, 34, 16, 37, 57, 43
Solution:
Frequency distribution table
RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.1 2

Question 6.
A die was thrown 25 times and following scores were obtained:
1,5,2,4,3,6,1,4,2,5,1,6,2,6,3,5,4,1, 3, 2, 3, 6,1, 5, 2
Prepare a frequency table of the scores.
Solution:
Frequency distribution table
RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.1 3

Question 7.
In a study of number of accidents per day, the observations for 30 days were obtained as follows:
6,3,5,6,4,3, 2,5,4,2,4,2,1,2, 2,0,5,4,6,1,6,0, 5, 3, 6,1, 5, 5, 2, 6
Prepare a frequency distribution table.
Solution:
Frequency distribution table
RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.1 4

Question 8.
Prepare a frequency table of the following ages (in years) of 30 students of class VIII in your school:
13,14,13,12,14,13,14,15,13,14,13,14, 16,12,14,13,14,15,16,13,14,13,12,17,13, 12,13,13,13,14
Solution:
Frequency distribution table
RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.1 5

Question 9.
Following figures relate to the weekly wages (in Rs) of 15 workers in a factory :
300,250,200,250,200,150,350,200,250, 200,150, 300,150, 200, 250 Prepare a frequency table.
(i) What is the range in wages (in Rs) ?
(ii) How many workers are getting Rs 350 ?
(iii) How many workers are getting the minimum wages ?
Solution:
Frequency distribution table
RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.1 6
(i) Range = 350- 150 = 200
(ii) Number of workers getting Rs 350 = 1
(iii) Number of workers getting minimum wages = 3

Question 10.
Construct a frequency distribution table for the following marks obtained by 25 students in a history test in class Vin of a school:
9,17,12, 20,9,18, 25,17,19,9,12,9,12, 18, 17,19, 20, 25, 9,12,17,19, 19, 20, 9
(i) What is the range of marks ?
(ii) What is the highest mark ?
(iii) Which mark is occurring more frequently ?
Solution:
Frequency distribution table
RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.1 7
(i) Range = 25 – 9 = 16
(ii) Highest marks = 25
(iii) Marks occurring more frequently = 9

 

Hope given RD Sharma Class 8 Solutions Chapter 23 Data Handling I Ex 23.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4C

RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4C

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4C.

Other Exercises

Question 1.
Solution:
(i) We have : – 34 – 18 = – 52
(ii) We have : 25 – ( – 15) = 25 + 15 = 40
(iii) We have : – 43 – ( – 28) = – 43 + 28 = – 15
(iv) We have : ( – 37) – 68 = ( – 37) + ( – 68) = – 105
(v) We have : 0 – 219 = 0 + ( – 219) = – 219
(vi) We have : 0 – ( – 92) = 0 + 92 = 92
(vii) We have : – 250 – ( – 135) = ( – 250) + 135 = – 115
(viii) We have : – 287 – ( – 2768) = ( – 287) + 2768 = 2481
(ix) We have: – 271 – 6240 = ( – 271) + ( – 6240) = – 6511
(x) We have : 6250 – ( – 3012) = 6250 + 3012 = 9262

Question 2.
Solution:
The sum of – 1050 and 813.
= ( – 1050) + 813 = – 237
Required number = – 23 – ( – 237)
= ( – 23) + 237 = 214

Question 3.
Solution:
The sum of – 250 and 138
= ( – 250) + 138 = – 112
The sum of 136 and – 272
= 136 + ( – 272) = – 136
Required number = – 136 – ( – 112)
= ( – 136) + 112 = – 24

Question 4.
Solution:
The sum of 33 and – 47
= 33 + ( – 47)
= – 14
Required number = – 14 – ( – 84)
= ( – 14) + 84
= 70

Question 5.
Solution:
The difference of – 8 and – 68
= – 8 – ( – 68)
= ( – 8) + 68 = 60
Required sum = 60 + ( – 36)
= 24

Question 6.
Solution:
(i) We have :
[37 – ( – 8)] + [11 – ( – 30)]
= (37 + 8) + (11 + 30)
= 45 + 41
= 86
(ii) [ – 13 – ( – 17)] + [ – 22 – ( – 40)]
= ( – 13 + 17)+ ( – 22 + 40)
= 4 + 18
= 22

Question 7.
Solution:
We have :
34 – ( – 72) = 34 + 72 = 106 and ( – 72) – 34 = ( – 72) + ( – 34)
= – 106
Clearly, 34 – ( – 72) and ( – 72) – 34 are not equal.

Question 8.
Solution:
The sum of two integers = – 13
One number =170
The other number = – 13 – 170
= ( – 13) + ( – 170)
= – 183

Question 9.
Solution:
The sum of two integers = 65
One number = – 47
The other number = 65 – ( – 47)
= 65 + 47
= 112

Question 10.
Solution:
(i) True
(ii) True
(iii) The given statement is
– 14 > – 8 – ( – 7)
– 14 > – 8 + 7 .
– 14 > – 1 which is not true.
(iv) The given statement is – 5 – 2 > – 8
( – 5) + ( – 2) > – 8
– 7 > – 8 which is true
The given statement is true.
(v) The given statement is ( – 7) – 3 = ( – 3) – ( – 7)
( – 7) + ( – 3) = ( – 3) + 7
– 10 = 4
which is not true.
The given statement is false.

Question 11.
Solution:
The vertical distance between A and B = Distance of point A above sea level + distance of point B below sea level.
= 5700 m + 39600 m
= 45300 m.
The required distance between A and B
= 45300 metres.

Question 12.
Solution:
Temperature at 6 p.m. = 1°C
Temperature at mid-night = – 4°C
Required temperature fall = 1°C – ( – 4° C)
= 1°C + 4°C
= 5°C.

Hope given RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 24 Data Handling II Ex 24.1

RD Sharma Class 8 Solutions Chapter 24 Data Handling II (Graphical Representation of Data as Histograms) Ex 24.1

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 24 Data Handling II Ex 24.1

Question 1.
Given below is the frequency distribution of the heights of 50 students of a class :
RD Sharma Class 8 Solutions Chapter 24 Data Handling II Ex 24.1 1
Draw a histogram representing the above data.
Solution:
We represent class intervals along x-axis and frequency along y-axis. Taking suitable intervals along x-axis and y-axis we construct the rectangles as shown in the figure. This is the required histogram.
RD Sharma Class 8 Solutions Chapter 24 Data Handling II Ex 24.1 2

Question 2.
Draw a histogram of the following data :
RD Sharma Class 8 Solutions Chapter 24 Data Handling II Ex 24.1 3
Solution:
We represent class-intervals along x-axis and frequency along y-axis. Taking suitable intervals along x-axis andy-axis, we construct rectangles as shown in the figure. This is the required histogram.
RD Sharma Class 8 Solutions Chapter 24 Data Handling II Ex 24.1 4

Question 3.
Number of workshops organized by a school in different areas during the last five years is as follows :
RD Sharma Class 8 Solutions Chapter 24 Data Handling II Ex 24.1 5
Draw a histogram representing the above data.
Solution:
We represent years along x-axis and number of workshops along y-axis. Taking suitable intervals, we construct rectangles as shown in the figure. This is the required histogram.
RD Sharma Class 8 Solutions Chapter 24 Data Handling II Ex 24.1 6
RD Sharma Class 8 Solutions Chapter 24 Data Handling II Ex 24.1 7

Question 4.
In a hypothetical sample of 20 people the amounts of money with them were found to be as follows :
114, 108,100, 98, 101,109,117,119, 126, 131, 136, 143, 156, 169, 182, 195, 207, 219, 235, 118.
Draw the histogram of the frequency distribution (taking one of the class intervals as 50-100).
Solution:
Highest sample = 235
Lowest sample = 98
Range = 235-98 = 137
Now frequency distribution table will be as under:
RD Sharma Class 8 Solutions Chapter 24 Data Handling II Ex 24.1 8
We represent class intervals along x-axis and frequency along j’-axis. Taking suitable intervals, we construct a rectangles as shown in the figure. This is the required histogram.

Question 5.
Construct a histogram for the following data:
RD Sharma Class 8 Solutions Chapter 24 Data Handling II Ex 24.1 9
Solution:
We represent monthly school fee (in Rs) along x-axis and number of schools along y-axis. Taking suitable intervals, we construct rectangles as shown in the figure. This is the required histogram.
RD Sharma Class 8 Solutions Chapter 24 Data Handling II Ex 24.1 10

Question 6.
Draw a histogram for the daily earnings of 30 drug stores in the following table :
RD Sharma Class 8 Solutions Chapter 24 Data Handling II Ex 24.1 11
Solution:
We represent daily earnings (in Rs) along x-axis and number of stores along y-axis. Taking suitable intervals, we construct rectangles as shown in the figure. This is the required histogram.
RD Sharma Class 8 Solutions Chapter 24 Data Handling II Ex 24.1 12

Question 7.
Draw a histogram to represent the following data:
RD Sharma Class 8 Solutions Chapter 24 Data Handling II Ex 24.1 13
RD Sharma Class 8 Solutions Chapter 24 Data Handling II Ex 24.1 14
Solution:
We represent monthly salary (in Rs) along x-axis and number of teachers along y-axis. Taking suitable intervals we construct rectangles as shown in the figure. This is the required histogram
RD Sharma Class 8 Solutions Chapter 24 Data Handling II Ex 24.1 15

Question 8.
The following histogram shows the number of literate females in the age group of 10 to 40 years in a town :
(i) Write the age group in which the number of literate female is highest.
(ii) What is the class width ?
RD Sharma Class 8 Solutions Chapter 24 Data Handling II Ex 24.1 16
(iii) What is the lowest frequency ?
(iv) What are the class marks of the classes ?
(v) In which age group literate females are least ?
Solution:
(i) The age group in which the number of literate females is 15-20.
(ii) The class width is 5.
(iii) Lowest frequency is 320.
(iv) The class marks of the classes are
\(\frac { 10+15 }{ 2 }\) = \(\frac { 25 }{ 2 }\) =12.5, similarly other class marks will be 17.5,22.5,27.5,32.5,37.5
(v) The least literate females is in the class 10-15

Question 9.
The following histogram shows the monthly wages (in Rs) of workers in a factory:
RD Sharma Class 8 Solutions Chapter 24 Data Handling II Ex 24.1 17
(i) In which wage-group largest number of workers are being kept ? What is their number ?
(ii) What wages are the least number of workers getting ? What is the number of such workers ?
(iii) What is the total number of workers ?
(iv) What is the factory size ?
Solution:
(i) The largest number of workers are in wage group 950-1000 and is 8.
(ii) The least number of workers are in the wage group 900-950 and is 2.
(iii) Total number of workers is 40 (3 + 7 + 5 + 4 + 2 + 8 + 6 + 5)
(iv) The factory size is 50.

Question 10.
Below is the histogram depicting marks obtained by 43 students of a class :
(i) Write the number of students getting highest marks.
(ii) What is the class size ?
RD Sharma Class 8 Solutions Chapter 24 Data Handling II Ex 24.1 18
Solution:
(i) The number of students getting highest marks is 3.
(ii) The class size is 10.

Question 11.
The following histogram shows the frequency distribution of the ages of 22 teachers in a school:
RD Sharma Class 8 Solutions Chapter 24 Data Handling II Ex 24.1 19
(i) What is the number of eldest and youngest teachers in the school ?
(ii) Which age group teachers are more in the school and which least ?
(iii) What is the size of the classes ?
(iv) What are the class marks of the classes?
Solution:
(i) The number of eldest teacher is 1 and the number of youngest teacher is 2.
(ii) The teachers in age group 35-40 is most.
(iii) Size of classes is 5.
(iv) Class marks of class 20-25 is \(\frac { 20+25 }{ 2 }\)= \(\frac { 45 }{ 2 }\) = 22.5
and similarly others will be 27.5, 32.5, 37.5, 42.5, 47.5, 52.5.

Question 12.
The weekly wages of 30 workers in a factory are given:
830,835,890,810,835,836,869,845,898, 890, 820, 860, 832, 833, 855, 845, 804, 808, 812, 840, 885, 835, 835, 836, 878, 840, 868, 890, 806, 840
Mark a frequency table with intervals as 800-810,810-820 and so on, using tally marks.
Also, draw a histogram and answer the following questions:
(i) Which group has the maximum number of workers ?
(ii) How many workers earn Rs 850 and more ?
(iii) How many workers earn less than Rs 850?
Solution:
The frequency table will be as given below:
RD Sharma Class 8 Solutions Chapter 24 Data Handling II Ex 24.1 20
We represent wages (in Rs) along x-axis and number of workers along y-axis. Taking suitable intervals, we construct rectangles as shown in the figure. This is the required histogram.
(i) Maximum workers are in the wage group 830-840.
(ii) Number of workers getting Rs 850 and more are 1 + 3 + 1 + 1 + 4 = 10.
(iii) Number of workers getting less than Rs 850 are 3 + 2 + 1 + 9 + 5 = 20
RD Sharma Class 8 Solutions Chapter 24 Data Handling II Ex 24.1 21

Hope given RD Sharma Class 8 Solutions Chapter 24 Data Handling II Ex 24.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E

RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 2 Factors and Multiples Ex 2E.

Other Exercises

Find the L.C.M. of the numbers given below:

Question 1.
Solution:
We have
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 1.1
42 = 2 x 3 x 7
63 = 3 x 3 x 7
= 32 x 7
∴ L.C.M. of 42 and 63 = 2 x 32 x 7
= 2 x 9 x 7
= 18 x 7
= 126

Question 2.
Solution:
We have
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 2.1
So, 60 = 2 x 2 x 3 x 5
= 22 x 3 x 5
75 = 3 x 5 x 5 = 3 x 52
∴L.C.M. of 60 and 75 = 22 x 3 x 52
= 4 x 3 x 25
= 4 x 75 = 300

Question 3.
Solution:
We have
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 3.1
So, 12 = 2 x 2 x 3 = 22 x 3
18 = 2 x 3 x 3 = 2 x 32
20 = 2 x 2 x 5 = 22 x 5
∴L.C.M. of 12, 18 and 20 = 22 x 32 x 5
=4 x 9 x 5
= 20 x 9
= 180

Question 4.
Solution:
We have
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 4.1
36 = 2 x 2 x 3 x 3 = 22 x 32
60 = 2 x 2 x 3 x 5 = 22 x 3 x 5
72 = 2 x 2 x 2 x 3 x 3 = 23 x 32
∴ L.C.M. of 36, 60 and 72 = 23 x 32 x 5
=8 x 9 x 5
= 40 x 9
= 360

Question 5.
Solution:
We have
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 5.1
36 = 2 x 2 x 3 x 3 = 22 x 32
40 = 2 x 2 x 2 x 5 = 23 x 5
126 = 2 x 3 x 3 x 7 = 2 x 32 x 7
∴ L.C.M. of 36, 40 and 126 .
= 23 x 32 x 5 x 7
= 8 x 9 x 5 x 7
= 72 x 35
= 2520

Question 6.
Solution:
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 6.1
∴ L.C.M. of given numbers
= 2 x 2 x 2 x 7 x 2 x 5 x 11
= 8 x 14 x 55
= 112 x 55 = 6160

Question 7.
Solution:
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 7.1
∴L.C.M. of given numbers = 2 x 2 x 3 x 3 x 5 x 7
= 36 x 35
= 1260

Question 8.
Solution:
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 8.1
∴L.C.M. of given numbers
= 2 x 2 x 2 x 2 x 3 x 3 x 5 x 8
= 16 x 9 x 40
= 144 x 40
= 5760

Question 9.
Solution:
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 9.1
∴L.C.M. of given numbers = 2 x 2 x 2 x 2 x 2 x 3 x 3 x 2 x 3
= 32 x 54
= 1728

Find the H.C.F. and L.C.M. of :

Question 10.
Solution:
First we find the H.C.F. of the given numbers as under :
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 10.1
∴ H.C.F. of 117 and 221 = 13
Now L.C.M. = \(\frac { product\quad of\quad numbers }{ their\quad H.C.F } \)
= \(\frac { 117\times 221 }{ 13 } \)
= 9 x 221 = 1989
∴ H.C.F. = 13 and L.C.M. = 1989

Question 11.
Solution:
First we find the H.C.F. of 234 and 572 as under :
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 11.1
H.C.F. of 234 and 572 = 26
Now L.C.M. = \(\frac { product\quad of\quad numbers }{ their\quad H.C.F } \)
= \(\frac { 234\times 572 }{ 26 } \)
= 9 x 572
= 5148

Question 12.
Solution:
First we find the H.C.F. of 693 and 1078 as under :
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 12.1
H.C.F. of 693 and 1078 = 77 Product of numbers
Now L.C.M. = \(\frac { product\quad of\quad numbers }{ their\quad H.C.F } \)
= \(\frac { 693\times 1078 }{ 77 } \)
= 9 x 1078
= 9702
H.C.F. = 77 and L.C.M. = 9702

Question 13.
Solution:
First we find the H.C.F. of 145 and 232 as under :
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 13.1
H.C.F. of 145 and 232 = 29
Now L.C.M. = \(\frac { product\quad of\quad numbers }{ their\quad H.C.F } \)
= \(\frac { 145\times 232 }{ 29 } \)
= 5 x 232 = 1160
H.C.F. = 29 and L.C.M. = 1160

Question 14.
Solution:
First we find the H.C.F. of 861 and 1353 as under :
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 14.1
H.C.F. of 861 and 1353 = 123
Now L.C.M. = \(\frac { product\quad of\quad numbers }{ their\quad H.C.F } \)
= \(\frac { 861\times 1353 }{ 123 } \)
= 7 x 1353 = 9471
H.C.F. = 123 and L.C.M. = 9471

Question 15.
Solution:
First we find the H.C.F. of 2923 and 3239 as under :
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 15.1
H.C.F. of 2923 and 3239 = 79
Now L.C.M. = \(\frac { product\quad of\quad numbers }{ their\quad H.C.F } \)
= \(\frac { 2923\times 3239 }{ 79 } \)
= 37 x 3239= 119843
H.C.F. = 79 and L.C.M. = 119843

Question 16.
Solution:
We have
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 16.1
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 16.2
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 16.3

Question 17.
Solution:
We know that
L.C.M = \(\frac { product\quad of\quad the\quad number }{ their\quad H.C.F } \)
= \(\\ \frac { 2160 }{ 12 } \)
= 180

Question 18.
Solution:
We know that
L.C.M = \(\frac { product\quad of\quad the\quad number }{ their\quad H.C.F } \)
= \(\\ \frac { 2560 }{ 320 } \)
= 8

Question 19.
Solution:
We know that
One number x The other number
= H.C.F. x L.C.M.
.’. The other number
= \(\\ \frac { H.C.F\times L.C.M }{ One\quad number } \)
= \(\\ \frac { 145\times 2175 }{ 725 } \)
= \(\\ \frac { 2175 }{ 5 } \)
= 435
Required number = 435

Question 20.
Solution:
We know that
One number x The other number
= H.C.F. x L.C.M.
The other number
= \(\\ \frac { H.C.F\times L.C.M }{ One\quad number } \)
= \(\\ \frac { 131\times 8253 }{ 917 } \)
= \(\\ \frac { 8253 }{ 7 } \)
Required number = 1179

Question 21.
Solution:
Required least number = L.C.M. of 15, 20, 24, 32 and 36
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 21.1
L.C.M. = 3 x 2 x 2 x 2 x 5 x 4 x 3
= 24 x 60
= 1440
Hence, required least number = 1440

Question 22.
Solution:
Clearly, required least number = (L.C.M. of the given numbers + 9)
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 22.1
L.C.M. of the given numbers
= 4 x 5 x 5 x 2 x 3
= 600
Required least number
= 600 + 9
= 609

Question 23.
Solution:
First we find the L.C.M. of the given numbers as under :
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 23.1
L.C.M of the given numbers = 2 x 2 x 2 x 3 x 2 x 3 x 5
= 24 x 30 = 720
Now least number of five digits = 10000 Dividing 10000 by 720, we get
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 23.2
Clearly if we add 80 to 640, it will become 720 which is exactly divisible by 720.
Required least number of five digits = 10000 + 80 = 10080

Question 24.
Solution:
The greatest number of five digits exactly divisible by the given numbers = The greatest number of five digits exactly divisible by the L.C.M. of given numbers.
Now
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 24.1
L.C.M. of given numbers
= 2 x 2 x 3 x 3 x 5 x 2 = 360
Now greatest number of five digits = 99999
Dividing 99999 by 360, we get
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 24.2
Required greatest number of five digits
= 99999 – 279
= 99720

Question 25.
Solution:
Three bells will again toll together after an interval of time which is exactly divisible by 9, 12, 15 minutes.
Required time = L.C.M. of 9, 12, 15 minutes
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 25.1
L.C.M. of 9, 12, 15 minutes = 3 x 3 x 4 x 5 minutes
= 9 x 20 minutes
= 180 minutes
Required time = 180 minutes
= \(\\ \frac { 180 }{ 60 } \)
= 3 hours

Question 26.
Solution:
Required distance = L.C.M. of 36 cm, 48 cm and 54 cm
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 26.1
L.C.M. of 36 cm, 48 cm. 54 cm
= 2 x 2 x 3 x 3 x 4 x 3 cm
= 36 x 12 cm
= 432 cm
= 4 m 32 cm
Required distance = 4 m 32 cm

Question 27.
Solution:
Required time = L.C.M. of 48 seconds, 72 seconds and 108 seconds
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 27.1
L.C.M. of 48 sec., 72 sec. and 108 sec.
= 2 x 2 x 2 x 3 x 3 x 2 x 3 sec.
= 24 x 18 sec.
= 432 sec.
Required time = 432 sec.
= \(\\ \frac { 432 }{ 60 } \)
= 7 m in 12 sec

Question 28.
Solution:
Lengths of three rods = 45 cm, 50 cm and 75 cm
Required least length of the rope = L.C.M. of 45 cm, 50 cm, 75 cm
We have
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 28.1

Question 29.
Solution:
The time after which both the devices will beep together = L.C.M. of 15 minutes and 20 minutes
Now,
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 29.1
L.C.M. of 15 minutes and 20 minutes
= 5 x 3 x 4
= 60 minutes
= 1 hour
Both the devices will beep together after 1 hour from 6 a.m.
Required time = 6 + 1
= 7 a.m.

Question 30.
Solution:
The circumferences of four wheels = 50 cm, 60 cm, 75 cm and 100 cm
Required least distance = L.C.M. of 50 cm, 60 cm, 75 cm and 100 cm Now,
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 30.1
L.C.M. of 50 cm, 60 cm, 75 cm, 100 cm
= 2 x 2 x 3 x 5 x 5 cm
= 300 cm = 3 m
Required least distance = 3 m.

Hope given RS Aggarwal Solutions Class 6 Chapter 2 Factors and Multiples Ex 2E are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.1

RD Sharma Class 8 Solutions Chapter 21 Mensuration II (Volumes and Surface Areas of a Cubiod and a Cube) Ex 21.1

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.1

Other Exercises

Question 1.
Find the volume of a cuboid whose
(i) length = 12 cm, breadth = 8 cm, height = 6 cm
(ii) length = 1.2 m, breadth = 30 cm, height = 15 cm
(iii) length = 15 cm, breadth = 2.5 dm, height = 8 cm
RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.1 1
Solution:
In a cuboid,
(i) Length (l) = 12 cm
Breadth (b) = 8 cm
Height (h) = 6 cm
∴ Volume = Ibh = 12 x 8 x 6 cm3 = 576 cm3
(ii) Length (l) = 1.2 m = 120 cm
breadth (6) = 30 cm
Height (h) = 15 cm
∴ Volume = Ibh = 120 x 30 x 15 cm3 = 54000 cm3
(iii) Length (l) = 15 cm
Breadth (b) = 2.5 dm = 25 cm
Height (h) = 8 cm
∴ Volume = Ibh
= 15 x 25 x 8 cm3 = 3000 cm2

Question 2.
Find the volume of the cube whose side is
(i) 4 cm
(ii) 8 cm
(iii) 1.5 dm
(iv) 1.2 m
(v) 25 mm.
Solution:
(i) Side of a cube (a) = 4 cm
∴ Volume = a3 = (4)3 cm3 = 4 x 4 x 4 = 64 cm3
RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.1 2
(ii) Side of cube (a) = 8 cm
∴ Volume = a3 = (8)3 4 cm
= 8 x 8 x 8 cm3 = 512 cm3
(iii) Side of cube (a) = 1.5 dm = 15 cm
∴ Volume = a3 = (1.5)3 dm2 = (15)3 cm3
= 15 x 15 x 15 = 3375 cm3
(iv) Side of cube (a) = 1.2 m = 120 cm
∴ Volume = a3 = (120)3 cm3
= 120 x 120 x 120 = 1728000 cm3
(v) Side of cube (a) = 25 mm = 2.5 cm.
∴ Volume = a3 = (2.5)3 cm3
= 2.5 x 2.5 x 2.5 cm3 = 15.625 cm3

Question 3.
Find the height of a cuboid of volume 100 cm3 whose length and breadth are 5 cm and 4 cm respectively.
Solution:
Volume of a cuboid =100 cm3
Length (1) = 5 cm
and breadth (b) = 4 cm
RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.1 3

Question 4.
A cuboidal vessel is 10 cm long and 5 cm wide, how high it must be made to hold 300 cm3 of a liquid ?
Solution:
Volume of the liquid in the vessel = 300 cm3
Length (l)= 10 cm
Breadth (b) = 5 cm
RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.1 4

Question 5.
A milk container is 8 cm long and 50 cm wide. What should be its height so that it can hold 4 litres of milk ?
Solution:
Capacity of milk = 4 litres
∴ Volume of the container = 4 x 1000 cm3 = 4000 cm3
Length (l) = 8 cm
Width (b) = 50 cm
RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.1 5

Question 6.
A cuboidal wooden block contains 36 cm3 wood. If it be 4 cm long and 3 cm wide, find its height.
Solution:
Volume of wooden cuboid block = 36 cm3
Length (l) = 4 cm
Breadth (b) = 3 cm
RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.1 6

Question 7.
What will happen to the volume of a cube, if its edge is (i) halved (ii) trebled ?
Solution:
Let side of original cube = a cm
∴ Volume = a3 cm3
(i) In first case,
RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.1 7
(ii) In second case, when side (edge) is trebled, then side = 3a
∴ Volume = (3a)3 = 27a3
∴ It will be 27 times

Question 8.
What will happen to the volume of a cuboid if its (i) Length is doubled, height is same and breadth is halved ? (ii) Length is doubled, height is doubled and breadth is same ?
Solution:
Let l, b and h be the length, breadth and height of the given cuboid respectively.
∴ Volume = lbh.
(i) Length is doubled = 21
RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.1 8
∴ The volume will be the same.
(ii) Length is doubled = 21
breadth is same = b height is doubled = 2h
∴ Volume = 2l x b x 2h = 4 lbh
∴ Volume will be 4 times

Question 9.
Three cuboids of dimensions 5 cm x 6 cm x 7 cm, 4 cm x 7 cm * 8 cm and 2 cm x 3 cm x 13 cm are melted and a cube is made. Find the side of cube.
Solution:
Dimensions of first cuboid = 5 cm x 6 cm x 7 cm
∴ Volume = 5 x 6 x 7 = 210 cm3
Dimensions of second cuboid = 4 cm x 7 cm x 8 cm
∴ Volume = 4x 7 x 8 = 224 cm3
Dimensions of third cuboid = 2 cm x 3 cm x 13 cm
∴ Volume = 2 x 3 x 13 = 78 cm3
Total volume of three cubes = 210 + 224 + 78 cm3 = 512 cm3
∴ Volume of cube = 512 cm3
RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.1 9

Question 10.
Find the weight of solid rectangular iron piece of size 50 cm x 40 cm x 10 cm, if 1 cm3 of iron weighs 8 gm.
Solution:
Dimension of cuboidal iron piece = 50 cm x 40 cm x 10 cm
∴ Volume = 50 x 40 x 10 = 20000 cm3
Weight of 1 cm3 = 8 gm
∴ Total weight of piece = 20000 x 8 gm
RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.1 10

Question 11.
How many wooden cubical blocks of side 25 cm can be cut from a log of wood of size 3 m by 75 cm by 50 cm, assuming that there is no wastage ?
Solution:
Length of log (l) = 3 m = 300 cm.
Breadth (b) = 75 cm
and height (h) = 50 cm
∴ Volume of log = lbh = 300 x 75 x 50 cm3 = 1125000 cm3
Side of cubical block = 25 cm
∴ Volume of one block = a2 = 25 x 25 x 25 cm3 = 15625 cm3
∴ Number of blocks to be cut out
RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.1 11

Question 12.
A cuboidal block of silver is 9 cm long, 4 cm broad and 3.5 cm in height. From it, beads of volume 1.5 cm2 each are to be made. Find the number of beads that can be made from the block ?
Solution:
Length of block (l) = 9 cm
Breadth (b) = 4 cm
and height (h) = 3.5 cm
∴ Volume = l x b x h = 9 x 4 x 3.5 cm3 = 126 cm3
Volume of one bead = 1.5 cm3
∴ Number of beads = \(\frac { 126 }{ 105 }\) = 84

Question 13.
Find the number of cuboidal boxes measuring 2 cm by 3 cm by 10 cm which can be stored in a carton whose dimensions are 40 cm, 36 cm and 24 cm.
Solution:
Length of cuboidal box (l) = 2 cm
breadth (b) = 3 cm
and height (h) = 10 cm
∴ Volume = lx b x h = 2 x 3 x 10 = 60 cm3
Volume of carton = 40 x 36 x 24 cm3
= 34560 cm3
∴ Number of boxes to be height in the carton
RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.1 12

Question 14.
A cuboidal block of solid iron has dimensions 50 cm, 45 cm and 34 cm. How many cuboids of size 5 cm by 3 cm by 2 cm can be obtained from the block ? Assume cutting causes no wastage.
Solution:
Dimensions of block = 50 cm, 45 cm, 34 cm
∴ Volume = 50 x 45 x 34 = 76500 cm3
Size of cuboid = 5 cm x 3 cm x 2 cm
∴ Volume of cuboid =  5 x 3 x 2 = 30 cm3
RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.1 13

Question 15.
A cube A has side thrice as long as that of cube B ? What is the ratio of the volume of cube A to that of cube B ?
Solution:
Let side of cube B = a
Then Volume = a3
and side of cube A = 3a
Volume = (3a)3 = 3a x 3a x 2a = 27a3
∴ Ratio of volume’s A and B = 27a3 : a3
= 27 : 1

Question 16.
An ice-cream brick measures 20 cm by 10 cm by 7 cm. How many such bricks can be stored in a deep fridge whose inner dimensions are 100 cm by 50 cm by 42 cm ?
Solution:
Dimensions of ice cream brick = 20 cm x 10 cm x 7 cm
∴ Volume = 20 x 10 x 7 cm3 = 1400 cm3
Dimensions of inner of fridge = 100 cm x 50 cm x 42 cm = 210000 cm3
∴ Number of bricks to be kept in the fridge
RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.1 14

Question 17.
Suppose that there are two cubes, having edges 2 cm and 4 cm, respectively. Find the volume V1 and V2 of the cubes and compare them.
Solution:
Side of first cube (a) = 2 cm
∴ Volume (V1) = a3 = (2) = 8 cm3
Similarly side of second cube = 4 cm
and volume (V2) = (4)3 = 64 cm3
Now V2 = 64 cm3 = 8 x 8 cm3
= 8 x V1
⇒ V2 = 8V1

Question 18.
A tea-packet measures 10 cm x 6 cm x 4 cm.How many such tea-packets can be placed in a cardboard box of dimensions 50 cm x 30 cm x 0.2 m ?
Solution:
Dimensions of tea-packet = 10cm x 6cm x 4 cm
∴ Volume =10 x 6 x 4 = 240 cm3
Dimensions of box = 50 cm x 30 cm x 0.2 m
= 50 cm x30 cm x20 cm
∴ Volume = 50 x 30 x 20 = 30000 cm3
∴ Number of tea-packets to be kept = \(\frac { 30000 }{ 240 }\)

Question 19.
The weight of a metal block of size 5 cm by 4 cm by 3 cm is 1 kg. Find the weight of a block of the same metal of size 15 cm by 8 cm by 3 cm.
Solution:
Dimensions of a metal block = 5 cm x 4 cm x 3 cm = 5 x 4 x 3 = 60 cm3
Dimensions of a second block = 15 cm x 8 cm x 3 cm = 15 x 8 x 3 = 360 cm3
But weight of first block = 1 kg
∴ Weight of second block
= \(\frac { 1 }{ 16 }\) x 360 = 6 kg

Question 20.
How many soap cakes can be placed in a box of size 56 cm x 0.4 m x 0.25 m, it the size of soap cake is 7 cm x 5 cm x 2.5 cm ?
Solution:
Size of box = 56 cm x 0.4 m x 0.25 m = 56 cm x 40 cm x 25 cm
∴ Volume = 56 x 40 x 25 cm3 = 56000 cm3
Size of a soap cake = 7 cm x 5 cm x 2.5 cm
∴ Volume = 7 x 5 x 2.5 cm3 = 87.5 cm3
∴ Number of cakes to be kept in the box
= \(\frac { 56000 }{ 87.5 }\) = 640

Question 21.
The volume of a cuboid box is 48 cm3. If its height and length are 3 cm and 4 cm respectively, find its breadth.
Solution:
Volume of cuboid box = 48 cm3
Length (l) = 4 cm
Height = (h) = 3 cm
RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.1 15

Hope given RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4B

RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4B

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4B.

Other Exercises

Question 1.
Solution:
(i) On the number line we start from 0 and move 9 steps to the right to reach a point A. Now, starting from A, we move 6 steps to the left to reach a point B, as shown below :
RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4B 1.1
Now, B represents the integer 3
9 + ( – 6) = 3
(ii) On the number line, we start from 0 and move 3 steps to the left to reach a point A. Now, starting from A, we move 7 steps to the right to reach a point B, as shown below :
RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4B 1.2
And B represents the integer 4
( – 3) + 7 = 4
(iii) On the number line, we start from 0 and move 8 steps to the right to reach a point A. Now, starting from A, we move 8 steps to the left to reach a point B, as shown below :
RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4B 1.3
And, B represents the integer 0.
8 + ( – 8) = 0
(iv) On the number line, we start from 0 and move 1 step the left to reach a point A. Now, starting from point A, we move 3 steps to the left to reach g. point B, as shown below :
RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4B 1.4
And, B represents the integer – 4
( – 1) + ( – 3) = – 4.
(v) On the number line, we start from 0 and move 4 steps to the left to reach a point A. Now, starting from point A, we move 7 steps to the left to reach a point B, as shown below :
RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4B 1.5
And, B represents the integer -11.
( – 4) + ( – 7) = – 11
(vi) On the number line we start from 0 and move 2 steps to the left to reach a point A. Now, starting from A, we move 8 steps to the left to reach a point B, as shown below :
RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4B 1.6
And, B represents the integer – 10
( – 2) + ( – 8) = – 10
(vii) On the number line we start from 0 and move 3 steps to the right to reach a point A. Now, starting from A, we move 2 steps to the left to reach a point B and again starting from left to reach a point B and again starting from B, we move 4 steps to the left to reach a point C, as shown below :
RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4B 1.7
And, C represents the integer – 3
3 + ( – 2) + ( – 4) = – 3
(viii) On the number line we start from 0 and move 1 step to the left to reach a point A. Now, starting from A, we move 2 steps to the left to reach a point B and again starting from B, we move 3 steps to the left to reach point C, as shown below :
RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4B 1.8
And, C represents the integer – 6
( – 1) + ( – 2) + ( – 3) = – 6.
(ix) On the number line we start from 0 and move 5 steps to the right to reach a point A. Now, starting from A, we move 2 steps to the left to reach a point B and again starting from point B, we move 6 steps to the left to reach a point C, as shown below :
RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4B 1.9
And, C represents the integer – 3.
5 + (- 2) + (- 6) = – 3

Question 2.
Solution:
(i) (- 3) + ( – 9) = – 12
(Using the rule for addition of integers having like signs)
(ii) ( – 7) + ( – 8) = – 15
(Using the rule for addition of integers having like signs)
(iii) ( – 9) + 16 = 7
(Using the rule for addition of integers having unlike signs)
(iv) ( – 13) + 25 = 12
(Using the rule for addition of integers having unlike signs)
(v) 8 + ( – 17) = – 9
(Using the rule for addition of integers having unlike signs)
(vi) 2 + ( – 12) = – 10
(Using the rule for addition of integers having unlike signs)

Question 3.
Solution:
(i) Using the rule for addition of integers with like signs, we get:
RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4B 3.1
(ii) Using the rule for addition of integers with like signs, we get :
RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4B 3.2
(iii) Using the rule for addition of integers with like signs, we get :
RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4B 3.3
(iv) Using the rule for addition of integers with like signs, we get:
RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4B 3.4

Question 4.
Solution:
(i) Using the rule for addition of integers with unlike signs, we get:
RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4B 4.1
(ii) Using the rule for addition of integers with unlike signs, we get:
RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4B 4.2
(iii) Using the rule for addition of integers with unlike signs, we have
RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4B 4.3
(iv) Using the rule for addition of integers with unlike signs, we have
RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4B 4.4

Question 5.
Solution:
(i) Using the rule for addition of integers with unlike signs, we get :
RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4B 5.1
(ii) Using-the rule for addition of integers with unlike signs, we get
RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4B 5.2
(iii) Using the rule for addition of integers with unlike signs, we get :
RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4B 5.3
(iv) Using the rule for addition of integers with unlike signs, we get :
RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4B 5.4
(v) Using the rule for addition of integers with like signs, we get:
RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4B 5.5
(vi) Using the rule for addition of integers with unlike signs, we get :
RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4B 5.6
(vii) Using the rule for addition of integers with unlike signs, we get :
RS Aggarwal Class 6 Solutions Chapter 4 Integers Ex 4B 5.7
(viii) We have, ( – 18) + 25 + ( – 37)
= [( – 18) + 25] + ( – 37)
= 7 + ( – 37)
= – 30
(ix) We have, – 312 + 39 + 192
= ( – 312) + (39 + 192)
= ( – 312) + 231
= – 81
(x) We have ( – 51) + ( – 203) + 36 + ( – 28)
= [( – 51) + ( – 203)] + [36 + ( – 28)]
= ( – 254) + 8
= – 246

Question 6.
Solution:
(i) The additive inverse of – 57 is 57
(ii) The additive inverse of 183 is – 183
(iii) The additive inverse of 0 is 0
(iv) The additive inverse of – 1001 is 1001
(v) The additive inverse of 2054 is – 2054

Question 7.
Solution:
(i) Successor of 201 = 201 + 1 = 202
(ii) Successor of 70 = 70 + 1 = 71
(iii) Successor of – 5 = – 5 + 1 = – 4
(iv) Successor of – 99 = – 99 + 1 = – 98
(v) Successor of – 500 = – 500 + 1 = – 499 Ans.

Question 8.
Solution:
(i) Predecessor of 120 = 120 – 1 = 119
(ii) Predecessor of 79 = 79 – 1 = 78
(iii) Predecessor of – 8 = – 8 – 1 = – 9
(iv) Predecessor of – 141 = – 141 – 1 = – 142
(v) Predecessor of – 300 = – 300 – 1 = – 301 Ans.

Question 9.
Solution:
(i) ( – 7) + ( – 9) + 12 + ( – 16)
= – 7 – 9 + 12 – 16
= – 7 – 9 – 16 + 12
= – 32 + 12
= – 20
(ii) 37 + ( – 23) + ( – 65) + 9 + ( – 12)
= 37 – 23 – 65 + 9 – 12
= 37 + 9 – 23 – 65 – 12
= 46 – 100
= – 54
(iii) ( – 145) + 79 + ( – 265) + ( – 41) + 2
= – 145 + 79 – 265 – 41 + 2
= 79 + 2 – 145 – 265 – 41
= 81 – 451
= – 370
(iv) 1056 + ( – 798) + ( – 38) + 44 + ( – 1)
= 1056 – 798 – 38 + 44 – 1
= 1056 + 44 – 798 – 38 – 1
= 1100 – 837
= 263 Ans.

Question 10.
Solution:
Distance travelled from Patna to its north = 60 km
Distance travelled from that place to south of it = 90 km
Distance of the final place to Patna = 60 – 90
= – 30 km
= 30 km south
Ans.

Question 11.
Solution:
Total amount of pencils purchased = Rs. 30 + Rs. 25
= Rs 55
Total amount of pens purchased = Rs. 90
Total cost price = Rs. 55 + Rs. 90
= Rs. 145
Total sale price of pencils and pens = Rs 20 + Rs. 70
= Rs. 90
Loss = cost price – selling price
= Rs. 145 – Rs. 90
= Rs. 55 Ans.

Question 12.
Solution:
(i) True.
(ii) False : As if positive integer is greater then it will be positive.
(iii) True : As ( – a + a = 0).
(iv) False : As the sum of three integers can be zero or non-zero.
(v) False : As | – 5 | = 5 and | – 3 | = 3 and 5 ≮ 3.
(vi) False : | 8 – 5 | = | 3 | = 3 and | 8 | + | – 5 | = 8 + 5 = 13.

Question 13.
Solution:
(i) a + 6 = 0
Subtracting 6 from both sides,
a + 6 – 6 = 0 – 6
=> a = – 6
a = – 6.
(ii) 5 + a = 0
Subtracting 5 from both sides,
5 + a – 5 = 0 – 5
=> a = – 5
a = – 5
(iii) a + ( – 4) = 0
Adding 4 to both sides,
a + ( – 4) + 4 = 0 + 4
=> a = 4
a = 4
(iv) – 8 + a = 0
Adding 8 to both sides,
– 8 + a + 8 = 0 + 8
=> a – 8
a = 8 Ans.

Hope given RS Aggarwal Solutions Class 6 Chapter 4 Integers Ex 4B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.