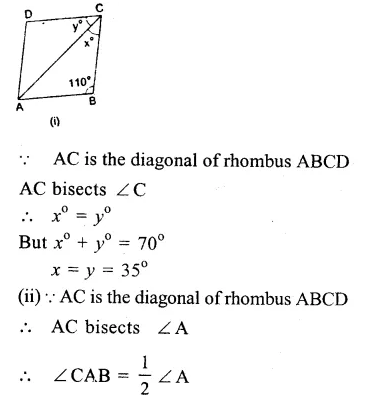
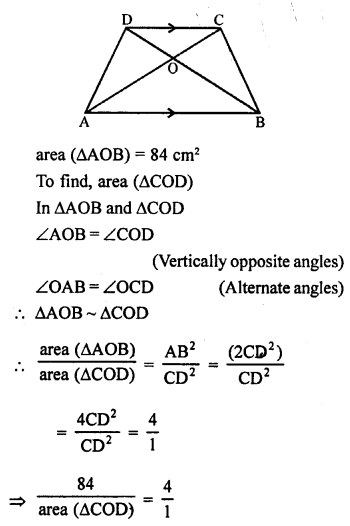
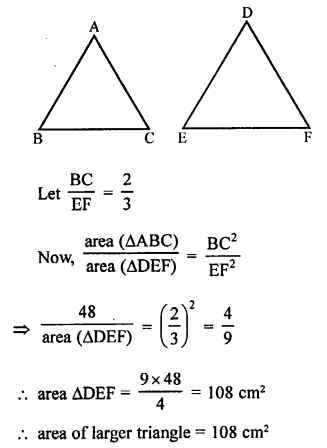
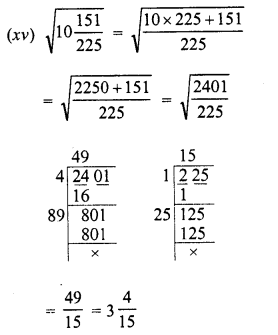
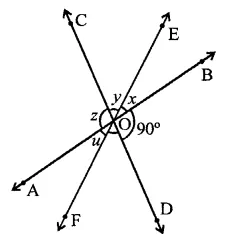
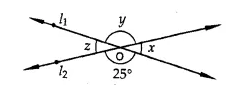
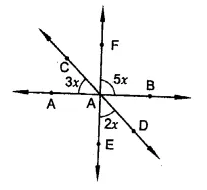
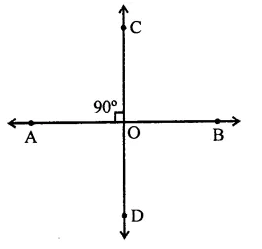
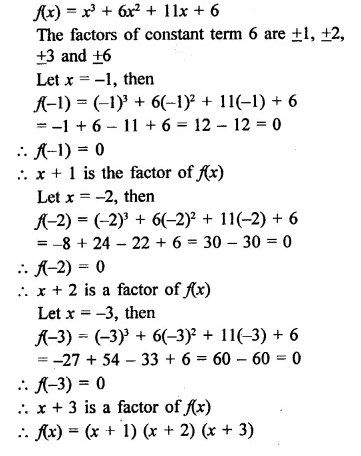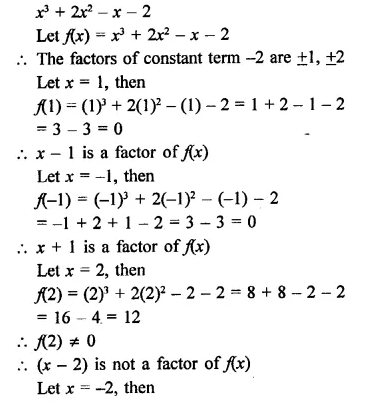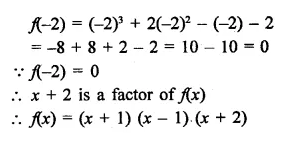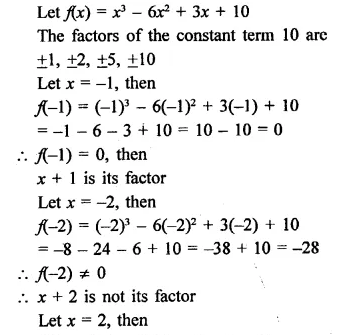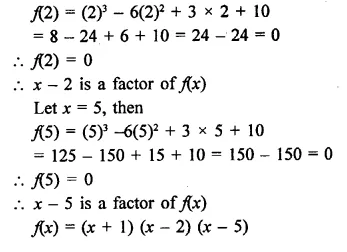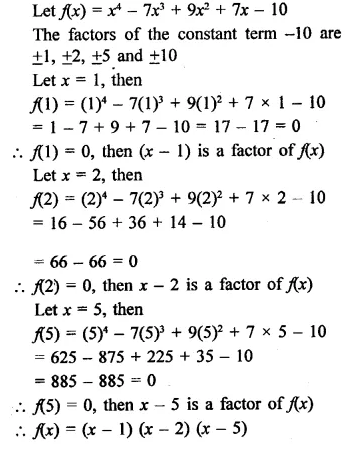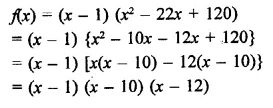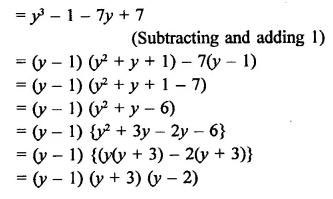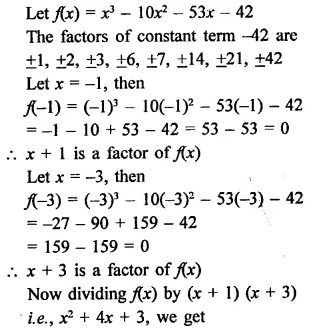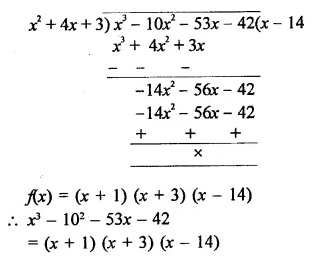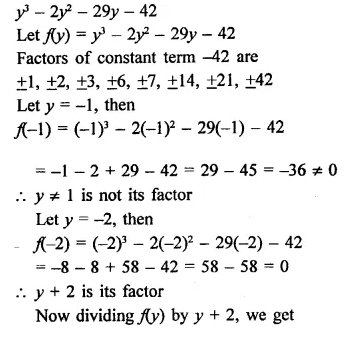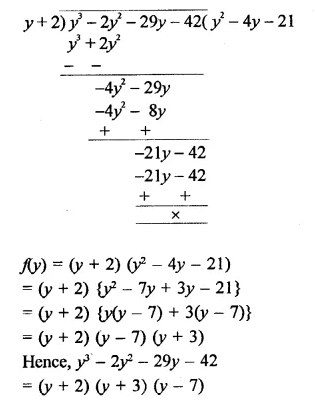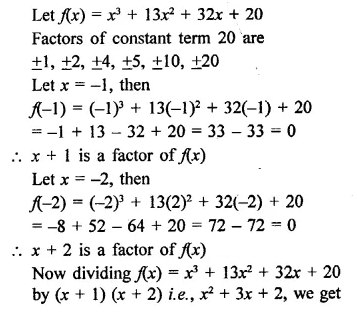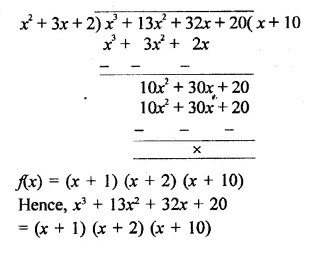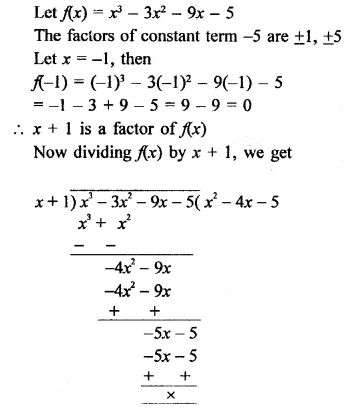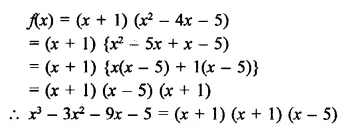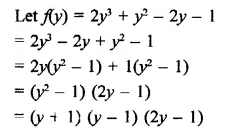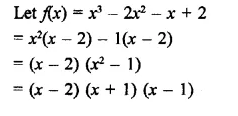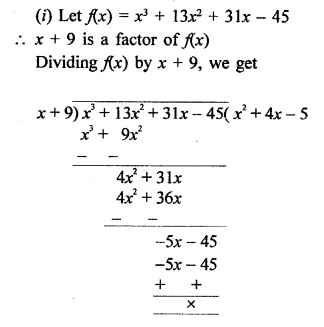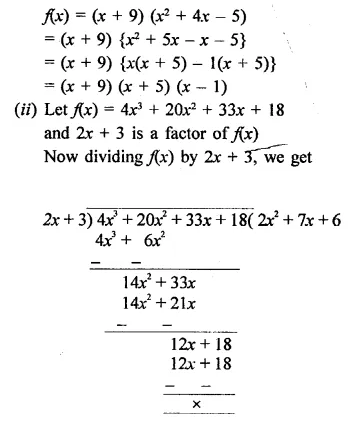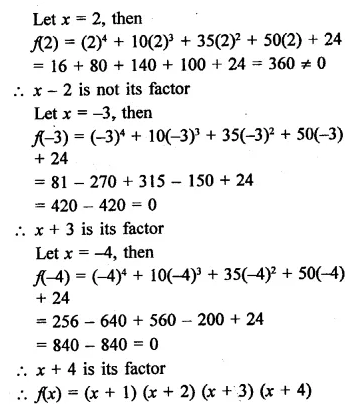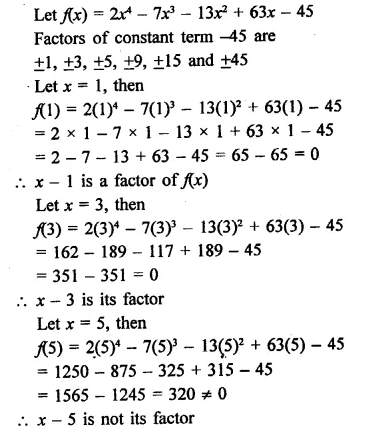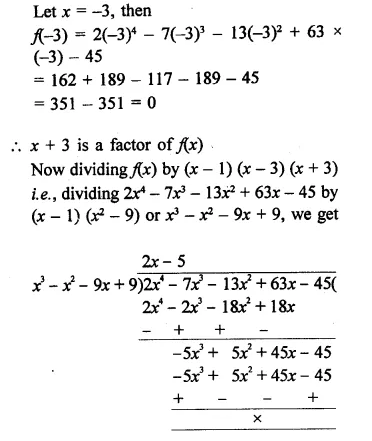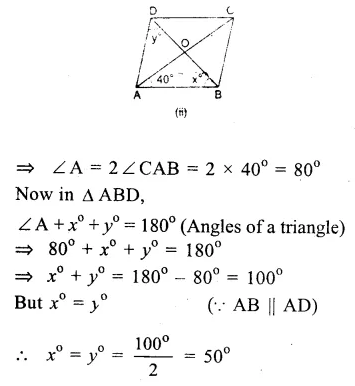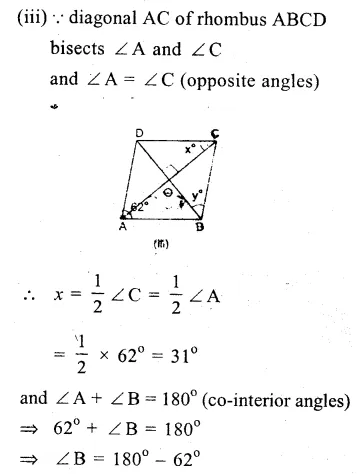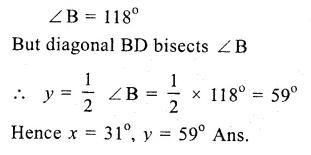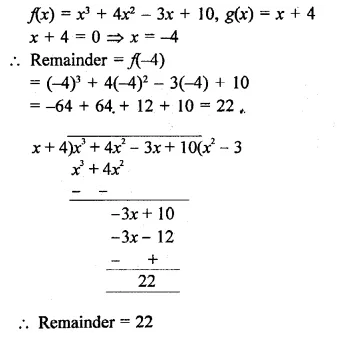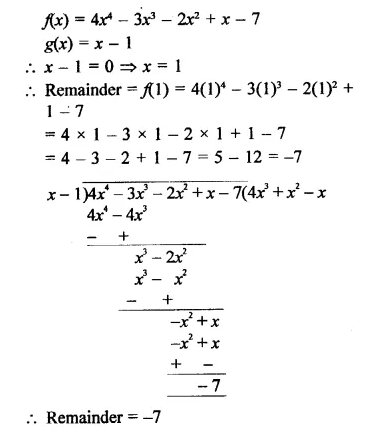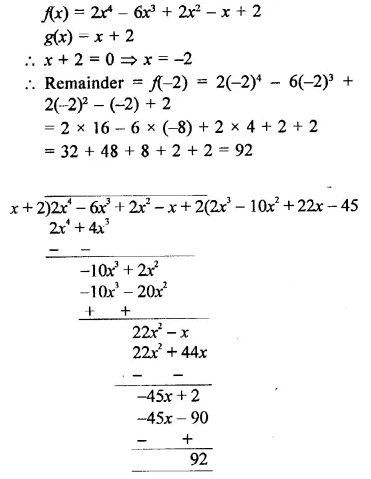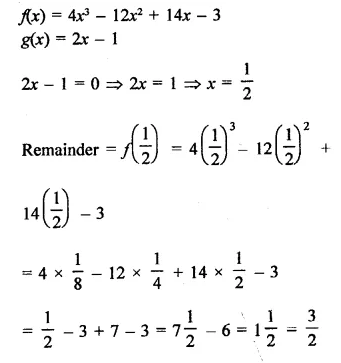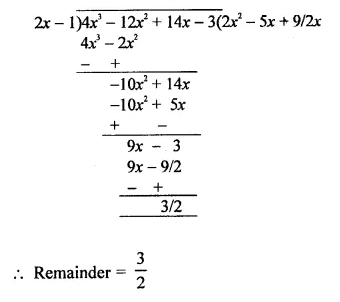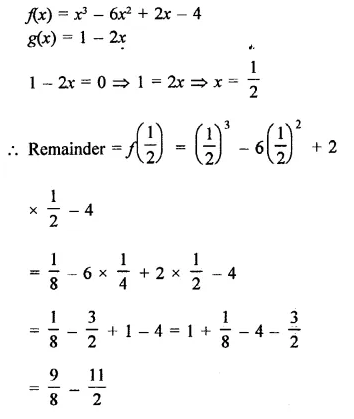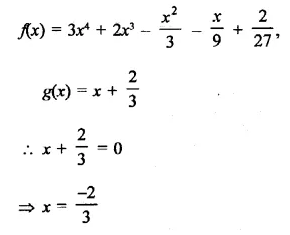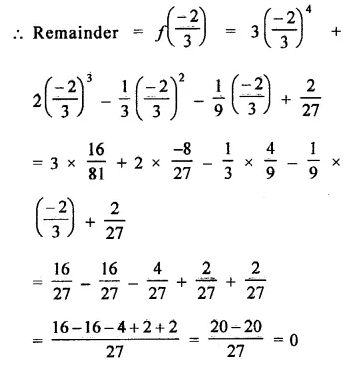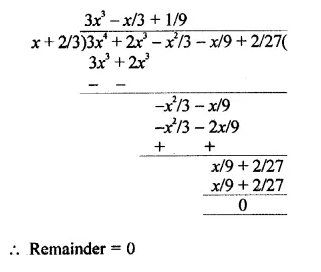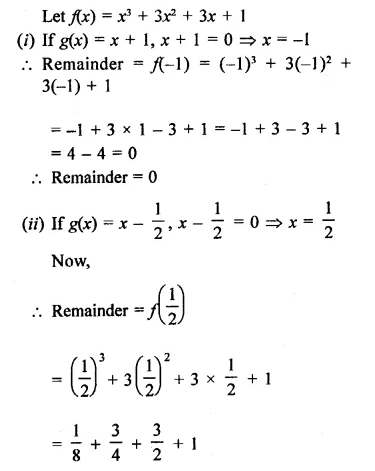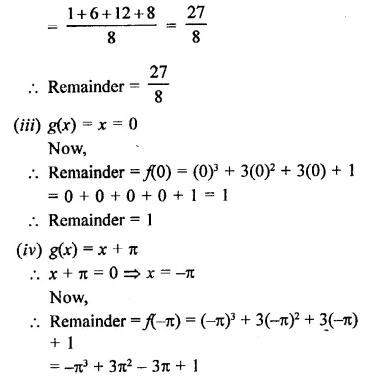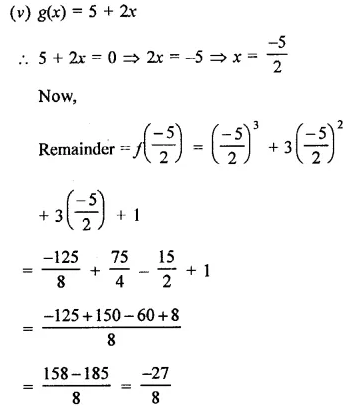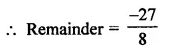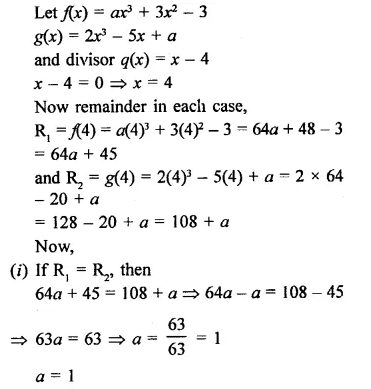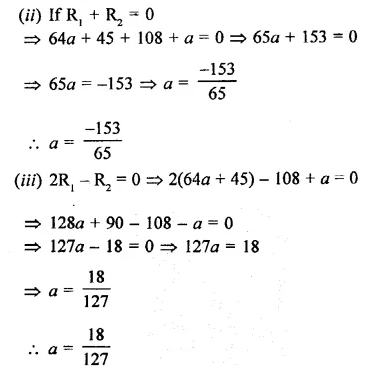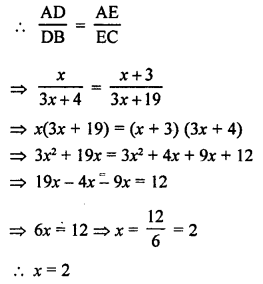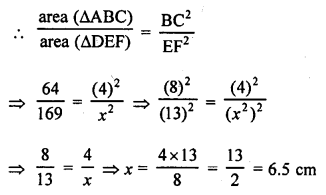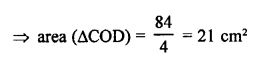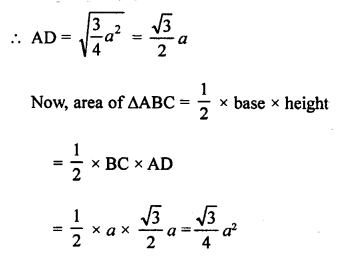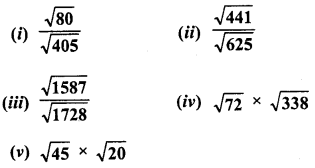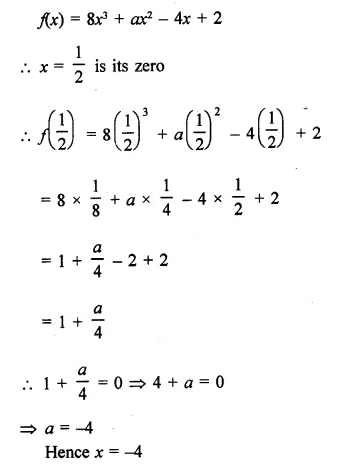RD Sharma Class 9 Solutions Chapter 8 Lines and Angles Ex 8.1
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 8 Lines and Angles Ex 8.1
Other Exercises
- RD Sharma Class 9 Solutions Chapter 8 Lines and Angles Ex 8.1
- RD Sharma Class 9 Solutions Chapter 8 Lines and Angles MCQS
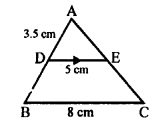
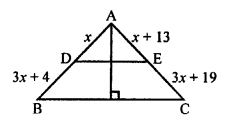
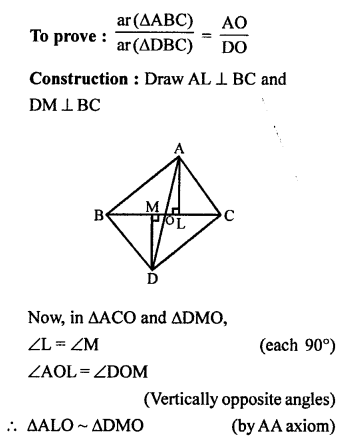
Question 1.
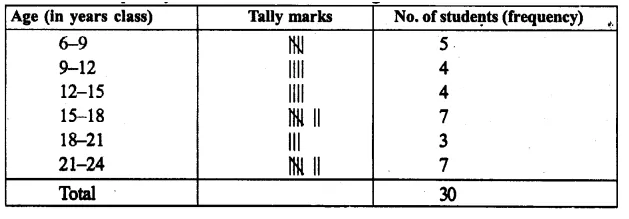
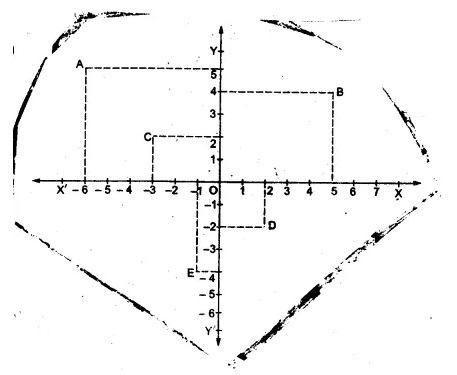
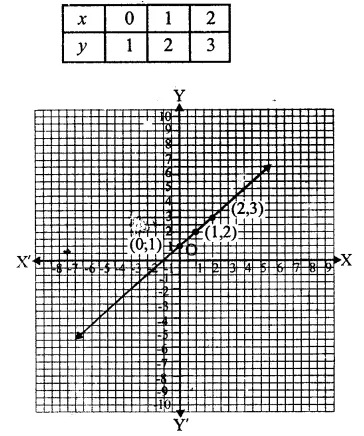
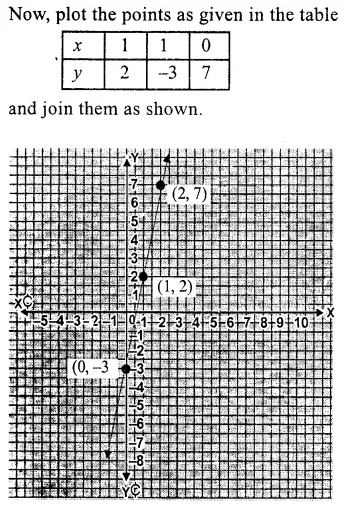
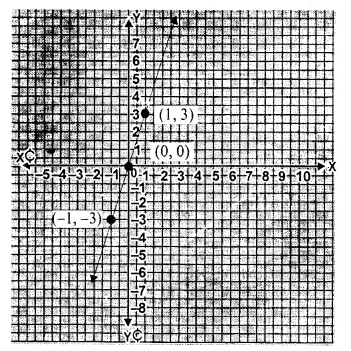
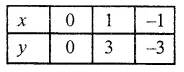
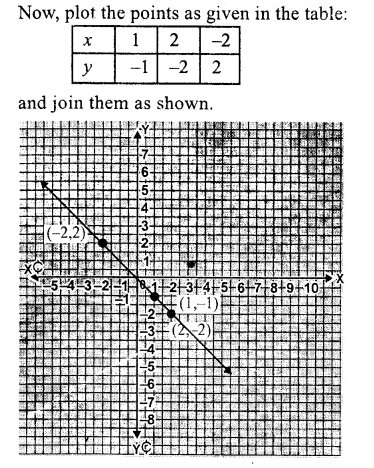
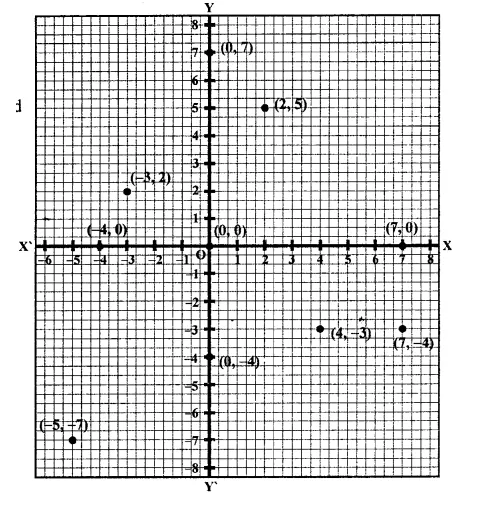
Plot the following points on the graph paper:
(i) (2, 5)
(ii) (4, -3)
(iii) (-5, -7)
(iv) (7, -4)
(v) (-3, 2)
(vi) (7, 0)
(vii) (-4, 0)
(viii) (0, 7)
(ix) (0, -4)
(x) (0, 0)
Solution:
The given points have been plotted on the graph as given below:
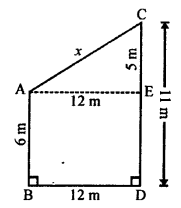
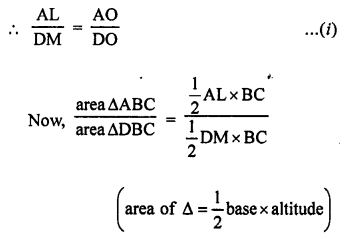
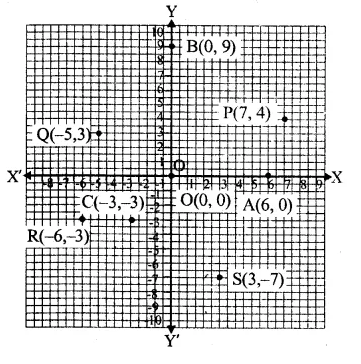
Question 2.
Write the coordinates of each of the following points marked in the graph paper.
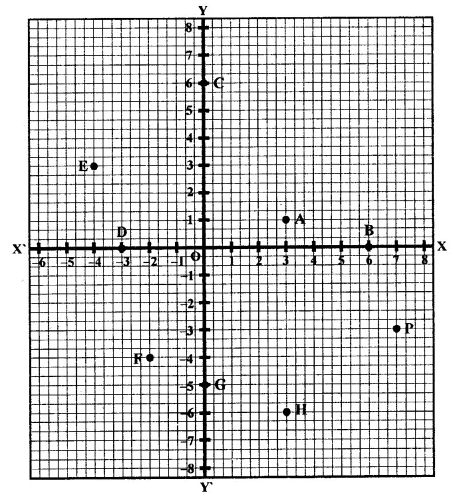
Solution:
The co-ordinates of the points given in the graph are A (3, 1), B (6, 0), C (0, 6), D (-3, 0), E (-4, 3), F (-2, -4), G (0, -5), H (3, -6), P (7, -3).
Hope given RD Sharma Class 9 Solutions Chapter 8 Lines and Angles Ex 8.1 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.