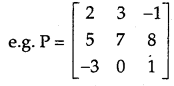Prasanna

We have given detailed NCERT Solutions for Class 9 Sanskrit Grammar Book सङ्ख्या Questions and Answers come in handy for quickly completing your homework.

Sanskrit Vyakaran Class 9 Solutions सङ्ख्या

अभ्यासः

प्रश्न 1.
अधोलिखित-वाक्येषु अङ्कानां स्थाने संख्यावाचकविशेषणैः रिक्तस्थानपूर्तिः करणीया
(i) एकस्मिन् तडागे (4) ………… मत्स्याः आसन्।
(ii) (1) ………. व्याधः तत्र आगतवान्।
(iii) अवदत् च श्वः अस्माकं (3) ………. भगिन्यः आगमिष्यन्ति सर्वान् मत्स्यान् गृहीत्वा नेष्यन्ति।
(iv) एकः वृद्धः मत्स्यः सर्वान् (4) ………. मत्स्यान् अकथयत् “नास्ति चिन्ता। श्वः कदापि न आगमिष्यति।
उत्तर:
(i) चत्वारः
(ii) एकः
(iii) तिस्रः
(iv) चतुरः।

प्रश्न 2.
अधोलिखितेषु वाक्येषु अङ्कानां स्थाने संख्यावाचकविशेषणैः रिक्तस्थानपूर्तिः क्रियताम्
एकदा
(i) ……… वृक्षे
(ii) ……… शुकाः निवसन्ति स्म।
(iii) ……….. कोकिले अपि समागते।
(iv) …………….खगेषु परस्परं घनिष्ठा मैत्री आसीत।
उत्तर:
(i) एकस्मिन्
(ii) त्रयः
(iii) द्वे
(iv) पञ्चसु।

प्रश्न 3.
अधोलिखितेषु वाक्येषु अङ्कानां स्थाने संख्यावाचकविशेषणैः रिक्तस्थानपूर्तिः क्रियताम्
एकेन छात्रेण वार्षिकपरीक्षायाम् संस्कृते (80)
(i) ………. अङ्का, गणिते (75)
(ii) ………. अङ्का विज्ञाने (60)
(iii) ……….. अङ्का योगे च (50)
(iv) …………. अङ्का लब्धाः । तेन संस्कृते सर्वाधिकाः अङ्का प्राप्ताः।
उत्तर:
(i) अशीतिः
(ii) पञ्चसप्ततिः
(iii) षष्टिः
(iv) पञ्चाशत्।

प्रश्न 4.
अधोलिखितेषु वाक्येषु अङ्कानां स्थाने संख्यावाचकविशेषणैः रिक्तस्थानपूर्तिः क्रियताम्
वयम् (28)
(i) ………….. छात्राः रेलयानेन पुरीनगरस्य यात्रायै गतवन्तः। अस्माभिः सह (3)
(ii) ……… अध्यापकाः (4)
(iii) …………. अध्यापिका च आसन्। पुरीनगरे मम (5)
(iv) ………. मित्रम् अपि वसति।
उत्तर:
(i) अष्टाविंशतिः
(ii) त्रयः
(iii) चतस्रः
(iv) एकम्।

प्रश्न 5.
अधोलिखितेषु वाक्येषु अङ्कानां स्थाने संख्यावाचकविशेषणैः रिक्तस्थानपूर्तिः क्रियताम्
सूर्यः
(1) ……….. अस्ति। सूर्यस्य
(2) …………. गती। जगतः
(3) ………… स्थितयः सृष्टि: विकास: प्रलयः च। कालस्य च
(4) …………….. युगानि।
उत्तर:
(1) एकः
(2) द्वे
(3) तिस्त्रः
(4) चत्वारि।

प्रश्न 6.
अङ्कानां स्थाने संस्कृतसंख्यावाचकविशेषणैः पूरयित्वा अधोलिखितानि वाक्यानि पुनः लिखत
(i) वेदाः ……… (4) मूषकाः अवसन्।
(ii) पुराणानि …………. (18) सन्ति।
(iii) रामायणे ……… (7) काण्डाः वर्तन्ते।
(iv) भासस्य ……….. (13) नाटकानि।
उत्तर:
(i) चत्वारः
(ii) अष्टादश
(iii) सप्त
(iv) त्रयोदश।

प्रश्न 7.
अधोलिखितानि वाक्यानि अङ्कानां स्थाने संस्कृतसंख्यावाचकविशेषणैः पूरयित्वा लिखत
(i) वर्षे (12) ………. मासाः भवन्ति।
(ii) मासे (30) …………… दिनानि भवन्ति।
(iii) सप्ताहे (7) ………. दिनानि सन्ति।
(iv) दिने (13) ………. नाटकानि।
उत्तर:
(i) द्वादश
(ii) त्रिंशत्
(iii) सप्त
(iv) त्रयोदश।

प्रश्न 8.
अधोलिखितानि वाक्यानि अङ्कानां स्थाने संस्कृतसंख्यावाचकविशेषणैः पूरयित्वा लिखत
(i) मनुष्यस्य शरीरे (2) ………. पादौ स्तः।
(ii) मनुष्यस्य मुखे (32) ………. दन्ताः सन्ति।
(iii) (1) ………. हस्ते, (5) ………. अमुल्यः सन्ति।
उत्तर:
(i) द्वौ
(ii) द्वात्रिंशत्
(iii) एकस्मिन्
(iv) पञ्च।

प्रश्न 9.
निम्नेषु वाक्येषु कोष्ठात् उपयुक्तसंख्याभिः रिक्तस्थानपूर्तिः क्रियताम्
(i) पाण्डवाः ……………. आसन्। (पञ्च/ पञ्चाः )
(ii) पुस्तकालये . .. मित्राणि पठन्ति। (त्रयः/त्रीणि)
(iii) वेदाः ……… सन्ति। (चत्वारि/चत्वारः)
(iv) ……… महिले फलानि आनयतः। (द्वे/ द्वौ) ।
उत्तर:
(i) पञ्च
(ii) त्रीणि
(iii) चत्वारः
(iv) द्वे ।

प्रश्न 10.
निम्नेषु वाक्येषु कोष्ठात् उपयुक्तसंख्याभिः रिक्तस्थानपूर्तिः क्रियताम्
(i) अश्वस्य …………… पादाः सन्ति। (चत्वारः/चतस्रः)
(ii) सप्ताहे ……………. दिवसाः भवन्ति। (सप्ताः /सप्त)
(iii) क्रीडाक्षेत्रे …………… मित्राणि क्रीडन्ति। (त्रयः/त्रीणि)
(iv) नरस्य हस्तौ ………… भवतः। (ढे/द्वौ)
उत्तर:
(i) चत्वारः
(ii) सप्त
(iii) त्रीणि
(iv) द्वौ।

प्रश्न 11.
निम्नेषु वाक्येषु कोष्ठात् उपयुक्तसंख्याभिः रिक्तस्थानपूर्तिः क्रियताम्
(i) अस्मिन् स्यूते ………. पुस्तके स्तः। (द्वौ / द्वे/द्वि)
(ii) तस्मिन् उद्याने ………. बालिकाः क्रीडन्ति। (तिस्रः/त्रीणि/त्रयः)
(iii) अत्र ………. वृक्षौ स्तः। (द्वे/ द्वौ / द्वि)
(iv) ……………… बालकाः पठन्ति। (चत्वारः/ चतस्त्र:/चतुर् )
उत्तर:
(i) द्वे
(ii) तिस्त्रः
(ii) द्वौ ।
(iv) चत्वारः।

प्रश्न 12.
निम्नेषु वाक्येषु कोष्ठात् उपयुक्तसंख्याभिः रिक्तस्थानपूर्तिः क्रियताम्
(i) अस्मिन् वृक्षे …………….. आम्राणि सन्ति। (चत्वारि /चतस्त्रः)
(ii) मम स्यूते सामान्ज्ञानस्य अपि ……………पुस्तकम् अस्ति। (एक:/एकम्/एका)
(iii) तत्र …………….. बालिकाः क्रीडन्ति। (तिस्रः/त्रीणि/त्रयः)
(iv) अत्र …………….. फले स्तः। (द्वौ / द्वे/द्वि)
उत्तर:
(i) चत्वारि
(ii) एकम्
(iii) तिस्रः
(iv) द्वे।

प्रश्न 13.
कोष्ठकात शुद्धम् उत्तरं विचित्य रिक्तस्थानानि परयत
मुखे …………….. नयने स्तः। (द्वौ / द्वे/द्वि) तत्र उद्याने …………….. बालाः भ्रमन्ति। (तिस्त्रः/त्रीणि/त्रयः) उद्याने ……. आम्रवृक्षः अस्ति। (एकं / एकः, एका) …….. छात्राः क्रीडन्ति। (चतस्रः/ चत्वारः/चतुर्)।
उत्तर:
(i) द्वे
(ii) तिस्रः
(iii) एकः
(iv) चत्वारः।

प्रश्न 14.
कोष्ठकात् शुद्धम् उत्तरं विचित्य रिक्तस्थानानि पूरयत मम हस्ते ……………. फले स्तः। (द्वौ / द्वे/द्वि) उद्याने …………….. बालिकाः क्रीडन्ति। (तिस्रः/त्रीणि/त्रयः) …………. मित्राणि सन्ति। (चत्वारः/चत्वारि, चतस्त्रः) गृहे …………….. लता शोभते। (एकं / एक:/एका)।
उत्तर:
(i) द्वे
(ii) तिस्रः
(iii) चत्वारि
(iv) एका।

प्रश्न 15.
कोष्ठकात् शुद्धम् उत्तरं विचित्य रिक्तस्थानानि पूरयत अस्मिन् वृक्षे …………….. काकौ तिष्ठतः। (द्वौ/ द्वे/द्वि) मम कक्षायां …………….. गायिकाः सन्ति। (तिस्त्रः/त्रयः/त्रीणि) सा ………… फलानि खादति। (चतस्रः/ चत्वारः, चत्वारि) त्वं …………. पुस्तके अत्र आनय (द्वौ / द्वे/ द्वौ)।
उत्तर:
(i) द्वौ
(ii) तिस्रः
(iii) चत्वारि
(iv) द्वे।

प्रश्न 16.
अधोलिखितानि वाक्यानि अङ्कानां स्थाने संस्कृतसंख्यावाचकविशेषणैः पूरयित्वा लिखत
(i) वेदाः ………… (4) सन्ति।
(ii) पुराणानि ………… (18) सन्ति ।
(iii) भास ………… (13) नाटकानि अलिखत्।
(iv) वृक्षे…………… (3) कोकिलाः सन्ति ।
उत्तर:
(i) चत्वारः
(ii) अष्टादश
(iii) त्रयोदश
(iv) त्रयः।

प्रश्न 17.
अधोलिखितानि वाक्येषु अङ्कानां स्थाने संस्कृतसंख्यावाचकविशेषणैः रिक्तस्थानपूर्ति संस्कृतेन कृत्वा लिखत
एकदा
(i) ………….. (1) वृक्षे
(ii) ………………..(4) कोकिला:
(iii) काकाः …………
(iv) ………… (2) च चटके आस्ताम्। येषु घनिष्ठा मैत्री अभवत्।
उत्तर:
(i) एकस्मिन्
(ii) चत्वारः
(iii) त्रयः
(iv) द्वे।

प्रश्न 18.
अङ्कानां स्थाने संस्कृतसंख्यावाचकविशेषणैः रिक्तस्थानपूर्ति संस्कृतेन कृत्वा पुनः लिखत
(i) मम विद्यालये (12) ………… कक्षाः सन्ति।
(ii) तेषु प्रायः (500) ………… छात्राः पठन्ति।
(iii) (50)………… अध्यापकाः परिश्रमेण अस्मान् पाठयन्ति।
(iv) गतवर्षे परीक्षापरिणामः (90) ……….. प्रतिशतम् आसीत्।
उत्तर:
(i) द्वादश
(ii) पञ्चशतम्
(iii) पञ्चाशत्
(iv) नवतिः ।

प्रश्न 19.
अधोलिखितेषु वाक्येषु अङ्कानां स्थाने संख्यावाचकविशेषणैः उचितरूपेण रिक्तस्थानपूर्तिः करणीया।
(नीचे दिए गए वाक्यों में अंकों के स्थान पर संख्यावाचक विशेषणों को लिखकर उचित रूप से रिक्त स्थान की पूर्ति कीजिए।
In the following sentences, fill in the blanks with the suitable numerical adjectives in place of numerals in Sanskrit.)

(i) गणिते (75) …………… अङ्काः विज्ञाने
(ii) (60) …….. अङ्गाः
(iii) योगे च (50) …………… अङ्काः लब्धाः । तेन संस्कृ सर्वाधिकाः अङ्काः प्राप्ताः।
(iv) वयम् (28) …………… छात्राः रेलयानेन पुरीनगर यात्रायै गतवन्तः।
(v) अस्माभिः सह (3) …………… अध्यापकाः
(vi) (4) ……. अध्यापिकाः च आसन्।
(vii) पुरीनगरे मम (1) …………… मित्रम् अपि वसति।
(viii) सूर्यः (1) …………… अस्ति ।
(ix) सूर्यस्य (2) …………… गती।
(x) जगतः (3) …………. स्थितयः सृष्टि विकासः प्रलयः च।
(xi) कालस्य च (4) ………युगानि।
(xii) वेदाः (4) ……… सन्ति।
(xiii) पुराणानि (18) …………… सन्ति ।
(xiv) रामायणे (7) …………… काण्डाः वर्तन्ते।
(xv) भासस्य (13) …………… नाटकानि।
(xvi) वर्षे (12) …….. मासाः भवन्ति।
(xvii) मासे (30) …………… दिनानि भवन्ति ।
(xviii) सप्ताहे (7) ………….. दिनानि सन्ति।
(xix) दिने (24) …………… होराः वर्तन्ते।
(xx) मनुष्यस्य शरीरे (2) …………… पादौ स्तः ।
(xxi) मनुष्यस्य मुखे (32) …………… दन्ताः सन्ति ।
(xxii) एकदा (1) …………… वृक्षे
(xxiii) (4) ……………….. कोकिला:
(xxiv) (3) …………… काका:
(xxv) (2) ……… च चटके आस्ताम्, तेषु घनिष्ठा मैत्री ……… आसीत्।
(xxvi) मम विद्यालये (12) ……… कक्षाः सन्ति।
(xxvii) तेषु प्रायः (500) ……… छात्राः पठन्ति ।
(xxviii) (50) ………अध्यापकाः परिश्रमेण अस्मान पाठयन्ति।
(xxix) गतवर्षे परीक्षापरिणामः (90)……… प्रतिशतम् आसीत्।
(xxx) रामायणस्य विपुल-साहित्यस्य कीर्तिः (10) ………. दिक्षु व्याप्ता।
(xxxi) उत्सवे प्रायः (100) ………. जनाः उपस्थिताः आसन्।
(xxxii) मञ्चे (4) ………………. विशिष्टाः अतिथयः आसन्।
(xxxiii) (10) …………. छात्रैः स्वागतगानं गीतम्।
(xxxiv) (3) ……………… बालिकाभिः श्लोक-पाठः कृतः।
(xxxv) अस्माकं पृथ्वी (7) ………. द्विपेषु विभक्ता।
(xxxvi) (3) …………. सागराः भारतभूमेः चरणप्रक्षालनं कुर्वन्ति।……….. नदीभिः पञ्चापप्रदेशः शोभते।
(xxxviii) (9) ………. ग्रहेषु पृथिवी अन्यतमः ग्रहः, तत्र भारतभूमिः विराजते।
(xxxix) (3) ………… महिलाः प्रतिदिनं शिव पूजां कुर्वन्ति।
(xxx) (2)………. भगिन्यौ सस्वरं गीतां पठतः।
(xxxi) गीता (1) …………….. महान ग्रन्थः अस्ति।
(xxxxii) अस्माकं ग्रामे (85) ………….. कृषकाः सन्ति ।
(xxxxiii) अकस्मात् (3) ………. कपोताः कुतश्चिद् उड्डीय समागताः। |
(xxxxiv) इदानीं वृक्षे (4) ………….. पक्षिणः सन्ति।
(xxxxu) विद्यालये दशमकक्षायां (42) ………….. छात्रा: संस्कृतं पठन्ति। |
(xxxxvi) तेषु (29) ……………. बालिकाः सन्ति ।
(xxxxvii) गत वर्षे (2) ……………. बालकौ।
(xxxxviii)(4) …………… बालिकाः च छात्रवृत्ति प्रार नुवन्।
(xxxxix) एकस्मिन् उद्याने (15) ……………. वृक्षाःआसन्।
(xxxxx) एकस्मिन् वृक्षे (2) ……………. वानरौ वसतः स्म।
(xxxxxi) तौ वानरौ (4) ……………. फलानि खादन्ति स्म।
(xxxxxii) तदैव एकस्मिन् वृक्षे (1) ……………… चटका अपि वसति स्म।
उत्तर:
(i) पञ्चसप्ततिः
(ii) षष्टिः
(iii) पञ्चाशत्
(iv) अष्टाविंशतिः
(v) त्रयः
(vi) चतस्रः
(vii) एकम्
(viii) एकः
(ix) द्वे
(x) तिस्त्रः
(xi) चत्वारि
(xii) चत्वारः
(xiii) अष्टादश
(xiv) सप्त
(xv) त्रयोदश
(xvi) द्वादश
(xvii) त्रिंशत्
(xviii) सप्त
(xix) चतुर्विंशतिः
(xx) द्वौ
(xxi) द्वात्रिंशत्
(xxii) एकस्मिन्
(xxiii) चत्वारः
(xxiv) त्रयः
(xxv) द्वे
(xxvi) द्वादश
(xxvii) पञ्चशतम्
(xxviii) पञ्चाशत्
(xxix) नवतिः
(xxx) दशसु
(xxxi) शतम्
(xxxii) चत्वारः
(xxxxiii) दशभिः
(xxxiv) तिसृभिः
(xxxv) सप्तसु
(xxxvi) त्रयः
(xxxvii) पज्चभि:
(xxxviii) नवसु
(xxxix) तिरत्र:
(xxxx) द्वे
(xxxxi) एकः
(xxxxii) पञ्चाशीतिः
(xxxxiii) त्रयः
(xxxxiv) चत्वारः
(xxxxv) द्विचत्वारिंशत्
(xxxxvi)नवविंशतिः/एकोनत्रिंशत्
(xxxxvii) द्वौ
(xxxxviii) चतस्त्रः
(xxxxix) पञ्चदश
(xxxxx) द्वौ
(xxxxxi)चत्वारि
(xxxxxii) एका।

बहुविकल्पीय प्रश्नाः

1. प्रदत्तेषु उत्तरेषु यत् उत्तरम् शुद्धम् अस्ति तत् अधस्तात् मञ्जूषायाः पदेभ्यः चीयताम्।
(दिए गए उत्तरों में से जो उत्तर शुद्ध है उसे नीचे के मंजूषा शब्दों से चुनिए।
Choose the appropriate answer from the options given below.)

1. (83) अस्य संस्कृते शुद्धम् रूपम् …………….. अस्ति।
(क) त्रिशीतिः
(ख) त्र्यशीतिः
(ग) त्रिणशीतिः
(घ) त्रयाशीतिः
उत्तर:
(ख) त्र्यशीतिः

2. वयम् (7) …………….. स्मः ।
(क) सप्त
(ख) सप्ताः
(ग) सप्तानि
(घ) सप्तः
उत्तर:
(क) सप्त

3. …………….. (4) नायिकाः नृत्यन्ति ।
(क) चत्वारि
(ख) चत्वारः
(ग) चतस्रः
(घ) चतुराः
उत्तर:
(ग) चतस्रः

4. मम समीपे ……………… (19) रुप्यकाणि सन्ति।
(क) एकोनविंशतिः
(ख) एकोनविशंति
(ग) एकोनविंशम्
(घ) एकोनाविंशतिः
उत्तर:
(क) एकोनविंशतिः

5. (54) अस्य संस्कृते शुद्धरूपम् ……………… अस्ति ।
(क) चतुश्पञ्चाशत्
(ख) चतुष्पंचाशत्
(ग) चतुःपञ्चाशत्
(घ) चतुस्पञ्चाशत्
उत्तर:
(ग) चतुःपञ्चाशत्

6. ……………… (2) पुस्तके आनय।
(क) द्वौ
(ख) द्वे
(ग) द्वि
(घ) द्वा
उत्तर:
(ख) द्वे

7. ………….. (3) ललनाः आनयन्ति।
(क) त्रीणि
(ख) त्रि
(ग) त्रयः
(घ) तिस्रः
उत्तर:
(घ) तिस्रः

8. भासेन …………….. (14) नाटकानि रचितानि।
(क) चतुर्दशम्
(ख) चतुर्दश
(ग) चतुर्दशानि
(घ) चतुर्दशाः
उत्तर:
(ख) चतुर्दश

9. (56) अस्य संस्कृते शुद्धम् रूपम् ……………… भवति ।
(क) षट्पञ्चाशत्
(ख) षटपञ्चाशत्
(ग) षणपंचाशत्
(घ) षड्पञ्चाशत्
उत्तर:
(क) षट्पञ्चाशत्

10. (99) अस्य शुद्धम् रूपम् …………….. अस्ति।
(क) नवणवतिः
(ख) नवानवतिः
(ग) नवौनवतिः
(घ) नवनवतिः
उत्तर:
(घ) नवनवतिः

11. (66) अस्य संस्कृते शुद्धम् रूपम् ……………… वर्तते।
(क) षट्षष्टि
(ख) षटाषष्टी:
(ग) षट्षष्टिः
(घ) षड्षष्टिः
उत्तर:
(ग) षट्षष्टिः

12. वृक्षात् …….(4) पत्राणि पतन्ति।
(क) चत्वारः
(ख) चत्वारि
(ग) चतस्रः
(घ) चतुरः
उत्तर:
(ख) चत्वारि

13. नव नव च ………….. (18) भवन्ति।
(क) अष्टादशम्
(ख) अष्टदशः
(ग) अष्टादश
(घ) अष्टादशाः
उत्तर:
(ग) अष्टादश

14. मह्यमपि ………….. (1) पेयम् दीयताम्।
(क) एका
(ख) एकम्
(ग) एकः
(घ) एकाम्
उत्तर:
(ख) एकम्

15. त्वम् ……………… (1) लेखम् लिख।
(क) एकः
(ख) एक
(ग) एकम्
(घ) एका
उत्तर:
(ग) एकम्

16. राजपथे………………. (4) वाहनानि सन्ति।
(क) चत्वारि
(ख) चत्वारः
(ग) चतस्रः
(घ) चतुरः
उत्तर:
(क) चत्वारि

17. त्वं मह्यम् ……………….. (3) पुस्तकानि आनय।
(क) त्रयः
(ख) त्रि
(ग) त्रयम्
(घ) त्रीणि
उत्तर:
(घ) त्रीणि

18. (71) अस्य संस्कृते शुद्धम् रूपम् ……………….. भवति ।
(क) एकासप्ततिः
(ख) एकसप्ततिः
(ग) एकासप्तति
(घ) एकसप्तयः।
उत्तर:
(ख) एकसप्ततिः

19. कुमारस्य …………. (6) मुखानि सन्ति।
(क) षड्म्
(ख) षट्
(ग) षडानि
(घ) षड्
उत्तर:
(घ) षड्

20. ………………. (17) अजाः चरन्ति ।
(क) सप्तदशाः
(ख) सप्तदश
(ग) सप्तदशः
(घ) सप्तदशम्
उत्तर:
(ख) सप्तदश

21. ……….. (94) पुस्तकानि सन्ति।
(क) चतुर्णवतिः
(ख) चतुर्नवति
(ग) चतुर्नवतिः
(घ) चर्तुनवति
उत्तर:
(क) चतुर्णवतिः

22. अस्याम् कक्षायाम् …………….. (60) छात्राः पठन्ति।
(क) षष्टिः
(ख) षष्टी
(ग) सष्टिः
(घ) षष्ठी
उत्तर:
(क) षष्टिः

23. तत्र ……………. (40) जनाः तिष्ठन्ति।
(क) चत्वारिंशत्
(ख) चत्वारिंसत्
(ग) चत्वारिषत्
(घ) चतवारींशत्
उत्तर:
(क) चत्वारिंशत्

24. पुस्तकालये …………. (3) मित्राणि पठन्ति।
(क) त्रयः
(ख) त्रीणि
(ग) तिस्त्र
(घ) त्रि
उत्तर:
(ख) त्रीणि

25. वेदाः ………… (4) सन्ति।
(क) चत्वारि
(ख) चत्वारः
(ग) चतुरः
(घ) चतस्त्रः
उत्तर:
(ख) चत्वारः

26. ………….. (2) महिले फलानि आनयतः।
(क) द्वे
(ख) द्वौ
(ग) द्वा
(घ) द्वयोः
उत्तर:
(क) द्वे

27. अश्वस्य ………. (4) पादाः सन्ति।
(क) चत्वारा:
(ख) चतस्रः
(ग) चत्वारः
(घ) चत्वारि
उत्तर:
(ग) चत्वारः

28. सप्ताहे ………….. (7) दिवसाः भवन्ति ।
(क) सप्तः
(ख) सप्त
(ग) सप्तम्
(घ) सप्ताः
उत्तर:
(ख) सप्त

29. क्रीडाक्षेत्रे …………. (3) मित्राणि क्रीडन्ति।
(क) त्रयः
(ख) तिस्रः
(ग) त्रि
(घ) त्रीणि
उत्तर:
(घ) त्रीणि

30. नरस्य हस्तौ ……………… (2) भवतः।
(क) द्वे
(ख) द्वौ
(ग) द्वि
(घ) द्वयोः
उत्तर:
(ख) द्वौ

31. पुरुषार्थाः …………. (4) सन्ति।
(क) चतस्रः
(ख) चत्वाराः
(ग) चत्वारः
(घ) चत्वारि
उत्तर:
(ग) चत्वारः

32. वित्तस्य ………… (3) गतयः भवन्ति।
(क) त्रयः
(ख) तिस्रः
(ग) त्रीणि
(घ) त्रि
उत्तर:
(ख) तिस्रः

33. ब्रह्मणः आयुः ………. (100) वर्षाणि।
(क) शत
(ख) शतानि
(ग) शतम्
(घ) शताः
उत्तर:
(ग) शतम्

34. हस्ते ……….. (5) अङ्गुल्यः भवन्ति।
(क) पञ्चं
(ख) पञ्चाः
(ग) पञ्चमं
(घ) पञ्च
उत्तर:
(घ) पञ्च

35. तस्मिन् उद्याने ………….. (3) बालिकाः क्रीडन्ति।
(क) तिस्त्रः
(ख) त्रीणि
(ग) त्रयः
(घ) त्रि
उत्तर:
(क) तिस्त्रः

36. अत्र ………………(2) वृक्षौ स्तः।
(क) द्वे
(ख) द्वौ
(ग) द्वि
(घ) द्वा
उत्तर:
(ख) द्वौ

37. ………………. (4) बालकाः पठन्ति ।
(क) चत्वारः
(ख) चतस्त्रः
(ग) चतुर्
(घ) चत्वारि
उत्तर:
(क) चत्वारः

38. अस्मिन् वृक्षे ………………(4) आम्राणि सन्ति ।
(क) चत्वारि
(ख) चत्वारः
(ग) चतस्रः
(घ) चतुराणि
उत्तर:
(क) चत्वारि

39. मम स्यूते सामान्यज्ञानस्य अपि ………………. (1) पुस्तकम् अस्ति।
(क) एकः
(ख) एक
(ग) एका
(घ) एकम्
उत्तर:
(घ) एकम्

40. तत्र ……….. (3) बालिकाः क्रीडन्ति।
(क) तिस्रः
(ख) त्रीणि
(ग) त्रयः
(घ) त्रयाः
उत्तर:
(क) तिस्रः

41. अत्र ……………(2) फले स्तः।
(क) द्वौ
(ख) द्वे
(ख) द्वे
(ग) द्वि
उत्तर:
(ख) द्वे

43. तत्र उद्याने ………… (3) बालाः भ्रमन्ति।
(क) तिस्रः
(ख) त्रयः
(ग) त्रीणि
(घ) त्रि
उत्तर:
(ख) त्रयः

44. उद्याने ……… (1) आम्रवृक्षः अस्ति।
(क) एकं
(ख) एका
(ग) एकां
(घ) एकः
उत्तर:
(घ) एकः

By going through these CBSE Class 12 Maths Notes Chapter 5 Continuity and Differentiability, students can recall all the concepts quickly.

Continuity and Differentiability Notes Class 12 Maths Chapter 5

Continuity (Definition): if f be a real-valued function on a subset of real numbers and let c be a point in its domain, then f is a continuous function at e, if

Obviously, if the left-hand limit and right-hand limit and value of the function at x = c exist and are equal to each other, i.e., if

then f is continuous at x = c.

Algebra of continuous functions:
Let f and g be two real functions, continuous at x = c, then

1. Sum of two functions is continuous at x = c, i.e., (f + g) (x), defined as f(x) + g(x), is continuous at x = c.
2. Difference of two functions is continuous at x = c, i.e., (f – g) (x), defined as f(x) – g(x), is continuous at x = c.
3. Product of two functions is continuous at x = c, i.e., (f g) (x), defined as f(x) . g(x) is continuous at x = c.
4. Quotient of two functions is continuous at x = c, (provided it is defined at x = c), i.e.,
   (\(\frac{f}{g}\))(x), defined as \(\frac{f(x)}{g(x)}\) [g(x) ≠ 0], is continuous at x = c.

However, if f(x) = λ, then
(a) λ.g, defined ty .g(x), is also continuous at x = c.
(b) Similr1y, if \(\frac{λ}{g}\) is defined as \(\frac{λ}{g}\) (x) = \(\frac{λ}{g(x)}\) , then \(\frac{λ}{g}\) is also continuous at x = c.

→ Differentiability: The concept of differentiability has been introduced in the lower class. Let us recall some important results.

→ Differentiability (Definition): Let f be a real function and c is a point in its domain. The derivative of f at c is defined as

Every differentiable function is continuous.

→ Algebra of Derivatives: Let u and v be two functions of x.

1. (u ± v)’ = u’ ± v’
2. (uv)’ = u’v + uv’
3. \(\left(\frac{u}{v}\right)^{\prime}=\frac{u^{\prime} v-u v^{\prime}}{v^{2}}\), where v ≠ 0.

→ Derivative of Composite Function: Let t be a real valued function which is a composite of two functions u and v, i.e., f = vou. Put u(x) = t and f= v(t).
∴ \(\frac{d f}{d x}=\frac{d v}{d t} \cdot \frac{d t}{d x}\)

→ Chain Rule: Let/be a real valued function which is a composite fimction of u, v and w, i.e., f(wov)ou.
Put u(x) = t, v(t) = s and f = w(s). Then,
\(\frac{d f}{d x}=\frac{d w}{d s} \cdot \frac{d s}{d t} \cdot \frac{d t}{d x}\).

→ Derivatives of Inverse Trigonometric Functions:

Functions	Domain	Derivatives
Sin-1x	[- 1, 1]	\( \frac{1}{\sqrt{1-x^{2}}} \)
Cos-1x	[- 1, 1]	\( -\frac{1}{\sqrt{1-x^{2}}} \)
tan-1x	R	\( \frac{1}{1+x^{2}} \)
Cot-1x	R	\( -\frac{1}{1+x^{2}} \)
Sec-1x	(-∞, – 1] ∪ [1, ∞)	\( \frac{1}{x \sqrt{x^{2}-1}} \)
Cosec-1x	(-∞, – 1] ∪ [1, ∞)	\( -\frac{1}{x \sqrt{x^{2}-1}} \)

Implicit Functions: An equation in form f(x, y) = 0, in which y is not expressible in terms of x, is called an implicit function of x and y.

Both sides of the equations are differentiated termwise. Then, from this equation, \(\frac{d y}{d x}\) is obtained. It may be noted that when a function of y occurs, then differentiate it w.r.t. y and multiply it by \(\frac{d y}{d x}\).

e.g., To find \(\frac{d y}{d x}\) from cos² y + sin xy = 1, we differentiate it as

Exponential Functions:

The exponential function, with positive base b > 1, is the function y = b^x.

1. The graph of y = 10^x is shown in the figure.
2. Domain = R
3. Range = R⁺
4. The point (0,1) always lies on the graph.
5. It is an increasing function, i.e., as we move from left to right, the graph rises above.
6. As x → – ∞, y → 0.
7. \(\frac{d}{dx}\) (a^x) = a^x log, a, \(\frac{d}{dx}\) e^x = e^x.

Logarithmic Functions:
Let b> 1 be a real number. b^x = a may be written as log_b a = x.

1. The graph of y = log₁₀ x is shown in the figure.
2. Domain = R⁺, Range = R.
3. It is an increasing function.
4. As x → 0, y → ∞.
5. The function y = e^x and y = log_e x are the mirror images of each other in the line y = x.
6. \(\frac{d}{dx}\) (loga x) = \(\frac{1}{x}\) l0ga e, \(\frac{d}{dx}\) loge x = \(\frac{1}{x}\)

→ Other properties of Logarithm are:

1. log_b pq = log_b p + log_b q
2. log_b \(\frac{p}{q}\) = log_a p – log_a q
3. log_b px = x log_b p – log_b q
4. log_a b = \(\frac{\log _{a} p}{\log _{b} p}\)

→ Logarithmic Differentiation:
Whenever the functions are given in the form

1. y = [u(x)]v(x) and
2. y = \(\frac{u(x) \times v(x)}{w(x)}\)

take log of both sides. Simplify and differentiate, e.g.,
Let y = (cos x)sin x, log y = sin x log cos x

Differentiating, \(\frac{1}{y}\) \(\frac{dy}{dx}\) = cos x log Cos x + sin x . – \(\frac{sin x}{cos x}\)
∴ \(\frac{dy}{dx}\) = (cos x)^{sin y} [cos x log cosx – sin x tan x].

→ Derivatives of Functions in Parametric Form: Let the given equations be x = f(t) and y = g(t), where t is the parameter. Then,

→ Second Order Derivative:
Let y = f(x), then \(\frac{dy}{dx}\) =f ‘(x).
If f ‘(x) is differentiable, then it is again differentiated.

Rolle’s Theorem:
Let f: [a, b] → R be continuous on closed interval [a, b] and differentiable on open interval (a, b) such that f(a) = f(b), where a and b are real numbers, then there exists some c ∈ (a, b) such that f ‘(c) = 0.

From the figure, we observe that f(a) = f(b). There exists a point c₁ ∈ (a, b) such that f ‘ (c) = 0, i.e., tangent at c1 is parallel to x-axis. Similarly, f(b) = f(c) → f ‘ (c₂) = 0.

→ Mean Value Theorem: Let f: [a, b] → R be a continuous function on the closed interval [a, b] and differentiable in the open interval (a, b). Then, there exists some c ∈ (a, b) such that
f ‘ (c) = \(\frac{f(b)-f(a)}{b-a}\)

Now, we know that \(\frac{f(b)-f(a)}{b-a}\) is the slope of secant drawn between A[a,f(a)] and B[b,f(b)]. We t k know that the slope of the line joining (x_1, y₁) and (x₂, y₂) is \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)

The theorem states that there is a point c ∈ (a, b), where f ‘(c) is equal to the slope of AB.

In other words, there exists a point c ∈ (a, b) such that tangent at x = c is parallel to AB.

1. CONTINUITY
(i) Left Continuity. A function ‘f ’ is left-continuous at x = c if \(\lim _{x \rightarrow c^{-}}\) f (x) = f(c).

(ii) Right Continuity. A function ‘f ’ is right-continuous at x = c if \(\lim _{x \rightarrow c^{+}}\) f (x) = f(c).

(iii) Continuity at a point. A function ‘ f ’ is continuous at x = c if
\(\lim _{x \rightarrow c^{-}}\) (x) = \(\lim _{x \rightarrow c^{+}}\) f(x) = f(c).

2. (i) Polynominal functions
(ii) Rational functions
(iii) Exponential functions
(iv) Trigonometric functions are all continuous at each point of their respective domain.

3. DIFFERENTIABILITY
(i) Left Derivative. A function ‘f ’ is said to possess left derivative at x = c if \(\lim _{h \rightarrow 0} \frac{f(c-h)-f(c)}{-h}\) exists finitely.

(ii) Right Derivative. A function ‘f ’ is said to possess right derivative at x = c if
\(\lim _{h \rightarrow 0} \frac{f(c+h)-f(c)}{h}\) exists finitely.
(iii) Derivative. A function is said to possess derivative at x = c if \(\lim _{h \rightarrow 0} \frac{f(c+h)-f(c)}{h}\) exists finitely.

4. CONTINUITY AND DERIVABILITY
A real valued function is finitely derivable at any point of its domain, it is necessarily continuous at that point. The converse is not true.

5. STANDARD RESULTS

(i) \(\frac{d}{d x}\) (xⁿ) = nx^n-1 ∀ x ∈ R
(ii) \(\frac{d}{d x}\) ((ax + b)n = n(ax + b)^{n – 1} . a ∀ x ∈ R
(iii) \(\frac{d}{d x}(|x|)=\frac{x}{|x|}\), x ≠ 0

6. GENERAL THEOREMS
(i) The derivative of a constant is zero.
(ii) An additive constant vanishes on differentiation i.e. if f(x) = g(x) + c, where ‘c’ is any constant, then f'(x) = g'(x).
(iii) If f(x) = ag(x), then f'(x) = ag'(x), where ‘a’ is a scalar.
(iv) If f(x) = g(x) + h(x), then f'(x) = g'(x) + h'(x).

Extension.
If f(x) = a₁f₁ ± a₂f₂ ……. ± a_nf_n(x), then :
f'(x) = a₁f₁‘(x) ± a₂f₂‘(x) ± ……. ± a_nf_n‘(x)

(v) If f(x) = \(\frac{g(x)}{h(x)}\), then f'(x) = g(x)h'(x) + g'(x)h(x)
(vi) If f(x) = \(\frac{g(x)}{h(x)}\), then f ‘(x) = \(\frac{h(x) g^{\prime}(x)-g(x) h^{\prime}(x)}{(h(x))^{2}}\), h(x) ≠ 0.
(vii) If f(x) = \(\frac{1}{h(x)}\), then f'(x) = \(-\frac{h(x)}{[h(x)]^{2}}\), h'(x) ≠ 0

7. IMPORTANT RESULTS

(i) (a) \(\frac{d}{d x}\) (sinx) = cos x and \(\frac{d}{d x}\) (cos x) = – sin x ∀ x ∈ R
(b) \(\frac{d}{d x}\) (tan x) = sec² x and \(\frac{d}{d x}\) (sec x) = sec x tan x ∀ x ∈ R except odd multiples of \(\frac{\pi}{2}\)
(c) \(\frac{d}{d x}\)(cot x) = – cosec² x and \(\frac{d}{d x}\) (cosec x) = -cosec x cot x ∀ x ∈ R except even multiple of \(\frac{\pi}{2}\)

(ii)
(a) \(\frac{d}{d x}\)(sin^-1x) = \(\frac{1}{\sqrt{1-x^{2}}}\), |x| < 1
(b) \(\frac{d}{d x}\)(cos^-1x) = \(-\frac{1}{\sqrt{1-x^{2}}}\), |x| < 1
(c) \(\frac{d}{d x}\)(tan^-1x) = \(\frac{1}{1+x^{2}}\) ∀ x ∈ R
(d) \(\frac{d}{d x}\)(cot^-1x) = \(-\frac{1}{1+x^{2}}\) ∀ x ∈ R
(e) \(\frac{d}{d x}\)(sec^-1x) = \(\frac{1}{|x| \sqrt{x^{2}-1}}\) x > 1 or x < -1
(f) \(\frac{d}{d x}\)cosec^-1x) = \(-\frac{1}{|x| \sqrt{x^{2}-1}}\), x > 1 or x < -1

(iii) (a) \(\frac{d}{d x}\) (a^x) = a^x log_e a, a > 0
(b) \(\frac{d}{d x}\)(e^x) = e^x
(c) \(\frac{d}{d x}\)(log_a x) = \(\frac{1}{x}\) log_a e, x > 0
(d) \(\frac{d}{d x}\) (log x) = \(\frac{1}{x}\), x>0.

8. CHAIN RULE
\(\frac{d}{d x}\) (f(g(x)) = f'(g(x)).g'(x)

9. PARAMETRIC EQUATIONS
\(\frac{d y}{d x}=\frac{d y / d t}{d x / d t}\), \(\frac{d x}{d t}\) ≠ 0
Or \(\frac{d y}{d x}=\frac{d y}{d t} \times \frac{d t}{d x}\)

10.MORE RESULTS

(i) \(\frac{d y}{d x}=\frac{1}{\frac{d x}{d y}}\)
(ii) \(\frac{d y}{d x} \times \frac{d x}{d y}=1\)

11. ROLLE’S THEOREM
If a function f(x) is :

(i) continuous in [a, b]
(ii) derivable in (a, b)
(iii) f (a) = f (b), then there exists at least one point ‘c’ in (a, b) such that f’ (c) = 0.

12. LAGRANGE’S MEAN VALUE THEROEM (LMV THEOREM OR MV THEOREM)
If a function f(x) is :
(i) continuous in [a, b]
(ii) derivable in (a, b), then there exists at least one point ‘c’ in (a, b) such that \(\frac{f(b)-f(a)}{b-a}=f^{\prime}(c)\)

By going through these CBSE Class 12 Maths Notes Chapter 4 Determinants, students can recall all the concepts quickly.

Determinants Notes Class 12 Maths Chapter 4

DETERMINANT:
Def.: Let A = [aij]n×n be a matrix of order n × n or simply as of order n. Now we can associate each square matrix with a unique number (real or complex). If M is a set of matrices and K is the set of real or complex numbers, then
f: M → K
or
f(A) = k, when A ∈ M and k ∈ K, which is written as
f(A) = | A | = det (A) = k.

Expansions of Determinants:
→ Determinant of order 1
Let A =[a]. Then, det A = a or | a | = a.

→ Determinant of order 2
Let A = \(\left[\begin{array}{ll}
a & b \\
c & d
\end{array}\right]\) is a matrix or order 2 × 2

Multiply the elements along the arrow, the products are written with alternate sign +, -, i.e.,
\(\left|\begin{array}{ll}
a & b \\
c & d
\end{array}\right|\) = (ad – bc)
Product with element a₁₁ = a and, a₂₂ = d is taken positive.

→ Determinant of order n
Let the determinant be

To expand this determinant, we take the following steps:

1. Take up the elements of a row (or column). Let it be in ith a row. Its elements are a₁₁, a₂₂,…, a_ij…, ai_in.
2. Corresponding to element a_ij we find a determinant M_ij, which is obtained by deleting the elements of ith row and jth column. The determinant Mij is called the minor of a_ij.
3. Sign of the product is (-1)^i+j. Thus, the expansion with the help of ith row = (-1)ⁱ⁺¹ a_i1 M_i1 + (-1)ⁱ⁺² a_i2 M_i2 +………… + (-1)^+j a_ij M_ij + ….. + (-1)i+n a_in M_in.

Now, consider the expansion of a determinant of third order,
i.e., \(\left|\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right|\)

1. The elements in the first row are a₁₁, a₁₂ and a₁₃.
2. M₁₁ is obtained by deleting 1st row and 1st column.
   

Adding the product elements and corresponding determinants with proper sign (-1)^i+j, we get the expansion of the determinant

The same result is obtained by taking the element of any other row or column. Similarly, the determinants of higher order may be expanded.

Properties of Determinants:
Property 1: If the rows and columns of a determinant are interchanged, the value of the determinant remains the same.
Thus, \(\left|\begin{array}{lll}
a_{1} & b_{1} & c_{1} \\
a_{2} & b_{2} & c_{2} \\
a_{3} & b_{3} & c_{3}
\end{array}\right|=\left|\begin{array}{lll}
a_{1} & a_{2} & a_{3} \\
b_{1} & b_{2} & b_{3} \\
c_{1} & c_{2} & c_{3}
\end{array}\right|\).

Property 2: If any two rows or columns of a determinant are interchanged, then sign of the determinant is changed.
Thus, \(-\left|\begin{array}{lll}
a_{2} & b_{2} & c_{2} \\
a_{1} & b_{1} & c_{1} \\
a_{3} & b_{3} & c_{3}
\end{array}\right|=\left|\begin{array}{lll}
a_{1} & b_{1} & c_{1} \\
a_{2} & b_{2} & c_{2} \\
a_{3} & b_{3} & c_{3}
\end{array}\right|\).

Property 3: If any two rows (columns) of a determinant are identical, the value of the determinant is zero.
Thus, \(\left|\begin{array}{lll}
a_{1} & a_{2} & a_{3} \\
a_{1} & a_{2} & a_{3} \\
b_{1} & b_{2} & b_{3}
\end{array}\right|\) = 0

Property 4: If each element of a row or column of a determinant is multiplied by a constant k, then its value is k times the given determinant.
Thus, \(\left|\begin{array}{lll}
k a_{1} & k a_{2} & k a_{3} \\
b_{1} & b_{2} & b_{3} \\
c_{1} & c_{2} & c_{3}
\end{array}\right|=k\left|\begin{array}{lll}
a_{1} & a_{2} & a_{3} \\
b_{1} & b_{2} & b_{3} \\
c_{1} & c_{2} & c_{3}
\end{array}\right|\).

Property 5: If the element of a row or column of a determinant are expressed as sum of two (or more terms), then the determinant can be expressed as sum of two (or more) determinants.

Property 6: If to each element of any row or column of a determinant, the equimultiples of corresponding elements of any other row or column are added, then the value of the determinant remains unchanged.

Area of a Triangle:
The area of a triangle whose vertices are (x₁, y₁), (x₂, y₂) and (x₃, y₃) is equal to \(\frac{1}{2}\) \(\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|\)

It may be noted:

• The area is positive. So, take the only absolute value.
• If the three points are collinear, the area of a triangle is taken as zero.

→ Minor of a determinant: In a determinant Δ, the minor of a_ij is obtained by deleting the ith row and jth column.
e.g. Minor of a₂₁ of \(\left|\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right|\)

= M₂₁ = \(\left|\begin{array}{ccc}
\ldots & a_{12} & a_{13} \\
\ldots & \ldots & \ldots \\
\ldots & a_{32} & a_{33}
\end{array}\right|=\left|\begin{array}{ll}
a_{12} & a_{13} \\
a_{32} & a_{33}
\end{array}\right|\)

Co-factor of an element of Determinant:
Co-factor of an element a., of determinant | a_ij |
= (-1)^i+j M_ij where M_ij is the minor of a_ij.

In det. \(\left|\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right|\), cofactor of a31 = (-1)3+1M31 = \(\left|\begin{array}{ll}
a_{12} & a_{13} \\
a_{22} & a_{23}
\end{array}\right|\)

→ Matrix of cofactors: By replacing the elements of a determinant with their cofactors, a matrix of cofactors is obtained.

→ Adjoint of a Matrix: The adjoint of a square matrix is the transpose of the matrix of cofactors.
If A_ij, is the cofactor of a., of det. A = | a_ij |, then

→ Singular Matrix: If | A | =0, the square matrix A is said to be singular.

→ Non-singular Matrix: If | A | ≠ 0, the square matrix A is known as a non-singular matrix.

→ Invertible Matrix: If AB = BA = I, then A is called the inverse of A which is written as B = A^-1. In this case, the square matrix A is said to be invertible.

Some Theorems:

1. If A is a square matrix, then A (adj A) = (adj A) A = AI.
2. If A and B are non-singular matrices, then AB and BA are also non-singular matrices.
3. | AB | = | A | | B |.
4. A square matrix A is invertible, if and only if A is non-singular.
5. A^-1 = \(\frac{1}{|A|}\) adj A.
6. (AB)^-1 = B^-1A^-1.
7. (a) (A’)^-1 .= (A^-1)’.
   (b) (A^-1)^-1 = A.
   (c) (XYZ)^-1 = Z^-1 Y^-1 X^-1.

Linear System of Equations:
→ Consistent system: The system of equations is said to be consistent, if it has one or more than one solutions.

→ Inconsistent system: The system of equations is said to be inconsistent, if it has no solution.
Consider the system of equations:
a₁x + b₁y + c₁z = d₁
a₂x + b₂y + c₂z = d₂
a₃x + b₃y + c₃z = d₃

Let A = \(\left[\begin{array}{lll}
a_{1} & b_{1} & c_{1} \\
a_{2} & b_{2} & c_{2} \\
a_{3} & b_{3} & c_{3}
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and B = \(\left[\begin{array}{l}
d_{1} \\
d_{2} \\
d_{3}
\end{array}\right]\)

The given system of equations can be written is
\(\left[\begin{array}{lll}
a_{1} & b_{1} & c_{1} \\
a_{2} & b_{2} & c_{2} \\
a_{3} & b_{3} & c_{3}
\end{array}\right]\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{l}
d_{1} \\
d_{2} \\
d_{3}
\end{array}\right]\)
or
AX = B.
∴ X = A-1B.

Consistency/Inconsistency of system cf equations:
(a) For a non-homogeneous system of equations AX ≠ O:

1. if | A | ≠ 0, AX = B has a unique solution.
2. If | A | = 0, let us find (adj A) B.
3. If (adj A)B ≠ 0, the system of equations is inconsistent.
4. If (adj A)B = 0, the system of equations has infinitely many solutions and hence consistent.

(b) For the homogeneous system of equations AX = O:

1. If | A | ≠ 0, the solution is x = 0, y = 0, z = 0. This is called the trivial solution. The system is consistent.
2. If | A | = 0, the system has infinitely many solutions. The system is consistent.

In such as case, we put one of the variables equal to k. Let z = k, then we find the values of x and y in terms of k.

1. DETERMINANT OF A SQUARE MATRIX

(i) If A = \(\left[\begin{array}{ll}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{array}\right]\), then det. A = \(\left|\begin{array}{ll}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{array}\right|\) = a₁₁a₂₂ – a₂₁a₁₂

(ii) If A = \(\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right]\), then det. A = a₁₁\(\left|\begin{array}{ll}
a_{22} & a_{23} \\
a_{32} & a_{33}
\end{array}\right|\) – a₁₂ \(\left|\begin{array}{ll}
a_{21} & a_{23} \\
a_{31} & a_{33}
\end{array}\right|\) + a₁₃ \(\left|\begin{array}{ll}
a_{21} & a_{22} \\
a_{31} & a_{32}
\end{array}\right|\)
= a₁₁a₂₂a₃₃ – a₂₃a₃₂a₁₁ – a₁₂a₂₁a₃₃ + a₁₂a₂₃a₁₁ + a₁₃a₂₁a₃₂ – a₁₃a₃₁a₂₂.

2. MINOR AND CO-FACTOR
(i) The minor of an element a_ij is a determinant, which is obtained by supressing die ith row and jth column. The minor of an element a_ij is denoted by M_ij.

(ii) The co-factor of an element is its minor with proper sign. The co-factor of an element a_ij is denoted by A_ij
A_ij =(-1)^i+jM_ij

3. PROPERTIES

(i) Reflection Property. The value of the determinant remains unaltered by interchanging its rows and columns.
(ii) Switching Property. If two adjacent rows (or columns) of a determinant are interchanged, then the sign of the determinant is changed.
(iii) Repetition Property. If two rows (or columns) of a determinant are identical, then its value is zero.
(iv) Scalar Multiple Property. If each element of a row (or column) of a determinant is multiplied f
by a constant ‘k’ then its value gets multiplied by the scalar ‘k’
(v) Sum Property. If each element of a row (or column) of a determinant is expressed as the sum
of two or more terms, then the determinant can be expressed as the sum of two or more determinants.
(vi) Invariance Property. If to any row (or column) of a determinant, a multiple of another row (or column) is added, the value of the determinant remains the same.
(vii) Factor Property. If a determinant Δ vanishes when for x is put a in those elements of Δ, which are polynomials in x, then (x – a) is a factor of Δ.

4. AREA OF A TRIANGLE

Area of a triangle whose vertices are (x₁, y₁), (x₂, y₂), (x₃, y₃) is given by:
D = \(\frac{1}{2}\left|\begin{array}{lll}
x_{1} & y_{1} & 1 \\
x_{2} & y_{2} & 1 \\
x_{3} & y_{3} & 1
\end{array}\right|\)
When the area of the triangle is zero, then the points are collinear.

5. ADJOINT OF A MATRIX

Let A = \(\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right]\), then adj, A = \(\left[\begin{array}{lll}
\mathrm{A}_{11} & \mathrm{~A}_{21} & \mathrm{~A}_{31} \\
\mathrm{~A}_{12} & \mathrm{~A}_{22} & \mathrm{~A}_{32} \\
\mathrm{~A}_{13} & \mathrm{~A}_{23} & \mathrm{~A}_{33}
\end{array}\right]\), where capital letters are co-factors of corresponding small letters.

6. INVERSE OF A MATRIX

Invertible Matrix. Any n-rowed square matrix A is said to be invertible if there exists an n-rowed matrix B such that
AB = BA = I_n
B is called the inverse of A and is denoted as A^-1.

Theorems.
(i) Inverse of every square matrix, if it exists, is unique.
(ii) A is invertible iff |A| ≠ 0
(iii) A^-1 = \(\frac{\operatorname{adj} . \mathrm{A}}{|\mathrm{A}|}\), if | A | ≠ 0.

PROPERTIES:

(i) (AB)^-1 =B^-1 A^-1
(ii) (A’)^-1 = (A^-1)’
(iii) (A^k)^-1 =(A^-1)^k, where k is any positive integer.

7. SINGULAR AND NON-SINGULAR MATRICES
A square matrix is said to be singular if |A| = 0 and non-singular if |A| ≠ 0.

8. SOLUTIONS OF EQUATIONS BY MATRIX METHOD To solve the equations :
\(\begin{array}{l}
a_{11} x_{1}+a_{12} x_{2}+\ldots \ldots+a_{1 n} x_{n}=b_{1} \\
a_{21} x_{1}+a_{22} x_{2}+\ldots \ldots+a_{2 n} x_{n}=b_{2} \\
\ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \\
a_{m 1} x_{1}+a_{m 2} x_{2}+\ldots \ldots+a_{m n} x_{n}=b_{m} .
\end{array}\)
Here X = A^-1B,
where A = \(\left[\begin{array}{cccc}
a_{11} & a_{12} & \ldots \ldots \ldots & a_{1 n} \\
a_{21} & a_{22} & \ldots \ldots \ldots & a_{2 n} \\
\ldots & \ldots \ldots \ldots \ldots & \\
a_{m 1} & a_{m 2} \ldots \ldots \ldots . & a_{m n}
\end{array}\right]\), X = \(\left[\begin{array}{c}
x_{1} \\
x_{2} \\
\cdots \\
x_{n}
\end{array}\right]\), B = \(\left[\begin{array}{c}
b_{1} \\
b_{2} \\
\ldots \\
b_{m}
\end{array}\right]\)

(i) If |A| ≠ 0, then the system is consistent and has a unique solution.
(ii) If | A | = 0 and (adj. A) B = O, (O being a zero matrix) then the system is consistent and has infinitely many solutions.
(iii) If | A | = 0 and (adj. A) B ≠ O, then the system is inconsistent and has no solution.

9. SOLUTION OF HOMOGENEOUS EQUATIONS
To solve the equations :
a₁x + b₁y + c₁z = 0
a₂x + b₂y + c₁z = 0
a₃x + b₃y + c₃z = 0.

Here AX = 0, where A = \(\left[\begin{array}{lll}
a_{1} & b_{1} & c_{1} \\
a_{2} & b_{2} & c_{2} \\
a_{3} & b_{3} & c_{3}
\end{array}\right]\) and X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\)

(i) If |A| ≠ 0, then system has only trivial solution.
(ii) If |A| = 0, the system has infinitely many solutions.

By going through these CBSE Class 12 Maths Notes Chapter 3 Matrices, students can recall all the concepts quickly.

Matrices Notes Class 12 Maths Chapter 3

Matrix (Definition): A matrix is defined as a rectangular array (arrangement) of numbers or functions.A
The matrices are denoted by capital letters as shown below:

→ Elements: The numbers or functions in a matrix are called its elements. In matrix A; 2, 5, 6, 4, 0 and \(\sqrt{3}\) are the elements.

→ Row: The elements lying in a horizontal line form a row. Matrix B has 3 rows viz: first row is (1, 3 + 2i, \(\frac{2}{3}\)) is (-5, 2.3, 7) and third row is (\(\sqrt{7}\) 4 -8).

→ Column: The elements lying in a vertical line form a column. Matrix A has three columns viz: first column is \(\left(\begin{array}{l}
2 \\
4
\end{array}\right)\), second is \(\left(\begin{array}{l}
5 \\
0
\end{array}\right)\) and third is \(\left(\begin{array}{c}
6 \\
\sqrt{3}
\end{array}\right)\)

→ Order of matrix: A matrix, having m rows and n columns, is said to be of the order m × n. The matrix A is of order 2 × 3, B is of order 3 × 3 and C is of order 3 × 2.

In general, a matrix of order m × n, i.e., consisting of m rows and n columns is denoted by A = [a_ij]_m×n.

A number of elements in the matrix [a_ij]_m×n are m × n and nth element = a_ij is that element that lies in the ith row and jth column.

Types of matrices:
→ Square Matrix: If in a matrix, the number of rows is equal to the number of columns, then the matrix is called a square matrix.

has 3 rows and 3 columns. Therefore, it is a square matrix.

In general, [a_ij]_n×n is a square matrix of order n. the elements a₁₁, a₂₂, a₃₃,…,a_ii…, a_nn are the elements of main diagonal. Thus, in the matrix P; 2, 7 and 1 are the diagonal elements.

→ Row Matrix: A matrix, which has one row is known as row matrix. [3 -1 i 2] is a row matrix, which has only one row.

→ Column Matrix: A matrix having one column is said to be is a column matrix.\(\left[\begin{array}{c}
-1 \\
3 \\
2
\end{array}\right]\) is a column matrix, since there is only one column in it.

→ Diagonal Matrix: A square matrix is called a diagonal matrix, if its non-diagonal elements are zero, i.e., a_ij = 0, when i ≠ 0, e.g. \(\left[\begin{array}{ll}
2 & 0 \\
0 & 1
\end{array}\right]\) is a diagonal matrix.

→ Scalar Matrix: It is a square matrix whose (a) diagonal elements are non-zero and equal (b) non-diagonals elements are zero, Le, a_ij = k ≠ 0 when j = j, a_ij = 0, when i ≠ j.\(\left[\begin{array}{lll}
2 & 0 & 0 \\
0 & 2 & 0 \\
0 & 0 & 2
\end{array}\right]\) is scalar matrix.

→ Unit or Identity Matrix: It is a square matrix in which each diagonal element is 1. i.e., a_ij = 1 when i = j and aij = 0 when i ≠ j.\(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\) is an Identity or Unit matrix.

→ Zero Matrix or Null Matrix: A matrix, in which all the elements are equal to zero, is called the zero matrix.\(\left[\begin{array}{lll}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0
\end{array}\right]\) is a zero matrix.

→ Comparable Matrices: Two matrices are said to be comparable, if they are of the same order. For example, \(\left[\begin{array}{ccc}
2 & 3 & -5 \\
4 & -2 & 6
\end{array}\right]\) and \(\left[\begin{array}{ccc}
i & 2 & x \\
3 & x^{2} & -1
\end{array}\right]\) are comparable matrices since each matrix is of order 2 × 3.

→ Equal Matrices: Two matrices are equal, if (a) they are of the same order (b) their corresponding elements are equal.

if p = 2, q = 3, r = 5, s = 7, t = 9 and u = 8.

OPERATIONS ON MATRICES:
→ Addition of Matrices: The sum of two matrices A and B of the same order is obtained by adding the corresponding elements. Thus,

→ Multiplication of a Matrix by a Scalar: If a matrix A = [a_ij]_m×n is multiplied by a scalar k, then the product kA is obtained by multiplying each element of A, by k. For example,

→ Negative of a Matrix: The negative of a matrix A = -A = (-1)A. For example,

→ Difference of two Matrices: If A and B are the matrices of the same order, then A – B = A + (-1)B = Sum of matrices A and -B.

→ Properties of Matrices Addition: Let A, B, and C be the matrices of the same order m × n.
(a) The commutation Law: A + B = B + A
(b) The Association Law: (A + B) + C = A + (B + C)
(c) The Existence of Additive Identity: Let Omxn be null matrix of order m × n.
A + O_m×n = O_m×n + A = A.
(d) The Existence of Additive Inverse: Let A = [aij]m×n. We have an order matrix – A = [-a_ij]_m×n such that A + (-A) = A – A = O_m×n
-A is called the additive inverse of A or negative of A.

→ Properties of Scalar Multiplication of a Matrix
Let A and B be the matrices of the same order m × n. Then,
(a) k(A + B) = kA + kB
(b) (k + l)A = kA+ lA

→ Multiplication of Matrices
Two matrices A and B are conformable for multiplication if the Tiber of columns in A is equal to the number of rows in B.
If A = [a_ij]_m×n then B = [b_ij]_n×p and AB = [c_ij]_m×p
C_ij = (ij), the element of AB = sum of the products of the elements of the ith row of A with corresponding elements oi jth column of B. Here, (ith row of A) (jth column of B).

No. of columns in A = No. of rows in B = 2 ⇒ A and B are comformable for multiplication. Let AB = [C_ij]_2×3
c₁₁ = (I row of A) × (I column of B)
= \(\left[\begin{array}{ll}
2 & 3
\end{array}\right]\left[\begin{array}{c}
-1 \\
2
\end{array}\right]\) = 2 × (-1) + 3 × 2 = -2 + 6 = 4

c₁₂ = (I row of A) × (II column of B)
= \(\left[\begin{array}{ll}
2 & 3
\end{array}\right]\left[\begin{array}{c}
2 \\
-3
\end{array}\right]\) = 2 × 2 + 3 × (-3) = 4 – 9 = -5

c₁₃ = (I row of A) × (III column of B)
= \(\left[\begin{array}{ll}
2 & 3
\end{array}\right]\left[\begin{array}{l}
4 \\
5
\end{array}\right]\) = 2 × 4 + 3 × 5 = 8 + 15 = 23

c₂₁ = (II row of A) × (I column of B)
= \(\left[\begin{array}{ll}
1 & 4
\end{array}\right]\left[\begin{array}{c}
-1 \\
2
\end{array}\right]\) = 1 × (-1) + 4 × 2 = -1 + 8 = 7

c₂₂ = (II row of A) × (III column of B)
= \(\left[\begin{array}{ll}
1 & 4
\end{array}\right]\left[\begin{array}{c}
2 \\
-3
\end{array}\right]\) = 1 × 2 + 4 × (-3) = 2 – 12 = -10

c₂₃ = (II row of A) × (III column j B)
= \(\left[\begin{array}{ll}
1 & 4
\end{array}\right]\left[\begin{array}{l}
4 \\
5
\end{array}\right]\) =1 × 4 + 4 × 5 = 4 + 20 = 24

→ Properties of Multiplication of Matrices
(a) The Associative Law:
Let A = [a_ij]_m×n, B = [b_ij]_n×p and C = [c_ij]_p×q.
Then, (AB)C = A(BC)

(b) The Distributive Law:

1. If A = [a_ij]_m×n, B = [b_ij]_n×p and C = [c_ij]_p×q, then A(B + C) = AB + AC.
2. If A = [a_ij]_m×n, B = [b_ij]_n×p and C = [c_ij]_p×q, then (A + B)C = AC + BC.

(c) The Existence of Multiplicative Identity:
Let A be a square matrix. There exists an identity matrix I of the same order such that IA = AI = A.

TRANSPOSE OF A MATRIX:
(a) Definition: Let A = [a_ij]_m×n. The matrix obtained by interchanging the rows and columns of A is called transpose of A. It is denoted by A’ or A^T.
For A = [a_ij]_m×n A’ = [aij]_n×m.

(b) Properties of Transpose of a Matrix Let A and B be the two matrices. Then,

1. (A’)’ = A
2. (kA)’ = kA’, where k is a scalar
3. (A + B)’ = A’ + B’ (whenever A + B is defined)
4. (AB)’ = B’A’ (whenever AB is defined)

SYMMETRIC AND SKEW SYMMETRIC MATRICES:
→ Symmetric Matrix: A square matrix A = [a_ij]_n×n is called symmetric, if A’ = A, i.e., for a_ji = a_ij e.g. \(\left[\begin{array}{ccc}
2 & 3 & 4 \\
3 & 1 & 5 \\
4 & 5 & -1
\end{array}\right]\) is a symmetric matrix.

→ Skew Symmetric Matrix: A square matrix A = [aij]n×n is skew symmetric, if A’ = -A for all i, j or a_ji = – a_ij\(\left[\begin{array}{ccc}
0 & 2 & -3 \\
-2 & 0 & 4 \\
3 & -4 & 0
\end{array}\right]\) a skew symmetric matrix.

→ Properties: Let A be a square matrix with real elements.
(a) A + A’ is symmetric.
(b) A – A’ is skew symrrtetric.
(c) A square matrix can be expressed as the sum of the symmetric and skew-symmetric matrix, i.e.,
A = \(\frac{1}{2}\) (A + A’) + \(\frac{1}{2}\) (A – A’)

ELEMENTARY TRANSFORMATIONS OF A MATRIX:
→ Interchange of ith row and jth row is denoted by R_i ↔ R_j. Similarly, interchange of the ith column with the jth column is denoted by C_i ↔ C_j.

→ Multiplication of each element of ith row by k is represented as R_i → kR_j. and when the ith column is multiplied by k, it is represented as C_i → kC_j.

→ Let the element of the ith row of A be added to the corresponding elements of the jth row multiplied by k. It is denoted by R_i → R_i + kR_j.

Similarly, in the case of columns when elements of the ith column are added to the corresponding elements of the jth column multiplied by k, then C_i → C_j + kC_j.

INVERTIBLE MATRICES:
(a) Definition: Let A be a square matrix of order n. If there exists another square matrix B of the same order such that AB = BA = I_n, then A is said to be invertible and B is called the inverse of A. It is denoted by A^-1. ⇒ B = A^-1.

(b) Inverse of a Matrix by Elementary Operations
Let B = A^-1 be the inverse of A.
i.e., I_n = BA
Multiplying I_n by A^-1, we get
A^-1I_n = I_n A^-1 = (BA)A^-1 = B(AA^-1)
= BI_n = B.
⇒ A^-1 = B.
e.g. Let us find the inverse of \(\left[\begin{array}{ll}
1 & 2 \\
2 & 2
\end{array}\right]\) by elementary operations we have: \(\left[\begin{array}{ll}
1 & 2 \\
2 & 2
\end{array}\right]=\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\) A

By elementary transformation, we change the matrix \(\left[\begin{array}{ll}
1 & 2 \\
2 & 2
\end{array}\right]\) so that we get identity matrix.

1. MATRIX
Def. A system of mn-numbers (real or complex) arranged in the form of an ordered set of m horizontal lines (called rows) and n vertical lines (called columns) is called an m x n matrix.

2. TYPES OF MATRICES

(i) Rectangular Matrix. Any m x n matrix (m≠n) is called a rectangular matrix.
(ii) Square Matrix. Any n x n matrix is called a square matrix of order n.
(iii) Row Matrix. Any 1 x n matrix is called a row matrix.
(iv) Column Matrix. Any m x 1 matrix is called a column matrix.
(v) Diagonal Matrix. A square matrix A = [a_ij ] is said to be a diagonal matrix if a_ij = 0 when i ≠ j.
(vi) Scalar Matrix. A diagonal matrix is said to be a scalar matrix if all its diagonal elements are equal.
(vii) Identity Matrix. A diagonal matrix is said to be an identity matrix if each of its diagonal elements is unity.
(viii) Zero Matrix. A matrix is said to be a zero matrix if each of its elements is zero.
(ix) Triangular Matrices.

(a) A square matrix A = [a_ij ] is said to be upper triangular matrix if a_ij =0 for i > j.
(b) A square matrix A = [a_ij ] is said to be lower triangular matrix if a_ij =0 for i < j.

3. EQUALITY OF MATRICES
Two matrices A = [a_ij ] and B = [b_ij] are said to be equal iff (i) they are of the same order (ii) their corresponding elements are equal.

4. OPERATIONS ON MATRICES

(i) Addition of Matrices.
Let A = [a_ij]_{m x n} and B = [b_ij]_{m x n} be two matrices. Then the sum A + B = C = [c_ij]_{m x n} , where c_ij + a_ij + b_ij for 1 ≤ i ≤ m, 1 ≤ j ≤ n

Key Point
Addition is defined only for matrices, which are of the same order.

(ii) Multiplication of a matrix by a scalar.
Let A be any m x n matrix and k be any scalar. Then m x n matrix obtained by multiplying each element by k is said to be scalar multiple of A by k and is denoted by kA or Ak.

(iii) Multiplication of Matrices.
Let A = [a_ij] be mxn matrix and B = [b_jk] be nxp matrix such that the number of columns of A equals the number of rows of B. Then matrix C = [c_ik] which is of the order m x p such that:

c_ik = \(\sum_{j=1}^{n} a_{i j} b_{j k}\) where i = 1,2, ….. m; p = 1, 2, 3,…………………k is called the product of the matrices A and B and is written as C = AB.

Key Point
Product AB is defined iff number of columns of A = number of rows of B.

5. TRANSPOSE OF A MATRIX
(i) Def. If A=[a_ij]_{m x n}, then the transpose of A, denoted by A’ (or A^t or A^T) is defined by n x m matrix obtained from A by writing the rows of A as columns and columns of A as rows in the same order.

(ii) Properties:

(a) (A’)’=A 1
(b) (A + B)’=A’+B’, A and B being of same type «
(c) (kA)’ = kA’, k being any scalar »
(d) (AB)’ = B’A’.

6. SYMMETRIC AND SKEW-SYMMETRIC MATRICES

(i) Symmetric Matrix.
Def. A square matrix A = [a_ij] is said to be symmetric if (i,j)th element is the same as its (j, i)th element.

Key Point is
A is symmetric if A’= A.

(ii) Skew-Symmetric Matrix.

A square matrix A = [a_ij] is said to be skew-symmetric if (i,j)th element is negative of its . (j, i)th element.

Key Point
A is skew-symmetric if A’ = – A.

We have given detailed NCERT Solutions for Class 10 Sanskrit Grammar Book प्रत्ययाः Questions and Answers come in handy for quickly completing your homework.

Sanskrit Vyakaran Class 10 Solutions प्रत्ययाः

अभ्यास:

I.
प्रश्न 1.
प्रत्ययं संयुज्य वियुज्य वा लिखत-

(i) दृश् + क्त्वा = ___________
(ii) प्रणम्य = ___________
(iii) उपविश्य = ___________
(iv) सोढुम् = ___________
(v) सह् + क्त्वा = ___________
(vi) आ + नी + ल्यप् = ___________
उत्तराणि:
(i) दृष्ट्वा
(ii) प्र + नम् + ल्यप्
(iii) उप + विश् + ल्यप्
(iv) सह + तुमुन्
(v) सोढ्वा
(vi) आनीय।

प्रश्न 2.
अधोलिखितवाक्येषु कोष्ठके प्रदत्त धातुषु क्त्वा / ल्यप् / तुमुन्-प्रत्ययानां प्रयोगेण निष्पन्नपदैः रिक्तस्थानानि पूरयत-

यथा- सः पुस्तकम् आदाय (आ + दा + ल्यप्) गच्छति।
सः पुस्तकं दत्त्वा (दा + क्त्वा) क्रीडति।
(i) रामः कन्दुकम् ___________ (आ + नी + ल्यप्) क्रीडति।
(ii) श्यामः कन्दुकम् ___________ (नी + क्त्वा) गच्छति।
(iii) रामः कन्दुकम् ___________ (ग्रह् + तुमुन्) श्यामम् अनुधावति।
(iv) श्यामः ___________ (वि + हस् + ल्यप्) कन्दुकम् ददाति।
(v) रामः कन्दुकम् ___________ (प्र + आप् + ल्यप्) पुनः प्रसन्नः भवति।
उत्तराणि:
(i) आनीय
(ii) नीत्वा
(iii) ग्रहीतुम्
(iv) विहस्य
(v) प्राप्य।

प्रश्न 3.
उदाहरणमनुसृत्य स्थूलपदेषु धातून् प्रत्ययान् च वियुज्य लिखत-

यथा- बालकः गुरुं नत्वा गच्छति। – नम् + क्त्वा
(i) सः अत्र आगत्य पठति। – ___________
(ii) त्वं कुत्र गत्वा क्रीडसि। – ___________
(iii) बालकः विहस्य वदति। – ___________
(iv) त्वं पस्तकं क्रेतुम् गच्छसि। – ___________
(v) छात्रः पठितुं विद्यालयं गच्छति। – ___________
(vi) नायक: निर्देशक द्रष्टुं गच्छति। – ___________
उत्तराणि:
(i) आ + गम् + ल्यप्
(ii) गम् + क्त्वा
(iii) वि + हस् + ल्यप्
(iv) क्रीण् + तुमुन्
(v) पठ् + तुमुन्
(vi) दृश् + तुमुन्।

प्रश्न 4.
‘क्त्वा’ प्रत्ययस्य प्रयोगेण वाक्यानि संयोजयत-

यथा- बालिका उद्यानं गच्छति। बालिका क्रीडिष्यति।
बालिका उद्यानं गत्वा क्रीडिष्यति।
(i) अहम् विद्यालयं गच्छामि। अहं पठिष्यामि।
(ii) सीता पुस्तकं पठति। सा ज्ञान प्राप्स्यति।
(iii) सः आपणं गच्छति। सः पुस्तकं क्रेष्यति।
(iv) रमेशः पुस्तकालयमगच्छत्। सः समाचारपत्रं पठति।
(v) देवदत्तः पाकशालामगच्छत्। सः भोजनं करोति।
उत्तराणि:
(i) अहं विद्यालयं गत्वा पठिष्यामि।
(ii) सीता पुस्तकं पठित्वा ज्ञान प्राप्स्यति।
(iii) सः आपणं गत्वा पुस्तकं क्रेष्यति।
(iv) रमेशः पुस्तकालयं गत्वा समाचारपत्रं पठति।
(v) देवदत्तः पाकशाला गत्वा भोजनं करोति।

प्रश्न 5.
‘तुमुन्’ प्रत्ययस्य योगेन वाक्यानि संयोजयत-

यथा- बालिका क्रीडिष्यति। सा उद्यानं गच्छति।
बालिका क्रीडितुम् उद्यानं गच्छति।
(i) अहम् पठिष्यामि। अहं पुस्तकं क्रीणामि।
(ii) बालिका परीक्षायाम् उत्तमानि अकानि प्राप्स्यति। सा परिश्रमेण पठति।
(iii) निशा क्रीडिष्यति। सा आपणात् कन्दुकमानयति।
(iv) माता भोजनं पचति। सा शाकमानयत्।
(v) आचार्यः पाठयति। सः कक्षामगच्छत्।
उत्तराणि:
(i) अहं पठितुं पुस्तकं क्रीणामि।
(ii) बालिका परीक्षायाम् उत्तमानि अकानि प्राप्तुं परिश्रमेण पठति।
(iii) निशा क्रीडितुम् आपणात् कन्दुकमानयति।
(iv) माता भोजनं पक्तुं शाकमानयत्।
(v) आचार्यः पाठयितुं कक्षामगच्छत्।

II.
प्रश्न 1.
प्रत्ययान् संयोज्य यथानिर्दिष्टं लिखत-

(i) पठ् + शतृ (पुं.)
(ii) लिख् + शतृ (स्त्री.)
(iii) सेव् + शानच् (स्त्री.)
(iv) सह् + शानच् (पुं.)
(v) वृत् + शानच् (पुं.)
(vi) हस् + शतृ (स्त्री.)
उत्तराणि:
(i) पठन्
(ii) लिखन्ती
(iii) सेवमाना
(iv) सहमानः
(v) वर्तमानः
(vi) हसन्ती

प्रश्न 2.
यथानिर्दिष्टं परिवर्तनं कृत्वा वाक्याने पुनः लिखत-

यथा- लिखन् बालकः पठति (स्त्रीलिङ्गे)
लिखन्ती बालिका पठति।
(i) क्रीडन् बालकः पतति। (स्त्रीलिङ्गे) ___________
(ii) उपविशन् छात्रः हसति। (स्त्रीलिङ्गे) ___________
(iii) धावन्ती बालिका क्रन्दति। (पुंल्लिङ्गे) ___________
(iv) सः चलन् खादति। (स्त्रीलिङ्गे) ___________
(v) अहम् नृत्यन् न गायामि। (स्त्रीलिङ्गे) ___________
(vi) त्वम् याचमाना न शोभसे। (पुंल्लिङ्गे) ___________
(vii) ते गच्छन्तः वार्ता कुर्वन्ति। (स्त्रीलिङ्गे) ___________
(viii) ते धावन्त्यौ भ्रमतः। (पुंल्लिङ्गे) ___________
उत्तराणि:
(i) क्रीडन्ती बालिका पतति।
(ii) उपविशन्ती छात्रा हसति।
(iii) धावन बालकः क्रन्दति।
(iv) सा चलन्ती खादति।
(v) अहम् नृत्यन्ती न गायामि।
(vi) त्वम् याचमानः न शोभसे।
(vii) ताः गच्छन्त्यः वार्ता कुर्वन्ति।
(viii) तो धावन्तौ भ्रमतः।

प्रश्न 3.
शतृप्रत्ययान्तस्य गच्छत्, गच्छन्ती शब्दयोः रूपाणि दृष्ट्वा पठत्, लिखत्, पठन्ती, लिखन्ती च इत्यादीनाम् शब्दानाम् रूपलेखनस्य अभ्यासं कुरुत-

उदाहरण-
(क) गच्छत् (पुंल्लिङ्गः)

(ख) गच्छन्ती (स्त्रीलिङ्गः)

उत्तराणि:
विद्यार्थी स्वयं पढ़े-लिखें और समझें।

प्रश्न 4.
कोष्ठके प्रदत्तशब्दानाम् उचितप्रयोगेण रिक्तस्थानानि पूरयत-

(i) ___________ बालिकायाः पुस्तकम् कुत्र अस्ति? (पठन्ती)
(ii) ___________ शिष्याम् आचार्या किञ्चिद् वदति। (हसन्ती)
(iii) ___________ छात्रैः हस्यते। (गच्छत्)
(iv) ___________ कलिकानाम् सौन्दर्यम् अपूर्वं वर्तते। (विकसन्ती)
(v) ___________ बालकाय वस्त्रं दीयते। (याचत्)
उत्तराणि:
(i) पठन्त्याः
(ii) हसन्ती
(ii) गच्छद्भिः
(iv) विकसन्तीनाम्
(v) याचते

प्रश्न 5.
उदाहरणमनुसृत्य शतृशानच्प्रत्ययौ प्रयुज्य वाक्यानि संयोजयत-

यथा- बालिका गच्छति/सा क्रीडति।
गच्छन्ती बालिका क्रीडति
(i) बालकः पठति। सः पाठं स्मरति।
(ii) शिशुः चलति। सः हसति।
(iii) रमा पठति। सा लिखति।
(iv) साधुः उपदिशति।/सः ज्ञानवार्ता करोति।
(v) याचकः याचते। सः मार्गे चलति।
उत्तराणि:
(i) बालकः पठन् पाठं स्मरति।
(ii) शिशुः चलन् हसति।
(iii) रमा पठन्ती लिखति।
(iv) साधुः उपदिशन् ज्ञान्वार्ता करोति।
(v) याचकः याचमानः मार्गे चलति।

III.
प्रश्न 1.
क्त-क्तवतु-प्रत्ययसंयोजनेन पदानि रचयित्वा वाक्यपूर्तिं कुरुत-

(i) बालकेन – ___________। (हस् + क्त)
(ii) बालकः – ___________। (हस् + क्तवतु)
(iii) शिक्षकेण छात्रः पठनाय – ___________। (कथ् + क्त)
(iv) शिक्षकाः छात्रान् पठनाय – ___________। (कथ् + क्तवतु)
(v) पुत्री पितरम् पुस्तकम् – ___________। (याच् + क्तवतु)
(vi) माता सुतायै भोजनं – ___________। (दा + क्तवतु)
(vii) मम जनकेन भिक्षुकाय रूप्यकाणि – ___________। (दा + क्त)
(viii) छात्रेण ऋषः ज्ञानोपदेशः – ___________। (श्रु + क्त)
उत्तराणि:
(i) हसितम्
(ii) हसितवान्
(iii) कथितः
(iv) कथितवन्तः
(v) याचितवती
(vi) दत्तवती
(vii) दत्तानि
(viii) श्रुतः

प्रश्न 2.
स्तम्भयोः यथोचितं योजयत-

उत्तराणि:

प्रश्न 3.
उदाहरणमनुसृत्य भूतकालिकक्रियाणां स्थाने क्तवतु प्रत्ययप्रयोगेण वाक्यपरिवर्तनं कुरुत-

यथा- अध्यापकः उद्दण्डं छात्रम् अदण्डयत्
अध्यापकः उद्दण्डं छात्रं दण्डितवान्।
(i) छात्रः कक्षायाम् उच्चैः अहसत्।
(ii) माता भोजनम् अपचत्।
(iii) काकः घटे पाषाणखण्डानि अक्षिपत्।
(iv) छात्राः बसयानस्य प्रतीक्षायाम् अतिष्ठन्।
(v) कन्याः उद्याने अक्रीडन्।
उत्तराणि:
(i) छात्रः कक्षायाम् उच्चैः दृष्टितवान्।
(ii) माता भोजनं पचितवती / पक्तवती।
(iii) काकः घटे पाषाणखण्डानिक्षिप्तवान्।
(iv) छात्राः बसयानस्य-प्रतीक्षायां स्थितवन्तः।
(v) कन्याः उद्यानि क्रीडितवत्यः।

प्रश्न 4.
उदाहरणमनुसृत्य भूतकालिकाक्रियाणां स्थाने वाक्यपरिवर्तनं कुरुत-

यथा- अध्यापकः छात्रम् पठनाया अकथयत्।
अध्यापकेन छात्रः पठनाया कथितः।
(i) वानरः मकराय जम्बूफलानि अयच्छत्।
(ii) मकरः वानरं गृहं चलितुम् अकथयत्।
(iii) नकुलः सर्पम् अमारयत्।
(iv) श्यामः लेखम् अलिखत्।
(v) रमा कथाम् अपठत्।
उत्तराणि:
(i) वानरेण मकराय जम्बूफलानि दत्तानि।
(ii) मकरेण वानरः गृहं चलितुम् कथितः।
(iii) नकुलैन सर्पः मारितः।
(iv) श्यामेन लेखः लिखितः।
(v) रमया कथा पठिता।

प्रश्न 5.
उदाहरणमनुसृत्य अशुद्धवाक्यानि शुद्धीकृत्य लिखत-

उत्तराणि:
(i) (i) मोहनः पुस्तकं नीतवान्।
(ii) मोहनेन पुस्तकं नीतम्।

(ii) (i) गीता पाठं पठितवती।
(i) गीतया पाठः पठितः।

(iii) (i) आचार्यः शिष्यम् उपदिष्टवान्।
(ii) आचार्येण शिष्यः उपदिष्टः।

(iv) (i) कन्या गृहे क्रीडितवती।
(ii) कन्यया गृहे क्रीडितम्।

(v) (i) सः भोजनं कृतवान्।
(ii) तेन भेजनं कृतम्।

IV.
प्रश्न 1.
कोष्ठके दत्तान् प्रकृतिप्रत्ययान् संयुज्य रिक्तस्थानानि पूरयत-

(i) रामस्य चरित्रं सर्वैः ___________ (अनु + कृ + अनीयर)
(ii) बालैः कन्दुकम् ___________ (क्रीड् + तव्यत्)
(ii) अस्माभिः गुरूपदेशः ___________ (श्रु + तव्यत्)
(iv) मया नौका ___________ (आ + रुह + अनीयर्)
(v) कः अत्र आगत्य ___________ (लिख + तव्यत्) लेख लेखिष्यति?
उत्तराणि:
(i) अनुकरणीयम्
(ii) क्रीडितव्यम्
(iii) श्रोतव्यः
(iv) आरोहणीया
(v) लेखितव्यं

प्रश्न 2.
कृ-कर्तव्यम्, करणीयम् इति उदाहरणमनुसृत्य अधोलिखिताभिः धातुभिः द्वे द्वे पदे रचयत-

(i) गम् ___________ ___________
(ii) स्मृ ___________ ___________
(iii) नी ___________ ___________
(iv) दृश् ___________ ___________
(v) दा ___________ ___________
उत्तराणि:
(i) गन्तव्यम्, गमनीयम्
(ii) स्मर्तव्यम्, स्मरणीयम्
(iii) नेतव्यम्, नयनीयम्
(iv) द्रष्टव्यम्, दर्शनीयम्
(v) दातव्यम्, दानीयम्

प्रश्न 3.
स्तम्भौ यथोचितं योजयत-

उत्तराणि:

प्रश्न 4.
यथास्थानं प्रकृतिप्रत्यययोग विभागं वा कुरुत-

(i) पेयम् ___________
(ii) दा + यत् ___________
(iii) सेव्यम् ___________
(iv) कृ + ण्यत् ___________
(v) कर्त्तव्यः ___________
(vi) प्र + आप् + तव्यत् ___________
(vii) स्मरणीयः ___________
(viii) हस् + अनीयर् ___________
(ix) लेखनीयम् ___________
(x) प्रच्छ् + तव्यत् ___________
उत्तराणि:
(i) पा + यत्
(ii) देयम्
(iii) सेव् + ण्यन्
(iv) कार्यम्
(v) कृ + तव्यत्
(vi) प्राप्तव्यत्
(vii) स्मृ + अनीयर्
(viii) हसनीयम्
(ix) लिख + अनीयर्
(x) प्रष्टव्यम्

प्रश्न 5.
शुद्धपदेन वाक्यपूर्ति कुरुत-

(i) जलम् ___________ (पातव्यम् / पीतव्यम्)
(ii) पाठ् ___________ (पठितव्यः / पठितव्यम्)
(iii) शत्र ___________ (जेतव्यः / जितव्यः)
(iv) असत्यवचनम् ___________ (त्याज्यम् / त्याज्य:)
(v) अपेयं जलम् ___________ (त्याग्यम् / त्याज्यम्)
(vi) धनम् ___________ (लभ्यम् / लभियम्)
उत्तराणि:
(i) पातव्यम्
(ii) पठितव्ययः
(ii) जेतव्यः
(iv) त्याज्यम्
(v) त्याज्यम्
(vi) लभ्यम्

V.
प्रश्न 1.
उदाहरणमनुसृत्य पदेषु प्रयुक्तान् प्रकृतिप्रत्ययान् लिखत-

उत्तराणि:
क्रमश:
प्रकृतिः-प्रत्ययः
(i) हस् – ल्युट्
(ii) पठ् – ण्वुल्
(iii) खाद् – ण्यत्
(iv) दृश् – ण्यत्
(v) भज् – क्तिन्
(vi) सौभाग्यशाल – इन्
(vii) नी – तृच्
(viii) गै – ण्वुल्

प्रश्न 2.
अधोलिखितप्रत्ययानां प्रयोगेण पञ्च, पञ्च पदानि रयचित्वा-

स्वपुस्तिकासु लिखत- तृच्, क्तिन्, ण्वुल्, ल्युट्, यत्।
उत्तराणि:
तृच – मातृ, गातृ, भर्तु, पठितृ पितृ।
क्तिन् – गतिः, बुद्धिः, मतिः, उक्तिः, श्रुतिः।
ण्वुल् – लेखकः, गायकः, धावकः, पाठकः, पाचकः।
ल्युट – पठनम्, दानम्, लेखनम्, चलनम्, पाणम्।
यत् – देयम्, भव्यम्, श्रव्यम्, चेयम्, नेयम्।

प्रश्न 3.
अधोलिखितवाक्येषु स्थूलपदेषु कः प्रत्ययः प्रयुक्तः इति कोष्ठकेभ्यः चित्वा लिखत-

(i) सज्जनानाम् उक्तिः पालनीया। (ल्युट / क्तिन्) ___________
(ii) सेचकः क्षेत्रं सिञ्चति। (ल्युट / ण्वुल्) ___________
(iii) श्रावकः कथां श्रावयति। (ल्युट / ण्वुल्) ___________
(iv) भक्तः भक्ति करोति। (ण्वुल् / क्तिन्) ___________
उत्तराणि:
(i) क्तिन्
(ii) ण्वुल्
(iii) ण्वुल्
(iv) क्तिन्

प्रश्न 4.
शुद्धरूपं चित्वा लिखत-

(i) गम् + क्तिन् – गति: / गमतिः
(ii) दा + तृच – दातृ / दानी
(iii) नी + ण्वुल् – नाविक: / नायकः
(iv) नृत् + ल्युट – नर्तक: / नर्तनम्
(v) दृश् + ल्युट – दृश्यम् / दर्शनम्
उत्तराणि:
(i) गतिः
(ii) दातृ
(iii) नायकः
(iv) नर्तनम्
(v) दर्शनम्

VI.
प्रश्न 1.
निम्नलिखितप्रयोगान् ध्यानेन पठित्वा स्थूलपदेषु प्रकृति-प्रत्यय विभागं कुरुत-

(i) कालिदासः कीर्तिमान् आसीत्। ___________
(ii) एतौ बालकौ बलवन्तौ स्तः। ___________
(iii) एते जनाः गुणवन्तः सन्ति। ___________
(iv) धनी सर्वत्र समादरं प्राप्नोति। ___________
(v) बलिनौ अन्यायं न सहतः। ___________
(vi) गुणिनः आत्मश्लाघां न कुर्वन्ति। ___________
(vii) पिता आकाशात् श्रेष्ठतरः। ___________
(viii) धरित्री मातृः अपि गंभीरतरा। ___________
(ix) कदलीफलम् आम्रात् मधुरतमम्। ___________
(x) हिमालयः भारतस्य उच्चतमः पर्वतः अस्ति। ___________
उत्तराणि:
(i) कीर्ति + मतुप्
(ii) बल + वतुप्
(iii) गुण + वतुप्
(iv) समादृ + अण्
(v) अ + नी + अण्
(vi) गुण + इनि (इन्)
(vii) श्रेष्ठ + तरप्
(viii) गंभीर + तरप्
(ix) मधुर + तमप्
(x) उच्च + तमप्

प्रश्न 2.
प्रत्ययं संयुज्य पदनिर्माणं कुरुत-

(i) श्री + मतुप ___________
(ii) शक्ति + मतुप् ___________
(iii) धन + वतुप् ___________
(iv) बल + वतुप् ___________
(v) गुरु + तल् ___________
(vi) सुन्दर + मयट ___________
(vii) पटु + तमप् ___________
(viii) मृत् + मयट ___________
(ix) वसुदेव + अण् ___________
(x) धर्म + ठक् ___________
(xi) मित्र + तल् ___________
(xii) विद्वस + त्व
उत्तराणि:
(i) श्रीमान
(ii) शक्तिमान्
(iii) धनवान्
(iv) बलवान्
(v) गुरुता
(vi) सुन्दरमयः
(vii) पटुतमः
(viii) मृण्मयः
(ix) वासुदेवः
(x) धार्मिकः
(xi) मित्रता
(xii) विद्वत्वम्

प्रश्न 3.
कोष्ठके दत्तैः पदैः रिक्तस्थानानि पूरयत-

(i) धर्मेन्द्रः बालाभ्याम् ___________ (प्रशस्यतर:/प्रशस्यतमः)
(ii) ___________ राज्ञः दशरथस्य राजगुरुः आसीत्। (वाशिष्ठः/वशिष्ठः)
(iii) बालिकासु माया ___________ (चतुरतरा/चतुरतमा)
(iv) पाण्डवानाम् ___________ दर्शनीयम् आसीत्। (युद्धकौशलम्/युद्ध कुशलम्)
(v) ___________ आभूषणम् बहुमूल्यं भवति। (स्वर्णमयः/स्वर्णमयम्)
(vi) ___________ आसीत्। (दानव:/दनुजः)
(vii) ___________ जनः औषधि सेवते। (व्याधित:/व्याधिः)
(viii) बालिकासु चंद्रकला ___________ वदति। (मुधरतरम्/मधुरतमम्)
(ix) बालकेषु विजयस्य टङ्कणगतिः नगा उठणगतिः ___________। (तीव्रतरा/तीव्रतमा)
उत्तराणि:
(i) प्रशस्यतरः
(ii) वशिष्ठः
(iii) चतुरतमा
(iv) युद्धकौशलम्
(v) स्वर्णमयम्
(vi) दानवः
(vii) व्याधित:
(viii) मधुरतमम्
(ix) तीव्रतमा

प्रश्न 4.
विशेष्यविशेषणे परस्परं योजयत-

उत्तराणि:

प्रश्न 5.
उदाहरणमनुसृत्य अशुद्धवाक्यानि शुद्धीकृत्य लिखत-

उत्तराणि:
(i) मधुर, तमप्
(ii) तीव्र, तरप्
(iii) वसुदेव, अण्
(iv) कर्म, ठक्
(v) दन्त, यत्
(vi) मृत्, मयट
(vii) पियासा, इतच्
(viii) लघु, तल्
(ix) वीर, तमप्
(x) नदी, तसिल्

प्रश्न 6.
अधोलिखितेषु शब्देषु तसिल्प्रत्ययं संयुज्य वाक्यरचनां कुरुत-

पर्वतः, नगरम्, भूमिः, भानुः, नदी
उत्तराणि:
पर्वतः + तसिल् = पर्वततः – नदी पर्वततः निस्सरति।
नगरम् + तसिल् = नगरतः – यात्री नगरतः गच्छति।
भूमिः + तसिल् = भूमितः – पादपाः भूमितः जायन्ते।
भानुः + तसिल् = भानुतः – प्रकाशः भानुतः भवति।
नदी + तसिल = नदीतः – नदीतः जलं प्राप्नोति।

VII.
प्रश्न 1.
निर्देशानुसारं लिङ्गपरिवर्तनं कुरुत-

(i) बालक ___________ (स्त्री.)
(ii) अराध्या ___________ (पुं.)
(iii) प्रथमा ___________ (पुं.)
(iv) साधक ___________ (स्त्री.)
(v) आचार्या ___________ (पुं.)
(vi) धातृ ___________ (स्त्री.)
उत्तराणि:
(i) बालिकाः
(ii) अराध्यः
(ii) प्रथमः
(iv) साधिका
(v) आचार्यः
(vi) धात्री

अभ्यासः

1. कोष्ठे दत्तान् प्रकृतिप्रत्ययान् योजयित्वा रिक्तस्थानपूर्तिः करणीया-

प्रश्न 1.
सर्वेषां मानवाना सेवा (i) ___________ (कृ + शानच्) वृक्षाः केषां न (ii) ___________ (वन्द + अनीयर)। (iii) ___________ (छाया + वतुप्) वृक्षाः मार्गे श्रान्तपथिकेभ्यः आश्रयं यच्छन्ति। (iv) ___________ (कोकिल + टाप्) च आम्रवृक्षे मधुरस्वरेण गायन्ति। यथा (v) ___________ (फल + इन् ) वृक्षाः नमन्ति तथैव गुणिनः जनाः अपि नमेयुः।
उत्तराणि:
(i) कुर्वाणाः
(ii) वन्दनीयाः
(iii) छायावन्तः
(iv) कोकिलाः
(v) फलिनः (अर्धाङ्ग प्रत्यययोगार्थं अर्धाङ्ग च शुद्धविभक्ति-वचनप्रयोगार्थं निर्धारितम् )।

प्रश्न 2.
(i) मम देशः (शक्ति + मतुप्) ___________ भवेत्।
(ii) जगति (विश्वबन्धु + तल्) ___________ भवेत।
(iii) दीनजनान् (सेव् + शानच्) ___________ जनाः पुण्यं लभन्ते।
(iv) अस्माभिः (वस् + तव्यत्) ___________।
(v) (पवित्र + टाप्) ___________ गङ्गा प्रदूषिता न कर्तव्या।
उत्तराणि:
(i) शक्तिमान्
(ii) विश्वबन्धुता
(iii) सेवमाना:
(iv) उषितव्यम्
(v) पवित्रा।

प्रश्न 3.
(i) विद्यार्थिभिः यथासमयं विद्यालयम् ___________। (गम् + तव्यत्)
(ii) उद्यमस्य ___________ (महत् + त्व) सर्वविदितम् एव।
(iii) ये छात्राः सर्वं वर्ष परिश्रमं कुर्वन्ति तेषा कृते ___________ (वर्ष + ठक् + ङीप्) परीक्षा भयं न जनयति।
(iv) ___________ (बुद्धि + मतुप्) छात्राः पुरुषार्थे विश्वसन्ति न तु केवलं भाग्ये।
(v) त्वम् कर्तव्यनिष्ठः ___________ (अधिकार + इन्) असि।
उत्तराणि:
(i) गन्तव्यम्
(ii) महत्त्वम्
(iii) वार्षिकी
(iv) बुद्धिमन्तः
(v) अधिकारी।

प्रश्न 4.
जानासि अस्माकं विद्यार्थिनां कानि (कृ + तव्यत्) (i) ___________? अस्माभिः विद्यालयस्य अनुशासनं (पाल् + अनीयर्) (ii) ___________। सर्वैः सहपाठिभिः सह (मित्र + तल्) (iii) ___________ आचरणीया। छात्रजीवने परिश्रमस्य (महत् + त्व) (iv) ___________ वर्तते। सत्यम् एव उक्तम्-(सुखार्थ + इन्) (v) ___________ कुतः विद्या?
उत्तराणि:
(i) कर्त्तव्यानि
(ii) पालनीयम्
(iii) मित्रता
(iv) महत्त्वम्
(v) सुखार्थिनः।

प्रश्न 5.
पर्यावरणस्य (महत् + त्व) (i) ___________ कः न जानाति? परं निरन्तरं (वृध् + शानच् ) (ii) ___________ प्रदूषणेन मानवजातिः विविधैः रोगैः आक्रान्ता अस्ति। अस्माभिः (ज्ञा + तव्यत् ) (iii) ___________ यत् पर्यावरणस्य रक्षणे एव अस्माकं रक्षणम्। एतदर्थं (जन + तल्) (iv) ___________ जागरूका कर्तव्या। स्थाने-स्थाने वृक्षारोपणम् अवश्यम् (कृ + अनीयर् ) (v) ___________ यतो हि वृक्षाः पर्यावरणरक्षणे अस्माकं सहायकाः सन्ति।
उत्तराणि:
(i) महत्त्वम्
(ii) वर्धमानेन
(iii) ज्ञातव्यम्
(iv) जनता
(v) करणीयम्।

प्रश्न 6.
(i) आर्यपुत्र! क्षत्रधर्मम् (अनु + स्मृ + शतृ) ___________ मां शोकसागरात् रक्षा।
(ii) जनैः सौन्दर्यमयी सृष्टि: दूषिता न (कृ + तव्यत्) ___________।
(ii) पुस्तकेषु किमपि न (लिख्+ अनीयर्) ___________।
(iv) मनुष्यः (समाज + ठक्) ___________ प्राणी अस्ति।
(v) (धन + मतुप्) ___________ नरः सर्वत्र मानं लभते।
उत्तराणि:
(i) अनुस्मरन्
(ii) कर्त्तव्या
(iii) लेखनीयम्
(iv) सामाजिकः
(v) धनवान्।

प्रश्न 7.
(i) कष्टानि (सह् + शानच्) ___________ वीराः कीर्तिं लभन्ते।
(ii) नमन्ति (फल + इन्) ___________ वृक्षाः।
(iii) (बल + मतुप्) ___________ हि आशा।
(iv) गुरोः (गुरु + त्व) ___________ वर्णयितुं न शक्यते।
(v) प्रकृतेः (रमणीया + तल्) ___________ दर्शनीया अस्ति।
उत्तराणि:
(i) सहमानाः
(ii) फलिनः
(iii) बलवती
(iv) गुरुत्वं
(v) रमणीयता।

प्रश्न 8.
(i) (शिष्य + टाप्) ___________ जलेन लताः सिञ्चति।
(ii) (दान + इन् ) ___________ मानं त्यजेत्।
(iii) (प्रयत् + शानच् ) ___________ जनः साफल्यम् आप्नोति।
(iv) (सप्ताह + ठक्) ___________ अवकाशः रविवारे भवति।
(v) (लौकिक + ङीप) ___________ उन्नतिः यशः वर्धयति।
उत्तराणि:
(i) शिष्या
(ii) दानी
(iii) प्रयतमानः
(iv) साप्ताहिकः
(v) लौकिकी।

प्रश्न 9.
(i) छात्रैः समये विद्यालयः (गम् + तव्यत्) ___________।
(ii) अद्य अस्माकं (वर्ष + ठक् + ङीप्) ___________ परीक्षा आरभते।
(iii) पर्यावरणस्य (महत् + त्व) ___________ सर्वे जानन्ति।
(iv) (बुद्धि + मतुप्) ___________ नरः सर्वत्र मानं लभते।
(v) जनकं (सेव् + शानच् ) ___________ पुत्रः प्रसन्नः अस्ति।
उत्तराणि:
(i) गन्तव्यः
(ii) वार्षिकी
(iii) महत्त्वं
(iv) बुद्धिमान्
(v) सेवमानः।

प्रश्न 10.
(i) नृपेण प्रजाः पाल् + अनीयर ___________।
(ii) आचार्य गुरु + त्व वर्णयितुं न शक्यते ___________।
(iii) पुरस्कारं लभ् + शानच् छात्रः प्रसन्नः भवति ___________।
(iv) मनुष्यः समाज + ठक् प्राणी अस्ति ___________।
(v) प्रकृतेः रमणीय + तल दर्शनीया अस्ति ___________।
उत्तराणि:
(i) पालनीयाः
(ii) गुरुत्वम्
(iii) लभमानः
(iv) सामाजिकः
(v) रमणीयता।

प्रश्न 11.
वानरयूथस्य स्वामी उवाच-जीवितं (i) ___________ (वाञ्छ् + शतृ) नरः कलहयुक्तं गृहं त्यजेत्। तेन तत्र न (ii) ___________ (स्था + तव्यत्)। (iii) ___________ (गुण + इन् ) जनाः कलहकारिभिः जनैः सह (iv) ___________ (मित्र + तल ) न कुर्वन्ति। ते सर्वदा (v) ___________ (धर्म + ठक् + ङीप् ) वृत्तिं धायन्ति।
उत्तराणि:
(i) वाञ्छन्
(ii) स्थातव्यम्
(iii) गुणिनः
(iv) मित्रताम्
(v) धार्मिकीम्।

2. अधोलिखिते कथने स्थूलाक्षरपदानां ‘प्रकृतिम् प्रत्ययम्’ च विभाज्य रिक्तस्थाने लिख्यताम्।

1. एकदा पितरं सेवमानः ___________ पुत्रः तमपृच्छत्-हे पितः! संसारे कः पूज्यते?
2. पिता अवदत्-गुणवान् ___________ सर्वत्र पूज्यते।
3. यः समाज सेवते स वन्दनीयः ___________ भवति।
4. सः सेवायाः महत्त्वं ___________ सम्यक् जानाति।
5. अतः सर्वै मानवतायाः ___________ सेवा।
6. कर्तव्या।
7. भारते अनेकानि दर्शनीयानि ___________ स्थानानि सन्ति।
8. तेषां रमणीयतां ___________ दृष्ट्वा जनाः विस्मताः भवन्ति।
9. परन्तु कश्चित् गुणवान् ___________ एव ऐतिहासिकस्थलाना।
10. महत्त्वं ___________ जानाति। धनी ___________ पुरुषः यत्र-तत्र भ्रमणं कृत्वा वस्तूनां संग्रह करोति।
11. एतेषां स्थानां यात्रा कर्त्तव्या ___________।
12. त्वया सन्तुलितः आहारः कर्तव्यः ___________।
13. तव कृशता ___________ मां तदति।
14. जीवने विद्याः अपि महत्त्वं ___________ वर्तते।
15. तर्हि त्वया सद्ग्रन्थाः अपि पठनीयाः ___________।
16. पठनेन नरः गुणवान् ___________ भवति।
17. किं त्वं जानासि कालस्य महत्त्वम् ___________?
18. कालः तु सततं चक्रवत् परिवर्तमानः ___________ वर्तते।
19. ये जनाः अस्य अस्थिरताम् ___________ अनुभूय वकार्याणि यथासमय।
20. कुर्वन्ति ते एव बुद्धिमन्तः ___________।
21. जनाः वन्दनीयाः ___________ भवन्ति।
22. कार्यं तु सदैव ध्यानेन एव करणीयम् ___________।
23. फलिनः ___________ वृक्षाः एव सदैव नमन्ति।
24. शिक्षायाः महत्त्वं ___________ तु अद्वितीयम् एव।
25. वर्धमानाः ___________ बालाः नयन्ति।
26. अजा ___________ शनैः शनैः चलति।
27. कार्यं सदैव शीघ्रं परन्तु धैर्येण कर्त्तव्यम् ___________।
28. वर्धमाना ___________ बालिका शीघ्रं-शीघ्रं धावति।
29. गुणिनः ___________ जनाः सदैव वन्दनीयाः।
30. वृक्षाणां महत्त्वं ___________ कः न जानाति।
31. कोकिला ___________ मधुरस्वरेण गायति।
32. पुस्तकानाम् अध्ययनम् करणीयम् ___________।
33. मन्त्रिणः ___________ सदसि भाषन्ते।
34. वर्तमाना ___________ शिक्षापद्धतिः सुकरा।
35. त्वं स्व-अज्ञानतां ___________ मा दर्शय।
36. नर्तकी ___________ शोभनं नृत्यति।
37. अस्माभिः सेवकाः पोषणीयाः ___________।
38. पक्षिण: ___________ वृक्षेषु तिष्ठन्ति।
39. पृथिव्याः गुरुत्त्वं ___________ सर्वे जानन्ति।
40. सेवमानाः ___________ सेवकाः धनं लभन्ते।
41. अश्वा ___________ वरं धारयति।
42. बालकैः गुरवः नन्तव्याः ___________
43. कार्यं कुर्वाणाः ___________ छात्राः अङ्कान् लभन्ते।
44. भाग्यशालिनः ___________ जनाः विश्रामं कुर्वन्ति।
45. गायिका ___________ मधुरं गायति।
46. पुस्तकानां महत्तां ___________ कः न जानाति?
उत्तराणि:
1. सेव+ शानच्।
2. गुण + मतुप्।
3. वन्द् + अनीयर।
4. महत् + त्व।
5. मानव + तल्।
6. कृ + तव्यत्।
7. दृश् + अनीयर।
8. रम् + अनीयर् + तल्।
9. गुण + मतुप।
10. महत् + त्व / धन + इन्।
11. कृ + तव्यत् + टाप्।
12. कृ + तव्यत्।
13. कृश + तल।
14. महत् + त्व।
15. पठ् + अनीयर।
16. गुण + मतुप।
17. महत् + त्व।
18. परि + वृत् + शानच्।
19. अस्थिर + तल।
20. बुद्धि + मतुप्।
21. वन्द् + अनीयर।
22. कृ + अनीयर।
23. फल + इन्।
24. महत् + त्व।
25. वृध् + शानच्।
26. अज + टा।
27. कृ+ तव्यत्।
28. वृध् + शानच्।
29. गुण + इन्।
30. महत् + त्व।
31. कोकिल + टाप्।
32. कृ + अनीयर।
33. मन्त्र + इन् (णिनि)।
34. वर्तमान + टाप्।
35. अज्ञान + तल्।
36. नर्तक + ङीप्।
37. पुष (पोष्) + अनीयर।
38. पक्ष + इन्।
39. गुरु + त्व।
40. सेव् + शानच्।
41. अश्व + टाप्।
42. नम् + तव्यम्।
43. कृ + शानच्।
44. भाग्यशाली + इन्।
45. गायक + ङीप्।
46. महत् + तल्।

3. विधिलिङ्ग-क्रियापदस्य स्थाने ‘तव्यत्’ प्रत्ययस्य प्रयोगं कृत्वा पुनः वाक्यानि लेखनीयानि।

उत्तराणि:
(i) विजयया, भोजनम्, कर्त्तव्यम्।
(ii) तेन, गुरुः, नन्तव्यः।
(iii) बालिकाभिः, उद्याने, क्रीडितव्यम्।
(iv) जनैः, प्रधानमन्त्रिकोषे धनं, दातव्यम्।
(v) अस्माभिः, पुस्तकानि, पठितव्यानि।
(vi) युष्माभिः, समाचारपत्राणि, द्रष्टव्यानि।

4. अधः वाक्येषु तव्यत्/अनीयर् प्रत्ययस्य प्रयोगं कृत्वा पुनः तानि लिख्यन्ताम्।
उदाहरणम् सः अत्र प्रवेशं न कुर्यात्।
(क) तव्यत् – तेन अत्र प्रवेशः न कर्तव्यः।
(ख) अनीयर् – तेन अत्र प्रवेशः न करणीयः।

(i) दर्शकाः पशून् न पीडयेयुः।
(क) तव्यत् – _______________________
(ख) अनीयर् – _______________________
(ii) पथिकः बसयानात् हस्तं बहिः न कुर्यात्?
(क) तव्यत् – _______________________
(ख) अनीयर् – _______________________
(iii) गोविन्दः ग्रन्थालये ग्रन्थं उच्चैः न पठेत।
(क) तव्यत् – _______________________
(ख) अनीयर् – _______________________
उत्तराणि:
(i) (क) दर्शकैः पशवः न पीडितव्याः।
(ख) दर्शकैः पशवः न पीडनीयाः।
(ii) (क) पथिकेन बसयानात् हस्तः बहिः न कर्तव्यः।
(ख) पथिकेन बसयानात् हस्तः बहिः न करणीयः।
(iii) (क) गोविन्देन ग्रन्थालये ग्रन्थः उच्चैः न पठितव्यः।
(ख) गोविन्देन ग्रन्थालये ग्रन्थः उच्चैः न पठनीयः।

5. अनीयर् प्रत्ययस्य स्थाने तव्यत् प्रत्ययस्य प्रयोगः करणीयः।

उत्तराणि:
(i) नृपेण, प्रजाः, पालयितव्याः।
(ii) त्वया, धर्मग्रन्थाः, श्रोतव्याः।
(iii) अस्माभिः, अपरेषां गुणाः, एव अनुकर्त्तव्याः।
(iv) कृषकैः, पशवः, स्नेहेन रक्षितव्याः।
(v) छात्रैः प्रातः, उत्थाय ईशः, स्मर्तव्यः।

6. ‘क’ स्तम्भे विशेषणानि ‘ख’ स्तम्भे विशेष्यानि सन्ति तेषां उचितमेलनं करुत।

उत्तराणि:

7. कोष्ठके दत्तानां धातूनां शानच्-प्रत्ययान्त-रूपेण रिक्तस्थानानि पूरयत-

यथा- वन्दमानः स आशिष लभते। (वन्द्)
(i) शनैः ___________ सा वैभवं प्राप्नोति। (वृध् / वर्ध)
(ii) ___________ नक्षत्रैः आकाशः दीव्यति। (प्र + काश्)
(iii) कष्टानि ___________ वीराः कीर्तिं लभन्ते। (सह)
(iv) ___________ वृक्षेभ्यः पुष्पाणि पतन्ति। (कम्प्)
(v) ___________ जनाः साफल्यम् आप्नुवन्ति। (प्र + यत्)
उत्तराणि:
(i) वर्धमाना
(ii) प्रकाशमानैः
(iii) सहमानाः
(iv) कम्पमानेभ्यः
(v) प्रयतमानाः।

8. किं भवन्तः उपर्युक्तपदानामर्थं जानन्ति? पश्यन्तु अत्र, उदाहरणम् च अनुसृत्य रिक्तस्थानं पूरयन्तु-
पदानि अर्थः

उत्तराणि:

9. अधः एतेषां पदानां सम्यक् परिचयम् उदाहरणम् अनुसृत्य लिखत।

उत्तराणि:

10. अधः प्रदत्तशब्दैः सह उदाहरणम् अनुसृत्य ‘इन्’ प्रत्ययं योजयित्वा लिखत-

उत्तराणि:

11. कोष्ठकाद् उचितपदम् आदाय रिक्तस्थानपूर्तिः क्रियताम्-

यथा- अभिमानी मानं न लभते। (अभिमानी / अभिमानिन:)
(i) ___________ सदा सम्मान्याः भवन्ति। (विज्ञानी / विज्ञानिन:)
(ii) ___________ शान्तिम् न प्राप्नोति। (लोभिनः / लोभी)
(iii) ___________ धन्याः लोके। (दानी / दानिनः)
(iv) ___________ विवेकः नश्यति। (क्रोधी / क्रोधिन:)
(v) किं कुलेन विशालेन विद्याहीनस्य ___________ (देही / देहिनः)
(vi) ___________ जनः सर्वप्रियः भवति। (विनोदिनः / विनोदी)
(vii) सर्वे भवन्तु ___________ (सुखी / सुखिनः)
(viii) ___________ इयम् बाला। (व्यवसायी / व्यवसायिनी)
उत्तराणि:
(i) विज्ञानिनः
(ii) लोभी
(iii) दानिनः
(iv) क्रोधिनः
(v) देहिनः
(vi) विनोदी
(vii) सुखिनः
(viii) व्यवसायिनी

12. अधोलिखितेषु वाक्येषु स्थूलाक्षरपदेषु प्रकृति-प्रत्ययविभागं कुरुत-

उत्तराणि:
(i) बल + मतुप् + ङीप्
(ii) उद्योग + इन्
(iii) गुण + इन्
(iv) नीति + ठक् + ङीप्
(v) नीति + मतुप्
(vi) उदार + तल्
(vii) विद्वस् + त्व, नृप + त्व

13. अधोलिखितानां विशेष्याणां विशेषणपदानि कोष्ठकात् चित्वा लिखत-

उत्तराणि:
(i) नैतिकः
(ii) प्रायोगिकः
(iii) मासिकी
(iv) औपचारिकम्
(v) मौलिकी
(vi) प्राकृतिकम्
(vii) प्राथमिकः
(viii) आध्यात्मिकी

14. अधोलिखित-शब्दैः सह ‘त्व’-प्रत्ययम् योजयत-

यथा- पृथु + त्व = पृथुत्वम्
(i) लघु + त्व = ___________
(ii) मनुष्य + त्व = ___________
(iii) विशाल + त्व = ___________
(iv) कवि + त्व = ___________
(v) दीन + त्व = ___________
(vi) क्षत्रिय + त्व = ___________
(vii) वीर + त्व = ___________
(viii) शम + त्व = ___________
उत्तराणि:
(i) लघुत्वम्
(ii) मनुष्यत्वम्
(iii) विशालत्वम्
(iv) कवित्वम्
(v) दीनत्वम्
(vi) क्षत्रियत्वम्
(vii) वीरत्वम्
(viii) शमत्वम्।

15. अधः मञ्जूषायां प्रदत्तैः शब्दैः सह ‘तल्’ प्रत्ययं संयोज्य यथोचितं रिक्तस्थानानि पूरयत।

यथा- क्रूरता तु सदैव निन्दनीया एव भवति।
क्रूर, चञ्चल, दक्ष, स्वच्छ, उष्ण, निर्धन, रमणीय
(i) अपने ___________ शीतकाले रोचते।
(ii) ___________ दु:खदायिनी भवति।
(iii) गृहस्य ___________ आनन्ददायिनी भवति।
(iv) प्रकृतेः ___________ मनोरमा अस्ति।
(v) मनसः ___________ वानरस्य इव भवति।
(vi) गणितविषये अशोकस्य ___________ प्रशंसनीया वर्तते।
उत्तराणि:
(i) उष्णता
(ii) निर्धनता
(iii) स्वच्छता
(iv) रमणीयता
(v) चञ्चलता
(vi) दक्षता

16. ‘त्व’ – ‘तल्’ – प्रत्ययान्तानि पदानि मञ्जूषायाः चित्वा यथोचितम् रिक्तस्थानानि पूरयत-

यथा- पवनस्य शीतलताम् अनुभूय मनः प्रसीदति।
चञ्चलत्वम्, मित्रता, वीरता, महत्त्वम्, पशुत्वम्
(i) विद्यायाः ___________ को न जानाति?
(ii) कृष्णसुदाम्नोः ___________ जगति आदर्श स्थापयति।
(iii) दुष्प्रयुक्ता वाणी मनुष्यस्य ___________ प्रकटयति।
(iv) मनसः ___________ वशीकरणीयम्।
(v) लवस्य ___________ अद्भुता आसीत्।
उत्तराणि:
(i) महत्त्वम्
(ii) मित्रता
(iii) पशुत्वम्
(iv) चञ्चलत्वम्
(v) वीरता

17. अधोलिखिताः सूक्तीः पठित्वा ‘तल्-त्व-प्रत्ययान्तानि पदानि रेखाङ्कितानि कुरुत-

यथा-
(i) ऐश्वर्यस्य विभूषणम् सुजनता।
(ii) न कालस्य अस्ति बन्धुत्वम्।
(iii) अविवेकिता तु अनर्थाय एव भवति।
(iv) अहो! बालकस्य ईदृशी निपुणता।
(v) न अस्ति अमरत्वम् हि कस्यचित् प्राणिनः भुवि।
(vi) क्षणे क्षणे यत् नवताम् उपैति तदेव रूपं रमणीयतायाः।
(vii) विद्वत्वम् च नृपत्वम् च नैव तुल्यम् कदाचन।
उत्तराणि:
(iii) अविवेकता
(iv) निपुणता
(v) अमरत्वम्
(vi) नवताम्, रमणीयतायाः
(vii) विद्वत्वम्, नृपत्वम्।

18. अधोलिखितेषु वाक्येषु स्थूलाक्षरपदानां मूलशब्दं प्रत्ययं च पृथक् कृत्य लिखत-


उत्तराणि:
(i) अनुपम + टाप्
(ii) उज्ज्वल + टाप्
(ii) प्रसन्न + टाप्
(iv) शुभद + टाप्
(v) धन्य + टाप्

19. अधोलिखितेषु वाक्येषु निर्दिष्टशब्दैः सह ‘ङीप्’ प्रत्ययं प्रयुज्य वाक्यानि पूरयत-

यथा- श्रीमती (श्रीमत् + ङीप्) हेमा नाट्योत्सवे दीप प्रज्वालयति।
(i) (कुमार + ङीप) ___________ वन्दना पुष्पगुच्छैः तस्याः स्वागतं करोति।
(ii) एका (किशोर + ङीप्) ___________ भरतनाट्यम् प्रस्तौति।
(iii) तया सह (नृत्यत् + ङीप्) ___________ देविका अस्ति।
(iv) मञ्चे (गायत् + ङीप्) ___________ सधा अस्ति।
(v) (मनोहारिन् + ङीप्) ___________ एषा नाट्यप्रस्तुतिः।
उत्तराणि:
(i) कुमारी
(ii) किशोरी
(iii) नृत्यन्ती
(iv) गायन्ती
(v) मनोहारिणी

20. अधोलिखितेषु वाक्येषु स्थूलाक्षरपदानां मूलशब्दं स्त्रीप्रत्ययं च पृथक्कृत्य लिखत-

उत्तराणि:
(i) तरुण + ङीप्
(ii) कुमार + ङीप्
(iii) एतादृश + ङीप्
(vi) पतत् + ङीप्

21. स्थूलपदानाम् ‘प्रकृतिप्रत्ययः’ पृथक् संयोगो कृत्वा उत्तरपुस्तिकायाम् लिखत।

(स्थूल पदों के प्रकृति-प्रत्यय अलग अथवा संयुक्त करके उत्तर पुस्तिका में लिखिए। Separate or join suffixes in the bold words and write answer in the answer sheet.)
(i) कोकिल + टाप् च आम्रवृक्षे मधुरस्वरेण गायन्ति।
(ii) जगति विश्वबन्धु + तल् भवेत्।
(iii) दीनजनान् सेव् + शानच् जनाः पुण्यं लभन्ते।
(iv) गङ्गा पवित्र + टाप् अतः प्रदूषिता न कर्तव्या।
(v) ये छात्राः सर्वं वर्ष परिश्रमं कुर्वन्ति तेभ्यं वर्ष + ठक् + डीप परीक्षा भयं न जनयति।
(vi) त्वम् कर्तव्यनिष्ठ अधिकार + इन् असि।
(vii) सर्वैः सहपाठिभिः सह मित्र + तल आचरणीया।
(viii) छात्रजीवने परिश्रमस्य महत् + त्व वर्तते।
(ix) परं निरन्तरं वृध् + शानच् प्रदूषणेन मानवजातिः विविधैः रोगैः आक्रान्ता अस्ति।
(x) कष्टानि सह् + शानच् वीराः कीर्तिं लभन्ते।
(xi) गुरोः गुरु + त्व वर्णयितुं न शक्यते।
(xii) प्रकृतेः रमणीय + तल् दर्शनीया अस्ति।
(xiii) शिष्य + टाप् जलेन लताः सिञ्चति।
(xiv) संसारे प्र + यत् + शानच् जनः साफल्यम् आप्नोति।
(xv) लौकिक + ङीप उन्नतिः यश: वर्धयति।
उत्तराणि:
(i) कोकिला:
(ii) विश्वबन्धुता
(iii) सेवमानाः
(iv) पवित्रा
(v) वार्षिकी
(vi) अधिकारी
(vii) मित्रता
(viii) महत्त्वं
(ix) वर्धमानेन
(x) सहमानाः
(xi) गुरुत्वं
(xii) रमणीयता
(xiii) शिष्या
(xiv) प्रयतमानः
(xv) लौकिकी

बहुविकल्पीय प्रश्नाः

1. प्रदत्तेषु उत्तरेषु प्रत्ययानुसारम् विकल्पेषु यत् उत्तरम् शुद्धम् अस्ति तत् चीयताम्।

(दिए गए उत्तरों में से प्रत्यय के अनुसार विकल्पों में से जो उत्तर शुद्ध है, उसे चुनिए। Choose the answer that you consider the most appropriate from the options given below to complete the sentence.)

प्रश्न 1.
कृषकैः पशवः स्नेहेन ___________ (रक्षितव्याः)।
(क) रक्ष् + तव्यत्
(ख) रक्ष् + तव्य
(ग) रक्ष् + तव्यः
(घ) रक्षि + तव्यत्।
उत्तराणि:
(क) रक्ष् + तव्यत्

प्रश्न 2.
पितरः सदैव ___________ (वन्द + अनीयर)।
(क) वन्दनीयः
(ख) वन्दनीयाः
(ग) वन्दनीया
(घ) वन्दनीयम्।
उत्तराणि:
(ख) वन्दनीयाः

प्रश्न 3.
___________ (छाया + मतुप्) वृक्षाः मार्गे श्रान्तपथिकेभ्यः आश्रयं यच्छन्ति।
(क) छायावान्
(ख) छायावन्तः
(ग) छायावन्तम्
(घ) छायावतः।
उत्तराणि:
(ख) छायावन्तः

प्रश्न 4.
यथा ___________ (फल + इन्) वृक्षाः नमन्ति तथैव गुणिनः जनाः अपि नमेयुः।
(क) फली
(ख) फलिनौ
(ग) फलिनः
(घ) फलिनाः।
उत्तराणि:
(ग) फलिनः

प्रश्न 5.
अस्माभिः परस्परं स्नेहेन (वस् + तव्यत्) ___________।
(क) वसितव्यः
(ख) वसितव्या
(ग) वसितव्यम्
(घ) उषितव्यम्।
उत्तराणि:
(घ) उषितव्यम्।

प्रश्न 6.
विद्यार्थिभिः यथासमयं विद्यालयः ___________ ( गम् + तव्यत्)।
(क) गन्तव्यम्
(ख) गन्तव्यः
(ग) गन्तव्या
(घ) गन्तव्याः
उत्तराणि:
(ख) गन्तव्यः

प्रश्न 7.
जानासि, अस्माकं विद्यार्थिनां कानि (कृ + तव्यत्) ___________?
(क) कर्तव्यम्
(ख) कर्तव्यौ
(ग) कर्तव्यानि
(घ) कर्तव्याः
उत्तराणि:
(ग) कर्तव्यानि

प्रश्न 8.
अस्माभिः विद्यालयस्य अनुशासनं (पाल् + अनीयर्) ___________
(क) पालनीयम्
(ख) पालनीयः
(ग) पालनीया
(घ) पालनीयन्ति।
उत्तराणि:
(क) पालनीयम्

प्रश्न 9.
सत्यम् एव उक्तम्, ___________ (सुखार्थ + इन्) कुतः विद्या?
(क) सुखार्थी
(ख) सुखार्थीम्
(ग) सुखार्थिन:
(घ) सुखार्थिने।
उत्तराणि:
(घ) सुखार्थिने।

प्रश्न 10.
जनैः सौन्दर्यमयी सृष्टि: दूषिता न (कृ + तव्यत्) ___________
(क) कर्तव्यः
(ख) कर्तव्यम्
(ग) कर्तव्या
(घ) कर्तव्याः
उत्तराणि:
(ग) कर्तव्या

प्रश्न 11.
पुस्तकेषु किमपि न (लिख + अनीयर) ___________।
(क) लेखनीयः
(ख) लेखनीयम्
(ग) लेखनीया
(घ) लेखनीयाः।
उत्तराणि:
(ख) लेखनीयम्

प्रश्न 12.
मनुष्यः (समाज + ठक्) ___________ प्राणी अस्ति।
(क) सामाजिकः
(ख) सामाजिकी
(ग) सामाजिकम्
(घ) सामाजिकाः।
उत्तराणि:
(क) सामाजिकः

प्रश्न 13.
(बुद्धि + मतुप्) ___________ नरः सर्वत्र मानं लभते।
(क) बुद्धिमत्
(ख) बुद्धिमान्
(ग) बुद्धिमन्तः
(घ) बुद्धिमतः।
उत्तराणि:
(ख) बुद्धिमान्

प्रश्न 14.
नमन्ति (फल + इन्) ___________ वृक्षाः।
(क) फलिनः
(ब) फली
(ग) फलिनौ
(घ) फलिनाः।
उत्तराणि:
(क) फलिनः

प्रश्न 15.
(बल + मतुप) ___________ हि आशा।
(क) बलवान्
(ख) बलवत्
(ग) बलवती
(घ) बलवतः।
उत्तराणि:
(ग) बलवती

प्रश्न 16.
(दान + इन्) ___________ मानं त्यजेत्।
(क) दानिन्
(ख) दानी
(ग) दानिनः
(घ) दनिनीम्।
उत्तराणि:
(ख) दानी

प्रश्न 17.
(सप्ताह + ठक्) ___________ अवकाशः रविवारे भवति।
(क) साप्ताहिक:
(ख) साप्ताहिकी
(ग) साप्ताहिकम्
(घ) साप्ताहिकाः।
उत्तराणि:
(क) साप्ताहिक:

2. स्थूलपदानाम् ‘प्रकृतिप्रत्ययः’ पृथक् संयोगो कृत्वा विकल्पेभ्यः शुद्धं उत्तरं चित्त्वा उत्तरपुस्तिकायाम् लिखत।

(स्थूल पदों के प्रकृति-प्रत्यय अलग अथवा संयुक्त करके विकल्पों से शुद्ध उत्तर को चुनकर उत्तर-पुस्तिका में लिखिए। Separate or join suffixes in the bold words and write answer appropriate from the options given below in the answer sheet.)

प्रश्न 1.
राजसभायाम् मन्त्र + इन् भाषयन्ति।
(क) मन्त्रिन्
(ख) मन्त्रिण:
(ग) मन्त्री
(घ) मन्त्रि।
उत्तराणि:
(ख) मन्त्रिण:

प्रश्न 2.
तया भोजनं पच् + तव्यत्।
(क) पचितव्यम्
(ख) पक्तव्यम्
(ग) पचतव्यम्
(घ) पन्तव्यम्।
उत्तराणि:
(ख) पक्तव्यम्

प्रश्न 3.
नागरिकाः देशम् रक्षन्ति।
(क) नगर + ठक्
(ख) नागर + इक
(ग) नगर + इक्
(घ) नागरि + इक।
उत्तराणि:
(क) नगर + ठक्

प्रश्न 4.
पठनेन नर: गुणवान् भवति।
(क) गुण + वतुप्
(ख) गुण + मत्
(ग) गुण + मतुप्
(घ) गुण + वत्।
उत्तराणि:
(ग) गुण + मतुप्

प्रश्न 5.
ते जनाः वन्दनीयाः भवन्ति।
(क) वद् + अनीयर्
(ख) वन्द् + अनीयर्
(ग) वन्द् + अनीयः
(घ) वन्द + अनीयस्।
उत्तराणि:
(ख) वन्द् + अनीयर्

प्रश्न 6.
कार्यं तु सदैव ध्यानेन एव करणीयम्।
(क) कृ + अनीयर्
(ख) कृ + अणीयर्
(ग) कर् + अनीयर्
(घ) कर् + अणीयम्।
उत्तराणि:
(क) कृ + अनीयर्

प्रश्न 7.
कार्यं सदैव शीघ्रं परन्तु धैर्येण कर्तव्यम्।
(क) कर्त + व्यत्
(ख) कर्तृ + तव्यम
(ग) कृ + तव्यत्
(घ) कृ + त्वयत्।
उत्तराणि:
(ग) कृ + तव्यत्

प्रश्न 8.
पुस्तकानाम् अध्ययनम् करणीयम्।
(क) कर् + अनीयम्
(ख) कृ + अनीयम
(ग) कृ + अनीयर्
(घ) कृ + अनीयत्।
उत्तराणि:
(ग) कृ + अनीयर्

प्रश्न 9.
अस्माभिः सेवकाः पोषणीयाः।
(क) पोष् + अनीयाः
(ख) पोष् + अनीयत्
(ग) पुष् + अनीयर्
(घ) पोष् + अनीयर।
उत्तराणि:
(घ) पोष् + अनीयर।

प्रश्न 10.
बालकैः गुरवः नन्तव्याः।
(क) नम् + तव्यत्
(ख) नम् + तव्याः
(ग) नन् + तव्यत्
(घ) नन् + तव्याः
उत्तराणि:
(क) नम् + तव्यत्

प्रश्न 11.
बालिकाभिः राष्ट्रगीतं ___________ (गै + तव्यत्)
(क) गीतव्यम्
(ख) गातव्यम्
(ग) गैतव्यम्
(घ) गेतव्यम्।
उत्तराणि:
(ख) गातव्यम्

प्रश्न 12.
त्वया शुद्धं जलं पातव्यम्।
(क) पा + तव्यत्
(ख) पा + तव्यम्
(ग) पा + तव्य
(घ) पा + तव्याः
उत्तराणि:
(क) पा + तव्यत्

प्रश्न 13.
मुनिभिः तप: करणीयम्।
(क) कृ + अनीयम्
(ख) कृ + अनीयत्
(ग) कृ + अनीय
(घ) कृ + अनीयर।
उत्तराणि:
(घ) कृ + अनीयर।

प्रश्न 14.
न्यायाधीशेन न्यायः ___________ (कृ + अनीयर्)।
(क) करणीय
(ख) करणीयर्
(ग) करणीयः
(घ) करणीया।
उत्तराणि:
(ग) करणीयः

प्रश्न 15.
भवत्या पाठः लेखनीयः।
(क) लिख् + अनीय
(ख) लिख् + अनीयर्
(ग) लेख् + अनीयर्
(घ) लेख + अनीयम्।
उत्तराणि:
(ख) लिख् + अनीयर्

प्रश्न 16.
अस्माभिः लता आरोपयितव्याः।
(क) आरोप् + तव्यः
(ख) आरुप् + तव्याः
(ग) आ + रोप् + तव्यत्
(घ) आरोप + तव्याः
उत्तराणि:
(ग) आ + रोप् + तव्यत्

प्रश्न 17.
पत्रवाहकेन पत्राणि ___________ (आ + नी + तव्यत्)।
(क) आनीतव्यानि
(ख) आनेतव्यानि
(ग) आनेतव्यम्
(घ) आनेतव्यः।
उत्तराणि:
(ख) आनेतव्यानि

प्रश्न 18.
राज्ञा प्रजाः पालनीयाः।
(क) पाल् + अनीयर्
(ख) पाल् + अनीयाः
(ग) पाल् + अनीयम्
(घ) पालय् + अनीयत्।
उत्तराणि:
(क) पाल् + अनीयर्

प्रश्न 19.
छात्रैः समये विद्यालयः (गम् + तव्यत्) ___________।
(क) गम्तव्यः
(ख) गन्तव्यः
(ग) गन्तव्या
(घ) गन्तव्याः।
उत्तराणि:
(ख) गन्तव्यः

प्रश्न 20.
(बुद्धि + मतुप) ___________ नरः सर्वत्र मानं लभते।
(क) बुद्धिमतः
(ख) बुद्धिमन्तः
(ग) बुद्धिमन्
(घ) बुद्धिमान्।
उत्तराणि:
(घ) बुद्धिमान्।

प्रश्न 21.
नृपेण प्रजाः (पाल् + अनीयर्) ___________।
(क) पालनीया
(ख) पालनीयम्
(ग) पालनीयः
(घ) पालनीयाः।
उत्तराणि:
(घ) पालनीयाः।

प्रश्न 22.
मनुष्यः (समाज + ठक्) ___________ प्राणी अस्ति।
(क) सामाजिकी
(ख) समाजिकी
(ग) समाजिकः
(घ) सामाजिकः।
उत्तराणि:
(घ) सामाजिकः।

प्रश्न 23.
तेन तत्र न ___________ (स्था + तव्यत्)।
(क) स्थातव्यः
(ख) स्थातव्यम्
(ग) स्थातव्या
(घ) स्थातव्याः।
उत्तराणि:
(ख) स्थातव्यम्

प्रश्न 24.
एकदा राजा तं ___________ (बुद्धि + मतुप्) द्रष्टुं-
(क) बुद्धिमान्
(ख) बुद्धिमानं
(ग) बुद्धिमन्तं
(घ) बुद्धिमत।
उत्तराणि:
(ग) बुद्धिमन्तं

प्रश्न 25.
तस्य कुटीरम् ___________ (गम् + तव्यत्) इति निश्चितवान्।
(क) गन्तव्यम्
(ख) गन्तव्यः
(ग) गन्तव्याः
(घ) गन्तव्यत्।
उत्तराणि:
(क) गन्तव्यम्

प्रश्न 26.
तत्र गत्वा तस्य ___________ (दरिद्र + तल्) दूरीकर्तुं सः तस्मै स्वर्णमुद्राः अयच्छत्।
(क) दरिद्रताः
(ख) दरिद्रता
(ग) दरिद्रतम्
(घ) दरिद्रताम्।
उत्तराणि:
(घ) दरिद्रताम्।

प्रश्न 27.
कैयटः अवदत्-धनस्य ___________ (लोभ + इन्) जनाः आसक्ताः भूत्वा दु:खिनः भवन्ति। अतः मम आनन्दं मा नाशयतु इति।
(क) लोभिनः
(ख) लोभी
(ग) लोभिन्
(घ) लोभि।
उत्तराणि:
(क) लोभिनः

प्रश्न 28.
सर्वे एव ___________ (दुःख + इन्) आसन्।
(क) दुःखीः
(ख) दुखिन्
(ग) दुःखी
(घ) दुःखिनः।
उत्तराणि:
(घ) दुःखिनः।

प्रश्न 29.
___________ (कृ + अनीयर्)। एकः अन्यः अवदत्, ‘कः करिष्यति?
(क) करनीयम्
(ख) करणीयम्
(ग) करणीयः
(घ) करणीया।
उत्तराणि:
(ख) करणीयम्

प्रश्न 30.
वयं वाटिकां प्रति गच्छामः। ऋतुराजः वसन्तः ___________ (दृश् + अनीयर्)
(क) दर्शनीयः
(ख) दृशनीयः
(ग) दृशनीयम्
(घ) दर्शनीयम्।
उत्तराणि:
(क) दर्शनीयः

प्रश्न 31.
प्रातःकाले उद्यानस्य शोभा खलु ___________ (दृश + अनीयर)।
(क) दृशनीयः
(ख) दर्शनीया
(ग) दृशनीया
(घ) दर्शनीयः।
उत्तराणि:
(ख) दर्शनीया

प्रश्न 32.
___________ (गुण + इन्) जनाः तेषां सज्जनानाम् आदरं कुर्वन्ति।
(क) गुणि
(ख) गुणिनः
(ग) गुणिनौ
(घ) गुणीः।
उत्तराणि:
(ख) गुणिनः

3. कोष्ठकेषु प्रदत्तान् प्रकृतिप्रत्ययान् योजयित्वा रिक्तस्थान पूर्तिः करणीया।

(कोष्ठक में दिए गए प्रकृति-प्रत्ययों को जोड़कर रिक्त स्थानों की पूर्ति कीजिए। Fill in the blanks by adding suffixes given in the brackets.)

प्रश्न 1.
अध्यापक:- ___________ (बुद्धि + मतुप्) छात्राः! संसारेऽस्मिन् कः श्रेष्ठः?
(क) बुद्धिमन्तः
(ख) बुद्धिमानाः
(ग) बुद्धिवन्तः
(घ) बुद्धिमान्।
उत्तराणि:
(क) बुद्धिमन्तः

प्रश्न 2.
यः ___________ (रूप + मतुप्) नरः भवति जनाः तम् एव श्रेष्ठ मन्यन्ते।
(क) रूपवान्
(ख) रूपमान्
(ग) रूपवानः
(घ) धनमानः।
उत्तराणि:
(क) रूपवान्

प्रश्न 3.
___________ (सदाचार + मतुप्), विवेकी-
(क) सदाचारमान्
(ख) सदाचारवान्
(ग) सदाचारवन्तः
(घ) सदाचारमन्तः।
उत्तराणि:
(ख) सदाचारवान्

प्रश्न 4.
___________ (नीति + मतुप्)
(क) नीतिवान्
(ख) नीतीमान्
(ग) नीतिमान्
(घ) नीतीवान्।
उत्तराणि:
(ग) नीतिमान्

प्रश्न 5.
___________ (चरित्र + मतुप्) च जनः एव सर्वोत्तमः भवति।
(क) चरित्रवान्
(ख) चरित्रवान
(ग) चरित्रमान
(घ) चरित्रमानः।
उत्तराणि:
(क) चरित्रवान्

प्रश्न 6.
यः सत्यवादी ___________ (निष्ठा + मतुप्)
(क) निष्ठावन्तः
(ख) निष्ठावतः
(ग) निष्ठावान्
(घ) निष्ठावान।
उत्तराणि:
(ग) निष्ठावान्

प्रश्न 7.
___________ (विनय + मतुप्)
(क) विनयी
(ख) विनयवान्
(ग) विनयमान्
(घ) विनयवान।
उत्तराणि:
(ख) विनयवान्

प्रश्न 8.
___________ (गुण + मतुप्) श्रेष्ठः च मन्यते।
(क) गुणवान्
(ख) गुणमान्
(ग) गुणवान
(घ) गुणमान।
उत्तराणि:
(क) गुणवान्

प्रश्न 9.
वीराः अभ्युदये ___________ (धैर्य + मतुप्) भवन्ति।
(क) धैर्यवन्तः
(ख) धैर्यवानाः
(ग) धैर्यवताः
(घ) धैर्यमन्तः।
उत्तराणि:
(क) धैर्यवन्तः

4. स्थूलपदानाम् ‘प्रकृतिप्रत्ययः’ पृथक् संयोगो कृत्वा विकल्पेभ्यः शुद्धं उत्तरं चित्त्वा उत्तरपुस्तिकायाम् लिखत।

(स्थूल पदों के प्रकृति-प्रत्यय अलग अथवा संयुक्त करके विकल्पों से शुद्ध उत्तर को चुनकर उत्तर-पुस्तिका में लिखिए। Separate or join suffixes in the bold words and write answer appropriate from the options given below in the answer sheet.)

प्रश्न 1.
पुत्र! तव कृशता मां तुदति।
(क) कृश + तल्
(ख) कृश + ता
(ग) कृश + शत् + आ
(घ) कृ + शता।
उत्तराणि:
(क) कृश + तल्

प्रश्न 2.
विद्यालये बालकाः मोदमानाः पठन्ति।
(क) मोद् + शानच्
(ख) मुद् + शानच्
(ग) मुद् + मानाः
(घ) मुद् + मतुप्।
उत्तराणि:
(ख) मुद् + शानच्

प्रश्न 3.
छात्रैः कथा लेखितव्या।
(क) लिख् + तव्या
(ख) लिख् + तव्यत्
(ग) लिख् + तव्यत् + टाप्
(घ) लेख् + तव्यत्।
उत्तराणि:
(ग) लिख् + तव्यत् + टाप्

प्रश्न 4.
वीरः युद्धयमानः वीरगतिं आप्नोत्।
(क) युद्ध + मानम्
(ख) युध् + मानत्
(ग) युध् + शानच्
(घ) युद्ध + शानच्।
उत्तराणि:
(ग) युध् + शानच्

प्रश्न 5.
देवम् वन्दमानाः ललनाः प्रसीदन्ति।
(क) वन्द + शानच्
(ख) वन्द् + शानच्
(ग) वन्द् + शानच् + टाप्
(घ) वन्द + मानाः।
उत्तराणि:
(ग) वन्द् + शानच् + टाप्

प्रश्न 6.
तत्र जायमानः बालकः कीदृशो भविष्यति?
(क) जा + शानच्
(ख) जन् + शानच्
(ग) ज्ञा + शानच्
(घ) ज्ञान + शानच्।
उत्तराणि:
(ख) जन् + शानच्

प्रश्न 7.
सीता रामेण सह वनं गच्छन्ती आसीत्।
(क) गम् + शतृ + ङीप्
(ख) गम् + ङीप्
(ग) गम् + शतृ
(घ) गम् + शानच् + ङीप्।
उत्तराणि:
(क) गम् + शतृ + ङीप्

प्रश्न 8.
गङ्गा नदी हिमालयात् उद्भवति।
(क) नद् + ङीप्
(ख) नद + इन्
(ग) नद + ङीप्
(घ) नद् + इन।
उत्तराणि:
(ग) नद + ङीप्

प्रश्न 9.
रूपवती भार्या कस्मै न रोचते?
(क) रूपवत + मतुप्
(ख) रूपवत + ङीप्
(ग) रूपवत् + इन्
(घ) रूप + मतुप् + ङीप्।
उत्तराणि:
(घ) रूप + मतुप् + ङीप्।

प्रश्न 10.
जीवने विद्यायाः अपि महत्त्वं वर्तते।
(क) महत् + त्वं
(ख) महत् + त्व
(ग) महत्त्व + मतुप्
(घ) महत्त + त्व।
उत्तराणि:
(ख) महत् + त्व

प्रश्न 11.
ये जनाः अस्य अस्थिरताम् अनुभूय स्वकार्याणि यथासमयं कुर्वन्ति ते एव बुद्धिमन्तः भवन्ति।
(क) अस्थिर + ता
(ख) अस्थिर + तल्
(ग) अस्थिर + टाप्
(घ) अस्थिरता + आ।
उत्तराणि:
(ख) अस्थिर + तल्

प्रश्न 12.
जनाः तीव्र धावन्तः गच्छन्ति।
(क) धाव + अन्तः
(ख) धा + वन्तः
(ग) धाव् + शतृ
(घ) धाव् + शानच्।
उत्तराणि:
(ग) धाव् + शतृ

प्रश्न 13.
गृहं गच्छन्त्यः छात्राः प्रसीदन्ति।
(क) गम् + शतृ
(ख) गम् + शतृ + ङीप्
(ग) गम् + ङीप्
(घ) गम् + शत् + टाप्।
उत्तराणि:
(ख) गम् + शतृ + ङीप्

प्रश्न 14.
कालः सदैव गम्यमानः वर्तते।
(क) गम् + शानच्
(ख) गम् + शतृ
(ग) गम् + मतुप्
(घ) गम् + ठक्।
उत्तराणि:
(क) गम् + शानच्

प्रश्न 15.
किं त्वं जानासि कालस्य महत्त्वम्?
(क) महत् + तव
(ख) महत् + तवं
(ग) महत् + त्वं
(घ) महत् + त्व।
उत्तराणि:
(घ) महत् + त्व।

प्रश्न 16.
आगता पर्वसु प्रिया दीपावलिः।
(क) प्रिय + आ
(ख) प्रिय + आप
(ग) प्रिय + टाप्
(घ) प्रिय + डाप्।
उत्तराणि:
(ग) प्रिय + टाप्

प्रश्न 17.
विपणीनां शोभा अनुपमा भविष्यति।
(क) अनुपम + टाप्
(ख) अनुपम + आप्
(ग) अनुपम + चाप्
(घ) अनुपम + ठक्
उत्तराणि:
(क) अनुपम + टाप्

प्रश्न 18.
धन्या इयं दीपावलिः प्रकाशपुञ्जा।
(क) धन्य् + टाप्
(ख) धन्य + टाप्
(ग) धन्या + टाप्
(घ) धन्या + आ।
उत्तराणि:
(ख) धन्य + टाप्

प्रश्न 19.
मधुरा वाणी प्रीणयति मनः।
(क) मधुर + टाप्
(ख) मधुर + आप्
(ग) मधुर + आ
(घ) मधुर + चाप।
उत्तराणि:
(क) मधुर + टाप्

प्रश्न 20.
कुलागना सदा सम्मानस्य अधिकारिणी।
(क) अधिकारी + ई
(ख) अधिकारी + ङीप्
(ग) अधिकार + इन्
(घ) अधिकार + ई।
उत्तराणि:
(ख) अधिकारी + ङीप्

प्रश्न 21.
सताम् बुद्धिः हितकारिणी भवति।
(क) हितकारिन् + ङीप
(ख) हितकर + ङीप्
(ग) हितकारी + ई
(घ) हितकरी + इन्।
उत्तराणि:
(क) हितकारिन् + ङीप

प्रश्न 22.
नैतिकी शिक्षा आवश्यकी।
(क) नैतिक + ईङ्
(ख) नैतिक + ङीप्
(ग) नैतिक + इन्
(घ) नीति + इक् + इन्।
उत्तराणि:
(ख) नैतिक + ङीप्

प्रश्न 23.
शिक्षायाः महत्त्वं तु अद्वितीयम् एव।
(क) मह + त्वं
(ख) महा + त्वं
(ग) महत् + त्व
(घ) महत् + त्वं
उत्तराणि:
(ग) महत् + त्व

प्रश्न 24.
अजा शनैः शनैः चलति।
(क) अजः + टाप्
(ख) अजा + टाप्
(ग) अजः + आप्
(घ) अजः + आ।
उत्तराणि:
(क) अजः + टाप्

प्रश्न 25.
गुणिनः जनाः सदैव वन्दनीयाः भवन्ति।
(क) गुण + इनः
(ख) गुण + इन्
(ग) गुण + ईन्
(घ) गुणी + इन्।
उत्तराणि:
(ख) गुण + इन्

प्रश्न 26.
कोकिला मधुरस्वरेण गायति।
(क) कोकिल + आप्
(ख) कोकिला + टाप्
(ग) कोकिला + आ
(घ) कोकिलः + टाप्।
उत्तराणि:
(घ) कोकिलः + टाप्।

प्रश्न 27.
फलिनः वृक्षाः एव सदैव नमन्ति।
(क) फल + इन्
(ख) फली + इन्
(ग) फल + इनः
(घ) फल + ङीप्।
उत्तराणि:
(क) फल + इन्

प्रश्न 28.
वर्धमाना बालिका शीघ्रं-शीघ्रं धावति।
(क) वृध् + शानच्
(ख) वृध् + शानच् + टाप्
(ग) वृध् + टाप्
(घ) वृध् + माना।
उत्तराणि:
(ख) वृध् + शानच् + टाप्

प्रश्न 29.
नर्तकी शोभनं नृत्यति।
(क) नृत् + अक् + ई
(ख) नर्तक + ङीप्
(ग) नर्तक + ईङ्।
(घ) नृत् + ङीप्।
उत्तराणि:
(ख) नर्तक + ङीप्

प्रश्न 30.
पृथिव्याः गुरुत्वं सर्वे जानन्ति।
(क) गुरु + त्व
(ख) गुरु + त्वं
(ग) गुरु + त्तवं
(घ) गुरु + त्तव।
उत्तराणि:
(क) गुरु + त्व

प्रश्न 31.
अश्वा वरं धारयति।
(क) अश्व + आ
(ख) अश् + वा
(ग) अश्व + टाप्
(घ) अश्व + टा।
उत्तराणि:
(ग) अश्व + टाप्

प्रश्न 32.
भाग्यशालिनः जनाः विश्रामं कुर्वन्ति।
(क) भाग्यशाली + इनः
(ख) भाग्यशाली + इन्
(ग) भाग्यशाल + इन्
(घ) भाग्यशाली + ईन्।
उत्तराणि:
(ग) भाग्यशाल + इन्

प्रश्न 33.
पुस्तकानां महत्तां कः न जानाति।
(क) महत् + ताम्
(ख) महत् + तल्
(ग) महत् + ताल्
(घ) महत् + ता।
उत्तराणि:
(ख) महत् + तल्

प्रश्न 34.
त्वं मां स्व-अज्ञानतां मा दर्शय।
(क) अज्ञान + ता
(ख) अज्ञान + ताम्
(ग) अज्ञान + तल्
(घ) अज्ञानता + तल्।
उत्तराणि:
(ग) अज्ञान + तल्

प्रश्न 35.
पक्षिण: वृक्षेषु तिष्ठन्ति।
(क) पक्षि + ङीप्
(ख) पक्ष + इन्
(ग) पक्ष् + ईञ्
(घ) पक्ष् + इणः।
उत्तराणि:
(ख) पक्ष + इन्

प्रश्न 36.
कार्यं कुर्वाणाः छात्राः अङ्कान् लभन्ते।
(क) कृ + शानच्
(ख) कृ + शतृ
(ग) कृ + मतुप्
(घ) कृ + टाप्।
उत्तराणि:
(क) कृ + शानच्

प्रश्न 37.
सेवमानाः सेवकाः धनं लभन्ते।
(क) सेव् + मानाः
(ख) सेवमान् + टाप्
(ग) सेव् + शानच्
(घ) सेव् + शत।
उत्तराणि:
(ग) सेव् + शानच्

प्रश्न 38.
दीपिका क्रीडायाम् ___________ (कुशल + टाप्) अस्ति।
(क) कुशलता
(ख) कुशलय
(ग) कुशला
(घ) कुशलताम्।
उत्तराणि:
(ग) कुशला

प्रश्न 39.
प्रभा-दीपिकयोः माता ___________ (चिकित्सक + टाप) अस्ति।
(क) चिकित्सका
(ख) चिकित्सकाः
(ग) चिकित्सकः
(घ) चिकित्सिका।
उत्तराणि:
(घ) चिकित्सिका।

प्रश्न 40.
सा समाजस्य ___________ (सेवक + टाप्) अपि अस्ति।
(क) सेवका
(ख) सेविका
(ग) सेविकः
(घ) सेवकी।
उत्तराणि:
(ख) सेविका

प्रश्न 41.
सा तु स्वभावेन अतीव ___________ (सरल + टाप) अस्ति।
(क) सरलता
(ख) सरला
(ग) सरलटा
(घ) सरलताप।
उत्तराणि:
(ख) सरला

प्रश्न 42.
अद्य अस्माकं (वर्ष + ठक् + ङीप्) ___________ परीक्षा आरभते।
(क) वार्षिकी
(ख) वर्षिकी
(ग) वार्षकी
(घ) वर्षकी।
उत्तराणि:
(क) वार्षिकी

प्रश्न 43.
जनकं (सेव् + शानच्) ___________ पुत्रः प्रसन्नोऽस्ति।
(क) सेववानः
(ख) सेवमानः
(ग) सेव्यमानः
(घ) सेव्यवानः।
उत्तराणि:
(ख) सेवमानः

प्रश्न 44.
पुरस्कारं (लभ् + शानच्) ___________ छात्रः प्रसन्नः भवति।
(क) लभमानः
(ख) लभमानं
(ग) लभमानाः
(घ) लभमाना।
उत्तराणि:
(क) लभमानः

प्रश्न 45.
प्रकृतेः (रमणीय + तल्) ___________ दर्शनीया अस्ति।
(क) रमणीयता
(ख) रमणीयतां
(ग) रमणीया
(घ) रमणीयां।
उत्तराणि:
(क) रमणीयता

प्रश्न 46.
वानरयूथस्य स्वामी उवाच-जीवितं ___________ (वाञ्छ् + शतृ) नरः कलहयुक्तं गृहं त्यजेत्।
(क) वाञ्छत्
(ख) वाञ्छन्
(ग) वाञ्छनः
(घ) वाञ्छद्।
उत्तराणि:
(ख) वाञ्छन्

प्रश्न 47.
ते ___________ (मित्र + तल्) न कुर्वन्ति।
(क) मित्रता
(ख) मित्रता
(ग) मित्रतया
(घ) मित्रताल
उत्तराणि:
(क) मित्रता

प्रश्न 48.
एक कैयटः नाम विद्वान् आसीत्। सः प्रातः ___________ (कृ + शतृ) शास्त्राणाम् अध्ययने रतः भवति स्म।
(क) कुर्वन्
(ख) कुर्वत्
(ग) कुर्वन्तः
(घ) कुर्वद्।
उत्तराणि:
(क) कुर्वन्

प्रश्न 49.
एकस्यां सभायां बहवः मूषकाः चिन्ता ___________ (कृ + शतृ) उपविष्टाः।
(क) कुर्वन्तः
(ख) कुर्वन्
(ग) कुर्वत्
(घ) कुर्वन्ताः।
उत्तराणि:
(क) कुर्वन्तः

प्रश्न 50.
एका वृद्धा ___________ (मूषक + टाप) अवदत्-अस्याः कण्ठे घण्टिकाबन्धनं।
(क) मूषका
(ख) मूषकी
(ग) मूषिका
(घ) मूषिकाम्।
उत्तराणि:
(ग) मूषिका

प्रश्न 51.
पुष्पाणां ___________ (रमणीय + त्व) दृष्ट्वा मनः प्रसन्नं भवति।
(क) रमणीयतां
(ख) रमणीयत्वः
(ग) रमणीयत्वं
(घ) रमणीयत्व।
उत्तराणि:
(ग) रमणीयत्वं

प्रश्न 52.
शीघ्रं शीघ्रं ___________ (चल् + शतृ) जनाः प्रसन्नाः भवन्ति।
(क) चलन्
(ख) चलन्तम्
(ग) चलतः
(घ) चलन्तः।
उत्तराणि:
(घ) चलन्तः।

प्रश्न 53.
ते वायोः ___________ (शीतल + तल्) अनुभवन्ति।
(क) शीतलताः
(ख) शीतलतां
(ग) शीतलता
(घ) शीतलतया।
उत्तराणि:
(ख) शीतलतां

प्रश्न 54.
बालकाः ___________ (बालक + टाप्) च कन्दुकेन क्रीडन्ति।
(क) बालिका
(ख) बालिकाः
(ग) बालिका
(घ) बलिकया।
उत्तराणि:
(ख) बालिकाः

प्रश्न 55.
___________ (आचार्य + टाप्) अपि तेभ्यः क्रुध्यति।
(क) आचार्या
(ख) आचार्यया
(ग) आचार्याम्
(घ) आचार्याः।
उत्तराणि:
(क) आचार्या

प्रश्न 56.
जीवने शिक्षायाः सर्वाधिकं ___________ (महत् + त्व) वर्तते।
(क) महत्त्वः
(ख) महत्त्वो
(ग) महत्त्वं
(घ) महत्तम्।
उत्तराणि:
(ग) महत्त्वं

प्रश्न 57.
परोपकारं ___________ (कृ + शानच्) देशस्य सर्वदा हितम् एव चिन्तयन्ति।
(क) कुर्वाणाः
(ख) कुर्वाणा
(ग) कुर्वाणं
(घ) कुर्वाणः।
उत्तराणि:
(क) कुर्वाणाः

प्रश्न 58.
तस्य क्षितौ ___________ (प्रलुठ् + शतृ) वह्नि-ज्वालाः समुत्थिताः।
(क) प्रलुठताः
(ख) प्रलुठन्
(ग) प्रलुठत्
(घ) प्रलुठतः।
उत्तराणि:
(घ) प्रलुठतः।

प्रश्न 59.
उद्यमस्य ___________ (महत् + त्व) सर्वविदितम् एव।
(क) महत्त्वः
(ख) महत्त्वम्
(ग) महत्त्वा
(घ) महत्त्व।
उत्तराणि:
(ख) महत्त्वम्

प्रश्न 60.
प्रकाशमानः चन्द्रः शोभते।
(क) प्र + काश् + शानच्
(ख) प्रकाश + शानच्
(ग) प्रकाश + मतुप्
(घ) प्रकाश + वतुप।
उत्तराणि:
(क) प्र+ काश् + शानच्

5. अधोलिखितेषु वाक्येषु ‘टाप्’ प्रत्ययान्तानि पदानि चित्वा लिखत-

(‘टाप्’ प्रत्यय युक्त शब्दों को चुनकर लिखिए। Choose and write the ‘Taap’ suffix.)

प्रश्न 1.
अमृतजला इयं गङ्गा पवित्रा।
(क) अमृतजला
(ख) इयं
(ग) गङ्गा
(घ) पवित्रा।
उत्तराणि:
(घ) पवित्रा।

प्रश्न 2.
भक्तैः सदा तु चिरं सेवमाना।
(क) सदा
(ख) भक्तैः
(ग) सेवमाना
(घ) चिरं।
उत्तराणि:
(ग) सेवमाना

प्रश्न 3.
कथं नु एतस्याः शोभा विचित्रा।
(क) कथं
(ख) विचित्रा
(ग) शोभा
(घ) एतस्याः
उत्तराणि:
(ख) विचित्रा

प्रश्न 4.
भागीरथी भवतु मे पूर्णकामा।
(क) मे
(ख) पूर्णकामा
(ग) भवतु
(घ) भागीरथी।
उत्तराणि:
(ख) पूर्णकामा

6. ‘त्व’ – ‘तल्’ – प्रत्ययान्तानि पदानि चित्वा यथोचितं रिक्तस्थानानि पूरयत-

(‘त्व’ – ‘तल’ प्रत्ययान्त पद से रिक्त स्थान भरिए। Fill in the blanks with ‘Twa’- ‘Tal’ suffixes.)

प्रश्न 1.
विद्यायाः ___________ को न जानाति?
(क) वीरता
(ख) महत्त्वम्
(ग) चञ्चलत्वम्
(घ) मित्रता।
उत्तराणि:
(ख) महत्त्वम्

प्रश्न 2.
कृष्णसुदाम्नो: ___________ जगति आदर्श स्थापयति।
(क) वीरता?
(ख) पशुत्त्वम्
(ग) मित्रता
(घ) महत्वम्।
उत्तराणि:
(ग) मित्रता

By going through these CBSE Class 12 Maths Notes Chapter 1 Relations and Functions, students can recall all the concepts quickly.

Relations and Functions Notes Class 12 Maths Chapter 1

RELATION
1. Types of Relations
→ Empty Relation: A relation in a set A is known as empty relation, if no element of A is related to any element of A, i.e., R = Φ ⊆ A × A. e.g.

Let the set A = {1, 2,3,4,5) and R is given by
R= {(a,b): a – b = 20}

There is no pair (a, b) that satisfies the condition
a – b = 20.
⇒ The relation R is the empty relation.

→ Universal Relation: A relation R in a set A is called a universal relation, if each element of A is related to every element of A, i.e.,
R = A × A. e.g.
Let the set A = {1, 2,3, 4,5} and R is given by R = {(a, b): ab > 0}
Here, R = {(a, b): ab > 0} is the whole set A × A as all pairs (a, b) in A × A satisfy ab > 0.
Thus, this is the universal relation.

→ A relation R in a set A is called
(a) reflexive: if (a, a) ∈ R for every a ∈ A.
(b) symmetric: ii (a, b) ∈ R implies that (b, a) ∈ R for all a, b ∈ A.
(c) transitive: if (a, b) ∈ R and (b, c) e R implies that (a, c) ∈ R for all a,b,c ∈ A.

→ Equivalence Relation: A relation R in A is an equivalence relation if R is reflexive, symmetric, and transitive. For example:
(1) Let T be the set of all triangles in a plane with R a relation in T given by
R = ((T₁, T₂): T₁ is similar to T₂)
(a) R is reflexive since every triangle is similar to itself.

(b) (T₁, T₂) ∈ R ⇒ T₁ is similar to T₂.
(T₂, T₃) ∈ R ⇒ T₂ is similar to T₁
Therefore, R is symmetric.

(c) (T₁, T₂) and (T₂, T₃) lies in R
⇒ T₁ is similar to T₂ and T₂ is similar to T₃, which means T₁ is similar to T₃,
i.e., (T₁, T₃) lies in R.
∴ R is transitive.
Now R is reflexive, symmetric, and transitive, therefore R is an equivalence relation.

(2) Consider the set A = {1,2,3,4} and the relation R = {(1,1), (2, 2), (3,3), (4, 4), (1, 2), (2, 3), (3, 4)}.
(a) Now (1,1), (2, 2), (3, 3), (4, 4) lie in R. Relation R is reflexive.
(b) (1, 2) lies in R but (2,1) does not lie in it.
∴ It is not symmetric.
(c) (1,2), (2, 3) lie in R but (1, 3) does not lie in it. Therefore, R is not transitive.
Here, R is reflexive but neither symmetric nor transitive. Therefore, R is not an equivalence relation.

2. Equivalence Class [a] containing a
For an arbitrary equivalence relation R in an arbitrary set X, R divides X into mutually disjoint subsets A_i, which are known as partitions or sub-divisions of X satisfying:
(a) All elements of A_i are related to each other for all i.
(b) No element of A_i is related to any element of A_j, i ≠ j.
(c) ∪ A_j = X and A_i ∩ A. = Φ, i ≠ j.

The subsets Af are said to be equivalence classes.
Example: Let R be the relation defined in the set A = {p, q, s, t, e, o, u} by
R = {(a, b): both a and b are either consonants or vowels,
Here, R is an equivalence relation.
(a) Any element ∈ A is either consonant or vowel,
i.e., (a, a) ∈ R ⇒ R is reflexive.

(b) If (a, b) ∈ R ⇒ a and b both are either consonants or vowels ⇒ (b, a) e R.
∴ R is symmetric.

(c) If (a, b) ∈ R and (b, c) ∈ R, then a, b; b, c both pairs are either consonants or vowels.
i.e., a, b, c all are either consonants or vowels.
⇒ (a, c) ∈ R.
∴ R is transitive.
Thus, R is an equivalence relation.

Further, all the elements of (p, q, s, t) are related to each other as all the elements of this subset are consonants.

Similarly, all the elements of {e, i, o, u } are related to each other as all of them are vowels. But no element of {p, q, s, t} can be related to any element of {e, i, o, u}, since the elements of {p, q, s, t} are all consonants and the elements of {e, i, o, u} are all vowels. {p, q, s, t} is an equivalence class.denoted by an element as {p}. Similarly, {e, i, o, u} is an equivalence class denoted by an element [e).

FUNCTIONS
1. Types of Functions
→ One-one (or Injective): A function f: X → Y is said to be one-one (or injective), if the images of the distinct elements of X under/are distinct, i.e., for every x₁, x₂ ∈ X, if f(x₁) = f(x₂) implies that x₁ = x₂.

Each element of X has a distinct image in Y. Such a function or a mapping is one-one.

→ Onto (or surjective): A function f: X →Y is called onto, if every element of Y is the image of some element of X under f, i.e., for all y ∈ Y, there exists an element x in X such that f(x) = y.

Corresponding to each element of Y, there is a pre-image in X. Such a mapping is onto.

→ One-one and Onto (Bijective): A function f: X to Y is known as one-one and onto (or bijective), if f is both one-one and onto.

Here,f is both one-one and onto. Therefore,f is said to be one-one onto function or bijective function.

2. Composition of Functions
Let f: A → B and g: B → C be the two functions. The composition of f and g is defined as. gof: A → C, such that
gof(x) = g{f(x)}, for all x ∈ A.

A function f: X → Y is said to be invertible if there exists a function g: Y → X such that gof = I_x and fog = I_y. The function g is called the inverse of f. It is denoted by f^-1.

Inverse or composite function: If f: X →Y and g: Y → Z be the two invertible functions, then gof is also invertible such that (gof)^-1 = f^-1og^-1

BINARY OPERATION
→ Binary Operation: A binary operation on a set A is a function X: A × A → A, defined by × (a,b) = a × b, e.g., ×: R × R → R is given by (a, b) → a + b. Here +, — and x are the functions but + : R × R →, R, written as (a, b) → \(\frac{a}{b}\) is not a function. It is not a binary operation, since it is not defined for b = O.

→ Commutative Binary Operation: A binary operation × on the set A is commutative,if for every a,b ∈ A, a × b = b × a.

→ Associative Binary Operation: A binary operation × on the set A is associative, if (a × b) × c = a × (b × c).
It may be noted that associative property, a × b × c × d, … is not defined unless brackets are used.

→ An Identity Element e for Binary Operation: Let ×: A × A → A be a binary operation. There exists an element e ∈ A such that a × e = a = e × a, for all a ∈ A.

The element e is known as the identity element. It should be noted that 0 is the identity element for addition but not for natural numbers N, since 0 ∉ N.

→ The inverse of an element a: Let ×: A × A → A be a binary operation with identity element e in A. An element a ∈ A is invertible w.r.t. binary operation ×, if there exists an element b in A such that a × b = e = b × a. The element b is said to be the inverse of a. It is denoted by a^-1, e.g.,

– a is the inverse of a for the operation of addition +.
\(\frac{1}{a}\) (a ≠ 0) is the inverse of a for multiplication.

1. RELATIONS

(i) Relation. A relation R from a set A to a set B is a subset of A x B.

(ii) Classification of Relations : a
(a) Reflexive Relation. A relation R in a set E is said to be reflexive if xRx ∀ x ∈ E.
(b) Symmetric Relation. A relation R in a set E is said to be symmetric if:
xRy = yRx ∀ x, y ∈ E.
(c) Transitive Relation. A relation R in a set E is said to be transitive if:
vRy and yRz ⇒ xRz ∀ x, y, z ∈ E.
(d) Equivalence Relation. A relation R in a set E is said to be an equivalence relation if it is :

• reflexive
• symmetric and
• transitive.

2. FUNCTIONS

(i) Let X and Y be two non-empty sets. Then ‘f’ is a rule, which associates to each element x in X . a unique element y in Y.
(a) The unique element y of Y is called the value of f at x.
(b) The element x of X is called pre-image of y.
(c) The set X is called the domain of f
(d) The set of images of elements of X under f is called the range of f.

(ii) (a) D_f = {x : x ∈ R, f(x) ∈ R}
(b) R_f = {f(x):x ∈ D_f}
(c) f is one-one iff x₁ = x₂
⇒ f(x₁) = f(x₂) for x₁, x₂ ∈ D_f
or iff x₁ ≠ x₂
⇒ f(x₁) ≠ f(x₂) for x₁, x₂ ∈ D_f
(d) f is invertible iff f is one-one onto and D_f^-1 = R_f, R_f^-1= DR_f.

3. ALGEBRA OF FUNCTIONS

Let f and g be two functions. Then
(i) (f+g) (x) =f(x) + g(x); D_f+g = D_f ∩ D_g
(ii) (f- g) (x) = f(x) – g(x); D_f-g = D_f ∩ D_g
(iii) (fg) (x) =f(x) g(x); D_fg = D_f ∩ D_g
(iv) \(\left(\frac{f}{g}\right) x=\frac{f(x)}{g(x)}\); D_f/g = D_f ∩ D_g – {x:x∈D_g, g(x) = 0}

We have given detailed NCERT Solutions for Class 10 Sanskrit Grammar Book समयलेखनम् Questions and Answers come in handy for quickly completing your homework.

Sanskrit Vyakaran Class 10 Solutions समयलेखनम्

अभ्यास:

प्रश्न 1.
भवान् ग्रीष्मावकाशे दिल्लीतः प्रयागराजम् गन्तुम् इच्छति, तत्र किं किं रेलयानम् कतिवादने गच्छति इति अधः घटिकां दृष्ट्वा तत्प्रस्थानकालम् रिक्तस्थाने निर्दिशत-

यथा-
7:15 A.M.

‘पुरी एक्सप्रेस’ प्रातः पादोनसप्तवादने।

8:00 A.M.

(i) ‘कालका मेल’ प्रातः __________ वादने।

3:30 P.M.

(ii) ‘जनता एक्सप्रेस’ अपराह्ने __________ वादने।

9:30P.M.

(iii) ‘प्रयागराज-एक्सप्रेस’ रात्री __________ वादने।

10:15 P.M.

(iv) ‘दिल्ली-हावड़ा मेल’ रात्रौ __________ वादने।
उत्तराणि:
(i) अष्ट
(ii) सार्धत्रि
(iii) सार्ध नव
(iv) सपाद-दश।

प्रश्न 2.
भवतः विद्यालये बालसभा अस्ति। तत्र कः कार्यक्रमः कतिवादने भविष्यति इति घटिकां दृष्ट्वा रिक्तस्थाने लिखत।

यथा-
7:30

प्रातः सार्धसप्तवादने सरस्वती प्रार्थना गीतानि च।

7:45

(i) प्रात: __________ वाद-विवाद प्रतियोगिताया: उद्घाटनम्।

8:00

(ii) __________ वादने निर्णायकैः टिप्पणयः।

11:15

__________ वादने प्राचार्येण निर्णस्य घोषणा।

11:30

(iv) ततः __________ वादने धन्यवाद्-ज्ञापनम्।
उत्तराणि:
(i) पादोन-अष्टवादने
(ii) अष्टवादने
(iii) सपाद-एकादश-वादने
(iv) सार्धएकादशवादने।

प्रश्न 3.
भवतः विद्यालयस्य वार्षिकोत्सवः अस्ति। तत्र कः कार्यक्रमः कतिवादने भविष्यति इति समयं दृष्ट्वा रिक्तस्थाने लिखत।

यथा-
9:00

प्रातः नववादने अतिथीनां स्वागतम्।

9:15

(i) प्रातः __________ वादने सरस्वती-वन्दना।

9:30

__________ वादने सांस्कृतिक-कार्यक्रमः।

10:45

(iii) प्रात: __________ वादने प्रधानाचार्येण वार्षिकविवरणस्य प्रस्तुतीकरणम्।

11:00

(iv) प्रातः __________ मुख्यातिथिना पुरस्कारवितरणम्।
उत्तराणि:
(i) सपादनववादने
(ii) सार्धनववादने
(iii) पादोन-एकादशवादने
(iv) एकादशवादने।

प्रश्न 4.
कोष्ठके दत्तं समयं संस्कृतेन लिखत यत् तव पितामही कदा किं कार्यं करोति-

यथा-
(9:00) – मम पितामही रात्रौ नववादने स्वपिति।
(5:00) – (i) सा प्रातः __________ वादने उत्तिष्ठति।
(6:30) – (ii) __________ वादने ईशवन्दनां करोति।
(2:15) – (iii) यदा अहम् __________ वादने विद्यालयतः आगच्छमि सा मया सह भोजनं करोति।
(2:45) – (iv) __________ वादने विश्राम करोति।
उत्तराणि:
(i) पञ्च
(ii) सार्धषड्
(iii) सपादद्वि
(iv) पादोनत्रि।

प्रश्न 5.
भवतः विद्यालयस्य संस्कृतश्लोकोच्चारण-प्रतियोगिता अस्ति। तत्र कः कार्यक्रमः कतिवादने भविष्यति इति कोष्ठके दत्तम् संस्कृतेन समयं रिक्तस्थाने लिखत-

यथा-
(9:30) – सार्धनववादनपर्यन्तम् सर्वे प्रतियोगिनः सभागारे उपस्थिताः भविष्यन्ति।
(10:15) – (i) प्रात: __________ वादने दीपप्रज्वालनं सरस्वतीवन्दना च।
(10:30) – (ii) प्रातः __________ वादने श्लोकप्रतियोगितायाः उद्घाटनम्।
(12:45) – (iii) प्रातः __________ निर्णस्य घोषणा।
(1:00) – (iv) प्रातः __________ पुरस्कारवितरणम् धन्यवादज्ञापनम् च।
उत्तराणि:
(i) सपाददश
(ii) सार्धदश
(iii) पादोन-एकवादने
(iv) एकवादने।

प्रश्न 6.
दूरदर्शने संस्कृतस्य कार्यक्रमः भाषामन्दाकिनी-चैनले प्रातः सार्धषड्वादने (6.30) प्रारभते। एकस्मिन् दिने कार्यक्रमः इत्थं प्रकाशितः समयं दृष्ट्वा रिक्तस्थानपूर्तिं कृत्वा वाक्यानि पुनः लिखत-
7:00

(i) प्रातः __________ वादने “शिक्षकः” तस्य रचनात्मकता च।

7:15

(ii) __________ वादने ‘काव्यानि’।

7:45

(iii) प्रातः __________ वादने ‘आलेख-लेखनम्’।

8:30

(iv) प्रातः __________ वादने कार्यक्रमः समाप्तः भविष्यति।
उत्तराणि:
(i) सप्त
(ii) सपादसप्त
(iii) पादोनाष्ट
(iv) सार्धाष्ट।

प्रश्न 7.
एकदा अस्माकं विद्यायालये क्षेत्रीय-स्तरकाव्यालिः प्रतियोगिता आयोजिता। अधः समयं दृष्ट्वा शब्देषु समयं लिखित्वा कार्यक्रमं पुनः उत्तरपुस्तिकायां लिखत।

9:30

(i) पञ्जीकरणं प्रातः __________ प्रारभत।

10:15

(ii) काव्यालिप्रतियोगिता __________ आरभत।

11:45

(iii) चायपानं __________ अभवत्।

1:00

(iv) __________ प्रतियोगिता समाप्ता जाता।
उत्तराणि:
(i) सार्धनववादने
(ii) सपाददशवादने
(iii) पादोन-द्वादशवादने
(iv) एकवादने।

प्रश्न 8.
दूरदर्शने चैनले विविध-समाचाराणां प्रसारणसमयः लिखितः। समय-सारिणीं दृष्ट्वा रिक्तस्थानपूर्ति कृत्वा उत्तरपुस्तिकायां लिखत-
दूरदर्शनस्य समाचाराणां समयसारिणी

(i) उर्दूसमाचाराः __________ वादने प्रसार्यन्ते।
(ii) समय सारिणी-अनुसारं संस्कृतसमाचाराणां प्रसारणं __________ वादने भवति।
(iii) हिन्दीसमाचाराः __________ वादने प्रसारिताः भवन्ति।
(iv) आंग्लसमाचाराणां प्रसारणसमयः __________ वादने अस्ति।
उत्तराणि:
(i) पादोनत्रि
(ii) दश
(iii) सार्ध-अष्ट
(iv) सपादति।

प्रश्न 9.
घटिकां दृष्ट्वा रिक्तस्थानेषु लिखत, विकासः कदा किं-किं करोति?

यथा-

विकासः प्रातः सार्धचतुर्वादने उत्तिष्ठति।

(i) सः नित्यं __________ वादने भ्रमणाय गच्छति।

(ii) सः प्रातः __________ वादने विद्यालयं गच्छति।

(iii) विकासः __________ वादने विद्यालयात् आगच्छति।

(iv) सः रात्रौ __________ वादने स्वपिति।
उत्तराणि:
(i) पञ्च
(ii) सार्धसप्त
(iii) सपाद एक
(iv) दश।

प्रश्न 10.
घटिकां दृष्ट्वा लिखत, अनिलः कदा किं-किं आचरति?

(i) सः प्रातः __________ वादने व्यायाम करोति।

(ii) सः __________ वादने विद्यायालयं गच्छति।

(iii) सः __________ वादने गृहम् आगच्छति।

(iv) अनिलः सायं __________ वादने उद्याने क्रीडति।
उत्तराणि:
(i) षट्
(ii) अष्ट
(ii) सार्धत्रि
(iv) पञ्च।

प्रश्न 11.
घटिकां दृष्ट्वा रिक्तस्थानेषु लिखत, मोहितः कदा किं-किं करोति?

यथा-

मोहितः साय: पञ्चवादने क्रीडति।

(i) सः प्रातः __________ वादने उत्तिष्ठति।

(ii) सः __________ वादने प्रातराशं करोति।

(iii) सः __________ वादने विद्यायालयात् आगच्छति।

(iv) सः __________ वादने गृहकार्यं करोति।
उत्तराणि:
(i) षड्
(ii) सार्धअष्ट
(iii) सार्धद्वि
(iv) चतुर्।

प्रश्न 12.
घटिकां दृष्ट्वा रिक्तस्थानेषु लिखत, सुधा कदा किं-किं करोति?

यथा-

सुधा सायं षड्वादने क्रीडति।

(i) सा नित्यं __________ वादने उत्तिष्ठति।

(ii) सा प्रातः __________ वादने भ्रमणाय गच्छति।

(iii) सा __________ वादने विद्यालयं गच्छति।

(iv) सा __________ वादने विद्यायालयात् आगच्छति।
उत्तराणि:
(i) पञ्च
(ii) सार्धपञ्च
(iii) अष्ट
(iv) द्वि।

प्रश्न 13.
उदाहरणानुसारं समयं दृष्ट्वा लिखत यत् रेलयानं कतिवादने प्रस्थानं करिष्यति-

यथा-

12:15 P.M. (मध्याह्न) यथा-मध्याह्ने सपादद्वादशवादने।
(i)

4:15 P.M. (मध्याह्ने) मध्याह्ने __________ वादने।

(ii)

7:00 A.M. (प्रात:) प्रातः __________ वादने।

(iii)

1:30 P.M. (मध्याह्न) मध्याह्ने __________ वादने।

(iv)

10:45 A.M. (प्रातः) प्रातः __________ वादने।

(v)

2:30 P.M. (मध्याह्ने) मध्याह्ने __________ वादने।

(vi)

8:00 A.M. (प्रात:) प्रातः __________ वादने।

(vii)

1:15 P.M. (मध्याह्न) मध्याह्ने __________ वादने।

(viii)

10:30 A.M. (प्रातः) प्रातः __________ वादने।
उत्तराणि-
(i) सपादचतुर्
(ii) सप्त
(iii) सार्ध-एक
(iv) पादोन-एकादश।
(v) सार्ध-द्वि
(vi) अष्ट
(vii) सपाद-एक
(viii) सार्ध-दश।

प्रश्न 14.
उदाहरणानुसारं समयं दृष्ट्वा लिखत, यत् बसयानं कति वादने प्रस्थानं करिष्यति-

यथा-

9:30 A.M. (प्रातः)प्रातः सार्धनव वादने। – उदाहरणम्

(i)

5:15 A.M. (प्रातः) प्रातः __________ वादने।

(ii)

11:00 P.M. (सायम्) सायम् __________ वादने।

(iii)

3:45 P.M. (सायम्) सायम् __________ वादने।

(iv)

8:00 P.M. (सायम्) सायम् __________ वादने।
उत्तराणि:
(i) सपाद पञ्च
(ii) एकादश
(iii) पादोनचतुर्
(iv) अष्ट।

प्रश्न 15.
उदाहरणानुसारं समयं दृष्ट्वा स्वदिनचर्यां वर्णय-

यथा-
6:00 A.M. (प्रातः)

प्रातः षड्वादने शय्या त्यजामि। – उदाहरणम्

7:15 A.M. (प्रातः)

(i) प्रात: __________ वादने विद्यायालयम् गच्छामि।

12:45 P.M. (मध्याह्न)

(ii) मध्याह्ने __________ वादने विद्यायालयात् गृहम् आगच्छामि।

2:30 P.M. (मध्याह्ने)

(iii) मध्याह्ने __________ वादने क्रीडायै गच्छामि।

9:00 P.M. (रात्रौ)

(iv) रात्रौ __________ वादने भोजनं करोमि।
उत्तराणि:
(i) सपाद-सप्त
(ii) पादोन एक
(iii) सार्धद्वि
(iv) नव।

प्रश्न 16.
उदाहरणानुसारं समयं दृष्ट्वा लिखत, यत्क्रीडायाः आरंभः कदा भविष्यति?

यथा- 11:15 A.M. (प्रातः)

यथा-प्रातः एकादश वादने।

1:30 P.M. (मध्याह्ने)

(i) मध्याह्ने __________ वादने।

2:45 P.M. (अपराह्ने)

(ii) अपराह्ने __________ वादने।

4:00 P.M. (सायम्)

(iii) सायम् __________ वादने।

9:15 P.M (रात्रौ)

(iv) रात्रौ __________ वादने।
उत्तराणि:
(i) सार्ध-एक
(ii) पादोन त्रि
(iii) चतुर्
(iv) सपादनव।

प्रश्न 17.
अधः घटिका दृष्ट्वा संस्कृतभाषया समयं पूरयित्वा कार्यक्रमम् उत्तरपुस्तिकायां लिखत-

(i) विद्यालये मुख्यातिथिः __________ वादने आगमिष्यति।

(ii) __________ वादने पुष्पगुच्छै: मुख्यातिथेः स्वागतं भविष्यति।

(iii) __________ वादने सांस्कृतिककार्यक्रमः आरप्स्यते।

(iv) __________ वादने मुख्यतिथिः पुरस्कारवितरणं करिष्यति।
उत्तराणि:
(i) दश
(ii) सपाद दश
(iii) पादोन एकादश
(iv) सार्धद्वादश।

प्रश्न 18.
अधः समयं दृष्ट्वा समयं लिखत यत् मैट्रोरेलयानं कतिवादने कुत्र तिष्ठति?
9:00 बजे

(i) मैट्रोरेलयानं __________ वादने शाहदरा मैट्रोरेलयाने तिष्ठति।

10:15 बजे

(ii) एतत् __________ वादने कशमीरीगेटे आगच्छति।

10:30 बजे

(iii) __________ वादने तीसहजार्याम् आगच्छति।

11:45 बजे

(iv) एतत् __________ वादने रिठालारेलयानस्थाने आगमिष्यामि।
उत्तराणि:
(i) नव
(ii) सपाददश
(iii) सार्धदश
(iv) पादोन-द्वादश।

प्रश्न 19.
विद्यालयस्य समयसारिणम् उचित समयवादकैः पदैः पूरयित्वा लिखत-

(i) 7:30 प्रातः
प्रातः __________ वादने प्रार्थना।
(ii) 10:00 प्रातः
प्रातः __________ अर्धावकाशः।
(iii) 10:15 प्रातः
प्रातः __________ वादने पञ्चमः कालांशः।
(iv) 12:45 मध्याह्ने
मध्याह्ने __________ वादने पूर्णः अवकाशः।
उत्तराणि:
(i) सार्ध-सप्त
(ii) दशवादने
(iii) सपाददश
(iv) पादोनैक।

प्रश्न 20.
अधोलिखितवाक्येषु अङ्कानां स्थाने संस्कृतपदेषु समयं लिखत-

प्रश्न 1.
(i) उर्दूसमाचाराः (2.45) __________ वादने प्रसार्यन्ते।
(ii) समयसारिणी-अनुसारं संस्कृतसमाचाराणां प्रसारणं (10.00) __________ वादने भवति।
(iii) हिन्दी समाचाराः (8.30) __________ वादने प्रसारिताः भवन्ति।
(iv) आंग्लसमाचाराणां प्रसारणसमयः (2.15) __________ वादने अस्ति।
(v) सः प्रातः (6.00) __________ वादने व्यायाम करोति।
(vi) सः (8.00) __________ वादने विद्यालयं गच्छति।
(vii) सः (3.30) __________ वादने गृहम् आगच्छति।
(viii) अनिलः सायं (5.00) __________ वादने उद्याने क्रीडति।
(ix) सा नित्यं (5.00) __________ वादने उत्तिष्ठति।
(x) सः प्रातः (5.30) __________ वादने भ्रमणाय गच्छति।
(xi) सा (8.00) __________ वादने विद्यालयं गच्छति।
(xii) सा (2.00) __________ वादने विद्यालयात् आगच्छति।
(xiii) मध्याह्ने (4.15) __________ वादने।
(xiv) प्रातः (5.00) __________ वादने।
(xv) मध्याह्ने (1.30) __________ वादने।
(xvi) प्रातः (10.45) __________ वादने।
(xvii) मध्याह्ने (2.30) __________ वादने आन्ध्रप्रदेश एक्सप्रेस।
(xviii) प्रातः (8.00) __________ वादने महामाया एक्सप्रेस।
(xix) मध्याह्न (1.15) __________ वादने गोमती एक्सप्रेस।
(xx) प्रातः (10.45) __________ वादने पंजाब एक्सप्रेस।
(xxi) मध्याह्ने (1.30) __________ वादने।
(xxii) अपराह्ने (2.45) __________ वादने।
(xxiii) सायम् (4.00) __________ वादने।
(xxiv) रात्रौ (9.15) __________ वादने।
उत्तराणि:
(i) पादोनत्रयो
(ii) दश
(iii) सार्धअष्ट
(iv) सपादद्वि
(v) षड्
(vi) अष्ट
(vii) सार्धत्रयो,
(viii) पञ्च
(ix) पञ्च
(x) सार्धपञ्च
(xi) अष्ट
(xii) द्वि
(xiii) सपादचतुर्
(xiv) पञ्च
(xv) सार्धएक
(xvi) पादोनएकादश।
(xvii) सार्धद्वि
(xviii) अष्ट
(xix) सपादएक
(xx) पादोनएकादश
(xxi) सार्ध एक
(xxii) पादोनत्रि
(xxiii) चतुर्
(xxiv) सपादनव

प्रश्न 2.
(i) विद्यालये मुख्यातिथि: (10.00) __________ वादने आगमिष्यति।
(ii) (10.15) __________ वादने पुष्पगुच्छै: मुख्यातिथेः स्वागतं भविष्यति।
(iii) (10.45) __________ वादने सांस्कृतिक कार्यक्रमः आरप्स्यते।
(iv) (12.30) __________ वादने मुख्यातिथिः पुरस्कारवितरणं करिष्यति।
उत्तराणि:
(i) दश
(ii) सपाददश
(iii) पादोनएकादश
(iv) सार्धद्वादश

प्रश्न 3.
(i) 7.30 प्रातः __________ वादने प्रार्थना।
(ii) 10.00 प्रातः __________ अर्धावकाशः।
(iii) 10.15 प्रातः __________ वादने पञ्चमः कालांशः।
(iv) 12.45 मध्याह्ने __________ वादने पूर्णः अवकाशः।
उत्तराणि:
(i) सार्धसप्त
(ii) दशवादने
(iii) सपाददश
(iv) पादोनएक

प्रश्न 4.
(i) सायं 7.30 __________ वादने सामुदायिकभवने आगमनम्।
(ii) सायं 8.00 __________ वादने कवितापाठः।
(iii) रात्री 9.15 __________ वादने प्रतिभोजनम्।
(iv) रात्रौ 9.45 __________ वादने प्रसादवितरणम् प्रस्थानं च।
उत्तराणि:
(i) सार्धसप्त
(ii) अष्ट
(iii) सपादनव
(iv) पादोनदश

प्रश्न 5.
प्रातः (i) 10.30 __________ वादने मुख्यातिथेः आगमनम्।
प्रातः (ii) 11.00 __________ वादने पारितोषिक वितरणम्।
मध्याह्ने (iii) 12.15 __________ वादने मुख्यातिथे भाषणम्, सांस्कृतिक-कार्यक्रमश्च।
मध्याह्ने (iv) 1.45 __________ प्रीतिभोजनम्।
उत्तराणि:
(i) सार्धदश
(ii) एकादश
(iii) सपादद्वादश
(iv) पादोनद्विवादने

प्रश्न 6.
(i) प्रातः 7.30 __________ वादने प्रार्थना-सभा।
(ii) प्रात: 10.00 __________ वादने अर्धावकाशः।
(iii) मध्याह्न 11.45 __________ वादने विविधाः क्रीडाः।
(iv) मध्याह्न 1.15 __________ वादने पूर्णावकाशः।
उत्तराणि:
(i) सार्धसप्त
(ii) दश
(iii) पादोनद्वादश
(iv) सपादएक

प्रश्न 7.
(i) 6.15 __________ सायम् अतिथीनाम् आगमनम्, जलपानम्।
(ii) 7.30 __________ सायम् काव्यगोष्ठी।
(iii) 8.45 __________ सायम् भक्तिसङ्गीतम्।
(iv) 10.00 __________ सायम् समापनम्।
उत्तराणि:
(i) सपादषड्वादने
(ii) सार्धसप्तवादने
(iii) पादोननववादने
(iv) दशवादने

प्रश्न 8.
प्रातः (i) 8.30 __________ वादने प्रार्थना।
प्रातः (ii) 8.45 __________ ध्वजारोहणं, भाषणानि च।
प्रातः (iii) 11.15 __________ जलपानम्।
मध्याह्ने (iv) 12.00 __________ भ्रमणाय प्रस्थानम्।
उत्तराणि:
(i) सार्धअष्ट
(ii) पादोननववादने
(iii) सपादएकादश
(iv) द्वादशवादने

प्रश्न 9.
प्रातः (i) 6.30 __________ वादने ईशवन्दना।
प्रातः (ii) 7.45 __________ वादने उपाहारः।
प्रातः (iii) 8.15 __________ वादने संस्कृतसम्भाषण-अभ्यासः।
प्रात: (iv) 11.00 __________ वादने वर्तनीसंशोधनम्।
उत्तराणि:
(i) सार्धषड्
(ii) पादोनअष्ट
(iii) सपादअष्ट
(iv) एकादश

प्रश्न 10.
(i) प्रात: 9.45 __________ वादने दीपप्रज्वालनम्।
(ii) प्रात: 10.15 __________ वादने अतिथेः स्वागतम्।
(iii) प्रातः 10.30 __________ वादने नाटकाभिनयः।
(iv) मध्याह्न 3.00 __________ वादने कार्यक्रमसमाप्तिः।
उत्तराणि:
(i) पादोनदश
(ii) सपाददश
(iii) सार्धदश
(iv) त्रि(त्रयो)

बहुविकल्पीय प्रश्नाः

1. घटिकायाः समयम् दृष्ट्वा प्रदत्तविकल्पेभ्यः शुद्धम् समयम् चित्वा एवं उचितं समयं लिखित्वा रिक्तस्थानम् पूरयत।
(घड़ी में समय देखकर दिए गए विकल्पों में से शुद्ध उत्तर चुनकर तथा उचित समय लिखकर रिक्त स्थान पूरा कीजिए। See the clock and fill the correct time in the blanks by choosing correct options.)

प्रश्न 1.
(i) देवशर्मा __________ वादने उत्तिष्ठति।

(क) पञ्च
(ख) षष्ठ
(ग) सप्त
(घ) अष्ट
उत्तराणि:
पञ्च

(ii) सः __________ वादने स्नानं करोति।

(क) सार्धषड्
(ग) सार्धपञ्च
(ख) सार्धषट्
(घ) सार्धचतुर्।
उत्तराणि:
(ग) सार्धपञ्च

(iii) सः __________ वादने पाठयति।

(क) पादोन-पञ्च
(ग) पादोन-सप्त
(ख) पादोन-षड्
(घ) पादोन-चतुर्।
उत्तराणि:
(ख) पादोनषड्

(iv) सः __________ वादने विद्यालयम् गच्छति।

(क) सपादअष्ट
(ख) सपादसप्त
(ग) सपादैक
(घ) सपादषड्
उत्तराणि:
(ख) सपादसप्त

प्रश्न 2.
(i) सुरेन्द्र __________ वादने निजकार्यात् निवृत्तः भवति।

(क) पञ्च
(ग) सप्त
(ख) षड्
(घ) नव
उत्तराणि:
(ग) सप्त

(ii) सः __________ वादने समाचारान् आकर्णयति।

(क) सार्धअष्ट
(ग) सार्धनव
(ख) सार्धसप्त
(घ) सार्धदश।
उत्तराणि:
(क) सार्धअष्ट

(iii) सः __________ वादने रात्रिभोजनम् करोति।

(क) सपादनव
(ग) सपादषड्
(ख) सपाददश
(घ) सपादसप्त
उत्तराणि:
(क) सपादनव

(iv) सः __________ वादने शयनाय गच्छति।

(क) पादोन-नव
(ग) सपाद-नव
(ख) पादोन-एकादश
(घ) पादोन-दश।
उत्तराणि:
(घ) पादोनदश।

प्रश्न 3.
(i) गोपालदासः __________ वादने देवालयम् गच्छति।

(क) सपादपञ्च
(ग) सपादषड्
(ख) सपादचतुर्
(घ) सपादसप्त।
उत्तराणि:
(क) सपादपञ्च

(ii) सः __________ वादनपर्यन्तम् कीर्तनं करोति।

(क) सार्धषड्
(ग) सार्धअष्ट
(ख) सार्धपञ्च
(घ) सार्धनव
उत्तराणि:
(क) सार्धषड्

(iii) सः __________ वादने देवालयात् आगच्छति।

(क) पादोनअष्ट
(ग) पादोननव
(ख) पादानसप्त
(घ) पादोनपञ्च
उत्तराणि:
(ख) पादोनसप्त

(iv) सः __________ वादने कार्यालयम् गच्छति।

(क) अष्ट
(ख) नव
(ग) दश
(घ) द्वादश।
उत्तराणि:
(ख) नव

प्रश्न 4.
(i) प्रातः __________ वाद-विवाद प्रतियोगितायाः उद्घाटनम्।

(क) पादोन-सप्तवादने
(ख) सार्धसप्तवादने
(ग) पादोन-अष्टवादने
(घ) सपादअष्टवादने
उत्तराणि:
(ग) पादोन अष्टवादने

(ii) __________ वादने निर्णायकैः टिप्पणयः।

(क) नव
(ख) दश
(घ) द्वादश
(ग) अष्ट
उत्तराणि:
(ख) अष्ट

(iii) __________ वादने प्राचार्येण निर्णयस्य घोषणा।

(क) पादोन-एकादश
(ख) सपाद-एकादश
(ग) सार्धएकादश
(घ) एकादश।
उत्तराणि:
(ख) सपाद-एकादश

(iv) ततः __________ वादने धन्यवाद ज्ञापनम्।

(क) सार्धएकादश
(ख) सार्धद्वादश
(ग) सार्धषड्
(घ) सार्धपञ्च
उत्तराणि:
(क) सार्धएकादश

प्रश्न 5.
(i) प्रातः __________ वादने सरस्वती-वन्दना।

(क) सपादअष्ट
(ख) सपादनव
(ग) सपाददश
(घ) सपादएकादश
उत्तराणि:
(ख) सपादनव

(ii) प्रातः __________ वादने सांस्कृतिक कार्यक्रमाः।

(क) सार्धनव
(ख) सपादनव
(ग) पादोन-नव
(घ) नव
उत्तराणि:
(क) सार्धनव

(iii) प्रातः __________ वादने प्रधानाचार्येण वार्षिकविवरणस्य प्रस्तुतीकरणम्।

(क) पादोनएकादश
(ख) पादोनद्वादश
(ग) पादोननव
(घ) पादोनपञ्च
उत्तराणि:
(क) पादोनएकादश

(iv) प्रात: __________ मुख्यातिथिना पुरस्कारवितरणम्।

(क) सार्धएकादशवादने
(ख) सार्धदशवादने
(ग) एकादशवादने
(घ) दशवादने
उत्तराणि:
(ग) एकादशवादने

प्रश्न 6.
(i) सा प्रातः __________ वादने उत्तिष्ठति।

(क) पञ्च
(ख) षष्ठ
(ग) नव
(घ) दश
उत्तराणि:
(क) पञ्च

(ii) __________ वादने ईशवन्दनां करोति।

(क) सार्धषट्
(ख) सार्धषड्
(ग) षड्
(घ) पादोन-षड्
उत्तराणि:
(ख) सार्धषड्

(iii) यदा अहम् __________ वादने विद्यालयतः आगच्छामि सा मया सह भोजनं करोति।

(क) सपादद्वि
(ख) सार्धद्वि
(ग) सार्धद्वौ
(घ) सार्धद्वा।
उत्तराणि:
(क) सपादद्वि

(iv) __________ वादने विश्रामं करोति।

(क) पादोनत्रयो
(ख) पादोनपञ्च
(ग) पादोनसप्त
(घ) पादोनअष्ट
उत्तराणि:
(क) पादोनत्रयो

प्रश्न 7.
(i) प्रातः __________ वादने “शिक्षकः तस्य रचनात्मकता च”।

(क) सप्त
(ख) सार्धसप्त
(ग) पादोन-सप्त
(घ) सपादसप्त।
उत्तराणि:
(क) सप्त

(ii) प्रातः __________ वादने ‘काव्यानि’।

(क) सप्तसपाद
(ख) पादोन-सप्त
(ग) सपादसप्त
(घ) सार्धसप्त।
उत्तराणि:
(ग) सपादसप्त

(iii) प्रात. __________ वादने ‘आलेख-लेखनम्’।

(क) पादोनअष्ट
(ख) पादोनसप्त
(ग) पादोनपञ्च
(घ) पादोननव
उत्तराणि:
(क) पादोनअष्ट

(iv) प्रात: __________ वादने कार्यक्रमः समाप्तः भविष्यति।

(क) सार्धअष्ट
(ख) सार्धनव
(ग) सार्धपञ्च
(घ) सार्धदश
उत्तराणि:
(क) सार्धअष्ट

प्रश्न 8.
(i) पंजीकरणं प्रात: __________ प्रारभत।

(क) सार्धनववादने
(ख) सार्धअष्टवादने
(ग) सार्धदशवादने
(घ) सार्धपञ्चवादने
उत्तराणि:
(क) सार्धनववादने

(ii) काव्यालिप्रतियोगिता __________ आरभत।

(क) सार्धदशवादने
(ख) दशसपादवादने
(ग) सपाददशवादने
(घ) पादोन-दशवादने।
उत्तराणि:
(ग) सपाददशवादने

(iii) चायपानं __________ अभवत्।

(क) पादोनद्वादशवादने
(ग) पादोनदशवादने
(ख) पादोननववादने
(घ) पादोनपञ्चवादने
उत्तराणि:
(क) पादोनद्वादशवादने

(iv) __________ प्रतियोगिता समाप्ता जाता।

(क) एकवादने
(ख) द्वादशवादने
(ग) द्विवादने
(घ) एकादशवादने।
उत्तराणि:
(क) एकवादने

By going through these CBSE Class 12 Maths Notes Chapter 13 Probability, students can recall all the concepts quickly.

Probability Notes Class 12 Maths Chapter 13

1. Conditional Probability:
Let E and F be two events with a random experiment. Then, the probability of occurrence of E under the condition that F has already occurred and P(F) ≠ 0 is called the conditional probability. It is denoted by P(E/F).

The conditional probability P(E/F) is given by
P(E/F) = \(\frac{\mathrm{P}(\mathrm{E} \cap \mathrm{F})}{\mathrm{P}(\mathrm{F})}\) , when P(F) ≠ 0.

→ Properties:

1. 0 ≤ P(E/F) ≤ 1
2. P(F/F) = 1
3. P(A ∪ B/F) = P(A/F) + P(B/F) – P(A n B/F)
   If A and B are disjoint events,
   then P(A ∪ B/F) = P(A/F) + P(B/F).
4. P(E/F) = 1 – P(E/F)

2. Multiplications Probability:
1. Multiplication Theorem on Probability:
Let E and F be two events associated with sample space S. P(E ∩ F) denotes the probability of the event that both E and F occur, which is given by P(E ∩ F) = P(E) P(F/E) = P(F) P(E/F) provided P(E) ≠ 0 and P(F) ≠ 0.
This result is known as the multiplication theorem on probability.

2. Multiplication rule of probability for more than two events:
Let E, F and G be the three events of sample space. Then, P(E ∩F ∩G) = P(E).P(F/E) P[G/(E ∩ F)]

3. Independent Events:

1. Two events E and F are said to be independent, if P(E/F) = P(E) and P(F/E) = P(F), provided P(E) ≠ 0 and P(F) ≠ 0.
   We know that P(E ∩ F)= P(E). P(F/E) and P(E ∩ F) = P(F). P(E/F).
2. Events E and F are independent if P(E ∩ F) = P(E) × P(F).
3. Three events E, F and G are said to be independent or mutually independent, if
   P(E∩F∩G)= P(E). P(F). P(G)

4. Partition of a Sample Space:
A set of events E₁, E₂,……….., E_n is said to represent a partition of sample S, if

1. E_i ∩ F_j = Φ, if i ≠ j, i, j = 1, 2,……….. ,n .
2. E₁ ∪ E₂ ∪ E₃ ∪ …. ∪ E_n = S
3. P(E_i) > 0 for all i = 1, 2,……., n

For example, E and E’ (complement of E) form a partition of sample space S, because
E∩E’ = Φ and E∪E’ = S.

5. Theorem of Total Probability:
Let E₁, E₂,…….., E_n be a partition of sample space and each event has a non-zero probability.
If A be any event associated with S, then
P(A) = P(E₁) P(A/E₁) + P(E₂) P(A/E₂) + P(E₃) P(A/E₃) +…….. + P(E_n) P(A/E_n)

6. Bayes’ Theorem:
Let E₁, E₂,…………, E_n be the n events forming a partition of sample space S, i.e., E₁, E₂,………, E( are pairwise disjoint and E₁ ∪ E₂ ∪………. ∪
E_n = S and A is any event of non-zero probability, then

7. A Few Terminologies:

1. Hypothesis: When Bayes’ Theorem is applied, the events E₁, E₂,……………., E_n is said to be a hypothesis.
2. Priori Probability: The probabilities P(E₁), P(E₂),…………., P(E_n) is called priori.
3. Posteriori Probability: The conditional probability P(E./A) is known as the posterior probability of hypothesis E.

8. Random Variable:
A random variable is a real-valued function whose domain is the sample space of a random experiment.
For example, let us consider the experiment of tossing a coin three times.

The sample space of the experiment is
S{TTT, TTH, THT, HTT, HHT, HTH, THH, HHH}

If x denotes the number of heads obtained, then X is the random variable for each outcome.
X(0) = {TTT}
X(1) = {TTH, THT, HTT}
X(2) = {HHT, HTH, THH}
X(3) = {HHH}

9. Probability Distribution of a Random Variable:
Let real numbers x₁, x₂,…………., x_n be the possible values of random variable and p₁, p₂,……………, p_n be probabilities corresponding to each value of the random variable X. Then the probability distribution is

It may be noted that

1. p_i > 0
2. Sum of probabilities p₁ + p₂ +………….+ p_n = 1

Example: Three cards are drawn successively with replacement from a well-shuffled pack of 52 cards. A random variable denotes the number of spades on three cards. Determine the probability distribution of X.
P(S) = P(Drawing a spade) = \(\frac{13}{52}=\frac{1}{4}\)
P(F) = P(Drawing not a space = 1 – \(\frac{1}{4}=\frac{3}{4}\)
P(X = 0) =P(FFF) = \(\left(\frac{3}{4}\right)^{3}=\frac{27}{64}\)
P(X = 1) = 3 × \(\left(\frac{1}{4} \times \frac{3}{4} \times \frac{3}{4}\right)=\frac{27}{64}\)

∵ X = 1 ⇒{SFF, FSF, FFS}
X = 2 ⇒ {SSF, SFS, FSS}
∴ P(X – 2) = 3 × \(\left(\frac{1}{4} \times \frac{1}{4} \times \frac{3}{4}\right)=\frac{9}{64}\)

When X = 3 ⇒ {SSS}
P(X = 3) = \(\frac{1}{4} \times \frac{1}{4} \times \frac{1}{4}=\frac{1}{64}\)
∴ Probability distribution is

10. Mean of Random Variable:
Let X be the random variable whose possible values are x₁, x₂,……….,x_n. If p₁, p₂,……….., p_n are the corresponding probabilities, then the mean of X denoted by p is given by
|
The mean of a random variable X is also called the expected value of X, denoted by E(x).
For the experiment of drawing a spade in three cards, the expected value ‘

11. Variance of a Random Variable:
Let X be the random variable with possible values of X: x₁ x₂,……x_n occur whose probabilities are p₁, p₂,………., p_n respectively.
Let μ = E(x) be the mean of X. The variance of X, denoted by Var (X) or σx2, is defined as

12. Bernoulli Trial:
Trials of a random experiment are said to be Bernoulli’s Trials if they satisfy the following conditions:

1. The trials should be independent.
2. Each trial has exactly two outcomes viz. success or failure.
3. The probability of success remains the same in each trial.
4. The number of trials is finite.

Example: An urn contains 6 red and 5 white balls. Four balls are drawn successively. Find whether the trials of drawing balls are Bernoulli trials when after each draw the ball draw is

1. replaced
2. not replaced in the urn.

1. If drawing a red ball with replacement is a success, in each trial the probability of success = \(\frac{6}{11}\).
Therefore, drawing a ball with replacement is a Bernoulli trial.

2. In the second attempt, when the ball is not replaced, the probability of success = \(\frac{5}{10}\).

In thired attempt, the probability of success = \(\frac{4}{9}\).
Thus, probability changes at each trial. Hence, in this case, it is not a Bernoulli trial.

13. Binomial Distribution:
The probability distribution of a number of successes in an experiment consisting of n Bernoulli trials is obtained by binomial expansion of (q + p)ⁿ.
Such a probability distribution may be written as:

This probability distribution is called binomial distribution with parameters n and p.

14. Probability Function:
The probability of x success is denoted by P(x). In a binomial distribution P(x) is given by
P(x) = ⁿC_x q^n-x p^x, x = 0,1, 2,…., n and q = 1 – p.
The function P(x) is known as the probability function of the binomial distribution.

1. DEFINITIONS

(i) Random Experiment of Trial. The performance of an experiment is called a trial.
(ii) Event. The possible outcomes of a trial are called events.
(iii) Equally likely Events. The events are said to be equally likely if there is no reason to expect
any one in preference to any other.
(iv ) Exhaustive Events. It is the total number of all possible outcomes of any trial.
(v) Mutually Exclusive Events. Two or more events are said to be mutually exclusive if they
cannot happen simultaneously in a trial. s:
(vi) Favourable Events. The cases which ensure the occurrence of the events are called favourable.
(vii) Sample Space. The set of all possible outcomes of an experiment is called a sample space.
( viii) Probability of occurrences of event A, denoted by P (A), is defined as :
P(A) = \(\frac{\text { No. of favourable cases }}{\text { No. of exhaustive cases }}=\frac{n(\mathrm{~A})}{n(\mathrm{~S})}\)

2. THEOREMS .

(i) In a random experiment, if S be the sample space and A an event, then :
(I) P (A) ≥ 0. (II) P (Φ) = 0 and (III) P (S) = 1.
(ii) If A and B are mutually exclusive events, then P (A ∩ B) = 0.
(iii) If A and B are two mutually exclusive events, then P (A) + P (B) – 1.
(iv) If A and B are mutually exclusive events, then : P (A ∪ B) = P ( A) + P ( B). s
(v) For any two events A and B. P (A ∪ B) = P (A) + P (B) – P (A ∩ B).
(vi) For each event A. P (\(\overline{\mathrm{A}}\)) = 1 – P (A), where (\(\overline{\mathrm{A}}\)) is the complementary event. 1;
( vii) 0 ≤ P (A) ≤ 1.

3. MORE DEFINITIONS
(i) Compound Event. The simultaneous happening of two or more events is called a compound event if they occur in connection with each other. I

(ii) Conditional Probability. Let A and B be two events associated with the same sample spat e then
P (A/B) = \(\frac { No. of elementary events favourable to B which are also favourable to A }{ No. of elementary events favourable to B }\)
Theorem. P (A/B) = \(\frac{P(A \cap B)}{P(B)}\)
P(B/A) = \(\frac{P(A \cap B)}{P(A)}\)

(iii) Independent Events. Two events are said to be independent if the occurrence of one does not a depend upon the occurrence of the other.
Theorem. P (A ∩ B) = P (A) P (B) when A, B are independent.

4. If A₁, A₁, …………A_r be r events, then the probability when at least one event happens
= 1 – \(\mathbf{P}\left(\overline{\mathbf{A}_{1}}\right) \mathrm{P}\left(\overline{\mathbf{A}_{2}}\right) \ldots \cdot \mathbf{P}\left(\overline{\mathrm{A}}_{r}\right)\)

5. BAYES’ FORMULA
If E₁, E₂,…., E_n are mutually exclusive and exhaustive events and A is any event that occurs with E₁, E₂, …. , E_n, then :
P(E₁/A) = \(\frac{\mathrm{P}\left(\mathrm{E}_{1}\right) \mathrm{P}\left(\mathrm{A} / \mathrm{E}_{1}\right)}{\mathrm{P}\left(\mathrm{E}_{1}\right) \mathrm{P}\left(\mathrm{A} / \mathrm{E}_{1}\right)+\mathrm{P}\left(\mathrm{E}_{2}\right) \mathrm{P}\left(\mathrm{A} / \mathrm{E}_{2}\right)+\ldots \ldots \ldots+\mathrm{P}\left(\mathrm{E}_{n}\right) \mathrm{P}\left(\mathrm{A} / \mathrm{E}_{n}\right)}\)

6. MEAN AND VARIANCE OF RANDOM VARIABLE.
Mean (μ) = Σx_ip_i
Variance (σ²) = Σ(x_i – μ)²p_i = Σx_i² p_i – μ²

By going through these CBSE Class 9 Sanskrit Notes Chapter 2 स्वर्णकाकः Summary, Notes, word meanings, translation in Hindi, students can recall all the concepts quickly.

Class 9 Sanskrit Chapter 2 स्वर्णकाकः Summary Notes

स्वर्णकाकः  Summary

प्रस्तुत पाठ पद्मशास्त्री जी द्वारा रचित ‘विश्वकथाशतकम्’ नामक कथा संग्रह से लिया गया है। इस कथा में सुनहरे पंखों वाले एक कौए के माध्यम से लोभ और उसके दुष्परिणाम का वर्णन किया गया है। साथ में त्याग और उसके लाभ के बारे में बताया गया है। कथा का सार इस प्रकार है

किसी गाँव में एक बुढ़िया रहती थी। उसने एक दिन थाली में चावल रखकर अपनी पुत्री से कहा-पुत्री, पंछियों से इसकी रक्षा करना। उसी समय एक विचित्र कौआ वहाँ आकर चावल खाने लगा। उस कन्या ने कौवे को मना किया तो उसने उसे एक पीपल के वृक्ष के पास आने के लिए कहा। कौवे ने उस लड़की की ईमानदारी से प्रसन्न होकर उसे हीरे-जवाहरात दिए।

उसी गाँव में एक लालची बुढ़िया भी रहती थी। वह सारे रहस्य जान गई। उसने ईर्ष्या वश उसी प्रकार का नाटक किया। उसकी बेटी घमंडी थी। कौवे के कहने पर उसने स्वर्णमय सोपान की माँग की। उस लड़की की हीन इच्छा को जानकर कौवे ने उसके सामने तीन पेटियाँ रख दीं। लोभ से भरी हुई उस लड़की ने सबसे बड़ी पेटी उठा ली। ज्यों ही उसने उसे खोला, त्योंही उसमें से काला साँप निकला। उस दिन से उस लड़की ने लालच का त्याग कर दिया।

स्वर्णकाकः Word Meanings Translation in Hindi

1. पुरा कस्मिंश्चिद् ग्रामे एका निर्धना वृद्धा स्त्री न्यवसत्। तस्याः च एका दुहिता विनम्रा मनोहरा चासीत्। एकदा माता स्थाल्यां तण्डुलान् निक्षिप्य पुत्रीम् आदिशत्। “सूर्यातपे तण्डुलान् खगेभ्यो रक्षा” किञ्चित् कालादनन्तरम् एको विचित्रः काकः समुड्डीय तस्याः समीपम् अगच्छत्।

शब्दार्थाः –
पुरा – प्राचीन काल में
निक्षिप्त – रखकर
कस्मिंश्चिद् – किसी (में)
आदिदेश – आदेश दिया
निर्धना – ग़रीब,
सूर्यातपे – सूरज की धूप में
न्यवसत् – रहती थी
खगेभ्यः – पक्षियों से
दुहिता – पुत्री
किञ्चिद् – कुछ
विनम्रा – नम्र स्वभाव वाली
कालात् – समय से (के)
मनोहरा – सुंदर
अनन्तरम् – बाद में
एकदा – एक बार
समुड्डीय – उड़कर
स्थाल्याम् – थाली में
तण्डुलान् – चावलों को।

अर्थ –
प्राचीन समय में किसी गाँव में एक निर्धन (ग़रीब) बुढ़िया स्त्री रहती थी। उसकी एक नम्र स्वभाव वाली और सुंदर बेटी थी। एक बार माँ ने थाली में चावलों को रखकर पुत्री को आज्ञा दी – सूर्य की गर्मी में चावलों की पक्षियों से रक्षा करो। कुछ समय बाद एक विचित्र कौआ उड़कर वहाँ आया।

अव्ययानां वाक्येषु प्रयोगः – 
अव्ययः वाक्येषु प्रयोगः
पुरा – पुरा रामः अयोध्यायाः नृपः आसीत्।
च् – श्रीकृष्णः बलरामश्च च् भ्रातरौ आस्ताम्।
अनन्तरम् – स्नानात् अनन्तरं शरीराङ्गानि स्वच्छानि भवन्ति।

विशेषण – विशेष्य – चयनम् –
विशेषणम् – विशेष्यः
कस्मिंश्चित् – ग्रामे
एका, विनम्रा, मनोहरा – दुहिता
एका, निर्धना, वृद्धा – स्त्री
एकः, विचित्रः – काकः

2. नैतादृशः स्वर्णपक्षो रजतचञ्चुः स्वर्णकाकस्तया पूर्वं दृष्टः। तं तण्डुलान् खादन्तं हसन्तञ्च विलोक्य बालिका रोदितुमारब्धा। तं निवारयन्ती सा प्रार्थयत् “तण्डुलान् मा भक्षय। मदीया माता अतीव निर्धना वर्तते।” स्वर्णपक्षः काकः प्रोवाच, “मा शुचः। सूर्योदयात्प्राग् ग्रामाबहिः पिप्पलवृक्षमनु त्वया आगन्तव्यम्। अहं तुभ्यं तण्डुलमूल्यं दास्यामि।” प्रहर्षिता बालिका निद्रामपि न लेभे।

शब्दार्थाः –
एतादृशः – ऐसा (इस तरह का)
स्वर्णपक्षः – सोने, के पंख वाला
रजतचञ्चुः-चाँदी की चोंच वाला
पूर्वम् – पहले
खादन्तम् – खाते हुए को
प्रोवाच – बोला/बोली
हसन्तम् – हँसते हुए को
शुचः – शोक करो,
दितम् – रोना
प्राग – पहले
आरब्धा – शुरू कर दिया
पिप्पलक्षमन – पीपल के वृक्ष के, पीछे
निवारयन्ती – हटाती हुई
आगन्तव्यम् – आना
प्रार्थयत् – प्रार्थना की
तुभ्यम् – तुम्हें
भक्षय – खाओ
प्रहर्षिता – प्रसन्न
मदीया – मेरी
निद्राम् – नींद को
अतीव – बहुत अधिक
लेभे – ले पाई

अर्थ –
उसके द्वारा ऐसा सोने के पंखों वाला और चाँदी की चोंच वाला सोने का कौआ पहले नहीं देखा गया था। उसको चावलों को खाते और हँसते हुए देखकर लड़की ने रोना शुरू कर दिया। उसको हटाती हुई उसने प्रार्थना की-चावलों को मत खाओ। मेरी माँ बहुत गरीब है। सोने के पंख वाला कौआ बोला, शोक मत करो। सूर्योदय से पहले गाँव के बाहर पीपल के वृक्ष के पीछे तुम आना। मैं तुम्हें चावलों का मूल्य (कीमत) दे दूँगा। प्रसन्नता से भरी लड़की नींद भी नहीं ले पाई।

विशेषण – विशेष्य – चयनम् –
विशेषणम् – विशेष्यः
एतादृशः, स्वर्णपक्षः, रजतचञ्चुः – स्वर्णकाकः
निवारयन्ती – सा
स्वर्णपक्षः – काकः
खादन्तम्, हसन्तम् – तम्
मदीया, निर्धना – माता
प्रहर्षिता – बालिका

अव्ययानां वाक्येषु प्रयोगः –
पूर्वम् – सः बालकः पूर्वम् अत्र नागच्छत्।
विलोक्य – पितरम् विलोक्य पुत्रः प्रसन्नः अभवत्।
अतीव – अधुना अहम् अतीव श्रान्तः अस्मि।
मा – त्वं तत्र मा गच्छ।
बहिः – सः ग्रामात् बहिः निरगच्छत्।
अनु – विद्यालयम् अनु छात्राः तिष्ठन्ति।
अपि – ते अपि गुणिनः सन्ति।

3. सूर्योदयात्पूर्वमेव सा तत्रोपस्थिता। वृक्षस्योपरि विलोक्य सा च आश्चर्यचकिता सञ्जाता यत् तत्र स्वर्णमयः प्रासादो वर्तते। यदा काकः शयित्वा प्रबुद्धस्तदा तेन. स्वर्णगवाक्षात्कथितं “हंहो बाले! त्वमागता, तिष्ठ, अहं त्वत्कृते सोपानमवतारयामि, तत्कथय स्वर्णमयं रजतमयम् ताम्रमयं वा?” कन्या अवदत्”अहं निर्धनमातुः दुहिता अस्मि। ताम्रसोपानेनैव आगमिष्यामि।” परं स्वर्णसोपानेन सा स्वर्ण-भवनम् आरोहत।

शब्दार्थाः –
पूर्वमेव – पहले से ही
हहो – अरे/हे
उपस्थिता – उपस्थित थी
आगता – आ गई।
वृक्षस्योपरि – वृक्ष के ऊपर
त्वत्कते – तम्हारे लिए.
आश्चर्यचकिता – हैरान,
अवतारयामि – उतारता हूँ.
सजाता – हो गई.
उत – और
स्वर्णमयः – सोने से बना,
प्रावोचत् – बोली,
प्रासादः – महल,
मातः – माँ की,
वर्तते – है,
दुहिता – बेटी
शयित्वा – सोकर,
ताम्रसोपानेन – ताँबे की सीढ़ी से,
प्रबुद्धः – जागा,
स्वर्णभवनम् – सोने के महल में,
स्वर्णगवाक्षात् – सोने की खिड़की से
आससाद – पहुँची।

अर्थ –
सूर्योदय से पहले ही वह (लड़की) वहाँ पहुँच गई। वृक्ष के ऊपर देखकर वह आश्चर्यचकित हो गई कि वहाँ सोने का महल है। जब कौआ सोकर उठा तब उसने सोने की खिड़की से झाँककर कहा–अरे बालिका! तुम आ गई, ठहरो, मैं तुम्हारे लिए सीढ़ी को उतारता हूँ, तो कहो सोने की, चाँदी की अथवा ताँबे की, किसकी उतारूँ? कन्या बोली-मैं निर्धन (ग़रीब) माँ की बेटी हूँ। ताँबे की सीढ़ी से ही आऊँगी। परंतु सोने की सीढ़ी से वह स्वर्णभवन में पहुँची।

अव्ययानां वाक्येषु प्रयोगः –
पूर्वम् – खगाः सायं कालात् पूर्वमे व स्वनीडमागच्छन्ति
तत्र – सः तत्र गच्छति तत्र तस्य माता अस्ति।
उपरि – गृहस्य उपरि खगाः तिष्ठन्ति।
यत् – अहं कथयामि यत् त्वं तत्र तिष्ठ।
यदा – यदा श्रीकृष्णः उपदिशति।
तदा – तदा अर्जुनः युद्धम् अकरोत्।
वा – सुखे वा दु:खे वा सदैव शान्तः भवेत्।
एव – माता एव पुत्रस्य हितं करोति।
यद्यपि सः खञ्जोऽस्ति परम् अतीव तत्परो प्रतीयते।

विशेषण – विशेष्य – चयनम् –
विशेषणम् – विशेष्यः
आश्चर्यचकिता – सा
प्रबुद्धः – काकः
स्वर्णमयः – प्रासादः
स्वर्णमयम् – भवनम्

4. चिरकालं भवने चित्रविचित्रवस्तूनि सज्जितानि दृष्ट्वा सा विस्मयं गता। श्रान्तां तां विलोक्य काकः अवदत् “पूर्वं लघुप्रातराशः क्रियताम्-वद त्वं स्वर्णस्थाल्यां भोजनं करिष्यसि किं वा रजतस्थाल्याम् उत ताम्रस्थाल्याम्”? बालिका अवदत्-ताम्रस्थाल्याम् एव अहं-“निर्धना भोजनं करिष्यामि।” तदा सा आश्चर्यचकिता सजाता यदा स्वर्णकाकेन स्वर्णस्थाल्यां भोजनं पर्यवेषितम्। न एतादृशम् स्वादु भोजनमद्यावधि बालिका खादितवती। काकोऽवदत्-बालिके! अहमिच्छामि यत् त्वम् सर्वदा अत्रैव तिष्ठ परं तव माता तु एकाकिनी वर्तते। अतः “त्वं शीघ्रमेव स्वगृहं गच्छ।”

शब्दार्थाः –
चिरकालम – बहुत देर तक
स्वर्णस्थाल्याम – सोने की थाली में
सज्जितानि – सजी हुई
रजतस्थाल्याम् – चाँदी की थाली में
विस्मयम् – हैरानी को
उत – या/अथवा
गता – प्राप्त हुई
व्याजहार – बोली/बोला
श्रान्ताम् – थकी हुई को
निर्धना – ग़रीब
विलोक्य – देखकर
आश्चर्यचकिता – हैरान
प्राह – बोला
सज्जाता – हो गई
पूर्वम् – पहले
पर्यवेषितम – परोसा (दिया)
लघप्रातराश: – थोडा नाश्ता (जलपान)
एतादक – ऐसा
क्रियताम – करो
स्वादु – स्वादिष्ट
अद्यावधि – आजतक
सर्वदा – सदा (हमेशा)
खादितवती – खाई भी
अत्रैव (अत्र+एव) – यहीं
ब्रूते – बोला, एकाकिनी-अकेली।

अर्थ –
बहुत देर तक भवन में चित्रविचित्र (अनोखी) वस्तुओं को सजी हुई देखकर वह हैरान रह गई। उसको थकी हुई देखकर कौआ बोला-पहले थोड़ा नाश्ता करो-बोलो तुम सोने की थाली में भोजन करोगी या चाँदी की थाली में या ताँबे की थाली में? लड़की बोली-ताँबे की थाली में ही मैं ग़रीब भोजन करूँगी (खाना खाऊँगी)। तब वह कन्या और आश्चर्यचकित हो गई जब सोने के कौवे ने सोने की थाली में (उसे) भोजन परोसा। ऐसा स्वादिष्ट भोजन आज तक उस लड़की ने नहीं खाया था। कौआ बोला-हे बालिका (लडकी)! मैं चाहता हूँ कि तुम हमेशा यहीं रहो परंतु तुम्हारी माँ अकेली है। तुम जल्दी ही अपने घर को जाओ।

अव्ययानां वाक्येषु प्रयोगः –
पूर्वम् – ग्रामात् पूर्वम् जलाशयः विद्यते।
वा – बाल:भवेत् बालिका वा, सम्पूर्ण स्नेहं कुर्यात्।
एव – एव मम भागिनी वर्तते।
यदा-तदा – यदा बालः गृहं गमिष्यति तदा भोजनं खादिष्यति।
अद्यावधि – रामम् इव अद्यावधि कश्चिदपि न अभवत्।
च – भ्राता भगिनी च विद्यालयं गच्छतः।
अत्र – अत्र मम जन्मस्थानम् अस्ति।
शीघ्रम् – अधुना अहं विद्यालयं शीघ्रं गच्छामि।

विशेषण – विशेष्य – चयनम् –
विशेषणम् – विशेष्यः
सज्जितानि – चित्रविचित्रवस्तूनि
निर्धना – अहम्
एतादृक् स्वादु – भोजनाम
श्रान्ताम् – ताम्
सा, आश्चर्यचकिता – कन्या
एकाकिनी – माता

5. इत्युक्त्वा काकः कक्षाभ्यन्तरात् तिस्त्रः मञ्जूषाः निस्सार्य तां प्रत्यवदत्-“बालिके! यथेच्छं गृहाण मञ्जूषामेकाम्।” लघुतमा मञ्जूषां प्रगृह्य बालिकया कथितम् इयत् एव मदीयतण्डुलानां मूल्यम्। गृहमागत्य तया मञ्जूषा समुद्घाटिता, तस्यां महार्हाणि हीरकाणि विलोक्य सा प्रहर्षिता तद्दिनाद्धनिका च सञ्जाता।

शब्दार्था: –
इत्युक्त्वा – ऐसा कहकर के
कक्षाभ्यन्तरात् – कमरे के अंदर से
मञ्जूषा: – बक्से
निस्सार्य – निकालकर
प्रत्यवदत् – बोला
यथेच्छम् – इच्छापूर्वक (इच्छा के अनुसार)
लघुतमाम् – सबसे छोटी (को)
प्रगृह्य – लेकर
इयदेव – इतना ही
मदीय – मेरे
समुद्घाटिता – खोला (खोला गया)
महार्हाणि – महँगे (बहुमूल्य)
प्रहर्षिता – प्रसन्न हो गई
तद्दिनात् – उसी दिन से
सञ्जाता – हो गई।

अर्थ –
ऐसा कहकर कौए ने कमरे के अंदर से तीन बक्से निकालकर उसको कहा- हे कन्या! अपनी इच्छा से एक संदूक ले लो। सबसे छोटी संदूक को लेकर लड़की ने कहा-यही मेरे चावलों की कीमत है। घर आकर उसने संदूक को खोला, उसमें बहुत कीमती (मूल्यवान) हीरों को देखकर वह बहुत खुश हुई और उसी दिन से वह धनी हो गई।

अव्ययानां वाक्येष प्रयोग –
अव्ययः – वाक्येषु प्रयोगः
इति –  इति कथयित्वा छात्रः विद्यालयम् अगच्छत्।
एव – त्वम् एव मम बन्धुः वर्तते।
च – रामः श्यामः च मित्रे स्तः।

विशेषण-विशेष्य चयनम –
तिस्त्रः – मञ्जूषाः
इयत्मू – ल्यम्
प्रहर्षिता, धनिका – सा
एकाम् – मञ्जूषाम्
महार्हाणि – हीरकाणि

6. तस्मिन्नेव ग्रामे एका परा लुब्धा वृद्धा न्यवसत्। तस्या अपि एका पुत्री आसीत्। ईर्ण्यया सा तस्य स्वर्णकाकस्य रहस्यम् ज्ञातवती। सूर्यातपे तण्डुलान् निक्षिप्य तयापि स्वसुता रक्षार्थं नियुक्ता। तथैव स्वर्णपक्षः काकः तण्डुलान् भक्षयन् तामपि तत्रैवाकारयत्। प्रातस्तत्र गत्वा सा काकं निर्भर्त्सयन्ती प्रावोचत्-“भो नीचकाक! अहमागता, मह्यं तण्डुलमूल्यं प्रयच्छ।” काकोऽब्रवीत्-“अहं त्वत्कृते सोपानम् अवतारयामि। तत्कथय स्वर्णमयं रजतमयं ताम्रमयं वा।” गर्वितया बालिकया प्रोक्तम्- “स्वर्णमयेन सोपानेन अहम् आगच्छामि।” परं स्वर्णकाकस्तत्कृते ताम्रमयं सोपानमेव प्रायच्छत्। स्वर्णकाकस्तां भोजनमपि ताम्रभाजने एव अकारयत्।

शब्दार्था: –
तस्मिन्नेव – उसी
निर्भर्त्सयन्ती – बुरा-भला कहती हुई
अपरा – दूसरी
प्रावोचत् – बोला
न्यवसत् – रहती थी
आगता – आ गई
रहस्यम् – गुप्त बात को
मह्यम् – मुझे
अभिज्ञातवती – जान गई
त्वत्कृते – तुम्हारे लिए
सूर्यातपे – सूर्य की धूप में
सोपानम् – सीढ़ी को
निक्षिप्य – रखकर/फैलाकर
अवतारयामि – उतारता हूँ
स्वसुता – अपनी पुत्री
तत्कथय – तो कहो
रक्षार्थम् – रखवाली के लिए
गर्वितया – घमंडी
नियुक्ता – बिठा दी
प्रोक्तम् – कहा गया/ कहा
तथैव – वैसे ही
तत्कृते – उसके लिए
भक्षयन् – खाते हुए
प्रायच्छत् – दिया
तत्रैव – वहीं
ताम्रभाजने – ताँबे के पात्र में
आवारयत् – बुलाया,
अकारयत् – कराया।

अर्थ –
उसी गाँव में एक दूसरी लालची बुढ़िया स्त्री रहती थी। उसकी भी एक बेटी थी। ईर्ष्या से उसने उस सोने के कौए का रहस्य जान लिया। सूर्य की धूप में चावलों को रखकर (फैलाकर) उसने भी अपनी बेटी को उसकी रक्षा के लिए बिठा (नियुक्त कर) दिया। वैसे ही सोने के पंख वाले कौए ने चावलों को खाते हुए उसको (लड़की को) भी या। सबह वहाँ जाकर वह कौए को बरा-भला कहती हई बोली- हे नीच कौए! मैं आ गई हूँ, मुझे चावलों का मल्य दो। कौआ बोला- मैं तुम्हारे लिए सीढी उतारता हूँ। तो कहो सोने से बनी हुई, चाँदी से बनी हुई अथवा ताँबे से बनी हुई। घमंडी लड़की बोली- सोने से बनी हुई सीढ़ी से मैं आती हूँ परंतु सोने के कौए ने उसे ताँबे से बनी हुई सीढ़ी ही दी। सोने के कौए ने उसे भोजन भी ताँबे के बर्तन में कराया।

अव्ययानां वाक्येषु प्रयोगः –
एव – एषः एव मम भ्राता अस्ति।
अपि – त्वम् अपि स्वकथां श्रावय!
तथैव – बालकः अपि तथैव करोति यथा तस्य पिता करोति।
तत्रैव – रामः तत्रैव तिष्ठति यत्र तस्य गुरुः आदिशत्
तत्र – त्वमपि तत्र गच्छ!
हि – त्वं हि नः पिता वर्तसे।

विशेषण – विशेष्य – चयनम् –
विशेषणम् – विशेष्य
तस्मिन् – ग्रामे
एका – पुत्री
निर्भर्त्सयन्ती – सा
गर्वितया – बालिकया
एका, अपरा, लुब्धा – वृद्धा
स्वर्णपक्षः – काक:
स्वर्णमयम्/ताम्रमयम् /रजतमयम् – सोपानम्
स्वर्णमयेन – सोपानेन

7. प्रतिनिवृत्तिकाले स्वर्णकाकेन कक्षाभ्यन्तरात् तिम्रः मञ्जूषाः तत्पुरः समुत्क्षिप्ताः। लोभाविष्टा सा बृहत्तमा मञ्जूषां गृहीतवती। गृहमागत्य सा तर्षिता यावद् मञ्जूषामुद्घाटयति तावत् तस्यां भीषणः कृष्णसर्पो विलोकितः। लुब्धया बालिकया लोभस्य फलं प्राप्तम्। तदनन्तरं सा लोभं पर्यत्यजत्।

शब्दार्थाः –
प्रतिनिवृत्तिकाले – वापस जाते समय
लोभाविष्टा – लालची
कक्षाभ्यन्तरात् – कमरे के अंदर से
बृहत्तमाम् – सबसे बड़ी
तिस्त्रः – तीन
गृहीतवती – ले ली
मञ्जूषाः – संदूकें (पेटियाँ),
तर्षिता – व्याकुल
तत्पुरः – उसके सामने
उद्घाटितवती – खोला/खोली
समुत्क्षिप्ताः – रख दी
भीषण:- भयानक
कृष्णसर्पः – काला साँप
विलोकितः – देखा
लुब्धया – लालची
प्राप्तम् – प्राप्त किया गया
पर्यत्यजत् – छोड़ दिया।

अर्थ –
वापस होते समय सोने के कौए ने कमरे के अंदर से तीन पेटियाँ (संदूकें) उसके सामने रख दीं। लालची लड़की ने सबसे बड़ी पेटी ले ली। घर आकर व्याकुल वह जब संदूक खोलती है तो उसमें अचानक काला साँप देखा। लालची लड़की ने लालच का फल पाया। उसके बाद उसने लालच छोड़ दी।

अव्ययानां वाक्येषु प्रयोगः –
अव्ययः – वाक्येषु प्रयोगः
तत्पुरः – रामः बालकं दृष्ट्वा तत्पुरः भोजनम् कृतवान्।
यावद् – यावद् सः पठिष्यति।
तावत् – तावत् तस्य जीवनम् उन्नति करिष्यति।
अनन्तरम् – पठनात् अनन्तरं सः अधिकारी अभवत्।

विशेषण – विशेष्य – चयनम् –
विशेषणम् – विशेष्यः
तिस्रः – मज्जूषाः
बृहत्तमाम् – मञ्जूषाम्
भीषणः – कृष्णसर्पः
लोभाविष्टा – सा
तर्षिता – सा
लुब्धया – बालिकया

By going through these CBSE Class 11 Maths Notes Chapter 1 Sets Class 11 Notes, students can recall all the concepts quickly.

Sets Notes Class 11 Maths Chapter 1

Set: Any well-defined collection of objects, which are different from each other, and which we can see or think of is called a set.

Members of a set: The objects which belong to a set are called its members or elements.

Representation of a set: There are two ways by which the , sets can be represented :
(a) Tabular form or Roster form : Here, the elements of a
set are actually written down, separated by commas and enclosed * within braces (i.e., curly brackets). Thus,

(i) V, the set of vowels in the English alphabet = {a, e, i, o, u},
(ii) A, the set of odd natural numbers < 10 = {1, 3, 5, 7, 9),
(iii) N, the set of natural numbers = {1, 2, 3,…}.

(b) The set builder form : In this form, we list the property or properties satisfied by the elements of the set. Thus,
(i) M = {2, 3,.5, 7, 11, 13, 17, 191 = {x : x is a prime number < 20).

(ii) A = 16, 7, 8, 9, 10, 11} = {x| ∈ N, 5 < x < 12}, where ∈ stands for ‘belongs to’ and ‘ | ’ stands for ‘such that’.

It may be noted that while writing the set in roster form, an element is not generally repeated. For example, the set of letters of the word ‘SCHOOL’ is (S, C, H, O, L}.

Empty set or null set or void set : A set consisting of no element at all is called the empty set or the null set or the void | set. It is denoted by Φ (Phai). In roster form, it is written as = { }.
Examples : (i) (x : x ∈ N, 1 < x < 2} = Φ.
(ii) {x : x ∈ R, x² = – 1} = Φ.

Finite Set: A set in which the process of counting of elements surely comes to an end, is called a finite set.
Examples : ii) {x : x ∈ N, x < 500) (ii) Set of all trees on earth.

Infinite Set: A set, in which the process of counting of elements never comes to an end, is called an infinite set. Examples : (i) {x : x ∈ N, x > 50), (ii) {x : x ∈ Z, x < 1}.

Equal Sets : Two sets A and B are said to be equal, if every element of A is in B and every element of B is in A. It is written as A = B.
Examples: (i) {1, 2, 5} = {2, 1, 5} = {5, 1, 2)
(ii) {1, 2, 3, 1} = {1, 2, 3} = {1, 1, 2, 2, 3} etc.
[∵ The repetition of elements in a set is meaningless]

Equivalent Sets : Two finite sets A and B are said to be equivalent, if n(A) = n(B), where n(A) or n(B) is the number of elements in set A or B. It is written as A ↔ B.
Example: If A = {1, 2, 3} and B = {a, b, c}. Then, A ↔ B as n(A) = n(B) = 3.

Whenever A = B, then n(A) = n(B). Thus, equal sets are always equivalent. But, equivalent sets need not be equal.

Disjoint Sets : Two sets are said to be disjoint, if they have no element in common.
Example : A = {1, 3, 5} and B = {2, 4, 6) are disjoint sets.

Subset: If A and B are two sets given in such a way that every element of A is in B, then A is a subset of set B and it is written as A ⊂ B (read as ‘A is contained in B’)
If at least one element of A does not belong to B, then A is not a subset of B. It is written as A ⊄ B.
Example : If A = {1, 2, 3} and B = {3, 2, 4, 1), then A ⊂ B.

Subsets of Set of Real Numbers R :
There are many important subsets of R. Some of them are given below :
(i) The set of natural numbers = N = {1, 2, 3, 4, 5, ….)

(ii) The set of integers Z is
Z = {…., – 3, – 2, – 1, 0, 1, 2, 3, ….}

(iii) The set of rational numbers Q.
Q = {x: x = \(\frac{p}{q}\), p,q ∈ Z and q ≠ 0

(iv) Set of irrational numbers
T = {x : x e R and x ∉ Q} = R – Q.

Members of T are such as √2, √5, √7,…., π, etc.
Here, we observe that
N ⊂ Z ⊂ Q ⊂ R, T ⊂ R, N ⊄ T.
INTERVAL AS SUBSET OF R.
Let a, b ∈ R and a < b.

Open Interval : The set of real numbers {y : a <y < b} is called an open interval and is denoted by (a, b). Here all the points between a and b belong to the open interval (a, b), but a and b do not, belong to this interval.

Closed Interval: Closed interval is defined as {a, b = [x : a ≤ x ≤ b}.
All the points between a and b and the points a and b belong to \a,b).

Closed on the left and open to right: [a, b) = {x:a ≤ x < b}.
All the points between a and b and the point a belong to fa, b) but b does not belong to this interval.

Open on the left and closed to the right:
(a, b] = {x:a < x ≤ b}.
All the points between a and b and the point b belong to (a, 6] but a does not belong to it.

Super Set: If A is subset of B, then we say that B is a super set of A and is written as B ⊃ A.’

Some results on subsets :

• Every set is a subset of itself, i.e.,A⊂A, B⊂B, etc.
• The empty set is a subset of every set, i.e., Φ ⊂ A, Φ ⊂ B, etc.
• If A = B, then A ⊂ B and B ⊂ A.
• If A ⊂ B and B ⊂ A, then A = B.
• If A contains n elements, then A has 2ⁿ subsets.

Power Set : The collection of all subsets of a set A is called the power set of A. It is denoted by P(A). In P(A), every element is a set.

Proper Subset : If A is a subset of B but A ≠ B, then A is called a proper subset et P and is written as A ⊂ B. Thus, A is a proper subset of B only when every elemént of A is in B and B has at least one extra element than A.

Example: If A {1, 2. 3) and B = (1, 2, 3, 4). Then, A ⊂ B and A ≠ B. Therefore A ⊂ B.

Note : If A is a subset of B and A = B, then A is not a proper subset of B. In such a case, it is denoted as A ⊆ B.

Some results on proper subsets:

• If A ⊂ B and A ≠ B, then A ⊂ B.
• No set is a proper subset of itself.
• Φ is a proper subset of every set except itself.
• Φ has no proper subset.
• A set having n elements has (2ⁿ – 1) proper subsets.

Universal Set : If there are some sets under consideration, then there happens to be a set which is a superset of each one of the given sets. Such a set is called the universal set and it is denoted by U or ξ

Venn Diagrams : Most of the relationships between sets can be represented by means of diagrams. Figures representing sets in the form of enclosed region in the plane are called Venn diagrams. In these diagrams, the universal set is usually represented by a rectangular region and its subsets by bounded regions inside this rectangular region.

Venn Diagrams In Different Situations

1. A ⊂ U, where U is the universal set.

2. Two intersecting subsets of a universal set U.

3. Two disjoint subsets of a universal set U.

4. A⊂B⊂U, where U is the universal set.

Operation of sets : The main set operations are

1. Union of sets
2. Intersection of sets
3. Difference of sets.

Union of two sets: The union of two
sets A and B, denoted by A u B (read as A union B), is the set of all those elements which are either in A or in B or in both.

Symbolically:
A∪B = {x:x ∈ A or x ∈ B}.
Example: If A = {1, 2, 3, 4} and B = {2, 4, 6, 8}. Then,
A ∪ B = {1, 2, 3, 4}∪{2, 4, 6, 8} = {1, 2, 3, 4, 6, 8}.

Some results on union of sets :

• A⊂A⊂B and B⊂A∪B.
• If A ⊂B, then A∪B⊂B.

Intersection of sets : The intersection of two sets A and B, denoted by A ∩ B (read as A intersection B), is the set of all elements common to both A and B.

Symbolically:
A ∩ B=[x:x ∈ A and x ∈ B).
Example: If A = (1, 2, 3, 4} and B = {2, 4, 6, 8). Then,
A ∩ B = (l, 2,3, 4}∩{2, 4, 6,8} = {2, 4}.

Disjoint Sets : Two sets A and B are said to be disjoint, if A ∩ B = Φ. ,
If A ∩ B ≠ Φ, then A and B are called overlapping or intersecting sets.

Difference of two sets : The difference of two sets A a.nd B, denoted by A – B (read as A minus B), is the set of all those elements of A which are not in B.

Symbolically :
A-B = {x:x∈A and x ∉ B}.
Example: If A = {1, 2, 3, 4, 6, 12} and B = {1, 2, 4, 8, 16). Then,
A – B = {3, 6,12} and B – A = {8, 16}.
Note : In general A – B ≠ B – A.

Laws of Set Operations:

1. Commutative Laws : For any two sets A and B, we have :
(i) A∪B = B∪A (ii) A ∩ B = B ∩ A.

2. Associative Laws: For any three sets A, B and C, we have :
(i) (A∪B)∪C = A∪(B∪C), {ii) (A∩B)∩C = A∩(B∩C).

3. Distributive Laws : For any three sets A, B and C, we have:
(i) A∪(B∩C) = (A∪B)∩(A∪C).
(ii) A∩(B∪C) = (A∩B)∪(A∩C).

4. Idempotent Laws : If A is any set, then
(i) A∩A = A (ii) A∪A = A,

5. Identity Laws : If A is any subset of a universal set U and Φ is the null set, then
(i) A∩U = A (ii) A∩Φ = Φ
(iii) A∪Φ = A (iv) A∪U = U.

Complement of a set : If U be a Universal set and A is the subset of U, then complement of A with respect to U, denoted by A’ or A^c, is defined as A’ = {x 😡 ∈ U and x ∉ A}, i.e., the complement of A is the set of elements of U which are not the elements of A.

Properties of Complements:
(i) Complement Laws.
(a) A∪A’ = U (b) A∩A’ = Φ

(ii) De Morgan’s Laws.
(a) (A ∪ B)’ = A’∩ B’ (b) (A∩B)’=A’∪B’

(iii) Law of double Complementation (a)(A’)’ = A

(iv) Complement of Φ and ∪
(a) Φ’ = U (b) U’ = Φ.

Cardinal Number : n, the number of elements in a set is called the cardinal number of the set, denoted by n(A).

Example : A = {1, 2, 3, 4, 5} n(A) = 5, since A has 5 elements.

Cardinal Properties of Sets:

(а) n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
If A and B are disjoint , then
n(A ∪ B) = n(A) + n(B)

(b) n[A∪B∪C] = n(A) + n(B) + n(C) – n(A∩B) – n(B∩C) – n(C∩A) + n(A ∩B ∩ C).