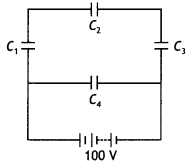
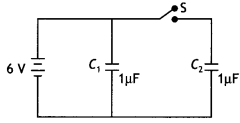
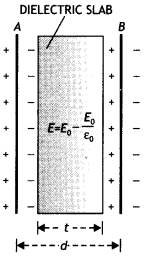
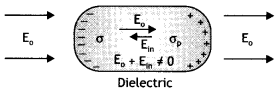
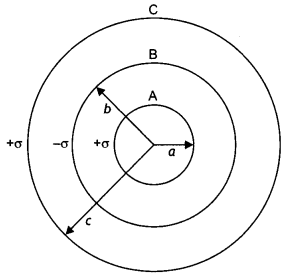
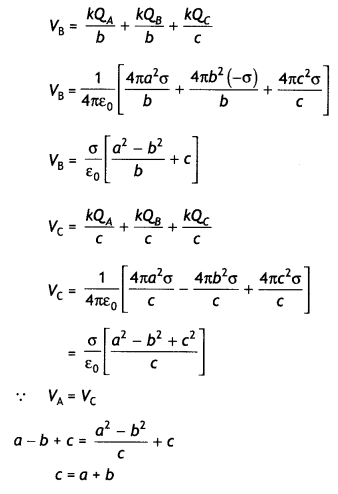
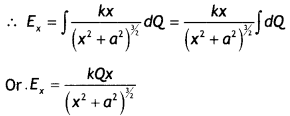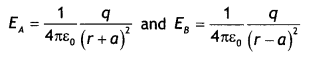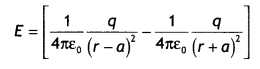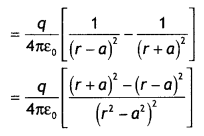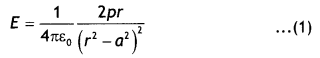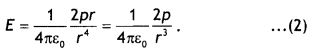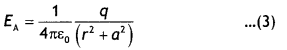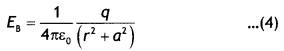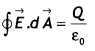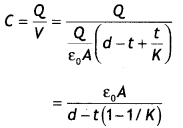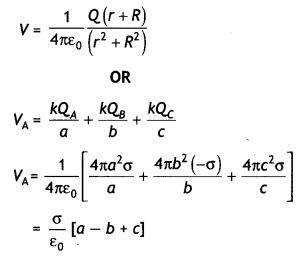Here we are providing Class 12 Physics Important Extra Questions and Answers Chapter 5 Magnetism and Matter. Important Questions for Class 12 Physics with Answers are the best resource for students which helps in Class 12 board exams.
Class 12 Physics Chapter 5 Important Extra Questions Magnetism and Matter
Magnetism and Matter Important Extra Questions Very Short Answer Type
Question 1.
A small magnetic needle pivoted at the center is free to rotate In a magnetic meridian. At what place will the needle
be vertical?
Answer:
At the potes
Question 2.
What is the angle of dip at a place where the horizontal and vertical components of the earth’s magnetic field are equal?
Answer:
450
Question 3.
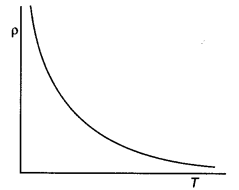
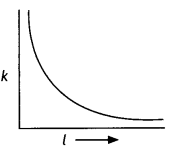
How does the intensity of a paramagnetic sample vary with temperature?
Answer:
it decreases with the increase in temperature.
Question 4.
What should be the orientation of a magnetic dipole in a uniform magnetic field so that its potential energy is maximum?
Answer:
It should be anti-parallel to the applied magnetic field.
Question 5.
What is the value of angle of dip at a place on the surface of the earth where the ratio of the vertical component to the horizontal component of the earth’s magnetic field is 1/\(\sqrt{3}\)?
Answer:
Using the expression tan δ = \(\frac{B_{V}}{B_{H}}=\frac{1}{\sqrt{3}}\)
Therefore, δ = 30°
Question 6.
Where on the surface of the earth is the angle of dip 90°? (CBSE Al 2011)
Answer:
Poles.
Question 7.
Where on the surface of the earth is the angle dip zero? (CBSE Al 2011)
Answer:
Magnetic equator
Question 8.
What are permanent magnets? Give one example. (CBSE Delhi 2013)
Answer:
It is an arrangement that has a permanent dipole moment, e.g. bar magnet.
Question 9.
At a place, the horizontal component of the earth’s magnetic field is B, and the angle of dip is 60°. What is the value of the horizontal component of the earth’s magnetic field at the equator? (CBSE Delhi 2017)
Answer:
Zero.
Question 10.
Is the steady electric current the only source of the magnetic field? Justify your answer. (CBSE Delhi 2013C)
Answer:
No, the magnetic field is also produced by alternating current.
Question 11.
Write one important property of a paramagnetic material. (CBSEAI2019)
OR
Do the diamagnetic substances have a resultant magnetic moment in an atom in the absence of an external magnetic field?
Answer:
It moves from the weaker to the stronger regions of the magnetic field.
OR
No
Question 12.
Steel is preferred for making permanent magnets, whereas soft iron is preferred for making electromagnets. Give one reason.
Answer:
- The Retentivity of steel is more than that of soft iron.
- Soft iron has a smaller value of coercivity than steel.
Question 13.
Define angle of inclination at a given place due to the earth’s magnetic field. (CBSE 2019C)
Answer:
The angle of inclination is the angle at which the earth’s magnetic field at a given place makes with the horizontal line in the magnetic meridian.
Question 14.
Relative permeability of a material p = 0.5. Identify the nature of the magnetic material and write its relation to magnetic susceptibility. (CBSE Delhi 2014C)
Answer:
Paramagnetic.
Susceptibility is small and greater than one.
Magnetism and Matter Important Extra Questions Short Answer Type
Question 1.
(a) Define the term magnetic susceptibility and write its relation in terms of relative magnetic permeability.
Answer:
It refers to the ease with which a substance can be magnetized. It is defined as the ratio of the intensity of magnetization to the magnetizing field. The required relation is µr = 1 + χm
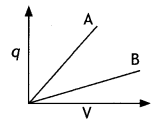
(b) Two magnetic materials A and B have relative magnetic permeabilities of 0. 96 and 500. Identify the magnetic materials A and B. (CBSE Al, Delhi 2018C)
Answer:
A: Paramagnetic,
B: Ferromagnetic
Question 2.
A magnetic needle free to rotate in a vertical position orients itself with its axis vertical at a certain place on the earth. What are the values of
(a) the angle of dip and
(b) the horizontal component of the earth’s magnetic field at this place? Where will this place be on the earth?
Answer:
The angle of dip is 90° and the horizontal component of the earth’s magnetic field is zero. This place is the magnetic pole of the earth.
Question 3.
Out of the two magnetic materials ‘A’ has relative permeability slightly greater than unity while ‘B’ has less than unity. Identify the nature of the materials ‘A’ and ‘B’. Will their susceptibilities be positive or negative? (CBSE Delhi 2014)
Answer:
- ‘A’ is paramagnetic and ‘B’ is diamagnetic.
- ‘A’ will have positive susceptibility while
- ‘B’ will have negative susceptibility.
Question 4.
A magnetic needle free to rotate in a vertical plane parallel to the magnetic meridian has its northern tip down at 60° with the horizontal. The horizontal component of the earth’s magnetic field at the place is known to be 0.4 G. Determine the magnitude of the earth’s magnetic field at the place. (CBSE Delhi 2011)
Answer:
Given δ = 30°, BH = 0.4 G, B = ?
Using the expression
BH = Bcos δ we have
B = \(\frac{B_{H}}{\cos \delta}=\frac{0.4}{\cos 30^{\circ}}=\frac{0.4}{\sqrt{3} / 2}=\frac{0.8}{\sqrt{3}}\) G
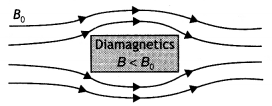
Question 5.
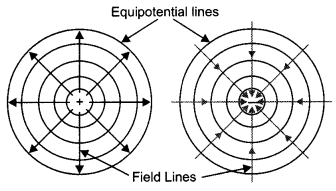
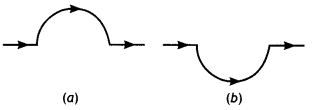
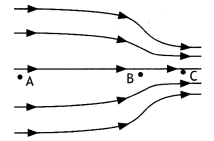
The susceptibility of a magnetic material is -0.085. Identify the type of magnetic material. A specimen of this material is kept in a non-uniform magnetic field. Draw the modified field pattern.
Answer:
The material is a diamagnetic material as diamagnetic materials have negative susceptibility. The modified field pattern is as shown below.
Question 6.
A uniform magnetic field gets modified as shown below when two specimens X and Y are placed in it.
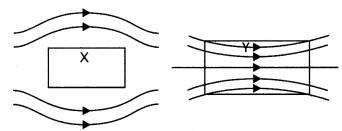
(a) Identify the two specimens X and Y.
Answer:
X is a diamagnetic substance and Y is a paramagnetic substance.
(b) State the reason for the behavior of the field lines in X and Y.
Answer:
This is because the permeability of a diamagnetic substance is less than one and that of a paramagnetic substance is greater than one.
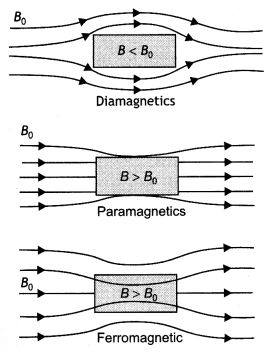
Question 7.
Three identical specimens of magnetic materials nickel, antimony, and aluminum are kept in a non-uniform magnetic field. Draw the modification in the field lines in each case. Justify your answer.
Answer:
Nickel is ferromagnetic, antimony is diamagnetic and aluminium is paramagnetic. Therefore, they will show the behavior as shown in the following figures.
Question 8.
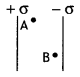
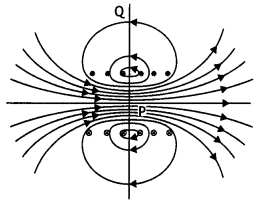
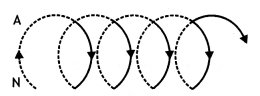
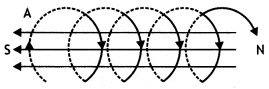
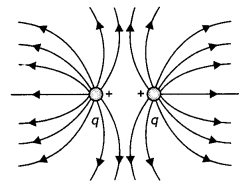
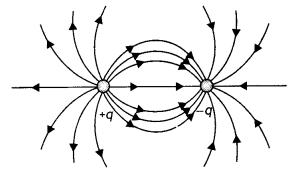
Define neutral point. Draw lines of force when two identical magnets are placed at a finite distance apart with their N-poles facing each other. Locate the neutral points.
Answer:
It is a point near a magnet where the magnetic field of the earth is completely balanced by the magnetic field of the magnet. The figure is as shown below.
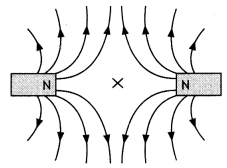
The cross indicates the neutral point.
Question 9.
The susceptibility of a magnetic material is -2.6 x 10-5. Identify the type of magnetic material and state its two properties. (CBSE Delhi 2012)
Answer:
Diamagnetic:
- Very small and negative susceptibility
- Permeability is less than one.
Magnetism and Matter Important Extra Questions Long Answer Type
Question 1.
Write the expression for the magnetic dipole moment for a closed current loop. Give its SI unit. Derive an expression for the torque experienced by a magnetic dipole in a uniform magnetic field.
Answer:
The required expression is m = nIA.
It is measured in A m².
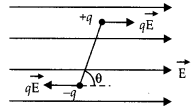
Consider a uniform magnetic field of strength B. Let a magnetic dipole be suspended in it such that its axis makes an angle 6 with the field as shown in the figure below. If ‘m’ is the strength of each pole, the two poles experience two equal and opposite force ‘B’ each. These forces constitute a couple that tends to rotate the dipole. Suppose the couple exerts a torque of magnitude τ.
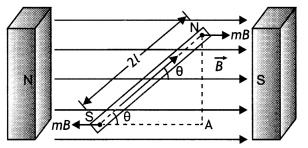
Then
τ = either force × arm of the couple
= mB × AN = mB × 2 L sin θ
or
Since m × 2L is the magnetic dipole moment of the magnet.
Therefore τ = MB sin θ in vector form
we have \(\vec{τ}\) = \(\vec{M}\) × \(\vec{B}\)
Question 2.
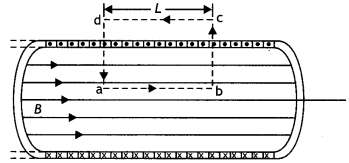
(a) State Gauss’s law for magnetism. Explain Its significance.
Answer:
(a) Gauss’s Law for magnetism states that “The total flux of the magnetic field, through any closed surface, is aLways
zero, i.e. ∮\(\vec{B}\).\(\vec{dL}\) = 0
This law implies that magnetic monopoles do not exist” or magnetic field lines form closed loops.
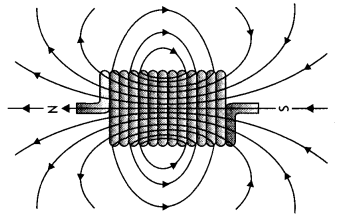
(b) Write the four Important properties of the magnetic field lines due to a bar magnet. (CBSE Delhi 2019)
Answer:
Four properties of magnetic field lines are as follows:
- Magnetic field lines always form continuous closed loops.
- The tangent to the magnetic field line at a given point represents the direction of the net magnetic field at that point.
- The larger the number of field lines crossing per unit area, the stronger is the magnitude of the magnetic field.
- Magnetic field lines do not intersect.
Question 3.
A short bar magnet placed with its axis at 30° with an external field of 800 G experiences a torque of 0.016 Nm.
(a) What is the magnetic moment of the magnet?
Answer:
(a) From equation τ = mB sin θ,
For θ = 30°, sin θ = 0.5
Thus, 0.016 = m × 800 × 10-4 × 0.5 or m = 160 × 2/800 = 0.40 Am²
(b) What is the work done in moving it from its most stable to a most unstable position?
Answer:
From equation U= -mB cos θ, the most stable position is for θ = 0° and the most unstable position is for θ = 180°.
Work done is given by
W = Um (θ = 180°) – Um for (θ = 0°)
= 2 mB = 2 × 0.40 × 800 × 10-4
= 0.064 J
(c) The bar magnet is replaced by a solenoid of cross-sectional area 2 × 10-4 m² and 1000 turns but of the same magnetic moment. Determine the current flowing through the solenoid. (NCERT Delhi 2005C)
Answer:
From part (i), m = 0.40 Am² Using equation m = NIA.
0.40 = 1000 × l × 2 × 10-4
l = 2 A
Question 4.
(a) What happens if a bar magnet is cut into two pieces: (i) transverse to its length and (ii) along its length?
Answer:
(a) In either case one gets two magnets each with a north pole and a south pole.
(b) A magnetized needle in a uniform magnetic field experiences a torque but no net force. An iron nail near a bar magnet, however, experiences a force of attraction in addition to torque. Why?
Answer:
The needle experiences no net force because the field is uniform.
The iron nail experiences a non¬uniform field due to the bar magnet. There is an induced magnetic moment in the nail; therefore, it experiences both force and torque.
The net force is attractive because the induced south pole (say) in the nail is closer to the north pole of the magnet than the induced north pole.
Question 5.
Name the elements of the earth’s magnetic field at a place. Explain their meaning.
Answer:
The elements required to completely specify the earth’s magnetic field are called magnetic elements. These elements are:
(a) Declination (θ)
(b) Dip or inclination (δ)
(c) Horizontal component of the earth’s magnetic field (BH).
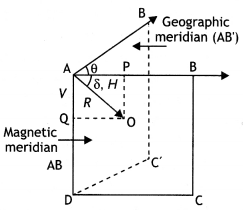
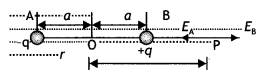
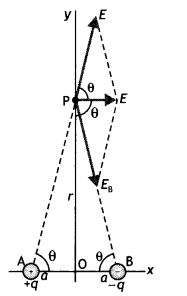
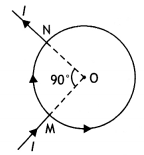
(a) Declination (θ): Declination at a place is defined as the acute angle between the magnetic meridian and the geographic meridian.
In the figure above ∠BAB’ = θ is called the angle of declination. There are several periodic variations in the value of declination for a given location.
(b) Dip (δ): Dip at a place is defined as the angle between the direction of the total intensity of the earth’s magnetic field and a horizontal line in the magnetic meridian at that place. It is denoted by 8.
Suppose a freely suspended magnet aligns itself along the direction AB as shown in the figure, then this gives the direction of the earth’s total magnetic field at that place. Then the angle ∠BAO = δ is called the angle of dip or simply dip at that point.
(c) Horizontal component of the earth’s magnetic field (BH): It is the component of the total intensity of the earth’s magnetic field along a horizontal line in the magnetic meridian. It is denoted by BH or H.
Question 6.
Name the three types of magnetic materials which behave differently when placed in a non-uniform magnetic field. Give two properties for each of them.
Answer:
The three types of magnetic materials are
(a) Diamagnetic
(b) Paramagnetic and
(c) Ferromagnetic
| Diamagnetic | Paramagnetic | Ferromagnetic |
| These are the substances that are feebly repelled by a magnet, e.g., Bi, Zn, Cu, Ag, Au, diamond, C, NaCI, H20, Hg, N2, H2, etc. Exhibited by solids, liquids, and gases. | These are the substances that are feebly attracted by a magnet, e.g., AL, Na, Pt, Mn, CuCL2, O2, etc. Exhibited by solids, liquids, and gases. | These are the substances that are strongly attracted by a magnet, e.g., Fe, Ni, Co, Fe304, etc. Exhibited by solids only, that too crystalline. |
| When a diamagnetic substance is placed in a magnetizing field, the Lines of force prefer not to pass through the substance. | When a paramagnetic substance is placed in a magnetizing field, the Lines of force prefer to pass through the substance. | When a ferromagnetic substance is placed in a magnetizing field, the Lines of force prefer to pass through the substance. |
Question 7.
The susceptibility of a magnetic material is 0-9853. Identify the type of magnetic material. Draw the modification of the field pattern on keeping a piece of this material in a uniform magnetic field. (CBSEAI, Delhi 2018)
Answer:
We know that the susceptibility of a paramagnetic substance is positive but small. Hence, the given magnetic material is paramagnetic in nature.
When a specimen of a paramagnetic substance is placed in a magnetizing field, the magnetic field lines prefer to pass through the specimen rather than through air. Thus, magnetic induction 6 inside the sample is more than the magnetic induction B0 outside the sample.
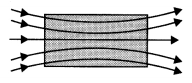
Question 8.
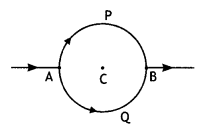
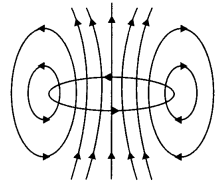
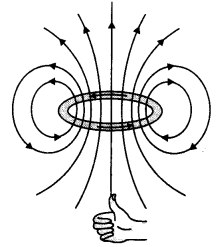
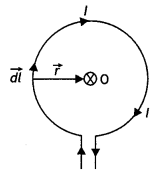
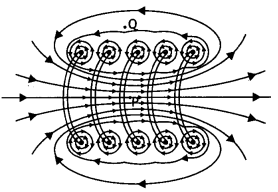
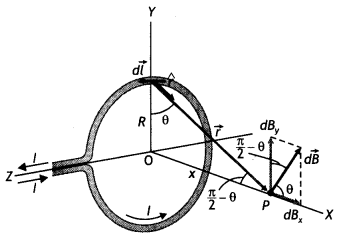
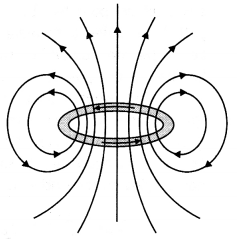
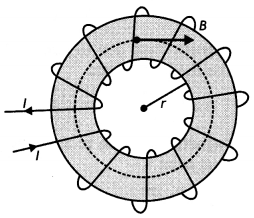
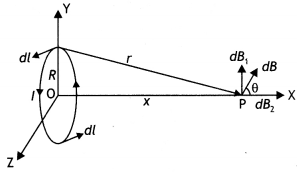
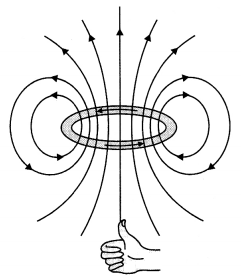
(a) Draw the magnetic field lines due to a circular loop of area \(\vec{A}\) carrying current l. Show that it acts as a bar magnet of magnetic moment \(\vec{m}\) = I \(\vec{A}\).
Answer:
(a) The magnetic field lines are as shown.
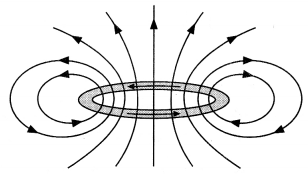
Magnetic field due to circular loop on its axis at far off points B = \(\frac{\mu_{0}}{4 \pi} \frac{2 l A}{x^{3}}\)
Magnetic field due to a bar magnet at its axial point is B = \(\frac{\mu_{0}}{4 \pi} \frac{2 m}{x^{3}}\)
Comparing the above two we have m = IA
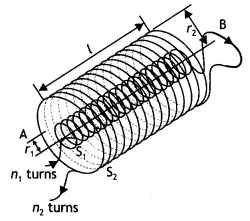
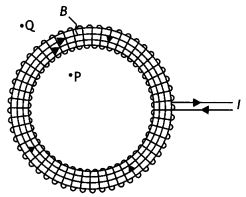
(b) Derive the expression for the magnetic field due to a solenoid of length ‘21’, radius ‘a’ having ‘n’ number of turns per unit length and carrying a steady current T at a point on the axial line, distant ‘r’ from the center of the solenoid. How does this expression compare with the axial magnetic field due to a bar magnet of the magnetic moment ‘m’? (CBSEAI 2015)
Answer:
(b) By the-Biot-Savarts law, the magnetic field at point P on the axis of the solenoid due to a small element of length dx at a distance ‘x’ from the center of the solenoid is
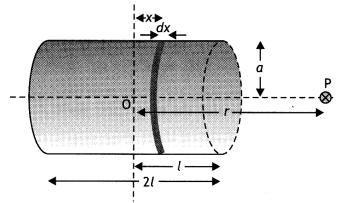
dB = \(\frac{\mu_{0} n d x / a^{2}}{2\left[(r-x)^{2}+a^{2}\right]^{3 / 2}}\)
Hence total magnetic field is given by
B = ∫dB = \(\frac{\mu_{0} / a^{2} n^{+L}}{2} \int_{-L}^{d x} \frac{d x}{\left[(r-x)^{2}+a^{2}\right]^{3 / 2}}\)
For r >> a (R >> L)
We have
B = ∫dB = \(\frac{\mu_{0} / a^{2} n^{+L}}{2 r^{3}} \int_{-L}^{+L} d x=\frac{\mu_{0} \ln }{2} \frac{2 L a^{2}}{r^{3}}\)
Magnetic moment of a solenoid
m = (n × 2L) I (πa²)
Therefore,
B = \(\frac{\mu_{0}}{4 \pi} \frac{2 m}{r^{3}}\) as that of a bar magnet.
Numerical Problems :
- Torque on a magnetic dipole τ = MB sin θ
- Potential energy of a magnetic dipole U = – MB cos θ
- \(B_{H}^{2}+B_{v}^{2}=B^{2}\)
- tan θ = \(\frac{B_{V}}{B_{H}}\)
- H = B cos δ
- V = B sin δ
Question 1.
A bar magnet of the magnetic moment 6 J T1 is aligned at 60° with a uniform external magnetic field of 0 – 44 T. Calculate
(a) the work is done in turning the magnet to align its magnetic moment (i) normal to the magnetic field and (ii) opposite to the magnetic field and
Answer:

(b) the torque on the magnet in the final orientation in case (ii). (CBSEAI, Delhi 2018)
Answer:
τ = M × B sin θ2
= 6 × 0.44 × sin 180° = 0
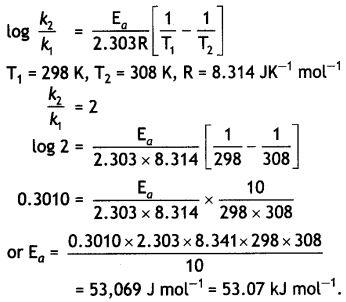
Question 2.
A short bar magnet placed with its axis at 30° with a uniform external magnetic field of 0.25 T experiences a torque of magnitude equal to 4.5 x 10-2 J. What is the magnitude of the magnetic moment of the magnet?
Answer:
Given θ = 30°, B = 0.25 T, τ = 4.5 × 10-2 J,M = ?
Using the expression τ = MB sin θ we have
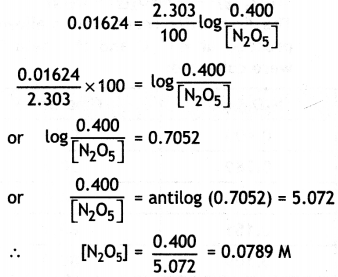
M = \(\frac{\tau}{B \sin \theta}=\frac{4.5 \times 10^{-2}}{0.25 \times \sin 30^{\circ}}\) = 0.36 J T-1


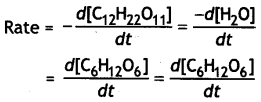

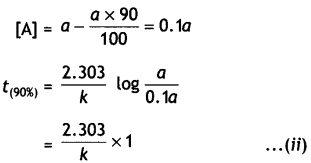
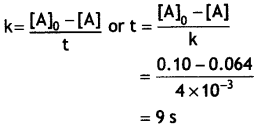
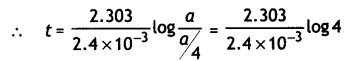
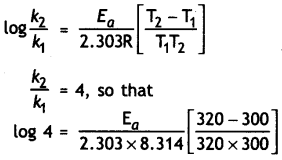
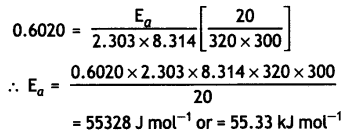
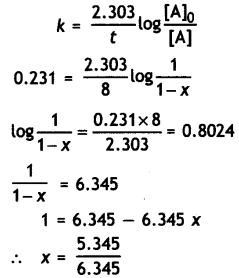
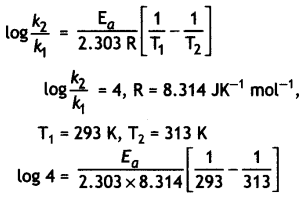






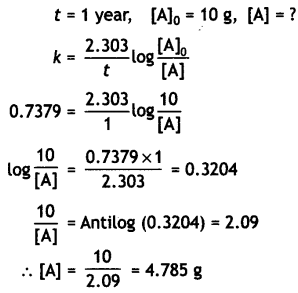


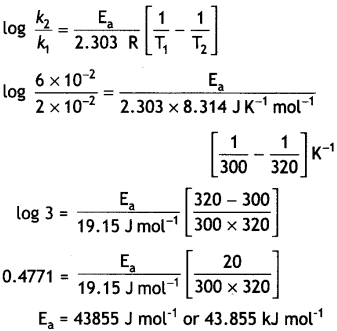


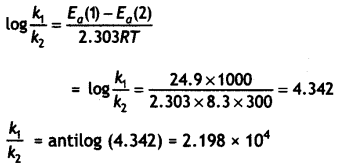

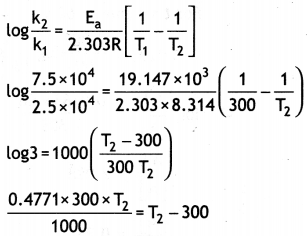




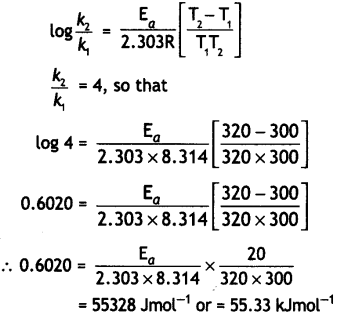



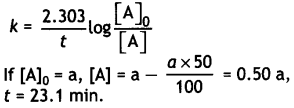





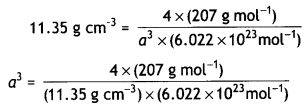
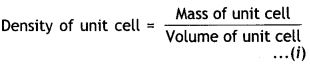

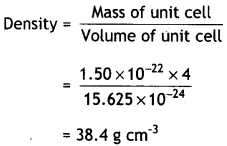
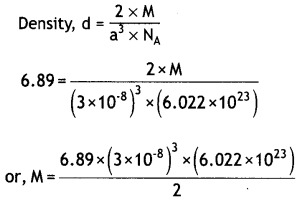
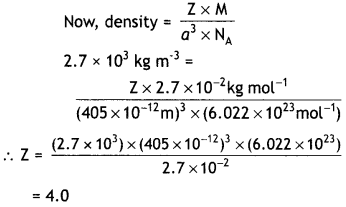

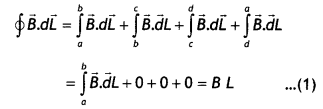
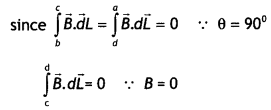
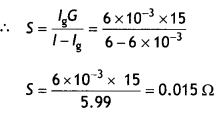
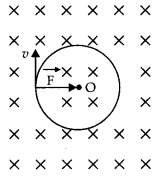
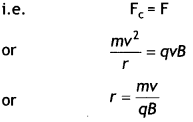
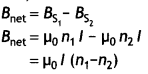
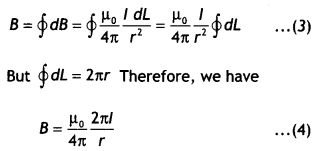
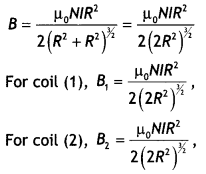
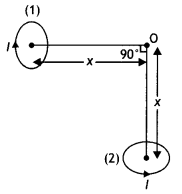
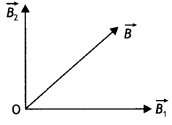
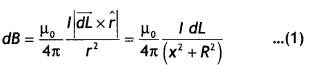
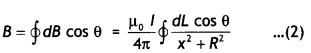
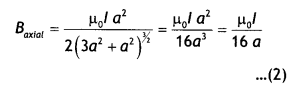
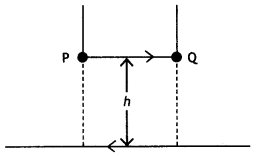
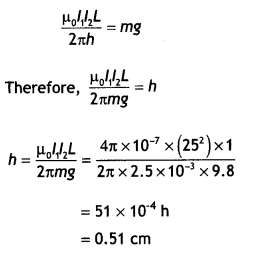
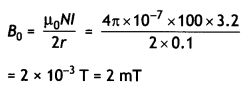
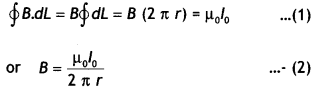
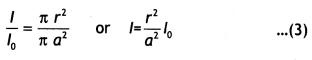
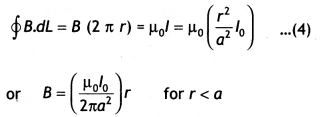
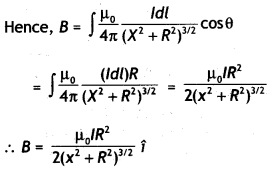
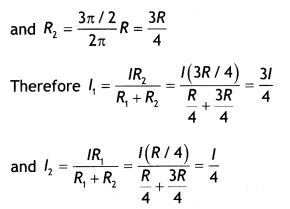
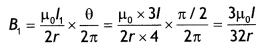
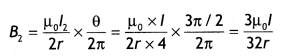
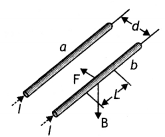
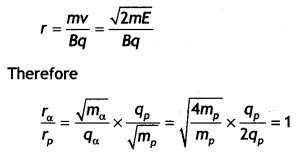
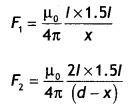
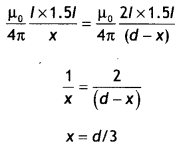
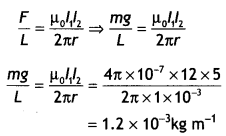
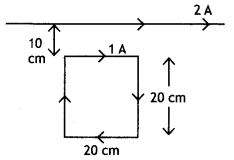
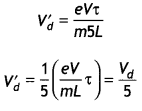
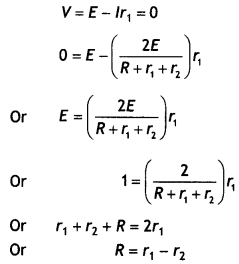
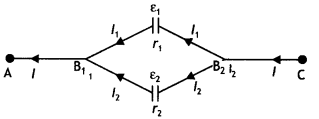
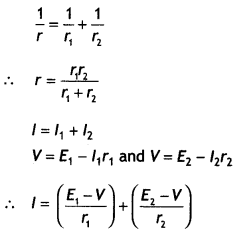
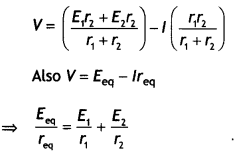
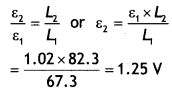
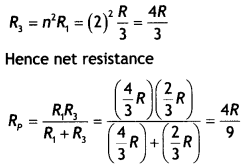
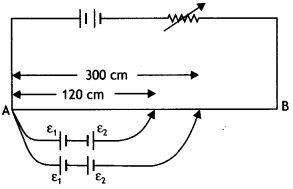
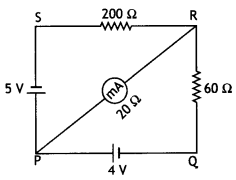
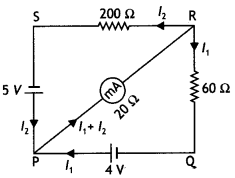
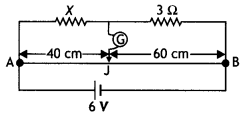
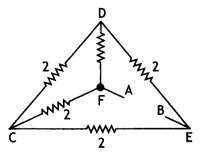
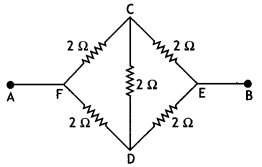
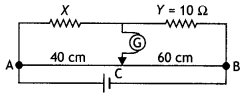
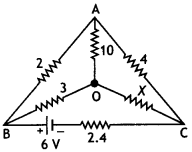

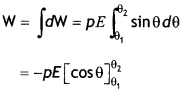
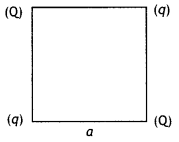
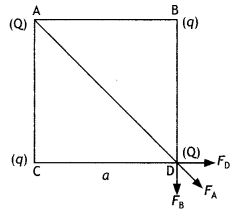
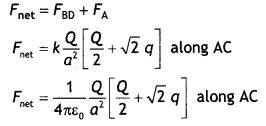
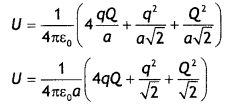
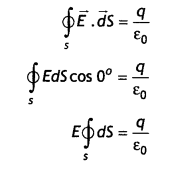
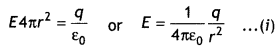
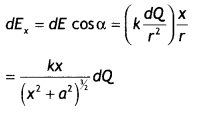 …(2)
…(2)