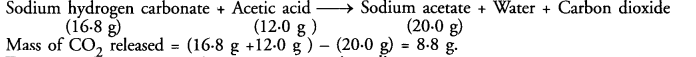HOTS Questions for Class 9 Science Chapter 7 Diversity in Living Organisms
These Solutions are part of HOTS Questions for Class 9 Science. Here we have given HOTS Questions for Class 9 Science Chapter 7 Diversity in Living Organisms
Question 1.
(a) Identify figures A to F.
(b) Which one of them is unicellular and eukaryotic organism ?
(c) Which one of them shows
- Heterotrophic nutrition
- Mixotrophic nutrition ?
(d) Which one of them is non-vascular embryophyte ?
(e) In which of them, xylem lacks vessels while phloem is devoid of companion cells ?
(f) In which of them endosperm is halpoid ?
(g) Which of them is commonly called
- Bread Mould
- Male Shield Fern ?
Answer:
(a) Identification.
A-Fern (Male Shield Fern, Dryopteris)
B-Moss (Funaria).
C—Pinus.
D—Spirogyra.
E—Euglena.
F-Rhizopus.
(b) Unicellular Eukaryotic Organism. Euglena.
(c)
- Heterotrophic Nutrition. Rhizopus.
- Mixotrophic Nutrition. Euglena.
(d) Non-vascular Embryophyte. Moss (Funaria)
(e) Xylem without Vessels and Phloem without Companion Cells. Pinus.
(f) Haploid Endosperm. Pinus
(g)
- Bread Mould._Rhizopus.
- Male Shield Fern. Dryopteris.
More Resources
- HOTS Questions for Class 9 Science
- NCERT Solutions for Class 9 Science
- Value Based Questions in Science for Class 9
- NCERT Exemplar Solutions for Class 9 Science
- Previous Year Question Papers for CBSE Class 9 Science
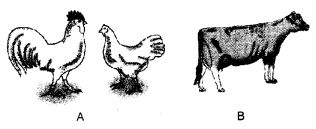
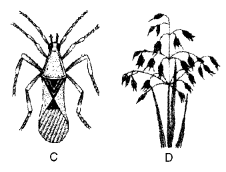
Question 2.
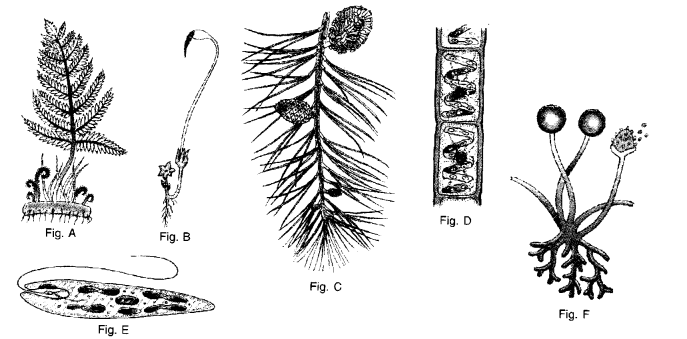
(a) Identify figure A to D.
(b) Which one belongs to
- Platyhelminthes
- Arthropoda
- Annelida ?
(c) Which one of them has
- Tissue level organisation
- Primitive organ level organisation ?
(d) Which one of them has
- Flame cells as exretory organs
- Nephridia as excretory organs ?
(e) Which one of them has poison claw ?
(f) Which one of them is
- Diploblastic
- Triploblastic ?
Answer:
(a) Identification.
A-Centipede.
B-Hydra.
C-Liverfluke {Fasciola).
D- Earthworm {Pheretima posthuma).
(b)
- Plathyhelminthes—Liverfluke (Fasciola)
- Arthropoda-Centipede (Scolopendra).
- Annelida-Earthworm {Pheretima posthuma).
(c)
- Tissue Level Organisation. Hydra.
- Primitive Organ Level Organisation. Liverfluke (Fasciola)
(d)
- Flame Cells. Liverfluke (Fasciola)
- Nephridia. Earthworm {Pheretima posthuma)
(e) Poison Claw. Centipede {Scolopendra)
(f)
- Diploblastic. Hydra.
- Triploblastic. Liverfluke {Fasciola), Centipede (Scolopendra), Earthworm {Pheretima posthuma).
Question 3.
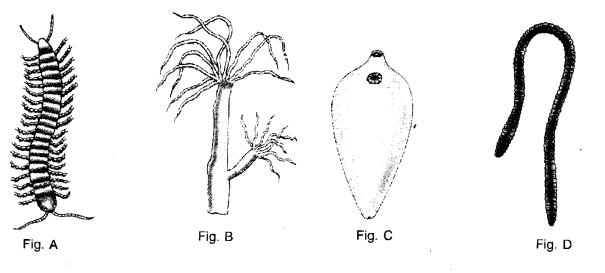
(a) Identify the figure and write down the phylum to which it belongs.
(b) Which type of
- Locomotory organ is present in it.
Circulatory system is present in it.
(c) Which type of symmetry is present ?
Answer:
(a) Identification. Pila (Apple Snail). Phylum. Mollusca.
(b)
- Locomotory Organ. Foot,
- Circulatory System. Open (Haemocoel).
(c) Symmetry. Asymmetry due to torsion (spirally coiled).
Question 4.
(a) Label W, X, Y and Z.
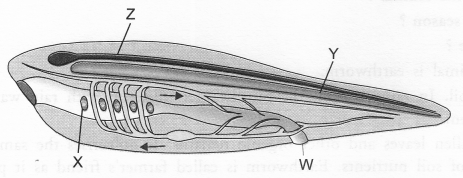
(b) Identify the above diagram.
(c) Name the phylum in which notochord is present.
(d) Name the subphylum in which notochord is present throughout life.
Answer:
(a) W-Anus.
X-Gill slits.
Y-Notochord.
Z-Nerve cord.
(b) Identification. Basic characteristics of chordates.
(c) Phylum with Notochord. Chordata.
(d) Subphylum with Notochord throughout Life. Cephalochordata.
Hope given HOTS Questions for Class 9 Science Chapter 7 Diversity in Living Organisms are helpful to complete your science homework.
If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.
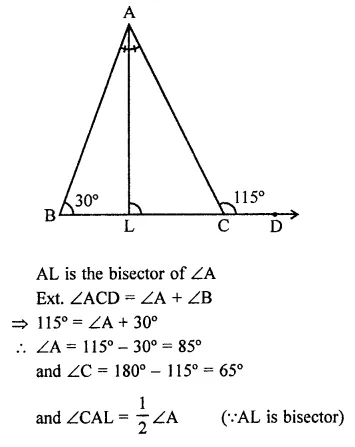
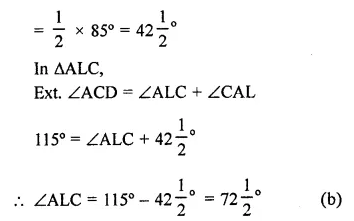
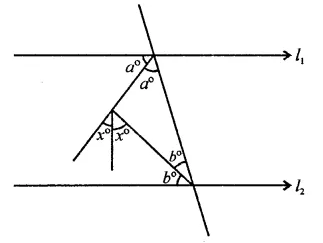
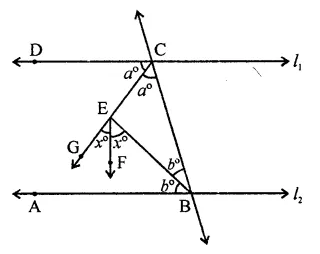
 Solution:
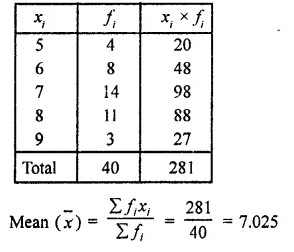
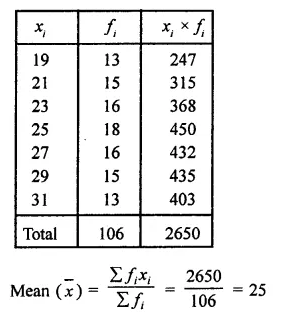
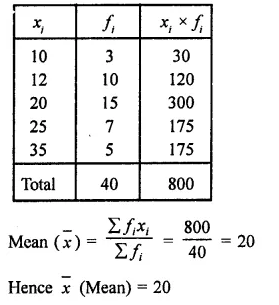
Solution:
















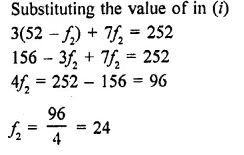


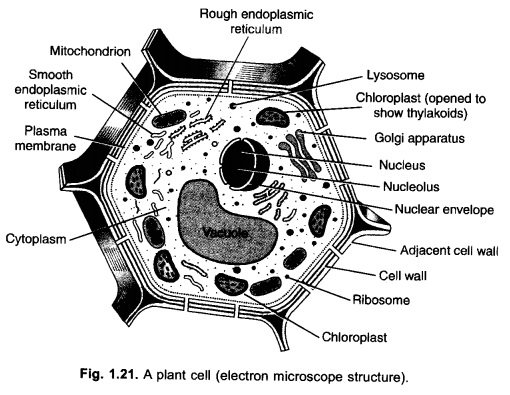
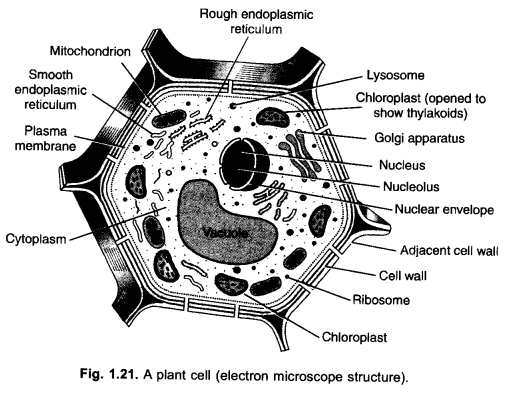

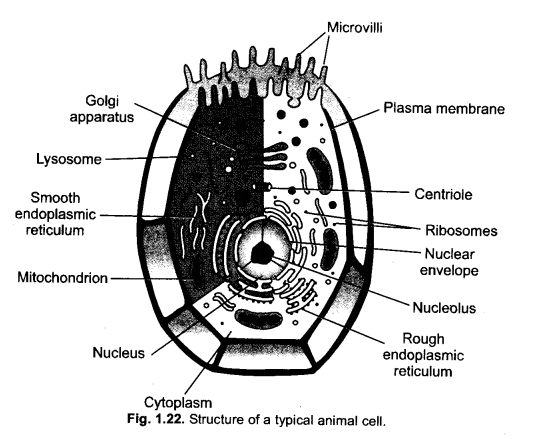
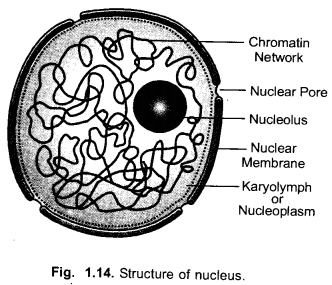

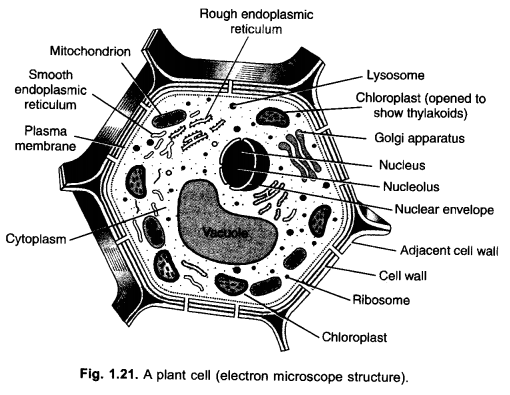
 (b) Membrane Biosynthesis : Both the types of E.R. take part in membrane biosynthesis. Rough endoplasmic reticulum synthesises proteins which are passed over to Golgi apparatus for glycolisation. Smooth endoplasmic reticulum forms lipids over its surface. They are also transported to Golgi apparatus. Golgi apparatus builds membrane with the help of lipids and proteins.
(b) Membrane Biosynthesis : Both the types of E.R. take part in membrane biosynthesis. Rough endoplasmic reticulum synthesises proteins which are passed over to Golgi apparatus for glycolisation. Smooth endoplasmic reticulum forms lipids over its surface. They are also transported to Golgi apparatus. Golgi apparatus builds membrane with the help of lipids and proteins.