Category: CBSE Class 9

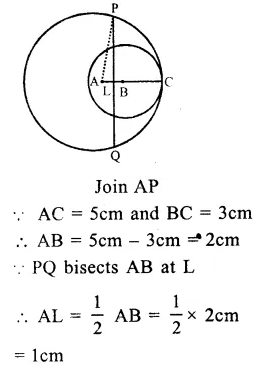
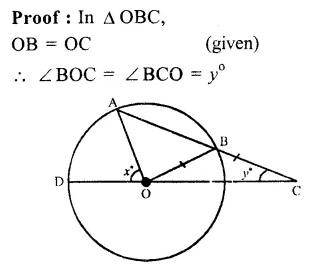
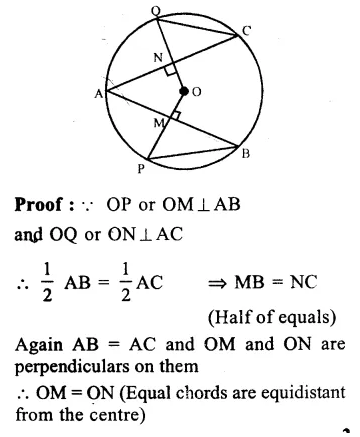
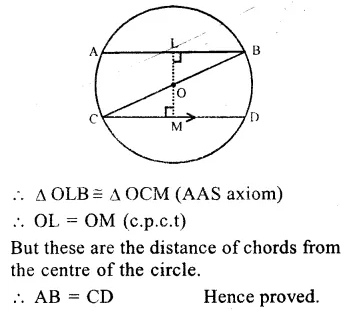
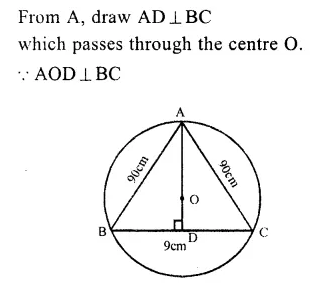
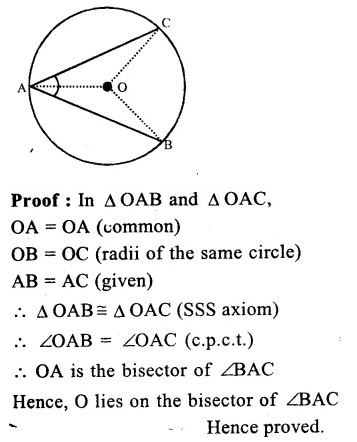
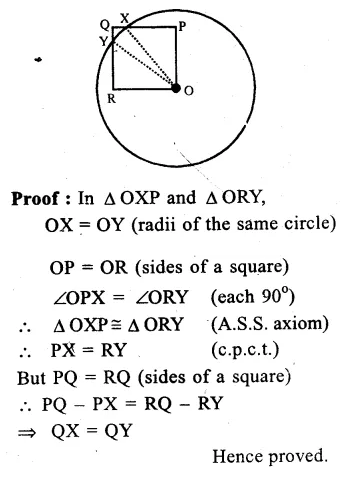
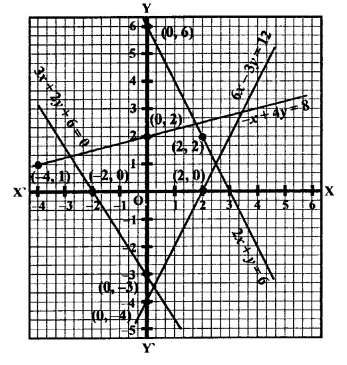
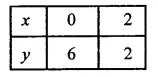
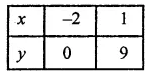
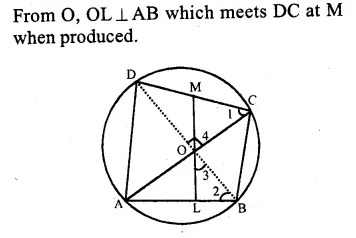
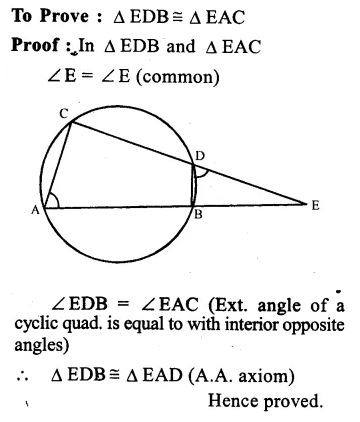
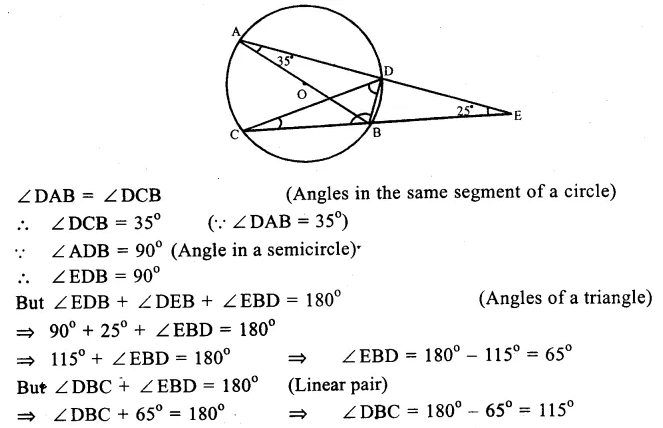
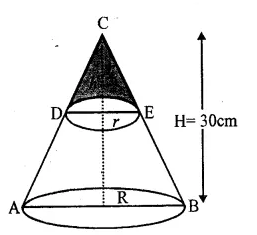
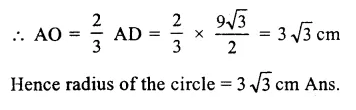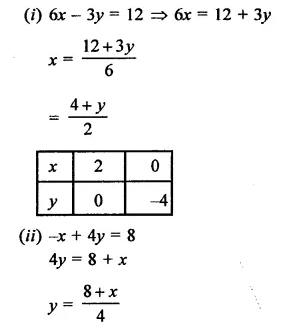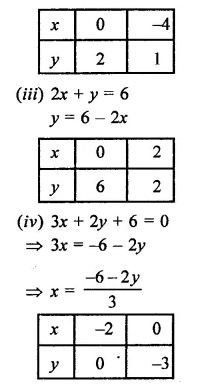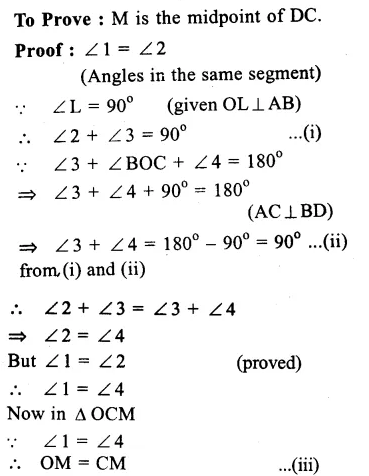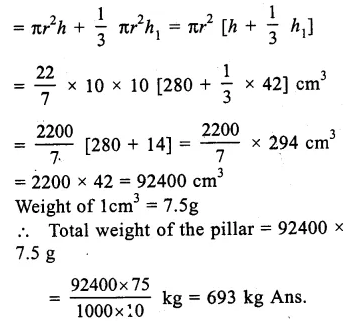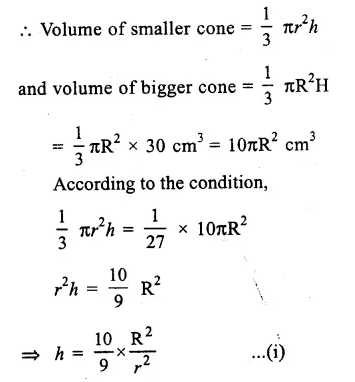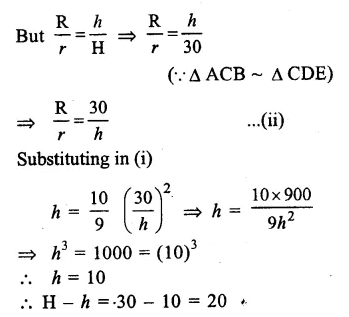RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles VSAQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles VSAQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.1
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.2
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.3
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.4
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles VSAQS
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles MCQS

Question 1.
Define complementary angles.
Solution:
Two angles whose sum is 90°, are called complementary angles.

Question 2.
Define supplementary angles.
Solution:
Two angles whose sum is 180°, are called supplementary angles.

Question 3.
Define adjacent angles.
Solution:
Two angles which have common vertex and one arm common are called adjacent angles.

Question 4.
The complement of an acute angles is…….
Solution:
The complement of an acute angles is an acute angle.

Question 5.
The supplement of an acute angles is………
Solution:
The supplement of an acute angles is a obtuse angle.

Question 6.
The supplement of a right angle is…….
Solution:
The supplement of a right angle is a right angle.

Question 7.
Write the complement of an angle of measure x°.
Solution:
The complement of x° is (90° – x)°

Question 8.
Write the supplement of an angle of measure 2y°.
Solution:
The supplement of 2y° is (180° – 2y)°

Question 9.
If a wheel has six spokes equally spaced, then find the measure of the angle between two adjacent spokes.
Solution:
Total measure of angle around a point = 360°
Number of spokes = 6
∴ Angle between the two adjacent spokes = \(\frac { { 360 }^{ \circ } }{ 6 }\) = 60°

Question 10.
An angle is equal to its supplement. Determine its measure.
Solution:
Let required angle = x°
Then its supplement angle = 180° – x
x = 180° – x
⇒ x + x = 180°
⇒  2x = 180° ⇒  x = \(\frac { { 180 }^{ \circ } }{ 2 }\) = 90°
∴ Required angle = 90°

Question 11.
An angle is equal to five times its complement. Determine its measure.
Solution:
Let required measure of angle = x°
∴  Its complement angle = 90° – x
∴  x = 5(90° – x)
⇒  x = 450° – 5x
⇒  x + 5x = 450°
⇒  6x = 450°
⇒ x = \(\frac { { 450 }^{ \circ } }{ 6 }\) = 75°
∴ Required angle = 75°

Question 12.
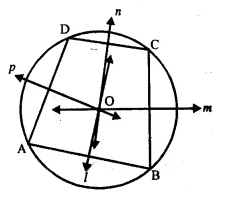
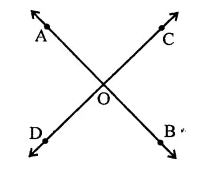
How many pairs of adjacent angles are formed when two lines intersect in a point?
Solution:
If two lines AB and CD intersect at a point O, then pairs of two adjacent angles are, ∠AOC and ∠COB, ∠COB and ∠BOD, ∠BOD and DOA, ∠DOA and ∠ZAOC
i.e, 4 pairs

Hope given RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency MCQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency MCQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.1
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.2
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.3
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.4
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency VSAQS
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency MCQS

Mark the correct alternative in each of the following:

Question 1.
Which one of the following is not a measure of central value?
(a) Mean
(b) Range
(c) Median
(d) Mode
Solution:
Range (b)

Question 2.
The mean of n observations is \(\overline { X } \) . If k is added to each observation, then the new mean is
(a) \(\overline { X } \)
(b) \(\overline { X } \) + k
(c) \(\overline { X } \) – k
(d) k\(\overline { X } \)
Solution:
Mean of n observation = \(\overline { X } \)
By adding k to each observation the new mean will be \(\overline { X } \) + k (b)

Question 3.
The mean of n observations is \(\overline { X } \) . If each observation is multiplied by k, the mean of new observations is
(a) k\(\overline { X } \)
(b) \(\frac { \overline { X } }{ k } \)
(c) \(\overline { X } \) + k
(d) \(\overline { X } \) – k
Solution:
Mean of n observations = \(\overline { X } \)
By multiplying each observation by k,
the new mean = k\(\overline { X } \) (a)

Question 4.
The mean of a set of seven numbers is 81. If one of the numbers is discarded, the mean of the remaining numbers is 78. The value of discarded number is
(a) 98
(b) 99
(c) 100
(d) 101
Solution:
Mean of 7 numbers = 81
Total = 7 x 81 = 567
By discarding one number, the mean of the remaining 7 – 1 = 6 numbers = 78
Total = 6 x 78 = 468
Discarded number = 567 – 468 = 99 (b)

Question 5.
For which set of numbers do the mean, median and mode all have the same value?
(a) 2, 2, 2, 2, 4
(b) 1, 3, 3, 3, 5
(c) 1, 1, 2, 5, 6
(d) 1, 1, 1, 2, 5
Solution:
a) In set 2, 2, 2, 2, 4

Mode = 3 as it come in maximum times
This set has mean, median and mode same (b)

Question 6.
For the set of numbers 2, 2, 4, 5 and 12, which of the following statements is true?
(a) Mean = Median
(b) Mean > Mode
(c) Mean < Mode
(d) Mode = Median
Solution:
The given set is 2, 2, 4, 5, 12

Question 7.
If the arithmetic mean of 7, 5, 13, x and 9 is 10, then the value of x is
(a) 10
(b) 12
(c) 14
(d) 16
Solution:
Arithmetic mean of 7, 5, 13, x, 9 is 10

Question 8.
If the mean of five observations x, x + 2, x + 4, x + 6, x + 8, is 11, then the mean of first three observations is
(a) 9
(b) 11
(c) 13
(d) none of these
Solution:
Mean = 11
But mean of x, x + 2, x + 4, x+ 6, x + 8

Question 9.
Mode is
(a) least frequent value
(b) middle most value
(c) most frequent value
(d) none of these
Solution:
Mode is most frequent value (c)

Question 10.
The following is the data of wages per day: 5, 4, 7, 5, 8, 8, 8, 5, 7, 9, 5, 7, 9, 10, 8 The mode of the data is
(a) 7
(b) 5
(c) 8
(d) 10
Solution:
Wages per day
5, 4, 7, 5, 8, 8, 8, 5, 7, 9, 5, 7, 9, 10, 8
=> 4, 5, 5, 5, 5, 7, 7, 7, 8, 8, 8, 8, 9, 9, 10
Here 8 comes in maximum times
Mode = 8 (c)

Question 11.
The median of the following data :
is ,
(a) 0
(b) -1.5
(c) 2
(d) 3.5
Solution:
Arranging in ascending order,
-3, -3, -1, 0, 2, 2, 2, 5, 5, 5, 5, 6, 6, 6

Question 12.
The algebraic sum of the deviations of a set of n values from their mean is
(a) 0
(b) n – 1
(c) n
(d) n + 1
Solution:
The algebraic sum of deviation of a set of n values from that mean

Question 13.
A, B, C are three sets of values of X:
A : 2, 3, 7, 1, 3, 2, 3
B: 7, 5, 9, 12, 5, 3, 8
C: 4, 4, 11, 7 ,2, 3, 4
Which one of the following statements is
correct?
(a) Mean of A = Mode of C
(b) Mean of C = Median of B
(c) Median of B = Mode of A
(d) Mean, Median and Mode of A are equal.
Solution:
Arranging the sets in ascending order
A{2, 3, 7, 1,3,2,3)
= {1, 2, 2, 3, 3, 3, 7)
B = {7, 5, 9, 12, 5, 3, 8)
= {3, 5, 5, 7, 8, 9, 12)
C = {4, 4, 11,7,2,3,4)
= {2, 3, 4, 4, 4, 7, 11)

Mode = 5 {as it comes max times}
(c) Mean of set C = \(\\ \frac { 2+3+4+4+4+7+11 }{ 7 } \)
= \(\\ \frac { 35 }{ 7 } \) = 5
Median = \(\\ \frac { 7+1 }{ 2 } \) th =\(\\ \frac { 8 }{ 2 } \) =4th term = 4
Mode =4 {as it comes max times}
In set A,mean = median = mode = 3 (d)

Question 14.
The empirical relation between mean, mode and median is
(a) Mode = 3 Median — 2 Mean
(b) Mode 2 Median — 3 Mean
(c) Median 3 Mode — 2 Mean
(d) Mean = 3 Median —2 Mode
Solution:
The empirical relations between mean, mode
and median is
Mode = 3 Median — 2 Mean (a)

Question 15.
The mean of a, b, c, d and e is 28. If the mean of a, c, and e is 24, what is the mean of b and d?
(a) 31
(b) 32
(c) 33
(d) 34
Solution:
Mean of a, b, c, d and e = 28
Total of a, b, c, d and e = 28 x 5 = 140
Mean of a, c and e is = 24
Total of a, c, e = 24 x 3 = 72
Total of b and d = 140 – 72 = 68
Mean = \(\\ \frac { 68 }{ 2 } \) = 34 (d)

Hope given RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.4

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.4

Other Exercises

• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.1
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.2
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.3
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.4
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency VSAQS
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency MCQS

Question 1.
Find out the mode of the following marks obtained by 15 students in a class:
Marks : 4, 6, 5, 7, 9, 8, 10, 4, 7, 6, 5, 9, 8, 7, 7.
Solution:
Marks obtained are in ascending order,
4, 4, 5, 5, 6, 6, 7, 7, 7, 7, 8, 8, 9, 9, 10
Here we see that 7 is the number which is maximum times i.e. 4 times
Mode = 7

Question 2.
Find the mode for the following data:
125, 175, 225, 125, 225, 175, 325, 125, 375, 225, 125
Solution:
Arranging in ascending order,
125, 125, 125, 125, 175, 175, 225, 225, 225, 325, 375
We see that, 125 is the number which is in maximum times
Mode = 125

Question 3.
Find the mode for the following series:
7.5, 7.3, 7.2, 7.2, 7.4, 7.7, 7.7, 7.5, 7.3, 7.2, 7.6, 7.2
Solution:
Arranging in ascending order,
7.2, 7.2, 7.2, 7.2, 7.3, 7.3, 7.4, 7.5, 7.5, 7.6, 7.7, 7.7
We see that 7.2 comes in maximum times
Mode = 7.2

Question 4.
Find the mode of the following data in each case:
(i) 14, 25, 14, 28, 18, 17, 18, 14, 23, 22, 14, 18
(ii) 7, 9, 12, 13, 7, 12, 15, 7, 12, 7, 25, 18, 7
Solution:
(i) 14, 25, 14, 28, 18, 17, 18, 14, 23, 22, 14, 18
Arranging in ascending order,
14, 14, 14,. 14, 17, 18, 18, 18, 22, 23, 25, 28
Here we see that 14 comes in maximum times
Mode = 14
(ii) 7, 9, 12, 13, 7, 12, 15, 7, 12, 7, 25, 18, 7
Arranging in order,
7, 7, 7, 7, 7, 9, 12, 12, 12, 13, 15, 18, 25
Here we see that 7 comes in maximum times
Mode = 7

Question 5.
The demand of different shirt sizes, as obtained by a survey, is given below:

Find the modal shirt sizes, as observed from the survey.
Solution:
From the given data

From above, we see that
Modal size is 39 as it has maximum times persons

Hope given RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry VSAQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry VSAQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.1
• RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2
• RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry VSAQS
• RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry MCQS

Question 1.
Define a triangle.
Solution:
A figure bounded by three lines segments in a plane is called a triangle.

Question 2.
Write the sum of the angles of an obtuse triangle.
Solution:
The sum of angles of an obtuse triangle is 180°.

Question 3.
In ∆ABC, if ∠B = 60°, ∠C = 80° and the bisectors of angles ∠ABC and ∠ACB meet at a point O, then find the measure of ∠BOC.
Solution:
In ∆ABC, ∠B = 60°, ∠C = 80°
OB and OC are the bisectors of ∠B and ∠C
∵ ∠A + ∠B + ∠C = 180° (Sum of angles of a triangle)
⇒ ∠A + 60° + 80° = 180°
⇒ ∠A + 140° = 180°
∴ ∠A = 180°- 140° = 40°

= 90° + – x 40° = 90° + 20° = 110°

Question 4.
If the angles of a triangle are in the ratio 2:1:3. Then find the measure of smallest angle.
Solution:
Sum of angles of a triangle = 180°
Ratio in the angles = 2 : 1 : 3
Let first angle = 2x
Second angle = x
and third angle = 3x
∴ 2x + x + 3x = 180° ⇒ 6x = 180°
∴ x = \(\frac { { 180 }^{ \circ } }{ 6 }\)  = 30°
∴ First angle = 2x = 2 x 30° = 60°
Second angle = x = 30°
and third angle = 3x = 3 x 30° = 90°
Hence angles are 60°, 30°, 90°

Question 5.
State exterior angle theorem.
Solution:
Given : In ∆ABC, side BC is produced to D

To prove : ∠ACD = ∠A + ∠B
Proof: In ∆ABC,
∠A + ∠B + ∠ACB = 180° …(i) (Sum of angles of a triangle)
and ∠ACD + ∠ACB = 180° …(ii) (Linear pair)
From (i) and (ii)
∠ACD + ∠ACB = ∠A + ∠B + ∠ACB
∠ACD = ∠A + ∠B
Hence proved.

Question 6.
The sum of two angles of a triangle is equal to its third angle. Determine the measure of the third angle.
Solution:
In ∆ABC,
∠A + ∠C = ∠B

But ∠A + ∠B + ∠C = 180° (Sum of angles of a triangle)
∴ ∠B + ∠A + ∠C = 180°
⇒ ∠B + ∠B = 180°
⇒ 2∠B = 180°
⇒ ∠B = \(\frac { { 180 }^{ \circ } }{ 2 }\)  = 90°
∴ Third angle = 90°

Question 7.
In the figure, if AB || CD, EF || BC, ∠BAC = 65° and ∠DHF = 35°, find ∠AGH.

Solution:
Given : In figure, AB || CD, EF || BC ∠BAC = 65°, ∠DHF = 35°

∵ EF || BC
∴ ∠A = ∠ACH (Alternate angle)
∴ ∠ACH = 65°
∵∠GHC = ∠DHF
(Vertically opposite angles)
∴ ∠GHC = 35°
Now in ∆GCH,
Ext. ∠AGH = ∠GCH + ∠GHC
= 65° + 35° = 100°

Question 8.
In the figure, if AB || DE and BD || FG such that ∠FGH = 125° and ∠B = 55°, find x and y.

Solution:
In the figure, AB || DF, BD || FG

∠FGH = 125° and ∠B = 55°
∠FGH + FGE = 180° (Linear pair)
⇒ 125° + y – 180°
⇒ y= 180°- 125° = 55°
∵ BA || FD and BD || FG
∠B = ∠F = 55°
Now in ∆EFG,
∠F + ∠FEG + ∠FGE = 180°
(Angles of a triangle)
⇒ 55° + x + 55° = 180°
⇒ x+ 110°= 180°
∴ x= 180°- 110° = 70°
Hence x = 70, y = 55°

Question 9.
If the angles A, B and C of ∆ABC satisfy the relation B – A = C – B, then find the measure of ∠B.
Solution:
In ∆ABC,
∠A + ∠B + ∠C= 180° …(i)
and B – A = C – B

⇒ B + B = A + C ⇒ 2B = A + C
From (i),
B + 2B = 180° ⇒ 3B = 180°
∠B = \(\frac { { 180 }^{ \circ } }{ 3 }\) = 60°
Hence ∠B = 60°

Question 10.
In ∆ABC, if bisectors of ∠ABC and ∠ACB intersect at O at angle of 120°, then find the measure of ∠A.
Solution:
In ∆ABC, bisectors of ∠B and ∠C intersect at O and ∠BOC = 120°

But ∠BOC = 90°+ \(\frac { 1 }{ 2 }\)
90°+ \(\frac { 1 }{ 2 }\) ∠A= 120°
⇒ \(\frac { 1 }{ 2 }\) ∠A= 120°-90° = 30°
∴ ∠A = 2 x 30° = 60°

Question 11.
If the side BC of ∆ABC is produced on both sides, then write the difference between the sum of the exterior angles so formed and ∠A.
Solution:
In ∆ABC, side BC is produced on both sides forming exterior ∠ABE and ∠ACD
Ext. ∠ABE = ∠A + ∠ACB
and Ext. ∠ACD = ∠ABC + ∠A

Adding we get,
∠ABE + ∠ACD = ∠A + ∠ACB + ∠A + ∠ABC
⇒ ∠ABE + ∠ACD – ∠A = ∠A 4- ∠ACB + ∠A + ∠ABC – ∠A (Subtracting ∠A from both sides)
= ∠A + ∠ABC + ∠ACB = ∠A + ∠B + ∠C = 180° (Sum of angles of a triangle)

Question 12.
In a triangle ABC, if AB = AC and AB is produced to D such that BD = BC, find ∠ACD: ∠ADC.
Solution:
In ∆ABC, AB = AC
AB is produced to D such that BD = BC
DC are joined
In ∆ABC, AB = AC
∴ ∠ABC = ∠ACB
In ∆ BCD, BD = BC
∴ ∠BDC = ∠BCD
and Ext. ∠ABC = ∠BDC + ∠BCD = 2∠BDC (∵ ∠BDC = ∠BCD)
⇒ ∠ACB = 2∠BCD (∵ ∠ABC = ∠ACB)
Adding ∠BDC to both sides
⇒ ∠ACB + ∠BDC = 2∠BDC + ∠BDC
⇒ ∠ACB + ∠BCD = 3 ∠BDC (∵ ∠BDC = ∠BCD)
⇒ ∠ACB = 3∠BDC

Question 13.
In the figure, side BC of AABC is produced to point D such that bisectors of ∠ABC and ∠ACD meet at a point E. If ∠BAC = 68°, find ∠BEC.

Solution:
In the figure,

side BC of ∆ABC is produced to D such that bisectors of ∠ABC and ∠ACD meet at E
∠BAC = 68°
In ∆ABC,
Ext. ∠ACD = ∠A + ∠B
⇒ \(\frac { 1 }{ 2 }\) ∠ACD = \(\frac { 1 }{ 2 }\) ∠A + \(\frac { 1 }{ 2 }\) ∠B
⇒ ∠2= \(\frac { 1 }{ 2 }\) ∠A + ∠1 …(i)
But in ∆BCE,
Ext. ∠2 = ∠E + ∠l
⇒ ∠E + ∠l = ∠2 = \(\frac { 1 }{ 2 }\) ∠A + ∠l [From (i)]
⇒ ∠E = \(\frac { 1 }{ 2 }\) ∠A = \(\frac { { 68 }^{ \circ } }{ 2 }\)  =34°

Hope given RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.4

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.4

Other Exercises

• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.1
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.2
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.3
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.4
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials VSAQS
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials MCQS

In each of the following, use factor Theorem to find whether polynomial g(x) is a factor of polynomial f(x) or, not: (1-7)
Question 1.
f(x) = x³ – 6x² + 11x – 6; g(x) = x – 3
Solution:
We know that if g(x) is a factor of p(x),
then the remainder will be zero. Now,
f(x) = x³ – 6x² + 11x – 6; g(x) = x -3
Let x – 3 = 0, then x = 3
∴ Remainder = f(3)
= (3)³ – 6(3)² +11 x 3 – 6
= 27-54 + 33 -6
= 60 – 60 – 0
∵  Remainder is zero,
∴ x – 3 is a factor of f(x)

Question 2.
f(x) = 3X⁴ + 17x³ + 9x² – 7x – 10; g(x) = x + 5
Solution:
f(x) = 3x⁴ + 17X³ + 9x² – 7x – 10; g(x) = x + 5
Let x + 5 = 0, then x = -5
∴  Remainder = f(-5) = 3(-5)⁴ + 17(-5)³ + 9(-5)² – 7(-5) – 10
= 3 x 625 + 17 x (-125) + 9 x (25) – 7 x (-5) – 10
= 1875 -2125 + 225 + 35 – 10
= 2135 – 2135 = 0
∵  Remainder = 0
∴ (x + 5) is a factor of f(x)

Question 3.
f(x) = x⁵ + 3x⁴ – x³ – 3x² + 5x + 15, g(x) = x + 3
Solution:
f(x) = x⁵ + 3X⁴ – x³ – 3x² + 5x + 15, g(x) = x + 3
Let x + 3 = 0, then x = -3
∴ Remainder = f(-3)
= (-3)⁵ + 3(-3)⁴ – (-3)³ – 3(-3)² + 5(-3) + 15
= -243 + 3 x 81 -(-27)-3 x 9 + 5(-3) + 15
= -243 +243 + 27-27- 15 + 15
= 285 – 285 = 0
∵  Remainder = 0
∴  (x + 3) is a factor of f(x)

Question 4.
f(x) = x³ – 6x² – 19x + 84, g(x) = x – 7
Solution:
f(x) = x³ – 6x² – 19x + 84, g(x) = x – 7
Let x – 7 = 0, then x = 7
∴  Remainder = f(7)
= (7)³ – 6(7)² – 19 x 7 + 84
= 343 – 294 – 133 + 84
= 343 + 84 – 294 – 133
= 427 – 427 = 0
∴  Remainder = 0
∴ (x – 7) is a factor of f(x)

Question 5.
f(x) = 3x³  + x² – 20x + 12, g(x) = 3x – 2
Solution:

Question 6.
f(x) = 2x³ – 9x² + x + 12, g(x) = 3 – 2x
Solution:
f(x) = 2x³ – 9x² + x + 12, g(x) = 3 – 2x

Question 7.
f(x) = x³ – 6x² + 11x – 6, g(x) = x² – 3x + 2
Solution:
g(x) = x² – 3x + 2
= x² – x – 2x + 2
= x(x – 1) – 2(x – 1)
= (x – 1) (x – 2)
If x – 1 = 0, then x = 1
‍∴ f(1) = (1)³ – 6(1)² + 11(1) – 6
= 1-6+11-6= 12- 12 = 0
‍∴ Remainder is zero
‍∴ x – 1 is a factor of f(x)
and if x – 2 = 0, then x = 2
∴ f(2) = (2)³ – 6(2)² + 11(2)-6
= 8 – 24 + 22 – 6 = 30 – 30 = 0
‍∴ Remainder = 0
‍∴ x – 2 is also a factor of f(x)

Question 8.
Show that (x – 2), (x + 3) and (x – 4) are factors of x³ – 3x² – 10x + 24.
Solution:
f(x) = x³ – 3x² – 10x + 24
Let x – 2 = 0, then x = 2
Now f(2) = (2)³ – 3(2)² – 10 x 2 + 24
= 8 – 12 – 20 + 24 = 32 – 32 = 0
‍∴ Remainder = 0
‍∴ (x – 2) is the factor of f(x)
If x + 3 = 0, then x = -3
Now, f(-3) = (-3)³ – 3(-3)² – 10 (-3) + 24
= -27 -27 + 30 + 24
= -54 + 54 = 0
∴ Remainder = 0
∴ (x + 3) is a factor of f(x)
If x – 4 = 0, then x = 4
Now f(4) = (4)³ – 3(4)² – 10 x 4 + 24 = 64-48 -40 + 24
= 88 – 88 = 0
∴ Remainder = 0
∴ (x – 4) is a factor of (x)
Hence (x – 2), (x + 3) and (x – 4) are the factors of f(x)

Question 9.
Show that (x + 4), (x – 3) and (x – 7) are factors of x³ – 6x² – 19x + 84.
Solution:
Let f(x) = x³ – 6x² – 19x + 84
If x + 4 = 0, then x = -4
Now, f(-4) = (-4)³ – 6(-4)² – 19(-4) + 84
= -64 – 96 + 76 + 84
= 160 – 160 = 0
∴ Remainder = 0
∴ (x + 4) is a factor of f(x)
If x – 3 = 0, then x = 3
Now, f(3) = (3)³ – 6(3)² – 19 x 3 + 84
= 27 – 54 – 57 + 84
= 111 -111=0
∴ Remainder = 0
∴ (x – 3) is a factor of f(x)
and if x – 7 = 0, then x = 7
Now, f(7) = (7)³ – 6(7)² – 19 x 7 + 84
= 343 – 294 – 133 + 84
= 427 – 427 = 0
∴ Remainder = 0
∴ (x – 7) is also a factor of f(x)
Hence (x + 4), (x – 3), (x – 7) are the factors of f(x)

Question 10.
For what value of a (x – 5) is a factor of x³ – 3x² + ax – 10?
Solution:
f(x) = x³ – 3x² + ax – 10
Let x – 5 = 0, then x = 5
Now, f(5) = (5)³ – 3(5)² + a x 5 – 10
= 125 – 75 + 5a – 10
= 125 – 85 + 5a = 40 + 5a
∴ (x – 5) is a factor of fix)
∴ Remainder = 0
⇒  40 + 5a = 0 ⇒  5a = -40
⇒ a = \(\frac { -40 }{ 5 }\)= -8
Hence a = -8

Question 11.
Find the value of a such that (x – 4) is a factor of 5x³ – 7x² – ax – 28.
Solution:
Let f(x) =  5x³ – 7x² – ax – 28
and Let x – 4 = 0, then x = 4
Now, f(4) = 5(4)³ – 7(4)² – a x 4 – 28
= 5 x 64 – 7 x 16 – 4a – 28
= 320 – 112 – 4a – 28
= 320 – 140 – 4a
= 180 – 4a
∴ (x – 4) is a factor of f(x)
∴ Remainder = 0
⇒  180 -4a = 0
⇒  4a = 180
⇒  a = \(\frac { 180 }{ 4 }\) =  45
∴  a = 45

Question 12.
Find the value of a, if x + 2 is a factor of 4x⁴ + 2x³ – 3x² + 8x + 5a.
Solution:
Let f(x) = 4x⁴ + 2x³ – 3x² + 8x + 5a
and Let x + 2 = 0, then x = -2
Now, f(-2) = 4(-2)⁴ + 2(-2)³ – 3(-2)² + 8 x ( 2) + 5a
= 4 x 16 + 2(-8) – 3(4) + 8 (-2) + 5a
= 64- 16- 12- 16 +5a
= 64 – 44 + 5a
= 20 + 5a
∴  (x + 2) is a factor of fix)
∴  Remainder = 0
⇒  20 + 5a = 0 ⇒  5a = -20
⇒  a =\(\frac { -20 }{ 5 }\)  = -4
∴ a = -4

Question 13.
Find the value of k if x – 3 is a factor of k²x³ – kx² + 3kx – k.
Solution:
Let f(x) = k²x³ – kx² + 3kx – k
and Let x – 3 = 0, then x = 3
Now,f(3) = k²(3)³ – k(3)² + 3k(3) – k
= 27k² – 9k + 9k-k
= 27k²-k
∴ x – 3 is a factor of fix)
∴ Remainder = 0
∴ 27k² – k = 0
⇒ k(27k – 1) = 0 Either k = 0
or 21k – 1 = 0
⇒ 21k = 1
∴  k= \(\frac { 1 }{ 27 }\)
∴  k = 0,\(\frac { 1 }{ 27 }\)

Question 14.
Find the values of a and b, if x² – 4 is a factor of ax⁴ + 2x³ – 3x² + bx – 4.
Solution:
f(x) = ax⁴ + 2x³ – 3x² + bx – 4
Factors of x² – 4 = (x)² – (2)²
= (x + 2) (x – 2)
If x + 2 = 0, then x = -2
Now, f(-2) = a(-2)⁴ + 2(-2)³ – 3(-2)² + b(-2) – 4
16a- 16 – 12-26-4
= 16a -2b-32
∵ x + 2 is a factor of f(x)
∴ Remainder = 0
⇒  16a – 2b – 32 = 0
⇒ 8a – b – 16 = 0
⇒ 8a – b = 16         …(i)
Again x – 2 = 0, then x = 2
Now f(2) = a x (2)⁴ + 2(2)³ – 3(2)² + b x 2-4
= 16a + 16- 12 + 26-4
= 16a + 2b
∵  x – 2 is a factor of f(x)
∴ Remainder = 0
⇒  16a + 2b = 0
⇒ 8a + b= 0                             …(ii)
Adding (i) and (ii),
⇒ 16a = 16
⇒ a = \(\frac { 16 }{ 16 }\) = 1
From (ii) 8 x 1 + b = 0
⇒ 8 + b = 0
⇒  b = – 8
∴ a = 1, b = -8

Question 15.
Find α and β, if x + 1 and x + 2 are factors of x³ + 3x² – 2αx +β.
Solution:
Let f(x) = x³ + 3x² – 2αx + β
and Let x + 1 = 0 then x = -1
Now,f(-1) = (1)³ + 3(-1)² – 2α (-1) +β
= -1 + 3 + 2α + β
= 2 + 2α + β
∵  x + 1 is a factor of f(x)
∴  Remainder = 0
∴ 2 + 2α + β = 0
⇒  2α + β = -2                    …(i)
Again, let x + 2 = 0, then x = -2
Now, f(-2) = (-2)³ + 3(-2)² – 2α(-2) + β
= -8 + 12 + 4α+ β
= 4 + 4α+ β
∵ x + 2 is a factor of(x)
∴ Remainder = 0
∴ 4+ 4α + β = 0
⇒  4α + β = -4 …(ii)
Subtracting (i) from (ii),
2α = -2
⇒  α = \(\frac { -2 }{ 2 }\) = -1
From (ii), 4(-1) + β = -4
-4 + β= -4
⇒  β =-4+ 4 = 0
∴  α = -1, β = 0

Question 16.
If x – 2 is a factor of each of the following two polynomials, find the values of a in each case:
(i) x³ – 2ax² + ax – 1
(ii) x⁵ – 3x⁴ – ax³ + 3ax² + 2ax + 4
Solution:
(i) Let f(x) = x³ – 2ax² + ax – 1 and g(x) = x – 2
and let x – 2 = 0, then x = 2
∴ x – 2 is its factor
∴ Remainder = 0
f(2) = (2)³ – 2a x (2)² + a x 2 – 1
= 8-8a+ 2a-1 = 7-6a
∴ 7 – 6a = 0
⇒  6a = 7
⇒ a = \(\frac { 7 }{ 6 }\)
∴ a =  \(\frac { 7 }{ 6 }\)
(ii) Let f(x) = x⁵ – 3x⁴ – ax³ + 3 ax² + 2ax + 4 and g(x) = x – 2
Let x – 2 = 0, then x=2
∴ f(2) = (2)⁵ – 3(2)⁴ – a(2³) + 3a (2)² + 2a x 2 + 4
= 32 – 48 – 8a + 12a + 4a + 4
= -12 + 8a
∴ Remainder = 0
∴ -12 + 8a = 0
⇒ 8a= 12
⇒ a = \(\frac { 12 }{ 8 }\) = \(\frac { 3 }{ 2 }\)
∴ Hence a = \(\frac { 3 }{ 2 }\)

Question 17.
In each of the following two polynomials, find the values of a, if x – a is a factor:
(i) x⁶ – ax⁵ + x⁴-ax³ + 3x-a + 2
(ii) x⁵ – a²x³ + 2x + a + 1
Solution:
(i) Let f(x) ⁼ x⁶ – ax⁵+x⁴-ax³ + 3x-a + 2 and g(x) = x – a
∴ x – a is a factor
∴ x – a = 0
⇒ x = a
Now f(a) = a⁶-a x a⁵ + a⁴-a x a³ + 3a – a + 2
= a⁶-a⁶ + a⁴-a⁴ + 2a + 2
= 2a + 2
∴ x + a is a factor of p(x)
∴ Remainder = 0

Question 18.
In each of the following, two polynomials, find the value of a, if x + a is a factor.
(i)  x³ + ax² – 2x + a + 4
(ii) x⁴ – a²r + 3x – a
Solution:

Question 19.
Find the values of p and q so that x⁴ + px³ + 2x² – 3x + q is divisible by (x² – 1).
Solution:

Question 20.
Find the values of a and b so that (x + 1) and (x – 1) are factors of x⁴ + ax³ 3x² + 2x + b.
Solution:

Question 21.
If x³ + ax² – bx + 10 is divisible by x² – 3x + 2, find the values of a and b.
Solution:

Question 22.
If both x + 1 and x – 1 are factors of ax³ + x² – 2x + b, find the values of a and b.
Solution:

Question 23.
What must be added to x³ – 3x² – 12x + 19 so that the result is exactly divisibly by x² + x – 6?
Solution:

Question 24.
What must be subtracted from x³ – 6x² – 15x + 80-so that the result is exactly divisible by x² + x – 12?
Solution:

Question 25.
What must be added to 3x³ + x² – 22x + 9 so that the result is exactly divisible by 3x² + 7x – 6?
Solution:

Hope given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.4

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.4

Other Exercises

• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.1
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.2
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.3
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.4
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry VSAQS
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry MCQS

Question 1.
Give the geometric representations of the following equations.
(a) on the number line
(b) on the cartesian plane.
(i) x – 2
(ii) y + 3 = 0
(iii) y = 3
(iv) 2x + 9 = 0
(v) 3x – 5 = 0
Solution:
(i) x = 2
(i) on the number line

(ii) x = 2 is a line parallel to 7-axis at a distance of 2 units to right of y-axis.

(ii) y = -3 is a line parallel to x-axis at a distance of 3 units below x-axis.

(iii) y = 3
(i) y = 3

(ii) y = 3 is a line parallel to x-axis at a distance of 3 units above x-axis.


x = -4.5 is a line parallel to 7-axis at a distance of 4.5 units to left of y-axis.


(ii) x = 1\(\frac { 2 }{ 3 }\) is a line parallel to y-axis at a  distance of 1\(\frac { 2 }{ 3 }\) unit to right side of y-axis.

Question 2.
Give the geometrical representation of 2x + 13 = 0 as an equation in
(i) One variable
(ii) Two variables
Solution:
(i) In one variable,
2x + 13 = 0
⇒ 2x = – 13
⇒ x = \(\frac { -13 }{ 2 }\)

is a line parallel to y-axis at a distance of -6 \(\frac { 1 }{ 2 }\) units on the left side of y-axis.

Question 3.
Solve the equation 3x + 2 = x -8, and represent on
(i) the number line
(ii) the Cartesian plane.
Solution:
3x + 2 = x – 8
⇒  3x – x = -8 – 2
⇒  2x = -10
⇒  x = \(\frac { -10 }{ 2 }\) = -5
(i) on the number line s = -5

(ii) x = -5 is a line parallel to  y-axis at a distance of 5 knot’s left of y-axis.

Question 4.
Write the equal of the line that is parallel to x-axis and passing through the points.
(i) (0, 3)                     
(ii)  (0, -4)
(iii) (2, -5)                     
(iv)    (3, 4)
Solution:
∵  A line parallel to x-axis will be of the type y = a
∴ (i) y = 3
(ii) y = -4
(iii) y = -5 and y = 4 are equations of the lines parallel to x-axis

Question 5.
Write the equation of the line that is parallel to y-axis and passing through the points.
(i) (4, 0)                      
(ii) (-2, 0)
(iii) (3, 5)                    
(iv) (-4, -3)
Solution:
∵  A line parallel to y-axis will be of the type x = a
∴  (i) x = 4, (ii)  x = -2, x = 3 and x = -4 are the equations of the lines parallel to y-axis.

Hope given RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.3

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.3

Other Exercises

• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.1
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.2
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.3
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.4
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry VSAQS
• RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry MCQS

Question 1.
Draw the graph of each of the following linear equations in two variables.

Solution:
(i)x + y = 4
x = 4 – y
If y = 0, then x = 4
If y = 4, then x = 0
Now plot the points (4, 0) and (0, 4) on the graph and join them ro get the graph of the given equation

(ii)x – y = 2
x = 2 +y
If y = 0, then x = 2 and if y = 1,
Then x = 2 + 1 = 3

Now plot the points (2, 0) and (3, 1) on the graph and join them to get the graph of the equation.

(iii) -x+y = 6 ⇒  y = 6+x

If x = 0, then y = 6 + 0 = 6
If x = -1, then y = 6 – 1 = 5

Now plot the points (0, 6) and (-1, 5) on the graph and join them to get a graph of the line.
(iv) y = 2x
If x = 0, then y =  2 x 0 = 0
If x = 1, then y = 2 x 1 = 2


Now plot the points (0, 0) and (1, 2) on the graph and join them to get the graph of the line.


Now plot the points (5, 0) and (0, 3) on the graph and join them to get the graph of the line.

Now plot the points (4, 0) and (2, -3) on the graph and join them to get the graph of the line.


Now plot the points (-1, 2) and (2, 3) on the graph and join then to get the graph of the line.


Now plot the points (1, 0) and (-1, 1) on the graph and join then to get the graph of the line.

Question 2.
Give the equations of two lines passing through (3, 12). How many more such lines are there, and why ?
Solution:
∵  Points (3, 12) lies on the lines passing through the points
∴ Solutions is x = 3,y- 12
∴  Possible equation can be
x + y = 15
-x+y = 9
4x-y = 0
3x – y + 3 = 0

Question 3.
A three-wheeler scooter charges ₹15 for first kilometer and ₹8 each for every subsequent kilometer. For a distance of x km, an amount of ₹y is paid. Write the linear equation representing the above information.
Solution:
Charges for the first kilometer = ₹15
Charges for next 1 km = ₹8
Distance = x km
and total amount = ₹y
∴ Linear equation will be,
15 + (x- 1) x 8 =y
⇒  15 + 8x – 8 = y
⇒   7 + 8x = y
∴  y = 8x + 7

Question 4.
Plot the points (3, 5) and (-1, 3) on a graph paper and verify that the straight line passing through these points also passes through the point (1, 4).
Solution:

Points (3, 5) and (-1, 3) have been plotted on the graph and joined to get a line. We see that die point (1,4) also lies out.

Question 5.
From the choices given below, choose the equation whose graph is given in figure.
(i) y = x                   
(ii) x + y = 0
(iii) y = 2x                   
(iv) 2 + 3y = 7x
Solution:

From the graph, we see that Points (-1, 1) and (1, -1) be on the graph of the line these will satisfy the equation of the line
∴  -x = y ⇒ x+ y = 0
i.e, required equation
∵ x + y = 0 is the graph of the equation.

Question 6.
From the choices given below, choose the equation whose graph is given in figure.
(i) y = x + 2              
(ii) y = x – 2
(ii) y = -x + 2           
(iv) x + 2y = 6
Solution:
From the graph
Points (-1,3) and (2, 0) lie on the graph of the line
Now there points, by observation, satisfy the equation y= -x+2
∴ Required equation is y = -x + 2 whose graph is given.

Question 7.
If the point (2, -2) lies on the graph of the linear equation 5x + ky =4, find the value of k.
Solution:
∵  Point (2, -2) lies on the graph of the linear equation 5x + ky = 4
∴  It will satisfy it
∴ Now substituting the values of x and y 5 x 2 + k (-2) = 4
⇒ 10 – 2k = 4 ⇒  -2k = 4 – 10 = -6 -6
⇒ k= \(\frac { -6 }{ -2 }\) =3
Hence k = 3

Question 8.
Draw the graph of the equation 2x + 3p = 12. From the graph find the co-ordinates of the point.
(i) whose y -coordinates is 3
(ii) whose x-coordinates is -3
Solution:


Plot the points (6, 0) and (0, 4) on the graph and join them to get the graph if the line.
(i) If y = 3, then draw perpendicular from y = 3 to the line, which get meets it at P then x-coordinate of p will be
∴ coordinates of P are ( \(\frac { 3 }{ 2 }\) ,3)
(ii) If x = -3, draw perpendicular from x = -3 to the line, which meets it Q.
The y coordinates of Q will be y = 6
∴ co-ordinates of Q are (-3, 6)

Question 9.
Draw the graph of each of the equations given below. Also, find the coordinates of the points where the graph cuts the coordinates axes:
(i) 6x – 3y = 12        
(ii) -x + 4y = 8
(iii) 2x + y = 6          
(iv) 3x + 2y + 6 = 0
Solution:


Now plot the points of each equation and join then we get four lines as shown on the graphs.
Equation (i) cuts the axes at (2, 0) and (0, -4)
Equation (ii) cuts the axes at (-8, 0) and (0, 2)
Equation (iii) cuts the axes at (3, 0), (0, 6) and
Equation (iv), cuts the axes at (-2, 0) and (0,-3)

Question 10.
A lending library has a fixed charges for the first three days and an additional charge for each day thereafter. Aarushi paid ₹27 for a book kept for seven days. If fixed charges are ₹x and per day charges are ₹y. Write the linear equation representing the above information.
Solution:
Let fixed charges for first 3 days = ₹x
and additional charges for each day = ₹y
Total period = 7 days
and amount charges = ₹27
∴ x + (7 – 3) x y  = 27
⇒  x + 4y = 27
Hence x + 4y = 27

Question 11.
A number is 27 more than the number obtained by reversing its digits. If its unit’s and ten’s digit are x and y respectively, write the linear equation representing the above statement.
Solution:
Let unit’s digit = x
and tens digit = y
∴  Number = x + 10y
By reversing the digits, units digit = y
and ten’s digit = x
∴  number = y + 10x
Now difference of these two numbers = 27 (x + 10y) – (y +10x) = 27
x + 10y – y – 10x = 27
⇒  -9x + 9y – 27 = 0
⇒ x-_y + 3 = 0                   (Dividing by -9)
Hence equation is x – y + 3 = 0

Question 12.
The sum of a two digit number and the number obtained by reversing the order of its digits is 121. If units and ten’s digit of the number are x and y respectively, then write the linear equation representing the above statement.
Solution:
Let unit digit = x
and tens digit = y
∴ Number = x + 10y
By reversing the digits,
units digit = y
and tens digit = x
∴ Number =y+ 10x
Now sum of these two numbers = 121
∴ x + 10y + y + 10x = 121
⇒  1 lx + 11y = 121
⇒  x + y = 11                        (Dividing by 11)
∴  x + y = 11

Question 13.
Draw the graph of the equation 2x + y = 6. Shade the region bounded by the graph and the coordinate axes. Also find the area of the shaded region.
Solution:
2x + y = 6
⇒  y = 6 – 2x
If x = 0, then y = 6- 2 x 0 = 6 – 0 = 6
If x = 2, then y = 6- 2 x 2 = 6- 4 = 2

Now plot the points (0, 6) and (2, 2) on the graph and join them to get a line which intersects x-axis at (3, 0) and y-axis at (0,6)
Now co-ordinates if vertices of the shaded portion are (6, 0) (0, 0) and (3, 0) Now area of the shaded region.

Question 14.
Draw the graph of the equation  \(\frac { x }{ 3 }\) +  \(\frac { y }{ 4 }\)  = 1 Also find the area of the triangle formed by the line and the co-ordinate axes.
Solution:

Now plot the points (3, 0) and (0, 4) and join them to get a line which interest x-axis at A (3, 0) and y-axis at B (0, 4)

Question 15.
Draw the graph of y = | x |
Solution:
y = | x |

⇒   y = x       [∵ | x |=x]
∴  Now taking z points.


Now plot the points (1, 1) (2, 2) and (3, 3) and join them to get a graph of a line.

Question 16.
Draw the graph of y = | x | + 2
Solution:
y – | x | + 2
⇒  y = x + 2         [| x | = x]
If x = 0, then y = 0 + 2 = 2
If x = 1, then y = 1+2 = 3
If x = 2, then y = 2 + 2 = 4

Now plot the points (0, 2), (1, 3) and (2, 4) on the graph and join them to get a line.

Question 17.
Draw the graphs of the following linear equation on the same graph paper.
2x + 3y = 12, x -y = 1
Find the co-ordinates of the vertices of the triangle formed by the two straight lines and the y-axis. Also find the area of the triangle.
Solution:

Now plot the points (6, 0) (0, 4) on the graph to get a line.

Now plot the points (1, 0) and (2, 1) on the graph to get another line.
Area of the triangle FEB so formed,
= \(\frac { 1 }{ 2 }\) FB x FL = \(\frac { 1 }{ 2 }\) x 5 x 3
= \(\frac { 15 }{ 2 }\)
= 7.5 sq. units
co-ordinates of E, F, B are E (3, 2), (0, -1) and (0, 4)

Question 18.
 Draw the graphs of the linear equations 4x – 3y + 4 = 0 and 4x + 3y – 20 = 0. Find the area bounded by these lines and x-axis.
Solution:



Now plot the points (5, 0) and (2, 4)and join them to get a line we see that the ΔABC is formed by bounding there line with x-axis.

Question 19.
The path of a train A is given by the equation 3x + 4y – 12 = 0 and the path of another train B is given by the equation 6jc + 8y – 48 = 0. Represent this situation graphically.
Solution:
Path of the train A = 3x + 4y – 12 = 0
Path of the train B = 6x + 8y – 48 = 0
Now, 3x + 4y – 12 = 0


Now plot the points (4, 0) and (0, 3) on the graph and join them to get a line, and 6x + 8y – 48 = 0
⇒  6x = 48 – 8y

Now plot the points (0, 6) and (4, 3) on the graph and join them to get another line.

Question 20.
Ravish tells his daughter Aarushi, “Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be”. If present ages of Aarushi and Ravish are x and y years respectively, represent this situation algebraically as well as graphically.
Solution:
Present age of Aarushi = x years
and age of Ravish = y years
7 years ago,
age of Aarushi = x – 7
years and age of Ravish =y-7 years
∴ y- 7 = 7 (X – 7)
⇒  y – 7 = 7x – 49
⇒  7x – y = -7 + 49  = 42
7x – y = 42
⇒  y = 7x – 42
If x = 6, then
y = 7 x 6 – 42 = 42 – 42 = 0,
If x = 7, then
y = 7 x 7 – 42 – 49 – 42 = -7

Plot the points (6, 0) (7, -7) on the graph and join them.
After 3 years,
age of Aarushi = x + 3
and age of Ravish = y + 3
⇒  y + 3 = 3(x + 3)
⇒ y + 3 = 3x + 9
⇒ y = 3x+ 9-3
⇒ y = 3x + 6
If x = -2, then y = 3 x (-2) + 6 =6-6=0
If x = 1, then y = 3 x (1) + 6 =3+6=9

Plot the points (1, 9), (-2, 0) on the graph Arundeep’s Mathematics (R.D.) 9th and join them to get another line.

Question 21.
Aarushi was driving a car with uniform speed of 60 km/h. Draw distance-time graph. From the graph, find the distance travelled by Aarushi in.
(i) 2\(\frac { 1 }{ 2 }\) Hours             
(ii) \(\frac { 1 }{ 2 }\) Hour
Solution:
Speed of car = 60 km / h.

Now plot the points (60, 1), (120, 2) are the graph and join then to get the graph of line.
From the graph, we see that

Hope given RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.