RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals VSAQS
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals VSAQS
Other Exercises
- RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.1
- RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.2
- RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3
- RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals VSAQS
- RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS
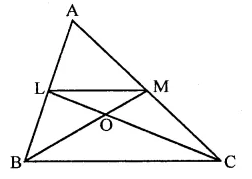
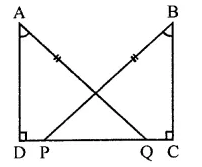
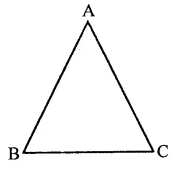
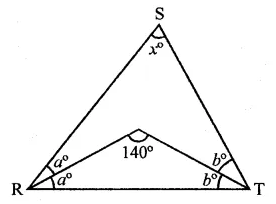
Question 1.
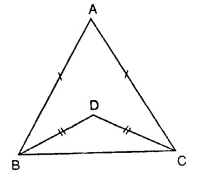
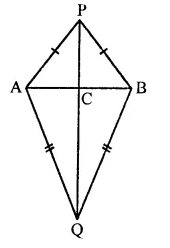
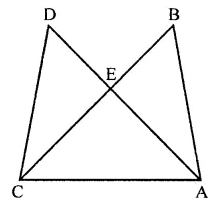
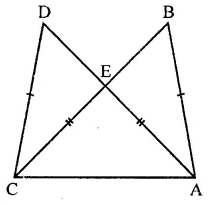
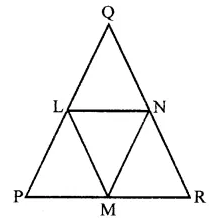
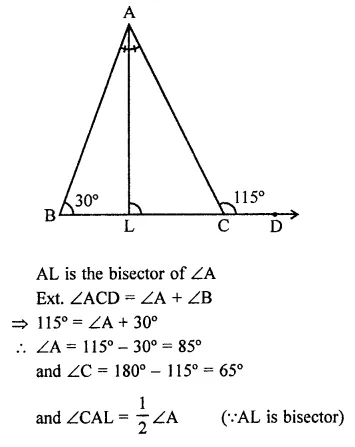
If ABC and BDE are two equilateral triangles such that D is the mid-ponit of BC, then find ar(∆ABC) : ar(∆BDE).
Solution:
ABC and BDE are two equilateral triangles and D is the mid-point of BC
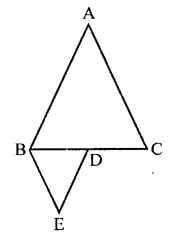
Let each side of AABC = a
Then BD = \(\frac { a }{ 2 }\)
∴ Each side of triangle BDE will be \(\frac { a }{ 2 }\)
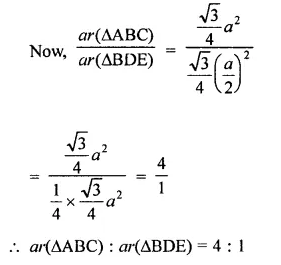
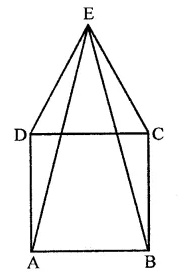
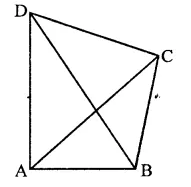
Question 2.
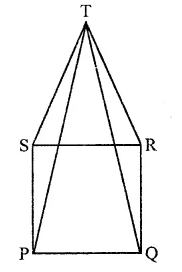
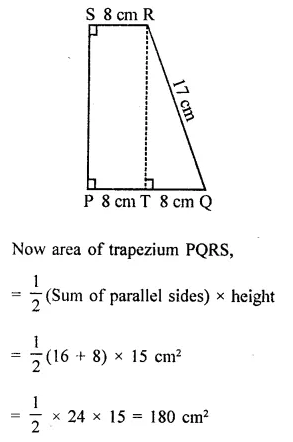
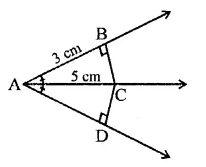
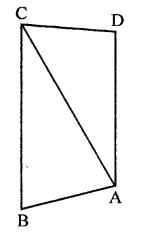
In the figure, ABCD is a rectangle in which CD = 6 cm, AD = 8 cm. Find the area of parallelogram CDEF.
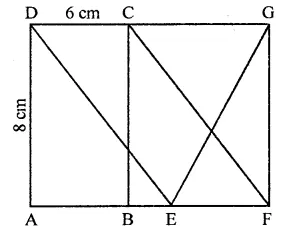
Solution:
In rectangle ABCD,
CD = 6 cm, AD = 8 cm
∴ Area of rectangle ABCD = CD x AD
= 6 x 8 = 48 cm2
∵ DC || AB and AB is produced to F and DC is produced to G
∴ DG || AF
∵ Rectangle ABCD and ||gm CDEF are on the same base CD and between the same parallels
∴ ar(||gm CDEF) = ar(rect. ABCD)
= 48 cm2
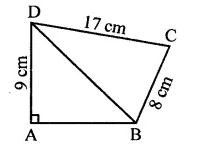
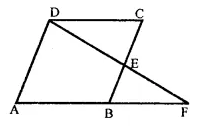
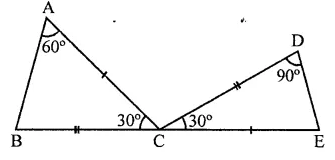
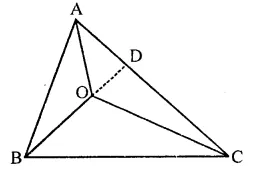
Question 3.
In the figure of Q. No. 2, find the area of ∆GEF.
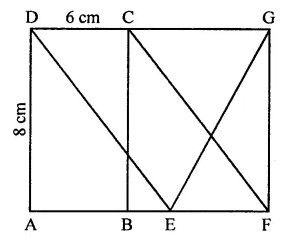
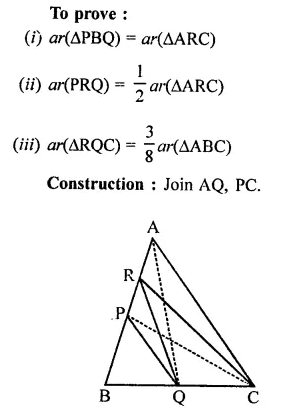
Solution:

Question 4.
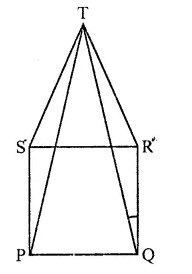
In the figure, ABCD is a rectangle with sides AB = 10 cm and AD = 5 cm. Find the area of ∆EFG.
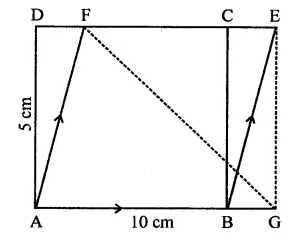
Solution:
ABCD is a rectangle in which
AB = 10 cm, AD = 5 cm
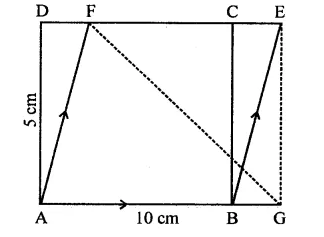
∵ ABCD is a rectangle
∴DC || AB,
DC is produced to E and AB is produced to G
∴DE || AG
∵ Rectangle ABCD and ||gm ABEF are on the same base AB and between the same parallels
∴ ar(rect. ABCD) = ar(||gm ABEF)
= AB x AD = 10 x 5 = 50 cm2
Now ||gm ABEF and AEFG are on the same
base EF and between the same parallels
∴ area ∆EFG = \(\frac { 1 }{ 2 }\) ar(||gm ABEF)
= \(\frac { 1 }{ 2 }\) x 50 = 25 cm2
Question 5.
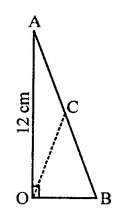
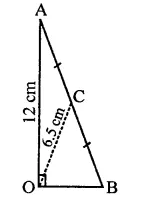
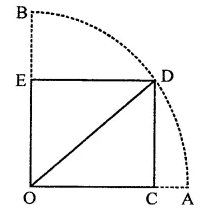
PQRS is a rectangle inscribed in a quadrant of a circle of radius 13 cm. A is any point on PQ. If PS = 5 cm, then find or(∆RAS).
Solution:
In quadrant PLRM, rectangle PQRS is in scribed
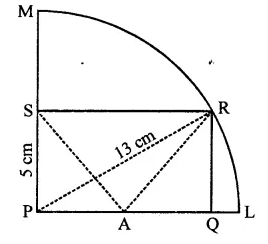
Radius of the circle = 13 cm
A is any point on PQ
AR and AS are joined, PS = 5 cm
In right ∆PRS,
PR2 = PS2 + SR2
⇒ (132 = (5)2+ SR2
⇒ 169 = 25 + SR2
⇒ SR2 = 169 – 25 = 144 = (12)2
∴ SR = 12 cm
Area of rect. PQRS = PS x SR = 5x 12 = 60 cm2
∵ Rectangle PQRS and ARAS are on the same
base SR and between the same parallels
∴ Area ARAS = \(\frac { 1 }{ 2 }\) area rect. PQRS 1
= \(\frac { 1 }{ 2 }\) x 60 = 30 cm2
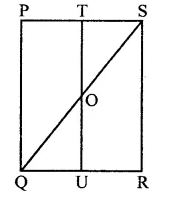
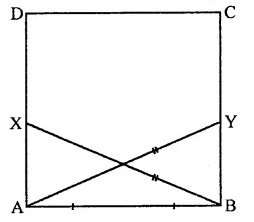
Question 6.
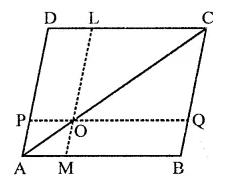
In square ABCD, P and Q are mid-point of AB and CD respectively. If AB = 8 cm and PQ and BD intersect at O, then find area of ∆OPB.
Solution:
In sq. ABCD, P and Q are the mid points of sides AB and CD respectively PQ and BD are joined which intersect each other at O
Side of square AB = 8 cm
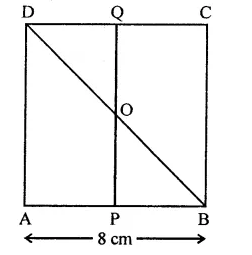
∴ Area of square ABCD = (side)2
∵ Diagonal BD bisects the square into two triangle equal in area
∴ Area ∆ABD = \(\frac { 1 }{ 2 }\) x area of square ABCD
= \(\frac { 1 }{ 2 }\) x 64 = 32 cm2
∵ P is mid point of AB of AABD, and PQ || AD
∴ O is the mid point of BD
∴ OP = \(\frac { 1 }{ 2 }\)AD = \(\frac { 1 }{ 2 }\) x 8 = 4 cm
and PB = \(\frac { 1 }{ 2 }\) AB = \(\frac { 1 }{ 2 }\) x 8 = 4 cm
∴ Area ∆OPB = \(\frac { 1 }{ 2 }\)PB x OP
= \(\frac { 1 }{ 2 }\) x4x4 = 8 cm2
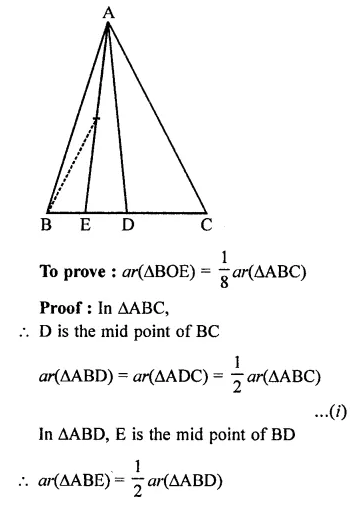
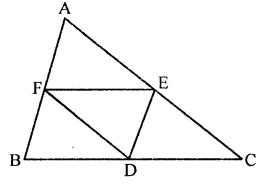
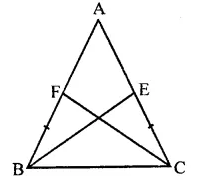
Question 7.
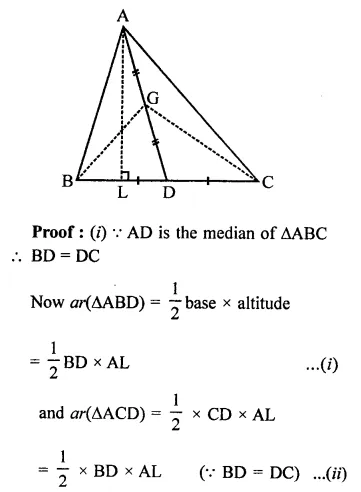
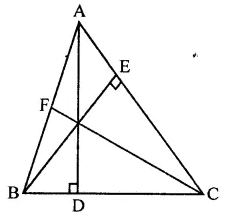
ABC is a triangle in which D is the mid-point of BC. E and F are mid-points of DC and AE respectively. If area of ∆ABC is 16 cm2, find the area of ∆DEF.
Solution:
In ∆ABC, D is mid point of BC. E and F are the mid points of DC and AE respectively area of ∆ABC = 16 cm2
FD is joined
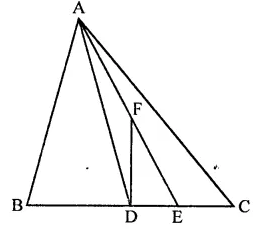
∵ D is mid point of BC
∴ AD is the median and median divides the triangle into two triangles equal in area
area ∆ADC = \(\frac { 1 }{ 2 }\) ar(∆ABC)
= \(\frac { 1 }{ 2 }\) x 16 = 8 cm2
Similarly, E is mid point of DC
∴ area (∆ADE) = \(\frac { 1 }{ 2 }\) ar(∆ADC)
= \(\frac { 1 }{ 2 }\) x 8 = 4 cm2
∵ F is mid point of AE of ∆ADE
∴ ar(∆DEF) = \(\frac { 1 }{ 2 }\)area (∆ADE)
= \(\frac { 1 }{ 2 }\) x 4 = 2 cm2
Question 8.
PQRS is a trapezium having PS and QR as parallel sides. A is any point on PQ and B is a point on SR such that AB || QR. If area of ∆PBQ is 17 cm2, find the area of ∆ASR.
Solution:
In trapezium PQRS,
PS || QR
A and B are points on sides PQ and SR
Such that AB || QR
area of ∆PBQ = 17 cm2
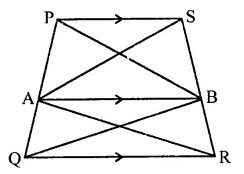
∆ABQ and ∆ABR are on the same base AB and between the same parallels
∴ ar(∆ABQ) = ar(∆ABR) …(i)
Similarly, ∆ABP and ∆ABS are on the same base and between the same parallels
∴ ar(ABP) = ar(∆ABS) …(ii)
Adding (i) and (ii)
ar( ∆ABQ) + ar( ∆ABP)
= ar(∆ABR) + ar(∆ABS)
⇒ ar(∆PBQ) = ar(∆ASR)
Put ar(PBQ) = 17 cm2
∴ ar(∆ASR) = 17 cm2
Question 9.
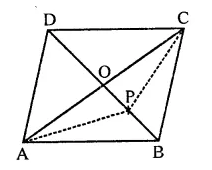
ABCD is a parallelogram. P is the mid-point of AB. BD and CP intersect at Q such that CQ : QP = 3 : 1. If ar(∆PBQ) = 10 cm2, find the area of parallelogram ABCD.
Solution:
In ||gm ABCD, P is mid point on AB,
PC and BD intersect each other at Q
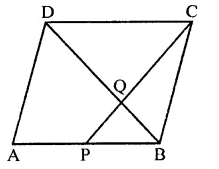
CQ : QP = 3 : 1
ar(∆PBQ) = 10 cm2
In ||gm ABCD,
BD is its diagonal
∴ ar(∆ABD) = ar(∆BCD) = \(\frac { 1 }{ 2 }\) ar ||gm ABCD
∴ ar(||gm ABCD) = 2ar(∆ABD) …(i)
In ∆PBC CQ : QP = 3 : 1
∵ ∆PBQ and ∆CQB have same vertice B
∴ 3 x area ∆PBQ = ar(∆CBQ)
⇒ area(∆CBQ) = 3 x 10 = 30 cm2
∴ ar(∆PBC) = 30 + 10 = 40 cm2
Now ∆ABD and ∆PBC are between the
same parallel but base PB = \(\frac { 1 }{ 2 }\) AB
∴ ar(∆ABD) = 2ar(∆PBC)
= 2 x 40 = 80 cm2
But ar(||gm ABCD) = 2ar(∆ABD)
= 2 x 80 = 160 cm2
Question 10.
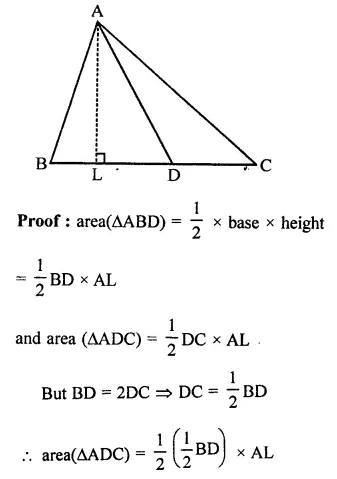
P is any point on base BC of ∆ABC and D is the mid-point of BC. DE is drawn parallel to PA to meet AC at E. If ar(∆ABC) = 12 cm2, then find area of ∆EPC.
Solution:
P is any point on base of ∆ABC
D is mid point of BC
DE || PA drawn which meet AC at E
ar(∆ABC) = 12 cm2
AD and PE are joined
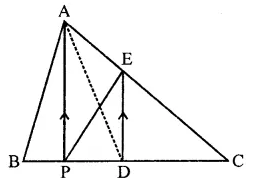
∵ D is mid point of BC
∴ AD is median
∴ ar(∆ABD) = ar(∆ACD)
= \(\frac { 1 }{ 2 }\) (∆ABC) = \(\frac { 1 }{ 2 }\) x 12 = 6 cm2 …(i)
∵ ∆PED and ∆ADE are on the same base DE and between the same parallels
∴ ar(∆PED) = ar(∆ADE)
Adding ar(∆DCE) to both sides,
ar(∆PED) + ar(∆DCE) = ar(∆ADE) + ar(∆DCE)
ar(∆EPC) = ar(∆ACD)
⇒ ar(∆EPC) = ar(∆ABD) = 6 cm2 [From (i)]
∴ ar(∆EPC) = 6 cm2
Hope given RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals VSAQS are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.


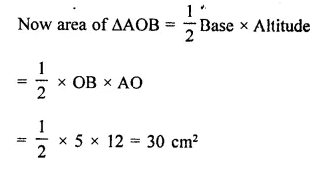
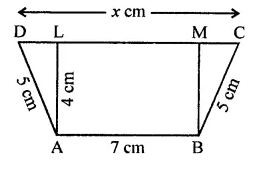
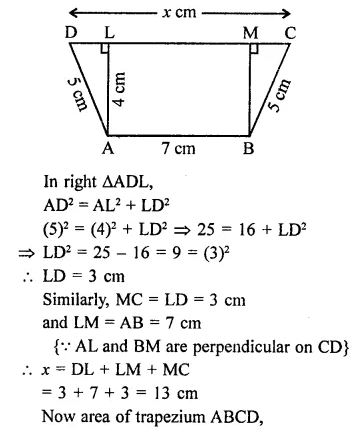
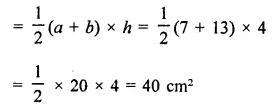



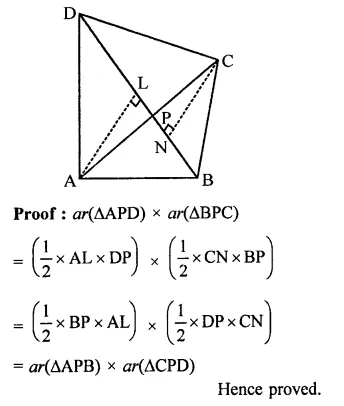
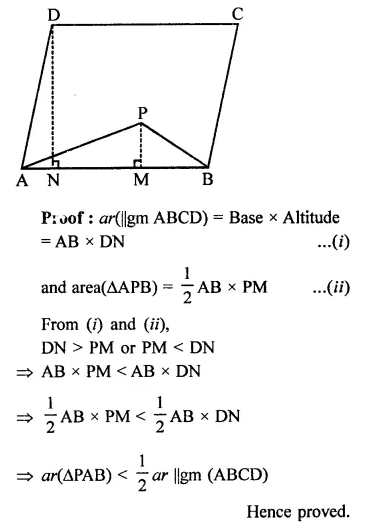
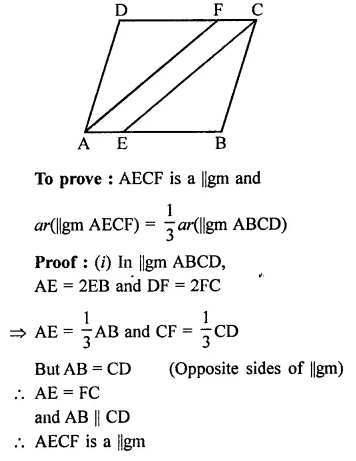

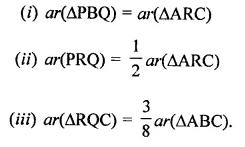



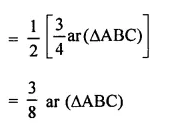
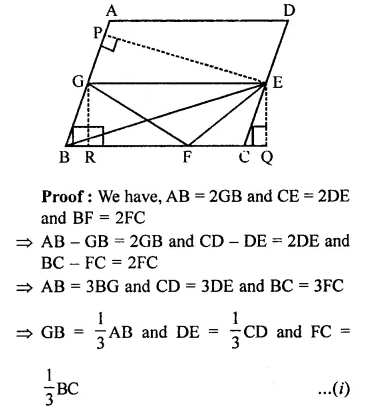
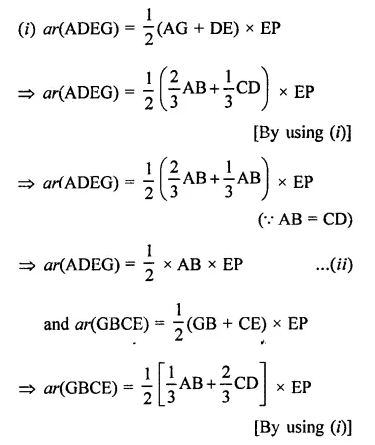
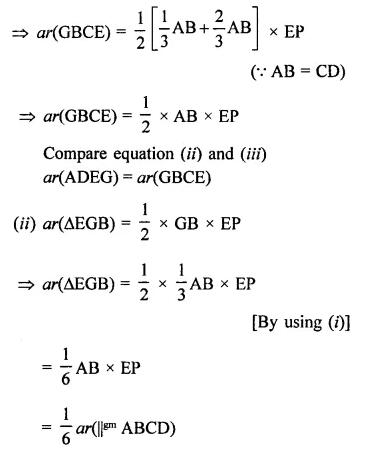
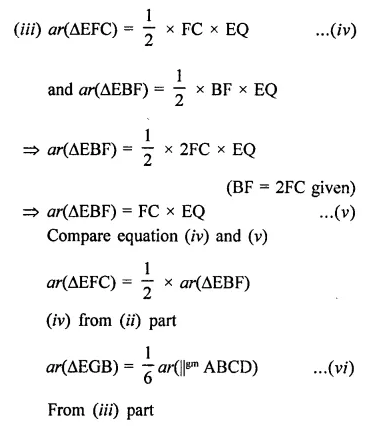
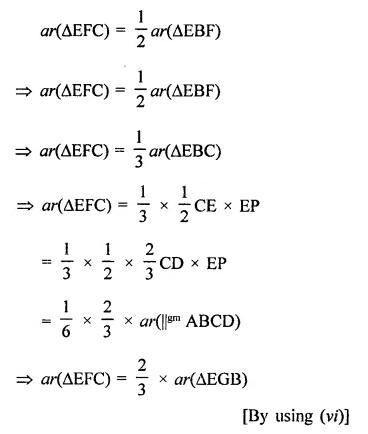

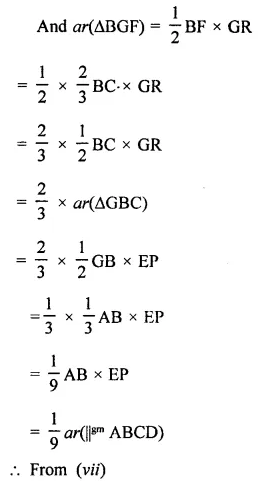
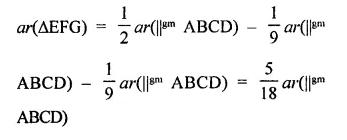

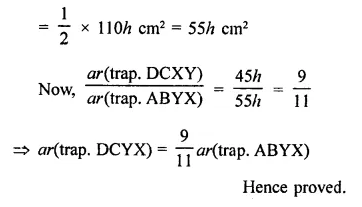
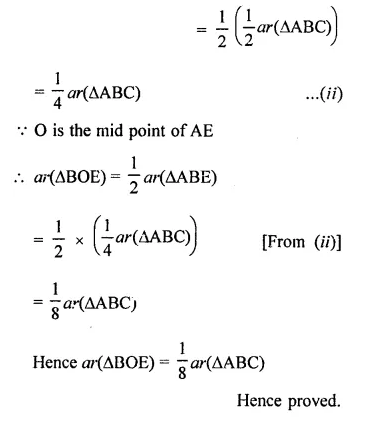
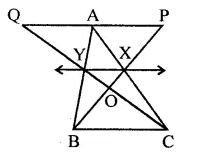






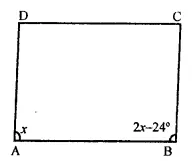
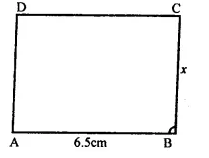
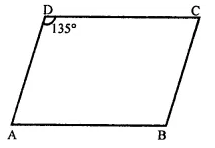
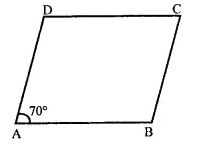
 Solution:
Solution: