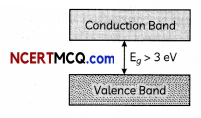
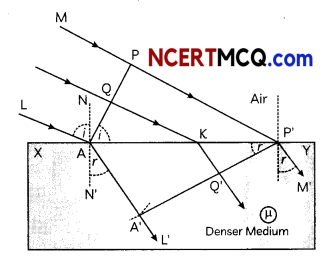
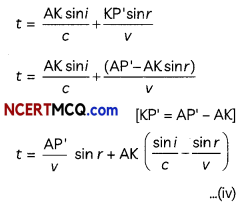
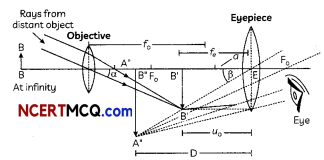
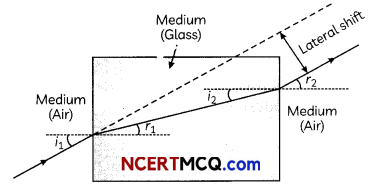
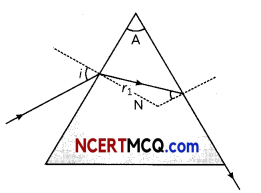
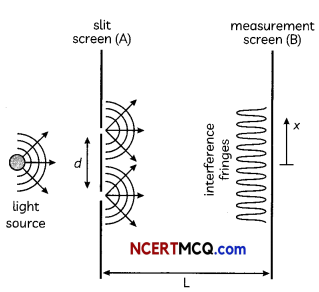
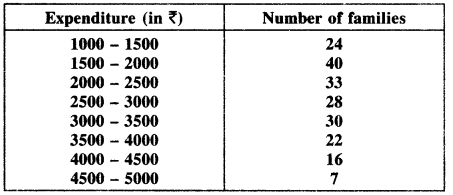
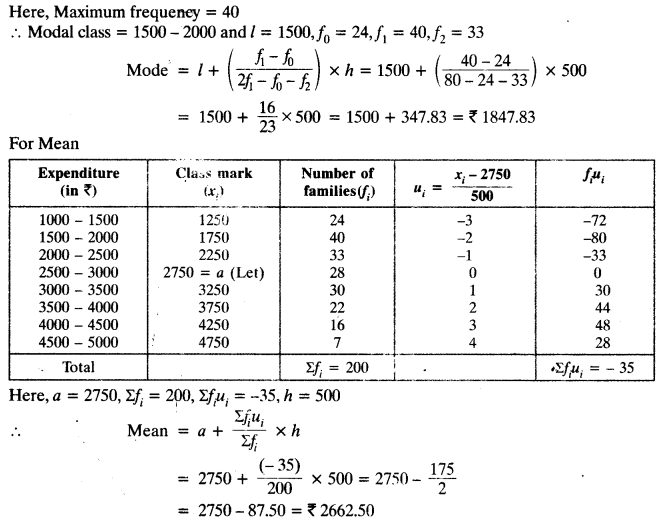
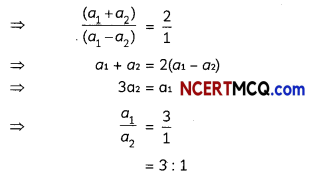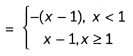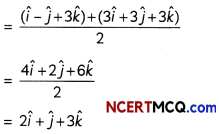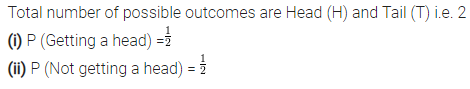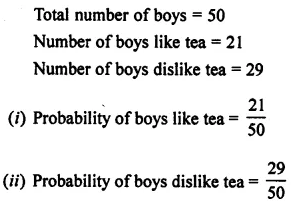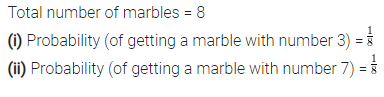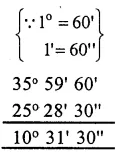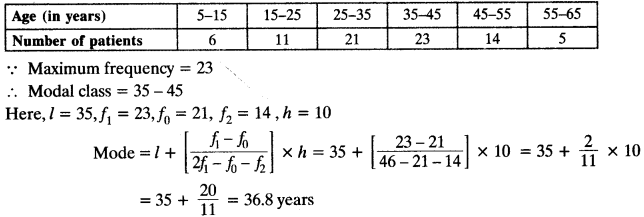Get Latest Edition of RD Sharma Solutions Pdf Download on LearnInsta.com. It provides step by step solutions RD Sharma Solutions Pdf Download. You can download the RD Sharma Solutions with Free PDF download option, which contains chapter wise solutions. In RD Sharma Solutions all questions are solved and explained by expert Mathematic teachers as per CBSE board guidelines. By studying these RD Sharma Solutions you can easily get good marks in CBSE Board Examinations.
We feel deeply indebted to all of you for giving such a tremendous response to the RD Sharma Solutions. It will be my sincere endeavour to keep on serving you through new editions also.
- RD Sharma Class 12 Solutions
- RD Sharma Class 11 Solutions
- RD Sharma Class 10 Solutions
- RD Sharma Class 9 Solutions
- RD Sharma Class 8 Solutions
Salient features of the RD Sharma Solutions:
- The RD Sharma Solutions has been rearranged and revised as per the CCE guidelines.
- As per CCE Guidelines the contents have been divided into two terms.
- Formative Assessments in the form of Very Short Answer Type Questions (VSAQs), Multiple Choice Type Questions (MCQs) and Summary have been given at the end of each chapter. As per the CCE Guidelines, Formative Assessment is a tool used by the teacher to continuously monitor a student’s progress in a non-threatening and supportive environment. If used effectively, it can improve a student’s performance tremendously, while raising the self-esteem of the student and reducing the work load of the teacher.
- Summative Assessments (Sample Papers) have been given at the end of each term. The Summative Assessment is a Terminal Assessment of the performance of the student at the end of each term. It is done on the basis of a written test at the end of each term covering the entire syllabus for the respective term.
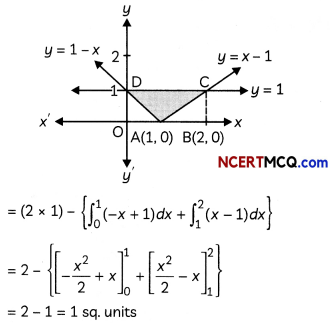
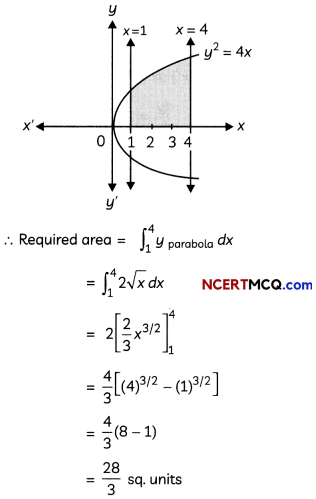
- All NCERT textbook problems have been marked as [NCERT].

Our sincere advice to the students that in each chapter first they should go through the theory and concepts thoroughly, then they should attempt to solve the illustrative examples without looking at their solutions. Students should consult the solutions only when they are unable to solve on their own. The exercises given at the end of each section should be attempted at the time of revision of the chapter.
Please send your feedback, suggestions or queries through e-mail to learninstaa@gmail.com.