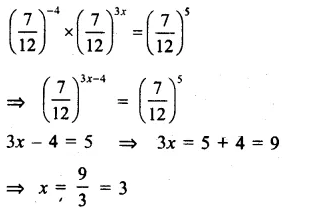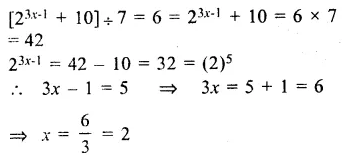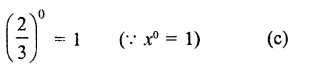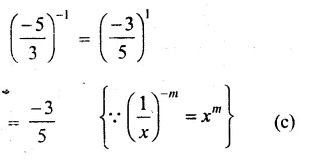RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3B
These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3B.
Other Exercises
- RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3A
- RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3B
- RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3C
- RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3D
- RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3E
- RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3F
- RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3G
- RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3H
Question 1.
Solution:
We know that a number ending in 2, 3, 7 or 8 is never a perfect square. So, (i) 5372, (ii) 5963, (iii) 8457, (iv) 9468 cannot be perfect square
Again number ending in an odd number of zeros is also never a perfect square.
Among (v) 360, (vi) 64000, (vii) 2500000 each one has odd zeros at its end. So, there cannot be a perfect square.
Question 2.
Solution:
We know that the square of an even number is also an even number.
(i) 196 (iii) 900, (v) 324 are the squares of even numbers.
Question 3.
Solution:
We know that square.of an odd number is alway is an odd number and square of an even number is always an even number.
Therefore the (ii) 961, (iv) 8649 (v) 4225 are squares of odd numbers.
Question 4.
Solution:
We know that sum of the first n odd natural numbers = n² Therefore.
(i) ∵ It ends with 13
and 1 + 3 + 5 + 7 + 9 + 11 + 13 is the sum of first 7 odd numbers
∵Its sum = (7)² = 49
(ii) 1 + 3 + 5 + 7 + 9+ 11 + 13 + 15 + 17 + 19
Here, n = 10
∵Sum = n² = (10)² = 100
(iii) (1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23)
Here, n = 12
Sum = n² = (12)² = 144 Ans.
Question 5.
Solution:
(i) 81 = (9)² = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 (Sum of first 9 odd numbers)
(ii) 100 = (10)² =1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 (Sum of first 10 odd numbers)
Question 6.
Solution:
We know that 2m, m² – 1 and m² + 1 is a Pythagorean triplet where m > 1
(i) One number = 6
∵ 2m = 6 => m = 3
∵ Other members of triplet will be
m² – 1 = (3)² – 1 = 9 – 1 = 8
and m² + 1 = (3)² + 1 = 9 + 1 = 10
∵ Pythagorean triplet is 6, 8, 10
(ii) Let 2m = 14 = m = \(\\ \frac { 14 }{ 2 } \) = 7
m² – 1 = (7)² – 1 = 49 – 1 = 48
and m² + 1 = (7)² + 1 = 49 + 1 = 50
∵Pythagorean triplet = 14, 48, 50
(iii) Let 2m = 16 => m = 8
m² – 1 = (8)² – 1 = 64 – 1 = 63
and m² + 1 = (8)² + 1 = 64 + 1 = 65
∵Pythagorean triplet =16, 63, 65
(iv) Let 2m = 20 => m = 10
∵m² – 1 = (10)² – 1 = 100 – 1 = 99
and m² + 1 = (10)² + 1 = 100 + 1 = 101
∵Pythagorean triplet = 20, 99, 101 Ans.
Question 7.
Solution:
We know that :
(n + 1)² – n² = {(n + 1) + n}
Therefore :
(i) (38)² – (37)² = 38 + 37 = 75
(ii) (75)² – (74)² = 75 + 74 = 149
(iii) (92)² – (91)² = 92 + 91 = 183
(iv) (105)² – (104)² = 105 + 104 = 209
(v) (141)² – (140)² = 141 + 140 = 281
(vi) (218)² – (217)² = 218 + 217 = 435
Question 8.
Solution:
We know that (a + b)² = a² + 2ab + b²
(i) (310)² = (300 + 10)²
= (300)² + 2 x 300 x 10 + (10)²
= 90000 + 6000 + 100 = 96100
(ii) (508)² = (500 + 8)²
= (500)² + 2 x 500 x 8 + (8)²
= 250000 + 8000 + 64 = 258064
(iii) (630)² = (600 + 30)²
= (600)² + 2 x 600 x 30 + (30)²
= 360000 + 36000 + 900 = 396900
Question 9.
Solution:
We know that (a – b)² = a² – 2ab + b²
(i) (196)² = (200 – 4)²
= (200)² – 2 x 200 x 4 + (4)²
= 40000 – 1600 + 16
= 40016 – 1600 = 38416
(ii) (689)² = (700 – 11)²
= (700)² – 2 x 700 x 11 +(11)²
= 490000 – 15400 + 121
= 490121 – 15400 = 474721
(iii) (891)² = (900 – 9)²
= (900)² – 2 x 900 x 9 + (9)²
= 810000 – 16200 + 81
= 810081 – 16200 = 793881
Question 10.
Solution:
Using (a – b) (a + b) = a² – b²
(i) 69 x 71 = (70 – 1) (70 + 1)
= (70)² – (1)² = 4900 – 1
= 4899
(ii) 94 x 106 = (100 – 6) (100 + 6)
= (100)² – (6)²
= 10000 – 36 = 9964
Question 11.
Solution:
Using (a – b) (a + b) – a² – b²
(i) 88 x 92 = (90 – 2) (90 + 2)
= (90)² – (2)²
= 8100 – 4 = 8096
(ii) 78 x 82 = (80 – 2) (80 + 2)
= (80)² – (2)²
= 6400 – 4 = 6396
Question 12.
Solution:
(i) The square of an even number is even
(ii) The square of an odd number is odd
(iii) The square of a proper fraction is less than the given fraction.
(iv) n² = the sum of first n odd natural numbers. Ans.
Question 13.
Solution:
(i) False: No. of digits of a perfect square can be even or odd.
(ii) False: Square of a prime number is not a prime number.
(iii) False: It is not always possible.
(iv) False: It is not always possible.
(v) True: The product of two squares is always a perfect square.
Hope given RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3B are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.
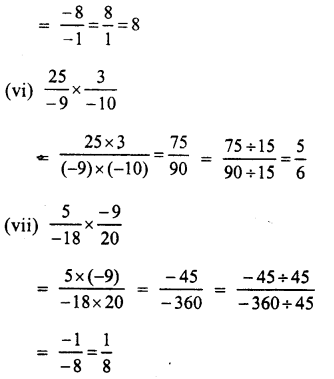
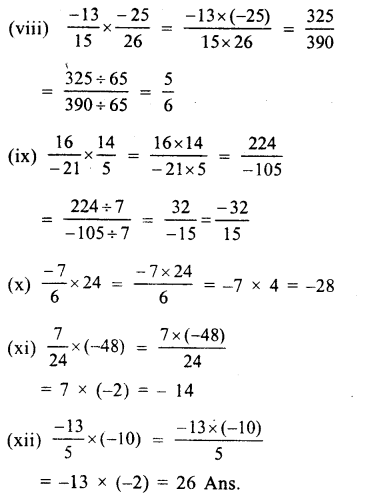
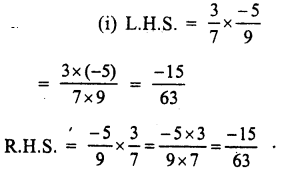
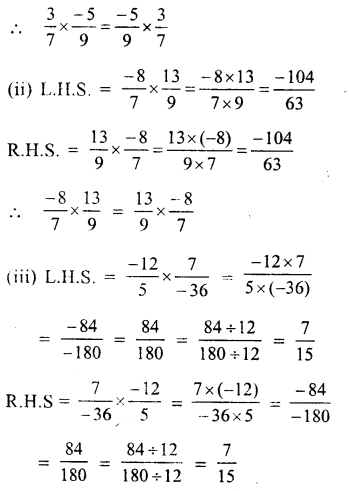



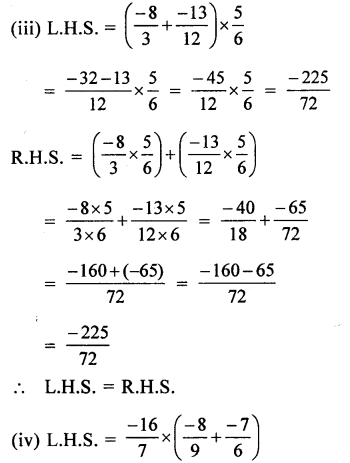
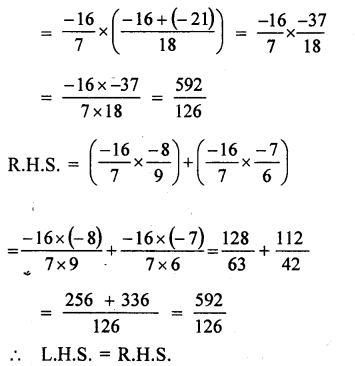


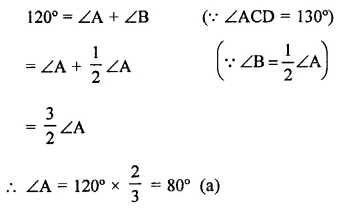
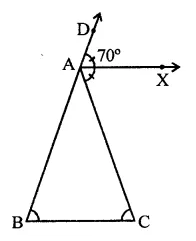
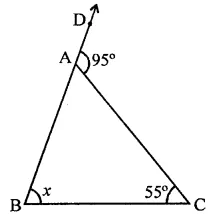
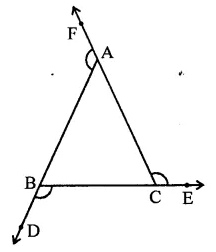
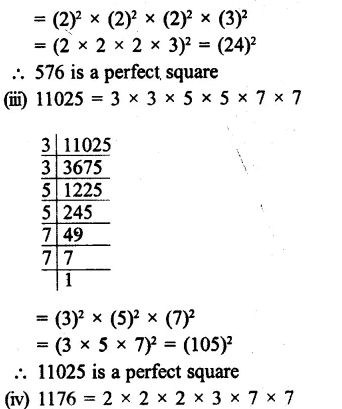



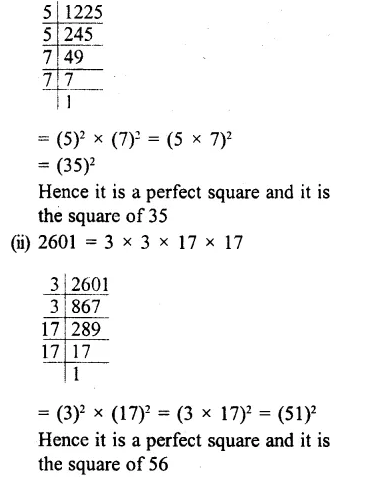
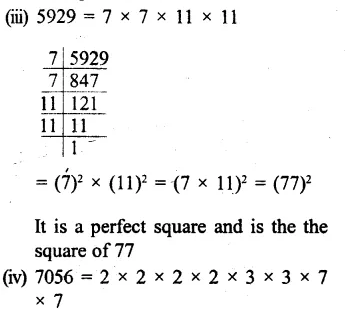
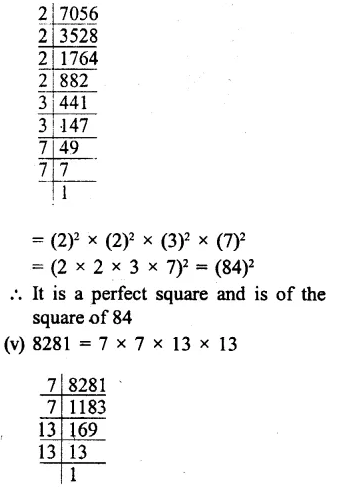



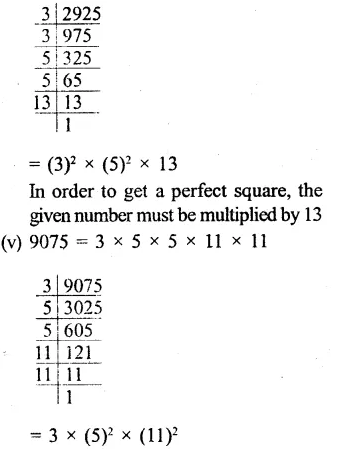


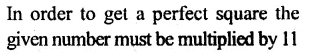
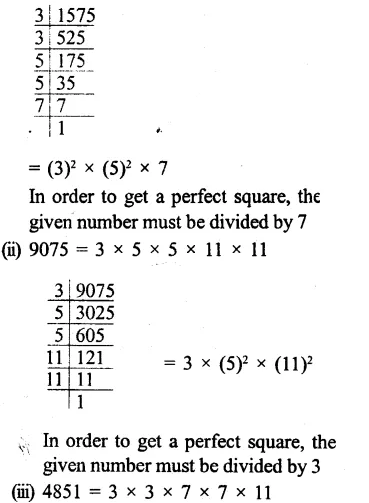
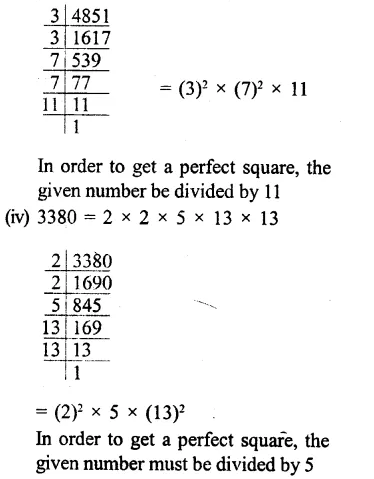



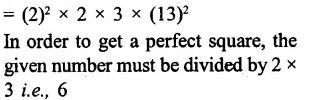
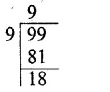
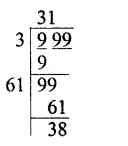
 Solution:
Solution: