Prasanna

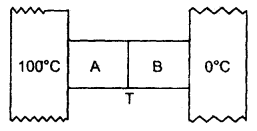
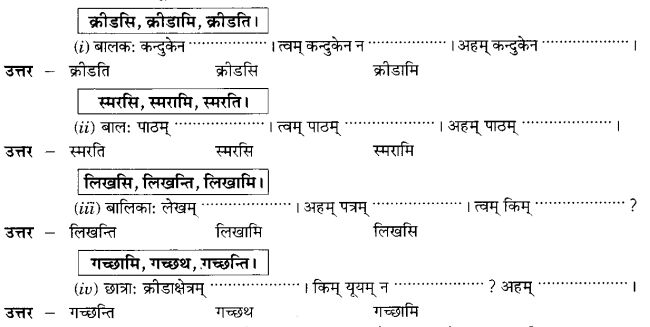
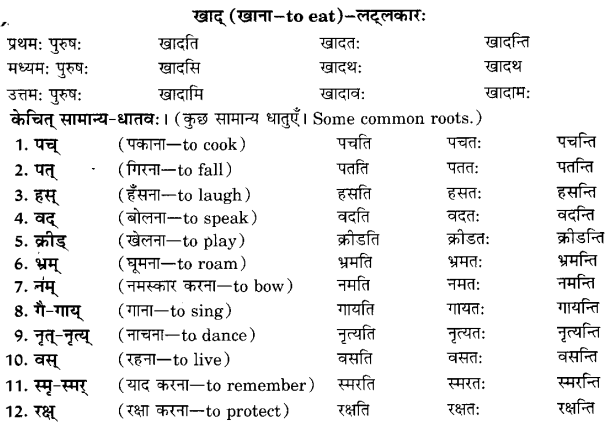
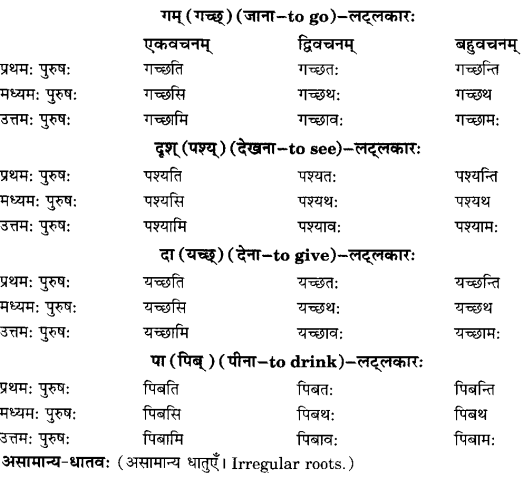
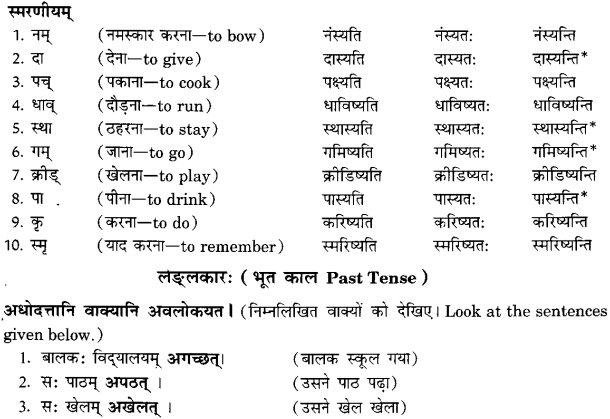
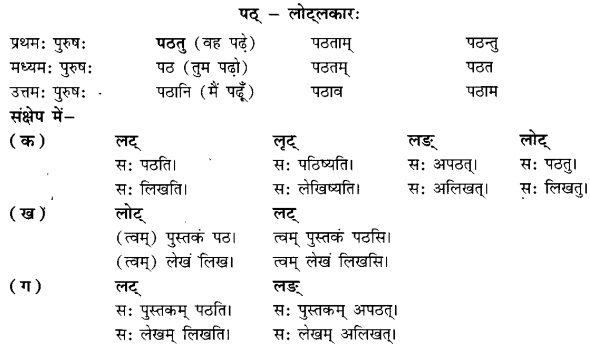
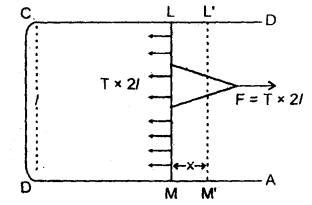
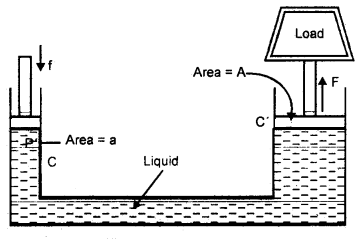
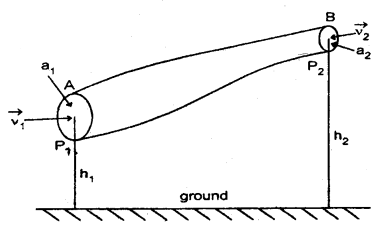
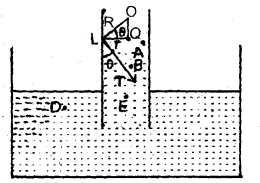
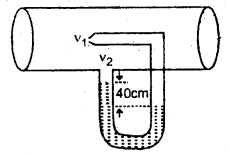
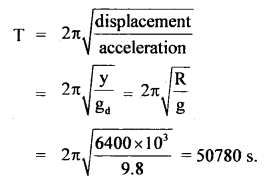
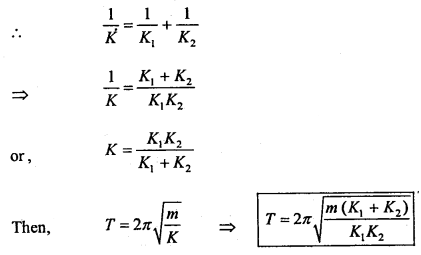
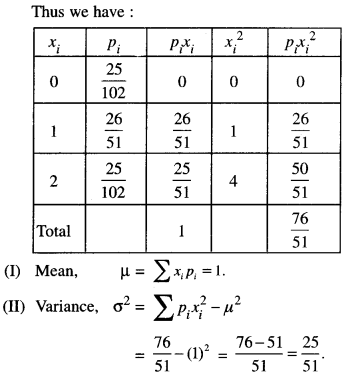
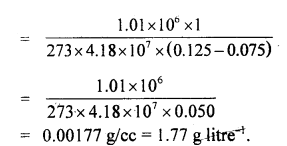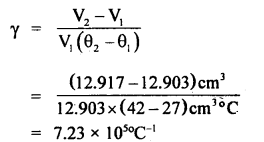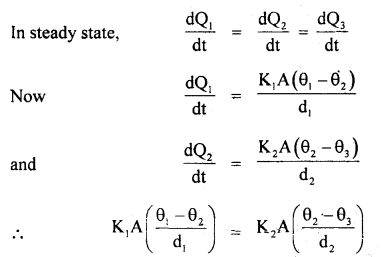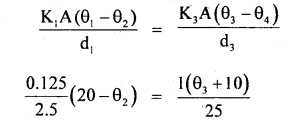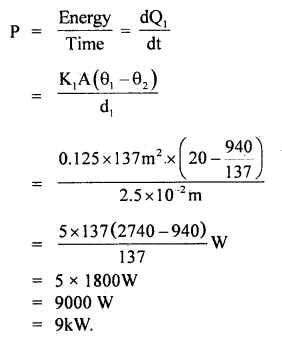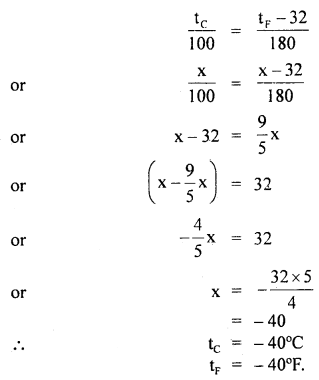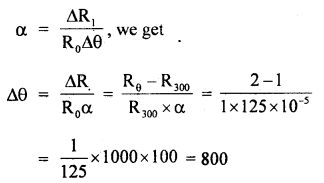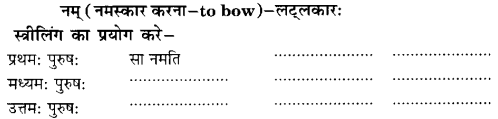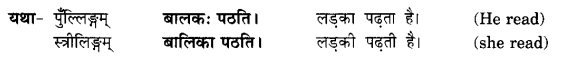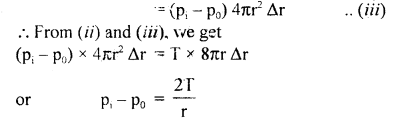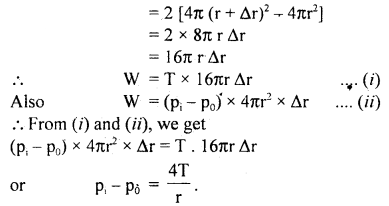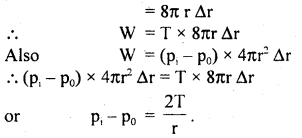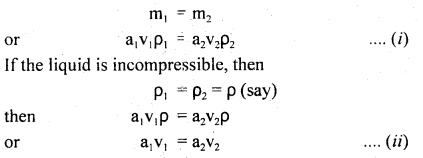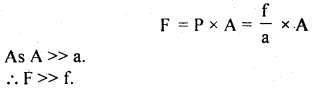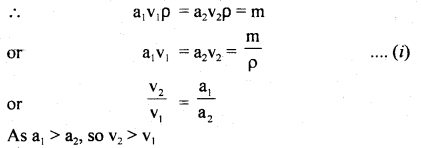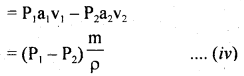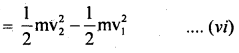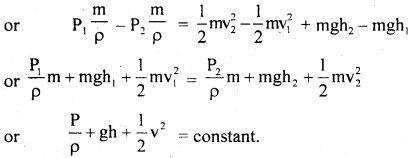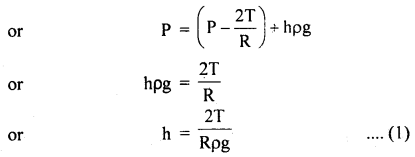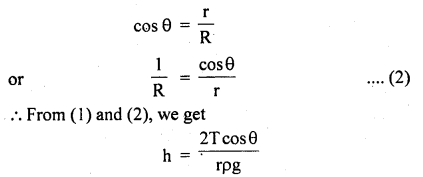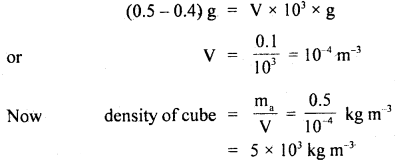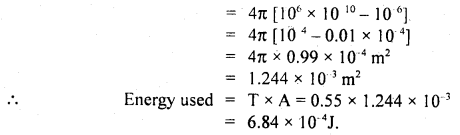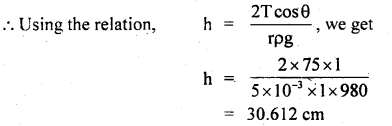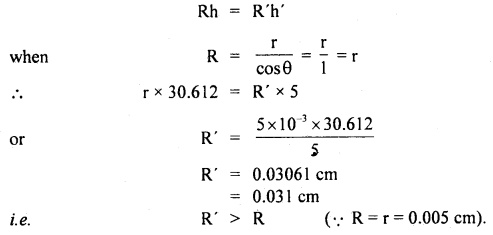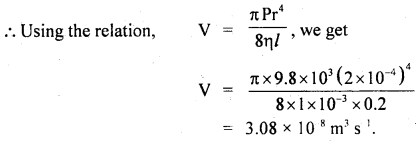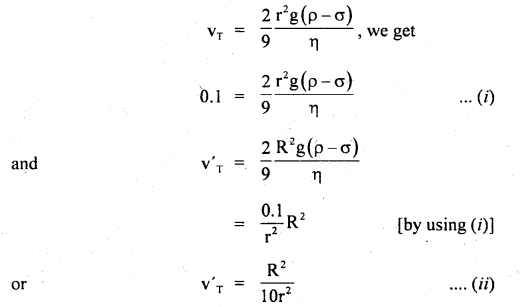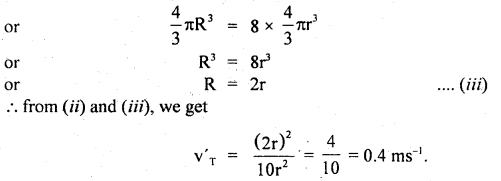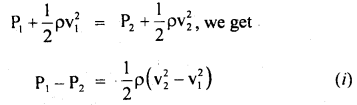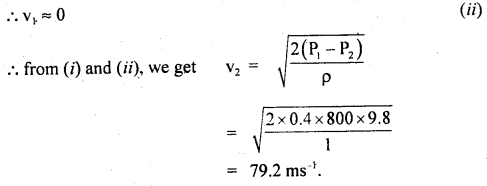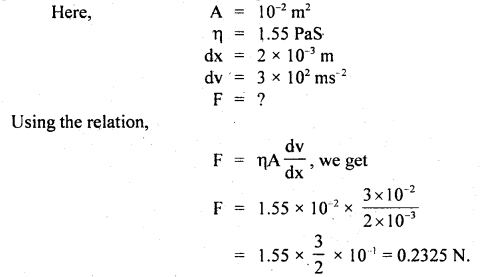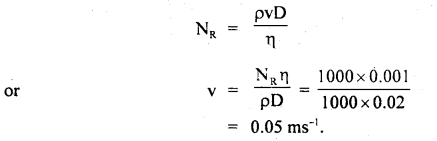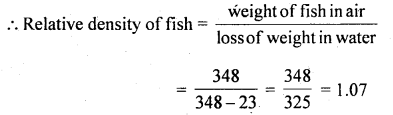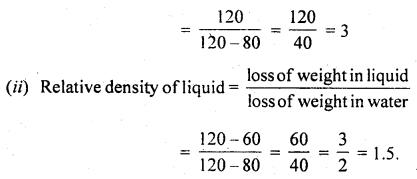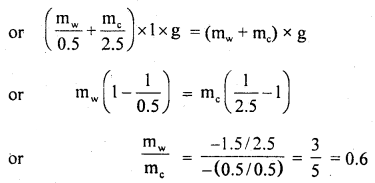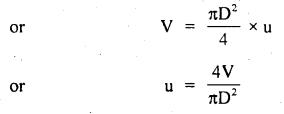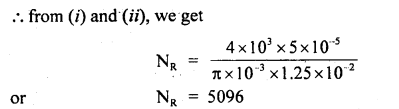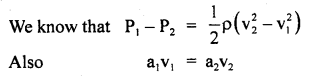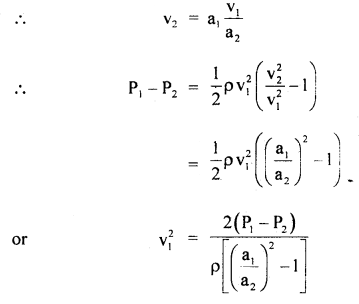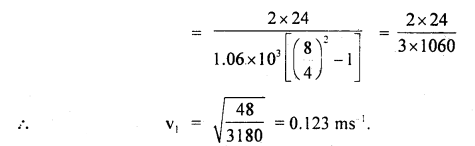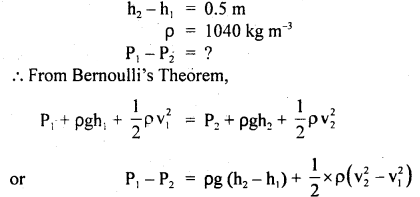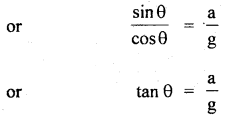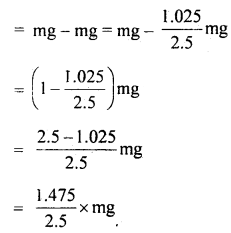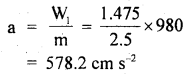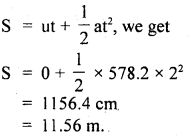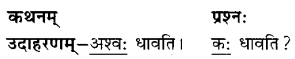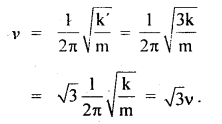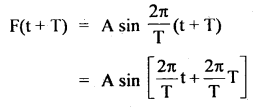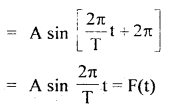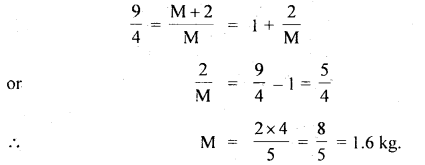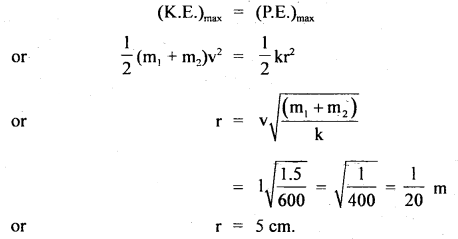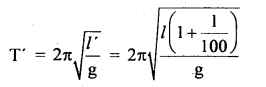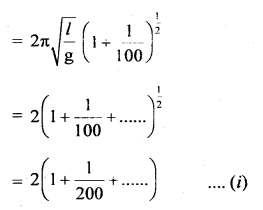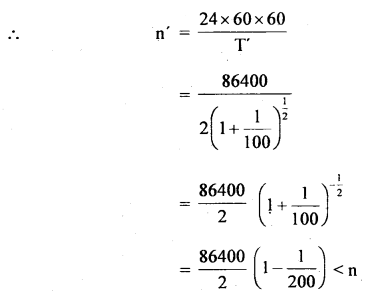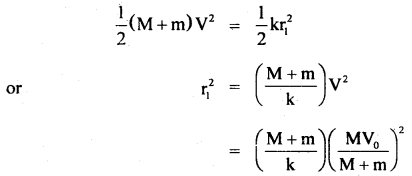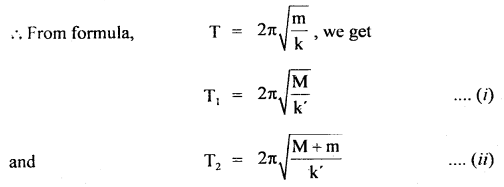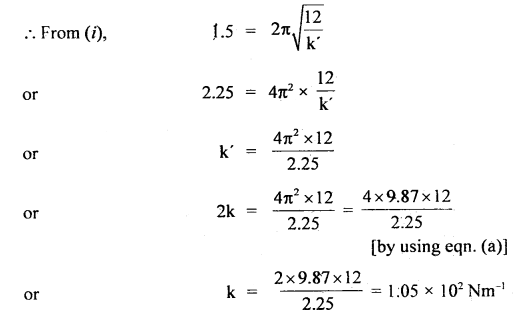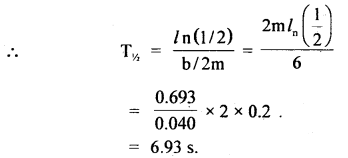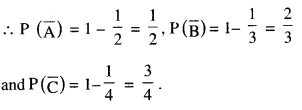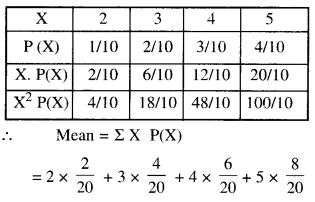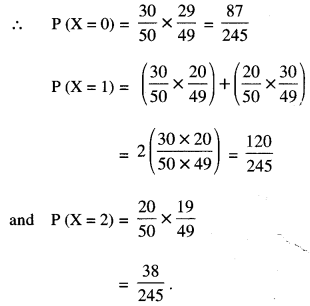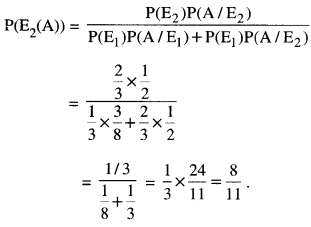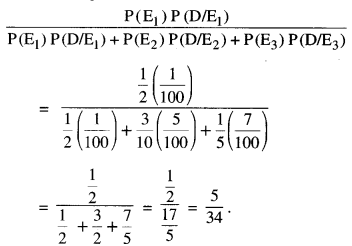We have given detailed NCERT Solutions for Class 10 Sanskrit Abhyasvan Bhav Sanskrit Class 10 Solutions Chapter 11 वाच्यम् Questions and Answers come in handy for quickly completing your homework.

Abhyasvan Bhav Sanskrit Class 10 Solutions Chapter 11 वाच्यम्

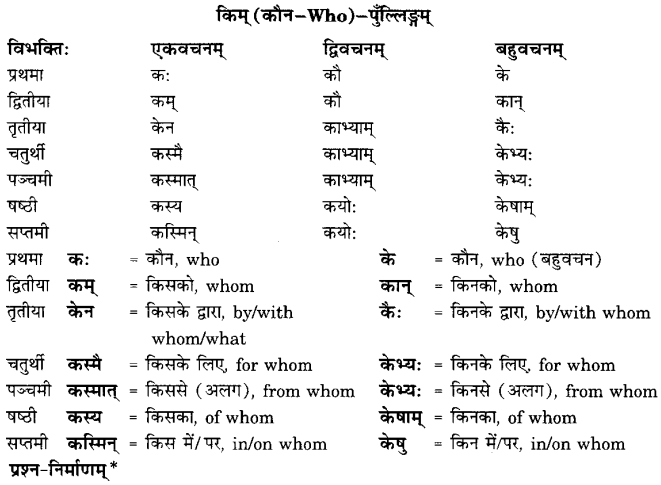
अभ्यासः

प्रश्न 1.
अधोलिखितवाक्येषु कर्तृपदं परिवर्त्य वाक्यानि लिखत-

(i) बालकः पायसं खादति।
_________ पायसः खाद्यते।
उत्तरम्:
बालकेन

(ii) अहं फलं खादामि।
_________ फलं खाद्यते।
उत्तरम्:
मया

(iii) त्वं किं शृणोषि?
_________ किं श्रूयते?
उत्तरम्:
त्वया

(iv) आवां चित्राणि पश्यावः।
_________ चित्राणि दृश्यन्ते।
उत्तरम्:
आवाभ्याम्

(v) वयं पाठं स्मरामः।
_________ पाठः स्मर्यते।
उत्तरम्:
अस्माभिः

(vi) बालकौ धावतः।
_________ धाव्यते।
उत्तरम्:
बालकाभ्याम्

(vii) कुक्कुराः इतस्ततः भ्रमन्ति।
_________ इतस्ततः भ्रम्यते।
उत्तरम्:
कुक्कुरैः

(viii) गजः शनैः शनैः चलति।
_________ शनैः शनैः चल्यते।
उत्तरम्:
गजेन

(ix) वानरः कूर्दति।
_________ कूर्यते।
उत्तरम्:
वानरेण

(x) अहं शाटिकां क्रीणामि।
_________ शाटिका क्रीयते।
उत्तरम्:
मया

प्रश्न 2.
अधोलिखितवाक्येषु कर्मपदं परिवर्त्य वाक्यानि लिखत-

(i) श्रमिकः भारं वहति।
श्रमिकेण _________ उह्यते।
उत्तरम्:
भारः

(ii) सः पाषाणं त्रोटयति।
तेन _________ त्रोट्यते।
उत्तरम्:
पाषाणः

(iii) सा गीतं गायति।
तया _________ गीयते।
उत्तरम्:
गीतं

(iv) माता रोटिकां पचति
मात्रा _________ पच्यते।
उत्तरम्:
रोटिका

(v) पिता फलानि आनयति।
पिता _________ आनीयन्ते।
उत्तरम्:
फलानि

(vi) सेवकः सेवां करोति।
सेवकेन _________ क्रियते।
उत्तरम्:
सेवा

(vii) चिकित्सक: उपचारं करोति।
चिकित्सकेन _________ क्रियते।
उत्तरम्:
उपचारः

(viii) नीलिमा पाठं स्मरति।
नीलिमया _________ स्मर्यते।
उत्तरम्:
पाठः

(ix) अहं गृहं गच्छामि।
मया _________ गम्यते।
उत्तरम्:
गृह

(x) आवां लेखान् लिखावः।
आवाम्यां _________ लिख्यन्ते।
उत्तरम्:
लेखाः

प्रश्न 3.
अधोलिखितवाक्येषु क्रियापदपरिवर्तनं कृत्वा वाक्यानि लिखत-

(i) अहं जलं पिबामि।
मया जलं _________।
उत्तरम्:
पीयते

(ii) आवां विद्यालयं गच्छावः
आवाभ्यां विद्यालयः _________।
उत्तरम्:
गम्यते

(iii) वयं ग्रामं गच्छामः।
अस्माभिः ग्रामः _________।
उत्तरम्:
गम्यते

(iv) त्वं फलानि खादसि।
त्वया फलानि _________।
उत्तरम्:
खाद्यान्ते

(v) छात्रः अध्ययनं करोति।
छात्रेण अध्ययनं _________।
उत्तरम्:
क्रियते

(vi) अहं श्रान्तः भवामि।
मया श्रान्तः _________।
उत्तरम्:
भूयते

(vii) बालकः क्रीडति।
बालकेन _________।
उत्तरम्:
क्रीड्यते

(viii) शिष्यः गुरुं सेवते।
शिष्येण गुरुः _________।
उत्तरम्:
सेव्यते

(ix) पाचकः भोजनं पचति।
पाचकेन भोजनं _________।
उत्तरम्:
पञ्चते

(x) धावकः धावति।
धावकेन _________।
उत्तरम्:
धाव्यते

Here we are providing Class 11 Physics Important Extra Questions and Answers Chapter 11 Mechanical Properties of Fluids. Important Questions for Class 11 Physics with Answers are the best resource for students which helps in Class 11 board exams.

Class 11 Physics Chapter 11 Important Extra Questions Thermal Properties of Matter

Thermal Properties of Matter Important Extra Questions Very Short Answer Type

Question 1.
The fact that the triple point of a substance is unique is used in modern thermometry. How?
Answer:
In modern thermometry, the triple point of water is a standard fixed point.

Question 2.
Is it possible for a body to have a negative temperature on the Kelvin scale? Why?
Answer:
No. Because absolute zero of temperature is the minimum possible temperature on the Kelvin scale.

Question 3.
(a) Why telephone wires are often given snag?
Answer:
It is done to allow for safe contraction in winter.

(b) The temperature of a gas is increased by 8°C. What is the corresponding change on the Kelvin scale?
Answer:
8 K.

Question 4.
There ¡s a hole in a metal disc. What happens to the size of the hole if the metal disc is heated?
Answer:
The size of the hole increases on heating the metal disc.

Question 5.
Milk is poured into a cup of tea and is mixed with a spoon. Is this an example of a reversible process? Why?
Answer:
No. When milk is poured into tea, some work is done which is not recoverable. So the process is not reversible.

Question 6.
The top of a lake is frozen. Air ¡n contact with it is at -15°C. What do you expect the maximum temperature of water in contact with the lower surface ice? What do you expect the maximum temperature of water at the bottom of the lake?
Answer:
0°C, 4°C.

Question 7.
How does the heat energy from the sun reaches Earth?
Answer:
It reaches by radiation.

Question 8.
Why does not the Earth become as hot as the Sun although it has been receiving heat from the Sun for ages?
Answer:
Earth loses heat by convection and radiation.

Question 9.
Why felt rather than air is employed for thermal insulation?
Answer:
In the air, loss of heat by convection is possible. But convection currents cannot be set up in felt.

Question 10.
What are the three modes of transmission of heat energy from one point to another point?
Answer:
Conduction, Convection and Radiation.

Question 11.
Name suitable thermometers for measuring:
(a) – 80°C,
Answer:
gas thermometer,

(b) 50°C,
Answer:
mercury thermometer,

(c) 700°C,
Answer:
Platinum resistance thermometer,

(d) 1500°C.
Answer:
radiation pyrometer.

Question 12.
Why a thick glass tumbler cracks when boiling liquid is poured into it?
Answer:
Its inner and outer surfaces undergo uneven expansion due to the poor conductivity of glass, hence it cracks.

Question 13.
What is the basic principle of a thermometer?
Answer:
The variation of some physical property of a substance with temperature constitutes the basic principle of the thermometer.

Question 14.
Out of mass, radius and volume of a metal ball, which one suffers maximum and minimum expansion on heating? Why?
Answer:
Volume and radius suffer maximum and minimum expansions respectively as γ = 3α.

Question 15.
The higher and lower fixed points on a thermometer are separated by 160 mm. If the length of the mercury thread above the lower point is 40 mm, then what is the temperature reading?
Answer:
The temperature reading = \(\frac{100 \times 40}{160}\) =25.

Question 16.
Two thermometers are constructed in the same way except that one has a spherical bulb and the other an elongated cylindrical bulb. Which of the two will respond quickly to temperature changes.
Answer:
The thermometer with a cylindrical bulb will respond quickly as the area of the cylindrical bulb is greater than the area of the spherical bulb.

Question 17.
Why a gas is cooled when expanded?
Answer:
Due to a decrease in internal energy, gas is cooled.

Question 18.
Why two layers of cloth of equal thickness provide warmer covering than a single layer of cloth of double thickness?
Answer:
This is because the air enclosed between the two layers of cloth acts as a good heat insulator.

Question 19.
Why snow is a better heat insulator than ice?
Answer:
Snow has air enclosed in it which reduces the chances of loss of heat by convection, hence it is a better heat insulator than ice.

Question 20.
Why water in a metallic pot can be boiled quickly if the bottom of the pot is made black and rough than a highly polished surface?
Answer:
The black and rough surface is a better absorber of heat than a highly polished surface.

Question 21.
Pieces of glass and copper are heated to the same temperature. Why does the piece of copper feel hotter OIL touching?
Answer:
Since copper is a better conductor of he, than gases, so copper transmits heat quickly to the hand and hence it feels hotter on touching.

Question 22.
Why people in the desert wear heavy clothes?
Answer:
Because they protect them from both heat and cold.

Question 23.
Why a wooden table fixed with iron nails become loose after some time?
Answer:
Due to uneven expansion of wood and nail.

Question 24.
Wooden charcoal and a metal piece of the same dimension are heated in the same oven to the same temperature and then removed in the dark. Which one would shine more and why?
Answer:
The charcoal will shine more as it is a good absorber and good emitter, so it will emit more energy.

Question 25.
What is the condition for the difference between the length of a certain brass rod and that of a steel rod to be constant at all temperature?
Answer:
The condition is that the lengths of the rods are inversely proportional to the coefficients of linear expansion of the materials of the rods.

Question 26.
What is the cause of the hotness of a body?
Answer:
The K.E. of the molecules constituting the body causes its hotness.

Question 27.
When are two bodies said to be in thermal equilibrium?
Answer:
Two bodies are said to be in thermal equilibrium when they are at j the same temperature.

Question 28.
What is the value of the temperature coefficient for metals and alloys?
Answer:
Its value is always positive f_c > r metals and alloys.

Question 29.
What is the value of the temperature coefficient for insulators and semi-conductor?
Answer:
It is always negative for insulators and semiconductors.

Question 30.
Are Coefficients of thermal expansion constant for a given solid?
Answer:
No.

Question 31.
Out of a gas and mercury thermometer, which one is more sensitive?
Answer:
A gas thermometer is more sensitive.

Question 32.
At what temperature will wood and iron appear equally hot or equally cold?
Answer:
At the temperature of the human body, both wood and iron will appear equally hot or cold.

Question 33.
A liquid of cubical coefficient of expansion is heated in a vessel having a coefficient of linear expansion \(\frac{\gamma}{3}\). What would be the effect on the level of liquid?
Answer:
No effect.

Question 34.
Is a fur coat itself a source of heat or merely an insulator?
Answer:
It is merely an insulator.

Question 35.
Why fur coat is an insulator?
Answer:
Because it is a bad conductor of heat and prevents the outflow of body heat.

Question 36.
Why does a bullet heat up when it hits a target?
Answer:
It is because its K.E. is converted into heat energy.

Question 37.
How can you measure a temperature of less than 100 K?
Answer:
It can be measured by using a germanium resistance thermometer.

Question 38.
Why water at the bottom of a waterfall is warmer than at the top?
Answer:
It is because P.E. of stored water is converted into heat energy.

Question 39.
What is the S.I. unit of heat capacity?
Answer:
Joule/Kelvin (JK^-1) is the S.I. unit of heat capacity.

Question 40.
Name the substance that contracts on heating?
Answer:
Ice.

Question 41.
Why is a vacuum created between two glass walls of a thermos flask?
Answer:
It is done to prevent the transfer of heat by conduction and convection.

Question 42.
What happens to the K.E. of water which stops after being stirred?
Answer:
It is converted into heat energy.

Question 43.
Why do telephone wires become tight in winter?
Answer:
It becomes tight due to contraction in length with the fall of temperature.

Question 44.
How does the coefficient of cubical expansion of a gas changes with temperature?
Answer:
It decreases with the rise in temperature.

Question 45.
Why do dogs draw out their tongues in summer?
Answer:
They do so to create cooling by evaporation.

Question 46.
How does the boiling point of a liquid changes with temperature?
Answer:
It rises with an increase in temperature.

Question 47.
What is the effect of pressure on the melting point of ice?
Answer:
It is lowered due to the increase in pressure.

Question 48.
What is the thermal capacity of 40 g of copper of specific heat 0.3?
Answer:
It is for 12 cal.

Question 49.
When water is heated from 0° to 10°C, what happens to its volume?
Answer:
It first decreases and then increases.

Question 50.
Why the coefficient of cubical expansion of water is zero at 4°C?
Answer:
This is because the density of water is maximum at 4°C.

Thermal Properties of Matter Important Extra Questions Short Answer Type

Question 1.
Why gas thermometers are more sensitive than mercury thermometers?
Answer:
This is because the coefficient of expansion of a gas is very large as compared to the coefficient of expansion of mercury. For the same temperature change, the gas would undergo a much larger change in volume as compared to mercury.

Question 2.
Why the brake drum of an automobile gets heated up when the automobile moves down a hill at constant speed?
Answer:
Since the speed is constant so there is no change of kinetic energy. The loss in gravitational potential energy is partially the gain in the heat energy of the brake drum.

Question 3.
A solid is heated at a constant rate. The variation of temperature with heat input is shown in the figure here:

(а) What is represented by AB and CD?
Answer:
The portions AB and CD represent a change of state. This is because the supplied heat is unable to change the temperature. While AB represents a change of state from solid to liquid, the CD represents a change of state from liquid to vapour state.

(b) What conclusion would you draw1 if CD = 2AB?
Answer:
It indicates that the latent heat of vaporisation is twice the latent heat of fusion.

(c) What is represented by the slope of DE?
Answer:
Slope of DE represents the reciprocal of the thermal or heat capacity of the substance in vapour state i.e. slope 0f DE = \(\frac{d T}{d Q}=\frac{1}{m C}\)(∴ dQ = mCΔT).

(d) What conclusion would you draw from the fact that the slope of OA is greater than the slope of BC?
Answer:
Specific heat of the substance in the liquid state is greater than that in the solid-state as the slope of OA is more than that of BC i.e. \(\frac{1}{\mathrm{mC}_{1}}\) > \(\frac{1}{\mathrm{mC}_{2}}\) where C₁, C₂ are specific heats mC₁ mC₂ of the material in solid and liquid state respectively.

Question 4.
Define:
(a) Thermal conduction.
Answer:
It h defined as the process of the transfer of heat energy from one part of a solid. to another part at a lower temperature without the actual motion of the molecules. It is also called the conduction of heat.

(b) Coefficient of thermal conductivity of a material.
Answer:
It is defined as the quantity of heat flowing per second across the opposite faces of a unit cube made of that material when the opposite faces are maintained at a temperature difference of 1K or 1°C.

Question 5.
On what factors does the amount of heat flowing from the hot face to the cold face depend? How?
Answer:
If Q is the amount of heat flowing from hot to the cold face, then it is found to be:

1. directly proportional to the cross-sectional area (A) of the face
   i. e. Q ∝ A …(1)
2. directly proportional to the temperature difference between the two faces, i.e. Q ∝ Δθ ….(2)
3. directly proportional to the time t for which the heat flows i.e. Q ∝ t …. (3)
4. inversely proportional to the distance ‘d’ between the two faces
   i.e. Q ∝ \(\frac{1}{Δx}\) …(4)

Combining factors (1) to (4), we get
Q ∝ \(\frac{\mathrm{A} \Delta \theta}{\Delta \mathrm{x}}\)t
or
Q ∝ K A \(\frac{\Delta \theta}{\Delta \mathrm{x}}\)t
where K is the proportionality constant known as the coefficient – of thermal conductivity.

Question 6.
State Newton’s law of cooling and define the cooling curve. What is its importance?
Answer:
Newton’s law of cooling: States that the rate of loss of heat per unit surface area of a body is directly proportional to the temperature difference between the body and the surroundings provided the difference is not too large.

Cooling Curve: It is defined as a graph between the temperature of a body and the time. It is as shown in the figure here.

The slope of the tangent to the curve at any point gives the rate of fall of temperature.

Question 7.
Explain why heat is generated continuously in an electric heater but its temperature becomes constant after some time?
Answer:
When the electric heater is switched on, a stage is quickly reached when the rate at which heat is generated by an electric current becomes equal to the rate at which heat is lost by conduction, convection and radiation and hence a thermal equilibrium is established. Thus temperature becomes constant.

Question 8.
A woollen blanket keeps our body warm. The same blanket if wrapped around ice would keep ice cold. How do you explain this apparent paradox?
Answer:
Wool is a bad conductor of heat. Moreover wool encloses air in it which is a bad conductor. There can also be no loss of heat by convection. The woollen blanket keeps us warm by preventing the heat of the human body to flow outside and hence our body remains warm.

In the case of ice, the heat from outsiders prevented to flow inside and thus ice remains cold.

Question 9.
A liquid is generally heated from below. Why?
Answer:
When a liquid is heated, it becomes rarer due to a decrease in density and it rises up. Liquid from the upper part of the vessel comes down to take its place and thus convection currents are formed. If the liquid is heated at the top, no such convection currents will be formed and only the liquid in the upper part of the vessel will become hot. However, the temperature in the lower part of the vessel will rise slightly due to a small amount of heat conducted by the hot liquid in the upper part of the vessel.

Question 10.
If a drop of waterfalls on a very hot iron, it does not evaporate fora long time. Why?
Answer:
When a drop of waterfalls on a very hot iron, it gets insulated from the hot iron due to the formation of a thin layer of water vapour, which is a bad conductor in nature. It takes quite a long to evaporate as heat is conducted from hot iron to the drop through the layer of water vapour very slowly.

On the other hand, if a drop of waterfalls on an iron which is not very hot, then it comes in direct contact with the iron and evaporates immediately.

Question 11.
On a hot day, a car is left in sunlight with all the windows closed. After some time, it is found that the inside of the car is considerably warmer than the air outside. Explain why?
Answer:
Glass possesses the property of selective absorption of heat radiation. It also transmits about 50% of heat radiation coming from a hot source like the sun and is more or less opaque to the radiation from moderately hot bodies (at about 100°C or so). Due to this, when a car is left in the sun, heat radiation from the sun gets into the car but as the temperature inside the car is moderate, it cannot escape through its windows. Thus glass windows of the car trap the sun rays and because of this, the inside of the car becomes considerably warmer.

Question 12.
It takes longer to boil water with a flame in a satellite in gravitational field-free space, why? How it will be heated?
Answer:
Water boils with flame by the process of convection. Hot lighter particles raise up and heavier particles move down under gravity. In. a gravity-free space in the satellite, the particles cannot move down hence, water can’t be heated by convection.

It will be heated by conduction.

Question 13.
Find γ for polyatomic gas and hence determine its value for a triatomic gas in which the molecules are linearly arranged.
Answer:
The energy of a polyatomic gas having n degrees of freedom is given by
E = n × \(\frac{1}{2}\) kT × N =\(\frac{n}{2}\) RT

In case of a triatomic gas, n = 7
∴ γ = 1 + \(\frac{2}{7}\) = \(\frac{9}{7}\).

Question 14.
Food in a hot case remains warm for a long time during winter, how?
Answer:
The hot case is a double-walled vessel. The space between the walls is evacuated in a good hot case. The food container placed inside the hot case is made of crowning steel, thus neither the outside low-temperature air can enter the container nor the heat from inside can escape through the hot case by conduction or convection. The highly polished shining surface of the food container helps in stopping loss of heat due to radiation. Thus, the heat of the food is preserved for a long time and food remains hot in winter.

Question 15.
You might have seen beggars sleeping on footpaths or in open in winter with their hands and knees pulled inside. Similarly dogs too curl while sleeping in winter. How does such action help anybody?
Answer:
The heat radiated or emitted from a body at a given temperature depends on

1. the temperature difference between the body and the surrounding,
2. area of the body in contact with the surroundings and
3. the nature of the body.

For man and animals in winter (1) and (2) factors remain what they are. So, in order to preserve, their body heat they curl up to reduce the surface area in contact with cold air.

Question 16.
Many people enjoy bathing below Kempty fall in Mussoorie, even though the water is quite cold, explain?
Answer:
When water falls from a height, it loses its potential energy. This is converted into the kinetic energy of the water molecules. It is a known fact from the kinetic theory of gases that an increase in kinetic energy of the substance increases its temperature, hence the temperature of water at the bottom of the fall rises and it does not remain as cold as on the top. Therefore, people taking bath below the Kempty fall do not get frozen, they rather feel warm and enjoy bathing.

Question 17.
Cycle, scooter handles and steering wheels of four-wheelers have plastic, rubber or cotton thread coverings. Why?
Answer:
Cycle and scooter handle, as well as steering wheels of four-wheelers such as car, truck, tempo, are made of metals which are good conductors of heat. In winter when we hold them the body heat is conducted to them being at lower temperature and in summer their temperature is more than the body temperature, transfer heat to the human hands. In either case, the human being feels uncomfortable.

To avoid this heat transfer, those portions from where the driver holds the vehicle are covered with heat insulators such as plastic, rubber or cotton.

Thus, the driver is saved from cold or heat being felt in his hands.

Question 18.
Why metals like copper, iron, brass etc. are good conductors of heat whereas wood, cardboard, ply are not conductors of heat?
Answer:
Heat conductibility in solids apart from temperature depends on the availability of conducting particles i.e. free electrons. In metals like copper, brass and iron-free electrons are available but in insulators like wood, cardboard and ply free electrons are not available, so metal is good conductors of heat.

Question 19.
House in Rajasthan made of stone and lime are cooler than those made of brick and cement why?
Answer:
The thermal conductivity of lime is smaller than that of cement. Even though stone tends to be Rotter than a brick in the day time as much as. does the cement plaster. Similarly, on cold days or cold nights even during summer, the heat of the house is not allowed to escape out. The thickness of stone walls compared to brick walls is yet another factor in keeping the houses, cool or warm in opposite”conditions.

Question 20.
Housing on hills are either made of wood or have wooden lining and walls. Why? Why people in plains where temperature variations are extreme winter and summer do not use-wooden house?
Answer:
On hills, people make wooden houses or put wooden lining, on house walls to insulate the house from the extreme cold of winter because wood being a bad conductor of heat does not allow the heat of house to escape out or exchange low outside temperature with the high temperature inside.

In plains even though wooden houses are helpful in fulfilling the odd weather conditions yet because of other factors such as

• non-availability of plenty of wood and
• chances of catching fire etc. wooden houses are generally not built.

Question 21.
People who own cars know well if they close all glass windows of the car park it in the Sun, it remains very hot inside the car even after sunset. To keep inside the car cooler insulating screens are put inside the car covering, the winds screen and curtains are pulled on the glass of windows, explain.
Answer:
Glass at normal temperature say up to 100° is opaque to heat radiations. But if radiations are coming from a source having a high temperature (surface temperature of sun ~ 6000k), it becomes transparent. Thus heat from the sun enters the car but radiations from the car being at a lower temperature (~ 50°C) cannot escape out so it remains hot, glass is opaque for radiations at such low temperature and the car body is double-walled or lined with insulators also does not allow the inner body heat to escape, Thus inside of the car remains hot.

But when screen and curtains are put the solar radiations are either reflected back or get absorbed and the temperature inside the car does not rise too much. It remains bearable.

Question 22.
What are the various properties of a thermometric substance?
Answer:
Following are the properties of a thermometric substance:

1. They should have a high boiling point and low freezing point to provide for the measurement of a wide range of temperature.
2. It should not be volatile.
3. It should be a variable in abundance.
4. Its rate of expansion should be uniform so that the calibration becomes easier.
5. The coefficient of expansion of the substance should be high so that the thermometer may be sensitive.
6. It should be available in a pure state.
7. It should not stick to the side of the glass tube.
8. It should have good thermal conductivity.

Question 23.
It is generally very cold after the hail storm than during or before it. Why?
Answer:
After a hail storm, the ice balls melt by absorbing a lot of heat energy from the atmosphere, thus reducing its temperature. Hence there is very cold after the hail storm.

Question 24.
Why pendulums made of invar are used in clocks?
Answer:
Invar has a low value of the coefficient of linear expansion, so the length of the pendulum almost remains the same in different seasons and hence gives the correct time.

Question 25.
Should a thermometer bulb have a large heat capacity or a small heat capacity? Why?
Answer:
A thermometer bulb should have a small heat capacity. In case, if it has a large capacity, the temperature of the substance will get lowered due to a large amount of heat absorbed by the thermometer bulb.

Question 26.
Explain why the coefficient of cubical expansion of water is negative between 0°C and 4°C?
Answer:
This is because of the fact that the volume of water decreases between 0°C and 4°C and water contracts within this range of temperature.

Question 27.
Why good conductors of electricity are also good conductors of heat?
Answer:
Both thermal and electrical conductivity depends upon the number of free electrons which are in large number in good conductors of electricity.

Question 28.
How is a gas thermometer better than a mercury thermometer?
Answer:
A gas thermometer is better because it can measure very low and very high temperature while the range of mercury thermometer is limited due to its freezing point – 37°C and boiling point 357°C.

Question 29.
A vertical glass jar is filled with water at 10°C. It has one thermometer at the top and another at the bottom. The central region of the jar is gradually cooled. It is found that the bottom thermometer reads 4°C earlier than the top thermometer and the top thermometer reads 0°C earlier than the bottom thermometer. Why?
Answer:
This is because water expands on cooling from 4°C to 0°C, thus it becomes of highest density at 4°C and then its density goes down. So the bottom thermometer reads 4°C earlier as the temperature of water at the top will be more than 4°C.

Question 30.
Two spheres are m&de of the same metal and have the same mass. One is solid and the other is hollow. They are heated to the same temperature. What is the percentage increase in their diameters?
Answer:
It will be the same We both spheres as the expansion of solid is like photographic enlargement, so \(\frac{\Delta \mathrm{V}}{\mathrm{V}}\) = γΔθ.

Question 31.
Nam the effects produced by the heat given to a body.
Answer:
The following are the effects produced by the heat:

1. It changes the temperature of the body.
2. It changes the volume of the body.
3. It changes the state of the body.
4. It changes the physical and chemical properties of the body.
5. It produces light.
6. It generates electricity.

Thermal Properties of Matter Important Extra Questions Long Answer Type

Question 1.
(a) Define the following:
(i) Coefficient of linear expansion (α)
Answer:
α – It is defined as the change in the length per unit original length per unit change in temperature of the material of a solid rod.
i.e. α = \(\frac{\Delta l}{l_{0} \Delta \mathrm{T}}\)

(ii) Coefficient of superficial expansion (β)
Answer:
β – It is defined as the change in surface area per unit original surface area per unit change in the temperature of the material of the solid.
i.e. β = \(\frac{\Delta S}{S_{0} \Delta \mathrm{T}}\)

(iii) Coefficient of cubical expansion (γ)
Answer:
γ – It is defined as the change in volume per unit original volume per unit change in the temperature of the material of the solid.
γ = \(\frac{\Delta V}{V_{0} \Delta \mathrm{T}}\)

(b) Derive the relation α, β and γ.
Answer:
Relation between α and β

Consider a solid of length 1 cm at 0°C. Heat it by 1°C. If l0, lt be its length at 0°C and 1°C respectively, then
l_o = 1 cm
and
l₁ = l₀ + l_o ∝ Δt
= 1 + 1 × α × 1
= (1 + α) (∵ Δt = 1 – 0 = 1°C)

If S_o and S_t be its area at 0°C and 1°C respectively, then
So = l_o²= 1 cm²
S_t = l₁² = (1 + α)² cm²
∴ ΔS = S_t – S_o = (1 + α)² – 1

∴ By definition ,
β = \(\frac{\Delta \mathrm{S}}{\mathrm{S}_{0} \Delta \mathrm{T}}=\frac{(1+\alpha)^{2}-1}{1 \times 1}\)
= 1 + α² + 2α – 1 = α² + 2α
= 2α
(∵ α is very small, so α² is neglected)
or
α = \(\frac{\beta}{2}\) …(1)

Relation between α and γ:
Consider a cube of side 1 cm at 0°C. Heat it by 1°C
∴ l_o = 1 cm
and l₁ = l_o(1 + α Δt) = 1(1 + α × 1)
= (1 + α) cm

If V_o and V_t be its volumes at 0°C and 1°C respectively.
Then V_o = l_o³ = 1 cm³
and V_t = l_t³ = (1 + α)³
= 1 + α³ + 3α(1 + α)
= 1 + α³ + 3α + 3α²
= 1 + 3α
(∵ α is very small so square and higher powers are neglected.)
ΔV change in its volume, then
ΔV = V_t – V_o = 1 + 3α – l = 3α

∴ By definition,

Numerical Problems:

Question 1.
Calculate the increase in the temperature of the water which falls from a height of 100 m. Assume that 90% of the energy due to fall is converted into heat and is retained by water. J = 4.2 J cal^-1.
Answer:
Here, h = 100 m
Let m (kg) = mass of water

∴ Its P.E. at a height h = mgh
Energy of fall retained by water i.e. useful work done is given by,
W = 90% of mgh
= \(\frac{90}{100}\) mgh
= \(\frac{90}{100}\) × m × 9.8 × 100
= 882 m J.

∴ Heat retained, Q = \(\frac{W}{J}=\frac{m \times 882 J}{4.2 J c a l^{-1}}\)
= m × 210 cal …(i)
Specific heat of water C = 10 cal kg^-1 °C^-1

Let Δθ (°C) be the rise in the temperature of water.
∴ Heat gained, Q = mCΔθ
.= m × 10³ × Δθ
= m × Δθ × 10³ cal …. (ii)

∴ From (1) and (ii), we get
m × 210 = m × Δθ × 10³
or
Δθ = \(\frac{210}{10^{3}}\)= 0.21°C.

Question 2.
A clock with a steel pendulum has a time period of 2s at 20°C. If the temperature of the clock rises to 30°C, what will be the gain or loss per day? The coefficient of linear expansion of steel is
1.2 × 10^-5 C^-1
Answer:
Here α = 1.2 × 10^-1  °C^-1
Δt = 30 – 20= 10°C
T = 2s.

Using the relation, Δl = l α Δt, we get
\(\frac{\Delta l}{l}\) = α Δt
= 1.2 × 10^-5 × 10 = 1.2 × 10^-4 …. (i)
∴ T = 2π \(\sqrt{\frac{l}{g}}\) ….(ii)

If T’ be the time period of the pendulum, when l increases by Δl, then

∴ loss in time in one oscillation T’ – T
Hence loss in time in one day is given by

Question 3.
The thermal conductivity of brick is 1.7 W m^-1 K^-1 and that – of cement is 2.9 W m^-1 K^-1. What thickness of cement will have the same insulation as the brick of thickness 20 cm.
Answer:
Here, K_B = 1.7 W m^-1 K^-1
K_C = 2.9 W m^-1 K^-1
dB = 20 cm
dc = ?

We know that the heat flow is given by
Q = KA \(\frac{\Delta \theta}{\mathrm{d}}\) t

For the same insulation by the brick and the cement, Q, A, Δθ and t don’t change
Thus \(\frac{K}{d}\) should be a constant.

Question 4.
Two metal cubes A and B of the same size are arranged as shown in the figure. The extreme ends of the combination are maintained at the indicated temperatures. The arrangement is thermally insulated. The coefficient of thermal conductivity of A and B are 300 W/m°C and 200 W/m°C respectively. After a steady-state is reached, what will be the temperature of the interface?

Answer:
Let T (°C) be the temperature of the interface =?
Here, K₁ = 300 Wm^-1 °C^-1 for A
K₂ = 200 Wm^-1 °C^-1 for B

∴ Δθ₁ = 100 – T for A
Δθ₂ = T – 0 for B .
x = size of each cube A and B

∴ x₁ = x₂ = x
Let a = area of cross-section of the faces between which there is the flow of heat

If \(\left(\frac{\Delta \mathrm{Q}_{1}}{\Delta \mathrm{t}}\right)_{\mathrm{A}}\) and \(\left(\frac{\Delta \mathrm{Q}_{2}}{\Delta \mathrm{t}}\right)_{\mathrm{B}}\) be the rate of.tlow of heat for A and B respectively, then in steady state,

Question 5.
The heat of combustion of ethane gas is 373 Kcal per mole. Assuming that 50% of heat is lost, how many litres of ethane measured at STP must be burnt to convert 50 kg of water at 10°G to steam at 100°C? One mole of gas occupies 22.4 litres at S.T.P. Latent heat (L) of steam = 2.25 × 106 JK^-1.
Answer:
Here
L = 2.25 × 106 JK^-1
= \(\frac{2.25}{4.2}\) × 106 cal°C^-1

Q = Heat of Combustion
= 373 × 103 Cal/mole

C = 103 J Kg^-1 °C^-1
m = 50 kg
Δθ = 100- 10 = 90°C
V = 22.4 litres

If Q₁ = Total heat energy required to convert 50 kg of water at 10°C to steam at 100°C
Q₁ = mCΔθ + mL
= 5.0 × 1000 × 90 + 50 ×\(\frac{2.25 \times 10^{6}}{4.2}\)
= 4.5 × 106 + 26.79 × 106
= 31.29 × 106 cal

As 50% of heat is lost,
∴ total heat produced = \(\frac{100}{50}\) × 3.129 × 106

Let n = no. of moles of ethane to be burnt, then
n = \(\frac{2 \times 31.29 \times 10^{6}}{373 \times 10^{3}}\) mole

∴ Volume of ethane = nV
= \(\frac{2 \times 31.29 \times 10^{6}}{373 \times 10^{3}}\) × 22.4 litres
= 3758.2 litres.

Question 6.
Calculate the heat of combustion of coal when 10 g of coal on burning raises the temperature of 2 litres of water from 20°C to 55°C.
Answer:
Here, C = 1 cal g^-1 °C^-1
m = 2 × 10³ g
Δθ = 55 – 20 = 35°C
M = 10g

If Q be the heat produced, then
Q = mCΔθ
= 2 × 10³ × 1 × 35
= 70 × 10³ cal

∴ If Q₁ be the heat of combustion, then
Q₁ = \(\frac{Q}{M}=\frac{70 \times 10^{3}}{10}\) = 7000 cal g^-1

Question 7.
Calculate two specific heats of a gas from the following data:
γ = \(\frac{\mathbf{C}_{\mathrm{P}}}{\mathbf{C}_{\mathbf{v}}}\) = 1.51, density of gas at NTP = 1.234 g litre J = 4.2 × 10⁷ erg cal^-1.
Answer:
\(\frac{\mathbf{C}_{\mathrm{P}}}{\mathbf{C}_{\mathbf{v}}}\) = 1.51
P = 1.013 × 10⁶ dyne cm^-2
T= 273K
ρ = 1.234 g litre^-1
m = 1 g

∴ V = \(\frac{\mathrm{m}}{\rho}=\frac{1}{1.234}\) litre
= \(\frac{1}{1.234 \times 10^{-3}}\)

Also we know that for 1g gas,

Question 8.
Specific heats of argon at constant pressure and volume are 0.125 cal g^-1 and 0.075 cal g^-1 respectively. Calculate the density of argon at N.T.P. (J = 4.18 × 10⁷ ergs/cal and normal pressure = 1.01 × 10⁶ dynes cm^-2.)
Answer:
Here, CP = 0.125 cal g^-1
Cv = 0.075 cal g^-1 J
J = 4.18 × 107 ergs cal^-1
P = 1.01 × 106 dyne cm^-2
d = density at NTP = ?
m = 1 g
T = 273 K

Using the relation,
C_p – C_v = \(\frac{r}{J}=\frac{P V}{T J}=\frac{P m}{d T J}\) (∵ V = \(\frac{m}{d}\))
d = \(\frac{P m}{\mathrm{~TJ}\left(\mathrm{C}_{r}-\mathrm{C}_{\mathrm{v}}\right)}\)

Question 9.
A piece of metal weighs 46 g in air. When it is immersed ¡n a liquid of specific gravity 124 at 27°C, it weighs 30g. When the temperature of the liquid is raised to42°C, the metal piece weighs 30.5 g. The specific gravity of the liquid at 42°C ¡s 1.20. Calculate the coefficient of linear expansion of the metal.
Answer:
Here, the Weight of the metal piece at 27°C in air 46 g
Weight of metal piece at 27°C in liquid =30 g
Weight of metal piece at 42°C in liquid = 30.5 g
α =?
Loss in weight of the metal = weight of liqiid displaced = 46 – 30
= 16 g.

The volume of metal at 27°C = Volume of liquid displaced at 27°C
or
V1 = \(\frac{16 g}{\text { specific gravity of liquid }}\)
= \(\frac{16 \mathrm{~g}}{1.24 \mathrm{gcm}^{-3}}\)
= 12.903 cm3

Similarly volume of metal piece at 42°C = V₂ = \(\frac{(46-30.5)}{1.2 \mathrm{gcm}^{-3}}\)
= 12.917 cm³

∴ Coefficient of cubical expansion of the metal

Since γ = 3α
∴ α = \(\frac{1}{3}\) γ = \(\frac{1}{3}\) × 2.41 × 10⁵ °C^-1
= 0.803 × 10⁵ °C^-1

Question 10.
In an industrial process, 10 kg of water per hour is to be heated from 20°C to 80°C. To do so, steam at 150°C is passed from a boiler into a copper coil immersed in water. The steam condenses in the coil and is returned to the boiler as water at 90°C. How many kg of steam is required per hour? Specific heat of steam = 1 Kcal kg^-1 °C^-1 and latent heat of steam = 540 Kcal kg^-1.
Answer:
C = sp. heat of steam
= 1 Kcal kg^-1 °c^-1

L = latent heat of steam
= 540 Kcal kg^-1

Let m (kg) = mass of steam required per hour.

Heat is given by steam first from 150°C to steam at 100°C = mCΔθ
= m × (150 – 100)Kcal = 50 m Kcal.

Then steam changes from steam at 100°C to water at 100°C and gives out heat = mL = 540 m Kcal.

After this water at 100°C gives heat is going to temperature 90°C = m (100 – 90) = 10m Kcal.

Total amount of heat given by the steam = 50 m + 540 m + 10 m = 600 m Kcal.
∴ 600 m K cal = 600 K cal
∴ m = 1 kilogram.

Question 11.
An electric heater is used in a room with a total wall area of 137 m² to maintain a temperature of +20°C inside it when the outside temperature is -10°C. The wall has three layers of different materials. The innermost layer is of wood of thickness 2.5 cm, the middle layer is of cement of thickness 1.0 cm and the outermost layer is of brick of thickness 25.0 cm. Find the power of the electric heater. Assume that there is no heat loss through the floor and ceiling. The thermal conductivity of wood, cement and brick are 0. 125,1.5 and 1.0 Wm^-1 °C^-1 respectively.
Answer:
Let the temperature inside the room be θ₁, at the interface of wood and cement be θ₂, at the interface of cement and brick θ₃ respectively. The outside temperature is θ₄.

Here, K₁ = 0.125 Wm^-1 °C, K₂ = 1.5 Wm^-1 °C^-1, K₃ = 1.0 Wm^-1 °C^-1 A = 137m2 , θ₁ = 20°C θ₄ = -10°C , d₁ = 2.5 cm, d₂ = 1.0 cm, d₃ = 25 cm.

∴ \(\frac{0.125\left(20-\theta_{2}\right)}{2.5}=\frac{1.5\left(\theta_{2}-\theta_{3}\right)}{1}\)
or
5(20 – θ₂) = 150(θ₂ – θ₃)
or
20 – θ₂ = 30(θ₂ – θ₃) ,
or
20 = 31θ₂ – 30θ₃

Similarly from

or
20 – θ₂ = \(\frac{4}{5}\) (θ₃ + 10)
or
θ₃ = \(\frac{5}{4}\) (20 – θ₂) – 10 …(2)

∴ From (1) and (2), we get
20 = 3lθ₂ – 30 × (20 – θ₂) + 30 × 10
or
80 = 124θ₂ – 150(20 – θ₂)+ 1200
= 274θ₂ – 3000 + 1200
or
274θ₂ = 18800

∴ θ₂ = \(\frac{940}{137}\) °C

∴ If P be the heater power, then

Question 12.
The opposite faces of a cubical block of iron of cross-section 4 cm2 are kept in contact with steam and melting ice. Calculate the amount of ice melted at the end of 10 minutes if K = 0.2 cal cm^-1 s^-1 °C^-1 for iron. Latent heat of fusion of ice = 80 cal g^-1.
Answer:
Here, L = latent heat of ice
= 80 cal g^-1
A = 4 cm² .
K = 0.2 cal cm^-1 s^-1 °C^-1
Δθ = θ₂ – θ₁ = 100 – 0 = 100°C
t = time = 10 minutes = 10 × 60 = 600s
d = \(\sqrt{4}\) =2 cm

Let m = amount of ice melted = ?
Using the relation, Q = \(\frac{\mathrm{K} \mathrm{A}\left(\theta_{2}-\theta_{1}\right) \mathrm{t}}{\mathrm{d}}\), we get

Q = \(\frac{0.2 \times 4 \times 100 \times 600}{2}\)
Q = 24000 cal …(i)
Also, Q = mL = m. 80 …(ii)

∴ From (i) and (ii), we get
m × 80 = 24000

∴ m = \(\frac{24000}{80}\) = 300 g.

Question 13.
Water is boiled in a rectangular steel tank of thickness 2 cm by a constant temperature furnace. Due to vaporisation, the water level falls at a steady rate of 1 cm in 9 minutes. Calculate the temperature of the furnace. Given the thermal conductivity of steel is 0.2 cal cm^-1 s^-1 °C^-1 and latent heat of steam is 540 cal.
Answer:
d = 2 cm
t = 9 minutes = 9 × 60 = 540 s
K = 0.2 cal cm^-1 s^-1 °C^-1
L = 540 cal.

Let A be the area of the bottom of the steel tank.
θ₁ = temperature of the tank which is in contact with the constant temperature furnace?
fall in level of water = 1cm

∴ volume of water evaporated, V = A × 1 = A cm³
ρ = density of water = 1 g/cm³

Mass of water evaporated, m = ρV – 1 × A = Ag .

Q = heat required to evaporate Ag of water in 9 minute = A × 540 cal.
Also, Q = \(\frac{\mathrm{KA}\left(\theta_{\mathrm{1}}-\theta_{2}\right) \mathrm{t}}{\mathrm{d}}\)
or
540A = \(\frac{0.2 \mathrm{~A} \times\left(\theta_{1}-\theta_{2}\right) 540}{2}\)
or
θ₁ – θ₂ = \(\frac{2}{0.2}\) = 10
Here, θ₂ = 100°C
θ₁ = θ₂ + 10 = 100 + 10= 110 °C.

Question 14.
A circular hole of a radius of 1 cm is drilled in a brass sheet kept at 293K. What will be the diameter of the hole when the sheet is heated to 393K? a for brass = 18 × 10^-6 K^-1.
Answer:
Here, α = 18 × 10^-6 K^-1
ΔT = 393 – 293 K = 100 K
r = radius = 1 cm
∴ D = 2r = diameter = 2 cm
and it acts as the original length l (say).

∴ Let D’ be the new diameter = ?
I f Δl be the increase in length, then using the relation,
Δl = αlΔt, we get
Δl = 18 × 10^-6 × 2 × 100 = 36 × 10^-4 cm

∴ increase in diameter, AD = Al = 36 × 10^-4 cm
∴ D’ = D + ΔD = 2 + 0.0036 = 2.0036cm.

Question 15.
Find the change in the length of the steel bridge of the original length of 200 m in a locality where temperature changes from 243 to 313K. a for steel = 11 × 10^-6 K^-1.
Answer:
Here, T₁ = 243 K
T₂ = 313 K
∴ ΔT = change in temperature
= T₂ – T₁ = 313 – 243 = 70 K
l = 200 m
α = 11 × 10^-6 K^-1

Let Δl = change in the length of the bridge = ?
∴ Δl = lα ΔT
= 200 × 11 × 10^-6 × 70
= 154 × 10^-3 m
= 0.154 m = 15.4 cm.

Question 16.
Equal volumes of copper and mercury have the same thermal capacity. Mercury has a specific heat of0.046 and a density of 13.6 g cm^-3. Calculate the density of copper having sp. heat 0.092.
Answer:
Let C₁ and C₂ be the sp. heat of mercury and copper respectively having densities ρ₁ and ρ₂
Here, ρ₁ = 13.6 g cm^-3
C₁ = 0.046
C₂ = 0.092
∴ ρ₂ =?

Let V = volume of copper and mercury.
If m₁ and m₂ be the mass of mercury and copper, then
m₁ = V × ρ₁
and
m₂ = V × ρ₂
Also let H₁ and H₂ be their respective thermal capacity, so using
Thermal capacity = mass × sp. heat, we get
H₁ = Vρ₁ × C₁
and
H₂ = Vρ₂ × C₂

As H₁ = H₂
Vρ₁C₁ = Vρ₂C₂
or
ρ₂ = ρ₁\(\frac{C_{1}}{C_{2}}=\frac{13.6 \times 0.046}{0.092}\)
= 6.8gcm³.

Question 17.
What would be the final temperature of the mixture when 5 g of ice at -10°C is mixed with 20 g of water at 30°C? Sp. the heat of ice is 0.5 and latent heat of water – 80 cal g^-1.
Answer:
Here, m1 = mass of water = 20 g
θ₁ = temperature of water = 30°C
θ₂ = temperature of ice = -10°C
C₁ = sp. heat of waterr = 1
C₂ = sp, heat of ice.= 0.5
m₂ = mass of ice = 5 g

Let θ = final temperatre of the mixture
L = latent heat of water = 80 cal g^-1

∴ Heat lost by water is given by
H₁ = 20 × 1 × (30 – θ) ….(1)
(∵ H = mCΔθ)

Heat required to raise 5 g of ice at -10°C to 0°C
H₂ = 5 × [0 – (-10)] × 0.5
= 5 × 10 × \(\frac{5}{10}\) = 25 cal ….(2)

Let H₃ = heat required to meet 5 g of ice at 0°C to water at 0°C
H₃ = m₂L
= 5 × 80 = 400 cal ….(3)

Also let H₄ = heat required to raise 5 g of water at 0°C to θ°C
∴ H₄ = 5 × 1 × θ = 5θ

∴ Total heat gained by ice = H₂ + H₃ + H₄
= 25 + 400 + 5θ

∴ Heat lost = Heat gained gives
20(30 – θ) = 425 + 5θ
or
600 – 200 = 425 + 5θ
or
600 – 425 = (20 + 5)θ
or
25θ = 175

∴ θ = \(\frac{175}{25}\) = 7 °C.

Question 18.
A faulty Celcius thermometer has lower and upper fixed points as 1°C and 101°C; it reads a certain temperature as 50°C. What is the correct temperature?
Answer:
Let Correct temp. = x°C
∴ \(\frac{x-0}{100-0}=\frac{50-1}{101-1}\)
or
\(\frac{x}{100}=\frac{49}{100}\)
or
x = 49°C.

Question 19.
At what temperature do the Celsius and Fahrenheit readings have the same numerical value?
Answer:
Let x be the required value in °C and °F.
i.e. t_F = t_c = x°

∴ Using the relation, \(\frac{\mathbf{C}-0}{100}=\frac{\mathrm{F}-32}{180}\), we get

Question 20.
At what temperature do the Kelvin and Fahrenheit readings have the same numerical value?
Answer:
Let x be the required value in °K and °F
t_K = t_F = x

Using the relation,

Question 21.
Express 37°C into Farenheit.
Answer:
Here, t_c = 37°C
t_F = ?
Using the relation, \(\frac{C-0}{100}=\frac{F-32}{180}\) we get
or
F – 32 = \(\frac{9}{5}\) × C
∴ F = \(\frac{9}{5}\)C + 32
= \(\frac{9}{5}\) × 37+32
= 66.6 + 32
= 98.6°F.

Question 22.
The temperature of a body is increased from 100°F to 910°F. What is the temperature range in the Kélvin scale?
Answer:
Here, Δt = (T₂ — T₁)°F
= 910 – 100°F
= 810°F

Using the relation, ΔC = \(\frac{5}{9}\) × ΔF
or
ΔC = \(\frac{5}{9}\) × 810 – 450
∴ ΔC = 450°K

Question 23.
A faulty thermometer has its fixed points marked as 50 and 95°. When it reads 590 what is the corresponding temperature in °C?
Answer:
Let x be the reading ¡n °C.
∴ \(\frac{x-0}{100-0}=\frac{59-5}{95-5}\)
or
\(\frac{x}{100}=\frac{54}{90}=\frac{3}{5}\)
or
x = \(\frac{3}{5}\) × 100 = 60°C.

Question 24.
The temperature coefficient of resistance of a Wire is 0.00125 per °C. At 300 K its resistance is 1 Q. At what temperature will the resistance of the wire be 2Ω?
Answer:
Here, α = 125 × 105 °C^-1
R₃₀₀ = 1Ω

Let R_θ be its resistance at θ°C
∴ R_θ = 2Ω
∴ Δθ = rise in its temp.

∴ Using the relation

or
θ – 300 = 800

∴ θ = 800 + 300 = 1100 K

Question 25.
Calculate the temperature difference in °F equivalent to temperature difference of 25°C.
Answer:
Here, ΔC = 25°C
ΔF =?
Using the relation, ΔF = \(\frac{9}{5}\) × ΔC, we get
ΔF = \(\frac{9}{5}\) × 25
= 45°F.

Value-Based Type:

Question 1.
Venkat having found his mother suffering from fever Venkat took her to the doctor for treatment. While checking the status, the doctor used a thermometer to know the temperature of the body. He kept the thermometer in the mouth of the patient and noted the reading as 102°F. The doctor gave the necessary medicines. After coming home, Venkat asked his mother, who Is a science teacher, why mercury is used in a thermometer when there are so many liquids. Then his mother explained the reason.
(a) Comment upon the values of the mother.
Answer:
Mother has an interest in educating her son and explained that Mercury has got the following properties for being used in their- monitors

1. The expansion of Mercury is fairly regular and uniform.
2. It is opaque and shining, hence can be easily seen through the glass tube.
3. Mercury is a good conductor of heat and has a low thermal capacity,
4. Mercury dose is not wet on the sides of the glass tube in which it is tilled.

(b) A newly designed thermometer has its lower fixed point and upper, the fixed point marked at 5° and 95° respectively. Compute the temperature on this scale corresponding to 50°C.
Answer:
Let θ be the temperature on the scale corresponding to θ = 50°C.
Then \(\frac{\theta-5}{95-5}=\frac{C-0}{100-0}=\frac{C}{100}\)
or
θ = 50°
Thus, the required temperature on the scale of the designed ther¬mometer is 50°.

Question 2.
Raman noticed that his grandfather to be suffering from fever. He took him to the doctor. The doctor gave him some pills. When the pills were used he sweated much, after some time became normal. Rahim enquired the Doctor about how his grandfather become normal.
(a) According to you what values are possessed by Raman?
Answer:
Raman is responsible and he has concern for others, inquisitiveness in gaining knowledge, curiosity

(b) A child running a temperature of 101°Fis given an Antipyrin which causes an increase in the rate of evaporation of the body. If the fever is brought down to 98° F in 20 m, what is the amount of heat lost by the body? The mass of the child is 30 kg.
Answer:
Loss in temperature (Dt) =101°F – 98°F = 3°F = 3 × \(\frac{5}{9}\) °C
= 1.67 °C
Specific heat of water (S) = 1000 Gal. kg^-1 °C^-1
m = 30 kg

∴ Heat lost by the body = ms Δt
= 30kg × 1000 Cal. kg^-1 °C^-1 × 1.67°C
=501000 Cal

Question 3.
Radha and Kavita are two friends of science stream. They were discussing the phenomena of cooling. Radha told that a hot body will lose its temperature more rapidly in a room where the temperature would be less. Kavita did a small activity by putting two j glasses having the same temperature in two different room of different room temperature and note down the temperature after 10 min. She found that Radha’s idea was correct.
(i) What values are exhibited by Kavita?
Answer:
Kavita’s values are:
Curiosity, Interested in the experiment. Habit to check the correctness of an idea.

(ii) Write the law relating to this phenomena.
Solution:
The rate of loss of heat depends on the difference in temperature between the body and its surroundings. Newton was the first to study.

According to Newton’s law of cooling, the rate of loss of heat (-dQ/dt) of the body is directly proportional 1o the difference of temperature DT = (T₂– T₁) of the body and the surrounding. The law holds goods only for the small difference in temperature.
i.e – \(\frac{dQ}{dt}\) = K(T₂ – T₁)

-ve sign implies that as time passes, temperature (T) decreases.

Question 4.
Anurag and Akash were discussing heat transfer. Anurag told that houses of concrete roofs get very hot during summer days because the thermal conductivity of concrete (though much smaller than that of metal) is still not small enough. Therefore, people usually prefer to give a layer of earth or foam insulation on the ceiling so that heat transfer is prohibited and keeps the room cooler. But Akash was not convinced by this idea. He told me that it is just to decorate the ceiling.
(i) What values are displayed by Anurag?
Answer:
Application of scientific reason, curiosity, the attitude of group discussion and problem-solving skill.

(ii) Whether Anurag was telling right or wrong?
Answer:
Yes, Anurag was telling right.

(iii) On what factors the amount of heat flowing from the hot face to the cold face depends?
Answer:
Heat flowing Q α A; A = Cross-sectional area
α Δθ ; Δθ = Temperature difference
α t ; t = time
α 1/Δx; Δx = Distance between the two face

On combining the above relations, we get.
i.e Q = \(\frac{\mathrm{KA} \Delta \theta}{\Delta x}\) t
Where K is the proportionality constant known as the coefficient of thermal conductivity

We have given detailed NCERT Solutions for Class 10 Sanskrit Abhyasvan Bhav Sanskrit Class 10 Solutions Chapter 10 समय: Questions and Answers come in handy for quickly completing your homework.

Abhyasvan Bhav Sanskrit Class 10 Solutions Chapter 10 समय:

अभ्यासः

प्रश्न 1.
अधोलिखितवाक्येषु उदाहरणानुसारं समयबोधकेषु पदेषु रिक्तस्थानानि पूरयत-

उदाहरणम्-
द्वितलीयरेलवाहनं ___________ (10:15) वादने जयपुरं प्राप्नोति।
द्वितयीयरेलवाहनं सपाददशवादने जयपुरं प्राप्नोति।
(i) पुरुषोत्तम-एक्सप्रेस इति रेलयानं ___________ (9:30) वादने पुरीतः प्रस्थानं करोति।
(ii) चेतक-एक्सप्रेस इति रेलयानं ___________ (4:45) वादने दिल्लीम् आगच्छति।
(iii) हावड़ा-एक्सप्रेस ___________ (11:00) वादने हावडास्थानकं प्राप्नोति।
(iv) रेलयानमेकं ___________ (8:15) उत्तराञ्चलं प्रति गच्छति।
उत्तरम्:
(i) सार्धनव
(ii) पादोनपञ्च
(iii) एकादश
(iv) सपादाष्टवादने

प्रश्न 2.
अधोलिखितवाक्येषु उदाहरणानुसारं समयबोधकेषु पदेषु रिक्तस्थानानि पूरयत-

उदाहरणम्-
माता प्रातः ___________ (5.00) वादने उत्तिष्ठति।
माता प्रातः पञ्चवादने उत्तिठति।
(i) राहुलः प्रातभ्रमणाय ___________ (6:15) वादने उद्यानं गच्छति।
(ii) मल्लिका ___________ (7:30) वादने प्रातराशं करोति।
(iii) अनन्या ___________ (5:45) वादने क्रीडति।
(iv) सर्वे ___________ (10:00) वादने शयनं कुर्वन्ति।
उत्तरम्:
(i) सवादषड्
(ii) सार्धसप्त
(iii) पदोनषड्
(iv) दश

प्रश्न 3.
अधोलिखितवाक्येषु समयबोधकेषु पदेषु रिक्तस्थानानि पूरयत-

उदाहरणम्-
प्रातः ___________ (7.00) वादनतः ___________ (7.45) वादनपर्यन्तं विद्यालये प्रार्थनासभा भवति।
उत्तरम्:
सप्त, पादोनाष्ट
प्रातः सप्तवादनतः पादोनाष्टवादनपर्यन्तं विद्यालये प्रार्थनासभा भवति।

(i) ___________ (8:15) वादनतः ___________ (9:00) वादनपर्यन्तं विज्ञानविषस्य कालांशः भवित।
(ii) वयं ___________ (9:00) वादनतः ___________ (9:45) वादनपर्यन्तं गणितविषयं पठामः।
(iii) ___________ (2:45) वादनतः ___________ (3:30) वादनपर्यन्तं हिन्दीभाषाकालांशः भवति।
(iv) सस्कृतशिक्षक: ___________ (10:15) वादने अध्यापयति।
उत्तरम्:
(i) सपादाष्ट, नव
(ii) नव, पादोन-दश
(iii) पादोन-त्रि, सार्धत्रि
(iv) सपाद-दश

प्रश्न 4.
अधोलिखितवाक्येषु समयबोधकेषु पदेषु रिक्तस्थानानि पूरयत-

उदाहरणम्-
छात्रः ___________ (5.00) वादने उत्तिष्ठति ___________ (6.15) वादने व्यायाम करोति।
छात्रः पञ्चवादने उत्तिष्ठति सपादषड्वादने व्यायाम करोति।
(i) छात्रः ___________ (7:30) वादने प्रातरांश कृत्वा ___________ (9:45) वादने विद्यालयं गच्छति।
(ii) ___________ (4:00) वादने गृहमागत्य ___________ (4:30) वादनपर्यन्तं विश्रामं करोतिः।
(iii) ___________ (5:00) वादने भोजनं कृत्वा ___________ (9:30) वादनपर्यन्तं अध्ययनं करोति।
(iv) रात्रौः ___________ (9:45) वादनतः ___________ (5:00) वादनपर्यन्तं शयनं करोति।
उत्तरम्:
(i) सार्धसप्त, पादोन दश
(ii) चतुर्, सार्धचतुर्
(iii) पञ्च, सार्धनव
(iv) पादोन दश, पञ्च

We have given detailed NCERT Solutions for Class 6 Sanskrit Grammar Book अव्ययपदानि Questions and Answers come in handy for quickly completing your homework.

Sanskrit Vyakaran Class 6 Solutions अव्ययपदानि

अभ्यासः

उत्तर:
(क) कुत्र
(ख) कदा
(ग) यदा-तदा
(घ) अद्य
(ङ) बहिः
(च) श्वः
(छ) सह
(ज) अधुना
(झ) प्रति
(ब) आम् ।अपि

प्रश्नः 2.
उचितेन अव्ययपदेन रिक्तस्थानपूर्तिं कुरुत। (उचित अव्यय-पद से रिक्त स्थान की पूर्ति कीजिए। Fill in the blanks with the suitable Indeclinable.)

प्रतिदिनम्, सायम्, श्वः।

(क)

(i) जनाः ……………….. भ्रमन्ति ।
(ii) अहं ……. ……. जन्तुशालाम् गमिष्यामि ।
(iii) किम् त्वम् …………………. खेलसि?
उत्तर:
(i) सायम्
(ii) श्वः
(iii) प्रतिदिनम्

शीघ्रम्, उच्चैः, शनैः-शनैः।

(ख)
(i) सिंहः …………………. गर्जति।
(ii) वृद्धः ……………….. चलति ।
(iii) अहम् ……………….. लिखामि।
उत्तर:
(i) उच्चैः
(ii) शनैः-शनैः
(iii) शीघ्रम्

नहि, आम्, च।

(ग)
(i) बालकाः बालिकाः …………. खेलन्ति।
(ii) …………..अहम् अपि खेलामि।
(iii) ………. अहं बहिः न गमिष्यामि।
उत्तर:
(i) च
(ii) आम्
(iii) नहि

प्रश्न: 3.
कोष्ठकात् उचितं विकल्पं चित्वा वाक्यपूर्तिं कुरुत। (कोष्ठक से उचित विकल्प चुनकर वाक्यों की पूर्ति कीजिए। Pick out the correct option from the bracket and complete the sentences.)

(i) यूयम् खेलितुम् ……………. गच्छथ? (कुतः, कुत्र, किम्)
(ii) ……….. प्रातः भवति खगाः …………. कूजन्ति। (यदा-तदा, यत्र-तत्र, शनैः-शनैः)
(iii) पितामही देवालयं ……………….. अगच्छत्। (विना, सह, प्रति)
(iv) आकाशे मेघाः ………….. गर्जन्ति। (उच्चैः , तीव्रम्, परस्परम्)
(v) ……. जनकः कार्यालयम् न गच्छति। (अद्य, हयः, श्वः)
उत्तर:
(i) कुत्र
(ii) यदा-तदा
(iii) प्रति
(iv) उच्चैः
(v) अद्य

एतानि वाक्यानि अवलोकयत। (इन वाक्यों को देखिए। Look at these sentences.)

1. किम् त्वम् अधुना संस्कृतम् पठसि?
2. आम्, अहम् अधुना संस्कृतम् पठामि।
3. छात्रा: कदा विद्यालयम् गच्छन्ति?
4. ते प्रातः विद्यालयम् गच्छन्ति ।
5. किम् त्वम् सायम् पठसि ?
6. नहि, अहम् सायम् क्रीडामि। उपर्युक्त वाक्यों में स्थूलाक्षरों में आए पद-अधुना, आम्, कदा, प्रातः, सायम्, नहि अव्यय हैं।

अव्यय वे पद होते हैं जिनका वाक्य-प्रयोग के समय रूप नहीं बदलता।

In the sentences given above the words in bold letters viz. अधुना, आम्, कदा, प्रातः, सायम्, नहि are all अव्यय-the Indeclinables. अव्यय are those words that do not change their form when used in a sentence. कुछ सामान्यतः प्रयोग में आने वाले अव्यय तथा उनका वाक्य-प्रयोग। (A few commonly used Indeclinables and their usage.)

We have given detailed NCERT Solutions for Class 6 Sanskrit Grammar Book क्रियापदानि तथा धातुरूपाणि Questions and Answers come in handy for quickly completing your homework.

Sanskrit Vyakaran Class 6 Solutions क्रियापदानि तथा धातुरूपाणि

अभ्यासः

प्रश्न 1.
(क) तालिकां पूरयत। (तालिका पूरी कीजिए। Complete the table.)

उत्तर:
प्रथम पुरुषः-धावति, धावन्ति, मध्यम पुरुष:धावसि, धावथ, उत्तम पुरुष:-धावामि, धावामः।

उत्तर:

(ख) रिक्तस्थानानि पूरयत। (रिक्त स्थान भरिए। Fill in the blanks.)

प्रश्न 2.
उदाहरणानुसारम् रिक्तस्थानानि पूरयत। (उदाहरण के अनुसार रिक्त स्थान भरिए। Fill in the blanks as per the example.)

प्रश्न 3.
रिक (रिक्त स्थान भरिए- Fill in the blanks.)

उत्तर:

उत्तर:

प्रश्न 4.
रेखाङ्कितक्रियापदम् संशोधयत- (रेखांकित क्रिया-पदों को शुद्ध कीजिए- Correct the underlined verbs.)

(क) सा दुग्धम् पिबिष्यति।। ……………….
(ख) अहम् बहिः खेलिष्यति। ……………
(ग) अहम् क्रीडितुम् गच्छिष्यामि। …………………..
(घ) त्वम् किं खादिष्यति? …………………..
(ङ) छात्र: लेखम् लिखिष्यति। …………………..
उत्तर:
(क) पास्यति
(ख) खेलिष्यामि
(ग) गमिष्यामि
(घ) खादिष्यसि
(ङ) लेखिष्यति प्रश्नः

प्रश्न 5.
उदाहरणम् अनुसृत्य वाक्यानि पुनः लिखत। (उदाहरण के अनुसार वाक्य को पुनः लिखिए। Rewrite the sentences as per the example.)

उदाहरणम् – बालकः खेलति। बालकः खेलिष्यति।

(क)
(i) सः किम् करोति? …………………..
(ii) अम्बा पचति। …………………..
(iii) अहम् नमामि। …………………..
(iv) वयम् धावामः। …………………..
(v) यूयम् क्रीडथ। …………………..
उत्तर:
(i) सः किम् करिष्यति?
(ii) अम्बा पक्ष्यति ।
(iii) अहम् नस्यामि ।
(vi) वयम् धाविष्यामः।
(v) यूयम् क्रीडिष्यथ।

(ख) उदाहरणम्- बालक: सत्यम् वदति। — बालकः सत्यम् अवदत् ।

(i) सा भोजनम् पचति । — ……………..
(ii) अजीजः गच्छति। — ……………..
(iii) सः मह्यम् यच्छति। — ……………..
(iv) सा त्वाम् वदति। — ……………..
(v) स्वामी सेवकम् पृच्छति। — ……………..
उत्तर:
(i) सा भोजनम् अपचत्।
(ii) अजीज: अगच्छत् ।
(iii) सः मह्यम् अयच्छत्।
(iv) सा त्वाम् अवदत् ।
(v) स्वामी सेवकम् अपृच्छत् ।

(ग) उदाहरणम् – बालक: खादतु। — बालकः खादति।

(i) सा लिखतु। — ……………..
(ii) छात्रः पठतु। — ……………..
(iii) बालिका क्रीडतु। — ……………..
(iv) अजीजः गच्छतु। — ……………..
(v) सः नमतु। — ……………..
उत्तर:
(i) सा लिखति।
(ii) छात्रः पठति।
(iii) बालिका क्रीडति ।
(iv) अजीजः गच्छति।
(v) सः नमति।

प्रश्न: 6.
निर्देशानुसारम् परिवर्तनम् कुरुत। (निर्देश के अनुसार परिवर्तन कीजिए ।Change as directed.)

उदाहरणम् – स: नमति। ( उ०पु०) अहम् नमामि।
(क) यूयम् धावथ। — (एकवचने) — ……………..
(ख) अहम् नमामि। — (द्विवचने) — ……………..
(ग) त्वम् वदसि। — (प्रथमपुरुषे) — ……………..
(घ) वयम् क्रीडिष्यामः। — (लट्लकारे) — ……………..
(ङ) युवाम् पठथः। — (लुट्लकारे) — ……………..
उत्तर:
(क) त्वम् धावसि।
(ख) आवाम् नमावः।
(ग) सः वदति।
(घ) वयम् क्रीडामः।
(ङ) युवाम् पठिष्यथः।

क्रियापदानि

अधोदत्तानि वाक्यानि अवलोकयत। (नीचे दिए गए वाक्यों को देखिए। Examine the sentences given below.)

उपरिलिखित वाक्यों में स्थूल शब्द क्रियापद हैं।
क्रियापद वे शब्द होते हैं जो क्रिया का बोध कराते हैं। प्रत्येक वाक्य में एक क्रियापद होता है। प्रत्येक क्रियापद धातु से बनता है और क्रिया के मूल रूप को धातु कहते हैं।

(In the sentences given at the beginning of the chapter the words in bold are verbs. The words which tell us about an action are called verbs. Simply put verbs are ‘doing’ words. Each sentence has a verb. Each verb is formed from a root.)

धातुरूपाणि

प्रत्येक धातु से अनेक क्रियापद बनते हैं। इसी को धातुरूप कहते हैं। नीचे ‘पठ्’ धातु के लट् लकार में रूप दिए गए हैं। लट् लकार का प्रयोग वर्तमान काल की क्रिया को दर्शाने के लिए किया जाता है।

(Many verb forms can be formed from a single root. This is called conjugation. Below are given the forms of the root पठ् in लट् लकार। लट् लकार is used to denote action in Present.

परिवर्तनशील-धातवः

(परिवर्तनशील धातुएँ, Roots that undergo a change.)

कुछ धातुएँ परिवर्तनशील होती हैं अर्थात् रूप चलाते समय उनमें परिवर्तन आता है; जैसे-गम् धातु का रूप चलाते समय ‘गच्छ्’ हो जाता है। (Some roots undergo a change, when they are conjugated e.g. the root गम् changes into गच्छ when conjugated.)

अवधेयम् – अंग्रेजी भाषा की तरह संस्कृत भाषा में भी कर्त्ता में लिङ्ग-भेद होने से क्रियापद में लिङ्ग भेद नहीं होता। (हिन्दी भाषा में क्रियापद में लिङ्ग-भेद होता है।)

(As in English, so also in Sanskrit there is no difference in the verb form whether the subject of the sentence is in Masculine or Feminine Gender.)

लट्लकारः
भविष्यत् काल-Future Tense

लृट् लकार का प्रयोग भविष्यत् काल की क्रिया को दर्शाने के लिए होता है। (लट् लकार is used to denote action in the future.)

उपर्युक्त वाक्यों में आए स्थूल पद-पठिष्यति, लेखिष्यति, खेलिष्यति-लृट् लकार के क्रियापद हैं जो क्रमश: पठ्, लिखु, खेल धातु से बने हैं। The words in bold are verbs of Future Tense (लुट्लकार)।

अवधेयम्-लुट लंकार में धातु के आगे लगने वाले प्रत्यय-ति, तः, अन्ति आदि वही होते हैं जो लट् लकार में धातु में जोड़े जाते हैं, किन्तु लृट् लकार में धातु और प्रत्यय के बीच ‘स्य’ अथवा ‘ष्य’ आ जाता है; यथा दा + स्य + ति = दास्यति; लिख + ष्य + ति = लेखिष्यति इत्यादि। (In लृट् लकार the root takes the same suffixes ति, तः, अन्ति etc., that are added in लट् लकार. But in लृट् लकार ‘स्य’ or ‘ष्य’ is inserted between the root and the suffix, when the root is conjugated.) नीचें कुछ धातुओं के लृट् लकार के रूप दिए गए हैं। (Given below is the conjugation of a few roots in लृट् लकार.)

उपर्युक्त वाक्यों में आए स्थूलपद-लङ्लकार के क्रियापद हैं जो क्रमशः गम्, पत्, खेल धातु से बने हैं। लङ्लकार का प्रयोग भूत काल की क्रिया को दर्शाने के लिए किया जाता है। लङ्लकार में धातु से पहले ‘अ’ जोड़ा जाता है। यथा- अवदत्, अनमत्, अलिखत् इत्यादि। उदाहरण रूप दिए गए क्रियापद प्रथम पुरुष एकवचन में हैं। अवलोकन हेतु लङ्लकार में पठ् धातु के तीनों पुरुषों के रूप नीचे दिए गए हैं यद्यपि इस कक्षा में प्रथम पुरुष, एकवचन के रूप पर ही ध्यान केंद्रित किया गया है।

उपर्युक्त वाक्यों में ‘पठ’, ‘आनय’, ‘लिख’ लोट् लकार, मध्यम पुरुष, एकवचन के रूप हैं। लोट्लकार का अधिकतम प्रयोग मध्यम पुरुष, एकवचन में होता है; कर्त्ता ‘त्वम्’ प्रायः लुप्त रहता है। अवलोकन हेतु पठ् धातु के लोट् लकार के रूप नीचे दिए गए हैं, यद्यपि सविस्तार चर्चा अगली कक्षाओं में होगी।

Here we are providing Class 11 Physics Important Extra Questions and Answers Chapter 10 Mechanical Properties of Fluids. Important Questions for Class 11 Physics with Answers are the best resource for students which helps in Class 11 board exams.

Class 11 Physics Chapter 10 Important Extra Questions Mechanical Properties of Fluids

Mechanical Properties of Fluids Important Extra Questions Very Short Answer Type

Question 1.
(a) Why density increases with the fall of temperature?
Answer:
Because the volume of the given mass decreases.

(b) Can you estimate the exact fractional volume of an ice cube in water when the system is falling freely? Why?
Answer:
No. The effective value of g in the given case is zero.

Question 2.
Why two holes are made to empty an oil tin?
Answer:
If only one hole is made, then the pressure inside the tin would be less than the atmospheric pressure. So oil would not come out. If two holes are made, then the pressure inside the tin is equal to atmospheric pressure.

Question 3.
(a) What is one torr of pressure?
Answer:
It is the pressure exerted by 1 mm of mercury column.

(b) Suppose a few’ drops of water are introduced in the barometer tube, what would be the effect on the barometric height?
Answer:
The barometric height would decrease due to the pressure of water vapors.

Question 4.
(a) What are the values of systolic and diastolic blood pressure of a healthy human being?
Answer:
Nearly 120 mm of Hg and 80 mm of Hg respectively.

(b) At what temperature is the density of water maximum and what is its value?
Answer:
At 4°C and the maximum value is 10³ kg m^-3.

Question 5.
What is indicated by:
(a) Gradual increase of atmospheric pressure?
Answer:
It indicates dry weather.

(b) Gradual fall of atmospheric pressure?
Answer:
This indicates the possibility of rain as the atmospheric pressure falls when the water vapors increase in air.

(c) Sudden fall of atmospheric pressure?
Answer:
It indicates the possibility of a storm.

Question 6.
Why water does not come out of a dropper unless its rubber head is pressed hard?
Answer:
Water would come out only if the pressure exerted on the rubber head is greater than the atmospheric pressure.

Question 7.
What is 105 Nm^-2 pressure called? What is the value of 1 torr?
Answer:
It is called 1 bar. Torr is the unit of atmospheric pressure.
1 torr = 1 mm of Hg column
= 1.33 × 10^-4 Nm^-2
= 1.33 × 10^-3dyne cm^-2.

Question 8.
(a) Why Hg is used in the barometer?
Answer:
Due to the large density of mercury, the barometer is of convenient size.

(b) A steel ball is floating in a trough of mercury. If we fill the empty part of the trough with water, what will happen to the steel ball?
Answer:
It will move up.

Question 9.
The two thigh bones (femurs) each of cross-section area 10cm² support the upper part of a human body of mass 40 Kg. Estimate the pressure sustained by the femurs.
Answer:

Question 10.
How can you check whether the barometer tube contains air or not?
Answer:
The barometer tube is raised or lowered in a trough of mercury. If the height of the mercury column changes, then the barometric tube contains air.

Question 11.
When air is blown in between the two balls suspended from a string such that they don’t touch each other, the balls come nearer to each other. Why?
Answer:
Pressure decreases with an increase in velocity between the balls.

Question 12.
What is the effect of temperature on the viscosity of liquid?
Answer:
The viscosity of liquid decreases with the increase in temperature and vice-versa.

Question 13.
Why you can’t remove the filter paper from the funnel shown here by blowing from the narrow end?
Answer:
When the air enters the wider and velocity is reduced and pressure is increased.

Question 14.
Why a raindrop falling freely does not acquire a high velocity?
Answer:
This is because the raindrop acquires terminal velocity after having fallen through a certain height.

Question 15.
(a) Why do the clouds float in the sky?
Answer:
They have zero terminal velocity.

(b) Why machines are sometimes jammed in winter?
Answer:
Due to change in viscosity with temperature.

(c) Why a hot liquid moves faster than a cold liquid?
Answer:
Due to a decrease in viscosity with an increase in temperature.

Question 16.
(a) A flask contains glycerine and the other one contains water. Both are stirred rapidly and kept on the table. In which flask will the liquid come to rest earlier than the other one and why?
Answer:
Glycerine due to greater viscosity.

(b) What is the effect on the viscosity of a gas of the temperature?
Answer:
There is a decrease in the viscosity of gas with the decrease in temperature and increases with an increase in temperature.

Question 17.
How does the viscous force between two layers of a liquid depend upon the relative velocity between two layers?
Answer:
The viscous force between two layers increases with the ¡ñcreasc in relative velocity.

Question 18.
(a) Why firefighters have a jet attached to the head of their water pipes?
Answer:
This is done to increase the velocity of water flowing out of the pipe.

(b) Why the airplanes and cars are given a streamlined shape?
Answer:
This is done to reduce the backward drag of the atmosphere.

Question 19.
People living in houses far removed from a municipal water tank often find it difficult to get water on the top floor even if it is situated lower than the level of water tank. Why?
Answer:
This is because there is a loss of pressure when water is flowing.

Question 20.
(a) Why a small air bubble rises slowly through a liquid whereas the bigger one rises rapidly?
Answer:
Terminal velocity is proportional to the square of radius i.e. v_T ∝ R².

(b) Why flags flutter on a windy day?
Answer:
Velocity increases and pressure decreases on a windy day.

Question 21.
(a) Why more viscous mobile oil is used in summer than in winter in scooters?
Answer:
Due to high temperature, viscosity is less, so more viscous oil is used in summer than in winter.

(b) Why air bubble in a liquid rises up?
Answer:
Because the terminal velocity of the air bubble is negative.

Question 22.
What are the values of Reynolds number (N_g) for different types of flows?
Answer:
For streamline or laminar flow 0 < N_R < 2000, for turbulent flow, N_R > 3000

If NR lies between 2000 to 3000, the flow is unstable i.e. change from streamline flow to turbulent flow.

Question 23.
Explain why:
(a) Is sand drier than clay?
Answer:
Due to capillary action.

(b) Is it that a needle may float on clear water but will sink when some detergent is added to water?
Answer:
The detergents reduce surface tension.

(c) Mercury (Hg) does not wet glass?
Answer:
For cohesion is greater than the force of adhesion.

(d) Two mercury drops coalesce when brought together?
Answer:
Due to the strong force of cohesion.

(e) The end of a glass rod becomes round on heating?
Answer:
Due to surface tension.

(f) Antiseptics have low surface tension.
Answer:
As they have to spread over a large area.

(g) Oil is poured to calm sea waves?
Answer:
When oil is poured on water, the surface tension of water is reduced, thus water tends to spread over a larger area.

(h) Is it possible to produce a fairly vertical film of soap solution but not of water?
Answer:
It is due to the reason that the surface tension of soap solution is lesser as compared to the surface tension of water and thus it spreads over a larger area.

(i) Is it easier to spray water when soap is added to it?
Answer:
Due to less surface tension.

Question 24.
(a) Why the liquid in the surface film has special importance?
Answer:
The phenomenon of surface tension is due to the given portion i.e. surface film of the liquid.

(b) Why cotton dresses should be preferred in summer?
Answer:
Due to the reason that they have fine pores which act as capillaries for the sweat.

Question 25.
(a) What shape does a liquid take when it weighs nothing?
Answer:
Spherical shape.

(b) Why the nib of a pen is split?
Answer:
For capillary action.

Question 26.
What is the effect:
(a) of highly soluble impurities on the surface tension of a liquid?
Answer:
The surface tension is increased.

(b) of less soluble impurities on the surface tension of a liquid?
Answer:
The surface tension decreases.

(c) on the angle of contact when the temperature of a liquid is increased?
Answer:
The angle of contact decreases.

Question 27.
Is the pressure:
(a) of air inside a soap bubble greater than the atmospheric pressure?
Answer:
Yes.

(b) inside a mercury drop greater than the atmospheric pressure?
Answer:
Yes.

(c) A cylinder is filled with non-viscous liquid of density p, height h, and a hole is made at a height h2 from the bottom of the cylinder? What is the velocity of the liquid coming out of the hole?
Answer:
\(\sqrt{2 \mathrm{~g}\left(\mathrm{~h}_{1}-\mathrm{h}_{2}\right)}\)

Question 28.
(a) What happens to the work done to increase the surface area?
Answer:
It is stored as potential energy.

(b) What is the work done in blowing a soap bubble of radius. r and surface tension T?
Answer:
8πr²T.

Question 29.
(a) How trees draw water from the ground?
Answer:
Trees draw water from the ground by capillary action.

(b) The radius of a capillary tube is doubled. What change will take place in the height of the capillary rise?
Answer:
Capillary rise will be halved as h ∝ \(\frac{1}{r}\)

(c) In the capillary tube water descends and not rises. Guess the material of the capillary tube.
Answer:
Paraffin wax.

Question 30.
(a) Smaller the angle of contact better is the detergent. Is it correct?
Answer:
Yes, because the smaller the angle of contact, the more is the area over which it can spread.

(b) When a glass window is smeared with glycerine, the raindrops don’t stick to the glass. Why?
Answer:
The smearing of glycerine increases the angle of contact from acute to obtuse.

Question 31.
(a) Why is it difficult to fill mercury in the glass tube of a mercury thermometer?
Answer:
This is because mercury descends and not ascends in the glass tube.

(b) Can you decide whether a liquid will rise or get depressed in a capillary tube by observing the shape of the liquid meniscus?
Answer:
If the liquid meniscus is concave then the liquid will rise and if it is convex, then the liquid will be depressed.

Question 32.
(a) Why water rises to different heights in capillaries of different bores?
Answer:
This is because the capillary rise is inversely proportional to the radius of the capillary tube.

(b) Why clothes become waterproof when the wax is rubbed on them?
Answer:
When the wax is rubbed on clothes, the capillaries formed in the threads disappear.

Question 33.
Why Teflon is coated on the surface of a non-stick pan?
Answer:
The Teflon coating increases the angle of contact from acute to obtuse as the adhesive force between Teflon and most of the dishes is very small as compared to uncoated pan and dishes.

Question 34.
‘How a damp proof layer increases the life of the plaster of the wall?
Answer:
Bricks have fine capillaries through which water rises. The damp-proof layer breaks these capillaries.

Question 35.
Why wet ink is absorbed by blotting paper?
Answer:
Blotting paper has fine pores which act as capillaries. The ink rises in these capillaries and hence is absorbed by the blotting paper.

Question 36.
Why greased cotton soaks less than ordinary cotton?
Answer:
This because the presence of grease reduces the effect of surface tension.

Question 37.
A capillary tube is dipped vertically in water in a state of weightlessness. To what height shall the water rise?
Answer:
The water shall rise to the full available length of the capillary tube.

Question 38.
Why the addition of flux makes soldering easy?
Answer:
The addition of flux reduces the surface tension of the molten tin. So the molten tin can spread easily. This makes soldering easy.

Question 39.
A tiny liquid drop is spherical but a larger drop has an oval shape. Why?
Answer:
In the case of a tiny drop, the force of surface tension dominates the force of gravity. But in the case of a large drop, the force of gravity dominates the force of surface tension.

Question 40.
If instead of freshwater, seawater is filled in the tank, will the velocity of efflux change?
Answer:
No, because the velocity of efflux is independent of the density of the liquid.

Question 41.
What is coming out of a hole made in the wall of a freshwater tank? If the size of the hole is increased,
(a) will the velocity of efflux of water change?
Answer:
The velocity of efflux will remain the same as it only depends upon the depth of orifice below the free surface of the water.

(b) will the volume of the water come out per second change?
Answer:
The volume will change since the volume of the liquid flowing out per second is equal to the product of the area of the hole and the velocity of the liquid flowing out.

Question 42.
(a) What is the effect on the equilibrium of a physical balance when air is blown below one pan?
Answer:
Velocity increases and thus pressure will decrease below that pan, hence it will go down.

(b) At what temperature, the surface tension of a liquid is zero?
Answer:
At the critical temperature, the surface tension of a liquid is zero.

Question 43.
What is the effect of solute on the surface tension of liquid?
Answer:
In case, the solute is very easily soluble, then the surface tension of liquid increases e.g. when salt is dissolved in water. If the solute is less soluble, then the surface tension of liquid decreases e.g. by adding soap or phenol in water.

Question 44.
What is the effect of pressure on the coefficient of viscosity of fluids?
Answer:
With the increase in pressure, the viscosity of liquids increases but the viscosity of water decreases, whereas the viscosity of gases remains unchanged.

Question 45.
Why the force required by a man to move his limbs immersed in water is smaller than the force required for the same movement in air?
Answer:
The upthrust of water apparently reduces the weight of a man in the water. So it is easier for him to move his limbs in water than in air.

Question 46.
What is:
(a) velocity head,
Answer:
\(\frac{\mathrm{v}^{2}}{2 \mathrm{~g}}\)

(b) pressure head,
Answer:
\(\frac{P}{\rho g}\)

(c) gravitational head?
Answer:
h

(d) Write down the following liquids in the order of increasing surface tension at a given temperature: w^ter, mercury, soap solution?
Answer:
soap solution, water, mercury.

(e) Is Bernoulli’s Theorem valid for viscous liquids?
Answer:
No.

Question 47.
What are the characteristics of a non-viscous fluid?
Answer:

1. It must be incompressible i.e. density should be constant.
2. It should have no viscosity.

Question 48.
Why hot soup tastes better than cold soup?
Answer:
Hot soup has comparatively less surface tension than cold soap. So hot soap spreads over a larger area than cold soap.

Question 49.
(a) Define critical velocity.
Answer:
It is defined as the velocity of flow of a liquid up to which its flow is streamlined and above which its flow becomes turbulent.
i.e. V_c = \(\frac{N_{R} \eta}{\rho D}\)

(b) What is Reynolds number?
Answer:
It is a pure number that determines the nature of the flow of the liquid through a pipe.
N_R = \(\frac{\mathrm{V}_{\mathrm{c}} \rho \mathrm{D}}{\eta}\)

Question 50.
The accumulation of snow on the wings of an airplane reduces the lift. Why?
Answer:
When snow accumulates on the wings of an airplane, the structure of the wings no longer remains as that of an aerofoil. Hence, the lift is reduced.

Mechanical Properties of Fluids Important Extra Questions Short Answer Type

Question 1.
A glass bulb is balanced by an iron weight in an extremely sensitive beam balance covered by a bell jar. What shall happen when the bell jar is evacuated?
Answer:
The upthrust on the bulb is larger than the upthrust on the iron weight. When the bell jar has evacuated the upthrust on both the bulb and the iron weight become zero. Clearly, the bulb is affected more than the iron weight. Thus the pan containing the bulb shall go down.

Question 2.
It is easier to swim in seawater than in river water. Why?
Answer:
Due to the presence of salt, the density of seawater is more than that of river water. Hence seawater offers more upthrust as compared to river water. Therefore a lesser portion of our body is submerged in, seawater as compared to river water. Hence it is easier to swim in sea-water than in river water.

Question 3.
Does Archimedes’ Principle hold in a vessel in free fall or in a satellite moving in a circular orbit?
Answer:
A vessel in free fall or in a satellite moving in a circular orbit is in the state of weightlessness. It means the value of ‘g’ is zero. Thus the weight of the vessel and upthrust will be zero. Hence Archimedes’ Principle does not hold good.

Question 4.
A block of wood floats in a pan of water in an elevator. When the elevator starts from rest and accelerates downward, does the 1 block floats higher above the water surface? What happens when the elevator accelerates upward? *
Answer:
When the elevator accelerates downward, the weight of the block of wood decreases. Hence it will float higher above the water’s surface.

When the elevator accelerates upward, the weight of the block increases, and hence it will float lower the water surface.

Question 5.
The thrust on a human being due to atmospheric pressure is about 15 tons. How human being can withstand such an enormous thrust while it is impossible for him to carry a load of even one ton?
Answer:
There is a large number of pores and openings on the skin of a body. Through these openings, air goes within the system and there is free communication between the inside and the outside. The presence of; the air inside the body counterbalances the pressure outside.

Question 6.
Why are sleepers used below the rails? Explain.
Answer:
When sleepers are placed below the rails, the area of the cross- p section is increased. We know that P = F/A, so when the train runs on the rails, the pressure exerted on the ground due to the weight of the train is small because of a large area of cross-section of the sleeper. Hence the ground will not yield under the weight of the train.

Question 7.
The passengers are advised to remove the ink from their f pens while going up in an airplane. Explain why?
Answer:
With the increase in height, the atmospheric pressure decreases. The ink in the pen is filled at the atmospheric pressure on the surface of the earth. So as the plane rises up, the pressure decreases \ and the ink will flow out of the pen from higher pressure to the low ‘pressure region. This will spoil the clothes of passengers.

Question 8.
Why a sinking ship often turns over as it becomes immersed in water?
Answer:
When the ship is floating, the metacenter of the ship is above the center of gravity. While sinking the ship takes in water and as a result, the center of gravity is raised above the metacenter. The ship turns over due to the couple formed by the weight and the buoyant force.

Question 9.
Explain why a balloon filled with helium does not rise in the air indefinitely but halts after a certain height?
Answer:
The balloon initially rises in the air because the weight of the displaced air i.e> upthrust is greater than the weight of the helium and the balloon. Since the density of air decreases with height, therefore, the balloon halts at a particular height where the density of air is such that the weight of air displaced is just equal to the weight of helium gas and the balloon. Hence the net force acting on the balloon is zero and the balloon stops rising.

Question 10.
A light ball can remain suspended in a vertical jet of water flow?
Answer:
The region where the ball and the vertical jet of water are in contact is a region of low pressure because of higher velocity. The pressure on the other side of the ball is larger. Due, to the pressure difference, the ball remains suspended.

Question 11.
In the case of an emergency, a vacuum brake is used to stop the train. How does this brake work?
Answer:
Steam at high pressure is made to enter the cylinder of the vacuum brake. Due to high velocity, pressure decreases in accordance with Bernoulli’s principle. Due to this decrease in pressure, the piston gets lifted. Hence the brake gets lifted.

Question 12.
Why dust generally settles down in a closed room?
Answer:
Dust particles may be regarded as tiny spheres. They acquire terminal velocity after having fallen through some distance in the air. Since the terminal velocity varies directly as the square of the radius therefore the terminal velocity of dust particles is very small. So they settle down gradually.

Question 13.
How will the rise of a liquid be affected if the top of the capillary tube is closed?
Answer:
The air trapped between the meniscus of the liquid and the closed end of the tube will be compressed. The compressed air shall oppose the rise of liquid in the tube.

Question 14.
What are buoyancy and the center of buoyancy?
Answer:

1. The upward thrust acting on the body immersed in a liquid is called buoyancy or buoyant force.
2. The center of buoyancy is the center of gravity of the displaced liquid by the body when immersed in a liquid.

Question 15.
Under what conditions:
(a) Centre of buoyancy coincides with the center of gravity?
Answer:
For a solid body of uniform density, the center of gravity coincides with the center of buoyancy.

(b) The center of buoyancy does not coincide with the center of gravity?
Answer:
For a solid body having different densities over different parts, its center of gravity does not coincide with the
center of buoyancy.

Question 16.
Why small pieces of camphor dance about on the surface of the water?
Answer:
When the camphor is dissolved in water, the surface tension of water is reduced. Since camphor has an irregular shape therefore it may dissolve more at one end than at the other end. This produces an unbalanced force due to which it moves. When it reaches a different region, the same process is repeated.

Question 17.
On what factors does the critical velocity of the liquid depend?
Answer:
Critical velocity (v_c) of a liquid is:

1. Directly proportional to the coefficient of viscosity of the liquid.
2. Inversely proportional to the density of the liquid i.e. v_c ∝ \(\frac{1}{ρ}\)
3. Inversely proportional to the diameter of the tube through which it flows
   i. e. vc ∝ \(\frac{1}{D}\)

Question 18.
What are the two forces which determine the shape of a liquid drop?
Answer:
The shape of a liquid drop is determined by the interplay of two forces – gravitational force and the force of surface tension. The gravitational force tries to flatten the drop so that the center of gravity comes at the lowest point.

On the other hand, the force of surface tension tends to give the drop a spherical shape.

Question 19.
A drop of oil placed on the surface of water spreads out. But a drop of water placed on oil contracts to a spherical shape. Explain both the phenomenon
Answer:
A drop of oil placed on the surface of water spreads because the force of adhesion between water molecules and oil molecules dominates the cohesive force-of oil molecules. So oil drop on water spreads.

On the other hand, the cohesive force of water molecules dominates the adhesive force between water and oil molecules. So drop of water c on oil contracts to a spherical shape.

Question 20.
Why are the droplets of mercury when brought in contact pulled together to form a bigger drop? Also, a state with reasons whether the temperature of this bigger drop will be the same or more or less than the temperature of the smaller drop.
Answer:
It is due to large cohesive forces acting between the molecules of mercury that the droplets of mercury when brought in contact pulled together to form a bigger drop.

Question 21.
Oil spreads over the surface of the water. Why?
Answer:
The surface tension of oil is smaller than that of water. When oil is dropped on the surface of the water, the force stretches the oil drops on all sides. Hence the oil spreads over the surface of the water.

Question 22.
Why is it easier to skate on ice than on a smooth aluminum sheet?
Answer:
The ice below the feet of the person smelts on account of increased pressure. Tiny drops of water are formed. These behave like ‘rollers’ and thus it is easier to skate on ice. No such thing is possible in the case of aluminum sheets.

Question 23.
What are the factors on which angle of contact depends?
Answer:
It depends upon the following factors:

1. The nature of the solid and the liquid in contact.
2. The cleanliness of the surfaces in contact.
3. The medium above the free surface of the liquid.

Question 24.
Prove Archimedes’ Principle mathematically.
Answer:
Let W₁ and W₂ be the weights of the body in the air and when completely immersed in a liquid respectively.

∴ Loss in weight of body inside the liquid = W₁ – W₂.

Proof: Let h = height of a body lying at a depth X below the free surface of a liquid of density p.
Let a = area of the face of the body parallel to the horizontal.

If P₁ and P₂ be the pressures at the upper and lower face of the
P₁ = x ρg ….(i)
P₂ = (x + h) ρg …(ii)

If F₁ and F₂ be the thrust on the upper and lower face of the body, then
F₁ = P₁a = xρag …(iii)
and acts vertically downward.

and F₂ = P₂a = (x + h) ρag …. (iv)
and acts vertically upward.

As F₂ > F₁, so net thrust acts on the body in the upward direction and is called upthrust (U)

As V = volume of the body = volume of liquid displaced by the body, so Vρ is the mass of the liquid displaced
∴ Vρg = weight of the displaced liquid

Thus loss in weight of the body when sunk in the liquid = weight of the liquid displaced.

Question 25.
Derive the condition of floatation of the body.
Answer:
When a body floats in a liquid with a part submerged in the liquid, the weight of the liquid displaced by the submerged part is always equal to the weight of the body.

Let V = volume of the body
σ = density of its material
ρ = density of the liquid in which the body floats such that its volume V ‘ is outside the liquid

Then the volume of the body inside the liquid = V – V’
Weight of the displaced liquid = (V – V’) ρg
Also weight of the body = Vσg

For the body to float,
weight of the liquid displaced by the submerged part = weight of the body.

Question 26.
(a) Why the wings of an airplane are rounded outwards (i.e. more curved) while flattened inwards? What is this shape called?
Answer:
The special design of the wings which is slightly convex upward and concave downward increases velocity at the upper surface and decreases it at the lower surface. So according to Bernoulli’s Theorem, the pressure on the upper side is less than the pressure on the lower side.

This difference of pressure provides the additional thrust on the foil called lift. This is called airfoil or aerofoil. It is a solid piece that is so shaped that it an upward vertical. force is produced on it when it moves horizontally through the air.

(b) What is an ideal liquid?
Answer:
A liquid is said to be ideal if:

1. It is incompressible.
2. It is non-viscous.
3. Its flow is steady i.e. stream-line.

Question 27.
What is a hydrostatic paradox? Explain. Is it really a paradox?
Answer:
It is defined as the inability of a liquid to flow from a vessel having more liquid to a vessel having lesser liquid when the liquid level is the same. Consider three vessels of different shapes but the same base area as shown., The level of water is kept the same in A, B, and C. So the quantity of water is different in the vessels. However, the thrust on the bottom is the same in all of them. It may appear paradoxical

We know that

1. the pressure at a point depends on the height of the liquid column.
2. It does not depend on the quantity of the liquid and
3. thrust is the product of pressure and area of the surface. ,

In the given three cases the pressure at the base is hρg and since the area of the base is the same in all the three cases hence the thrust = hρg a where a = area of the base

So, we see that the thrust is the same in A, B, and C even though the quantity of liquid is different in them.

No. In fact, there is no paradox as such because the pressure depends on the depth of point and not on the quantity of liquid. Here O₁, O₂, and O₃ lie in the same horizontal plane, so the pressure is the same.

Question 28.
State Pascal’s law. How does it get changed in the presence of gravity?
Answer:
Pascal’s law states that for a liquid in equilibrium, the pressure is the same everywhere (provided the effect of gravity can be neglected), It may also be stated as “the pressure applied anywhere on an enclosed fluid is transmitted equally in all directions throughout the fluid”.

Effect of gravity: Consider a liquid of density p contained in a vessel. Let us find the pressure difference between the points x and y. Let us imagine a cylinder of liquid whose faces 1 and 2 are at height h. The cylinder is in equilibrium.

Let P₁ = Pressure at face 1, pressure P₂ at face 2 and the weight of the liquid in cylinder mg. Here m is the mass of the imaginary fluid cylinder. If F, and F, be the forces on the upper and lower faces of the cylinder, then F₁ = P₁ A₁, F₂ = P₂A₂. As the cylinder of liquid is in equilibrium, so the net force on it is zero.
i.e. (F₁ + mg) – F₂ = 0
or P₁A + mg – P₂A = 0
or (P₂ – P₁)A = mg

where A is the base area of the imaginary cylinder. Since mass of the liquid cylinder
m = Vρ = Ahρ (∵ V = Ah)
∴ (P₂ – P₁)A = Ahρg
or (P₂ – P₁) = hρg

If the point x lies on the surface, then P₁ = 0 and Let P₂ = P
∴ P = hρg
Equation (1) gives the expression for the pressure applied by a liquid column of height h.

Question 29.
Draw a diagram showing the construction of a hydraulic brake.$Iow does it work?
Answer:
The diagram showing various parts of a hydraulic brake is given here.

On applying foot pressure on the pedal, the brake fluid flows*from the master cylinder transmitting the pressure from P₁ to P₂ equally.

This expands the brake shoe and stops the wheel. When pressure is released at the foot pedals, the spring brings the brake shoe to its original position and brake fluid is forced back to the master cylinder.

Question 30.
Stake’s law deals with spherical bodies moving through a viscous fluid. Give its statement and derive it dimensionally.
Answer:
Stake’s law may be stated as “the viscous drag experienced by a spherical body of radius r moving in a fluid of viscosity η with a terminal velocity v is given by
F = 6πηrv

Derivation: Let F depends on η, r, and v, we can write
F = kη_ar_bv_c ….(1)
where k = Proportionality constant.
On writing dimensional formula on both sides, we have

∴ a = 1, b = 1, c = 1

∴ Putting values of a, b, c in equation (1), we get
F = kη₁r₁V₁
= kηrv.

For spherical bodies Stoke found k to be 6π
∴ F = 6ηπrv
Hence, derived.

Mechanical Properties of Fluids Important Extra Questions Long Answer Type

Question 1.
(a) Derive the expression for excess pressure inside:
(i) a liquid drop.
Answer:
Let r = radius of a spherical liquid drop of center O.
T – surface tension of the liquid. Let p_i and p₀ be the values of pressure inside and outside the drop.

∴ Excess of pressure inside the liquid drop = p_i – p₀

Let Δr be the increase in its radius due to excess pressure. It has one free surface outside it.
∴ increase in surface area of the liquid drop.
= 4π (r + Δr)² – 4πr²
= 4π [r² +(Δr)² + 2r Δr – r²]
= 8πr Δr ….(i)
(∵ Δr is small Δr² is neglected.)

∴ increase in surface energy of the drop is
W = surface tension × increase in area
= T × 8πr Δr ….(ii)

Also W = Force due to excess of pressure × displacement
= Excess of pressure × area of drop × increase in radius

(ii) a liquid bubble.
Answer:
In a liquid bubble: A liquid bubble has air both inside and outside it and therefore it has two free surfaces.
r, Δr, T = ? as above
Thus increase in its surface area

(iii) an air bubble.
Answer:
Inside an air bubble: Air bubble is formed inside the liquid, thus an air bubble has one free surface inside it and a liquid is outside.
If r = radius of the air bubble.
Δr = increase in its radius due to excess pressure (p_i – p₀) inside it.
T = surface tension of the liquid in which bubble is formed.

∴ increase in surface area

(b) Derive the relation between the surface tension and the surface energy.
Answer:
Let ABCD be a rectangular frame of wire. Let LM be a slidable cross-piece. Now dip the wireframe in the soap solution so that a film is formed over the frame. Due to surface tension, -the film has a tendency to shrink, and thereby, the cross-piece LM will be pulled in an inward direction which can be kept in its position by applying an equal and opposite force F on it.
F = T × 2l
where T = surface tension and l = length of LM.

It has been taken 2l as the film has two free surfaces.
Let x = small distance by which LM moves to L’M’.

∴ 21 × x = increase in the area of the film if W – work done in increasing the area by 2l × x, then
W = F × x = (T × 2l) × x

If U be the surface energy, then by definition
U = \(\frac{\text { Work done in increasing the surface area }}{\text { increase in surface area }}\)
= \(\frac{\mathrm{T} \times 2 l \times \mathrm{x}}{2 l \times \mathrm{x}}\)
U = T
Thus U is numerically equal to the surface energy.

Question 2.
(a) Derive the expression for terminal velocity.
Answer:
When a spherical body is dropped in a viscous fluid, it is first accelerated and then the acceleration becomes zero and it attains a constant velocity VT called terminal velocity.

Let r = radius of the spherical body falling through a viscous medium having a coefficient of viscosity η and density σ.
Let ρ = density of the material of the body.

The various forces acting on it are:
(i) its weight (W) acting in a vertically downward direction and

(ii) Upthrust (U) equal to the weight of the fluid displaced and is given by
U = \(\frac{4π}{3}\)r3 σg …..(ii)
and its acts vertically upward.

(iii) Viscous force (F) acting upward and according to Stoke’s Law,
F = 6πηrv₁ …. (iii)

where v_T = terminal velocity
when the body attains v_T, the net force on it is zero.
i.e. upward force = downward force

(b) Derive the equation of continuity.
Answer:
Consider a liquid flowing through a pipe AB of the varying area of cross-section.

Let a₁ and a₂ be its area of the cross-section at points A and B respectively.

Let v₁ and v₂ be the velocities of the liquid at A and B respectively whereas ρ₁ and ρ₂ are the densities of the liquid at A and B respectively.

∴ The volume of liquid entering per second at point A = a₁v₁
and Volume of liquid leaving per second at point B = a₂V₂

∴ masses of the liquid per second entering at A and leaving at B are given by
m₁ = a₁v₁ρ₁
and m₂ = a₂v₂ρ₂

If there is no source or sink of the liquid along the length of the pipe, then

Equation (ii) is the required expression for the equation of continuity for the steady flow of an incompressible and non-viscous liquid.

(c) Describe the principle and action of a hydraulic lift giving a simple diagram.
Answer:
Principle: This device uses Pascal’s law. It is an arrangement used to multiply force. It consists of two cylinders C and C’ of different areas of cross-section fitted with frictionless pistons connected to each other with a pipe.

Action: In hydraulic lift greater force is generated using a smaller force.

Let a, A = area of cross-section of smaller and bigger cylinders respectively,
f = force applied on the smaller piston.
P = pressure applied on the liquid f
∴ P = \(\frac{f}{a}\)

According to Pascal’s law, the same pressure is transmitted to the larger piston.
If F be the force transmitted to the larger piston, then

Thus a heavy load placed on the larger piston is lifted easily.

Question 3.
(a) Prove mathematically Bernoulli’s Theorem.
Answer:
It states that

Proof: Imagine an incompressible and non-viscous liquid flowing through a pipe AB of varying cross¬sectional area as shown in Fig. It enters from A and leaves

Let a₁ and a₂ be its area of the cross-section at A and B respectively such that a₁ > a₂.

P₁ and P₂ be the pressures due to liquid at ends A and B respectively such that P₁ > P₂ as the liquid flows from high to low pressure.

Also, let v₁ and v₂ be the velocities of the liquid at A and B respectively.
ρ = density of the liquid,
m = mass of liquid flowing per second from A to B.

Work done per second on the liquid at end A
= pressure × area × velocity
= P₁a₁v₁ …. (ii)
and work done per second by the liquid at end B
= P₂a₂v₂ …. (iii)

∴ Net work done per second on the liquid by the pressure energy in moving the liquid from A to B

When m flows in one second from end A to B, its height increases from h₁ to h₂, and velocity increases from v₁ to
v₂.

∴ increase in potential energy / second from end A to B
= mgh₂ – mgh₁ …. (v)

∴ increase in K.L. second from end A to B

∴ According to the work-energy theorem, work done by pressure energy/second = increase in (K.E. + P.E.) per second

(b) Derive the Ascent formula.
Answer:
Let r = radius of a capillary tube immersed in a liquid
like water having surface tension T.
θ = angle of contact
ρ = density of liquid
R = radius of the meniscus
P = atmospheric pressure
Let h = height up to which the liquid rises in the capillary tube.

Let A and B be two points in the capillary tube where A is just above the meniscus and B is just below it. Now the pressure on the convex side is less than that on the concave side.
Pressure at A = P
Pressure at B = P – \(\frac{2T}{R}\)

The liquid rises in the capillary tube so that pressure at points D and E which lie at the same horizontal level in the liquid become equal.

i.e. Pressure at E = Pressure at D = P
∴ Pressure at E = Pressure at B + Pressure due to liquid column of height h

To calculate R: Let O be the center of curvature of the liquid meniscus.
∴ θ = angle of contact

Now in rt. angled ΔOQL

which is the required formula.

Numerical Problems:

Question 1.
Express standard atmospheric pressure in
(a) Nm^-2
(b) bars
(c) millibars
(d) Torr
Answer:
We know that standard atmospheric pressure is
P = 76 cm of Hg
h = 760 cm = 0.76 m
p = 13.6 × 10³ kg m^-3
g = 9.8 ms^-2

Question 2.
A piece of alloy haš a mass of 250 g in air. When immersed in water, it has an apparent weight of 1.96 N and when immersed in oil, it has an apparent weight of 2.16 N. Calculate the density of
(a) metal
Answer:
Weight of metal in the air.

weight of metal in water,
W_w = 1.96N
weight of metal in oil, W_oil = 2.16N

(a) weight of water displaced = W_a – W_w
= 2.45 – 1.96 = 0.49 N

∴ mass of water displaced,

= 5000 kg m³
= 5 gm cm³

(b) oil.
Answer:

Question 3.
A copper cube of mass 0.50 kg is weighed in water (ρ = 10³ kg m^-3). The mass comes out to be 0.40 kg. Is the cube hollow or solid? Given density of copper = 8.96 × 10³ kg m^-3.
Answer:
Let V be the volume of the cube, then according to Archimedes’ principle,
Loss of weight in water = weight of water displaced …. (i)

Here, mass in air, m_a = 0.5 kg
mass in water, m_w = 0.4 kg …. (ii)
ρ of water = 10³ kg m³.
∴ From (i) and (ii), we get

which is less than the density of copper (8.96 × 10³ kg m^-3). So the cube must be hollow.

Question 4.
A piece of pure gold (ρ = 9.3 g cm^-3) is suspected to be hollow. It weighs 38.250 g in air and 33.865 in water. Calculate the volume of the hollow portion in gold, if any.
Answer:
Density of pure gold, ρ = 9.3 g cm³ ,
mass of gold piece, M = 3 8.250 g

∴ volume of the gold piece, V = \(\frac{\mathrm{M}}{\mathrm{p}}=\frac{38.250}{9.3}\)
= 4.113 cm³

Also mass of gold piece in water
m’ = 33.865 g
∴ apparent loss in mass of the gold piece in water = (M – m’)
= (38.250 – 33.865)g
= 4.3.85 g

ρ_water = 1 g Cm^-3

∴ volume of displaced water = \(\frac{\mathrm{m}}{\rho}=\frac{4.385}{1}\)cm^-3
= 4.385 cm^-3

∴ volume of the hollow portion in the gold piece
= 4.385 – 4.113
= 0.272 cm^-3.

Question 5.
A glass plate of length 20 cm, breadth 4 cm, and thickness 0.4 cm weights 40 g in air. If it is held vertically with the long side horizontal and the plate half breadth immersed in water, what will be its apparent weight, the surface tension of water = 70 dyne cm^-1.
Answer:
Here, l = 20 m, b = 4 cm , t = 0.4 cm, T = 70 dyne cm^-1

Following three forces are acting on the plate:

1. Weight of the plate, W = 40 grand actings vertically downward.
2. Force due to surface tension acting vertically downward.

If F be the force due to surface tension, then

(iii) Upthrust, U = Vρg


∴ Net weight = W + F – U
= 40 + 2.9143 – 16
= 26.9143 gf

Question 6.
(a) What is the work done in blowing a soap bubble of diameter 0.07 m?

Answer:
(a) Here, initial radius of soap bubble, r₁ = 0
Final radius of soap bubble, r₂ = 0.035 m (∵ D₂ = 0.07m)
Increase in surface area of soap bubble

surface tension of soap solution = T = 0.04 Nm^-1
∴ work done to blow soap bubble = increase in area × T
= 0.0308 × 0.04
= 1.232 × 10^-3

(b) If 3.6960 × 10³ J of work is done to blow it further, find the new radius. Surface tension of soap solution is 0.04 Nm1.
Answer:
Let r be the new radius =?

Question 7.
Aspherical mercury drop of 10^-3 m radius is sprayed into million drops of the same size. Find the energy used in doing so. Surface tension of Hg = 0.55 Nm^-1.
Answer:
Here, R = 10^-3 m
Number of small drops, n = 106
T = 0.55 Nm^-1

Let r = radius of small drop
Since volume before spraying = volume after spraying

Also the surface area of bigger drop = 4πR²
The surface area of 106 smaller drops = 106 × πr²

∴ increase in surface area,

Question 8.
A liquid drop of diameter D breaks up into 27 tiny drops. Find the resulting change in energy.
Answer:
Let R be the radius of a bigger drop.
and r be the radius of smaller drop.


∴ Increase in area = 3πD² – πD² = 2πD²
T = surface tension of the liquid

∴ increase in energy = increase in area × T
= 2πD² × T.

Question 9.
Find the height to which water at 4°C will rise in a capillary tube of 10^-3 m diameter. Take g = 9.8 ms^-1. Angle of contact, θ = 0° and T = 0.072 Nm^-1.
Answer:
Here,

Question 10.
If a 5 cm long capillary tube with 0.1 mm internal diameter and open at both ends is slightly dipped in water having surface tension = 75 dynes cm^-1, explain whether water will flow out of the upper end of the capillary or not.
Answer:
Here,

Let h = height up to which water rises =?

Let h’ be the height of the capillary tube
∴ h’ = 5 cm
‘ Now water will rise to ..the upper end but will not overflow. It will adjust its radius of curvature (R) such that

Question 11.
Water is escaping from a vessel through a horizontal capillary tube 20 cm long and 0.2 mm radius at a point 100 cm below the free surface of the water in the vessel. Calculate the rate of flow if the coefficient of viscosity of water is 1 × 10^-3 PaS.
Answer:
Here, l = 20 cm = 0.20 m
r = 0.2mm = 2 × 10⁴ m
h = 100 cm = 1 m
p = 10³ kg m³
η = 1 × 10³ PaS
∴ P = hpg= 1 × 10³ × 9.8 Nm^-2

Let V = rate of flow = volume of water flowing per second =?

Question 12.
8 spherical raindrops of equal size are falling vertically through the air with a terminal velocity of 6.1 ms^-1. What should be the velocity if these 8 drops were to combine to form a bigger spherical drop.
Answer:
Here, v_T = 0.1 ms^-1
= terminal vol. of small drop

Let v ‘T be the terminal velocity of bigger drop Let r and R be the radius of smaller and bigger drop respectively.
Using the relation,

Also volume of bigger drop = Volume of 8 small drops

Question 13.
A pitot tube is mounted on an airplane wing to measure the speed of the plane. The tube contains alcohol and shows a level difference of 40 cm as shown here. What is the speed of the plane relative to air? Given relative density of alcohol = 0.8 and density of air = 1 kg m^-3.

Answer:
Here, the density of air, ρ = 1 kg m^-3
relative density of alcohol = 0.8

∴ density of alcohol = 0.8 × 10³ kg m^-3
Let P₁ = pressure of air at the nozzle.
P₂ = pressure of air at the other end.

P₁ – P₂ = 40 cm of alcohol
= 0.4 m of alcohol
= 0.4 × density of alcohol × g
= 0.4 × 800 × 9.8 Nm^-2.

Let v1 and v2 be the velocity of air at the nozzle and another end respectively. Then using Bernoulli’s theorem,

Now as the nozzle of the tube is parallel to the direction of motion of air,

Question 14.
A piece of metal 102 m2 ¡n area rests on a layer of Castrol oil 2 × 10 m thick whose η = 1.55 PaS. Calculate the horizontal force required to move the plate with a speed of 3 × 10² ms^-1.
Answer:

Question 15.
What should be the maximum average velocity of water in a tube of diameter 2 cm so that flow is laminar? The viscosity of water is 0.001 Nm^-2s.
Answer:
Here, D = 2 cm = 0.02 m
ρ = 10³ kg m³
η = 0.001 Nm^-2 s
= 10^-3 Nm^-2 s

Flow of water will be laminar if
N_R = 1000
where N_R is Reynold number

Let v = maximum average velocity.
∴ Using the relation

Question 16.
A non-viscous liquid flows through a horizontal pipe of varying cross-section at the rate of 22 m^-3 s^-1. Calculate the velocity at the cross-section where the radius is 5 cm.
Answer:
Here, the volume of liquid flowing per second,

Question 17.
(a) A fish weighs 348 g in air and 23 g in pure water. Calculate the relative density of fish.
Answer:
Here, the weight of fish in air = 348 g
weight of fish in water = 23 g

(b) A piece of solid weighs 120 g in air, 80 g in water, and 60 g in a liquid. Calculate the relative density of the solid and that of liquid.
Answer:
Here, the weight of solid in air = 120 g
weight of solid in water = 80 g
weight of liquid = 60 g

∴ (i) Relative density of solid

Question 18.
(a) A cubical block of wood of specific gravity 0.5 and a chunk of concrete of specific gravity 2.5 are fastened together. Calculate the ratio of the mass of wood to the mass of concrete which makes the combination float with its entire volume Submerged underwater.
Answer:
(a) Let m_w and m_c be the masses of wood and concrete respectively. Then according to law of floatation, Weight of the water displaced = weight of the body immersed.

(b) A spring balance reads 10 kg when a bucket of water is suspended from it. What is the reading on the spring? balance when:
(i) an ice cube of mass 1.5 kg is put into the bucket.
Answer:
When the ice cube is put in the bucket, then the total mass of the system suspended from the spring balance will be
10 kg + 1.5 kg = 11.5 kg
so the balance will read 11.5 kg.

(ii) an iron piece of mass 7.8 kg suspended by another string is immersed with half its volume inside the water in the bucket. (Relative density of iron = 7.8)?
Answer:
Relative density of iron = 7.8
so the density of iron = 7.8 × 10³ kg m^-1

This is the buoyant force experienced by iron pieces due to water. The iron piece will exert an equal force on the water in the downward direction. So the reading of the balance will increase by 0.5 kg. Thus the spring will read 10 kg +0.5 kg= 10.5 kg.

Question 19.
The flow rate from the tap of diameter 1.25 cm ¡s 3l/mm. The coefficient of viscosity of water is 10 PaS. Characterize the flow.
Answer:
The volume of liquid flowing per unit time = area × velocity



As N_R > 3000, so clearly, the flow will be turbulent.

Question 20.
The flow of blood in a large artery of an anesthetized dog is diverted through a Venturimeter. The wider part of the meter has a cross-sectional area equal to that of the artery, A = 8 mm². The narrow part has an area, a = 4 mm². The pressure drop in the artery is 24 Pa. What is the speed of the blood in the artery? (Given: density of blood = 1.06 × 10³ kg m^-3).
Answer:
Here, a₂= a = 4 mm²
a₁ = A =8 mm²
r = 1.06 × 10³ kg m^-3
P₁ – P₂ = 24 Pa
v₁ = ?

Question 21.
Calculate the minimum pressure required to force the blood from the heart to the top of the head (vertical distance 0.5 m). Assume the density of blood to be 1040 kg m^-3. Friction is neglected, g = 9.8 ms^-2.
Answer:
Here,

let v₁ = v₂ for minimum pressure difference

Question 22.
The density of air in the atmosphere decreases with height and can be expressed by the relation p = ρ₀e^-αh where ρ₀ is the density at sea level, a is the constant and h is the height. Calculate the atmospheric pressure at sea level. Assume g to be constant. The numerical values of constants are g = 9.8 ms^-2, ρ₀ = 1.3 kg m^-3 α = 1.2 × 10^-4 m^-1.
Answer:
Here, g = 9.8 ms^-2
ρ₀ = 1.3 kg m^-3
α = 1.2 × 10-4 m^-1
ρ = ρ₀e^-αh

Let dp = pressure due to small air column of length dh at a height h, then
dP = ρ dh g = (ρ₀e^-αh) g dh

∴ Total atmospheric pressure is given by

Question 23.
A ring is cut from a platinum tube having 8.5 cm internal and 8.7 cm external diameter. It is supported horizontally from a pan of balance so that it comes in contact with water in a glass vessel. What is the surface tension of water if an extra 3.97 g weight is required to pull it away from water (g = 980 ms^-2)?
Answer:
Here, m = 3.97 gm
r₁ = 8.5 cm
r₂ = 8.7 cm
T = ?
The water is in contact with the inner and outer circumference of the ring. To pull it out, work has to be done against forces due to surface tension.

Question 24.
Consider the horizontal acceleration of a mass of liquid in an open tank. Acceleration of this kind causes the liquid surface to drop at the front of the tank and to rise at the rear. Show that the liquid surface slopes at an angle θ with the horizontal where tan θ = \(\frac{a}{g}\), where ‘a’ is the horizontal acceleration, g
Answer:
This situation is shown in the figure here.

Let a liquid molecule of mass m lies at point P on the sloped surface AB of the liquid.
The different forces acting on this molecule are shown in the figure.
The force ma is due to the reaction and mg is the weight of the molecule.

For equilibrium of the molecule along the sloped surface AB,
ma cos θ = mg cos(90 – θ)
= mg sin θ

As the surface AB is in equilibrium, sp every liquid molecule on it is at rest.
The surface AB becomes inclined to the horizontal at angle 0 s.t.
tan θ = \(\frac{a}{g}\)

Question 25.
A stone of density 2.5 g cm^-3 completely immersed in seawater is allowed to sink from rest. Calculate the depth to which the stone would sink in 2s. The specific gravity of seawater is 1.025 and acceleration due to gravity is 980 cm s^-2. Neglect the effect of friction.
Answer:
Here, g = 980 cm s^-2 .
ρ₁ = density of stone = 2.5 g cm^-3.
Specific gravity of sea water = 1.025
∴ ρ₂ = density of sea water = 1.025 g cm^-3.

Now let m = mass of stone.
∴ V = volume of stone = \(\frac{\mathrm{m}}{\rho}=\frac{\mathrm{m}}{2.5}\) cm .
and this is equal to the volume of the displaced seawater.

∴ M = mass of seawater displaced.
= ρ₂ × V
= 1.025 × \(\frac{m}{2.5}\) gram

∴ Weight of sea water displaced = \(\frac{1.025 \times \mathrm{m}}{2.5}\) × g
If W₁ be the weight of the stone in seawater, then
W₁ = weight of stone – the weight of seawater displaced.

∴ Downward acceleration ‘a’ of stone in seawater is given by

Now let S = depth to which stone sinks. t = 2s, u = 0

∴ Using the relation,

Value-Based Type:

Question 1.
Krishna went sightseeing to a nearby river along with his physics teacher. He noticed that the wind was blowing from the side and the sailboat still continue to move forward. He was surprised. He asked his physics teacher an explanation of this situation. The teacher has noticed his “interest explained the concept through a small example.

The physics of sailing is very interesting in that sailboats do not need the wind to push from behind in order to move. The wind can blow from the side and the sailboat can still move forward.

The answer lies in the well-known principle of aerodynamic
lift Imagine you are a passenger in a car as it’s moving along, and you place your right hand out the window, ff you tilt your hand in the clockwise sense your hand will be pushed backward and up. This is due to the force of the air which has a sideways component and upwards component (therefore your hand is pushed backward and up).
(a) What values could you find- in Krishna?
Answer:
Krishna is very interested in learning the subject; also he is interested in knowing how science helps in understanding the day-to-day experiences, observant, has the courage to ask questions.

(b) Also explain what the Magnus effect is.
Answer:
The difference in velocities of air above the ball is relatively larger than below. Hence, there is a pressure difference between the lower and upper faces and there is a net upward force on the ball. This dynamic lift due to spinning is called the Magnus effect.

Question 2.
Seema’s mother was suffering from blood pressure but she did not consult any doctor. Prabha was a student of class XI who came to Visit Seema’s mother. Seema was upset as her mother did not want to go to hospital. Prabha convinced her mother by telling the effects of blood pressure on the heart. Finally, both of them able to brought Seema’s mother to a hospital and consulted a doctor.
(i) What values were displayed by Seema?
Answer:
Seema’s values are:
Caring, Sensible, love, and affection to her mother.

(ii) What values were exhibited by Prabha?
Answer:
Prabha’s values are Good knowledge of diseases and their ef- feet, a Helping attitude, willingness to convince and serve someone who needs, Friendly behavior, etc.

(iii) State Bernoulli’s theorem.
Answer:
It states that the total energy (sum of pressure energy, K.E, and P.E) per unit mass is always constant for an ideal fluid.
i.e. \(\frac{\mathrm{P}}{\mathrm{\rho}}\) + gh + \(\frac{1}{2}\)v² = constant

Question 3.
Salma’s little sister was crying. Then she took a piece of camphor and put it in water. By seeing the camphor piece dancing on surface on the surface of the water, the little one stopped crying.
(a) What can you say about the qualities of Salma?
Answer:
Salma is responsible, helps her mother in looking after her younger sister.

(b) Why do small pieces of camphor dance on the surface of the water?
Answer:
When camphor is dissolved in water, the surface tension of water is reduced, Since camphor has an irregular shape, therefore, it may dissolve more at one end than at the other end. This produces an unbalanced force due to which it moves. When it reaches a different region, the same process is repeated.

(c) Define surface tension.
Answer:
It is the property of the liquid by virtue of which the free surface of the liquid at rest tends to have minimum area and as such it behaves like a stretched elastic membrane.

Question 4.
(a)Savitawas surprised to see oil spreading onto the surface of the water and asked her mother to explain why oil spreads onto the surface of the water. Her mother explained to her daughter the reason behind it. By going through the explanation she thought of learning more about the other scientific phenomenon also. What qualities do you can find in Savita?
Answer:
She has inquisitiveness; she wants to know the scientific reason behind the phenomena.

(b) Oil spreads over the surface of water whereas water does not spread over the surface of the oil. Why?
Answer:
The surface tension of the water is more than that of oil, therefore when oil is poured over water the greater value of surface tension of water, pulls the oil in all directions. On the other hand, when water is poured over oil, it does not spread over it because the surface tension of oil is less than that of water.

Question 5.
Vineet saw his uncle planting seeds in the land. His uncle does not know the methods of growing plants. Then he decided to make his uncle aware of this. He explained the importance of plowing the land before planting the seeds. Uncle is convinced with his ideas. He planted accordingly. The plants are grown successfully.
(a) What can you say about Vineet?
Answer:
Vineet has good knowledge of agriculture. He is very much interested in putting his ideas into practice, uses his knowledge to convince his uncle.

(b) What is the utility of plowing a field? Does it help the soil to retain moisture?
Answer:
When the field is plowed, the capillaries are broken. So water cannot rise to the surface and the soil is able to retain its moisture.

We have given detailed NCERT Solutions for Class 6 Sanskrit Grammar Book सर्वनाम शब्द-रूपाणि तथा वाक्यप्रयोगः Questions and Answers come in handy for quickly completing your homework.

Sanskrit Vyakaran Class 6 Solutions सर्वनाम शब्द-रूपाणि तथा वाक्यप्रयोगः

अभ्यासः

प्रश्न 1.
‘तत्’ सर्वनाम-शब्दस्य उचितेन रूपेण वाक्यानि पूरयत। (तत् सर्वनाम के उचित रूप द्वारा वाक्य पूरे कीजिए। Complete the sentences with the appropriate form of the pronoun तत्..)

उदाहरणम्-सुनील: धावति। —- सः पतति।

(क) सुदीप्तिः क्रीडति। ……. न पतति। (सः, सा, तत्)
(ख) बालकाः खादन्ति। …………………… हसन्ति अपि। (ते, ताः, सः)
(ग) फलम् पतति। ………………….. मधरम अस्ति । (सः, तत्, तम्)
(घ) छात्रौ गच्छतः। (ते, तौ, सा)
(ङ) बालिकाः गच्छन्ति। …………………. बसयानेन गच्छन्ति। (ते, सा, ता:)
उत्तर:
(क) सा
(ख) ते
(ग) तत्
(घ) तौ
(ङ) ताः

प्रश्न 2.
उदाहरणानुसारं सर्वनामपदं संशोध्य वाक्यानि पुनः लिखत। (उदाहरण के अनुसार सर्वनाम-पद शुद्ध करके वाक्य को पुनः लिखिए। Correct the pronoun and rewrite the sentences as per the example.)

उदाहरणम् – एषः कमलानि। — एतानि कमलानि।
(क) एतत् वृक्षः। — ………….
(ख) एषा पुस्तकम्। — ………….
(ग) एतत् बालिके। — ………….
(घ) एषः बालकाः। — ………….
(ङ) एषा: अध्यापिकाः। — ………….
उत्तर:
(क) एषः वृक्षः
(ख) एतत् पुस्तकम्,
(ग) एते बालिके
(घ) एते
(ङ) एषा अध्यापिका।

प्रश्न 3.
किम् सर्वनाम-शब्दरूप-सहायतया प्रश्नान् पूरयत। (किम् सर्वनाम शब्दरूप की सहायता से प्रश्न पूरे कीजिए। Complete the following questions with the help of किम् शब्दरूप.)


उत्तर:
(क) के, (ख) कम्, (ग) केन, (घ) कस्मै (ङ) कस्मात् (च) कस्य (छ) कस्मिन्

प्रश्न 4.
प्रदत्त सर्वनामपदेभ्यः उचितं विकल्पं चित्वा रिक्तस्थानानि पूरयत। (दिए गए सर्वनाम पदों में से उचित विकल्प चुनकर रिक्त स्थान भरिए। Fick out the appropriate option from among the pronouns given and fill in the blanks.)

(क)
(i) ………. छात्रस्य नाम तन्मयः अस्ति। (सः, तम्, तस्य)
(ii) गुरुः ………. छात्रम् वदति। (सा, तम्, तेन)
(ii) …………. छात्रात् कलमम् आनय। (तस्मात्, तेन, तस्मै)
(iv) ………. गृहे अहम् वसामि। (ते, तम्, तस्मिन्)
(v) …………. छात्राय पुस्तकम् यच्छ। (तस्मिन्, कस्मै, तस्मै)
उत्तर:
(i) तस्य
(ii) तम्
(iii) तस्मात्
(iv) तस्मिन्
(v) तस्मै

(ख)
(i) एतत् ………. गृहम्। (मम्, माम्, मम)
(ii) किम् एतत् ………. पुस्तकम्? (त्वम्, त्वाम्, तव)
(iii) त्वम् ………. मित्राय उपहारम् आनेष्यसि? (कम्, किम्, कस्मै)
(iv) सः बालकः ………. वृक्षात् अपतत्? (कः, कस्मात्, केन)
(v) व्याघ्राः …………. वने सन्ति? (के, किम्, कस्मिन्)
उत्तर:
(i) मम
(ii) तव
(iii) कस्मै
(iv) कस्मात्
(v) कस्मिन्

प्रश्न: 5.
अधोदत्तायां तालिकायां उचित सर्वनामपदैः रिक्तस्थानपूर्ति कुरुत। (निम्नलिखित तालिका में उचित सर्वनामपद द्वारा रिक्त स्थानों की पूर्ति कीजिए॥ Fill in the blanks in the table given below with the appropriate pronoun forms.)

बालक शब्द- संज्ञापद (पुंल्लिग) एकवचन रूपाणि निर्देशानुसार पूरयत

उत्तर:

अधोदत्तानि वाक्यानि अवलोकयत। (नीचे दिए गए वाक्यों को देखिए । Examine the sentences given below.)

1. विभा पठति । सा न लिखति।
2. अरविन्दः लिखति। सः न पठति ।
3. तत् फलम् मधुरम्।
4. एषः वृक्षः।
5. एषा वाटिका।
3. तत् फलम् मधुरम्।
6. एतत् फलम्।
उपर्युक्त वाक्यों में स्थूल अक्षरों में आए शब्द सर्वनाम हैं।

सर्वनाम वे शब्द होते हैं जो संज्ञा के स्थान पर प्रयोग में लाए जाते हैं।

अवधेयम् – संस्कृत में सर्वनाम शब्द का पूर्व निर्धारित लिङ्ग नहीं होता है। सर्वनाम शब्द जिस शब्द के साथ प्रयुक्त होता है उसी का लिङ्ग अपना लेता है। अतः सर्वनाम शब्दों के रूप तीनों लिङ्गों में चलते हैं। संज्ञा

In the sentences given at the beginning of the chapter the words in bold letters are Pronouns. Pronouns are words which are used in place of nouns. In San skrit, the pronoun takes the gender of the word with which it is used. Therefore, Pronouns are declined in all three genders.

शब्दरूप-सर्वनाम

तत्, एतत्, किम् सर्वनाम हैं। नीचे इनके रूप दिए गए हैं।

Here we are providing Class 11 Physics Important Extra Questions and Answers Chapter 14 Oscillations. Important Questions for Class 11 Physics with Answers are the best resource for students which helps in Class 11 board exams.

Class 11 Physics Chapter 14 Important Extra Questions Oscillations

Oscillations Important Extra Questions Very Short Answer Type

Question 1.
(a) A particle has maximum velocity in the mean position and zero velocity at the extreme position. Is it a sure test for S.H.M.?
Answer:
No.

(b) Is restoring force necessary in S.H.M.?
Answer:
Yes.

Question 2.
Imagine a situation where the motion is not simple harmonic but the particle has maximum velocity in the mean position and zero velocity at the extreme position.
Answer:
Projection of a particle in non-uniform circular motion satisfies all the given conditions.

Question 3.
We know that in S.H.M., the time period is given by
T = 2π\(\sqrt{\frac{\text { Displacement }}{\text { Acceleration }}}\)
Does T depend upon displacement?
Answer:
No. T is independent of displacement as the displacement term is also contained in acceleration.

Question 4.
(a) Two simple pendulums of equal lengths cross each other at the mean position. What is their phase difference?
Answer:
180° i.e. it radians.

(b) Can a simple pendulum vibrate at the center of Earth? Why?
Answer:
No. This is because the value of g at the center of Earth is zero.

Question 5.
(a) A particle is in S.H.M. of amplitude 2 cm. At the extreme position, the force is 4N. What is the force at a mid-point i.e. midway between mean and extreme position?
Answer:
2N.

(b) What happens to the time period of a simple pendulum if its length is doubled?
Answer:
The time period is increased by a factor of 4l.

Question 6.
Can & simple pendulum be used in an artificial satellite? Why?
Answer:
No. This is because there exists a state of weightlessness in the artificial satellite.

Question 7.
What fraction of the total energy is potential energy when the displacement is one-half of the amplitude?
Answer:
\(\frac{1}{4}\left[\because \frac{P . E}{\text { Total energy }}=\frac{\frac{1}{2} \operatorname{m\omega}^{2}\left(\frac{a}{2}\right)^{2}}{\frac{1}{2} m \omega^{2} a^{2}}\right]\)

Question 8.
What fraction of the total energy is kinetic energy, when the displacement is one-half of the amplitude?
Answer:
\(\frac{3}{4}\left[\because \frac{\text { K.E. }}{\text { Total energy }}=\frac{\frac{1}{2} m \omega^{2}\left(a^{2}-\left(\frac{a}{2}\right)^{2}\right)}{\frac{1}{2} m \omega^{2} a^{2}}=\frac{3}{4}\right]\)

Question 9.
(a) When a particle oscillates simply harmonically, its potential energy varies periodically. If v be the frequency of oscillation of the particle, then what is the frequency of vibration of P.E.?
Answer:
2v

(b) A body executes S.H.M. with a period of \(\frac{11}{7}\) seconds and an amplitude of 0.025 m. What is the maximum value of acceleration?
Answer:

Question 10.
A body of mass m when hung on a spiral spring stretches it by 20 cm. What is its period of oscillation when pulled down, and released?
Answer:
T = 2π\(\sqrt{\frac{20}{980}}=\frac{2 \pi}{7} \mathrm{~s}=\frac{44}{49} \mathrm{~s}\)

Question 11.
A spring-mass system oscillating vertically has a time period T. What shall be the time period if oscillating horizontally?
Answer:
T i.e. it remains the same.

Question 12.
The time period of a body executing S.H.M. is 0.05 s and the amplitude of vibration is 4 cm. What is the maximum velocity of the body?
Answer:
1.6 π ms^-1

Question 13.
A spring-controlled wristwatch is taken from Earth to Moon. What shall be the effect on the watch?
Answer:
There will be no effect on g as the time period of spring is independent of g.

Question 14.
(a) At what displacement, the P.E. of a simple harmonic oscillator is maximum?
Answer:
At the extreme position.

(b) At what displacement, the K.E. of a simple harmonic oscillator is maximum? ‘
Answer:
At the mean position.

Question 15.
What is the total energy of a simple harmonic oscillator?
Answer:
\(\frac{1}{2}\)m ω² r², where r = amplitude, ω = angular frequency, m = mass of the oscillator.

Question 16.
Name the trigonometric functions which are suitable for the analytical treatment of periodic motions. ,
Answer:
Sine and Cosine functions or their linear combination.

Question 17.
How is acceleration (a) related to the displacement (y) in S.H.M.?
Answer:
aα – y.

Question 18.
At what position, the velocity of a particle executing S.H.M. is maximum?
Answer:
At mean position.

Question 19.
What is Force constant (k)? What are its units in the S.I. system?
Answer:
k = Force per unit displacement.
S.I unit of k is Nm^-1

Question 20.
(a) What ¡s the phase difference between displacement and velocity of a particle executing S.H.M.?
Answer:
90° or \(\frac{π}{2}\) radian.

(b) What is the phase difference between displacement and acceleration of a particle executing S.H.M.?
Answer:
180° or π radian.

Question 21.
(a) What will be the change in the time period of a loaded spring when taken to Moon?
Answer:
No change because T = 2π\(\sqrt{\frac{m}{k}}\) i.e. T ¡s independent of g.

(b) Why does the time period (T) of the swing not change when two boys sit on it instead of one?
Answer:
T is independent of the mass of the swing as T = 2π\(\sqrt{\frac{l}{g}}\).

Question 22.
Why are the vibrations of a simple pendulum damped?
Answer:
Because the energy of the pendulum is used to overcome air resistance.

Question 23.
A pendulum clock is taken on a lift moving down with a uniform Velocity. Will it gain dr lose time?
Answer:
It neither gains nor loses time.

Question 24.
What role do shock absorbers play in oscillations of vehicles on a bumpy road?
Answer:
They act as damping devices and save vehicles from resonant oscillations.

Question 25.
When do you apply force as the spring descends while swinging on a swing?
Answer:
To counter the effect of the damping force on the amplitude of oscillations of the swing at an appropriate point.

Question 26.
The time period of oscillation of a sphere hung from a wire attached to a rigid support and given slight rotation about the wire is given by T = 2π\(\sqrt{\frac{I}{C}}\). Which factor out of these is equivalent to the mass factor of an oscillator in S.H.M.?
Answer:
I (moment of inertia) of the sphere is equivalent to m, the mass of an ordinary oscillator in S.H.M.

Question 27.
At what points is the energy entirely K.E. and entirely P.E. in S.H.M.?
Answer:
At mean position and extreme position respectively.

Question 28.
What provides the restoring force for simple harmonic motion in the following cases?
(i) Simple pendulum.
(ii) Spring.
(iii) Column of mercury in a U-tube.
Answer:
The restoring force is provided by:
(a) gravity in simple pendulum i.e. weight of the pendulum.
(b) elasticity in spring.
(c) weight in the column of Hg in a U-tube.

Question 29.
Which single characteristics of a periodic motion distinguishes it as S.H.M?
Answer:
If acceleration is directly proportional to the negative- displacement, then the motion is said to be S.H.M.

Question 30.
(a) Does the bursting of air bubbles at the surface of boiling water show a periodic motion of the surface molecules?
Answer:
No.

(b) Do all periodic motions are S.H.M.?
Answer:
No.

Question 31.
At what point the velocity and acceleration are zero in S.H.M.?
Answer:
The velocity is zero at the extreme points of motion and acceleration is zero at the mean position of motion.

Question 32.
On what factors does the force constant of a spring depend?
Answer:
It Depends Upon the following factors:

1. Nature of the material of the spring.
2. Elasticity (i.e. coefficient of elasticity) of the material of spring.

Question 33.
Which factors determine the natural frequency of an oscillator?
Answer:
The dimensions and the elastic properties of the oscillator.

Question 34.
When a high-speed plane passes by, the windows of the plane start producing sound due to
(i) S.H.M.,
(ii) damped oscillations,
(iii) maintained oscillations. Why?
Answer:
(ii) Damped oscillations are caused due to air pressure on the glass window panes.

Question 35.
A motorcyclist while trying to loop a loop of maximum radius in a death trap goes round in the globe. Is it his projection on diameter in S.H.M.?
Answer:
Yes.

Question 36.
Sometimes on the screen of a cathode-ray oscilloscope, we see rectangular or triangular waves. Are these formed due to S.H.M. of the oscillator connected to it?
Answer:
No, these are not S.H.M. but are periodic waves.

Question 37.
Is oscillation of a mass suspended by a spring simple harmonic?
Answer:
Yes, only if the spring is perfectly elastic.

Question 38.
A diver wearing an electronic digital watch goes down into seawater with terminal velocity v. How will the time in the waterproof watch be affected?
Answer:
It will not be affected as its action is independent of gravity and buoyant force.

Question 39.
When is the tension maximum in the string of a simple pendulum?
Answer:
The tension in the string is maximum at the mean position because the tension in the string = mg cos θ = mg. (∵ θ = 0 at mean position).

Question 40.
Is the damping force constant on a system executing S.H.M.?
Answer:
No, because damping force depends upon velocity and it is more when the system moves fast and is less when the system moves slow.

Question 41.
What is the (a) distance covered by (b) displacement of, a body executing S.H.M. in a time equal to its period if its
amplitude is r?
Answer:
A body executing S.H.M. completes one vibration in a time equal to its period, so the body reaches its initial position after a time equal to its period.
Thus the
(a) total distance traveled is 4r and
(b) displacement is zero.

Question 42.
Can a motion be oscillatory but not simple harmonic? If yes give an example and if no explain, why?
Answer:
Yes. Uniform circular motion is an example of it.

Question 43.
How will the period of a pendulum change when its length is doubled?
Answer:
The time period becomes \(\sqrt{2}\) times the original value as T ∝ \(\sqrt{l}\).

Question 44.
Determine whether or not the following quantities can be in the same direction for a simple harmonic motion;
(a) displacement and velocity,
Answer:
Yes, when the particle in S.H.M. is moving from equilibrium position to extreme position.

(b) velocity and acceleration,
Answer:
Yes, when the particle executing S.H.M. is moving from an extreme position to a mean position.

(c) acceleration and displacement?
Answer:
No, because acceleration is always directed opposite to the displacement.,

Question 45.
Can a body have zero velocity and maximum acceleration in S.H.M.?
Answer:
Yes. In S.H.M., at the extreme position, the velocity of the body is zero and acceleration is maximum.

Question 46.
A passing airplane sometimes causes the rattling of windows of a house. Explain why?
Answer:
When the frequency of the sound waves produced by the engine of the airplane strikes the windows panes, they start vibrating due to forced oscillations. This causes rattling of windows.

Question 47.
Identify periodic, non-periodic, and S.H.M. out of the following:
(a) fluttering tree leaves due to wind.
Answer:
Non-periodic

(b) fluttering of honeybee’s wings for a microsecond.
Answer:
S.H.M.

(c) rising and falling of water drops at the bottom of a waterfall.
Answer:
Non-periodic

(d) the sound produced by a motorcycle in a small interval of time.
Answer:
Periodic

(e) the motion of the wheels of a canon during rapid fire.
Answer:
Periodic

(f) jerks in a machine gun during rapid fire.
Answer:
periodic

(g) vibrations of a drum membrane in a music band.
Answer:
Non-periodic.

Question 48.
Why pendulum clocks are not suitable for spaceships?
Answer:
The time period of a pendulum clock is given by
T = 2π\(\sqrt{\frac{l}{g}}\)

In a spaceship g = 0, so T = ∞,
It means the pendulum clock will not oscillate and hence are not suitable for spaceships.

Question 49.
A glass window may be broken by a distant explosion. Is it correct?
Answer:
Yes. The sound waves can cause forced vibrations in glass due to the difference between the frequency of sound waves and the natural frequency of the glass. This can break the glass window.

Question 50.
The bob of a simple pendulum is positively charged. The pendulum is made to oscillate over a negatively charged plate. How shall the time period change as compared to the natural time period of the simple pendulum?
Answer:
Due to the electric force of attraction between the bob and the plate, the effective value of acceleration due to gravity will increase T = 2π\(\sqrt{\frac{l}{g}}\) therefore T will decrease.

Oscillations Important Extra Questions Short Answer Type

Question 1.
Why does the body of a bus begin to rattle sometimes when the bus is accelerated?
Answer:
At some speed of the bus, the frequency of vibrations produced by the bus-engine is equal to the natural frequency of the bus. This produces resonant vibrations which have quite a large amplitude and\ence the bus begins to rattle.

Question 2.
The displacement of a particle in S.H.M. may be given by x = A sin (ωt + Φ) Show that if the time t is increased by \(\frac{2π}{ω}\), the value of x remains the same.
Answer:
The displacement of a particle in S.H.M. at a time t is given
x = A sin (ωt + Φ) …. (i)

Let x be the displacement of the-particle at time t’ = ( t + \(\frac{2π}{ω}\)),
To prove x₁ = x

From equation (i), we get
x₁ = A sin [ω( t + \(\frac{2π}{ω}\)) + Φ)]
= A sin [ωt + 2π + Φ]
= A sin [2π + (ωt + Φ)]
= A sin (ωt + Φ)
[ ∵ sin (2π + θ) = sin θ]

i.e. the displacement of the particle in S.H.M. is same for times t and t + \(\frac{2π}{ω}\) .
Hence proved.

Question 3.
A hollow sphere is filled with water through a small hole in it. It is hung by a long thread and as water slowly flows out of the hole at the bottom, one finds that the period of oscillations first increases and then decreases. Explain why?
Answer:
When the sphere is filled with water, its C.G. is at the center of the sphere. We know that the time period (T) of oscillation is directly proportional to the square root of the effective length of the pendulum
i.e. T ∝ \(\sqrt{l}\).

Due to the flow out of the water through the hole at the bottom of the sphere, the first effective length l increases, and then it decreases because of the lowering of the center of gravity in the first case and rising up in the second case. The first case corresponds to the lowering of the water level up to the center of the sphere. The second case corresponds to the lowering of the water level from the center of the sphere to its bottom.

Question 4.
A girl is swinging in the sitting position. How will the period ^ of the swing be changed if she stands up?
Answer:
This can be explained using the concept of a simple pendulum.
We know that the time period of a simple pendulum is given by
T = 2π \(\sqrt{\frac{l}{g}}\) i.e. T ∝ \(\sqrt{l}\)

When the girl stands up, the distance between the point of suspension arid the center of mass of the swinging body decreases i. e. l decreases, so l will also decrease.

Question 5.
At what displacement, a particle in S.H.M. possesses half K.E. and half P.E.?
Answer:
We know that in any position for a displacement of y from the mean position, the K.E. and P.E. are given by the expressions:
E_k = \(\frac{1}{2}\) mω² (r² – y²) ….(1)
E_p = \(\frac{1}{2}\)mω²y² …..(2)
Where m = mass of the particle
y = displacement from the mean position
ω = its angular frequency
r = amplitude of oscillation of the particle

Now for E_k = E_p, we get

Question 6.
Explain why marching troops are asked to break their steps while crossing a bridge?
Answer:
This is done so as to avoid setting the bridge into resonant oscillations of large amplitude. If troops march in step, then the frequency of the steps of the marching troops may become equal to the natural frequency of vibration of the bridge. Hence it may oscillate with high amplitude due to the phenomenon of resonance, resulting in damage to the bridge.

Question 7.
What is the direction of acceleration at the mean and extreme positions of an oscillating simple pendulum?
Answer:
When the simple pendulum oscillates, its bob moves along a circular path with the point of suspension at its center. At the mean position, bob possesses centripetal acceleration which acts along the thread towards the point of suspension. At an extreme position, the bob is at rest for a moment. The acceleration on the bob acts along the tangent to the circular path and is directed towards its mean position. This acceleration results due to the restoring force arising due to the weight of the bob.

Question 8.
You are provided with a light spring, a meter scale, and a known mass. How will you find the time period of oscillation of mass attached to the spring without the use of a clock?
Answer:
With the help of metre scale, we can note the length and extension produced. Since
F = – kl
and F = mg
or
∴ mg = – k l
or
\(\frac{\mathrm{m}}{\mathrm{k}}=\frac{l}{\mathrm{~g}}\) (numerically)
∴ T = 2π\(\sqrt{\frac{m}{k}}\) = 2π\(\sqrt{\frac{l}{g}}\) …(1)

∴ By knowing the extension l, T can be calculated from equation (1) w ithout the use of clock.

Question 9.
Why does the time period of a pendulum change when taken to the top of a mountain or deep in a mine? Will clocks keep the correct time?
Answer:
Time period of a pendulum is given by
T = 2π\(\sqrt{\frac{l}{g}}\)
As the value of ‘g’ on the top of a mountain or deep in a mine decreases, so the time period of the pendulum increases on the top of a mountain or deep in a mine and hence the pendulum clocks will run slow,

Question 10.
What is the source of potential energy in a loaded elastic spring?
Answer:
As the load is put at the end of the spring, it gets extended. To increase the length, the load does work against the elastic restoring force. This work done is stored in the spring in the form of its potential energy,

Question 11.
Why cannot we construct an ideal simple pendulum?
Answer:
An ideal simple pendulum is made up of a heavy point mass suspended to a weightless, inextensible string fastened to a rigid support. In actual practice geometrical point mass is not realized so is a weightless and inextensible string. Hence ideal simple pendulum cannot be constructed in actual practice.

Question 12.
When a fast railway train passes over a river bridge, we hear a loud sound, why?
Answer:
Fast railway train vibrations are passed to the air column between the bridge and the river water through railway lines and slippers. The vertical air column starts resonating with train vibrations, so a loud sound is heard. ‘

Question 13.
If the amplitude of vibration of an oscillator is made half, how will its time period and energy be affected?
Answer:
Since the time period of an oscillator is independent of its amplitude, so it remains unaffected. However, the total energy is directly proportional to the square of the amplitude, so the energy of the oscillator will become a quarter of its original value on making amplitude half.

Question 14.
A bead is mounted on a vertical stand placed attached to the rim of a record player and its shadow is cast on the wall with the help of light from a lamp. The record player is set in motion. Describe the motion of the shadow of the bead.
Answer:
As the bead executes circular motion with the record player, its shadow on the wall will execute whose period depends on the speed of rotation of the record player.

Question 15.
In Boyle’s law apparatus, if the open end tube is quickly moved up and down what will happen to the mercury column in the closed tube?
Answer:
Due to quick compression and expansion of air column above mercury column in the closed tube, the mercury column is set into damped harmonic motion. Damping is caused due to friction in the air layer and mercury with the glass wall.

Question 16.
Alcohol in a U-tube is executing S.H.M. of time period T. Now alcohol is replaced by water up to the same height in U-tube. What will be the effect on the time period?
Answer:
As the time period (T) of oscillation of a liquid column in a U-tube does not depend upon the density of the liquid, so T is independent of the nature of liquid in a U-tube, hence there will be no effect on the time-period of replacing alcohol by water.

Question 17.
A spring having a force constant k and a mass m is suspended. The spring is cut into three halves and the $ame mass is suspended from one of the halves. Is the frequency of vibration the same before and after the spring is cut? Give reason.
Answer:
No. This can be explained as follows:
The spring constant k = \(\frac{F}{x}\), when the spring is cut inito three parts, the hew force constant will be k’ = \(\frac{\mathrm{F}}{\frac{\mathrm{x}}{3}}=\frac{3 \mathrm{~F}}{\mathrm{x}}\) = 3k.

If v = frequency of oscillation when the spring was not divided,
Then

i.e. frequency of oscillation after cutting the spring into 3 parts is \(\sqrt{3}\) times the frequency of oscillation before cutting. It is now clear to us that this is due to the reason that v ∝ \(\sqrt{k}\) and k increases on cutting the spring, so frequency increases.

Question 18.
Oscillatory motion is periodic but the reverse is not always true. Justify.
Answer:
The motion of planets and comets like Hailey’s comet, satellites, merry-go-round, etc. all are periodic but not oscillatory as these are not to and fro motions about a mean position. But the motion of the simple pendulum is not only oscillatory but periodic too as it is also to and fro and repeats itself at regular intervals of time.

Question 19.
Why a restoring force is a must for S.H.M.?
Answer:
A restoring force is a force that restores or tends to restore or bring back a body or particle to its equilibrium position. When a body executing S.H.M. crosses its mean position due to its kinetic energy, the restoring force starts acting towards the equilibrium position and brings the oscillator towards the mean position from the extreme position of motion. The same thing happens when the body goes to the other side of the equilibrium position. So, a restoring force is a must for any oscillatory motion including S.H.M.

Question 20.
What is a periodic function, explain?
Answer:
A mathematical function that repeats itself after a definite period is called a periodic function, e.g. f (t) = f (t + T), here T = period of the function.

Let F(t) fie a periodic function such that F(t) = A sin \(\frac{2π}{T}\) t or F(t) = A cos \(\frac{2π}{T}\) t which are periodic functions. If t is replaced by t + T, we get once again the same value of the function. Thus


Hence f(t) is a periodic function having a time period T.

Question 21.
Distinguish between forced vibrations and maintained vibrations.
Answer:
A body vibrating under the effect of an external applied periodic force and oscillating with a frequency other than its natural frequency is said to be performing forced vibrations.

If energy is supplied to the oscillator at the same rate at which it is dissipated, the amplitude of the oscillator remains unchanged. Such oscillations are called maintained oscillations e.g. The oscillations of the pendulum clock of a watch or the balance wheel of a watch are examples of maintained oscillations.

Question 22.
Will a pendulum go slower or faster at
(a) Moon,
(b) planet Jupiter?
The time period of oscillation of a pendulum on Earth is given by
T_e = 2π\(\sqrt{\frac{1}{g_{e}}}\)
Answer:
(a) On moon gm = \(\frac{1}{6}\) of the Earth = \(\frac{\mathrm{g}_{\mathrm{c}}}{6}\).Since g_m < g_e, so T_m > T_e. Thus due to increase in time period of oscillation of pendulum, it will go slower on the moon.

(b) The value of acceleration due to gravity g_j on Jupiter is more than g_e, so the time period T_J of oscillation of the pendulum will be less than what it is on the earth. Thus due to a decrease in the time period of oscillation of a pendulum, it will go faster on Jupiter.

Question 23.
The mass M attached to a spring oscillates with a period of 2s. If the mass is increased by 2 kg, the period increases by 1 s. Find the initial mass m assuming that Hooke’s law is obeyed.
Answer:
Let the initial mass and time period be M and T respectively. If the Hook’s law is obeyed, then the oscillations of the spring will be simple harmonic having time period T given by
T = 2π\(\sqrt{\frac{M}{k}}\)

Given T = 2s
∴ 2 = 2π\(\sqrt{\frac{M}{k}}\); k = spring constant ….(1)

On increasing the mass by 2 kg, T’ = 2 + 1 = 3s.
∴ 3 = 2π\(\sqrt{\frac{M+2}{k}}\)

Squaring and dividing equation (2) by (1), we have

Question 24.
The displacement of a particle having periodic motion is given by
y = r sin ωt
Show that the motion of the particle is simple harmonic for small values of v.
Answer:
Since y = r sin(ωt – Φ) ….(1)
∴ \(\frac{dy}{dt}\) = rω cos(ωt – Φ) …(2)
and \(\frac{\mathrm{d}^{2} \mathrm{y}}{\mathrm{dt}^{2}}\) = – rω² sin(ωt – Φ)
= – ω² y …(3) [by (i)]

where,a = \(\frac{\mathrm{d}^{2} \mathrm{y}}{\mathrm{dt}^{2}}\) is called acceleration.
ω = angular frequency
∴ a = – ω²y

Now as a ∝ y and acts towards mean position. This is the characteristic of S.H.M. Hence the given equation y = r sin (ωt – Φ) represents an S.H.M. of the oscillator.

Question 25.
We have a very strong string and of sufficient length making a pendulum with a metal ball (e.g. a shot put). What will be the effect on the time period if
(a) the length of the pendulum is doubled and
Answer:
If the length of the pendulum is doubled, then
T = 2π\(\sqrt{\frac{2l}{g}}\)
= 2π\(\sqrt{\frac{l}{g}}\) \(\sqrt{2}\) = \(\sqrt{2}\)T.
The period of oscillation will increase.

(b) the ball is replaced by an elephant?
Answer:
Since mass does not come in relation to the time period of oscillation of a pendulum therefore instead of shot put if we make a pendulum of some length with an elephant there will be no effect on the time period of its oscillation.

Question 26.
The angular frequency of damped harmonic motion is given by ω = \(\sqrt{\frac{k}{m}-\left(\frac{b}{2 m}\right)^{2}}\) where b is know as damping constant. The displacement in such a motion is given by x = A e^-bt/2m cos (ωt + Φ) and the retarding force is F = – b v, where v is the speed of the particle. Could you guess from the given equations?
(a) How the amplitude of vibration change?
Answer:
The amplitude of vibration decreases continuously due to damping force. The amplitude decreases exponentially as is evident from the displacement equation the damping force is velocity-dependent.

(b) Does the time period of vibration change with displacement?
Answer:
The time period of oscillation does not change in damped oscillations.

Question 27.
Apart from the danger of being burnt which other factors make the re-entry of a space vehicle difficult in Earth’s atmosphere?
Answer:
The Earth’s thick atmospheric layer offers buoyant force and space vehicles suffer from damped harmonic oscillations, making the re-entry difficult.

Question 28.
If the amplitude of vibration is not small in the simple pendulum experiment will it not be executing periodic harmonic oscillations? How will the time period be affected?
Answer:
The simple pendulum will still be executing periodic harmonic oscillation even if the amplitude is large. However, the time period of oscillation will be slightly greater than what it is for small amplitudes
i.e. T > 2π\(\sqrt{\frac{l}{g}}\) ,

(The derivation of formulae is beyond the scope of this course),

Question 29.
Can you give some examples where an anharmonic oscillator does not possess potential energy?
Answer:
The thermal radiation enclosed in a black body of fixed dimensions and photons in solids behave like harmonic oscillators where they don’t have potential energy.

Question 30.
A man is standing on a platform executing S.H.M. in the vertical direction and attached to a weighing machine. Will there be any change in his weight?
Answer:
Depending on the motion of the platform from its mean position, the weight of the man will change when the platform moves down from the mean position to the lowermost point and return back to the mean position, ‘ the acceleration acts vertically upwards and hence the weight of the man j will increase. But when the platform moves up from its mean position to [ the uppermost point and returns back to the mean position, the acceleration in S.H.M. acts downwards, so the weight of the man is decreased.

Oscillations Important Extra Questions Long Answer Type

Question 1.
(a) What is the effect on the time period of a simple pendulum when:
(i) it is immersed in a liquid of density σ.
Answer:
Let p = density of the material of the pendulum bob.
σ = density of the liquid in which the pendulum bob is immersed such that p > σ. Let it is made oscillate with a time period T’. The effective value of ‘g’ in the liquid is given by

where T = time period of the simple pendulum when it oscillates in air.
or
\(\frac{\mathrm{T}^{\prime}}{\mathrm{T}}=\sqrt{\frac{\rho}{\rho-\sigma}}\)
∴ ρ > σ
or
ρ – σ > 0

∴ \(\frac{\rho}{\rho-\sigma}\) > 1
or
\(\frac{\mathrm{T}^{\prime}}{\mathrm{T}}\) > 1
or
T’ > T
i.e. its time period increases.

(ii) the temperature of wire through which the bob is suspended increased?
Answer:
When the temperature of the wire with which the bob of the pendulum is suspended increases, the length of the wire increases due to its thermal expansion. As
T ∝ \(\sqrt{l}\), so T will also increase as shown below:
Let l = original length of the wire
dθ = rise in its temperature
α = coefficient of linear expansion of the material of the wire
If l’ = new length
and dl = increase in its length = l’ – l, then

(Using Binomial expansion)
or increase in Time period = T’ – T = \(\frac{\mathrm{T} \alpha \mathrm{d} \theta}{2}\)

(b) Derive the differential equation of Simple Harmonic Oscillation.
Answer:
When an oscillator is displaced, say in the x-direction, the restoring force tends to bring it in its equilibrium position. It is well known that restoring force is directly proportional to the displacement, thus
Fα – x or F = – k x(t) .
where, the negative sign indicates! that the force always acts towards equilibrium position and opposes displacement, k is known as the force constant.

According to Newton’s law of motion if x (t) is the displacement then \(\frac{\mathrm{dx}(\mathrm{t})}{\mathrm{dt}}\) is the velocity and \(\frac{\mathrm{d}^{2} \mathrm{x}(\mathrm{t})}{\mathrm{dt}^{2}}\) is the acceleration of the oscillating particle.

Now Force = mass × acceleration

Equations (A) and (B) are known as the differential equations of simple harmonic oscillator, GO is the angular velocity given by
ω = \(\frac{2π}{T}\)
Also
ω = \(\sqrt{\frac{k}{m}}\)

So, the time period of oscillation of the oscillator is given by
\(\frac{2π}{T}\) = \(\sqrt{\frac{k}{m}}\)
or
T = 2π\(\sqrt{\frac{m}{k}}\)

(c) Distinguish briefly between natural, forced and , resonant vibrations. What are damped and undamped / vibrations?
Answer:
Natural vibrations: The vibrations of a body in the absence of any resistive, damping, or external) forces are said to be its natural vibrations. The body once vibrated continues to vibrate with its natùral frequency and undiminished amplitude.

Forced vibrations: A body at rest or vibrating with some frequency changes its frequency of vibration and amplitude when an external force is impressed on it. If the applied force is periodic the body oscillates with a period which is the period of the impressed force.

The vibrations of the body are not natural or free vibrations but are forced vibrations. If the external periodic force is removed, the body executes its natural oscillations after a while.

Resonant vibrations: If a body is set in vibrations such that a periodic force creates vibrations in it and the frequency of such vibrations becomes equal to the natural frequency of vibration of the body (i.e. the frequency of its free vibrations in the absence of the applied periodic force), its amplitude of vibration increases vigorously. The body is said to be in resonance with the second oscillating body or the applied periodic force.

The frequencies of the two oscillators become equal. Resonant oscillations are not only set up in mechanical oscillators but in electrical circuits and atomic oscillators too.

Damped vibrations: If a body vibrates in the presence of a resistive force such as fluid friction or electromagnetic damping force, its amplitude of oscillation decreases, and ultimately the oscillations die out i.e. the body stops oscillating. Such an oscillation is called damped oscillation as shown in the figure. The amplitude of vibration decreases with time.

Undamped Oscillations: The free oscillations of an oscillator in the absence of any resistive or damping force have constant amplitude over time. Such oscillations are called undamped oscillations. Most vibrations in ‘ daily life are damped vibrations because the oscillator experiences one or the other type of force acting on it. So, its vibrations become damped.

Question 2.
(a) Discuss the effect of driving force frequency on the driven frequency. How does friction affect the oscillation of an oscillator?
Answer:
Driving force is a time-dependent force represented by
F(t) = f_o cos 2πvt …..(1)
where v = frequency of driving force. This frequency is different from the natural frequency of the oscillation v_n of the oscillator. v_n is also called driven frequency. Thus motion depends on driving force.

Thus the motion of the particle is now under the action of: (a) linear restoring force, (b) time dependent (or periodic) force given in equation (1) so that using Newton’s law, we have for the oscillator:
ma(t) = – k x(t) + f_o cos2πvt …. (2)
and v_n² = \(\frac{1}{\mathrm{~T}^{2}}=\frac{\mathrm{k}}{4 \pi^{2} \mathrm{~m}}\) ….(3)

where m = mass of oscillator,
k = force constant,
v = frequency of the driving force,
ω = 2πvt,
vn = natural frequency of the oscillator,

Let the displacement be given by, x = C cos ωt,
where C = constant, .

This shows that the mass m will execute S.H.M. whose frequency is equal to the frequency of the driving force. The amplitude of oscillation too depends on the frequency of the driving force and is independent of time.

If there is a large difference between v and v_n, then the amplitude of oscillation will be too small. But if v_n ~ v, the amplitude of oscillation will become infinite, which does not actually happen as some sort of unaccounted force breaks the oscillations down. But if v – v_n, the amplitude becomes very large. This phenomenon is called resonance. There are several examples of resonance in daily life such as playing musical instruments, marching of troops in steps, etc.

Effect of the force of friction on S.H.M.: The real oscillations of almost all oscillators are known as damped oscillations. The energy of the system is continuously dissipated but nevertheless, oscillations remain periodic. This dampens oscillations. It is an additional restoring force that is proportional to the velocity of the particle rather than its displacement i.e. F = – bv(t), where b is a positive constant called damping constant. The oscillator is now under the combined action of F(t) and f(t) so that
ma(t) = – k x(t) – bv(t) …. (5)

The solution of this equation gives

(b) Derive an expression for
(1) angular velocity
(2) time period,
(3) frequency of a particle executing S.H.M. in terms of spring factor and inertia factor.
Answer:
Let m = mass of a particle executing S.H.M. The restoring force F is directly proportional to the displacement and acts opposite to it so that
F ∝ – x
or
F = – k x
where k is called the force constant. If the mass m is attached to an elastic spring, then k is called the spring constant for a given spring. From Newton’s second law of motion,
F = ma
Therefore F = ma = – kx
or
a = – \(\frac{k}{m}\)x
⇒ a ∝ – x

Hence the motion is S.H.M., we can write
a = – ω² x
where ω² = \(\frac{k}{m}\)
or
ω = \(\left(\frac{k}{m}\right)^{\frac{1}{2}}\)

This gives ω in terms of spring and constant mass factor.
we know that ω = \(\frac{2π}{T}\)

⇒ T = \(\frac{2π}{ω}\)

Substituting the value of ω from above we have
T = 2π\(\sqrt{\frac{m}{k}}\)

This is the expression for time period.
The frequency v = \(\frac{1}{T}\) = \(\frac{1}{2 \pi} \sqrt{\frac{\mathrm{k}}{\mathrm{m}}}\)

If the body executing S.H.M. has angular motion, then mass is replaced by the moment of inertia L and the force constant k is replaced by C, the restoring couple per unit twist, hence ω, T and v become
ω = \(\sqrt{\frac{C}{I}}\)

T = 2π\(\sqrt{\frac{C}{I}}\)
and v = \(\frac{1}{2 \pi} \sqrt{\frac{C}{I}}\)

Thus ω, T and v are found in terms of the spring factor and moment of inertia factor.

Question 3.
Calculate the effective spring constant and time period of a parallel and series combination of two different types of springs that are loaded.
Answer:
(a) When springs are connected in parallel with weight mg, hanging at the lower end.

Both the springs are pulled down through the same displacement say y.

Let F₁ and F₂ be the restoring forces acting on the spring.
Then F₁ = – k₁y
and F₂ = – k₂y

If F = total restoring force, then
F = F₁ + F₂
= – (k₁ + k₂)y ….(1)

Let k = spring constant of the combination, then
F = – ky ….(2)

∴ From (1) and (2), we get
k = k₁ + k₂

The motion of the weight will be simple harmonic in nature. Its time period is given by
T = 2π\(\sqrt{\frac{m}{k}}\)
= 2π\(\sqrt{\frac{\mathrm{m}}{\mathrm{k}_{1}+\mathrm{k}_{2}}}\)

(b) When the springs are connected in series, the springs suffer different displacement y₁ and y₂ when the weight mg is pulled down. But the restoring force is the same in each spring.
∴ F = – k₁y₁
and F = -k₂y₂

If k be the spring constant of the combination, then
F = -ky …..(4)
∴ From (3) and (4), we get
k = \(\frac{\mathbf{k}_{1} \mathbf{k}_{2}}{\mathbf{k}_{1}+\mathbf{k}_{2}}\) …(5)

If ‘a’ be the acceleration produced in the body of mass m, then
a = \(\frac{\mathrm{F}}{\mathrm{m}}=\frac{-\mathrm{k}}{\mathrm{m}}\)y ⇒ motion of S.H.M. having time period T given by

(c) The weight ‘mg’ is connected in between the two springs which themselves are connected in series.

When the weight is pulled to one side, one spring gets compressed and the other is extended by the same amount. The restoring force acts in the same direction due to both the springs.

Let y = extension or compression produced in the springs,
F₁, F₂ = restoring forces produced in the springs, then
F₁ = – k₁y
F₂ = – k₂y
If F = F₁ + F₂ = – (k₁ + k₂)y

If k = spring constant of the combination, then
F = – ky;
∴ k = k₁ + k₂
a = \(\frac{F}{m}\) = – \(\frac{\left(\mathrm{k}_{1}+\mathrm{k}_{2}\right)}{\mathrm{m}}\)y
and T = 2π\(\sqrt{\frac{M}{k}}\) = 2π\(\sqrt{\frac{M}{k_{1}+k_{2}}}\)

Question 4.
(a) Obtain the expression for a time period of a simple pendulum.
(b) Calculate the total energy of a particle executing S.H.M.
Answer:
(a) Let l = length of the string of the pendulum.
mg = weight of the bob acting vertically downward.
θ = angle by which the bob be displaced from the vertical position.
O = equilibrium position of the bob.

At any position P, the various forces acting on the bobs are:

1. mg, the weight of the bob acting in a vertically downward direction.
2. Tension (T) in the string acting along the string towards the support from which the pendulum is suspended.

mg is resolved into two rectangular components.

1. mg cos θ opposite to T.
2. mg sin θ perpendicular to T and directed towards the mean position O.

T – mg cos θ provides the centripetal force = \(\frac{\mathrm{mv}^{2}}{l}\) to the bob to move it in the circular path of radius l.

∴ T – mg cos θ = \(\frac{\mathrm{mv}^{2}}{l}\)
At extreme position P, bob is momentarily at rest i.e. v = 0

∴ T – mg cos θ = 0
or
T = mg cos θ ….(1)
mg sin θ provides restoring force (F), i.e.
F = – mg sin θ …. (2)

It acts towards the mean position. Here -ve sign shows that F tends to decrease θ. If θ is small, then
sin θ ~ θ
∴ F = – mg θ
Or
\(\frac{F}{m}\) = – gθ
or
a = – gθ = – g. \(\frac{x}{l}\) (∵ x = lθ)

where a = acceleration produced in the bob.
Now as a ∝ x and acts towards mean position, so its motion is S.H.M. having timC period (T) given by

T = 2π\(\sqrt{\frac{x}{a}}\) = 2π\(\sqrt{\frac{l}{g}}\)

(b) A particle executing S.H.M. has two types of energy

1. P.E. due to its displacement from mean position.
2. K.E. due to its velocity.

Let M = mass of the particle executing S.H.M.
r = amplitude of S.H.M.
ω = angular frequency of S.H.M.
y = displacement after a time t. k = force constant of S.H.M.
F = ky, restoring force acting at any position A.

Let the body is displaced from A to B s.t. AB = dy
If dW = work is done on the body when displaced by dy, then
dW = F dy = ky dy

If W = work done when the body is displaced through y, then

This work is stored in the particle in the form of P.E.
i.e. E₁ = P.E. = \(\frac{1}{2}\)ky²

KE. Let y = velocity of the particle executing S.H.M. at a displacement y from the mean position. Then
v = ω\(\sqrt{r^{2}-y^{2}}\)


Thus the total energy in S.H.M. remains constant.

Numerical Problems:

Question 1.
A particle executing S.H.M. along a straight line has a velocity of 4 ms^-1 at a distance of 3 m from its mean position and 3 ms^-1 at a distance of 4 m from it. Determine its angular speed and time period of oscillation.
Answer:
Here, y₁ = 3 m
v₁ = 4 ms^-1
y₂ = 4 m
v₂ = 3 ms^-1
ω =?

We know that the velocity of a particle executing S.H.M. is given by

∴ From (ii),
4 = ω \(\sqrt{25-9}\) = 4ω
∴ ω = 1 rad s^-1
∴ T = \(\frac{2π}{ω}\) = 2π second.

Question 2.
A harmonic oscillation is represented by y = 0.34 cos (3000 t + 0.74) where y and t are in cm and s respectively. Deduce
(i) amplitude,
(ii) frequency and angular frequency,
(iii) time period,
(iv) initial phase.
Answer:
The given equation is y 0.34 cos (3000 t + 0.74) …. (1)
Comparing eqn. (i) with the standard equation of displacement of harmonic oscillation,
y = r cos (ωt + Φ_o), we get
r = amplitude = 0.34 cm

Question 3.
A particle vibrates simply harmonically with an amplitude of 4 cm.
(a) Locate the position of the point where its speed is half its maximum speed.
(b) At what displacement ¡s P.E. = K.E.?
Answer:
Here, r = 4 cm
v_max = maximum speed of the particle
m = mass of the particle
(a) let v = speed of the particle when its displacement is y and
v = \(\frac{1}{2}\)v_max …(i)
Let y = required position w.r.t. mean pcsition =?

∴ maximum P.E = \(\frac{1}{2}\)kr²
Also maximum K.E = \(\frac{1}{2}\)mv²_max

According to the law of conservation of energy,

(b) Let y₁ be the displacement from the mean position at which
P.E.=KE.

Question 4.
A body of mass 12 kg is suspended by a coil spring of natural length 50 cm and force constant 2.0 × 10³ Nm^-1. What is the stretched length of the spring? 1f the body is pulled down further stretching the spring to a length of 59 cm and then released, what is the frequency of oscillation of the suspended mass? (Neglect the mass of the spring) .
Answer:
Here, k = 2 × 10³ Nm^-1
m = 12 kg
L = original length of the spring
= 50 cm = 0.50 m

Let l = elongation produced in the spring when 12 kg mass is suspended.
∴ F = kl = mg
or
l = \(\frac{\mathrm{mg}}{\mathrm{k}}=\frac{12 \times 9.8}{2 \times 10^{3}}\)
= 0.0588 m = 5.88 cm

∴ stretched length of the spring = L + l = 50.00 + 5.88 = 55.88 cm

The time period of a loaded spring does not change even if the spring is further stretched. So when it is stretched to 59 cm, its time period will be given by
T= 2π\(\sqrt{\frac{m}{k}}\)

∴ Frequency of oscillation is given by

Question 5.
A body of mass of 1.0 kg is suspended from a weightless spring having a force constant of 600 Nm^-1. Another body of mass 0.5 kg moving vertically upward hits the suspended body with a velocity of 3.0 ms^-1 and gets embedded in it. Find the frequency of oscillations and amplitude of motion.
Answer:
Here, m₁ = 1 kg
m₂ = 0.5 kg
k = force constant = 600 Nm^-1
v₁ = 0
v₂ = 3 ms^-1

As the mass m2 gets embedded after collision; so
m = total mass = inertia factor = m₁ + m₂ = 1 + 0.5 = 1.5 kg
If v = frequency of oscillation, then

According to the law of conservation of linear momentum, pf = pi.
(m₁ + m₂)V = m₁v₁ + m₂v₂ = m₂v₂ (∵ v₁ = 0)
∴ V = \(\frac{\mathrm{m}_{2} \mathrm{v}_{2}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}=\frac{0.5 \times 3}{1.5}\) = 1 ms^-1

Let r = amplitude of motion
Also according to the law of conservation of mechanical energy

Question 6.
(a) If the length of a second’s pendulum is increased by 1%, how many beats will it lose in one day?
(b) A pendulum clock normally shows the correct time. On an extremely cold day, its length decreases by 0.2%. Compute the error in time per day.
Answer:
(a) Time period of a pendulum is
T = 2π\(\sqrt{\frac{l}{g}}\)

For second’s pendulum, T = 2s
∴ 2 = 2π\(\sqrt{\frac{l}{g}}\) …(i)

Let l’ = new length of the second’s pendulum. When l is increased by 1%, then
l’ = l + l% of l = l +\(\frac{1}{100}\)l

If T’ = new time period, then


(Using Binomial Expansion Theorem)
= 2 + \(\frac{1}{100}\)

No. of oscillations initially produced by the pendulum is
n = no. of seconds in one day/time
= \(\frac{24 \times 60 \times 60}{2}=\frac{86400}{2}\) …(ii)

No. of oscillations produced by the pendulum after increasing its length.

Number of oscillations lost per day = no. of seconds lose per day
= 216 × 2 = 432 s.

(b) The correct time period of the pendulum clock 2s.
Let l be its correct length
∴ 2 = 2π\(\sqrt{\frac{l}{g}}\) ….(iii)

Decrease in length = 0.2% of l = \(\frac{2}{100}\)l
If l’ be the new length than
l’ = l – \(\frac{0.2}{100}\)l = l(1 – \(\frac{0.2}{100}\))

If T’ be the new time period, then

= (2 – \(\frac{0.2}{100}\)) < 2
∴ Clock gains time,
Time gained in 2 seconds = \(\frac{0.2}{100}\)s

∴ Time gained per day = \(\frac{0.2}{100}\) × \(\frac{1}{2}\) × 24 × 60 × 60 = 86.4 s.

Question 7.
A simple pendulum is made by attaching a 1 kg bob to a 5 cm copper wire of diameter 0.08 cm and it has a certain period of oscillation. Next, a 10 kg bob is substituted for a 1 kg bob. Calculate the change in period if any. Young’s modulus of Copper is 12.4 × 1010 Nm^-2.
Answer:
Here, F = mg
A = πr²
The original length of the pendulum, l = 5 m

Case I: m = 1 kg, l = 5 m, r = \(\frac{0.08}{2}\) cm = 0.04 cm = 4 × 10^-4 m, Y = 12.4 × 10¹⁰ Nm^-2
∴ Δl1 = \(\frac{1 \times 9.8 \times 5}{3.14 \times(0.04)^{2} \times 12.4 \times 10^{10}}\)
= 0.0787 × 10^-2 m
= 0.00079 m.

∴ Total length of the pendulum,
l₁ = l + Δl₁ = 5 m + 0.00079 m
= 5.00079 m.

If T1 be the initial time period of the pendulum, then
T₁ = 2π\(\sqrt{\frac{l_{1}}{g}}\)
= 2 × \(\frac{22}{7} \sqrt{\frac{5.00079}{9.8}}\)
= 6.28 × 0.714 = 4.486 s

CaseII: M = 10kg, l = 5 m, r = 0.04 × 10^-4m, Y = 12.4 × 1010 Nm^-2
∴ Δl₂ = \(\frac{10 \times 5 \times 9.8}{3.14 \times 16 \times 10^{-8} \times 12.4 \times 10^{10}}\)
= 0.0079 m
∴ l₂ = l + Δl₂ = 5 + 0.0079 = 5.0079 m

If T2 be the new time period of the pendulum, then
T₂ = 2π\(\sqrt{\frac{l_{2}}{g}}\)
= 2 × 3.14\(\sqrt{\frac{5.00079}{9.8}}\)
= 4.489 s.

∴ Increase in time = T₂ – T₁ = 4.489 – 4.486 = 0.003s.

Question 8.
A second’s pendulum is taken in a carriage. Find the period of oscillation when the carriage moves with an acceleration of 4 ms^-2.
(i) Vertically upwards,
(ii) Vertically downwards,
(iii) in a horizontal direction.
Answer:
Here, T = 2s
using T = 2π\(\sqrt{\frac{l}{g}}\), we get
∴ 2 = 2π\(\sqrt{\frac{l}{g}}\)
or
1 = 2π\(\frac{l}{g}\)
or
l = \(\frac{\mathrm{g}}{\pi^{2}}=\frac{9.8}{\pi^{2}}\) …(i)

(i) When carriage moves up, a = 4 ms^-2
∴ If T₁ be the time period, then

(ii) When the carriage moves down with a = 4 ms^-2
If T₂ be the time period, then

(iii) When the carriage moves horizontally, then g and a are at right angles to each other and hence the net acceleration is

Question 9.
A block is kept on a horizontal table. The table is undergoing S.H.M. of frequency 3 Hz in a horizontal plane. The coefficient of static friction between the block and the table surface is 0.72. Find the maximum amplitude of the table at which the block does not slip on the surface (g = 10 ms^-2).
Answer:
Here, v = 3 Hz.
μ = 0.72
g = 10 ms^-2

Maximum acceleration of the block is
amax = rω²
where r = amplitude of the table
ω = its angular frequency = 2πv
= 2π × 3

∴ Maximum force on the block is given by
F = mamax = mrω²

Frictional force on the block,
f_s = μmg

The block will not slip on the surface of the table if
F = f_s
or
mrω² = μmg
or
r = \(\frac{\mu g}{\omega^{2}}\)
or
r = \(\frac{0.72 \times 10.0}{(6 \pi)^{2}}\) = 0.02 m

Question 10.
The pendulum bob has a speed of 3 ms^-1 at its lowest position. The pendulum is 0.5 m long. What will be the speed of the bob when the length makes an angle of 60° with the vertical?
Answer:
Let m = mass of the bob
y = speed of the bob at the lowest position = 3ms^-1.

l = length of the pendulum
= 0.5 m = \(\frac{1}{2}\)m

∴ K.E at the lowest position O = \(\frac{1}{2}\)mv²
= \(\frac{1}{2}\)m × 3² = \(\frac{9}{2}\)m …(i)

When the length (i) makes an angle O ( 60°) to the vertical, the bob of the pendulum will have both K.E. and P.E.

If v₁ be the velocity of the bob in this position and h= height of the bob with respect to O, then
SC = l cos θ
∴ h = OS – SC = l – l cos θ
= l(l – cos θ)
= l(1 – \(\frac{1}{2}\))
= \(\frac{l}{2}=\frac{1}{2} \times \frac{1}{2}\)m
= \(\frac{1}{4}\)m.

Total energy of the bob = K.E. + P.E.
= \(\frac{1}{2}\)mv₁² + mgh
= \(\frac{1}{2}\)mv₁² + m × 9.8 × \(\frac{1}{4}\) …(iii)

∴ According to the law of conservation of energy,
K.E. at O = Total energy at A
\(\frac{9}{2}\) m = \(\frac{1}{2}\)mv12 + \(\frac{\mathrm{m} \times 9.8}{4}\)
or
v₁² = 9 – \(\frac{9.8}{2}\) = 9 – 4.9 = 4.1
∴ v₁ = 2.025 = 2.03 ms-1.

Question 11.
A person stands on a weighing machine placed on a horizontal platform. The machine reads 60 kg. When the platform executes S.H.M. at a frequency of 2.0 s^-1 and amplitude 5.0 cm, what will be the effect on the reading of the weighing machine? Take g = 10 ms^-2.
Answer:
Here, m = 60 kg
v = 2 s^-1
r = 5 cm = 0.05 m
ω = 2πv = 2π × 2 = 4π rad^-1 s

Here A and B are the extreme positions between which the platform vibrates and O = mean position.
∴ acceleration is maximum at A or B and is given by
a_max = rω² = 0.05 × (4π)²
= 0.05 × 16 × 9.87
= 7.9 ms^-2

∴ restoring force, F = ma_max
= m × 7.9 N
= 7.9 m N

At point A, both weight and restoring force are directed towards the mean position, so the effective weight is maximum at A i.e. reading will be maximum and is given by
W₁ = mg + ma_max = m(g + a_max)
= 60 (10 + 7.9)
= 60 × 17.9 N
= 1074.0 N
= 107.4 kgf

At point B, the weight and the restoring force are opposite to each other, so the effective weight i.e. reading of the weighing machine is minimum at B and is given by

Question 12.
If earth were a homogeneous sphere and a square hole was bored in it through its center, show that a body dropped in the hole will execute S.H.M. and calculate its period if the radius of earth = 6400 km.
Answer:
Let R = radius of earth 6400 × 10³ m
O = center of the earth

Let AB be a tunnel bored along the diameter of the earth and a body be dropped from point A.

Let it reaches point C at a depth d from the surface of the earth.
∴ OC = R — d = distance of the object from the center of earth displacement of the body.

If gd be the acceleration due to gravity at a depth ‘d’ then we know, that
g_d = g(1 – \(\frac{d}{R}\)) = g\frac{(R-d)}{R}\(\)

If R – d = y = displacement from O, then
g_d = \(\frac{g}{R}\)y

Now as the acceleration of the body is proportional to its displacement from the center of earth i.e. O. Hence the motion of the body is S.H.M. and its time period is given by

Question 13.
A horizontal spring block system of mass M executes S.H.M. When the block is passing through its equilibrium position, an object of mass m is put on it and the two move together. Find the new amplitude and frequency of vibration.
Answer:
The frequency of oscillation of spring block system of mass M is given by
v = \(\frac{1}{2 \pi} \sqrt{\frac{\mathrm{k}}{\mathrm{M}}}\) …..(i)
where k = force constant of the spring.

Let r = initial amplitude of oscillation.
V_o = velocity of the system in equilibrium position,
according to the law of conservation of energy,
∴ \(\frac{1}{2}\)MV₀² = \(\frac{1}{2}\)kr²
or
V_o = \(\sqrt{\frac{k}{M}}\)r ….(ii)

When mass m is put on the system, then total mass = M + m.

If V = velocity of the combination in equilibrium, then according to the law of conservation of linear momentum,
MV_o = (M + m)V
or
V = \(\frac{\mathrm{MV}_{0}}{\mathrm{M}+\mathrm{m}}\) ….(iii)

Let r₁ be the new amplitude, then


If v’ be the new frequency of oscillation, then
v’ = \(\frac{1}{2 \pi} \sqrt{\frac{\mathrm{k}}{\mathrm{M}+\mathrm{m}}}\)

Question 14.
A tray of mass 12 kg is supported by two parallel vertical identical springs. When the tray is pressed down slightly and released, it executes S.H.M. with a time period of 1.5 s. What is the force constant of each spring? When a block of mass m is placed in the tray, the period of S.H.M. changes to 3 s. What is the mass of the block?
Answer:
Let k be the spring constant of each of the identical springs connected in parallel.
M = mass of tray = 12 kg
T₁ = time period of oscillation of the tray = 1.5 s

Let T₂ = time period of oscillation of the tray + block of mass ‘m’
∴ T₂ = 3 s
m = ?
k =?

If k’ = spring constant of the combination, then
k’ = k + k = 2k (a)

Dividing (ii) and (i), we get

Question 15.
Two pendulums of lengths 100 cm and 110.25 cm start oscillating in phase simultaneously. After how many oscillations will they again be in phase together?
Answer:
Here, l₁ = 100 cm
l₂ = 110.25 cm
using T = 2π\(\sqrt{\frac{l}{g}}\)

For smaller pendulum, T₁ = 2π\(\sqrt{\frac{100}{g}}\) …(i)

For larger pendulum, T₂ = 2π\(\sqrt{\frac{110.25}{g}}\) …(ii)
where T₁ and T₂ are the time periods of the two pendulums.

Let these pendulums oscillate in phase again if the larger pendulum completes n oscilLations, It means the smaller pendulum must complete (n + 1) oscillations.
nT₂ = (n + 1)T₁

Hence both pendulums will again oscillate in phase after 20 oscillations of the larger or 21 oscillations of the smaller pendulum.

Question 16.
Springs of spring constants k, 2k, 4k., 8k, are connected in series. A mass m kg ¡s attached to the lowér end to the last spring and the system is allowed to vibrate. Calculate the approximate time period of vibration.
Answer:
The time period of vibration of series loaded spring is given by
T = 2π\(\sqrt{\frac{\mathrm{m}}{\mathrm{k}_{\mathrm{s}}}}\) …(1)
Where k is the force constant of the series combination of springs.

In a series combination of springs, the combined spring constant k is given by

or
ks = \(\frac{k}{2}\)

m mass attached to the lower end of the spring.
∴ From (1) and (2), we get
T = 2π\(\sqrt{\frac{2 m}{k}}\)

Question 17.
A point particle of mass 0.1 kg is executing S.H.M. of amplitude 0.1 m. When the particle passes through the mean position, its kinetic energy is 8 × 10^-2 J. Obtain the equation of motion of this article if the initial phase of oscillation is 45°
Answer:
Since the kinetic energy is maximum at the mean position and is equal to

The standard equation of motion of a particle executing S.H.M. is
y = A sin(ωt + Φ₂)
or
x = A cos(ωt + Φ₂)
Given r = 0.1 m, ω = 4 rad s-1 and Φ₂ = 45° = \(\frac{π}{4}\)

∴ The required cquation of motion is
y = 0.1 sin (4t + \(\frac{π}{4}\))
or
x = 0.1 cos (4t + \(\frac{π}{4}\)).

Question 18.
A cubical body (side 0.1 m and mass 0.002 kg) floats in water. It is pressed and then released so that it oscillates vertically. Show that the motion of the body is simple harmonic and And the time period.
Answer:
Here, m = mass of body = 0.002 kg
L = side of body = 0.1 m
In the absence of any given indication it is assumed that the body floats (just sunk), so

The mass of water displaced = volume × density of water
= V ρ = (0.1 )3 ρ.

The upward thrust exerted by water displaced
i.e. buoyant force = Vρg=(0.1 )3 × 10³ × 9.8 (∴ ρ ofwater = 10³ kg m³)
W₁ = Downward weight = mg
Net downward force, F = (0.002 g -Vρg)
or
F = [0.002g – (1)³ × 10³g
= (0.002 – 1)g
= – 0.998 × 9.8 N …. (1)

Suppose the block is depressed by y,
hence restoring force F₁ = – (0.1 + y)k

When the body floats on the water the force acting is F = 0.1 k, where k is the force constant
The net downward force
F – F’ = 0.1 k – (0.1 + y)k
= – yk ….(2)

Thus force ∝ (- y)
Force = ma, where a = acceleration of the body.
∴ ma = – y k
or a = – \(\frac{k}{m}\) y
m
or a ∝ -y …. (3)

Hence the motion-ofthe block is S.H.M.
The time period of oscillation is given by
T = 2π\(\frac{m}{k}\) …(4)

From eqn. (1), k = \(\frac{\mathrm{F}}{\mathrm{L}}=\frac{0.998 \times 9.8}{0.1}\)Nm^-1 …(5)
m = 0.002 kg

∴ T = 2π\(\sqrt{\frac{0.002 \mathrm{~kg} \times 0.1}{0.998 \times 9.8 \mathrm{Nm}_{1}}}\)
= 0.0284 s.

Question 19.
Two simple harmonic motions are represented by the following equations:
y₁ = 10 sin \(\frac{π}{4}\) (12t + 1); y² = 5 (sin 3πt + \(\sqrt{3}\) cos 3πt).
(a) Find out the ratio of their amplitudes.
(b) What are the time periods of two motions?
(c) Also find the phase difference between two motions.
Answer:
The two given displacements may be written as

(a) The amplitudes of the two S.H.M. are A₁ = 10 units. and A₂ = 10 units
Hence \(\frac{\mathrm{A}_{1}}{\mathrm{~A}_{2}}=\frac{10}{10}\) = 1

(b) Comparing the given equation with the normal sine function of S.H.M.
i.e. y = A sin(\(\frac{2πt}{T}\) + Φ) …(3)

Here we get \(\frac{2πt}{T}\) = 3πt
or
T = \(\frac{2}{3}\) s

i.e. Time period for two motions is same i.e. T = 0.67 s.

(c) Phase difference between two motions:
Phase (Φ₁) of motion represented by y₁ is
Φ₁ = 3πt + \(\frac{π}{4}\) …(4)

Phase (Φ₂) of motion represented by y₂ is
Φ₂ = 3πt + \(\frac{π}{3}\) …(5)

∴ Phase difference is given by
dΦ = Φ₂ – Φ₁ = (3πt + \(\frac{π}{3}\)) – (3πt + \(\frac{π}{4}\))
= (4 – 3)\(\frac{π}{12}\)
= \(\frac{π}{12}\) = 15°

Question 20.
Two particles execute- S.H.M. of the same amplitude at time period along the same straight line. They cross each other in opposite directions at half the amplitude. What is the phase difference between them?
Answer:
Let the displacement of one particle executing S.H.M. be
y₁ = A sin ωt …. (1)

when y₁ = \(\frac{A}{2}\)
From equation (1), we get.
\(\frac{A}{2}\) = A sin ωt
or
sin ωt = \(\frac{1}{2}\) = sin 30°
∴ ωt = 30° = \(\frac{π}{6}\) radian.

If Φ₁ be the phase of first particle then Φ = \(\frac{π}{6}\) radian. Also let the displacement of second particle executing S.H.M. be
y₁ = r sin (π – ωt) = r sin Φ₂ ….(2)
where Φ₂ = π – ωt = π – \(\frac{π}{6}\) = \(\frac{5}{6}\)π radian

If dΦ be the phase difference between the two particle when they cross each other, then
dΦ = Φ₂ – Φ₁
= \(\frac{5}{6}\)π – \(\frac{π}{6}\) = \(\frac{4π}{6}\) = \(\frac{2}{3}\)π radian
= 120°.

Question 21.
A spring compressed by 10 cm develops a restoring force of 5N. A body of mass of 2 kg is placed on it. Find
(i) Force constant,
(ii) depression of a spring,
(iii) time period and
(iv) the frequency of oscillations, if the body is disturbed.
Answer:
Here, F = 5N
x = 10 cm = 0.1 m
m = 2 kg
(i) k = force constant = \(\frac{F}{x}=\frac{5 N}{0.1}\) = 50 Nm^-1.

(ii) depression, l = \(\frac{\mathrm{mg}}{\mathrm{k}}=\frac{2 \times 9.8}{50}\) = 0.392 m

(iii) T = 2π\(\sqrt{\frac{m}{k}}\) = 2π\(\sqrt{\frac{2}{50}}\) = \(\sqrt{\frac{2π}{5}}\)s

(iv) v = \(\frac{1}{\mathrm{~T}}=\frac{5}{2 \pi}\) Hz

Question 22.
The S.H.M. of a particle is given by the equation y = 3 sin cot + 4 cos cot. Find its amplitude.
Answer:
The equation y = 3 sin ωt + 4 cos ωt is due to the superposition of two waves,
y₁ = 3 sin ωt
and
y₂ = 4 cos ωt = 4 sin(ωt + \(\frac{π}{2}\))

If r₁ and r₂ be the amplitudes of the two w’aves respectively, then r₁= 3 units and r₂ = 4 units.
Φ = phase difference between them = \(\frac{π}{2}\)

If r be the amplitude of the resultant wave, then

Question 23.
Two masses m₁ = 1.0 kg and m₂ = 0.5 kg arc suspended together by a massless spring of spring constant k as shown in the figure. When masses are in equilibrium, m, is removed without disturbing the system. Calculate the amplitude of oscillation and angular frequency of m2. (g = 10 ms^-2 and k = 12.5 Nm^-1).
Answer:
Let y = extension in length of the spring when both m1 and m2 are suspended with it, then
(m₁ + m₂)g = ky
or
y = \(\frac{\left(m_{1}+m_{2}\right) g}{k}\) …(1)

Let y’ extension in the length of the spring when only m is suspended.
∴ m₂g = ky’
or
y’ = \(\frac{\mathrm{m}_{2} \mathrm{~g}}{\mathrm{k}}\) …(2)

(1) – (2) gives y – y’ = \(\frac{\left(m_{1}+m_{2}\right) g}{k}-\frac{m_{2} g}{k}=\frac{m_{1} g}{k}\)

This represents the amplitude of oscillation (r)
i.e. r = y – y’ = \(\frac{\mathrm{m}_{1} \mathrm{~g}}{\mathrm{k}}\) …(3)
Here, m₁ = 1.0 kg
k = 12.5 Nm^-1
g = 10 ms^-2

Putting these values in equation (3), we get
r = \(\frac{1 \times 10}{12.5}\) = 0.8 m

If ω be the angular frequency of m₂, then
ω = \(\sqrt{\frac{\mathrm{k}}{\mathrm{m}_{2}}}=\sqrt{\frac{12.5}{0.5}}\) (∵ m₂ = 0.5 kg)
ω = 5 s^-1.

Question 24.
Prove that T = 84.6 minutes for a simple pendulum of infinite length.
Answer:
T = 2π\(\sqrt{\frac{l}{g}}\) …(1)
eqn. (1) hold good till l << R (radius of the earth).

When l is large, the curvature of the earth had also to be taken into account. In that case,

Question 25.
For damped oscillator, m = 200 gm, k = 90 Nm b = 40 gs^-1.
Calculate (a) time period of oscillation,
(b) time is taken for its amplitude of vibration to become \(\frac{l}{2}\) of its initial value.
(c) time is taken for its mechanical energy to drop to half of its initial value.
Answer:
Here, m = 200 g = 0.200 kg
k = 90 Nm^-1
b = 40gs^-1.
(a) \(\sqrt{km}\) = \(\sqrt{90 \times 0.2}=\sqrt{18}\) = 4.243 kg s^-1
b = 0.04 kg s^-1
∴ b << \(\sqrt{km}\)

(b) Let T_1/2 = time taken for the amplitude to drop to half of its initial value.

(c) Let T’_1/2 be the time for its mechanical energy to drop to half of its initial value,
∴ Using equation,

which is just half of T_1/2. (i.e. decay period for amplitude).

Value-Based Type:

Question 1.
A sports teacher was training the children to march- past On their way they come across a bridge. Then the physical education teacher stopped the children from marching on the bridge.
(a) Comment upon the values of sports teachers.
Answer:
The sports teacher is responsible, cares not only for public property but also for children.

(b) Also explain what is meant by Resonance.
Answer:
When the frequency of marching coincides with the natural frequency of oscillation of the bridge then the bridge oscillates with maximum amplitude to such an extent that the bridge may even collapse. The condition is called “Resonance”.

Question 2.
The Physics teacher of class XI has assigned the work finding the resultant spring constant when two springs of spring constants K₁, K₂ are joined in series. Two students Sabita and Shirin. Sabita made a theoretical study as well as verified it experimentally. Whereas Shirin could not complete the work. When th~ teacher enquired the next day Sabita could give the answer. Whereas Shirin could not.
(a) Comment upon the qualities of Sabita.
Answer:
Sabita is Sincere and hardworking and has a scientific temper.

(b) Two springs are joined in series and connected to a mass m. If spring constants are Kj and K2, Calculate the period of oscillation of mass m.
Answer:
Since K₁ and K₂ are joined in series.

Question 3.
Adarsh a student of class XI has found the factors on which the time period of oscillation of a pendulum depends and arrived at the expression T – (constant) × (l/g)^1/2. He wants to know how the length of the pendulum gets affected on the surface of the moon for the same pendulum and arrived at the conclusion that it is 1/6.
(a) What values does Adarsh possesses?
Answer:
Adarsh is hardworking, thinks logically, having a scientific temper, able to find solutions with patience.

(b) The length of a second pendulum on the surface of the moon?
Answer:
Since l is proportional to ‘g’ the pendulum on the surface of the moon will be 1/6m.

Question 4.
In a physics class, the teacher told that everyone has to finish the homework and assignment within a weak. But only five students including Dinesh did their homework on time. A few questions from the assignment are as under:
(i) Derive the expression for velocity in S.H.M.
Answer:
Let the displacement in S.H.M is given by

(ii) On what factors time period of a simple pendulum depends.
Answer:
The time period of a simple pendulum depends on
(a) Length of the pendulum.
(b) The acceleration due to gravity.

(iii) What values are shown by Dinesh?
Answer:
Values shown by Dinesh are Punctuality and Sincerity.

Here we are providing Class 12 Maths Important Extra Questions and Answers Chapter 13 Probability. Class 12 Maths Important Questions are the best resource for students which helps in Class 12 board exams.

Class 12 Maths Chapter 13 Important Extra Questions Probability

Probability Important Extra Questions Very Short Answer Type

Question 1.
If A and B are two independent event, prove that A’ and B are also independent.
(C.B.S.E. Sample Paper 2018-19)
Solution:
Since A and B are independent events, [Given]
.-. P (A ∩ B) = P (A) . P(B) …(1)
Now P(A’∩B) = P (B) – P (A ∩ B)
= P(B) – P (A) P( ∩ B) [Using (1)]
= (1 – P(A)) P(B) = P(A’) P(B).
Hence, A’ and B are independent events.

Question 1.
One card is drawn from a pack of 52 cards so that each card is equally likely to be se-lected. Prove that the following cases are in-dependent :
(a) A : “The card drawn is a spade”
B : “The card drawn is an ace.”
(N.C.E.R.T.)
(b) A : “The card drawn is black”
B : “The card drawn is a king.”
(.N.C.E.R.T.)
Solution:
(a) P(A) =\(\frac{13}{52}=\frac{1}{4}\),P(B) = \(\frac{4}{52}=\frac{1}{13}\)
P(A∩B) = \(\frac{1}{52}=\frac{1}{4} \cdot \frac{1}{13}\) = p(A).p(B)
Hence, the events A and B are independent

(b) P(A) = \(\frac{26}{52}=\frac{1}{2}\), P(B) = \(\frac{4}{52}=\frac{1}{13}\)
P(A∩B) = \(\frac{2}{52}=\frac{1}{26}=\frac{1}{2} \cdot \frac{1}{13}\) = P(A).P(B)
Hence, the events A and B are independent

Question 3.
A pair of coins is tossed once. Find the probability of showing at least one head.
Solution:
S, Sample space = {HH, HT, TH, TT}
where H ≡ Head and T ≡ Tail.
∴ P (at least one head) = \(\frac { 3 }{ 4 }\) .

Question 4.
P(A) = 0.6, P(B) = 0. 5 and P(A/B) = 0.3, then find P(A∪ B)
(C.B.S.E. Sample Paper 2018-19)
Solution:
We have: P(A/B) = 0.3
\(\frac{P(A \cap B)}{P(B)}\) = 0.3
\(\frac{P(A \cap B)}{0.5}\) = 0.3
P (A ∩ B) = 0.5 x 0.3 = 0.15.
Now, P(A∪B) = P(A) + P(B) – P(A ∩ B)
= 0.6 + 0.5 – 0. 15
Hence, P (A ∪ B) = 1.1 – 0.15 = 0.95.

Question 5.
One bag contains 3 red and 5 black balls. Another bag contains 6 red and 4 black balls. A ball is transferred from first bag to the second bag and then a ball is drawn from the second bag. Find the probability that the ball drawn is red. (C.B.S.E. Sample Paper 2018-19)
Solution:
P(Red transferred and red drawn or black trans¬ferred red drawn)
\(\begin{array}{l}
=\frac{3}{8} \times \frac{7}{11}+\frac{5}{8} \times \frac{6}{11} \\
=\frac{21}{88}+\frac{30}{88}=\frac{51}{88}
\end{array}\)

Question 6.
Evaluate P(A ∪ B), if 2P(A) = P(B) = \(\frac { 5 }{ 13 }\) and P(A/B) = \(\frac { 2 }{ 5 }\) (C.B.S.E. 2018 C)
Solution:
P(A/B) = \(\frac{\mathrm{P}(\mathrm{A} \cap \mathrm{B})}{\mathrm{P}(\mathrm{B})}\) P(A∩B) = \(\frac{2}{11}\)
P(A∪B) = P(A) + P(B) – (A ∩ B)
= \(\frac{5}{26}+\frac{5}{13}-\frac{2}{13}=\frac{11}{26}\)

Probability Important Extra Questions Short Answer Type

Question 1.
Given that A and B are two independent events such that P(A) = 0.3 and P(B) = 0.5. Find P(A/B). (C.B.S.E. 2019 C)
Solution:
We have:
P(A)= 0.3 and P(B) = 0.5.
Now P(A ∩ B) = P(A). P(B)
[∵A and B are independent events]
= (0.3) (0.5) = 0.15.
Hence, P(A/B) = \(\frac{\mathrm{P}(\mathrm{A} \cap \mathrm{B})}{\mathrm{P}(\mathrm{B})}=\frac{0.15}{0.5}\) =0.3.

Question 2.
A bag contains 3 white and 2 red balls, another bag contains 4 white and 3 red balls. One ball is drawn at random from each bag.
Find the probability that the balls drawn are one white and one red.
(C.B.S.E. 2019 C)
Solution:
Reqd. probability
= P(White, Red) + P (Red, White)
\(\frac{3}{5} \times \frac{3}{7}+\frac{2}{5} \times \frac{4}{7}=\frac{9}{35}+\frac{8}{35}=\frac{17}{35}\)

Question 3.
The probabilities of A, B and C solving a problem independently are \(\frac{1}{2}, \frac{1}{3}\) and \(\frac{1}{4}\) respectively. If all the three try to solve the problem independently, find the probability that the problem is solved. (C.B.S.E. 2019 C)
Solution:
Given: P(A) = \(\frac{1}{2}\), P(B) = \(\frac{1}{3}\) and P(C) = \(\frac{1}{4}\)

Probability that the problem is solved
= Probability that the problem is solved by at least one person
= 1 – \(\mathrm{P}(\overline{\mathrm{A}}) \mathrm{P}(\overline{\mathrm{B}}) \mathrm{P}(\overline{\mathrm{C}})\)
= 1 – \(\frac{1}{2} \times \frac{2}{3} \times \frac{3}{4}\)= 1 – \(\frac{1}{4}=\frac{3}{4}\)

Question 4.
A die marked 1, 2, 3 in red and 4, 5, 6 in green is tossed. Let A be the event “number is even” and B be the event “number is marked red”. Find whether the events A and B are independent or not. {Delhi 2019)
Solution:
Here, A : number is even i.e.,
A = {2,4,6}
and B : number is red i.e.,
B = {1,2,3}
∴ P(A) = \(\frac{3}{6}=\frac{1}{2}\) and P(B) = \(\frac{3}{6}=\frac{1}{2}\)
And,
P(A ∩ B) = P(Number is even and red) = \(\frac { 1 }{ 6 }\) .
Thus, P(A ∩ B) ≠ P(A). P(B)
[∵ \(\frac{1}{6} \neq \frac{1}{2} \times \frac{1}{2}\) ]
Hence, the events A and B are not indepedent.

Question 5.
A die is thrown 6 times. If “getting an odd number” is a success, what is the probability of (i) 5 successes (ii) at most 5 successes? (Delhi 2019)
Solution:
Probability of getting an odd number is one 3 1
trial = \(\frac{3}{6}=\frac{1}{2}\) = p ( say)
Probability of getting an even number in one 3
trial = \(\frac{3}{6}=\frac{1}{2}\) = g(say) o l
Also, n = 6.

(i) P(5 successes) = P(5) = ⁶C₅ q¹ p⁵
(ii) P(at most 5 successes)
= P(0) + P(1) + … + P(5) = 1 – P(6)
= 1 – ⁶C₆ q⁰ p⁶
= 1 – \(\frac{1}{64}=\frac{63}{64}\)

Question 6.
The random variable ‘X’ has a probability distribution P(X) of the following form, where ‘k’ is some number :
\(\mathbf{P}(\mathbf{X}=\boldsymbol{x})=\left\{\begin{array}{l}
\boldsymbol{k}, \text { if } \boldsymbol{x}=\mathbf{0} \\
2 k, \text { if } x=1 \\
3 k, \text { if } x=2 \\
0, \text { otherwise. }
\end{array}\right.\)
Determine the value of ‘P. (Outside Delhi 2019)
Solution:
We have : P(X = 0) + P(X = 1) + P(X = 2) = 1
⇒ k + 2k + 3k = 1
⇒ 6k = 1.
Hence, k = \(\frac { 1 }{ 6 }\).

Question 7.
Out of 8 outstanding students of a school, in which there are 3 boys and 5 girls, a team of 4 students is to be selected for a quiz competiton. Find the probability that 2 boj and 2 girls are selected. (Outside Delhi 2019)
Solution:
Read, probability = \(\frac{{ }^{3} \mathrm{C}_{2} \times{ }^{5} \mathrm{C}_{2}}{{ }^{8} \mathrm{C}_{4}}\)
= \(\frac{3 \times 10}{70}=\frac{3}{7}\)

Question 8.
12 cards numbered 1 to 12 (one number on one card), are placed in a box and mixed up thoroughly. Then a card is drawn at ran¬dom from the box. If it is known that the number on the drawn card is greater than 5, find the probability that the card bears an odd number. {Outside Delhi 2019)
Solution:
Let the events be as :
A : Card bears an odd number.
B : Number on the card is greater than 5.
A∩B = {7, 9, 11}.
Hence, P(A/B) = \(\frac{P(A \cap B)}{P(B)}\)
= \(\frac{3 / 12}{7 / 12}=\frac{3}{7}\)

Question 9.
The probability of solving a specific problem independently by A and B are \(\frac { 1 }{ 3 }\) and \(\frac { 1 }{ 5 }\) respectively. If both try to solve the problem independently, find the probability that the problem is solved.
(iOutside Delhi 2019)
Solution:
P (Problem is solved)
= 1 – P (Problem is not solved)
= 1 – \(\left(1-\frac{1}{3}\right)\left(1-\frac{1}{5}\right)\)
= 1 – \(\frac{2}{3} \times \frac{4}{5}\)
= 1 – \(\frac{8}{15}=\frac{7}{15}\)

Probability Important Extra Questions Long Answer Type 1

Question 1.
A black and a red die are rolled together. Find the conditional probability of obtaining the sum 8, given that the red die resulted in a number less than 4. (C.B.S.E. 2018)
Solution:
Let the events be as:
E : Sum of numbers is 8
F : Number of red die less than 4.
E : {(2, 6), (3, 5), (4, 4), (5, 3), (6, 2)}
F = {(1, 1), (2, 1), … (6, 1), (1, 2), (2, 2), … (6, 2), (1, 3), (2, 3), … (6, 2) (6, 3)}
and E ∩ F = {(5, 3), (6, 2)}
P(E) = \(\frac{5}{36}\), P(F) = \(\frac{18}{36}\)
and P(E ∩ F) = \(\frac{2}{36}\).
Hence, P(E/F) = \(\frac{\mathrm{P}(\mathrm{E} \cap \mathrm{F})}{\mathrm{P}(\mathrm{F})}=\frac{2 / 36}{18 / 36}\)
= \(\frac{2}{18}=\frac{1}{9}\)

Question 2.
Two numbers are selected at random (with-out replacement) from the first five positive integers. Let X denote the larger of the two numbers obtained. Find the mean and vari-ance of X.
Solution:
The first five positive integers are 1, 2, 3, 4 and 5.
We select two positive numbers in 5 x 4 = 20 way.
Out of three, two numbers are selected at ran-dom.
Let ‘X’ denote the larger of the two numbers.
X can be 2, 3, 4 or 5.
∴ P (X = 2) = P (Larger number is 2)
{(1, 2), (2,1)} = \(\frac{2}{20}\)
Similarly, P(X = 3) = \(\frac{4}{20}\) ,
P(X = 4) = \(\frac{6}{20}\)
and P(X = 5) = \(\frac{8}{20}\)
Hence, the probability distribution is:

Question 3.
The probabilities of two students A and B coming to the school in time are \(\frac{3}{7}\) and \(\frac{5}{7}\) respectively. Assuming that the events, ‘A coming in time’ and ‘B coming in time’ are independent, find the probability of only one of them coming to the school in time. (A.I.C.B.S.E. 2013)
Solution:
We have : P(A) = Probability of student A coming to school in time = \(\frac{3}{7}\)
P(B) = Probability of student B coming to school in time = \(\frac{5}{7}\)
∴ \(\mathrm{P}(\overline{\mathrm{A}})=1-\frac{3}{7}=\frac{4}{7}\)
and \(\mathrm{P}(\overline{\mathrm{B}})=1-\frac{5}{7}=\frac{2}{7}\)
∴ Probability that only one of the students coming to school in time
= P(A ∩ \(\overline{\mathrm{B}}\)) + P( \(\overline{\mathbf{A}}\) ∩B)
= P(A)P(\(\overline{\mathrm{B}}\)) + P(\(\overline{\mathrm{B}}\))PB)
[∵ A and B are independent => A and \(\overline{\mathrm{B}}\) and \(\overline{\mathrm{A}}\) and B are also independent]
= \(\left(\frac{3}{7}\right)\left(\frac{2}{7}\right)+\left(\frac{4}{7}\right)\left(\frac{5}{7}\right)=\frac{26}{49}\)

Question 4.
A speaks truth in 80% cases and B speaks truth in 90% cases. In what percentage of cases are they likely to agree with each other in stating the same fact? (C.B.S.E. Sample Paper 2019-20)
Solution:
P(A) = \(\frac{80}{100}=\frac{4}{5}\)
and P( B) = \(\frac{90}{100}=\frac{9}{10}\)
P(\(\overline{\mathrm{A}}\)) = 1 – P(A) = 1 – \(\frac{4}{5}=\frac{1}{5}\)
P(\(\overline{\mathrm{B}}\)) = 1 – P(B) = 1 – \(\frac{9}{10}=\frac{1}{10}\)
∴ P(Agree) = P(Both speak the truth or both tell a lie)

Hence, the reqd. percentage = 74%.

Question 5.
A problem in Mathematics is given to three students whose chances of solving it are \(\frac{1}{2}, \frac{1}{3}, \frac{1}{4}\). What is the probability in the
following cases?
(i) that the problem is solved
(ii) only one of them solves it correctly
(iii) at least one of them may solve it.
Solution:
Let A, B, C be three events when a problem in
Mathematics is solved by three students.
Given : P(A) = \(\frac{1}{2}\), P(B) = \(\frac{1}{3}\), P(C) = \(\frac{1}{4}\).
.-. P(A) = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\), P(B) = 1 – \(\frac{1}{3}\) = \(\frac{2}{3}\)
and P(C) = 1 – \(\frac{1}{4}\) = \(\frac{3}{4}\).

(i) Probability that the problem is solved = Probability that the problem is solved by at least one student

(ii) Probability that only one solves it correctly = P(Aninc)+P(AnBnc)+P(AnBnc)

(iii) Probability that atleast one of them may solve the problem

Question 6.
In a set of 10 coins, 2 coins with heads on both sides. A coin is selected at random from this set and tossed five times. Of all the five times, the result was head, find the probability that the selected coin had heads on both sides. (A.I. C.B.S.E. 2015)
Solution:
Let the events be :
E₁ : Selecting a coin with two heads
E₂ : Selecting a normal coin and A : The coin falls head all the times.
Since E₁ and E₂ are mutually exclusive and by the data given in the problem, we have :
P(E₁) = \(\frac{2}{10}=\frac{1}{5}\)
P(A/E₂) = \(\frac{8}{10}=\frac{4}{5}\) = P(A/E₁) = 1
P(A/E₁) = 1
P(A/E₂) = \(\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}=\frac{1}{32}\)
Now P(A) = P(A ∩ E₁) + P(A ∩ E₂)
= P(E₁) P(A/ E₁) + P(E₂) P(A/ E₂)
= \(\frac{1}{5}+\frac{1}{40}=\frac{8+1}{40}=\frac{9}{40}\)

Question 7.
A person playsa game of tossing a coin thrice. For each head he is given XI by the organiser of the game and for each tail he has to give ₹1.50 to the organiser. Let ‘X’ denote the amount gained or lost by the person. Show that ‘X’ is a random variable and exhibit it as a function on the sample space of the experiment. (N.C.E.R.T.)
Solution:
Since ‘X’ is a number whose values are defined by the outcomes of the random experiment,
∴ ‘X’ is a random variable.
Now sample space is given by :
S = {HHH, HHT, HTH, THH, HIT, THT, TTH, ITT},
where H = Head and T = Tail.
Thus X (HHH) = 2 x 3 = ₹6
X (HHT) = X (HTH) = X (THH)
= 2×2-lxl.5 = ₹ 2.50
X (HTT) = X (THT) = X (TTH)
= lx2-2xl.5 = -₹l
and X (TTT) = -(3xl.5) = – ₹4.50.
Thus for each element of S, X takes a unique value.
∴ ‘X’ is a function on the sample space S having range = {6, 2.50, – 1, – 4.50}.

Question 8.
Two numbers are selected at random (without replacement) from first 7 natural numbers. If X denotes the smaller of the two numbers obtained, find the probability distribution of X. Also, find mean of the distribution.
(C.B.S.E. Sample Paper 2019-20)
Solution:
Let ‘X’ be the smaller of the two numbers obtained.
Thus, X takes values 1, 2, 3, 4, 5 and 6.

(ii) We have :

Question 9.
Two cards are drawn simultaneously (with-out replacement) from a well shuffled pack of 52 cards. Find the mean and variance of the number of red cards. (A.I.C.B.S.E. 2012)
Solution:
Here ‘X’ takes values 0, 1, 2

Question 10.
There is a group of 50 people who are patriotic out of which 20 believe in non-violence. Two persons are selected at random out of them, write the probability distribution for the selected persons who are non-violent. Also find the mean of the distribution.
Solution:
Let ‘X’ be the number of non-violent persons.
Here ‘X’ takes values 0, 1,2.
Thus no. of non-violent persons = 20
and no. of violent persons = 50 – 20 = 30.

Hence, probability distribution is given by :

Question 11.
Two groups are competing for the positions of the Board of Directors of a corporation. The probabilities that the first and second groups will win are 0.6 and 0.4 respectively. Further, if the first group wins, the probability of introducing a new product is 0.7 and the corresponding probability is 0.3 if the second group wins. Find the probability that the new product introduced was by the second group. (C.B.S.E. 2018 C)
Solution:
Let E₁ = First group wins, E₂ = Second group wins
H = Introduction of new product.
P(E₁) = 0.6, P(E₂) = 0.4
P(H/E₂) = 0.3 P(H/E₁) = 0.7
Now,
P(E₂/H) = \(\frac{\mathrm{P}\left(\mathrm{E}_{2}\right) \mathrm{P}\left(\mathrm{H} / \mathrm{E}_{2}\right)}{\mathrm{P}\left(\mathrm{E}_{2}\right) \mathrm{P}\left(\mathrm{H} / \mathrm{E}_{2}\right)+\mathrm{P}\left(\mathrm{E}_{1}\right) \mathrm{P}\left(\mathrm{H} / \mathrm{E}_{1}\right)}\)

Question 12.
From a lot of 20 bulbs which include 5 defectives, a sample of 3 bulbs is drawn at random, one by one with replacement. Find the probability distribution of the number of defective bulbs. Also, find the mean of the distribution. (C.B.S.E. 2018 C)
Solution:
Let X denote the number of defective bulbs.
X = 0, 1, 2, 3.
P(X = 0) = \(\left(\frac{15}{20}\right)^{3}=\frac{27}{64}\)
P(X = 1) = \(3\left(\frac{5}{20}\right)\left(\frac{15}{20}\right)^{2}=\frac{27}{64}\)
P(X = 2) = \(3\left(\frac{5}{20}\right)^{2}\left(\frac{15}{20}\right)=\frac{9}{64}\)
P(X = 3 )=\(\left(\frac{5}{20}\right)^{3}=\frac{1}{64}\)
Mean = ΣXP(X) = \(\frac{27}{64}+\frac{18}{64}+\frac{3}{64}=\frac{3}{4}\)

Probability Important Extra Questions Long Answer Type 2

Question 1.
In a hockey match t wo teams A and B scored same number of goals upto the end of the game, so to decide the winner, the referee asked both the captains to throw a die alternately and decided that the team, whose captain gets a six first, will be declared the winner. If the captain of team A was asked to start, find their respective probabilities of winning the match. (A.I.C.B.S.E. 2013)
Solution:
P(A), probability of A’s getting a six = \(\frac { 1 }{ 6 }\)
\(\mathrm{P}(\overline{\mathrm{A}})\), probability of A’s not getting a six
= 1 – \(\frac{1}{6}=\frac{5}{6}\)
Thus, P(A) = \(\frac{1}{6}\) \(\mathrm{P}(\overline{\mathrm{A}})\) = \(\frac{5}{6}\).
Similarly, P(B) = \(\frac{1}{6}\), \(\mathrm{P}(\overline{\mathrm{B}})\). = \(\frac{5}{6}\)

Question 2.
If A and B are two independent events such that:
\(\mathbf{P}(\overline{\mathbf{A}} \cap \mathbf{B})=\frac{2}{\mathbf{1 5}}\) and \(\mathbf{P}(\mathbf{A} \cap \overline{\mathbf{B}})=\frac{1}{\mathbf{6}}\), then find P(A) and P(B). (C.B.S.E. 2015)
Solution:
Since A and B are independent events,
\(\overline{\mathrm{A}}\) and B, A and \(\overline{\mathrm{B}}\) are also independent events.
Now \(P(\bar{A} \cap B)=\frac{2}{15}\) => \(\mathrm{P}(\overline{\mathrm{A}}) \mathrm{P}(\mathrm{B})=\frac{2}{15}\)
(1 – P(A)P(B) = \(\frac{2}{15}\)
P(B) – P(A))P(B) = \(\frac{2}{15}\) ………… (1)
And P(A∩\(\overline{\mathrm{B}}\))
P(A) \(\overline{\mathrm{B}}\) = \(\frac{1}{6}\)
P(A) (1 — P(B)) = \(\frac{1}{6}\)
P(A)-P(A)P(B) = \(\frac{1}{6}\) ………… (2)
Putting P(A) = x and P(B) = y in (1) and (2), we get
y – xy = \(\frac{2}{15}\)
and x – xy = \(\frac{1}{6}\) ………..(2)
Subtracting (2) from (1) y = y – x = \(\frac{2}{15}\) –\(\frac{1}{6}\)
⇒ y – x = \(\frac{-1}{30}\)
⇒ y = x – \(\frac{1}{30}\) ………… (3)
Putting in (1)’, \(x-\frac{1}{30}-x\left(x-\frac{1}{30}\right)=\frac{2}{15}\)
⇒ \(x-\frac{1}{30}-x^{2}+\frac{x}{30}=\frac{2}{15}\)
⇒ 30x – 1 – 30x² + x = 4
⇒ 30x² – 31x + 5 = 0.

If the girl tossed a coin .three times and exactly
1 tail shown, then: „ n
{HTH, HHT, THH} = 3
∴ P(A/E₁) = \(\frac { 3 }{ 8 }\)

Let A be the event that the girl obtained ex-actly one tail. If the girl tossed a coin only once and exactly 1 tail.
∴ P(A/E₂) = \(\frac { 1 }{ 2 }\)
By Bayes’ Theorem,

Question 6.
A manufacturer has three machine operators A, B and C. The first operator A produces 1 % of defective items, whereas the other two operators B and C produce 5% and 7% defective items respectively. A is on the job for 50% of the time, B on the job 30% of the time and C on the job for 20% of the time. All the items are put into one stockpile and then one item is chosen at random from this and is found to be defective. What is the probability that it was produced by A?
(Delhi 2019)
Solution:
Let the events be as below :
E₁ : Item produced by machine A.
E₂ : Item produced by machine B.
E₃ : Item produced by machine C. and D : Item drawn is defective.
We have to find P (E₁/D).
Now P(E₂) = \(\frac{50}{100}=\frac{1}{2}\) ,
P(E₂) = \(\frac{30}{100}=\frac{3}{10}\)
and P (E₃) = \(\frac{20}{100}=\frac{1}{5}\)
Also P(D/E₁) = \(\frac{1}{100}\)
P(D/E₂) = \(\frac{5}{100}\), P(D/E₃) = \(\frac{7}{100}\)
By Bayes’ Theorem,
P(E₁/D) =

Question 7.
Bag I contain 3 white and 4 black balls, while Bag II contains 5 white and 3 black balls. One ball is transferred at random from Bag I to Bag II and then a ball is drawn at random from Bag II. The ball is drawn is found to be white. Find the probability that the transferred ball is also white.
(C.B.S.E. 2019 C)
Solution:
Let the events be as below:
E₁ : 1 white ball is transferred from Bag I to Bag II
E₂ : 1 black ball is transferred from Bag I to Bag II
and A: 1 white ball is drawn from Bag II.

Question 8.
There are three coins. One is a two-headed coin (having head on both the faces), another is a biased coin that comes up heads 75% of the time and the third is an unbiased coin. One of the three coins is chosen at random and tossed. If it shows head, what is the probability that it was the two-headed coin? (C.B.S.E. Sample Paper 2018-19)
Solution:
Let the events be:
E₁ : coin is two headed
E₂ : coin is biased and
E₃ : coin is unbiased.
And, A : coin shows up head.
∴P(E₁) = P(E₂) = P(E₃) = \(\frac{1}{3}\)
and P(A/E₁) = 1, P(A/E₂) = \(\frac{75}{100}=\frac{3}{4}\)
and P(A/E₃) = \(\frac{1}{2}\)
By Bayes’ Theorem,
P(E₁/A) =

Hence, the required probability = \(\frac{4}{9}\)

Question 9.
Bag I contains 4 red and 2 green balls and Bag II contains 3 red and 5 green balls. One ball is transferred at random from Bag I to Bag II and then a ball is drawn at random from Bag II. The ball so drawn is found to be green in colour. Find the probability that the transferred ball is also green. (C.B.S.E. 2019 )
Solution:
Let the events be as below:
E₁ : 1 red ball is transferred from Bag I to Bag II
E₂ : 1 green ball is transferred from Bag I to Bag II
and A : 1 Green ball is drawn from Bag II.

Question 10.
There are three coins. One is a coin having tails on both faces, another is a biased coin that comes up tails 70% of the time and the third is an unbiased coin. One of the coins is chosen at random and tossed, it shows tail. Find the probability that it was a coin with tail on both the faces. (Outside Delhi 2019)
Solution:
Let the events be as below :
E₁ : Selected coin has tail on both faces
E₂ : Selected coin is biased
E₃ : Selected coin is unbiased and
A : Tail comes up.
Now P(E₁ ) = P(E₂ ) – P(E₃ ) = \(\frac{1}{3}\)

P(A/E₁) = 1,
P(A/E₂) = \(\frac{70}{100}=\frac{7}{10}\)
P(A/E₃) = \(\frac{1}{2}\)
By Bayes ’ Theorem :

Question 11.
Let a pair of dice be thrown and the random variable ‘X’ be the sum of the numbers that appear on the two dice. Find the mean (or expectation) of X. (N.C.E.R.T.)
Solution:
Clearly the sample space consists of 36 elementary events = {(x_i, y_i) ; x_i, y_i = 1, 2,…., 6}.
X, the random variable = Sum of the numbers on the two dice.
∴ ‘X’ takes values 2, 3,4, or 12.

Now P(X = 2) = P({1,1}) = \(\frac{1}{36}\)
P (X = 3) = P ({1,2}, {2,1}) =\(\frac{2}{36}\)
P (X = 4) = P {(1,3), (2,2), (3,1)} = \(\frac{3}{36}\)
P (X = 5) = P {(1,4),(2,3), (3,2),(4,1)} = \(\frac{4}{36}\)
P (X = 6) = P {(1,5), (2,4), (3,3), (4,2), (5,1)} = \(\frac{5}{36}\)
P (X = 7) = P {(1,6), (2,5), (3,4), (4,3), (5,2), (6,1)} = \(\frac{6}{36}\)
P (X = 8) = P {(2,6), (3,5), (4,4), (5, 3), (6,2)} = \(\frac{5}{36}\)
P (X = 9) = P {(3,6), (4,5), (5,4), (6,3)} = \(\frac{4}{36}\)
P (X = 10) = P {(4, 6), (5,5), (6,4)} = \(\frac{3}{36}\)
P (X = 11) = P {(5,6), (6,5)} = \(\frac{2}{36}\)
P (X = 12) = P {(6, 6} = \(\frac{1}{36}\)
Thus the probability distribution is:

= \(\frac{1}{36}\)(2 + 6 + 12 + 20 + 30 + 42 + 40 + 36 + 30 + 22 + 12) = \(\frac{1}{36}\) (252) = 7.
Hence, the required, mean = 7.

Question 12.
Find the mean and variance of the numbers obtained on a throw of an unbiased die.
(N.C.E.R.T.)
Solution:
Here sample space, S = {1, 2, 3, 4, 5, 6}.
Let ‘X’ denote the number obtained on the throw.
Thus ‘X’ takes values 1, 2, 3, 4, 5 or 6.
∴ P (1) = P (2) = = P(6) = \(\frac{1}{6}\).
∴ Probability distribution is :

Question 13.
Two cards are drawn simultaneously (or successively without replacement) from a well shuffled pack of 52 cards. Find the mean and variance of the number of kings. (C.B.S.E. Delhi 2019)
Solution:
Let X, number of kings = 0,1,2.
∴ P(X=0) = P (no king)
= \(\frac{48}{52} \times \frac{47}{51}=\frac{188}{221}\)
P(X = 1) = P (one king and one non-king)
= 2 x \(\frac{4}{52} \times \frac{48}{51}=\frac{32}{221}\)
P(X = 2) = P (two kings)
= \(\frac{4}{52} \times \frac{3}{51}=\frac{1}{221}\)
Hence, probability distribution is :

We have given detailed NCERT Solutions for Class 9 Sanskrit Grammar Book कारक उपपद विभक्ति प्रयोगा: Questions and Answers come in handy for quickly completing your homework.

Sanskrit Vyakaran Class 9 Solutions कारक उपपद विभक्ति प्रयोगा:

पाठ्यपुस्तकस्य (व्याकरणवीथिः)
अभ्यासकार्यम्

प्रश्न 1.
कोष्ठकेषु मूलशब्दाः प्रदत्ताः। तेषु उचितविभक्ती: योजयित्वा रिक्तस्थानाननि पूरयता

1. नास्ति ………………. समः शत्रुः। (क्रोध)
2. ……….. भीत: बालकः क्रदन्ति। (चौर)
3. अस्माकम् बालिका: ………………. निपुणाः सन्ति। (गायन)
4. माता ………………. स्निह्यति। (शिशु)
5. ………………. नमः। (सरस्वती)
6. अलम् ……….. । (विवाद)
7. धिक् देशस्य ……………….। (शत्रु)
8. पितरौ ………………. सर्वस्वं यच्छतः। (अस्मद्)
9. किम् ……… एतत् गीतं रोचते? (युष्मद्)
10. परितः वायुमण्डलम् अस्ति। (पृथ्वी) ………… बहिः छात्राः कोलाहलं कुर्वन्ति? (कक्षा)
उत्तर:
1. क्रोधेन
2. चौरात्
3. गायने
4. शिशौ
5. सरस्वत्यै
6. विवादेन
7. शत्रून्/शत्रुम्
8. अस्मभ्यम्
9. तुभ्यम्
10. पृथ्वीम्
11. कक्षायाः

प्रश्न 2.
कोष्ठकेभ्यः शुद्धम् उत्तरं चित्वा रिक्तस्थानपूर्तिं कुरुत

1. ………………. सह सीता वनम् अगच्छत्। (रामस्य/रामेण)
2. माता ………………. स्निह्यति। (माम/मयि)
3. ………………. मोदकं रोचते। (मोहनम्/मोहनाय)
4. …………… धनं ददाति। (रमेशम्/रमेशाय)
5. अध्यापिका ………………. पुस्तकं यच्छति। (सुलेखाम्/सुलेखायै)
6. ………………. परितः वृक्षाः सन्ति। (विद्यालयम्/विद्यालयस्य)
7. ………………. नमः। (गुरवे/गुरुम्) उत्तराणि
उत्तर:
1. रामेम्
2. मयि
3. मोहनाय
4. रमेशाय
5. सुलेखायै
6. विद्यालयम्
7. गुरवे।

प्रश्न 3.
उचितविभक्तिप्रयोगं कृत्वा अधोलिखितपदानां सहायतया वाक्यरचनां कुरुत

1. समम्
2. धिक्
3. विना
4. बहिः
5. निपुणः
6. अलम्
7. बिभेति।
उत्तर:
1. रामेण समम् सीता लक्ष्मणः च वनम् अगच्छताम्।
2. धिक् दुष्टम्।
3. धनं विना किमपि न भवति।
4. ग्रामात् बहिः त्डागोऽस्ति।
5. सः संस्कृते निपुणः अस्ति।
6. अलम् कोलाहलेन।
7. स:सिंहात् बिभेति।

प्रश्न 4.
‘क’ स्तम्भे शब्दाः दत्ताः सन्ति, ‘ख’ स्तम्भे च विभक्तयः। कास्य योगे का विभिक्तिः प्रयुज्यते इति। योजयित्वा लिखत

उत्तर:
1. (घ) चतुर्थी
2. (ज) तृतीया
3. (छ) चतुर्थी
4. (ग) पञ्चमी
5. (ख) चतुर्थी
6. (ञ) प्रथमा
7. तृतीया,
8. (झ) द्वितीया, तृतीया, पञ्चमी,
9. (च) तृतीया
10. (ङ) प्रथमा।

प्रश्न 5.
‘स्थूलपदानां’ स्थाने शुद्धपदं लिखत

1. अध्यापिकायाः परितः छात्राः सन्ति।
2. गोपालः शिवस्य सह वार्ता करोति।
3. महापुरुषम् नमः।
4. त्वाम् किम् रोचते?
5. सा गृहकर्मणः निपुणः।
उत्तर:
1. अध्यापिकाम्
2. शिवेन
3. महापुरुषाय
4. तुभ्यम्
5. गृहकर्मणि।

अतिरिक्तं कार्यम्

प्रश्न 1.
अधोलिखितेभ्यः शुद्धं पदं चित्वा रिक्तस्थानानि पूरयत।
(नीचे लिखे गए शब्दों में से उचित शब्द चुनकर रिक्त स्थानों की पूर्ति कीजिए।)
(Fill in the blanks with the suitable word choosing from the given words.)

1. पश्य! पश्य ! ………….. परितः पुष्पाणि न सन्ति।
(क) विद्यालयः
(ख) विद्यालयम्
(ग) विद्यालयस्य
(घ) विद्यालयेन
उत्तर:
(ख) विद्यालयम्

2. सज्जनाः …….. सह चलन्ति।
(क) सज्जनैः
(ख) सज्जनान्
(ग) सज्जनानाम्
(घ) सज्जनात्
उत्तर:
(क) सज्जनैः

3. सः पाठनकाले ………. बहिः गच्छति।
(क) कक्षायाः
(ख) कक्षायाम्
(ग) कक्षाम्
(घ) कक्षायै
उत्तर:
(क) कक्षायाः

4. कक्षायाम् …… परितः छात्रा: अतिष्ठन्।
(क) गुरुणा
(ख) गुरुम्
(ग) गुरोः
(घ) गुरौ
उत्तर:
(ख) गुरुम्

5. सः पुरुषः ……….. बिभेति।
(क) शत्रोः
(ख) शत्रुम्
(ग) शत्रवे
(घ) शत्रुणा
उत्तर:
(क) शत्रोः

6. ………… पृष्ठतः कः?
(क) ग्रामम्
(ख) ग्रामस्य
(ग) ग्रामाय
(घ) ग्रामात्
उत्तर:
(ख) ग्रामस्य

7. स: ………….. निपुणः।
(क) पठने
(ख) पठनाय
(ग) पठनेन
(घ) पठनस्य
उत्तर:
(क) पठने

8. सम्प्रति …………. परितः के?
(क) मम
(ख) माम्
(ग) अहम्
(घ) मह्यम्
उत्तर:
(ख) माम्

9. …………… बहिः उद्यानम् वर्तते।
(क) नगरस्य
(ख) नगरात्
(ग) नगरं
(घ) नगराय
उत्तर:
(ख) नगरात्

10. अधुना ……………. नृत्यम् रोचते।
(क) बालिकाम्
(ख) बालिकायै
(ग) बालिकायाम्
(घ) बालिके
उत्तर:
(ख) बालिकायै

11. सः …………… सह गच्छति।
(क) बालिकायाः
(ख) बालिकया
(ग) बालिकाय
(घ) बालिकायै
उत्तर:
(ख) बालिकया

12. सम्प्रति …………… विना न सफलता।
(क) परिश्रमात्
(ख) परिश्रमस्य
(ग) परिश्रमे
(घ) परिश्रमैः
उत्तर:
(क) परिश्रमात्

13. छात्राः कथयन्ति ……. नमः।
(क) अध्यापकम्
(ख) अध्यापकाय
(ग) अध्यापकेन
(घ) अध्यापकस्य
उत्तर:
(ख) अध्यापकाय

14. अध्यापकः …………. पुस्तकम् ददाति।
(क) छात्राय
(ख) छात्रम्
(ग) छात्रेण
(घ) छात्रात्
उत्तर:
(क) छात्राय

15. माता ……… क्रुप्यति।
(क) पुत्राय
(ख) पुत्रम्
(ग) पुत्रेण
(घ) पुत्रस्य
उत्तर:
(क) पुत्राय

16. बालकः …………. बिभेति।
(क) सिंहात्
(ख) सिंहस्य
(ग) सिंहम्
(घ) सिंहेन
उत्तर:
(क) सिंहात्

17. छात्राः ….. सह भ्रमणाय गच्छन्ति ।
(क) गुरोः
(ख) गुरुणा
(ग) गुरुम्
(घ) गुरवे
उत्तर:
(ख) गुरुणा

18. तस्यै ……………… पठनम् रोचते।
(क) छात्रायै
(ख) छात्रस्य
(ग) छात्रायाः
(घ) छात्रायाम्
उत्तर:
(क) छात्रायै

19. सीता ….. सह वनम् अगच्छत् ।
(क) रामस्य
(ख) रामेण
(ग) रामाय
(घ) रामम्
उत्तर:
(ख) रामेण

20. सम्भवतः अद्य ……. मोदकम् न रोचते।
(क) मम
(ख) मह्यम्
(ग) मत्
(घ) माम्
उत्तर:
(ख) मह्यम्

21. सः ………. निपुणः वर्तते।
(क) कार्यस्य
(ख) कार्ये
(ग) कार्यात्
(घ) कार्येण
उत्तर:
(ख) कार्ये

22. अहं कथयामि-वरुण ………… नमः।
(क) देवाय
(ख) देवम्
(ग) देवात्
(घ) देवेन
उत्तर:
(क) देवाय

23. राजा …………………. गाम् यच्छति।
(क) ब्राह्मणाय
(ख) ब्राह्मणम्
(ग) ब्राह्मणः
(घ) ब्राह्मणात्
उत्तर:
(क) ब्राह्मणाय

24. भिक्षुकः …………… बहिः देवालयः अस्ति।
(क) देवालयात्
(ख) देवालयम्
(ग) देवालयाय
(घ) देवालये उत्तराणि
उत्तर:
(क) देवालयात्

प्रश्न 2.
अधः संवादे कोष्ठकगतशब्देषु उचितविभक्तिं प्रयुज्य वाक्यानि पूरयत।
(नीचे लिखे संवाद में कोष्ठक के शब्दों में उचित विभक्ति का प्रयोग करके वाक्यों को पूरा कीजिए।
Complete the sen tences by using the suitable inflexion of the words from the brackets in the following dialogue.)

दीपकः — आम्। ……….. (युष्मद्) सह अन्ये के गच्छन्ति?

प्रभा — मम कक्षायाः प्रायः सर्वे छात्राः। पश्य, आगछन्ति ते।

दीपकः — आचार्यः अपि आगतः।

सर्वे छात्राः — ……………….. (आचार्य) नमः।

आचार्यः — नमस्ते नमस्ते! प्रसन्नाः भवत। बसयानम् .. …..(ग्राम)बहिः ……….
(चिकित्सालय) पुरतः स्थितम् अस्ति । सर्वे तत्र चलन्तु । बसयानम् इतः प्रातः 10.00 वादने प्रस्थास्यति ।

दीपकः — प्रभे! अहम् अपि त्वया सह गच्छामि। आगच्छ चलावः।

रमेशः —  त्वम् कस्मिन् विद्यालये पठसि?

सुरेशः — अहम् सर्वोदय विद्यालये पठामि ।

रमेशः — कीदृशः तव विद्यालयः?

सुरेशः — मम ………………. (विद्यालय) परितः वृक्षाः सन्ति।

रमेशः त्वम् विद्यालयं केन सह गच्छसि?

सुरेशः — अहम् विद्यालयं महेशेन सह गच्छामि।

रमेशः — परन्तु महेशः तु खञ्जः

अस्ति। — सुरेशः आम्। सः ……………….. (दण्ड) चलति।

रमेशः — हे महेश! तव माता प्रातः काले किं करोति त्वम् च किं करोषि?

सुरेशः — मम माता प्रातःकाले ओ३म् ……………… (गणेश) नमः इति मन्त्रेण पूजां करोति। अहम् स्वाध्यायं करोमि।

माला — रमेश! किं त्वमपि ……………. प्रति (कश्मीर) गमिष्यसि?

रमेशः — आम्। ……………. (युष्मद्)।
सह अन्ये के गमिष्यन्ति? ।

माला — मम कक्षायाः प्रायः सर्वे छात्राः सर्वाः छात्राश्च तत्र गमिष्यन्ति। पश्य, ते आगच्छन्ति ।

रमेशः — आचार्यः अपि आगच्छति।

छात्राः — ……. (आचार्य) नमः।

आचार्यः — नमस्ते, नमस्ते! प्रसन्नाः भवत। बसयानं तु ……………….. (ग्राम) बहिः ………………. (विद्यालय)
पुरतः स्थितम् अस्ति। सर्वे तत्र चलन्तु। बसयानम् इतः प्रातः 10.00 वादने प्रस्थास्यति।

उत्तर:
त्वया, आचार्याय, ग्रामात्, चिकित्सालयस्य, विद्यालयं, दण्डेन, गणेशाय, कश्मीरं, त्वया, आचार्याय, ग्रामात्, विद्यालयस्य

प्रश्न 3.
(क) कोष्ठकगतपदेषु उचितविभक्तिं प्रयुज्य वाक्यानि पूरयत।
(कोष्ठक में आए हए शब्दों में उचित विभक्ति को प्रयोग करके वाक्यों की पूर्ति कीजिए।) (Complete the sentences with the suitable inflexion of the words from the brackets.)

1. (i) ……………. (उद्यान) बहिः एकः जलाशयः अस्ति। (ii) तत्र विकसितानि कमलानि ……………. (जन) रोचन्ते। (iii) ……… (जलाशय) पुरतः एकः देवालयः अपि अस्ति। जनाः प्रतिदिनं तत्र गच्छन्ति। (iv) भो मित्र! पश्य, कीदृशः एषः सुन्दरः तडाग:? …………. (तडाग) परितः जम्बु-आमवृक्षाः सन्ति। (v) तडागे विकसितानि कमलानि …………. (अस्मद्) अतीव रोचन्ते। तडागे तरन्त्यः मीनाः बहु शोभन्ते।।
उत्तर:
(क)
(i) उद्यानात्
(ii) जनेभ्यः
(iii) जलाशयस्य
(iv) तडागं
(v) अस्मभ्यम्

2. (i) इदम् एकम् उद्यानम् अस्ति। ……………. (उद्यान) परितः वृक्षाः सन्ति। (ii) वृक्षः ……………. (लता) सह शोभते। (iii) ………….. (अस्मद्) पुष्पाणि रोचन्ते। (iv) वृक्षाः अपि ………… (पुष्प) ऋते न शोभन्ते। (v) …………. (उद्यान) बहिः देवालयः अपि अस्ति।
उत्तर:
(i) उद्यानम्
(ii) लताभिः
(iii) अस्मभ्यं
(iv) पुष्पेभ्यः
(v) उद्यानात्

(ख) मञ्जूषायाः उचितानि पदानि चित्वा अधोलिखितेषु अनुच्छेदेषु रिक्तस्थानानि पूरयन्तु।
(मञ्जूषा से उचित पदों को चुनकर नीचे लिखे अनुच्छेदों में खाली स्थानों को भरिए।)
(Fill in the blanks with the suitable words choosing from the given in box.)

1. संसारे जनाः स्व-स्व (i) ……………… कुशलाः भवेयुः यतः आधुनिके काले (ii) ……. विना कार्य न सरति। संसारं (iii) ………….. सुअवसराः प्रसृताः सन्ति। अतः जनाः (iv) …………… न बिभेत्य स्वमार्गेषु निरन्तरं चलेयुः। (v) …………. पृष्ठतः एव सफलता आगच्छति।
मञ्जूषा-परिश्रमात्, कार्येषु, परितः, श्रमस्य, श्रमात्।
उत्तर:
(i) कार्येषु
(ii) परिश्रमात्
(iii) परितः
(iv) श्रमात्
(v) श्रमस्य

2. मम (i) …………….. उभयतः हरिताः वृक्षाः सन्ति, (iii) ………….. बहिः एकं जलयन्त्रं वर्तते। सर्वे छात्राः शिक्षकेभ्यः कथयन्ति (iii) …. ………… मिलित्वा वार्तालाप कुर्वन्ति। (v) ……….. एकः अतीव निपुणः छात्रः अस्ति।
मञ्जूषा-सह, विद्यालयम्, तेषु, शिक्षकेभ्यः, तस्मात्।
उत्तर:
(i) विद्यालयम्
(ii) तस्मात्
(iii) शिक्षकेभ्यः
(iv) सह
(v) तेषु

प्रश्न 4.
अधोलिखितेष पदेष उचितं पदं चित्वा रिक्तस्थानानि परयत।
(नीचे लिखे पदों में से उचित पद चुनकर रिक्त स्थानों की पूर्ति कीजिए।)
(Fill in the blanks with the suitable word choosing from the given words.)

1. इयम् शान्तिसभा, अलम्
(क) कोलाहलेन
(ख) कोलाहलात्
(ग) कोलाहलाय
(घ) कोलाहलात्
उत्तर:
(क) कोलाहलेन

2. ……….. नमः।
(क) शिवम्
(ख) शिवाय
(ग) शिवात्
(घ) शिवेन
उत्तर:
(ख) शिवाय

3. ……….. परितः अग्निः ज्वलति।
(क) भवनम्
(ख) भवनस्य
(ग) भवनेन
(घ) भवनात्
उत्तर:
(क) भवनम्

4. ……… बहिः वाटिका अस्ति।
(क) गृहात्
(ख) गृहस्य
(ग) गृहम्
(घ) गृहेण
उत्तर:
(क) गृहात्

5. …….. बहिः रक्षकः तिष्ठति।
(क) गृहस्य
(ख) गृहात्
(ग) गृहम्
(घ) गृहेणे
उत्तर:
(ख) गृहात्

6. धनिकः ………… धनं यच्छति।
(क) याचकम्
(ख) याचकाय
(ग) याचकात्
(घ) याचकस्य
उत्तर:
(ख) याचकाय

7. सः …………….. बिभेति।
(क) सर्पस्य
(ख) सर्पात्
(ग) सर्पम्
(घ) सर्पण
उत्तर:
(ख) सर्पात्

8. …………. परित: आम्रवृक्षाः सन्ति।
(क) तडागम्
(ख) तडागेन
(ग) तडागे
(घ) तडागाय
उत्तर:
(क) तडागम्

9. ……….. नमः।
(क) शिवम्
(ख) शिवाय
(ग) शिवात्
(घ) शिवस्य
उत्तर:
(ख) शिवाय

प्रश्न 5.
अधोलिखितेभ्यः शुद्धं पदं चित्वा रिक्तस्थानानि पूरयत।
(नीचे दिए गए शब्दों में से उचित शब्द चुनकर रिक्त स्थानों की पूर्ति कीजिए।)
(Fill in the blanks with the suitable word choosing from the given words.)

1. अलम् ……………
(क) कोलाहलं
(ख) कोलाहलेन
(ग) कोलाहलात्
(घ) कोलाहलस्य
उत्तर:
(ख) कोलाहलेन

2. धिक ……..
(क) असत्यवादिने
(ख) असत्यवादिनम्
(ग) असत्यवादिन्
(घ) असत्यवादी
उत्तर:
(ख) असत्यवादिनम्

3. …….. मिष्ठान्नं रोचते।
(क) बालकं
(ख) बालकाय
(ग) बालकस्य
(घ) बालके
उत्तर:
(ख) बालकाय

4. सः बालकः …………. समया उपतिष्ठति।
(क) पुस्तकस्य
(ख) पुस्तकम्
(ग) पुस्तकेन
(घ) पुस्तकात्
उत्तर:
(ख) पुस्तकम्

5. माता …… स्निह्यति।
(क) पुत्रे
(ख) पुत्रम्
(ग) पुत्रेण
(घ) पुत्रात्
उत्तर:
(क) पुत्रे

6. अध्यापकः …………. विश्वसिति।
(क) छात्रम्
(ख) छात्रे
(ग) छात्रेण
(घ) छात्रात्
उत्तर:
(ग) छात्रेण

7. संसारे ……….. विना न ज्ञानम्।
(क) गुरुणा
(ख) गुरौ
(ग) गुरोः
(घ) गुरवे
उत्तर:
(क) गुरुणा

8. मृगः ………… प्रति धावति।
(क) ग्रामम्
(ख) ग्रामात्
(ग) ग्रामाय
(घ) ग्रामस्य
उत्तर:
(क) ग्रामम्

9. सा ……….. कुशला अस्ति।
(क) नृत्यम्
(ख) नृत्ये
(ग) नृत्येण
(घ) नृत्यस्य
उत्तर:
(ख) नृत्ये

10. धिक् …………. यः सीताम् अहरत् ।
(क) रावणम्
(ख) रावणेन
(ग) रावणाय
(घ) रावणः
उत्तर:
(क) रावणम्

11. अध्यापकः …………… कुप्यति।
(क) छात्राय
(ख) छात्रम्
(ग) छात्रेण
(घ) छात्रस्य
उत्तर:
(क) छात्राय

12. अलम् अति ………..
(क) वदनात्
(ख) वदनेन
(ग) वदनाय
(घ) वदनम्
उत्तर:
(ख) वदनेन

13. अध्यापकः ………………. प्रति अकथयत्।
(क) देवम्
(ख) देवेन
(ग) देवाय
(घ) देवात्
उत्तर:
(क) देवम्

14. अलम् वृथाः
(क) रोदनेन
(ख) रोदनात्
(ग) रोदनाय
(घ) रोदनात्
उत्तर:
(क) रोदनेन

15. तं …….. समया सुन्दरम् उद्यानं वर्तते।
(क) विद्यालयात्
(ख) विद्यालयम्
(ग) विद्यालयस्य
(घ) विद्यालये
उत्तर:
(ख) विद्यालयम्

16. बाल: …………… निकषा गच्छति।
(क) मातुः
(ख) मातरम्
(ग) माता
(घ) मात्रा
उत्तर:
(ख) मातरम्

17. कुत्र ………. विना जीवनम्?
(क) वायुना
(ख) वायोर
(ग) वायवे
(घ) वायौ
उत्तर:
(क) वायुना

18. ………. विना न जीवनम्।
(क) विद्यायाः
(ख) विद्यायै
(ग) विद्याम्
(घ) विद्यया
उत्तर:
(ग) विद्याम्

19. त्वं ………… निकषा गच्छसि?
(क) कस्य
(ख) कम्
(ग) किम्
(घ) केन
उत्तर:
(ख) कम्

20. ……….. विना जीवानां जीवनम् वृथा अस्ति।
(क) जलस्य
(ख) जलम्
(ग) जलेन
(घ) जलाय
उत्तर:
(ख) जलम्

21. धिक् तान् …………….. ।
(क) राक्षसाः
(ख) राक्षसान्
(ग) राक्षसेभ्यः
(घ) राक्षसैः
उत्तर:
(ख) राक्षसान्

22. अध्यापकः ………. स्निह्यति।
(क) छात्राय
(ख) छात्रे
(ग) छात्रेण
(घ) छात्रम्
उत्तर:
(ख) छात्रे

23. धिक् एतान् …………..
(क) जाल्मेभ्यः
(ख) जाल्मान्
(ग) जाल्मैः
(घ) जाल्मानाम्
उत्तर:
(ख) जाल्मान्

24. अलम् अनेन …………..|
(क) कथनम्
(ख) कथनेन
(ग) कथनाय
(घ) कथने
उत्तर:
(ख) कथनेन

25. त्वम् अधुना विना कथं पठिष्यसि?
(क) पुस्तकस्य
(ख) पुस्तकम्
(ग) पुस्तके
(घ) पुस्तकाय
उत्तर:
(ख) पुस्तकम्

प्रश्न 6.
अधः संवादे कोष्ठकगतशब्देष उचितविभक्तिं प्रयुज्य वाक्यानि पुरयत।
(नीचे लिखे संवाद में कोष्ठक के शब्दों में उचित विभक्ति का प्रयोग करके वाक्यों को पूरा कीजिए।)
Complete the sentences by using the suitable inflexion of the words from the brackets in the following dialogue.)
(i) प्रभा — दीपक! किम् त्वमपि ……….. (हरिद्वार) प्रति चलसि?
(ii) रमेशः – अतिशोभनम् ………….. (स्वाध्याय) मा प्रमदितव्यम्। (सहसा अध्यापक: आगच्छति वदति च अलम् …………… (वार्तालाप)
(iii) माला – रमेश! किं त्वमपि …………… (कश्मीर) प्रति चलसि?
उत्तर:
(i) हरिद्वार
(ii) स्वाध्यायात्, वार्तालापेन
(ii) कश्मीरं।

कारक के उदाहरण |
कारक – उपपद विभक्तीनां प्रयोगः

प्रयच्छ — मह्यम् तण्डुलमूल्यं प्रयच्छ।
कृते — अहं तव कृते सोपानम् उत्तारयामि।
स्वर्णमयेन सोपानेन — स्वर्णमयेन सोपानेन अहम् आगच्छामि।
प्रति — सः माम् प्रति आगच्छति।
अन्तिकम् (षष्ठी) — सः पितुः अन्तिकम् अगच्छत्।
न्यवेदयत् (द्वितीया) — पुत्रः पितरं न्यवेदयत्।
आज्ञया (तृतीया/करणकारक) पुत्रः पितुः — आज्ञया गृहम् अगच्छत्।
उपसर्पतः — श्वसुरौ विमलाम् उपसर्पतः।
शपामि — अहं गुरुः ईश्वरेण शपामि।
महानसम् — माता पुत्रीम महानसम् आनयति।
सप्राणपणम् — ते सर्वे सप्राणपणम् कार्यं कुर्वन्ति।
सह — पुरुषनिरीक्षकेण सह सोमप्रभा प्रविशति।
उप+चर् — वयम् एनाम् उपचरामः।
नि+दिश् — निरीक्षकः सोमप्रभां निर्दिश्य कथयति।

कारक एवं उपपदविभक्तीनां प्रयोगः

1. नेश्वरैरगुणैः समः!
अत्र समः कारणेन गुणैः शब्दे तृतीया विभक्तिः अस्ति।
सह साकं, साधु, समं इन शब्दों के कारण तृतीया विभक्ति का प्रयोग होता है।

2. मरालैः सह हंसाः क्रीडन्ति।
अत्र ‘सह’ कारणेन मरालैः शब्दे तृतीया विभक्तिः अस्ति ।
सह, साकं, सार्धं, समं, विना तथा अंगविकार के कारण शब्दों में तृतीया विभक्ति का प्रयोग होता है।

3. सह-तेन सह केलिभिः कालं क्षेप्तुं कोऽपि न आसीत्।
अत्र सह कारणेन ‘तेन’ शब्दे तृतीया विभक्तिः अस्ति ।

4. अलं स्वच्छन्दप्रलापेन!
अत्र अलम् कारणेन प्रलापेन शब्दे तृतीया विभक्ति अस्ति।

5. गम्यतामनेन सार्धम्।
अत्र सार्धं कारणेन अनेन शब्दे तृतीया विभक्ति अस्ति।

6. तेन अभ्यागतेन सह प्रस्थितः।
अत्र सह कारणेन अभ्यागतेन शब्दे तृतीया विभक्ति अस्ति।

7. मे शिशुः यः त्वया सह नदीं गतः।
अत्र गम् धातु कारणेन नदी शब्दे द्वितीया विभक्ति अस्ति।

8. नदीतटात् स श्येनेन हतः।
जब किसी के द्वारा कोई काम होता है तो तृतीया विभक्ति का प्रयोग होता है। यहाँ हतः के कारण श्येन शब्द में
तृतीया विभक्ति प्रयुक्त भक्ति हुआ है।

9. अलमलं तव श्रमेण।
अत्र अलमलं कारणेन श्रमेण शब्दे तृतीया विभक्तिः अस्ति ।

10. लिप्यक्षरज्ञानं विना केवलं तपोभिः कथं विद्यां प्राप्नोसि?
विना कारणेन ज्ञानं शब्दे द्वितीया वि० अस्ति।

11. अक्षरज्ञानं विनैव वैदुष्यम् अवाप्तुं इच्छसि।
अत्र विना कारणेन अक्षरज्ञानं शब्दे द्वितीया विभक्तिः अस्ति।

12. “नमः एतेभ्यः “।
अत्र नमः कारणाय ‘एतेभ्यः’ शब्दे चतुर्थी विभक्तिः प्रयुक्ता।

13. अलमलं तव श्रमेण।।
अत्र अलमलं कारणेन श्रमेण शब्दे तुतीया विभक्तिः अस्ति ।

14. लिप्यक्षरज्ञानं विना केवलं तपोभिः कथं विद्यां प्राप्नोसि?
अत्र विना कारणेन ज्ञानं शब्दे द्वितीया वि० अस्ति।

15. अक्षरज्ञानं विनैव वैदुष्यम् अवाप्तुम् इच्छसि।
अत्र विना कारणेन अक्षरज्ञानं शब्दे द्वितीया विभक्तिः अस्ति।

We have given detailed NCERT Solutions for Class 9 Sanskrit Grammar Book धातुरूपाणि Questions and Answers come in handy for quickly completing your homework.

Sanskrit Vyakaran Class 9 Solutions धातुरूपाणि

पाठ्यपुस्तकस्य (व्याकरणवीथिः) अभ्यासकार्यम्।

प्रश्न 1.
कोष्ठके प्रदत्तधातोः निर्दिष्टलकारे समुचितप्रयोगेणं वाक्यानि पूरयत
(i) बालकाः पुस्तकानि …………………। (पठ् – लट)
(ii) पुस्तकानि पठित्वा ते विद्वांसः …………………। (भू – लुट्)
(iii) यूयम् उद्याने कदा …………………। (क्रीड् – लङ्)
(iv) किम् आवाम् अद्य …………………। (भ्रम् – लोट)
(v) त्वम् ध्यानेन पाठं …………………। (पठ् – विधिलिङ्)
(vi) साधवः तपः …………………। (तप् – लट)
(vii) वयम् उत्तमान् अङ्कान् …………………। (लम् – लुट्)
(viii) नाटकं दृष्ट्वा सर्वे …………………। (मुद् – लङ)
(ix) पितरं वार्धक्ये पुत्रः अवश्यं …………………। (सेव् – लोट)
(x) हे प्रभो! संसारे कोऽपि भिक्षां न …………………। (याच् – विधिलिङ)
उत्तर:
(i) बालकाः पुस्तकानि पठन्ति।
(ii) पुस्तकानि पठित्वा ते विद्वांसः भविष्यन्ति।
(iii) यूयम् उद्याने कदा अक्रीडत।
(iv) किम् आवाम् अद्य भ्रमाव।
(v) त्वम् ध्यानेन पाठं पठेः।
(vi) साधवः तपः तपन्ति।
(vii) वयम् उत्तमान् अङ्कान् लप्स्यामहे।
(viii) नाटकं दृष्ट्वा सर्वे अमोदन्त।
(ix) पितरं वार्धक्ये पुत्रः अवश्यं सेवताम्।
(x) हे प्रभो! संसारे कोऽपि भिक्षां न याचेत।

प्रश्न 2.
कोष्ठकात् समुचितं क्रियापदं चित्वा वाक्यानि पूरयत
(i) अद्य युवाम् विद्यालयं किमर्थं न …………………। ? (अगच्छताम्/अगच्छतम्/अगच्छत)
(ii) पुरा जनाः संस्कृतभाषया …………………। (भाषन्ते/भाषामहे/अभाषन्त)
(iii) युयम् कं पाठम् ………………… ? (अपठत/अपठत्/अपठन्)
(iv) जीवोः सर्वेऽत्र …………………। भावयन्तः परस्परम्। (मोदताम्/मोदेताम्/मोदन्ताम्)
(v) कक्षायाम् सर्वे ध्यानेन ……………… । (पठतु/पठताम्/पठन्तु)
(vi) प्रभो! मह्यम् बुद्धिम् । ………. । (यच्छ/यच्छतम्/यच्छत)
(vii) वयं सदैव सुधीराः सुवीराः च …………………। (भवेव/भवेम/भवेयम्)
(viii) त्वं सायं कुत्र ………………..। ? (गमिष्यसि/गमिष्यय/गमिष्यथ)
(ix) विद्वान् सर्वत्र …………………। (पूज्यन्ते/पूज्येते/पूज्यते)
(x) अद्यत्वे समाचारपत्रस्य महत्वं सर्वे …………………। (जानाति/जानन्ति/जानासि)
उत्तर:
(i) अद्य युवाम् विद्यालयं किमर्थं न अगच्छतम्?
(ii) पुरा जनाः संस्कृतभाषया अभाषन्त।
(iii) यूयम् कं पाठम् अपठत?
(iv) जीवाः सर्वेऽत्र मोदन्ताम् भावयन्तः परस्परम्।
(v) कक्षायाम् सर्वे ध्यानेन पठन्तु।
(vi) प्रभो! मह्यम् बुद्धिम् यच्छ।
(vii) वयं सदैव सुधीराः सुवीराः च भवेम।
(viii) त्वं सायं कुत्र गमिष्यसि?
(ix) विद्वान् सर्वत्र पूज्यते।।
(x) अद्यत्वे समाचारपत्रस्य महत्वं सर्वे जानन्ति।

अतिरिक्तं कार्यम्

प्रश्न 1.
अधःप्रदत्तेषु धातुरूपेषु उचितैः धातुरूपैः रिक्तस्थानानि पूरयत।
(नीचे दिए गए धातु रूपों में से उचित धातुओं से रिक्त स्थानों की पूर्ति कीजिए।)
(Fill in the blanks with suitable verb-stems from the following words.)

1. स: नायकः ……………. (अस्-लङ्)
(क) अस्ति
(ख) आसीत्
(ग) भविष्यति
(घ) अस्तु
उत्तर:
(ख) आसीत्

2. त्वम् का ………..? (अस्-लट)
(क) असि
(ख) स्मः
(ग) स्थ
(घ) अस्ति
उत्तर:
(क) असि

3. भारतम् प्रगतिम् ………… (कृ-लुट)
(क) करोतु
(ख) करिष्यतः
(ग) करिष्यति
(घ) करिष्यथः
उत्तर:
(ग) करिष्यति

4. छात्राः पुस्तकानि ………….. (पठ्–लट)
(क) पठन्ति
(ख) पठन्तु
(ग) पठिष्यन्ति
(घ) पठेयुः
उत्तर:
(क) पठन्ति

5. त्वम् ह्यः कुत्र …………… (अस्-लङ्)
(क) आसीत्
(ख) आस्त
(ग) आसी:
(घ) आस्म
उत्तर:
(ग) आसी:

6. सः तत्र न……….. (पठ्-लङ्)
(क) अपठः
(ख) अपठत्
(ग) अपठत
(घ) अपठतम्
उत्तर:
(ख) अपठत्

7. माता पुत्र सेवाम् ……………. (कृ-लट)
(क) करोति
(ख) करोसि
(ग) करोतु
(घ) कुर्यात्
उत्तर:
(क) करोति

8. सेवकः स्वामिनम् ……….। (सेव्–लट्)
(क) सेवसे
(ख) सेवति
(ग) सेवते
(घ) सेवेथे
उत्तर:
(ग) सेवते

प्रश्न 2.
स्थूलपदानि आधुत्य उचितं लकारं लिखत।।
(मोटे शब्दों को आधार मानकर उचित लकार लिखिए।)
(Write original letter of the bold words.)

1.स्थानानि दर्शनीयानि सन्ति।
(क) लङ्
(ग) लट
(घ) लृट्
उत्तर:
(ग) लट

2. अत्र किम् आसीत् ?
(क) लङ्
(ख) लोट
(ग) लट्
(घ) लृट्
उत्तर:
(क) लङ्

3. सेवकाः सेवन्ते।
(क) लोट
(ख) लङ्
(ग) लुट्
(घ) लट्
उत्तर:
(घ) लट्

4. तत्र किम् भविष्यति?
(क) विधिलिङ्
(ख) लृट्
(ग) लट्
(घ) लङ्
उत्तर:
(ख) लृट्

5. यूयं रसं पास्यथ।
(क) लङ्
(ख) लट्
(ग) लृट्
(घ) लोट
उत्तर:
(ग) लृट्

6. सः पुस्तकं पठति।
(क) लट
(ख) लोट
(ग) लङ्
(घ) लृट्
उत्तर:
(क) लट

7. तौ राजानम् असेवताम्।
(क) लट्
(ख) विधिलिङ्
(ग) लङ्
(घ) लोट
उत्तर:
(ग) लङ्

8. त्वं गीतां पठ।
(क) लङ्
(ख) लोट
(ग) लृट्
(घ) विधिलिङ्
उत्तर:
(ख) लोट

9. युवाम् अमृतं पिबताम्।
(क) लट्
(ख) लङ्
(ग) लृट्
(घ) लोट
उत्तर:
(घ) लोट

10. सः राजानं सेवेत।
(क) लट्
(ख) लङ्
(ग) विधिलिङ्
(घ) लोट
उत्तर:
(ग) विधिलिङ्

11. अहं शास्त्रं पठेयम्। ___
(क) विधिलिङ्
(ख) लङ्
(ग) लट
(घ) लोट
उत्तर:
(क) विधिलिङ्

12. शिशुः असि खलु त्वम्। ___
(क) लोट
(ख) लट्
(ग) लङ्
(घ) लृट्
उत्तर:
(ख) लट्

13. युवां शान्तौ आस्ताम्।
(क) लङ्
(ख) लोट
(ग) लृट
(घ) विधिलिंङ्
उत्तर:
(क) लङ्

14. युवां धार्मिकौ भविष्यथः।
(क) लट्
(ख) लोट्
(ग) लुट
(घ) विधिलिंङ्
उत्तर:
(ग) लुट

15. सः प्रियदर्शी स्यात्।
(क) विधिलिङ्
(ख) लोट
(ग) लृट
(घ) लुट
उत्तर:
(क) विधिलिङ्

प्रश्न 3.
निम्नस्थूलपदानां शुद्धं वचनम् अधस्तात् पदेभ्यः चित्वा लिखत।
(निम्न मोटे छपे शब्दों के वचन नीचे लिखे पदों में से चुनकर लिखिए।)
(Write original letter of the bold words.)

1. तौ जलं पिबतः।
(क) एकवचनम्
(ख) द्विवचनम्
(ग) बहुवचनम्
उत्तर:
(ख) द्विवचनम्

2. तन्तुवायः कवितां करोति।
(क) एकवचनम्
(ख) द्विवचनम्
(ग) बहुवचनम्
उत्तर:
(क) एकवचनम्

3. सः राजानं सेवेत।
(क) एकवचनम्
(ख) द्विवचनम्
(ग) बहुवचनम्
उत्तर:
(क) एकवचनम्

4. अहं बद्ध परिकरः अस्मि।
(क) द्विवचनम्
(ख) एकवचनम्
(ग) बहुवचनम्
उत्तर:
(ख) एकवचनम्

5. त्वं रामायणम् अपठः।
(क) बहुवचनम्
(ख) एकवचनम्
(ग) बहुवचनम्
उत्तर:
(ख) एकवचनम्

6. युवाम् अमृतम् पिबतम्।
(क) बहुवचनम्
(ख) द्विवचनम्
(ग) एकवचनम्
उत्तर:
(ख) द्विवचनम्

7. सज्जनः अमित्रमपि उपकरोति।
(क) एकवचनम्
(ख) द्विवचनम्
(ग) बहुवचनम्
उत्तर:
(क) एकवचनम्

8. वयं विद्यालये अस्मि।
(क) बहुवचनम्
(ख) एकवचनम्
(ग) द्विवचनम्
उत्तर:
(क) बहुवचनम्

9. सज्जनाः पीडितान् सेवन्ते।
(क) एकवचनम्
(ख) द्विवचनम्
(ग) बहुवचनम्
उत्तर:
(क) एकवचनम्

10. ते सुखिनो भविष्यतः।
(क) एकवचनम्
(ख) बहुवचनम्
(ग) द्विवचनम्
उत्तर:
(ख) बहुवचनम्

11. युवाम् उद्यामिनौ स्याताम्।
(क) द्विवचनम्
(ख) बहुवचनम्
(ग) एकवचनम्
उत्तर:
(क) द्विवचनम्

12. त्वम् पठसि।
(क) एकवचनम्
(ख) द्विवचनम्
(ग) बहुवचनम्
उत्तर:
(क) एकवचनम्

प्रश्न 4.
अधोलिखिते कोष्ठके उचितधातुरूपैः सह वाक्यानि पूरयत।
(नीचे लिखे कोष्ठक में उचित धातु रूपों से वाक्य को पूरा कीजिए।)
(Complete the sentence with the following suitable verb-stems given in bracket.)
(i) कानने चत्रत्रः चटका: ….. (अस् + लङ्)
(ii) शिशवः दुग्धं ……….. (पा + विधिलिङ्)
(iii) तौ अधुना कि ……….. (कृ + लृट्)
(iv) त्वं परिश्रमी ……….. (अस् + विधिलिङ्)
(v) भारते कोऽपि शिक्षाविहीनः न …… (अस् + लङ)
(vi) तौ मधुरभाषिणौ ……….. (अस् + विधिलिङ्)
(vii) राष्ट्रभक्ताः एव देशस्य उन्नतिम् ……. (कृ + लट)
(viii) भारतं शक्तिसम्पन्नः देशः ……….. (अस् + लट)
उत्तर:
(i) आसन्
(ii) पिबेयुः
(ii) करिष्यावः
(iv) स्याः
(v) आसीत्
(vi) आस्ताम्
(vii) कुर्वन्ति
(viii) अस्ति

प्रश्न 5.
अधोलिखितेषु वाक्येषु कोष्ठकेषु प्रदत्तेन क्रियापदेन रिक्तस्थानं पूरयत।
(नीचे लिखे वाक्यों में कोष्ठकों में दिए गए क्रिया के उचित शब्दों से खाली स्थान भरिए।)
(Fill in the blanks of the following sentences with the suitable form of the bracket verb.)

(i) अहम् एकः छिन्नः द्रुमः ………… | (अस्-लट्लकारे)
(क) आसी:
(ख) अस्मि
(ग) अस्तु
(घ) स्तम्
उत्तर:
(ख) अस्मि

(ii) पुस्तकैः कि………………… (कृ-लुटलकारे)
(क) करिष्यति
(ख) करिष्यामि
(ग) करिष्यतः
(घ) करिष्यसि
उत्तर:
(घ) करिष्यसि

(iii) ह्यः मम गृहे विवाहोत्सवः ………….. (अस्-लङ्लकारे)
(क) आसीत्
(ख) अस्ति
(ग) आस्ताम्
(घ) आसन्
उत्तर:
(क) आसीत्

(iv) सः पुस्तकम् …………… (पल्-लट्लकारे)
(क) पठ्येत
(ख) पठन्ति
(ग) पठति
(घ) पठसि
उत्तर:
(ग) पठति

(v) राजकुमारौ उटजे न …………. (अस्-लट्लकारे)
(क) आसीत्
(ख) सन्तु
(ग) स्तः
(घ) आसम्
उत्तर:
(ग) स्तः

(vi) शिशुः दुग्धं ………. (पा-लुट्लकारे)
(क) पिबिष्यति
(ख) पास्यतः
(ग) पास्यति
(घ) पिबिष्यसि
उत्तर:
(ग) पास्यति

(vii) भोजः एकः प्रतापी राजा …… (अस्-लङ्लकारे)
(क) अस्ति
(ख) अभवत्
(ग) आसीत्
(घ) भविष्यति
उत्तर:
(ग) आसीत्

(viii) मोहनः नवमकक्षायाः छात्रः ……. (अस् धातु-लट्लकारे)
(क) अस्ति
(ख) आसीत्
(ग) भविष्यति
(घ) अस्तु
उत्तर:
(क) अस्ति

(ix) अहं कार्यरतः ………… (अस्-लङ्लकारे)
(क) आस्व
(ख) आसम्
(ग) आस्व
(घ) आसी:
उत्तर:
(ख) आसम्

(x) श्वः रविवासरः …………….. | (भू धातु-लुट्लकारे)
(क) आसीत्
(ख) अस्ति
(ग) भवेत्
(घ) भविष्यति
उत्तर:
(घ) भविष्यति

प्रश्न 6.
कोष्ठकात् मूलधातुं गृहीत्वा तस्य उचितधातुरूपैः वाक्यानि पूरयत।
(कोष्ठक से मूल धातु लेकर उसके उचित धातु रूपों से वाक्यों को पूरा कीजिए।)
(Complete the sentences with the suitable verb-stems from the bracket.)
(i) आवाम् स्वास्थौ ………… (अस, विधिलिङ्)
(ii) सेवकाः भृशं प्रयत्न …….. (कृ, लट)
(iii) ते पुस्तकम् ………… (पठ, लट्)
(iv) सः गुरुजनान् ………… (सेव्, लुट्)
उत्तर::
(i) स्याव
(ii) कुर्वन्ति
(iii) पठतः
(iv) सेविष्यते

प्रश्न 7.
निम्न रेखाङ्कितानाम् क्रियाणाम् उचितं वचनं लिखत।
(निम्न रेखांकित क्रियाओं के उचित वचन लिखिए।
Write suitable number of underline verbs.)
(i) वयं कुत्र स्मः?
(ii) त्वम् पठसि।
(ii) सः गुरुजनान् सेविष्यते।
(iv) यूयम् स्वकार्यं अकुरुत।
उत्तर::
(i) बहुवचनम्
(ii) एकवचनम्
(iii) एकवचनम्
(iv) बहुवचनम्

प्रश्न 8.
कोष्ठकात् मूलधातुं गृहीत्वा तस्य उचितधातु रूपै वाक्यानि पूरयत।
(कोष्ठक से मूलधातु लेकर उसके उचित धातु रूपों से वाक्य को पूरा कीजिए।)
(Complete the sentences with the suitable verb-stems form the bracket.)

1. सञ्जयः कस्मिन् विद्यालये ………? (पठ्-लङ्)
(क) अपठत्
(ख) पठति
(ग) पठिष्यति
(घ) पठतु
उत्तर:
(क) अपठत्

2. धृतराष्ट्रस्य शतं पुत्राः …………। (अस्-लङ)
(क) आसीत्
(ख) आस्ताम्
(ग) आसन्
(घ) आसी:
उत्तर:
(ग) आसन्

3. त्वम् दुग्धं किमर्थं न ………… । (पा-विधिलिङ्)
(क) पिबेत
(ख) पिबेः
(ग) पिबेताम्
(घ) पिबेम्
उत्तर:
(ख) पिबेः

4. बालकाः कोलाहलम् न …. ……….(कृ-लोट)
(क) कुर्वन्तु
(ख) कुरुतु
(ग) करोतु
(घ) कुर्युः
उत्तर:
(क) कुर्वन्तु

5. युवाम् संस्कृतम् ………….। (पठ्-लोट)
(क) पठतु
(ख) पठेताम्
(ग) पठतम्
(घ) पठताम्
उत्तर:
(ग) पठतम्

6. तौ माता-पितरौ प्रणाम …। (कृ-लोट)
(क) कुरुत
(ख) कुरुः
(ग) कुरुताम्
(घ) कुरुतः
उत्तर:
(ग) कुरुताम्

7. त्वम् प्रतिदिनं फलरसं ………। (पा—विधिलिङ्)
(क) पिबेः
(ख) पिबेत
(ग) पिबेसु
(घ) पिबताम्
उत्तर:
(क) पिबेः

8. वयम् प्रातः व्यायाम ………………… । (कृ-विधिलिङ्)
(क) कुर्यात
(ख) कुर्याः
(ग) कुर्याताम्
(घ) कुर्याम
उत्तर:
(घ) कुर्याम

9. युवाम् स्वपाठान् …………. । (पठ्-विधिलिङ)
(क) पठेतम्
(ख) पठेताम्
(ग) पठेयुः
(घ) पठेत
उत्तर:
(क) पठेतम्

10. कार्यम् अधुना एव …….। (कृ-विधि)
(क) कुर्यात्
(ख) कुर्यात
(ग) कुर्युः
(घ) करवाणि
उत्तर:
(क) कुर्यात्

11. चत्वारि दिनानि यावत् त्वं कुत्र …… । (अस्-लङ्)।
(क) आस्ताम्
(ख) आसीत्
(ग) आस्व
(घ) आसी:
उत्तर:
(घ) आसी:

12. श्रवणः पितरं ………..। (सेव्–लट)
(क) सेवामहे
(ख) सेवेथे
(ग) सेवते
(घ) सेवावहे
उत्तर:
(ग) सेवते

13. अहं दुग्धं न …………. (पा-लुट)
(क) पास्यसि
(ख) पास्यामि
(ग) पास्यतः
(घ) पास्यथ
उत्तर:
(ख) पास्यामि

14. भारतं ग्रामाणां देशः …………….. । (अस्-लट्)
(क) अस्ति
(ख) असि
(ग) अस्मि
(घ) सन्ति
उत्तर:
(क) अस्ति

15. शिष्टाः बालकाः सदा अध्यापकान् … (सेव-लट)
(क) सेवथे
(ख) सेवन्ते
(ग) सेवसे
(घ) सेवावहे
उत्तर:
(ख) सेवन्ते

प्रश्न 9.
स्थूलपदानि आधृत्य उचितं लकारं लिखत।
(मोटे शब्दों को आधार मानकर उचित लकार लिखिए।)
(Write original letter of the bold words.)

1. त्वम् मम मित्रम् असि।
(क) लोट
(ख) लट
(ग) विधिलिङ्
(घ) लृट।
उत्तर:
(ख) लट

2. बालकाः कोलाहलम् न कुर्वन्तु।
(क) लोट
(ख) लृट्
(ग) लट्
(घ) विधिलिङ
उत्तर:
(ग) लट्

3. तौ जलं पिबतः।
(क) लोट
(ख) विधिलिङ्
(ग) लट्
(घ) लृट्
उत्तर:
(ग) लट्

4. लोभं मा कुरुत।
(क) विधिलिङ्
(ख) लोट
(ग) लट
(घ) लङ्
उत्तर:
(ख) लोट

5. बालकाः पठन्तु।
(क) लोट
(ख) विधिलिङ्
(ग) लट्
(घ) लृट
उत्तर:
(क) लोट

प्रश्न 10.
निम्न स्थूलपदानां शुद्धं वचनम् अधस्तात् पदेभ्यः चित्वा लिखत।।
(निम्न मोटे छपे शब्दों के वचन नीचे लिखे पदों में से चुनकर लिखिए।)
(Write original letter of the bold words.)

1. त्वं रामायणम् अपठः।
(क) द्विवचनम्
(ख) एकवचनम्
(ग) बहुवचनम्
उत्तर:
(ख) एकवचनम्

2. राष्ट्रसवको असाव।
(क) द्विवचनम्
(ख) बहुवचनम्
(ग) एकवचनम्
उत्तर:
(क) द्विवचनम्

3. कम् अध्यायम् पठसि।
(क) द्विवचनम्
(ख) बहुवचनम्
(ग) एकवचनम्
उत्तर:
(ग) एकवचनम्

4. भारते अशोकः नाम्ना नृपः आसीत्।
(क) द्विवचनम्
(ख) एकवचनम्
(ग) बहुवचनम्
उत्तर:
(ख) एकवचनम्

5. निजकार्यं कुरु।
(क) बहुवचनम्
(ख) एकवचनम्
(ग) द्विवचनम्
उत्तर:
(ख) एकवचनम्