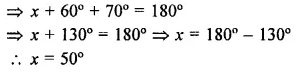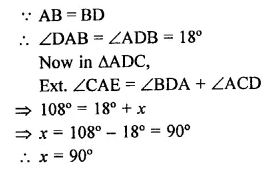Tag: Class 9 Maths RD Sharma Solutions

RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.1

Other Exercises

• RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.1
• RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.2
• RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.3
• RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.4
• RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS
• RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables MCQS

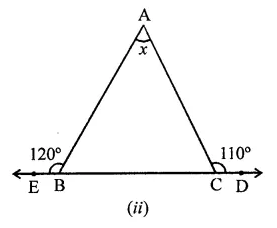
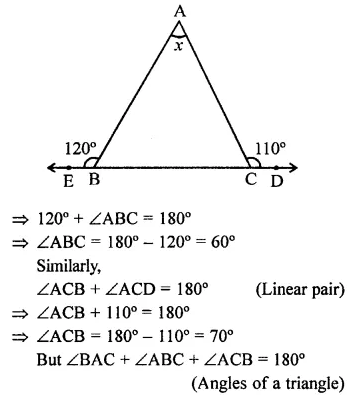
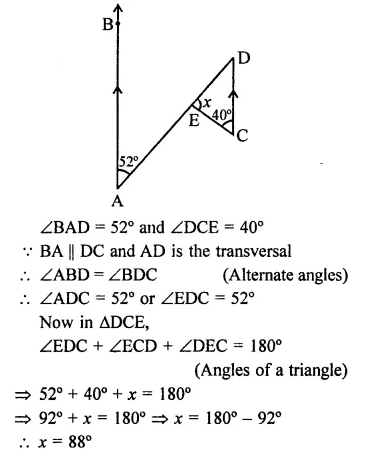
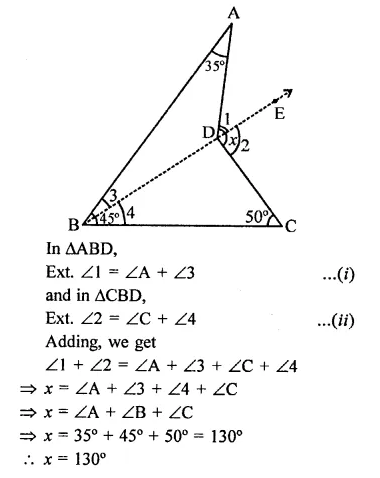
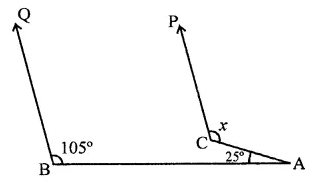
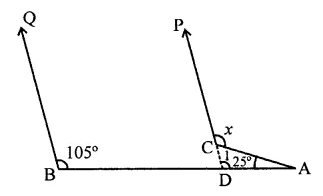
Question 1.
Three angles of a quadrilateral are respectively equal to 110°, 50° and 40°. Find its fourth angle.
Solution:
Sum of four angles of a quadrilateral = 360°
Three angles are = 110°, 50° and 40°
∴ Fourth angle = 360° – (110° + 50° + 40°)
= 360° – 200° = 160°

Question 2.
In a quadrilateral ABCD, the angles A, B, C and D are in the ratio 1 : 2 : 4 : 5. Find the measures of each angle of the quadrilateral.
Solution:
Sum of angles of a quadrilateral ABCD = 360°
Ratio in angles = 1 : 2 : 4 : 5
Let first angle = x
Second angle = 2x
Third angle = 4x
and fourth angle = 5x
∴ x + 2x + 4x + 5x = 360°
⇒ 12x = 360° ⇒ x = \(\frac { { 360 }^{ \circ } }{ 12 }\)  = 30°
∴ First angle = 30°
Second angle = 30° x 2 = 60°
Third angle = 30° x 4 = 120°
Fourth angle = 30° x 5 = 150°

Question 3.
The angles of a quadrilateral are in the ratio 3 : 5 : 9 : 13. Find all the angles of the quadrilateral. [NCERT]
Solution:
Sum of four angles of a quadrilateral = 360°
Ratio in the angles = 3 : 5 : 9 : 13
Let first angle = 3x
Then second angle = 5x
Third angle = 9x
and fourth angle = 13x
∴ 3x + 5x + 9x+ 13x = 360°
⇒ 30x = 360°
⇒ x = \(\frac { { 360 }^{ \circ } }{ 30 }\) = 12°
∴ First angle = 3x = 3 x 12° = 36°
Second angle = 5x = 5 x 12° = 60°
Third angle = 9x = 9 x 12° = 108°
Fourth angle = 13 x 12° = 156°

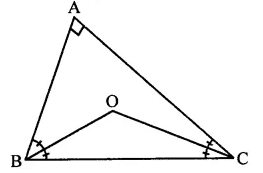
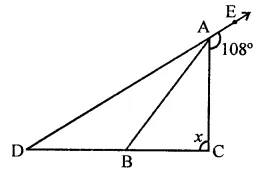
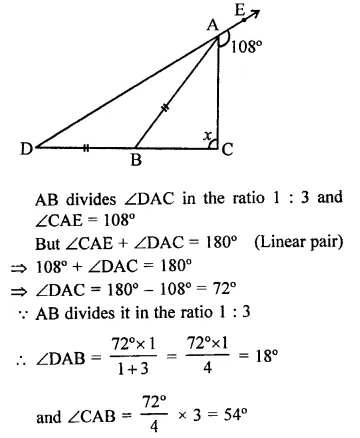
Question 4.
In a quadrilateral ABCD, CO and DO are the bisectors of ∠C and ∠D respectively.
Prove that ∠COD = \(\frac { 1 }{ 2 }\) (∠A + ∠B).
Solution:

 

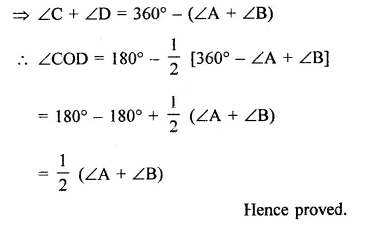
Hope given RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.2

Other Exercises

• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.1
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.2
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.3
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.4
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.5
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.6
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula VSAQS
• RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS

Question 1.
BD and CE are bisectors of ∠B and ∠C of an isosceles ∠ABC with AB = AC. Prove that BD = CE.
Solution:
Given : In ∆ABC, AB = AC
BD and CE are the bisectors of ∠B and ∠C respectively
To prove : BD = CE
Proof: In ∆ABC, AB = AC
∴ ∠B = ∠C (Angles opposite to equal sides)
∴ \(\frac { 1 }{ 2 }\) ∠B = \(\frac { 1 }{ 2 }\) ∠C

∠DBC = ∠ECB
Now, in ∆DBC and ∆EBC,
BC = BC (Common)
∠C = ∠B (Equal angles)
∠DBC = ∠ECB (Proved)
∴ ∆DBC ≅ ∆EBC (ASA axiom)
∴ BD = CE

Question 2.
In the figure, it is given that RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that: ∆RBT = ∆SAT.

Solution:
Given : In the figure, RT = TS
∠1 = 2∠2 and ∠4 = 2∠3
To prove : ∆RBT ≅ ∆SAT
Proof : ∵ ∠1 = ∠4 (Vertically opposite angles)
But ∠1 = 2∠2 and 4 = 2∠3
∴ 2∠2 = 2∠3 ⇒ ∠2 = ∠3
∵ RT = ST (Given)
∴∠R = ∠S (Angles opposite to equal sides)
∴ ∠R – ∠2 = ∠S – ∠3
⇒ ∠TRB = ∠AST
Now in ∆RBT and ∆SAT
∠TRB = ∠SAT (prove)
RT = ST (Given)
∠T = ∠T (Common)
∴ ∆RBT ≅ ∆SAT (SAS axiom)

Question 3.
Two lines AB and CD intersect at O such that BC is equal and parallel to AD. Prove that the lines AB and CD bisect at O.
Solution:
Given : Two lines AB and CD intersect each other at O such that AD = BC and AD \(\parallel\)
BC

To prove : AB and CD bisect each other
i. e. AO = OB and CO = OD
Proof: In ∆AOD and ∆BOC,
AD = BC (Given)
∠A = ∠B (Alternate angles)
∠D = ∠C (Alternate angles)
∴ ∆AOD ≅ ∆BOC (ASA axiom)
AO = OB and AO = OC (c.p.c.t.)
Hence AB and CD bisect each other.

Hope given RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.2

Other Exercises

• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.1
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.2
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.3
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.4
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency VSAQS
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency MCQS

Question 1.
Calculate the mean for the following distribution
x 5 6 7 8 9
f 4 8 14 11 3
Solution:

Question 2.
Find the mean of the following data:
x 19 21 23 25 27 29 31
f 13 15 16 18 16 15 13
Solution:

Question 3.
Find the mean of the following distribution:
x 10 12 20 25 35
f 3 10 15 7 5
Solution:

Question 4.
Five coins were simultaneously tossed 1000 times and at each toss the number of heads were observed. The number of tosses during which 0, 1, 2, 3, 4 and 5 heads were obtained are shown in the table below. Find the mean number of heads per toss.

Solution:

Question 5.
The mean of the following data is 20.6. Find the value of p.
x 10 15 p 25 35
f 3 10 25 7 5
Solution:
Mean = 20.6

Question 6.
If the mean of the following data is 15, find p?.
x 5 10 15 20 25
f 6 p 6 10 5
Solution:
Mean = 15

Question 7.
Find the value of p for the following distribution whose mean is 16.6.
x 8 12 15 p 20 25 30
f 12 16 20 24 16 8 4
Solution:
Mean = 16.6

Question 8.
Find the missing value of p for the following distribution whose mean is 12.58.
x 5 8 10 12 p 20 25
f 2 5 8 22 7 4 2
Solution:
Mean = 12.58

Question 9.
Find the missing frequency (p) for the following distribution whose mean is 7.68.
x 3 5 7 9 11 13
f 6 8 15 p 8 4
Solution:
Mean = 7.68

Question 10.
Find the value of p, if the mean of the following distribution is 20.
x 15 17 19 20 + p 23
f    2  3   4     5p     6
Solution:
Mean = 20

Question 11.
Candidates of four schools appear in a mathematics test. The data were as follows:

If the average score of the candidates of all the four schools is 66, find the number of candidates that appeared from school III.
Solution:
Let number of candidates in school III = p
Then total number of candidates in 4 schools = 60 + 48 + p + 40 = 148 + p
Average score of 4 schools = 66
∴Total score = (148 + p) x 66
Now mean score of 60 in school I = 75 .
∴Total = 60 x 75 = 4500
In school II, mean of 48 = 80
∴Total = 48 x 80 = 3840
In school III, mean of p = 55
∴Total = 55 x p = 55p
and in school IV, mean of 40 = 50
∴Total = 40 x 50 = 2000
Now total of candidates of 4 schools = 148 + p
and total score = 4500 + 3840 + 55p + 2000 = 10340 + 55p
∴10340 + 55p = (148 + p) x 66 = 9768 + 66p
=> 10340 – 9768 = 66p – 55p
=> 572 = 11p
∴ p = \(\frac { 572 }{ 11 } \)
Number of candidates in school III = 52

Question 12.
Find the missing frequencies in the following frequency distribution if it is known that the mean of the distribution is 50.
x 10 30 50 70 90
f 17 f1 32 f1 19
Total 120
Solution:
Mean = 50

Hope given RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.1

Other Exercises

• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.1
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.2
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.3
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.4
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency VSAQS
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency MCQS

Question 1.
If the heights of 5 persons are 140 cm, 150 cm, 152 cm, 158 cm and 161 cm respectively. Find the mean height.
Solution:
Heights of 5 persons are 140 cm, 150 cm, 152 cm, 158 cm and 161 cm

Question 2.
Find the mean of 994, 996, 998, 1002 and 1000.
Solution:
Mean of 994, 996, 998, 1002 and 1000

Question 3.
Find the mean of first five natural numbers.
Solution:
First five natural numbers are 1, 2, 3, 4, 5
∴ Mean = \(\overline { x } =\frac { 1+2+3+4+5 }{ 5 } =\frac { 15 }{ 5 } \) = 3

Question 4.
Find the mean all factors of 10.
Solution:
Factors of 10 = 1, 2, 5, 10
∴ Mean = \(\overline { x } =\frac { 1+2+5+10 }{ 4 } =\frac { 18 }{ 4 } \) = 4.5

Question 5.
Find the mean of first 10 even natural numbers.
Solution:
First 10 even natural numbers are 2, 4, 6, 8, 10, 12, 14, 16, 18, 20
∴ Mean = \(\overline { x } =\frac { 2+4+6+8+10+12+14+16+18+20 }{ 10 } =\frac { 110 }{ 10 } \) = 11

Question 6.
Find the mean of x, x + 2, x + 4, x + 6, x + 8.
Solution:
Sum = x + x + 2+ x + 4 + x + 6 + x + 8 = 5x + 20
∴ Mean = \(\overline { x } =\frac { \sum { { x }_{ i } } }{ n } \frac { 5x+20 }{ 5 } =x+4 \)

Question 7.
Find the mean of first five multiples of 3.
Solution:
First 5 multiples of 3 are = 3, 6, 9, 12, 15
∴ Mean = \(\overline { x } =\frac { 3+6+9+12+15 }{ 5 } =\frac { 45 }{ 5 } \) = 9

Question 8.
Following are the weights (in kg) or 10 new born babies in a hospital on a particular day:
3.4, 3.6, 4.2, 4.5, 3.9, 4.1, 3.8, 4.5, 4.4, 3.6. Find the mean \(\overline { X } \).
Solution:
Weights of 10 new bom babies are 3.4, 3.6, 4.2, 4.5, 3.9, 4.1, 3.8, 4.5, 4.4, 3.6
∴ Mean \(\overline { X } \) = \(\frac { 3.4+3.6+4.2+4.5+3.9+4.1+3.8+4.5+4.4+3.6 }{ 10 } \)
= \(\frac { 40.0 }{ 10 } \) = 4kg

Question 9.
The percentage of marks obtained by students of a class in mathematics are : 64, 36, 47, 23, 0, 19, 81, 93, 72, 35, 3, 1. Find their mean.
Solution:
Percentage of 12 students are 64, 36, 47, 23, 0, 19, 81, 93, 72, 35, 3, 1
∴ Mean \(\overline { X } \) = \(\frac { 64+36+47+23+0+19+81+93+72+35+3+1 }{ 12 } \)
= \(\frac { 474 }{ 12 } \) = 39.5

Question 10.
The numbers of children in 10 families of a locality are : 2, 4, 3, 4, 2, 0, 3, 5, 1, 1, 5. Find the mean number of children per family.
Solution:
Number of children in 10 families are 2, 4, 3, 4, 2, 0, 3, 5, 1, 1, 5
∴ Mean \(\overline { X } \) = \(\frac { 2+4+3+4+2+0+3+5+1+1+5 }{ 10 } \)
= \(\frac { 30 }{ 10 } \) = 3

Question 11.
Explain, by taking a suitable example, how the arithmetic mean alters by (i) adding a constant k to each term, (ii) subtracting a constant k from each them, (iii) multiplying each term by a constant k and (iv) dividing each term by a non-zero constant k.
Solution:
Let x1, x2, x3, x4, x5 are five numbers whose mean is \(\overline { x } \) i.e. = \(\frac { x1+x2+x3+x4+x5 }{ 5 } \) = \(\overline { x } \)


Hence we see that in each case, the mean is changed.

Question 12.
The mean of marks scored by 100 students was found to be 40. Later on its was discovered that a score of 53 was misread as 83. Find the correct mean.
Solution:
Mean score of 100 students = 40
∴Total = 100 x 40 = 4000
Difference in one score by mistake = 83 – 53 = 30
Actual total scores = 4000 – 300 = 3970
Actual mean = \(\frac { 3970 }{ 100 } \) = 39.70 = 39.7

Question 13.
The traffic police recorded the speed (in km/hr) of 10 motorists as 47, 53, 49, 60, 39, 42, 55, 57, 52, 48. Later on an error in recording instrument was found. Find the correct average speed of the motorists if the instrument recorded 5 km/hr less in each case.
Solution:
Speed of 10 motorist as recorded = 47, 53, 49, 60, 39, 42, 55, 57, 52, 48
Total of speed of 10 motorists = 47 + 53 + 49 + 60 + 39 + 42 + 55 +57 + 52 + 48 = 502

Question 14.
The mean of five numbers is 27. If one number is excluded, their mean is 25. Find the excluded number.
Solution:
Mean of 5 numbers = 27
Total = 27 x 5 = 135
By excluded one number, then mean of remaining 4 numbers = 25
Total = 4 x 25 = 100
Excluded number = 135 – 100 = 35

Question 15.
The mean weight per student in a group of 7 students is 55 kg. The individual weights of 6 of them (in kg) are 52, 54, 55, 53, 56 and 54. Find the weight of the seventh student.
Solution:
Mean weight of 7 students = 55 kg
Total weight of 7 students = 55 x 7 kg = 385 kg
Total weights of 6 students among them = 52 + 54 + 55 + 53 + 56 + 54 = 324 kg
Weight of 7th student = 385 – 324 = 61 kg

Question 16.
The mean weight of 8 numbers is 15. If each number is multiplied by 2, what will be the new mean?
Solution:
Weight of 8 numbers =15
By multiplying each number by 2, then the average will be = 15 x 2 = 30
New average = 30

Question 17.
The mean of 5 numbers is 18. If one number is excluded, their mean is 16. Find the excluded number.
Solution:
Mean of 5 numbers = 18
Total = 18 x 5 = 90
By excluding one number, the mean of remaining 5 – 1=4 numbers = 16
Total = 16 x 4 = 64
Excluded number = 90 – 64 = 26

Question 18.
The mean of 200 items was 50. Later on, it was discovered that the two items were misread as 92 and 8 instead of 192 and 88. Find the correct mean.
Solution:
Mean of 200 items = 50
Total = 50 x 200 = 10000
The number were misread as 92 instead of 192 and 8 instead of 88
Difference = 192 – 92 + 88 – 8 = 180
New total = 10000 + 180 = 10180
and new mean = \(\frac { 10180 }{ 200 } \) = 50.9

Question 19.
If M is the mean of x1, x2, xr3, x4, x5 and x6, prove that
(x1 – M) + (x2 – M) + (x3 – M) + (x4 – M) + (x5 – M) + (x6 – M) = 0.
Solution:
∵ M is the mean of x,, x2, x3, x4, x5, x6
Then M = \(\frac { x1+x2+x3+x4+x5+x6 }{ 6 } \)

Question 20.
Durations of sunshine (in hours) in Amritsar for first 10 days of August 1997 as reported by the Meteorological Department are given below:
9.6, 5.2, 3.5, 1.5, 1.6, 2.4, 2.6, 8.4, 10.3, 10.9
(i) Find the mean \(\overline { X }\)
(ii) Verify that \( \sum _{ i=1 }^{ 10 }{ \left( { x }_{ i }-\overline { X } \right) } \) = 0
Solution:
Duration of sun shine for 10 days (in hours)
= 9.6, 5.2, 3.5, 1.5, 1.6, 2.4, 2.6, 8.4, 10.3, 10.9

Question 21.
Find the values of n and X in each of the following cases:
(i) \(\sum _{ i=1 }^{ n }{ \left( { x }_{ i }-12 \right) } =-10\quad and\sum _{ i=1 }^{ n }{ \left( { x }_{ i }-3 \right) } =62\)
(ii) \(\sum _{ i=1 }^{ n }{ \left( { x }_{ i }-10 \right) } =30\quad and\sum _{ i=1 }^{ n }{ \left( { x }_{ i }-6 \right) } =150\)
Solution:
(i) \(\sum _{ i=1 }^{ n }{ \left( { x }_{ i }-12 \right) } =-10\)…(i)

Question 22.
The sums of the deviations of a set of n values x1, x2,… xn measured from 15 and -3 are -90 and 54 respectively. Find the value of n and mean.
Solution:
In first case,
(x1 – 15) + (x2 – 15) + (x3 – 15) + … + (xn – 15) = – 90
=> x1 + x2 + x3 + … + xn – 15 x n = – 90

Question 23.
Find the sum of the deviations of the variate values 3, 4, 6, 7, 8, 14 from their mean.
Solution:
Mean of 3, 4, 6, 7, 8, 14 = \(\frac { 42 }{ 6 } \) = 7

Question 24.
If \(\overline { X } \) is the mean of the ten natural numbers x1, x2, x3, …, x10, show that (x1 – \(\overline { X } \)) + (x2 – \(\overline { X } \)) + … + (x10 – \(\overline { X } \)) = 0.
Solution:
\(\overline { X } \) is the mean of 10 natural numbers
x1, x2, x3, …, x10

 

Hope given RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.1

Other Exercises

• RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.1
• RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2
• RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry VSAQS
• RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry MCQS

Question 1.
In a ∆ABC, if ∠A = 55°, ∠B = 40°, find ∠C.
Solution:
∵ Sum of three angles of a triangle is 180°
∴ In ∆ABC, ∠A = 55°, ∠B = 40°
But ∠A + ∠B + ∠C = 180° (Sum of angles of a triangle)

⇒ 55° + 40° + ∠C = 180°
⇒ 95° + ∠C = 180°
∴ ∠C= 180° -95° = 85°

Question 2.
If the angles of a triangle are in the ratio 1:2:3, determine three angles.
Solution:
Ratio in three angles of a triangle =1:2:3
Let first angle = x
Then second angle = 2x
and third angle = 3x
∴ x + 2x + 3x = 180° (Sum of angles of a triangle)
⇒6x = 180°
⇒x = \(\frac { { 180 }^{ \circ } }{ 6 }\)  = 30°
∴ First angle = x = 30°
Second angle = 2x = 2 x 30° = 60°
and third angle = 3x = 3 x 30° = 90°
∴ Angles are 30°, 60°, 90°

Question 3.
The angles of a triangle are (x – 40)°, (x – 20)° and (\(\frac { 1 }{ 2 }\) x – 10)°. Find the value of x.
Solution:
∵ Sum of three angles of a triangle = 180°
∴ (x – 40)° + (x – 20)° + (\(\frac { 1 }{ 2 }\)x-10)0 = 180°
⇒ x – 40° + x – 20° + \(\frac { 1 }{ 2 }\)x – 10° = 180°
⇒ x + x+ \(\frac { 1 }{ 2 }\)x – 70° = 180°
⇒ \(\frac { 5 }{ 2 }\)x = 180° + 70° = 250°
⇒ x = \(\frac { { 250 }^{ \circ }x 2 }{ 5 }\)  = 100°
∴ x = 100°

Question 4.
Two angles of a triangle are equal and the third angle is greater than each of those angles by 30°. Determine all the angles of the triangle.
Solution:
Let each of the two equal angles = x
Then third angle = x + 30°
But sum of the three angles of a triangle is 180°
∴ x + x + x + 30° = 180°
⇒ 3x + 30° = 180°
⇒3x = 150° ⇒x = \(\frac { { 150 }^{ \circ } }{ 3 }\) = 50°
∴ Each equal angle = 50°
and third angle = 50° + 30° = 80°
∴ Angles are 50°, 50° and 80°

Question 5.
If one angle of a triangle is equal to the sum of the other two, show that the triangle is a right triangle.
Solution:
In the triangle ABC,

∠B = ∠A + ∠C
But ∠A + ∠B + ∠C = 180°
⇒∠B + ∠A + ∠C = 180°
⇒∠B + ∠B = 180°
⇒2∠B = 180°
∴ ∠B = \(\frac { { 180 }^{ \circ } }{ 2 }\) = 90°
∵ One angle of the triangle is 90°
∴ ∆ABC is a right triangle.

Question 6.
Can a triangle have:
(i) Two right angles?
(ii) Two obtuse angles?
(iii) Two acute angles?
(iv) All angles more than 60°?
(v) All angles less than 60°?
(vi) All angles equal to 60°?
Justify your answer in each case.
Solution:
(i) In a triangle, two right-angles cannot be possible. We know that sum of three angles is 180° and if there are two right-angles, then the third angle will be zero which is not possible.
(ii) In a triangle, two obtuse angle cannot be possible. We know that the sum of the three angles of a triangle is 180° and if there are
two obtuse angle, then the third angle will be negative which is not possible.
(iii) In a triangle, two acute angles are possible as sum of three angles of a trianlge is 180°.
(iv) All angles more than 60°, they are also not possible as the sum will be more than 180°.
(v) All angles less than 60°. They are also not possible as the sum will be less than 180°.
(vi) All angles equal to 60°. This is possible as the sum will be 60° x 3 = 180°.

Question 7.
The angles of a triangle are arranged in ascending order of magnitude. If the difference between two consecutive angle is 10°, find the three angles.
Solution:
Let three angles of a triangle be x°, (x + 10)°, (x + 20)°
But sum of three angles of a triangle is 180°
∴ x + (x+ 10)° + (x + 20) = 180°
⇒ x + x+10°+ x + 20 = 180°
⇒ 3x + 30° = 180°
⇒ 3x = 180° – 30° = 150°
∴ x = \(\frac { { 180 }^{ \circ } }{ 2 }\) = 50°
∴ Angle are 50°, 50 + 10, 50 + 20
i.e. 50°, 60°, 70°

Question 8.
ABC is a triangle is which ∠A = 72°, the internal bisectors of angles B and C meet in O. Find the magnitude of ∠BOC.
Solution:
In ∆ABC, ∠A = 12° and bisectors of ∠B and ∠C meet at O

Now ∠B + ∠C = 180° – 12° = 108°
∵ OB and OC are the bisectors of ∠B and ∠C respectively
∴ ∠OBC + ∠OCB = \(\frac { 1 }{ 2 }\) (B + C)
= \(\frac { 1 }{ 2 }\) x 108° = 54°
But in ∆OBC,
∴ ∠OBC + ∠OCB + ∠BOC = 180°
⇒ 54° + ∠BOC = 180°
∠BOC = 180°-54°= 126°
OR
According to corollary,
∠BOC = 90°+ \(\frac { 1 }{ 2 }\) ∠A
= 90+ \(\frac { 1 }{ 2 }\) x 72° = 90° + 36° = 126°

Question 9.
The bisectors of base angles of a triangle cannot enclose a right angle in any case.
Solution:
In right ∆ABC, ∠A is the vertex angle and OB and OC are the bisectors of ∠B and ∠C respectively
To prove : ∠BOC cannot be a right angle
Proof: ∵ OB and OC are the bisectors of ∠B and ∠C respectively

∴ ∠BOC = 90° x \(\frac { 1 }{ 2 }\) ∠A
Let ∠BOC = 90°, then
\(\frac { 1 }{ 2 }\) ∠A = O
⇒∠A = O
Which is not possible because the points A, B and C will be on the same line Hence, ∠BOC cannot be a right angle.

Question 10.
If the bisectors of the base angles of a triangle enclose an angle of 135°. Prove that the triangle is a right triangle.
Solution:
Given : In ∆ABC, OB and OC are the bisectors of ∠B and ∠C and ∠BOC = 135°

To prove : ∆ABC is a right angled triangle
Proof: ∵ Bisectors of base angles ∠B and ∠C of the ∆ABC meet at O
∴ ∠BOC = 90°+ \(\frac { 1 }{ 2 }\)∠A
But ∠BOC =135°
∴ 90°+ \(\frac { 1 }{ 2 }\) ∠A = 135°
⇒ \(\frac { 1 }{ 2 }\)∠A= 135° -90° = 45°
∴ ∠A = 45° x 2 = 90°
∴ ∆ABC is a right angled triangle

Question 11.
In a ∆ABC, ∠ABC = ∠ACB and the bisectors of ∠ABC and ∠ACB intersect at O such that ∠BOC = 120°. Show that ∠A = ∠B = ∠C = 60°.
Solution:
Given : In ∠ABC, BO and CO are the bisectors of ∠B and ∠C respectively and ∠BOC = 120° and ∠ABC = ∠ACB

To prove : ∠A = ∠B = ∠C = 60°
Proof : ∵ BO and CO are the bisectors of ∠B and ∠C
∴ ∠BOC = 90° + \(\frac { 1 }{ 2 }\)∠A
But ∠BOC = 120°
∴ 90°+ \(\frac { 1 }{ 2 }\) ∠A = 120°
∴ \(\frac { 1 }{ 2 }\) ∠A = 120° – 90° = 30°
∴ ∠A = 60°
∵ ∠A + ∠B + ∠C = 180° (Angles of a triangle)
∠B + ∠C = 180° – 60° = 120° and ∠B = ∠C
∵ ∠B = ∠C = \(\frac { { 120 }^{ \circ } }{ 2 }\) = 60°
Hence ∠A = ∠B = ∠C = 60°

Question 12.
If each angle of a triangle is less than the sum of the other two, show that the triangle is acute angled.
Solution:
In a ∆ABC,
Let ∠A < ∠B + ∠C

⇒∠A + ∠A < ∠A + ∠B + ∠C
⇒ 2∠A < 180°
⇒ ∠A < 90° (∵ Sum of angles of a triangle is 180°)
Similarly, we can prove that
∠B < 90° and ∠C < 90°
∴ Each angle of the triangle are acute angle.

Hope given RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

 

RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency VSAQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency VSAQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.1
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.2
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.3
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.4
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency VSAQS
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency MCQS

Question 1.
If the ratio of mode and median of a certain data is 6 : 5, then find the ratio of its mean and median.
Solution:
We know that
Mode = 3 median – 2 mean…(i)
and \(\frac { mode }{ median } \) = \(\frac { 6 }{ 5 } \)
Mode = \(\frac { 6 }{ 5 } \)median
∴From (i), \(\frac { 6 }{ 5 } \) median = 3 median – 2 mean
=> 2 mean = 3 median – \(\frac { 6 }{ 5 } \)median
2 mean = \(\frac { 15-6 }{ 5 } \)median = \(\frac { 9 }{ 5 } \)median
\(\frac { mean }{ median } \) = \(\frac { 9 }{ 5X2 } \) = \(\frac { 9 }{ 10 } \)
∴Ratio = 9:10

Question 2.
If the mean of x + 2, 2x + 3, 3x + 4, 4x + 5 is x + 2, find x.
Solution:
Mean of x + 2, 2x + 3, 3x + 4, 4x + 5 = x + 2
=> \(\frac { x + 2+2x + 3+3x + 4+4x + 5 }{ 4 } \) = x + 2
=> 10x + 14 = 4x + 8
=> 10x – 4x = 8 – 14
=> 6x= – 6
∴ x = – 1

Question 3.
If the median of scores ,\(\frac { x }{ 2 } \), \(\frac { x }{ 3 } \), \(\frac { x }{ 4 } \), \(\frac { x }{ 5} \) and \(\frac { x }{ 6 } \) (where x > 0) is 6, then find the value \(\frac { x }{ 6 } \)
Solution:
\(\frac { x }{ 2 } \), \(\frac { x }{ 3 } \), \(\frac { x }{ 4 } \), \(\frac { x }{ 5} \), \(\frac { x }{ 6 } \)
Here n = 5
Median = \(\frac { n+1 }{ 2 } \) th term = \(\frac { 5+1 }{ 2 } \) th
\(\frac { 6 }{ 2 } \) = 3rd term = \(\frac { x }{ 4 } \)
\(\frac { x }{ 4 } \) = 6 => x = 24
\(\frac { x }{ 6 } \) = \(\frac { 24 }{ 6 } \) = 4
∴Hence = \(\frac { x }{ 6 } \) = 4

Question 4.
If the mean of 2, 4, 6, 8, x, y is 5, then find the value of x + y.
Solution:
Mean of 2, 4, 6, 8, x, y is 5
\(\frac { 2+4+6+8+x+y }{ 6 } \) = 5
\(\frac { 20+x+y }{ 6 } \) = 5
=> 20 + (x +y) = 30
=> x + y = 30 – 20 = 10
∴x + y = 10

Question 5.
If the mode of scores 3, 4, 3, 5, 4, 6, 6, x is 4, find the value of x.
Solution:
Mode of 3, 4, 3, 5, 4, 6, 6, x is 4
∴ 4 comes in maximum times
But here ,
3 2
4 2
5 1
6 2
3, 4 and 6 are equal in number
∴ x must be 4 so that it becomes in maximum times

Question 6.
If the median of 33, 28, 20. 25, 34, x is 29. find the maximum possible value of x.
Solution:
Median of 33, 28, 20, 25, 34, x is 29
Now arranging in ascending order 20, 25, 28, x, 33, 34
Here n = 6
Median = \(\frac { 1 }{ 2 } \left[ \frac { 6 }{ 2 } th\quad term+\left( \frac { 6 }{ 2 } +1 \right) th\quad term \right] \)
29 = \(\frac { 1 }{ 2 } \) [3rd term + 4th term]
29 = \(\frac { 1 }{ 2 } \) [28+x]
58 = 28 + x
=> x = 58 – 28 = 30
∴Possible value of x = 30

Question 7.
If the median of the scores 1, 2, x, 4, 5 (where 1 <2 <x <4 <5) is 3, then find the mean of the scores.
Solution:
Scores are 1, 2, x, 4, 5 and median 3
Here n = 5 which is odd
Median = \(\frac { n+1 }{ 2 } \) th term = \(\frac { 5+1 }{ 2 } \) = \(\frac { 6 }{ 2 } \) th
=> 3 = 3rd term = x
=> 3 = x
∴ x = 3
Mean of the score = \(\frac { 1+2+3+4+5 }{ 5 } \) = 3

Question 8.
If the ratio of mean and median of a certain data is 2 : 3, then find the ratio of its mode and mean.
Solution:
We know that mode = 3 median – 2 mean

\(\frac { mode }{ mean } \) = \(\frac { 5 }{ 2 } \)
Ratio in mode and mean = 5 : 2

Question 9.
The arithmetic mean and mode of a data are 24 and 12 respectively, then find the median of the data.
Solution:
Mean = 24
Mode = 12
We know that mode = 3 median – 2 mean
12 = 3 median – 2 x 24
12 = 3 median – 48
3 median 12 + 48 = 60
Median = \(\frac { 60 }{ 3 } \) = 20

Question 10.
If the difference of mode and median of a data is 24, then find the difference of median and mean.
Solution:
Mode – Median = 24
Mode = 24 + median
But mode = 3 median – 2 mean
3 median – 2 mean = 24 + median
3 median – median – 2 mean = 24
=> 2 median – 2 mean = 24
=> Median – Mean = 12 (Dividing by 2)

Hope given RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2

Other Exercises

• RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.1
• RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2
• RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry VSAQS
• RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry MCQS

Question 1.
The exterior angles obtained on producing the base of a triangle both ways are 104° and 136°. Find all the angles of the triangle.
Solution:
In ∆ABC, base BC is produced both ways to D and E respectivley forming ∠ABE = 104° and ∠ACD = 136°

Question 2.
In the figure, the sides BC, CA and AB of a ∆ABC have been produced to D, E and F respectively. If ∠ACD = 105° and ∠EAF = 45°, find all the angles of the ∆ABC.

Solution:
In ∆ABC, sides BC, CA and BA are produced to D, E and F respectively.
∠ACD = 105° and ∠EAF = 45°
∠ACD + ∠ACB = 180° (Linear pair)
⇒ 105° + ∠ACB = 180°
⇒ ∠ACB = 180°- 105° = 75°
∠BAC = ∠EAF (Vertically opposite angles)
= 45°
But ∠BAC + ∠ABC + ∠ACB = 180°
⇒ 45° + ∠ABC + 75° = 180°
⇒ 120° +∠ABC = 180°
⇒ ∠ABC = 180°- 120°
∴ ∠ABC = 60°
Hence ∠ABC = 60°, ∠BCA = 75°
and ∠BAC = 45°

Question 3.
Compute the value of x in each of the following figures:

Solution:
(i) In ∆ABC, sides BC and CA are produced to D and E respectively


(ii) In ∆ABC, side BC is produced to either side to D and E respectively
∠ABE = 120° and ∠ACD =110°
∵ ∠ABE + ∠ABC = 180° (Linear pair)

(iii) In the figure, BA || DC

Question 4.
In the figure, AC ⊥ CE and ∠A: ∠B : ∠C = 3:2:1, find the value of ∠ECD.

Solution:
In ∆ABC, ∠A : ∠B : ∠C = 3 : 2 : 1
BC is produced to D and CE ⊥ AC
∵ ∠A + ∠B + ∠C = 180° (Sum of angles of a triangles)
Let∠A = 3x, then ∠B = 2x and ∠C = x
∴ 3x + 2x + x = 180° ⇒ 6x = 180°
⇒ x = \(\frac { { 180 }^{ \circ } }{ 6 }\)  = 30°
∴ ∠A = 3x = 3 x 30° = 90°
∠B = 2x = 2 x 30° = 60°
∠C = x = 30°
In ∆ABC,
Ext. ∠ACD = ∠A + ∠B
⇒ 90° + ∠ECD = 90° + 60° = 150°
∴ ∠ECD = 150°-90° = 60°

Question 5.
In the figure, AB || DE, find ∠ACD.

Solution:
In the figure, AB || DE
AE and BD intersect each other at C ∠BAC = 30° and ∠CDE = 40°
∵ AB || DE
∴ ∠ABC = ∠CDE (Alternate angles)

⇒ ∠ABC = 40°
In ∆ABC, BC is produced
Ext. ∠ACD = Int. ∠A + ∠B
= 30° + 40° = 70°

Question 6.
Which of the following statements are true (T) and which are false (F):
(i) Sum of the three angles of a triangle is 180°.
(ii) A triangle can have two right angles.
(iii) All the angles of a triangle can be less than 60°.
(iv) All the angles of a triangle can be greater than 60°.
(v) All the angles of a triangle can be equal to 60°.
(vi) A triangle can have two obtuse angles.
(vii) A triangle can have at most one obtuse angles.
(viii) If one angle of a triangle is obtuse, then it cannot be a right angled triangle.
(ix) An exterior angle of a triangle is less than either of its interior opposite angles.
(x) An exterior angle of a triangle is equal to the sum of the two interior opposite angles.
(xi) An exterior angle of a triangle is greater than the opposite interior angles.
Solution:
(i) True.
(ii) False. A right triangle has only one right angle.
(iii) False. In this, the sum of three angles will be less than 180° which is not true.
(iv) False. In this, the sum of three angles will be more than 180° which is not true.
(v) True. As sum of three angles will be 180° which is true.
(vi) False. A triangle has only one obtuse angle.
(vii) True.
(viii)True.
(ix) False. Exterior angle of a triangle is always greater than its each interior opposite angles.
(x) True.
(xi) True.

Question 7.
Fill in the blanks to make the following statements true:
(i) Sum of the angles of a triangle is ………
(ii) An exterior angle of a triangle is equal to the two …….. opposite angles.
(iii) An exterior angle of a triangle is always …….. than either of the interior opposite angles.
(iv) A triangle cannot have more than ………. right angles.
(v) A triangles cannot have more than ……… obtuse angles.
Solution:
(i) Sum of the angles of a triangle is 180°.
(ii) An exterior angle of a triangle is equal to the two interior opposite angles.
(iii) An exterior angle of a triangle is always greater than either of the interior opposite angles.
(iv) A triangle cannot have more than one right angles.
(v) A triangles cannot have more than one obtuse angles.

Question 8.
In a ∆ABC, the internal bisectors of ∠B and ∠C meet at P and the external bisectors of ∠B and ∠C meet at Q. Prove that ∠BPC + ∠BQC = 180°.
Solution:
Given : In ∆ABC, sides AB and AC are produced to D and E respectively. Bisectors of interior ∠B and ∠C meet at P and bisectors of exterior angles B and C meet at Q.

To prove : ∠BPC + ∠BQC = 180°
Proof : ∵ PB and PC are the internal bisectors of ∠B and ∠C
∠BPC = 90°+ \(\frac { 1 }{ 2 }\) ∠A …(i)
Similarly, QB and QC are the bisectors of exterior angles B and C
∴ ∠BQC = 90° + \(\frac { 1 }{ 2 }\) ∠A …(ii)
Adding (i) and (ii),
∠BPC + ∠BQC = 90° + \(\frac { 1 }{ 2 }\) ∠A + 90° – \(\frac { 1 }{ 2 }\) ∠A
= 90° + 90° = 180°
Hence ∠BPC + ∠BQC = 180°

Question 9.
In the figure, compute the value of x.

Solution:
In the figure,
∠ABC = 45°, ∠BAD = 35° and ∠BCD = 50° Join BD and produce it E

Question 10.
In the figure, AB divides ∠D AC in the ratio 1 : 3 and AB = DB. Determine the value of x.

Solution:
In the figure AB = DB

Question 11.
ABC is a triangle. The bisector of the exterior angle at B and the bisector of ∠C intersect each other at D. Prove that ∠D = \(\frac { 1 }{ 2 }\) ∠A.
Solution:
Given : In ∠ABC, CB is produced to E bisectors of ext. ∠ABE and into ∠ACB meet at D.

Question 12.
In the figure, AM ⊥ BC and AN is the bisector of ∠A. If ∠B = 65° and ∠C = 33°, find ∠MAN.

Solution:

Question 13.
In a AABC, AD bisects ∠A and ∠C > ∠B. Prove that ∠ADB > ∠ADC.
Solution:
Given : In ∆ABC,
∠C > ∠B and AD is the bisector of ∠A

To prove : ∠ADB > ∠ADC
Proof: In ∆ABC, AD is the bisector of ∠A
∴ ∠1 = ∠2
In ∆ADC,
Ext. ∠ADB = ∠l+ ∠C
⇒ ∠C = ∠ADB – ∠1 …(i)
Similarly, in ∆ABD,
Ext. ∠ADC = ∠2 + ∠B
⇒ ∠B = ∠ADC – ∠2 …(ii)
From (i) and (ii)
∵ ∠C > ∠B (Given)
∴ (∠ADB – ∠1) > (∠ADC – ∠2)
But ∠1 = ∠2
∴ ∠ADB > ∠ADC

Question 14.
In ∆ABC, BD ⊥ AC and CE ⊥ AB. If BD and CE intersect at O, prove that ∠BOC = 180°-∠A.
Solution:
Given : In ∆ABC, BD ⊥ AC and CE⊥ AB BD and CE intersect each other at O

To prove : ∠BOC = 180° – ∠A
Proof: In quadrilateral ADOE
∠A + ∠D + ∠DOE + ∠E = 360° (Sum of angles of quadrilateral)
⇒ ∠A + 90° + ∠DOE + 90° = 360°
∠A + ∠DOE = 360° – 90° – 90° = 180°
But ∠BOC = ∠DOE (Vertically opposite angles)
⇒ ∠A + ∠BOC = 180°
∴ ∠BOC = 180° – ∠A

Question 15.
In the figure, AE bisects ∠CAD and ∠B = ∠C. Prove that AE || BC.

Solution:
Given : In AABC, BA is produced and AE is the bisector of ∠CAD
∠B = ∠C

To prove : AE || BC
Proof: In ∆ABC, BA is produced
∴ Ext. ∠CAD = ∠B + ∠C
⇒ 2∠EAC = ∠C + ∠C (∵ AE is the bisector of ∠CAE) (∵ ∠B = ∠C)
⇒ 2∠EAC = 2∠C
⇒ ∠EAC = ∠C
But there are alternate angles
∴ AE || BC

Hope given RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 25 Probability Ex 25.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 25 Probability Ex 25.1

Other Exercises

• RD Sharma Class 9 Solutions Chapter 25 Probability Ex 25.1
• RD Sharma Class 9 Solutions Chapter 25 Probability VSAQS
• RD Sharma Class 9 Solutions Chapter 25 Probability MCQS

Question 1.
A coin is tossed 1000 times with the following frequencies
Head : 455, Tail : 545.
Compute the probability for each event.
Solution:
Total number of events (m) 1000
(i) Possible events (m) 455
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 455 }{ 1000 } \)
= \(\frac { 91 }{ 200 } \) = 0.455
(ii) Possible events (m) = 545
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 545 }{ 1000 } \) = \(\frac { 109 }{ 200 } \) = 0.545

Question 2.
Two coins are tossed simultaneously 500 times with the following frequencies of different
outcomes:
Two heads : 95 times
One tail : 290 times
No head: 115 times
Find the probability of occurrence of each of these events.
Solution:
Two coins are tossed together simultaneously 500 times
∴ Total outcomes (n) 500
(i) 2 heads coming (m) = 95 times
∴Probability P(A) = \(\frac { m }{ n } \)
= \(\frac { No. of possible events }{ Total number of events } \)
= \(\frac { 95 }{ 500 } \) = \(\frac { 19 }{ 100 } \) = 0.19
(ii) One tail (m) = 290 times
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 290 }{ 500 } \) = \(\frac { 580 }{ 1000 } \) = \(\frac { 58 }{ 100 } \) = 0.58
(iii) No head (m) = 115 times
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 115 }{ 500 } \) = \(\frac { 23 }{ 100 } \) = 0.23

Question 3.
Three coins are tossed simultaneously 1oo times with the following frequencies of different outcomes:

If the three coins are simultaneously tossed again, compute the probability of:
(i) 2 heads coming up.
(ii) 3 heads coming up.
(iii) at least one head coming up.
(iv) getting more heads than tails.
(v) getting more tails than heads.
Solution:
Three coins are tossed simultaneously 100 times
Total out comes (n) = 100

(i) Probability of 2 heads coming up (m) = 36
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 36 }{ 100 } \) = 0.36
(ii) Probability of 3 heads (m) = 12
ProbabilityP(A)= \(\frac { m }{ n } \) = \(\frac { 12 }{ 100 } \) = 0.12
(iii) Probability of at least one head coming up (m) = 38 + 36 + 12 = 86
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 86 }{ 100 } \) = 0.86
(iv) Probability of getting more heads than tails (m) = 36 + 12 = 48
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 48 }{ 100 } \) = 0.48
(v) Getting more tails than heads (m) = 14 + 38 = 52
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 52 }{ 100 } \) = 0.52

Question 4.
1500 families with 2 children were selected randomly and the following data were recorded:

If a family is chosen at random, compute the probability that it has:
(i) No girl
(ii) 1 girl
(iii) 2 girls
(iv) at most one girl
(v) more girls than boys
Solution:
Total number of families (n) = 1500

(i) Probability of a family having no girls (m) = 211
∴Probability P(A)= \(\frac { m }{ n } \) = \(\frac { 211 }{ 1500 } \) = 0.1406
(ii) Probability of a family having one girl (in) = 814
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 814 }{ 1500 } \) = 0.5426
(iii) Probability of a family having 2 girls (m) = 475
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 475 }{ 1500 } \) = 0.3166
(iv) Probability of a family having at the most one girls
∴m = 814 + 211 = 1025
∴Probability P(A) =\(\frac { m }{ n } \) = \(\frac { 1025 }{ 1500 } \) = 0.6833
(v) Probability of a family having more girls than boys (m) = 475
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 475 }{ 1500 } \) = 0.3166

Question 5.
In a cricket match, a batsman hits a boundary 6 times out of 30 balls he plays. Find the probability that on a ball played:
(i) he hits boundary
(ii) he does not hit a boundary.
Solution:
Total balls played (n) 30
No. of boundaries = 6
(i) When the batsman hits the boundary = 6
∴m = 6
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 6 }{ 30 } \) = \(\frac { 1 }{ 5 } \) = 0.2
(ii) When the batsman does not hit the boundary (m) = 30 – 6 = 24
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 24 }{ 30 } \) = \(\frac { 4 }{ 5 } \) = 0.8

Question 6.
The percentage of marks obtained by a student in monthly unit tests are given below:

Find the probability that the student gets:
(i) more than 70% marks
(ii) less than 70% marks
(iii) a distinction.
Solution:
Percentage of marks obtain in

(i) Probability of getting more than 70% marks (m) = In unit test II, III, V = 3
Total unit test (n) = 5
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 3 }{ 5 } \) = 0.6
(ii) Getting less then 70% marks = units test I and IV
∴m = 2
Total unit test (n) = 5
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 2 }{ 5 } \) = 0.4
(iii) Getting a distinction = In test V (76 of marks)
∴m = 1
Total unit test (n) = 5
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 1 }{ 5 } \) = 0.2

Question 7.
To know the opinion of the students about Mathematics, a survey of 200 students was conducted. The data is recorded in the following table:

Find the probability that a student chosen at random
(i) likes Mathematics
(ii) does not like it.
Solution:
Total number of students (n) = 200

(i) Probability of students who like mathematics (m) = 135
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 135 }{ 200 } \) = 0.675
(ii) Probability of students who dislike mathematics (m) = 65
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 65 }{ 200 } \) = 0.325

Question 8.
The blood groups of 30 students of class IX are recorded as follows:
A, B, O, O, AB, O, A, O, B, A, O, B, A, O, O,
A, AB, O, A, A, O, O, AB, B, A, O, B, A, B, O,
A student is selected at random from the class from blood donation. Find the probability that the blood group of the student chosen is:
(i) A (ii) B (iii) AB (iv) O
Solution:
Total number of students of IX class = 30
No. of students of different blood groups
A AB B O
9 3 6 12

Question 9.
Eleven bags of wheat flour, each marked 5 kg, actually contained the following weights of flour
(in kg):
4.97, 5.05, 5.08, 5.03, 5.00, 5.06, 5.08, 4.98, 5.04, 5.07, 5.00
Find the probability that any of these bags chosen at random contains more than 5 kg of flour.
Solution:
Number of total bags (n) = 11
No. of bags having weight more than 5 kg (m) = 7
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 7 }{ 11 } \)

Question 10.
Following table shows the birth month of 40 students of class IX.

Find the probability that a student was born in August.
Solution:
Total number of students (n) = 40

Number of students who born in Aug. (m) = 6
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 6 }{ 40 } \) = \(\frac { 3 }{ 20 } \)

Question 11.
Given below is the frequency distribution table regarding the concentration of sulphur dioxide in the air in parts per million of a certain city for 30 days.

Find the probability of concentration of sulphur dioxide in the interval 0.12 – 0.16 on any of these days.
Solution:
Total number of days (n) = 30

Probability of cone, of S02 of the interval 0.12-0.16 (m) = 2
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 2 }{ 30 } \) = \(\frac { 1 }{ 15 } \)

Question 12.
A company selected 2400 families at random and survey them to determine a relationship between income level and the number of vehicles in a home. The information gathered is listed in the table below:

If a family is chosen, find the probability that the family is:
(i)earning Rs 10000-13000 per month and owning exactly 2 vehicles.
(ii)earning Rs 16000 or more per month and owning exactly I vehicle.
(iii)earning less than Rs 7000 per month and does not own any vehicle.
(iv)earning Rs 13000-16000 per month and owning more than 2 vehicle.
(v)owning not more than 1 vehicle.
(vi)owning at least one vehicle.
Solution:
Total number of families (n) = 2400

(i) Number of families earning income Rs 10000-13000 and owning exactly 2 vehicles (m) = 29
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 29 }{ 2400 } \)
(ii) Number of families earning income Rs 16000 or more having one vehicle (m) = 579
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 579 }{ 2400 } \)
(iii) Number of families earning income less than Rs 7000 having no own vehicle (m) = 10
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 10 }{ 2400 } \) = \(\frac { 1 }{ 240 } \)
(iv) Number of families having X13000 to X16000 having more than two vehicles (m) = 25
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 25 }{ 2400 } \) = \(\frac { 1 }{ 96 } \)
(v) Number of families owning not more than one vehicle (m)
= 10 + 1 + 2 + 1 + 160 + 305 + 533 + 469 + 579 = 2062
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 2062 }{ 2400 } \) = \(\frac { 1031 }{ 1200 } \)
(vi) Number of families owning at least one vechile (m) = 2048 + 192 + 110 = 2356
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 2356 }{ 2400 } \) = \(\frac { 589 }{ 600 } \)

Question 13.
The following table gives the life time of 400 neon lamps:

A bulb is selected at random. Find the probability that the life time of the selected bulb is: (i) less than 400 (ii) between 300 to 800 hours (iii) at least 700 hours.
Solution:
Total number of neon lamps (n) = 400

A bulb is chosen:
(i)No. of bulbs having life time less than 400 hours (m) = 14
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 14 }{ 400 } \) = \(\frac { 7 }{ 200 } \)
(ii)No. of bulbs having life time between 300 to 800 hours (m) = 14 + 56 + 60 + 86 + 74 = 290
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 290 }{ 400 } \) = \(\frac { 29 }{ 40 } \)
(iii)No. of bulbs having life time at least 700 hours (m) = 74 + 62 + 48 = 184
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 184 }{ 400 } \) = \(\frac { 23 }{ 50 } \)

Question 14.
Given below is the frequency distribution of wages (in Rs) of 30 workers in a certain factory:

A worker is selected at random. Find the probability that his wages are:
(i) less than Rs 150
(ii) at least Rs 210
(iii) more than or equal to 150 but less than Rs 210.
Solution:
Number of total workers (n) = 30

A worker is selected.
(i)No. of workers having less than Rs 150 (m) = 3 + 4 = 7
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 7 }{ 30 } \)
(ii)No. of workers having at least Rs 210 (m) = 4 + 3 = 7
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 7 }{ 30 } \)
(iii)No. of workers having more than or equal to Rs 150 but less than Rs 210 = 5 + 6 + 5 = 16
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 16 }{ 30 } \) = \(\frac { 8 }{ 15 } \)

 

Hope given RD Sharma Class 9 Solutions Chapter 25 Probability Ex 25.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.4

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.4

Other Exercises

• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.1
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.2
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.3
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.4
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles VSAQS
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles MCQS

Question 1.
In the figure, AB || CD and ∠1 and ∠2 are in the ratio 3 : 2. Determine all angles from 1 to 8.

Solution:
AB || CD and l is transversal ∠1 : ∠2 = 3 : 2
Let ∠1 = 3x
Then ∠2 = 2x
But ∠1 + ∠2 = 180° (Linear pair)
∴ 3x + 2x = 180° ⇒ 5x = 180°
⇒ x = \(\frac { { 180 }^{ \circ } }{ 5 }\)  = 36°
∴ ∠1 = 3x = 3 x 36° = 108°
∠2 = 2x = 2 x 36° = 72°
Now ∠1 = ∠3 and ∠2 = ∠4 (Vertically opposite angles)
∴ ∠3 = 108° and ∠4 = 72°
∠1 = ∠5 and ∠2 = ∠6 (Corresponding angles)
∴ ∠5 = 108°, ∠6 = 72°
Similarly, ∠4 = ∠8 and
∠3 = ∠7
∴ ∠8 = 72° and ∠7 = 108°
Hence, ∠1 = 108°, ∠2= 72°
∠3 = 108°, ∠4 = 72°
∠5 = 108°, ∠6 = 72°
∠7 = 108°, ∠8 = 12°

Question 2.
In the figure, l, m and n are parallel lines intersected by transversal p at X, Y and Z respectively. Find ∠l, ∠2 and ∠3.

Solution:
l || m || n and p is then transversal which intersects then at X, Y and Z respectively ∠4 = 120°
∠2 = ∠4 (Alternate angles)
∴ ∠2 = 120°
But ∠3 + ∠4 = 180° (Linear pair)
⇒ ∠3 + 120° = 180°
⇒ ∠3 = 180° – 120°
∴ ∠3 = 60°
But ∠l = ∠3 (Corresponding angles)
∴ ∠l = 60°
Hence ∠l = 60°, ∠2 = 120°, ∠3 = 60°

Question 3.
In the figure, if AB || CD and CD || EF, find ∠ACE.

Solution:
Given : In the figure, AB || CD and CD || EF
∠BAC = 70°, ∠CEF = 130°
∵ EF || CD
∴ ∠ECD + ∠CEF = 180° (Co-interior angles)
⇒ ∠ECD + 130° = 180°
∴ ∠ECD = 180° – 130° = 50°
∵ BA || CD
∴ ∠BAC = ∠ACD (Alternate angles)
∴ ∠ACD = 70° (∵ ∠BAC = 70°)
∵ ∠ACE = ∠ACD – ∠ECD = 70° – 50° = 20°

Question 4.
In the figure, state which lines are parallel and why.

Solution:
In the figure,
∵ ∠ACD = ∠CDE = 100°
But they are alternate angles
∴ AC || DE

Question 5.
In the figure, if l || m,n|| p and ∠1 = 85°, find ∠2.

Solution:
In the figure, l || m, n|| p and ∠1 = 85°
∵ n || p
∴ ∠1 = ∠3 (Corresponding anlges)
But ∠1 = 85°
∴ ∠3 = 85°
∵ m || 1
∠3 + ∠2 = 180° (Sum of co-interior angles)
⇒ 85° + ∠2 = 180°
⇒ ∠2 = 180° – 85° = 95°

Question 6.
If two straight lines are perpendicular to the same line, prove that they are parallel to each other.
Solution:

Question 7.
Two unequal angles of a parallelogram are in the ratio 2:3. Find all its angles in degrees.
Solution:
In ||gm ABCD,

∠A and ∠B are unequal
and ∠A : ∠B = 2 : 3
Let ∠A = 2x, then
∠B = 3x
But ∠A + ∠B = 180° (Co-interior angles)
∴ 2x + 3x = 180°
⇒ 5x = 180°
⇒ x = \(\frac { { 180 }^{ \circ } }{ 5 }\)  = 36°
∴ ∠A = 2x = 2 x 36° = 72°
∠B = 3x = 3 x 36° = 108°
But ∠A = ∠C and ∠B = ∠D (Opposite angles of a ||gm)
∴ ∠C = 72° and ∠D = 108°
Hence ∠A = 72°, ∠B = 108°, ∠C = 72°, ∠D = 108°

Question 8.
In each of the two lines is perpendicular to the same line, what kind of lines are they to each other?
Solution:
AB ⊥ line l and CD ⊥ line l

∴ ∠B = 90° and ∠D = 90°
∴ ∠B = ∠D
But there are corresponding angles
∴ AB || CD

Question 9.
In the figure, ∠1 = 60° and ∠2 = (\(\frac { 2 }{ 3 }\))3 a right angle. Prove that l || m.

Solution:
In the figure, a transversal n intersects two lines l and m
∠1 = 60° and
∠2 = \(\frac { 2 }{ 3 }\) rd of a right angle 2
= \(\frac { 2 }{ 3 }\) x 90° = 60°
∴ ∠1 = ∠2
But there are corresponding angles
∴ l || m

Question 10.
In the figure, if l || m || n and ∠1 = 60°, find ∠2.

Solution:
In the figure,

l || m || n and a transversal p, intersects them at P, Q and R respectively
∠1 = 60°
∴ ∠1 = ∠3 (Corresponding angles)
∴ ∠3 = 60°
But ∠3 + ∠4 = 180° (Linear pair)
60° + ∠4 = 180° ⇒ ∠4 = 180° – 60°
∴ ∠4 = 120°
But ∠2 = ∠4 (Alternate angles)
∴ ∠2 = 120°

Question 11.
Prove that the straight lines perpendicular to the same straight line are parallel to one another.
Solution:
Given : l is a line, AB ⊥ l and CD ⊥ l

Question 12.
The opposite sides of a quadrilateral are parallel. If one angle of the quadrilateral is 60°, find the other angles.
Solution:
In quadrilateral ABCD, AB || DC and AD || BC and ∠A = 60°

∵ AD || BC and AB || DC
∴ ABCD is a parallelogram
∴ ∠A + ∠B = 180° (Co-interior angles)
60° + ∠B = 180°
⇒ ∠B = 180°-60°= 120°
But ∠A = ∠C and ∠B = ∠D (Opposite angles of a ||gm)
∴ ∠C = 60° and ∠D = 120°
Hence ∠B = 120°, ∠C = 60° and ∠D = 120°

Question 13.
Two lines AB and CD intersect at O. If ∠AOC + ∠COB + ∠BOD = 270°, find the measure of ∠AOC, ∠COB, ∠BOD and ∠DOA.
Solution:
Two lines AB and CD intersect at O
and ∠AOC + ∠COB + ∠BOD = 270°
But ∠AOC + ∠COB + ∠BOD + ∠DOA = 360° (Angles at a point)

∴ 270° + ∠DOA = 360°
⇒ ∠DOA = 360° – 270° = 90°
But ∠DOA = ∠BOC (Vertically opposite angles)
∴ ∠BOC = 90°
But ∠DOA + ∠BOD = 180° (Linear pair)
⇒ 90° + ∠BOD = 180°
∴ ∠BOD= 180°-90° = 90° ,
But ∠BOD = ∠AOC (Vertically opposite angles)
∴ ∠AOC = 90°
Hence ∠AOC = 90°,
∠COB = 90°,
∠BOD = 90° and ∠DOA = 90°

Question 14.
In the figure, p is a transversal to lines m and n, ∠2 = 120° and ∠5 = 60°. Prove that m || n.

Solution:
Given : p is a transversal to the lines m and n
Forming ∠l, ∠2, ∠3, ∠4, ∠5, ∠6, ∠7 and ∠8
∠2 = 120°, and ∠5 = 60°
To prove : m || n
Proof : ∠2 + ∠3 = 180° (Linear pair)
⇒ 120°+ ∠3 = 180°
⇒ ∠3 = 180°- 120° = 60°
But ∠5 = 60°
∴ ∠3 = ∠5
But there are alternate angles
∴ m || n

Question 15.
In the figure, transversal l, intersects two lines m and n, ∠4 = 110° and ∠7 = 65°. Is m || n?

Solution:
A transversal l, intersects two lines m and n, forming ∠1, ∠2, ∠3, ∠4, ∠5, ∠6, ∠7 and ∠8
∠4 = 110° and ∠7 = 65°
To prove : Whether m || n or not
Proof : ∠4 = 110° and ∠7 = 65°
∠7 = ∠5 (Vertically opposite angles)
∴ ∠5 = 65°
Now ∠4 + ∠5 = 110° + 65° = 175°
∵ Sum of co-interior angles ∠4 and ∠5 is not 180°.
∴ m is not parallel to n

Question 16.
Which pair of lines in the figure are parallel? Give reasons.

Solution:
Given : In the figure, ∠A = 115°, ∠B = 65°, ∠C = 115° and ∠D = 65°
∵ ∠A + ∠B = 115°+ 65°= 180°
But these are co-interior angles,
∴ AD || BC
Similarly, ∠A + ∠D = 115° + 65° = 180°
∴ AB || DC

Question 17.
If l, m, n are three lines such that l ||m and n ⊥ l, prove that n ⊥ m.
Solution:
Given : l, m, n are three lines such that l || m and n ⊥ l

To prove : n ⊥ m
Proof : ∵ l || m and n is the transversal.
∴ ∠l = ∠2 (Corresponding angles)
But ∠1 = 90° (∵ n⊥l)
∴ ∠2 = 90°
∴ n ⊥ m

Question 18.
Which of the following statements are true (T) and which are false (F)? Give reasons.
(i) If two lines are intersected by a transversal, then corresponding angles are equal.
(ii) If two parallel lines are intersected by a transversal, then alternate interior angles are equal.
(iii) Two lines perpendicular to the same line are perpendicular to each other.
(iv) Two lines parallel to the same line are parallel to each other.
(v) If two parallel lines are intersected by a transversal, then the interior angles on the same side of the transversal are equal.
Solution:
(i) False. Because if lines are parallel, then it is possible.
(ii) True.
(iii) False. Not perpendicular but parallel to each other.
(iv) True.
(v) False. Sum of interior angles on the same side is 180° not are equal.

Question 19.
Fill in the blanks in each of the following to make the statement true:
(i) If two parallel lines are intersected by a transversal then each pair of corresponding angles are ……..
(ii) If two parallel lines are intersected by a transversal, then interior angles on the same side of the transversal are …….
(iii) Two lines perpendicular to the same line are ……… to each other.
(iv) Two lines parallel to the same line are ……… to each other.
(v) If a transversal intersects a pair of lines in such away that a pair of alternate angles are equal, then the lines are …….
(vi) If a transversal intersects a pair of lines in such away that the sum of interior angles on the same side of transversal is 180°, then the lines are …….
Solution:
(i) If two parallel lines are intersected by a transversal, then each pair of corresponding angles are equal.
(ii) If two parallel lines are intersected by a transversal, then interior angles on the same side of the transversal are supplementary.
(iii) Two lines perpendicular to the same line are parallel to each other.
(iv) Two lines parallel to the same line are parallel to each other.
(v) If a transversal intersects a pair of lines in such away that a pair of alternate angles are equal, then the lines are parallel.
(vi) If a transversal intersects a pair of lines in such away that the sum of interior angles on the same side of transversal is 180°, then the lines are parallel.

Question 20.
In the figure, AB || CD || EF and GH || KL. Find ∠HKL.

Solution:
In the figure, AB || CD || EF and KL || HG Produce LK and GH

∵ AB || CD and HK is transversal
∴ ∠1 = 25° (Alternate angles)
∠3 = 60° (Corresponding angles)
and ∠3 = ∠4 (Corresponding angles)
= 60°
But ∠4 + ∠5 = 180° (Linear pair)
⇒ 60° + ∠5 = 180°
⇒ ∠5 = 180° – 60° = 120°
∴ ∠HKL = ∠1 + ∠5 = 25° + 120° = 145°

Question 21.
In the figure, show that AB || EF.

Solution:
Given : In the figure, AB || EF
∠BAC = 57°, ∠ACE = 22°
∠ECD = 35° and ∠CEF =145°
To prove : AB || EF,
Proof : ∠ECD + ∠CEF = 35° + 145°
= 180°
But these are co-interior angles
∴ EF || CD
But AB || CD
∴ AB || EF

Question 22.
In the figure, PQ || AB and PR || BC. If ∠QPR = 102°. Determine ∠ABC. Give reasons.

Solution:
In the figure, PQ || AB and PR || BC
∠QPR = 102°
Produce BA to meet PR at D

∵ PQ || AB or DB
∴ ∠QPR = ∠ADR (Corresponding angles)
∴∠ADR = 102° or ∠BDR = 102°
∵ PR || BC
∴ ∠BDR + ∠DBC = 180°
(Sum of co-interior angles) ⇒ 102° + ∠DBC = 180°
⇒ ∠DBC = 180° – 102° = 78°
⇒ ∠ABC = 78°

Question 23.
Prove that if the two arms of an angle are perpendicular to the two arms of another angle, then the angles are either equal or supplementary.
Solution:
Given : In two angles ∠ABC and ∠DEF AB ⊥ DE and BC ⊥ EF
To prove: ∠ABC + ∠DEF = 180° or ∠ABC = ∠DEF
Construction : Produce the sides DE and EF of ∠DEF, to meet the sides of ∠ABC at H and G.


Proof: In figure (i) BGEH is a quadrilateral
∠BHE = 90° and ∠BGE = 90°
But sum of angles of a quadrilateral is 360°
∴ ∠HBG + ∠HEG = 360° – (90° + 90°)
= 360° – 180°= 180°
∴ ∠ABC and ∠DEF are supplementary
In figure (if) in quadrilateral BGEH,
∠BHE = 90° and ∠HEG = 90°
∴ ∠HBG + ∠HEG = 360° – (90° + 90°)
= 360°- 180° = 180° …(i)
But ∠HEF + ∠HEG = 180° …(ii) (Linear pair)
From (i) and (ii)
∴ ∠HEF = ∠HBG
⇒ ∠DEF = ∠ABC
Hence ∠ABC and ∠DEF are equal or supplementary

Question 24.
In the figure, lines AB and CD are parallel and P is any point as shown in the figure. Show that ∠ABP + ∠CDP = ∠DPB.

Solution:
Given : In the figure, AB || CD
P is a point between AB and CD PD
and PB are joined
To prove : ∠APB + ∠CDP = ∠DPB
Construction : Through P, draw PQ || AB or CD

Proof: ∵ AB || PQ
∴ ∠ABP = BPQ …(i) (Alternate angles)
Similarly,
CD || PQ
∴ ∠CDP = ∠DPQ …(ii)
(Alternate angles)
Adding (i) and (ii)
∠ABP + ∠CDP = ∠BPQ + ∠DPQ
Hence ∠ABP + ∠CDP = ∠DPB

Question 25.
In the figure, AB || CD and P is any point shown in the figure. Prove that:
∠ABP + ∠BPD + ∠CDP = 360°

Solution:
Given : AB || CD and P is any point as shown in the figure
To prove : ∠ABP + ∠BPD + ∠CDP = 360°
Construction : Through P, draw PQ || AB and CD

Proof : ∵ AB || PQ
∴ ∠ABP+ ∠BPQ= 180° ……(i) (Sum of co-interior angles)
Similarly, CD || PQ
∴ ∠QPD + ∠CDP = 180° …(ii)
Adding (i) and (ii)
∠ABP + ∠BPQ + ∠QPD + ∠CDP
= 180°+ 180° = 360°
⇒ ∠ABP + ∠BPD + ∠CDP = 360°

Question 26.
In the figure, arms BA and BC of ∠ABC are respectively parallel to arms ED and EF of ∠DEF. Prove that ∠ABC = ∠DEF.

Solution:
Given : In ∠ABC and ∠DEF. Their arms are parallel such that BA || ED and BC || EF
To prove : ∠ABC = ∠DEF
Construction : Produce BC to meet DE at G
Proof: AB || DE
∴ ∠ABC = ∠DGH…(i) (Corresponding angles)

BC or BH || EF
∴ ∠DGH = ∠DEF (ii) (Corresponding angles)
From (i) and (ii)
∠ABC = ∠DEF

Question 27.
In the figure, arms BA and BC of ∠ABC are respectively parallel to arms ED and EF of ∠DEF. Prove that ∠ABC + ∠DEF = 180°.

Solution:
Given: In ∠ABC = ∠DEF
BA || ED and BC || EF
To prove: ∠ABC = ∠DEF = 180°
Construction : Produce BC to H intersecting ED at G

Proof: ∵ AB || ED
∴ ∠ABC = ∠EGH …(i) (Corresponding angles)
∵ BC or BH || EF
∠EGH || ∠DEF = 180° (Sum of co-interior angles)
⇒ ∠ABC + ∠DEF = 180° [From (i)]
Hence proved.

Hope given RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 25 Probability VSAQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 25 Probability VSAQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 25 Probability Ex 25.1
• RD Sharma Class 9 Solutions Chapter 25 Probability VSAQS
• RD Sharma Class 9 Solutions Chapter 25 Probability MCQS

Question 1.
Define a trial.
Solution:
When we perform an experiment, it is called a trial of the experiment.

Question 2.
Define an elementary event.
Solution:
An outcome of a trial of an experiment is called an elementary event.

Question 3.
Define an event.
Solution:
An event association to a random experiment is said to occur in a trial.

Question 4.
Define probability of an event.
Solution:
In n trials of a random experiment if an event A happens m times, then probability of happening
of A is given by P(A) = \(\frac { m }{ n } \)

Question 5.
A bag contains 4 white balls and some red balls. If the probability of drawing a white ball from the bag is \(\frac { 2 }{ 5 } \), find the number of red balls in the bag
Solution:
No. of white balls = 4
Let number of red balls = x
Then total number of balls (n) = 4 white + x red = (4 + x) balls

Question 6.
A die is thrown 100 times. If the probability of getting an even number is \(\frac { 2 }{ 5 } \). How many times an odd number is obtained?
Solution:
Total number of a die is thrown = 100
Let an even number comes x times, then probability of an even number = \(\frac { x }{ 100 } \)

Question 7.
Three coins are tossed simultaneously 200 times with the following frequencies of different outcomes

Find the probability of getting at most two heads.
Solution:
Total number of three coins are tossed (n) = 200
Getting at the most 2 heads (m) = 72 + 77 + 28 = 177
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 177 }{ 200 } \)

Question 8.
In the Q. No. 7, what is the probability of getting at least two heads?
Solution:
Total number of possible events = 200
No. of events getting at the least = 2 heads (m) = 23 + 72 = 95
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 95 }{ 200 } \) = \(\frac { 19 }{ 40 } \)

Hope given RD Sharma Class 9 Solutions Chapter 25 Probability VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles MCQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles MCQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.1
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.2
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.3
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.4
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles VSAQS
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles MCQS

Mark the correct alternative in each of the following:
Question 1.
One angle is equal to three times its supplement. The measure of the angle is
(a) 130°
(b) 135°
(c) 90°
(d) 120°
Solution:
Let required angle = x
Then its supplement = (180° – x)
x = 3(180° – x) = 540° – 3x
⇒ x + 3x = 540°
⇒ 4x = 540°
⇒ x = \(\frac { { 540 }^{ \circ } }{ 4 }\)  = 135°
∴ Required angle = 135° (b)

Question 2.
Two straight lines AB and CD intersect one another at the point O. If ∠AOC + ∠COB + ∠BOD = 274°, then ∠AOD =
(a) 86°
(b) 90°
(c) 94°
(d) 137°
Solution:
Sum of angles at a point O = 360°
Sum of three angles ∠AOC + ∠COB + ∠BOD = 274°

∴ Fourth angle ∠AOD = 360° – 274°
= 86° (a)

Question 3.
Two straight lines AB and CD cut each other at O. If ∠BOD = 63°, then ∠BOC =
(a) 63°
(b) 117°
(c) 17°
(d) 153°
Solution:
CD is a line
∴ ∠BOD + ∠BOC = 180° (Linear pair)

⇒ 63° + ∠BOC = 180°
⇒ ∠BOC = 180° – 63°
∴ ∠BOC =117° (b)

Question 4.
Consider the following statements:
When two straight lines intersect:
(i) adjacent angles are complementary
(ii) adjacent angles are supplementary
(iii) opposite angles are equal
(iv) opposite angles are supplementary Of these statements
(a) (i) and (iii) are correct
(b) (ii) and (iii) are correct
(c) (i) and (iv) are correct
(d) (ii) and (iv) are correct
Solution:
Only (ii) and (iii) arc true. (b)

Question 5.
Given ∠POR = 3x and ∠QOR = 2x + 10°. If POQ is a striaght line, then the value of x is
(a) 30°
(b) 34°
(c) 36°
(d) none of these
Solution:
∵ POQ is a straight line
∴ ∠POR + ∠QOR = 180° (Linear pair)
⇒ 3x + 2x + 10° = 180°
⇒ 5x = 180 – 10° = 170°
∴ x = \(\frac { { 170 }^{ \circ } }{ 5 }\)  = 34° (b)

Question 6.
In the figure, AOB is a straight line. If ∠AOC + ∠BOD = 85°, then ∠COD =
(a) 85°
(b) 90°
(c) 95°
(d) 100°

Solution:
AOB is a straight line,
OC and OD are rays on it
and ∠AOC + ∠BOD = 85°
But ∠AOC + ∠BOD + ∠COD = 180°
⇒ 85° + ∠COD = 180°
∠COD = 180° – 85° = 95° (c)

Question 7.
In the figure, the value of y is
(a) 20°
(b) 30°
(c) 45°
(d) 60°

Solution:
In the figure,

y = x (Vertically opposite angles)
∠1 = 3x
∠2 = 3x
∴ 2(x + 3x + 2x) = 360° (Angles at a point)
2x + 6x + 4x = 360°
12x = 360° ⇒ x = \(\frac { { 360 }^{ \circ } }{ 12 }\)  = 30°
∴ y = x = 30° (b)

Question 8.
In the figure, the value of x is
(a) 12
(b) 15
(c) 20
(d) 30

Solution:
∠1 = 3x+ 10 (Vertically opposite angles)
But x + ∠1 + ∠2 = 180°

⇒ x + 3x + 10° + 90° = 180°
⇒ 4x = 180° – 10° – 90° = 80°
x = \(\frac { { 80 }^{ \circ } }{ 4 }\) = 20   (c)

Question 9.
In the figure, which of the following statements must be true?
(i) a + b = d + c
(ii) a + c + e = 180°
(iii) b + f= c + e
(a) (i) only
(b) (ii) only
(c) (iii) only
(d) (ii) and (iii) only

Solution:
In the figure,
(i) a + b = d + c
a° = d°
b° = e°
c°= f°
(ii) a + b + e = 180°
a + e + c = 180°
⇒ a + c + e = 180°
(iii) b + f= e + c
∴ (ii) and (iii) are true statements (d)

Question 10.
If two interior angles on the same side of a transversal intersecting two parallel lines are in the ratio 2:3, then the measure of the larger angle is
(a) 54°
(b) 120°
(c) 108°
(d) 136°
Solution:
In figure, l || m and p is transversal

= \(\frac { 3 }{ 5 }\) x 180° = 108° (c)

Question 11.
In the figure, if AB || CD, then the value of x is
(a) 20°
(b) 30°
(c) 45°
(d) 60°

Solution:
In the figure, AB || CD,
and / is transversal
∠1 = x (Vertically opposite angles)
and 120° + x + ∠1 = 180° (Co-interior angles)

Question 12.
Two lines AB and CD intersect at O. If ∠AOC + ∠COB + ∠BOD = 270°, then ∠AOC =
(a) 70°
(b) 80°
(c) 90°
(d) 180°
Solution:
Two lines AB and CD intersect at O

∠AOC + ∠COB + ∠BOD = 270° …(i)
But ∠AOC + ∠COB + ∠BOD + ∠DOA = 360° …(ii)
Subtracting (i) from (ii),
∠DOA = 360° – 270° = 90°
But ∠DOA + ∠AOC = 180°
∴ ∠AOC = 180° – 90° = 90° (c)

Question 13.
In the figure, PQ || RS, ∠AEF = 95°, ∠BHS = 110° and ∠ABC = x°. Then the value of x is
(a) 15°
(b) 25°
(c) 70°
(d) 35°

Solution:
In the figure,

PQ || RS, ∠AEF = 95°
∠BHS = 110°, ∠ABC = x
∵ PQ || RS,
∴ ∠AEF = ∠1 = 95° (Corresponding anlges)
But ∠1 + ∠2 = 180° (Linear pair)
⇒ ∠2 = 180° – ∠1 = 180° – 95° = 85°
In ∆AGH,
Ext. ∠BHS = ∠2 +x
⇒ 110° = 85° + x
⇒ x= 110°-85° = 25° (b)

Question 14.
In the figure, if l1 || l2, what is the value of x?
(a) 90°
(b) 85°
(c) 75°
(d) 70°

Solution:
In the figure,

∠1 = 58° (Vertically opposite angles)
Similarly, ∠2 = 37°
∵ l₁ || l₂, EF is transversal
∠GEF + EFD = 180° (Co-interior angles)
⇒ ∠2 + ∠l +x = 180°
⇒ 37° + 58° + x = 180°
⇒ 95° + x= 180°
x = 180°-95° = 85° (b)

Question 15.
In the figure, if l₁ || l₂, what is x + y in terms of w and z?
(a) 180-w + z
(b) 180° + w- z
(c) 180 -w- z
(d) 180 + w + z

Solution:
In the figure, l₁ || l₂

p and q are transversals
∴ w + x = 180° ⇒ x = 180° – w (Co-interior angle)
z = y (Alternate angles)
∴ x + y = 180° – w + z (a)

Question 16.
In the figure, if l₁ || l₂, what is the value of y?
(a) 100
(b) 120
(c) 135
(d) 150

Solution:
In the figure, l₁ || l₂ and l₃ is the transversal

Question 17.
In the figure, if l1 || l2 and l3 || l4 what is y in terms of x?
(a) 90 + x
(b) 90 + 2x
(c) 90 – \(\frac { x }{ 2 }\)
(d) 90 – 2x

Solution:
In the figure,

l₁ || l₂ and l₃ || l₄ and m is the angle bisector
∴ ∠2 = ∠3 = y
∵ l₁ || l₂
∠1 = x (Corresponding angles)
∵ l₃ || l₄
∴ ∠1 + (∠2 + ∠3) = 180° (Co-interior angles)
⇒ x + 2y= 180°
⇒ 2y= 180°-x
⇒ y = \(\frac { { 540 }^{ \circ }-x }{ 4 }\)
= 90° – \(\frac { x }{ 2 }\) (c)

Question 18.
In the figure, if 11| m, what is the value of x?
(a) 60
(b) 50
(c) 45
d) 30

Solution:
In the figure, l || m and n is the transversal

⇒ y = 25°
But 2y + 25° = x+ 15°
(Vertically opposite angles) ⇒ x = 2y + 25° – 15° = 2y+ 10°
= 2 x 25°+10° = 50°+10° = 60° (a)

Question 19.
In the figure, if AB || HF and DE || FG, then the measure of ∠FDE is
(a) 108°
(b) 80°
(c) 100°
(d) 90°

Solution:
In the figure,
AB || HF, DE || FG

∴ HF || AB
∠1 =28° (Corresponding angles)
But ∠1 + ∠FDE + 72° – 180° (Angles of a straight line)
⇒ 28° + ∠FDE + 72° = 180°
⇒ ∠FDE + 100° = 180°
⇒ ∠FDE = 180° – 100 = 80° (b)

Question 20.
In the figure, if lines l and m are parallel, then x =
(a) 20°
(b) 45°
(c) 65°
(d) 85°

Solution:
In the figure, l || m

∴ ∠1 =65° (Corresponding angles)
In ∆BCD,
Ext. ∠1 = x + 20°
⇒ 65° = x + 20°
⇒ x = 65° – 20°
⇒ x = 45° (b)

Question 21.
In the figure, if AB || CD, then x =
(a) 100°
(b) 105°
(c) 110°
(d) 115°

Solution:
In the figure, AB || CD
Through P, draw PQ || AB or CD

∠A + ∠1 = 180° (Co-interior angles)
⇒ 132° + ∠1 = 180°
⇒ ∠1 = 180°- 132° = 48°
∴ ∠2 = 148° – ∠1 = 148° – 48° = 100°
∵ DQ || CP
∴ ∠2 = x (Corresponding angles)
∴ x = 100° (a)

Question 22.
In tlie figure, if lines l and in are parallel lines, then x =
(a) 70°
(b) 100°
(c) 40°
(d) 30°

Solution:
In the figure, l || m

∠l =70° (Corresponding angles)
In ∆DEF,
Ext. ∠l = x + 30°
⇒ 70° = x + 30°
⇒ x = 70° – 30° = 40° (c)

Question 23.
In the figure, if l || m, then x =
(a) 105°
(b) 65°
(c) 40°
(d) 25°

Solution:
In the figure,
l || m and n is the transversal

∠1 = 65° (Alternate angles)
In ∆GHF,
Ext. x = ∠1 + 40° = 65° + 40°
⇒ x = 105°
∴ x = 105° (a)

Question 24.
In the figure, if lines l and m are parallel, then the value of x is
(a) 35°
(b) 55°
(c) 65°
(d) 75°

Solution:
In the figure, l || m
and PQ is the transversal

∠1 = 90°
In ∆EFG,
Ext. ∠G = ∠E + ∠F
⇒ 125° = x + ∠1 = x + 90°
⇒ x = 125° – 90° = 35° (a)

Question 25.
Two complementary angles are such that two times the measure of one is equal to three times the measure of the other. The measure of the smaller angle is
(a) 45°
(b) 30°
(c) 36°
(d) none of these
Solution:
Let first angle = x
Then its complementary angle = 90° – x
∴ 2x = 3(90° – x)
⇒ 2x = 270° – 3x
⇒ 2x + 3x = 270°
⇒ 5x = 270°
⇒ x = \(\frac { { 270 }^{ \circ } }{ 5 }\)  = 54°
∴ second angle = 90° – 54° = 36°
∴ smaller angle = 36° (c)

Question 26.

Solution:

Question 27.
In the figure, AB || CD || EF and GH || KL.
The measure of ∠HKL is
(a) 85°
(b) 135°
(c) 145°
(d) 215°

Solution:
In the figure, AB || CD || EF and GH || KL and GH is product to meet AB in L.

∵ AB || CD
∴ ∠1 = 25° (Alternate angle)
and GH || KL
∴ ∠4 = 60° (Corresponding angles)
∠5 = ∠4 = 60° (Vertically opposite angle)
∠5 + ∠2 = 180° (Co-interior anlges)
∴ ⇒ 60° + ∠2 = 180°
∠2 = 180° – 60° = 120°
Now ∠HKL = ∠1 + ∠2 = 25° + 120°
= 145° (c)

Question 28.
AB and CD are two parallel lines. PQ cuts AB and CD at E and F respectively. EL is the bisector of ∠FEB. If ∠LEB = 35°, then ∠CFQ will be
(a) 55°
(b) 70°
(c) 110°
(d) 130°
Solution:
AB || CD and PQ is the transversal EL is the bisector of ∠FEB and ∠LEB = 35°

∴ ∠FEB = 2 x 35° = 70°
∵ AB || CD
∴ ∠FEB + ∠EFD = 180°
(Co-interior angles)
70° + ∠EFD = 180°
∴ ∠EFD = 180°-70°= 110°
But ∠CFQ = ∠EFD
(Vertically opposite angles)
∴ ∠CFQ =110° (c)

Question 29.
In the figure, if line segment AB is parallel to the line segment CD, what is the value of y?
(a) 12
(b) 15
(c) 18
(d) 20

Solution:
In the figure, AB || CD
BD is transversal
∴ ∠ABD + ∠BDC = 180° (Co-interior angles)
⇒y + 2y+y + 5y = 180°
⇒ 9y = 180° ⇒ y = \(\frac { { 180 }^{ \circ } }{ 9 }\)  = 20° (d)

Question 30.
In the figure, if CP || DQ, then the measure of x is
(a) 130°
(b) 105°
(c) 175°
(d) 125°

Solution:
In the figure, CP || DQ
BA is transversal
Produce PC to meet BA at D

∵ QB || PD
∴ ∠D = 105° (Corresponding angles)
In ∆ADC,
Ext. ∠ACP = ∠CDA + ∠DAC
⇒ x = ∠1 + 25°
= 105° + 25° = 130° (a)

Hope given RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.