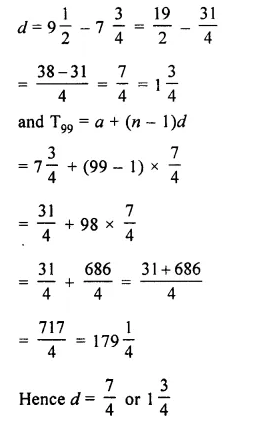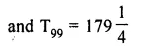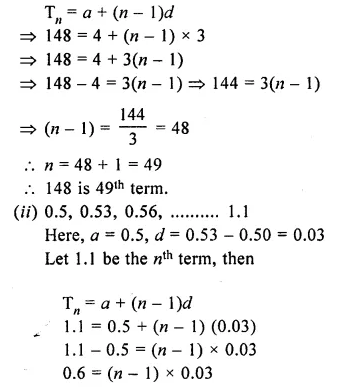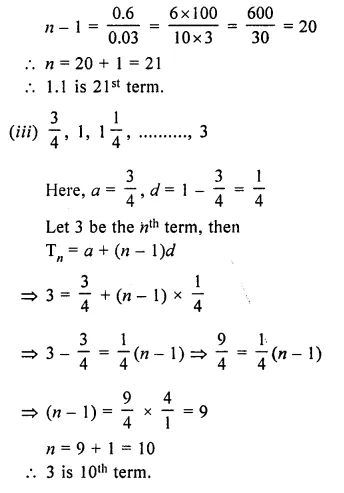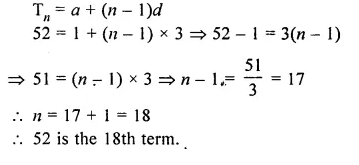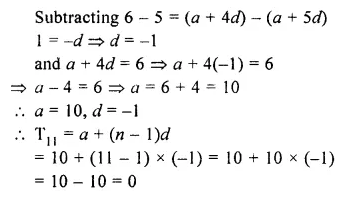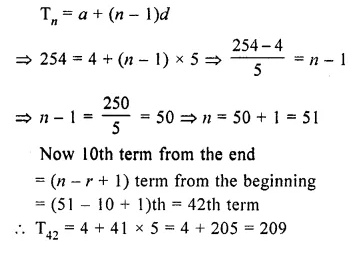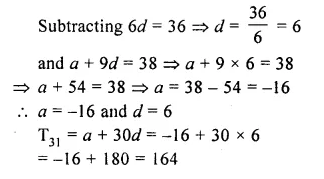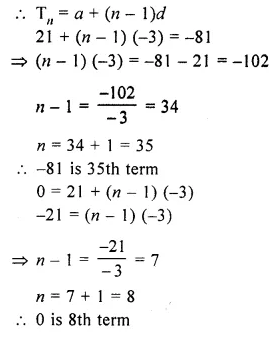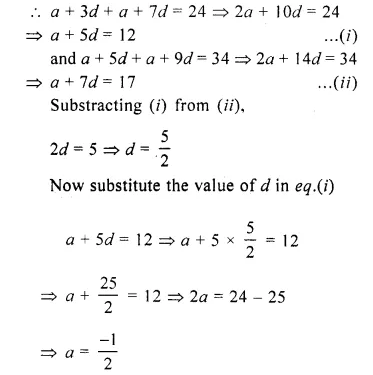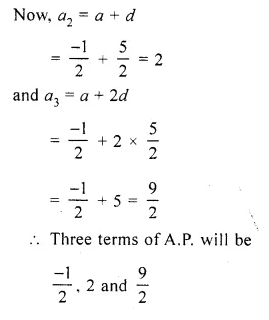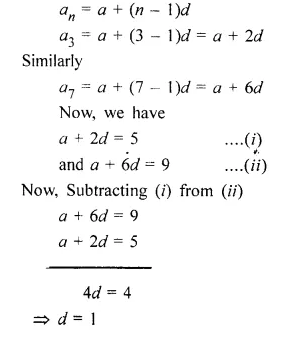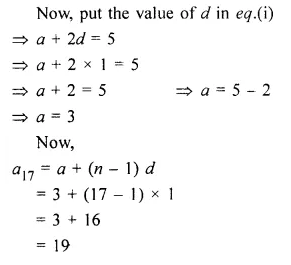Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10B
These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10B
Other Exercises
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10A
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10B
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10C
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10D
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10E
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10F
Question 1.
In an A.P., ten times of its tenth term is equal to thirty times of its 30th term. Find its 40th term.
Solution:
In an A.P.
10T10 = 30T30
We know that,
If m times of mth term = n times of nth term
Then its (m + n)th term = 0
∴ 10T10 = 30T30
Then T10+30 = 0 or T40 = 0
Question 2.
How many two-digit numbers are divisible by 3 ?
Solution:
Two digits numbers are 10 to 99
and two digits numbers which are divisible
by 3 are 12, 15, 18, 21,….99
Here a = 12, d = 3 and l = 99
Now, Tn = l = a + (n – 1 )d
99 = 12 + (n – 1) x 3
=> 99 – 12 = 3(n – 1)
=> 87 = 3(n – 1)
=> \(\\ \frac { 87 }{ 3 } \) = n – 1
=> n – 1 = 29
n = 29 + 1 = 30
Number of two digit number divisible by 3 = 30
Question 3.
Which term of A.P. 5, 15, 25, will be 130 more than its 31st term?
Solution:
A.P. is 5, 15, 25,….
Let Tn = T31 + 130
In A.P. a = 5, d = 15 – 5 = 10
∴ Tn = a + 30d + 130 = 5 + 30 x 10 +130
= 5 + 300 + 130 = 435
∴ n + (n – 1)d = 435
=> 5 + (n – 1) x 10 = 435
=> (n – 1) x 10 = 435 – 5 = 430
n – 1 = \(\\ \frac { 430 }{ 10 } \) = 43
n = 43 + 1 = 44
∴ The required term is 44th.
Question 4.
Find the value of p, if x, 2x + p and 3x + 6 are in A.P.
Solution:
A.P. is x, 2x + p, 3x + 6
2x + p – x = 3x + 6 – 2x + p
x + p = x – p + 6
=>2p = 6
=>p = \(\\ \frac { 6 }{ 2 } \) = 3
Hence p = 3
Question 5.
If the 3rd and the 9th terms of an arithmetic progression are 4 and – 8 respectively, which term of it is zero?
Solution:
In an A.P.
T3 = 4 and T9 = – 8
Let a be the first term and d be the common difference, then
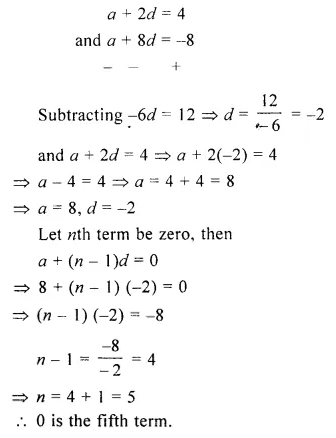
Question 6.
How many three-digit numbers ate divisible by 87 ?
Solution:
Three digits numbers are 100 to 999

999 – 42 = 957
Numbers divisible by 87 will be 174,….., 957
Let n be the number of required three digit number.
Here, a = 174 and d = 87
l = 957 = a + (n – l)d
= 174 + (n – 1) x 87
=> (n – 1) x 87 = 957 – 174 = 783
n – 1 = \(\\ \frac { 783 }{ 87 } \) = 9
n = 9 + 1 = 10
There are 10 such numbers.
Question 7.
For what value of n, the nth term of A.P. 63, 65, 67,….. and nth term of A.P. 3, 10, 17,…… are equal to each other?
Solution:
We are given,
nth term of 63, 65, 67, …….
=> nth term of 3, 10, 17,…….
=> In first A.P., a1 = 63, d1 = 2
and in second A.P., a2 = 3, d2 = 1
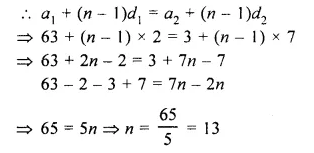
∴ Required nth term will be 13th
Question 8.
Determine the A.P. whose 3rd term is 16 and the 7th term exceeds the 5th term by 12.
Solution:
T3 = 16, and T7 = T5 + 12
Let a be the first term and d be the common difference
T3 = a + 2d – 16 …(i)
T7 = T5 + 12
a + 6d = a + 4d + 12
=> 6d – 4d = 12 => 2d – 12
=> d = \(\\ \frac { 12 }{ 2 } \) = 6
and in (i),
a + 6 x 2 = 16
=> a + 12 = 16
=>a = 16 – 12 = 4
A.P. will be 4, 10, 16, 22,……
Question 9.
If numbers n – 2, 4n – 1 and 5n + 2 are in A.P., find the value of n and its next two terms.
Solution:
n – 2, 4n – 1 and 5n + 2 are in A.P.
(4n – 1) – (n – 2) = (5n + 2) – (4n – 1)
=> 4n – 1 – n + 2 = 5n + 2 – 4n + 1
=> 4n – n – 5n + 4n = 2 + 1 + 1 – 2
=>2n = 2 =>n = \(\\ \frac { 2 }{ 2 } \) = 1
4n – 1 = 4 x 1 – 1 = 4 – 1 = 3
n – 2 = 1 – 2 = – 1
and 5n + 2 = 5 x 1 + 2 = 5 + 2 = 7
A.P. is – 1, 3, 7, ……
and next 2 terms will 11, 15
Question 10.
Determine the value of k for which k2 + 4k + 8, 2k2 + 3k + 6 and 3k2 + 4k + 4 are in A.P.
Solution:
k2 + 4k+ 8, 2k2 + 3k + 6 and 3k2 + 4k + 4 are in A.P.
(2k2 + 3k + 6) – (k2 + 4k + 8)
= (3k2 + 4k + 4) – (2k2 + 3k + 6)
=> 2k2 + 3k + 6 – k2 – 4k – 8
= 3k2 + 4k + 4 – 2k2 – 3k – 6
=> k2 – k – 2 = k2 + k – 2
=> k2 – k – k2 – k = – 2 + 2
=> – 2k = 0
=> k = 0
Hence k = 0
Question 11.
If a, b and c are in A.P. show that :
(i) 4a, 4b and 4c are in A.P.
(ii) a + 4, b + 4 and c + 4 are in A.P.
Solution:
a, b, c are in A.P.
2b = a + c
(i) 4a, 4b and 4c are in A.P.
If 2(4b) = 4a + 4c
If 8b = 4a + 4c
If 2b = a + c which is given
(ii) a + 4, b + 4 and c + 4 are in A.P.
If 2(b + 4) = a + 4 + c + 4
If 2b + 8 = a + c + 8
If 2b = a + c which is given
Question 12.
An A.P. consists of 57 terms of which 7th term is 13 and the last term is 108. Find the 45th term of this A.P.
Solution:
Number of terms in an A.P. = 57
T7 = 13, l= 108
To find T45
Let a be the first term and d be the common difference
=> a + 6d = 13 …(i)
a + (n – 1 )d= 108
=> a + (57 – 1 )d= 108
=> a + 56d = 108
Subtracting,
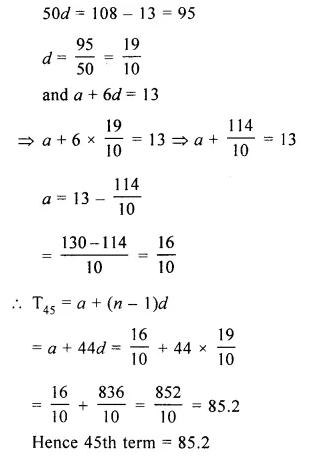
Question 13.
4th term of an A.P. is equal to 3 times its term and 7th term exceeds twice the 3rd term by 1. Find the first term and the common difference.
Solution:
In A.P
T4 = 3 x T1
T7 = 2 x T3 + 1
Let a be the first term and d be the common
difference

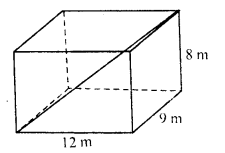
Question 14.
The sum of the 2nd term and the 7th term of an A.P. is 30. If its 15th term is 1 less than twice of its 8th term, find the A.P.
Solution:
In an A.P.
T2 + T7 = 30
T15 = 2T8 – 1
Let a be the first term and d be the common difference
a + d + a + 6d = 30
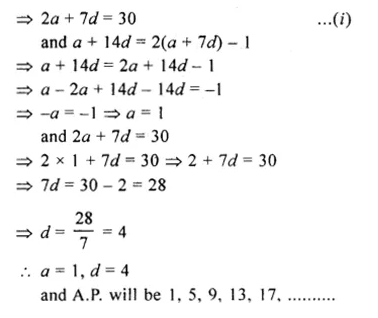
Question 15.
In an A.P., if mth term is n and nth term is m, show that its rth term is (m + n – r)
Solution:
In an A.P.
Tm = n and Tn = m
Let a be the first term and d be the common difference, then
Tm = a + (m – 1 )d = n

Question 16.
Which term of the A.P. 3, 10, 17,…..will be 84 more than its 13th term?
Solution:
A.P. is 3, 10, 17,….
Here, a = 2, d = 10 – 3 = 7

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10B are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.