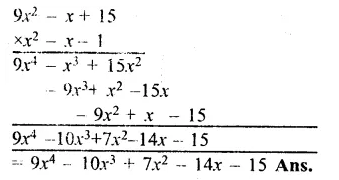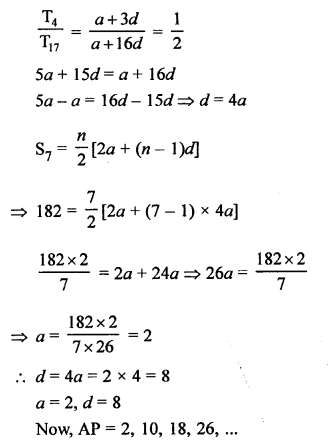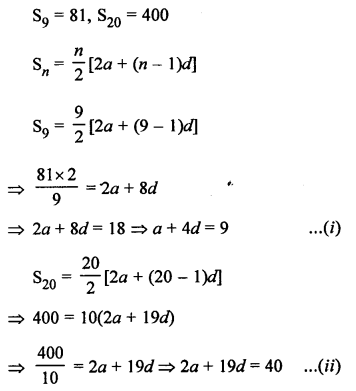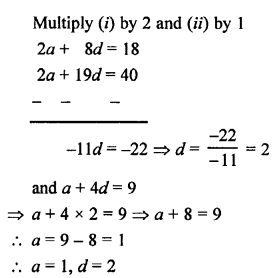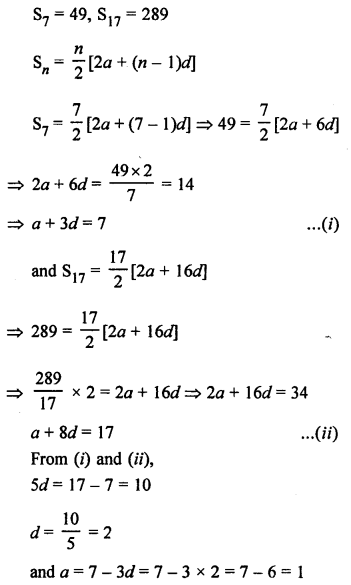Prasanna

RS Aggarwal Class 8 Solutions Chapter 6 Operations on Algebraic Expressions Ex 6D

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6D.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6A
• RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6B
• RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6C
• RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6D
• RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6E

Question 1.
Solution:
(i)(x + 6)(x + 6)
= (x + 6)²

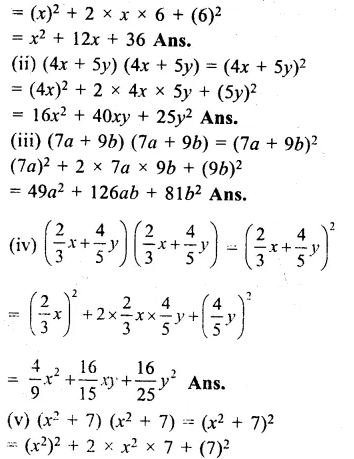
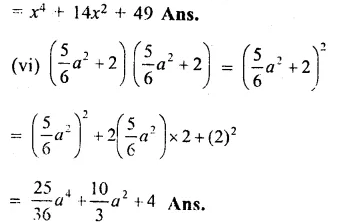
You can also Download NCERT Solutions for Class 8 English to help you to revise complete Syllabus and score more marks in your examinations.

Question 2.
Solution:
(i) (x – 4)(x – 4)
= (x – 4)²

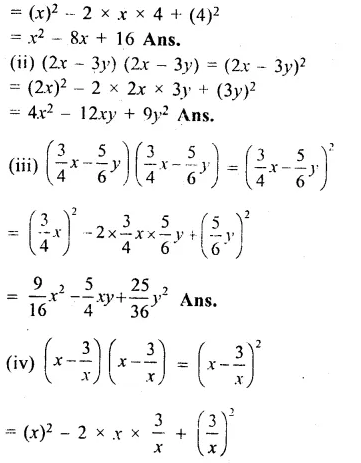
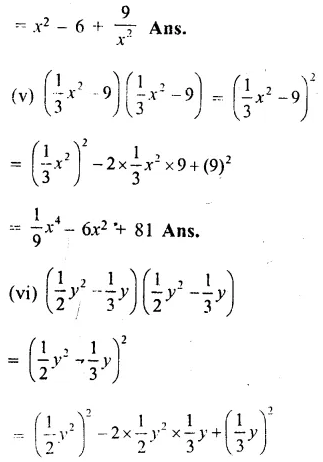
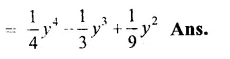
Question 3.
Solution:
(i)(8a + 3b)²
= (8a)² + 2 x 8a x 3b + (3b)²

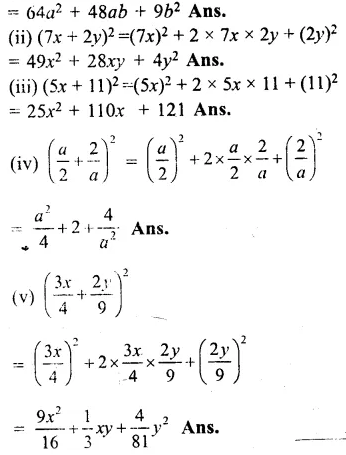
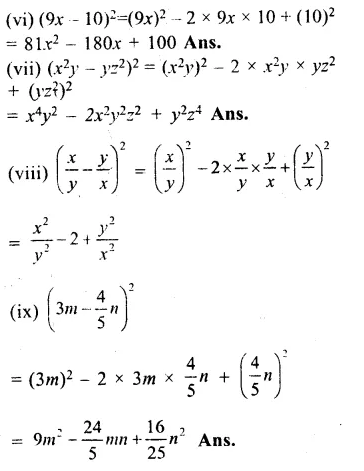
Question 4.
Solution:
(i)(x + 3)(x – 3)
= (x)² – (3)²

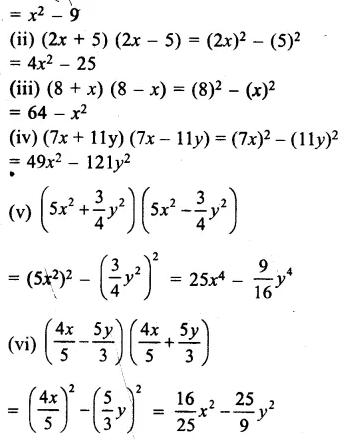
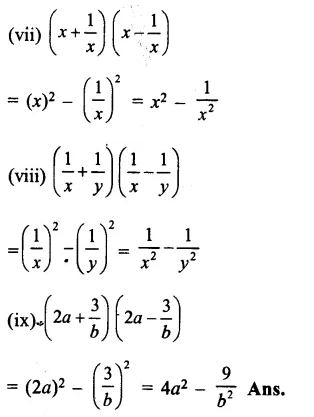
Question 5.
Solution:
(i) (54)²
= (50 + 4)²

Question 6.
Solution:
(i) (69)²
= (70 – 1)²

Question 7.
Solution:
(i)(82)² – (18)²
= (82 – 18)(82 – 18)

Question 8.
Solution:
9x² + 24x + 16
= (3x)² + 2 x 3x x 4 + (4)²
= (3x + 4)²
= (3 x 12 + 4)²
= (36 + 4)²
= (40)²
= 1600 Ans.

Question 9.
Solution:
64x² + 81y² + 144xy = (8x)² + (9y)² + 2 x 8x x 9y
= (8x + 9y)²
= \({ \left( 8\times 11+9\times \frac { 4 }{ 3 } \right) }^{ 2 }\)
= (88 + 12)²
= (100)²
= 10000 Ans.

Question 10.
Solution:
(36x² + 25y² – 60xy)
= (6x)² + (5y)² – 2 x 6x x 5y
= (6x – 5y)²
= \({ \left( 6\times \frac { 2 }{ 3 } -5\times \frac { 1 }{ 5 } \right) }^{ 2 } \)
= (4 – 1)²
= (3)² = 9

Question 11.
Solution:
\(\left( x+\frac { 1 }{ 4 } \right) =4 \)
Squaring on both sides

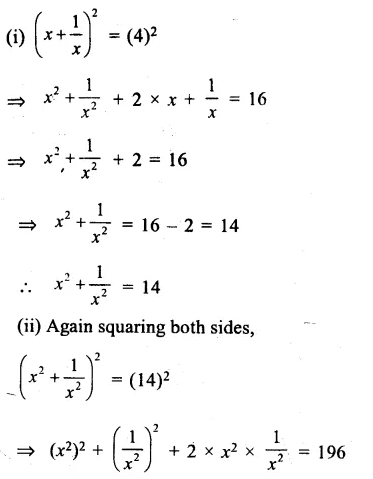
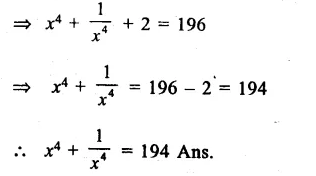
Question 12.
Solution:
\(\left( x-\frac { 1 }{ x } \right) =5 \)
(i) Squaring on both sides

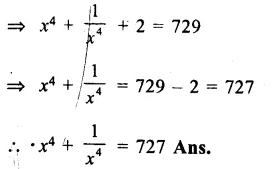
Question 13.
Solution:
(i) (x + 1) (x – 1) (x² + 1)
= {(x)² – (1)²} (x² + 1)
= (x² – 1) (x² + 1)
= (x²)² – (1)² = x⁴ – 1 Ans.
(ii) (x – 3) (x + 3) (x² + 9)
= {(x)² – (3)² } (x² + 9)
= (x² – 9) (x² + 9)
= (x²)² – (9)² = x⁴ – 81 Ans.
(iii) (3x – 2y) (3x + 2y) (9x² + 4y²)
= {(3x)² – (2y)²} (9x² + 4y²)
= (9x² – 4y²) (9x² + 4y²)
= (9x²)² – (4y²)²
= 81x⁴ – 16y⁴ Ans.
(iv) (2p + 3) (2p – 3) (4p² + 9)
= {(2p)² – (3)²} (4p² + 9)
= (4p² – 9) (4p² + 9)
= (4p²)² – (9)² = 16p⁴ – 81 Ans.

Question 14.
Solution:
x + y = 12
Squaring both sides,
(x + y)² = (12)²
=> x² + y² + 2xy = 144
=> x² + y² + 2 x 14 = 144
=> x² + y² + 28 = 144
=> x² + y² = 144 – 28 = 116
x² + y² = 116 Ans.

Question 15.
Solution:
x – y = 7
Squaring both sides,
(x – y)² = (7)²
=> x² + y² – 2xy = 49
=> x² + y² – 2 x 9 = 49
=> x² + y² – 18 = 49
=> x² + y² = 49 + 18 = 67
x² + y² = 67 Ans.

Hope given RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 6 Operations on Algebraic Expressions Ex 6B

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6B.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6A
• RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6B
• RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6C
• RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6D
• RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6E

Find each of the following products?

Question 1.
Solution:
(5x + 7) X (3x + 4) = 5x(3x + 4) + 7(3x + 4)
= 15x² + 20x + 21x + 28 = 15x² + 41x + 28 Ans.

Question 2.
Solution:
(4x + 9) X (x – 6) = 4x(x – 6) + 9(x – 6)
= 4x² – 24x + 9x – 54
= 4x² – 15x – 54 Ans.

Question 3.
Solution:
(2x + 5) X (4x – 3) = 2x(4x – 3) + 5(4x – 3)
= 8x² – 6x + 20x – 15
= 8x² + 14x – 15 Ans.

Question 4.
Solution:
(3y – 8) X (5y – 1) = 3y(5y – 1) – 8(5y – 1)
= 15y² – 3y – 40y + 8
= 15y² – 43y + 8 Ans.

Question 5.
Solution:
(7x + 2y) X (x + 4y)
= 7x(x + 4y) + 2y(x + 4y)
= 7x² + 28xy + 2xy + 8y²
= 7x² + 30xy + 8y² Ans.

Question 6.
Solution:
(9x + 5y) X (4x + 3y) = 9x(4x + 3y) + 5y(4x + 3y)
= 36x² + 27xy + 20xy + 15y²
= 36x² + 47xy + 15y² Ans.

Question 7.
Solution:
(3m – 4n) X (2m – 3n)
= 3m(2m – 3n) – 4n(2m – 3n)
= 6m² – 9mn – 8mn + 12n²
= 6m² – 17mn + 12n² Ans.

Question 8.
Solution:
(x² – a²) X (x – a)
= x²(x – a) – a²(x – a)
= x³ – x²a – xa² + a³ Ans.

Question 9.
Solution:
(x² – y²) X (x + 2y)
= x²(x + 2y) – y²(x + 2y)
= x³ + 2x²y – xy² – 2y³ Ans.

Question 10.
Solution:
(3p² + q²) X (2p² – 3q²)
= 3p²(2p² – 3q²) + q²(2p² – 3q²)
= 6p⁴ – 9p²q² + 2p²q² – 3q⁴
= 6p⁴ – 7p²q² – 3q⁴ Ans.

Question 11.
Solution:
(2x² – 5y²) X (x² + 3y²)
= 2x²(x² + 3y²) – 5y²(x² + 3y²)
= 2x⁴ + 6x²y² – 5x²y² – 15y⁴)
= 2x⁴ + x2y² – 15y⁴ Ans.

Question 12.
Solution:
(x³ – y³) X (x² + y²)
= x³(x² + y²) – y³(x² + y²)
= x⁵ + x³y² – x²y³ – y⁵ Ans.

Question 13.
Solution:
(x⁴ + y⁴) X (x² – y²)
= x⁴(x² – y²) + y⁴(x² – y²)
= x⁶ – x⁴y² + x²y⁴ – y⁶ Ans.

Question 14.
Solution:
\(\left( { x }^{ 4 }+\frac { 1 }{ { x }^{ 4 } } \right) \times \left( { x+ }\frac { 1 }{ { x } } \right)\)

Find each of the following products:

Question 15.
Solution:
(x² – 3x + 7) X (2x + 3)
= (x² – 3x + 7) (2x) + (x² – 3x + 7) X 3
= 2x³ – 6x + 14x + 3x² – 9x + 21
= 2x³ – 3x² + 5x + 21 Ans.

Question 16.
Solution:
(3x² + 5x – 9) X (3x – 5)
= 3x²(3x – 5x) + 5x(3x – 5) – 9(3x – 5)
= 9x³ – 15x² + 15x² – 25x – 27x + 45
= 9x³ – 52x + 45 Ans.

Question 17.
Solution:
(x² – xy + y²) X (x + y)
= (x² – xy + y²) X x + (x² – xy + y²) X y
= x³ – x²y + xy² + x²y – xy² + y³
= x³ + y³ Ans.

Question 18.
Solution:
(x² + xy + y²) X (x – y)
(x² + xy + y²) X x + (x² + xy + y²) X ( – y)
= x³ + x²y + xy² – x²y – xy² – y³
= x³ – y³ Ans.

Question 19.
Solution:
(x³ – 2x² + 5) X (4x – 1)
= (x³ – 2x² + 5) X 4x + (x³ – 2x² + 5) X ( – 1)
= 4x⁴ – 8x³ + 20x – x³ + 2x² – 5
= 4x⁴ – 9x³ + 2x² + 20x – 5 Ans.

Question 20.
Solution:
(9x² – x + 15) X (x² – 3)
(9x² – X + 15) X x² + (9x² – x + 15) X ( – 3)
= 9x⁴ – x³ + 15x² – 27x² + 3x – 45
= 9x⁴ – x³ – 12x² + 3x – 45 Ans.

Question 21.
Solution:
(x² – 5x + 8) X (x² + 2)
= (x² – 5x + 8) X x² + (x² – 5x + 8) X 2
= x⁴ – 5x³ + 8x² + 2x² – 10x + 16
= x⁴ – 5x³ + 10x² – 10x + 16 Ans.

Question 22.
Solution:
(x³ – 5x² + 3x + 1) X (x² – 3)
= (x³ – 5x² + 3x + 1) X x² + (x³ – 5x² + 3x + 1) X ( – 3)
= x⁵ – 5x⁴ + 3x³ + x² – 3x³ + 15x² – 9x – 3
= x⁵ – 5x⁴ + 16x² – 9x – 3 Ans.

Question 23.
Solution:
(3x + 2y – 4) X (x – y + 2)

Question 24.
Solution:
(x² – 5x + 8) X (x² + 2x – 3)

Question 25.
Solution:
(2x² + 3x – 7) X (3x² – 5x + 4)

Question 26.
Solution:
(9x² – x + 15) X (x² – x – 1)

Hope given RS Aggarwal Solutions Class 8 Chapter 6 Operations on Algebraic Expressions Ex 6B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4C

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 4 Cubes and Cube Roots Ex 4C.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 4 Cubes and Cube Roots Ex 4A
• RS Aggarwal Solutions Class 8 Chapter 4 Cubes and Cube Roots Ex 4B
• RS Aggarwal Solutions Class 8 Chapter 4 Cubes and Cube Roots Ex 4C
• RS Aggarwal Solutions Class 8 Chapter 4 Cubes and Cube Roots Ex 4D

Evaluate:

Question 1.
Solution:
\(\sqrt [ 3 ]{ 64 } \)
= \(\sqrt [ 3 ]{ 4X4X4 } \)
= \(\sqrt [ 3 ]{ { 4 }^{ 3 } } \)
= 4

Question 2.
Solution:
\(\sqrt [ 3 ]{ 343 } \)
= \(\sqrt [ 3 ]{ 7X7X7 } \)
= \(\sqrt [ 3 ]{ { 7 }^{ 3 } } \)
= 7

Question 3.
Solution:
\(\sqrt [ 3 ]{ 729 } \)

Question 4.
Solution:
\(\sqrt [ 3 ]{ 1728 } \)

Question 5.
Solution:
\(\sqrt [ 3 ]{ 9261 } \)

Question 6.
Solution:
\(\sqrt [ 3 ]{ 4096 } \)

Question 7.
Solution:
\(\sqrt [ 3 ]{ 8000 } \)

Question 8.
Solution:
\(\sqrt [ 3 ]{ 3375 } \)

Question 9.
Solution:
\(\sqrt [ 3 ]{ -216 } \)

Question 10.
Solution:
\(\sqrt [ 3 ]{ -512 } \)

Question 11.
Solution:
\(\sqrt [ 3 ]{ -1331 } \)

Question 12.
Solution:
\(\sqrt [ 3 ]{ \frac { 27 }{ 64 } } \)

Question 13.
Solution:
\(\sqrt [ 3 ]{ \frac { 125 }{ 216 } } \)

Question 14.
Solution:
\(\sqrt [ 3 ]{ \frac { -27 }{ 125 } } \)

Question 15.
Solution:
\(\sqrt [ 3 ]{ \frac { -64 }{ 343 } } \)

Question 16.
Solution:
\(\sqrt [ 3 ]{ 64\times 729 }\)

Question 17.
Solution:
\(\sqrt [ 3 ]{ \frac { 729 }{ 1000 } } \)

Question 18.
Solution:
\(\sqrt [ 3 ]{ \frac { -512 }{ 343 } } \)

Hope given RS Aggarwal Solutions Class 8 Chapter 4 Cubes and Cube Roots Ex 4C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 7 Factorisation Ex 7B

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 7 Factorisation Ex 7B.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 7 Factorisation Ex 7A
• RS Aggarwal Solutions Class 8 Chapter 7 Factorisation Ex 7B
• RS Aggarwal Solutions Class 8 Chapter 7 Factorisation Ex 7C
• RS Aggarwal Solutions Class 8 Chapter 7 Factorisation Ex 7D
• RS Aggarwal Solutions Class 8 Chapter 7 Factorisation Ex 7E

Question 1.
Solution:
x² – 36
= (x)² – (6)² { ∵ a² – b² = (a + b) (a – b)}
= (x + 6) (x – 6) Ans.

Question 2.
Solution:
4a² – 9
= (2a)² – (3)²
= (2a + 3) (2a – 3)
{ ∵ a² – b² = (a + b) (a – b)}

You can also Download NCERT Solutions for Class 8 English to help you to revise complete Syllabus and score more marks in your examinations.

Question 3.
Solution:
81 – 49x²
= (9)² – (7x)²
= (9 + 7x) (9 – 7x) { ∵ a² – b² = (a + b) (a – b)}

Question 4.
Solution:
= (2x)² – (3y)²
= (2x + 3y)(2x-3y)
{∵ a² – b² = (a + b) (a – b)}

Question 5.
Solution:
Using a² – b²
= (a + b) (a – b)
= 16a² – 225b²
= (4a)² – (15b)²
= (4a + 15b) (4b – 5b)

Question 6.
Solution:
Using a² – b²
= (a + b) (a – b)
= (3ab)² – (5)²
= (3ab + 5) (3ab – 5)

Question 7.
Solution:
Using a² – b² = (a + b) (a – b)
16a² – 144 = (4a)² = (12)²
= (4a + 12) (4a – 12)
= 4 (a + 3) x 4 (a – 3)
= 16 (a + 3) (a – 3)

Question 8.
Solution:
63a² – 112b²
= 7 (9a² – 16b²)
= 7 [(3a)² – (4b)²
= 7 (3a + 4b) (3a – 4b)

Question 9.
Solution:
20a² – 45b²
= 5 {4a² – 9b²}
= 5{(2a)² – (3b)²)
= 5(2a + 3b) (2a – 3b) Ans.

Question 10.
Solution:
12x² – 27
= 3(4x² – 9)
= 3{(2x)² – (3)²}
= 3(2x + 3) (2x – 3) Ans.

Question 11.
Solution:
x³ – 64x
= x(x² – 64)
= x{(x)² – (8)²}
= x(x + 8) (x – 8) Ans.

Question 12.
Solution:
16x⁵ – 144x³
= 16x³ [x² – 9]
= 16x³ [(x)² – (3)²]
= 16x³ (x + 3) (x – 3)

Question 13.
Solution:
3x⁵ – 48x³
= 3x³ {x² – 16}
= 3x³{(x)² – (4)²}
= 3x³ (x + 4) (x – 4) Ans.

Question 14.
Solution:
16p³ – 4p
= 4p [4p² – 1]
= 4p ((2p)² – (1)²]
= 4p(2p + 1)(2p – 1)

Question 15.
Solution:
63a²b² – 7
= 7(9a²b² – 1)
= 7{(3ab)² – (1)²)
= 7(3ab + 1) (3ab – 1) Ans.

Question 16.
Solution:
1 – (b – c)²
= (1)² – (b – c)²
= (1 + b + c) (1 – b + c) Ans.
{ ∵ a² – b² = (a + b) (a – b)}

Question 17.
Solution:
(2a + 3b)² – 16c²
= (2a + 3b)² – (4c)²
=(2a + 3b + 4c)(2a + 3b – 4c)Ans.
{ ∵ a² – b² = (a + b)(a – b)}

Question 18.
Solution:
(l + m)² – (l – m)²
= (l + m + l – m)(l + m – l + m)
{ ∵ a² – b² = (a + b)(a – b)}
= 2l x 2m = 4lm

Question 19.
Solution:
(2x + 5y)² – (1)²
=(2x + 5y + 1)(2x + 5y – 1)
{ ∵ a² – b² = (a + b)(a – b)}

Question 20.
Solution:
36c² – (5a + b)²
= (6c)² – (5a + b)²
{ ∵ a² – b² = (a + b)(a – b)}
= (6c + 5a + b)(6c – 5a – b)

Question 21.
Solution:
(3x – 4y)² – 25z²
= (3x – 4y)² – (5z)²
= (3x – 4y + 5z) (3x – 4y – 5z) Ans.

Question 22.
Solution:
x² – y² – 2y – 1
= x² – (y² + 2y + 1)
= (x)² – (y + 1)²
= (x + y + 1)(x – y – 1)Ans.

Question 23.
Solution:
25 – a² – b² – 2ab
= 25 – (a² + b² + 2ab)
= (5)² – (a + b)²
= (5 + a + b)(5 – a – b)Ans.

Question 24.
Solution:
25a² – 4b² + 28bc – 49c²
= 25a² – [4b² – 28bc + 49c²]
{ ∵ a² – 2ab + b² = (a – b)²}
= (5a)² – [(2b)² – 2 x 2b x 7c + (7c)²]
= (5a)² – (2b – 7c)²
{ ∵ (a² – b² = (a + b)(a – b)}
= (5a + 2b – 7c) (5a – 2b + 7c)

Question 25.
Solution:
9a² – b² + 4b – 4
= 9a² – (b² – 4b + 4)
= (3a)² – [(b)² – 2 x b x 2 + (2)²]
= (3a)² – (b – 2)²
{ ∵ a² – 2ab + b² = (a – b)²}
= (3a + b – 2)(3a – b + 2)
{ ∵ a² – b² = (a + b)(a – b)}

Question 26.
Solution:
(10)² – (x – 5)²
= (10)² – (x – 5)²
= (10 + x – 5)(10 – x + 5)
= (5 + x) (15 – x) Ans.

Question 27.
Solution:
{(405)² – (395)²}
= (405)² – (395)²
= (405 + 395) (405 – 395)
{ ∵ a² – b²(a + b) (a – b)}
= 800 x 10 = 8000

Question 28.
Solution:
(7.8)² – (2.2)²
= (7.8 + 2.2) (7.8 – 2.2)
= 10.0 x 5.6
= 56 Ans.

Hope given RS Aggarwal Solutions Class 8 Chapter 7 Factorisation Ex 7B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3D

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3D.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3A
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3B
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3C
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3D
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3E
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3F
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3G
• RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3H

Find the square root of each of the following numbers by using the method of prime factorization:

Question 1.
Solution:
225 = 3 x 3 x 5 x 5

Question 2.
Solution:
441 = 3 x 3 x 7 x 7

Question 3.
Solution:
729 =

Question 4.
Solution:
1296 = 2 x 2 x 2 x 2 x 3 x 3 x 3 x 3

Question 5.
Solution:
2025 =

Question 6.
Solution:
4096 =

Question 7.
Solution:
7056 = 2 x 2 x 2 x 2 x 3 x 3 x 7 x 7

Question 8.
Solution:
8100 =

Question 9.
Solution:
9216 =

Question 10.
Solution:
11025 =

Question 11.
Solution:
15876 =

Question 12.
Solution:
17424 =

Question 13.
Solution:
Factorizing 252, we get :
252 = \(\overline { 2X2 } X\overline { 3X3 } X7\)

To make it is a perfect square it must by multiplied by 7.
Square root of 252 x 7 = 1764
= 2 x 3 x 7 = 42 Ans.

Question 14.
Solution:
Factorizing 2925, we get :
2925 = \(\overline { 3X3 } X\overline { 5X5 } X13\)

To make it a perfect square it must be divided by 13.
2925 ÷ 13 = 225
Square root of 225 = 3 x 5 = 15 Ans.

Question 15.
Solution:
Let no. of rows = x
Then the number of plants in each row = x

Hence no. of rows = 35
and no. of plants in each row = 35

Question 16.
Solution:
Let no. of students in the class = x
Then contribution of each student = x

No. of students of the class = 34 Ans.

Question 17.
Solution:
L.C.M. of 6, 9, 15 and 20
= 2 x 3 x 5 x 2 x 3 = 180
180 = \(\overline { 2X2 } X\overline { 3X3 } X5\)

To make it a perfect square, it must be multiplied by 5
Product = 180 x 5 = 900
Hence, the least square number = 900 Ans.

Question 18.
Solution:
L.C.M. of 8, 12, 15, 20 = 2 x 2 x 2 x 3 x 5= 120
120 = \(\overline { 2X2 }\)X2X3X5
To make it a perfect square it must be multiplied by 2 x 3 x 5 = 30
Then least perfect square = 120 x 30 = 3600

Hope given RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 11 Arithmetic Progressions Ex 11C

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11C

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11A
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11B
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11C
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11D
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions MCQS

Question 1.
Solution:

Question 2.
Solution:

Question 3.
Solution:

Question 4.
Solution:
S_n = 3n² + 6n

Question 5.
Solution:
S_n = 3n² – n
S₁ = 3(1)² – 1 = 3 – 1 = 2
S₂ = 3(2)² – 2 = 12 – 2 = 10
T₂ = 10 – 2 = 8 and
T₁ = 2
(i) First term = 2
(ii) Common difference = 8 – 2 = 6
T_n = a + (n – 1) d = 2 + (n – 1) x 6
= 2 + 6n – 6 = 6n – 4

Question 6.
Solution:

Question 7.
Solution:
Let a be first term and d be the common difference of an AP.
Since, we have,
a_m = a + (m – 1) d = \(\frac { 1 }{ n }\) …(i)

Question 8.
Solution:
AP is 21, 18, 15,…
Here, a = 21,
d = 18 – 21 = -3,
sum = 0
Let number of terms be n, then

Question 9.
Solution:
AP is 9, 17, 25,…
Here, a = 9, d = 17 – 9 = 8
Sum of terms = 636
Let number of terms be n, then

Which is not possible being negative and fraction.
n = 12
Number of terms = 12

Question 10.
Solution:
AP is 63, 60, 57, 54,…
Here, a = 63, d = 60 – 63 = -3 and sum = 693
Let number of terms be n, then

22th term is zero.
There will be no effect on the sum.
Number of terms are 21 or 22.

Question 11.
Solution:

Question 12.
Solution:
Odd numbers between 0 and 50 are 1, 3, 5, 7, 9, …, 49
Here, a = 1, d = 3 – 1 = 2, l = 49

= \(\frac { 25 }{ 2 }\) x 50 = 25 x 25 = 625

Question 13.
Solution:
Numbers between 200 and 400 which are divisible by 7 will be 203, 210, 217,…, 399
Here, a = 203, d = 7, l = 399

Question 14.
Solution:
First forty positive integers are 0, 1, 2, 3, 4, …
and numbers divisible by 6 will be 6, 12, 18, 24, … to 40 terms
Here, a = 6, d = 12 – 6 = 6, n = 40 .

Question 15.
Solution:
First 15 multiples of 8 are 8, 16, 24, 32, … to 15 terms
Here, a = 8, d = 16 – 8 = 8 , n = 15

Question 16.
Solution:
Multiples of 9 lying between 300 and 700 = 306, 315, 324, 333, …, 693
Here, a = 306, d = 9, l = 693

Question 17.
Solution:
Three digit numbers are 100, 101, …, 999
and numbers divisible by 13, will be 104, 117, 130, …, 988
Here, a = 104, d = 13, l = 988
T_n (l) = a + (n – 1) d

Question 18.
Solution:
Even natural numbers are 2, 4, 6, 8, 10, …
Even natural numbers which are divisible by 5 will be
10, 20, 30, 40, … to 100 terms
Here, a = 10, d = 20 – 10 = 10, n = 100

Question 19.
Solution:

Question 20.
Solution:
Let a be the first term and d be the common difference of the AP, then

Question 21.
Solution:
Let a be the first term and d be the common difference, then

Question 22.
Solution:
Let a be the first term and d be the common difference, then

Question 23.
Solution:
In an AP
a = 17, d = 9, l = 350
Let number of terms be n, then

Question 24.
Solution:
Let a be the first term, d be the common difference, then

Question 25.
Solution:
In an AP, let a be the first term and d be the common difference, then

Question 26.
Solution:
Let a be the first term and d be the common difference of an AP, then

Question 27.
Solution:
Let a be first term and d be the common difference, then

Question 28.
Solution:
Let first term be a and d be the common difference in an AP, then

Question 29.
Solution:
Let a be the first term and d be the common difference of an AP, then

Question 30.
Solution:
Let a₁ and a₂ be the first terms of the two APs and d be the common difference, then
a₁ = 3, a₂ = 8

Question 31.
Solution:
Let a be the first term and d be the common difference, then
S₁₀ = -150

Question 32.
Solution:
Let a be the first term and d be the common difference, then

Question 33.
Solution:
Let a be the first term and d be the common difference of an AP, then

Question 34.
Solution:
(i) AP is 5, 12, 19,… to 50 terms
Here, a = 5, d = 12 – 5 = 7, n = 50

Question 35.
Solution:
Let a₁, a₂ be the first term and d₁, d₂ be common difference of the two AP’s respectively.
Given, ratio of sum of first n terms =

Question 36.
Solution:
Let a be the first term and d be the common difference of an AP.

Question 37.
Solution:

Question 38.
Solution:

Question 39.
Solution:
AP is -12, -9, -6,…, 21
Here, a = -12, d = -9 – (-12) = -9 + 12 = 3, l = 21

Question 40.
Solution:
S₁₄ = 1505
Let a be the first term and d be the common difference, then
a = 10

Question 41.
Solution:
Let a be the first term and d be the common difference of an AP, then

Question 42.
Solution:
In the school, there are 12 classes, class 1 to 12 and each class has two sections.
Each class plants double of the class
i.e. class 1 plants two plant, class 2 plants 4 plants, class 3 plants 6 plants, and so on.
So, total plants will be for each class each sections = 2 + 4 + 6 + 8 … + 24
Here, a = 2, d = 2, l = 24, n = 12

Each class has. two sections.
Plants will also be doubt
i.e. Total plants = 156 x 2 = 312

Question 43.
Solution:
In a potato race,
Bucket is at 5 m from first potato and then the distance between the two potatoes is 3m.
There are 10 potatoes.
The player, pick potato and put it in the bucket one by one.
Total distance in m to be covered, for 1st, 2nd, 3rd, … potato.

Question 44.
Solution:
Total number of trees = 25
Distance between them = 5 m in a line.
There is a water tank which is 10 m from the first tree.
A gardener waters these plants separately.
Total distance for going and coming back

Question 45.
Solution:
Total sum = ₹ 700
Number of cash prizes = 7
Each prize in ₹ 20 less than its preceding prize.
Let first prize = ₹ x
Then second prize = ₹ (x – 20)
Third prize = ₹ (x – 40) and so on.

Question 46.
Solution:
Total savings = ₹ 33000
Total period = 10 months
Each month, a man saved ₹ 100 more than its preceding of month.
Let he saves ₹ x in the first month.

Question 47.
Solution:
Total debt to be paid = ₹ 36000
No. of monthly installments = 40
After paying 30 installments, \(\frac { 1 }{ 3 }\) of his debt left
i.e. ₹ 36000 x \(\frac { 1 }{ 3 }\) = ₹ 12000
and amount paid = ₹ 36000 – ₹ 12000 = ₹ 24000
Monthly installments are in AP.
Let first installment = x
and common difference = d

Question 48.
Solution:
A contractor will pay the penalty for not doing the work in time.
For the first day = ₹ 200
For second day = ₹ 250
For third day = ₹ 300 and so on
The work was delayed for 30 days
Total penalty, he paid
200 + 250 + 300 + ….. to 30 terms
Here, a = 200, d = 50, n = 30
Total sum = \(\frac { n }{ 2 }\) [2a + (n – 1) d]
= \(\frac { 30 }{ 2 }\) [2 x 200 + (30 – 1) x 50]
= 15 [400 + 29 x 50]
= 15 [400 + 1450]
= 15 x 1850 = ₹ 27750

Question 49.
Solution:
Child will put 5 rupee on 1st day, 10 rupee (2 x 5 rupee)
on 2nd day, 15 rupee (3 x 5 rupee) on 3rd day etc.
Total saving = 190 coins = 190 x 5 = 950 rupee
The above problem can be written as Arithmetic Progression series
5, 10, 15, 20, ……
with a = 5, d = 5, S_n = 950
Let n be the last day when piggy bank become full.

⇒ n (n + 20) – 19 (n + 20) = 0
⇒ (n + 20) (n – 19) = 0
⇒ n + 20 = 0 or n – 19 = 0
⇒ n = -20 or n = 19
cannot be negative, hence n = 19
She can put money for 19 days.
Total saving is 950 rupees.

Hope given RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 11 Arithmetic Progressions Ex 11D

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11D

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11A
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11B
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11C
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11D
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions MCQS

Very-Short and Short-Answer Questions
Question 1.
Solution:
(3y – 1), (3y + 5) and (5y+ 1) are in AP
(3y + 5) – (3y – 1) = (5y + 1) – (3y + 5)
⇒ 2 (3y + 5) = (5y + 1) + (3y – 1)
⇒ 6y + 10 = 8y
⇒ 8y – 6y = 10
⇒ 2y = 10
⇒ y = 5
y = 5

Question 2.
Solution:
k, (2k – 1) and (2k + 1) are the three successive terms of an AP.
(2k – 1) – k = (2k + 1) – (2k – 1)
⇒ 2 (2k – 1) = 2k + 1 + k
⇒ 4k – 2 = 3k + 1
⇒ 4k – 3k = 1 + 2
⇒ k = 3
k = 3

Question 3.
Solution:
18, a, (b – 3) are in AP
⇒ a – 18 = b – 3 – a
⇒ a + a – b = -3 + 18
⇒ 2a – b = 15

Question 4.
Solution:
a, 9, b, 25 are in AP.
9 – a = b – 9 = 25 – b
b – 9 = 25 – b
⇒ b + b = 22 + 9 = 34
⇒ 2b = 34
⇒ b= 17
a – b = a – 9
⇒ 9 + 9 = a + b
⇒ a + b = 18
⇒ a + 17 = 18
⇒ a = 18 – 17 = 1
a = 18, b= 17

Question 5.
Solution:
(2n – 1), (3n + 2) and (6n – 1) are in AP
(3n + 2) – (2n – 1) = (6n – 1) – (3n + 2)
⇒ (3n + 2) + (3n + 2) = 6n – 1 + 2n – 1
6n + 4 = 8n – 2
⇒ 8n – 6n = 4 + 2
⇒ 2n = 6
⇒ n = 3
and numbers are
2 x 3 – 1 = 5
3 x 3 + 2 = 11
6 x 3 – 1 = 17
i.e. (5, 11, 17) are required numbers.

Question 6.
Solution:
Three digit numbers are 100 to 990 and numbers which are divisible by 7 will be
105, 112, 119, 126, …, 994
Here, a = 105, d= 7, l = 994
T_n = (l) = a + (n – 1) d
⇒ 994 = 105 + (n – 1) x 7
⇒ 994 – 105 = (n – 1) 7
⇒ (n – 1) x 7 = 889
⇒ n – 1 = 127
⇒ n = 127 + 1 = 128
Required numbers are 128

Question 7.
Solution:
Three digit numbers are 100 to 999
and numbers which are divisible by 9 will be
108, 117, 126, 135, …, 999
Here, a = 108, d= 9, l = 999
T_n (l) = a + (n – 1) d
⇒ 999 = 108 + (n – 1) x 9
⇒ (n – 1) x 9 = 999 – 108 = 891
⇒ n – 1 = 99
⇒ n = 99 + 1 = 100

Question 8.
Solution:
Sum of first m terms of an AP = 2m² + 3m
S_m = 2m² + 3m
S₁ = 2(1)² + 3 x 1 = 2 + 3 = 5
S₂ = 2(2)² + 3 x 2 = 8 + 6=14
S₃ = 2(3)² + 3 x 3 = 18 + 9 = 27
Now, T₂ = S₂ – S₁ = 14 – 5 = 9
Second term = 9

Question 9.
Solution:
AP is a, 3a, 5a, …
Here, a = a, d = 2a

Question 10.
Solution:
AP 2, 7, 12, 17, …… 47
Here, a = 2, d = 7 – 2 = 5, l = 47
nth term from the end = l – (n – 1 )d
5th term from the end = 47 – (5 – 1) x 5 = 47 – 4 x 5 = 47 – 20 = 27

Question 11.
Solution:
AP is 2, 7, 12, 17, …
Here, a = 2, d = 7 – 2 = 5
a_n = a + (n – 1) d = 2 + (n – 1) x 5 = 2 + 5n – 5 = 5n – 3
Now, a₃₀ = 2 + (30 – 1) x 5 = 2 + 29 x 5 = 2 + 145 = 147
and a₂₀ = 2 + (20 – 1) x 5 = 2 + 19 x 5 = 2 + 95 = 97
a₃₀ – a₂₀ = 147 – 97 = 50

Question 12.
Solution:
T_n = 3n + 5
T_n-1 = 3 (n – 1) + 5 = 3n – 3 + 5 = 3n + 2
d = T_n – T_n-1 = (3n + 5) – (3n + 2) = 3n + 5 – 3n – 2 = 3
Common difference = 3

Question 13.
Solution:
T_n = 7 – 4n
T_n-1 = 7 – 4(n – 1) = 7 – 4n + 4 = 11 – 4n
d = T_n – T_n-1 = (7 – 4n) – (11 – 4n) = 7 – 4n – 11 + 4n = -4
d = -4

Question 14.
Solution:
AP is √8, √18, √32, …..
⇒ √(4 x 2) , √(9 x 2) , √(16 x 2), ………

Question 15.
Solution:

Question 16.
Solution:
AP is 21, 18, 15, …n
Here, a = 21, d = 18 – 21 = -3, l = 0
T_n (l) = a + (n – 1) d
0 = 21 + (n – 1) x (-3)
0 = 21 – 3n + 3
⇒ 24 – 3n = 0
⇒ 3n = 24
⇒ n = 8 .
0 is the 8th term.

Question 17.
Solution:
First n natural numbers are 1, 2, 3, 4, 5, …, n
Here, a = 1, d = 1

Question 18.
Solution:
First n even natural numbers are 2, 4, 6, 8, 10, … n
Here, a = 2, d = 4 – 2 = 2

Question 19.
Solution:
In an AP
First term (a) = p
and common difference (d) = q
T₁₀ = a + (n – 1) d = p + (10 – 1) x q = (p + 9q)

Question 20.
Solution:

Question 21.
Solution:
2p + 1, 13, 5p – 3 are in AP, then
13 – (2p + 1) = (5p – 3) – 13
⇒ 13 – 2p – 1 = 5p – 3 – 13
⇒ 12 – 2p = 5p – 16
⇒ 5p + 2p = 12 + 16
⇒ 7p = 28
⇒ p = 4
P = 4

Question 22.
Solution:
(2p – 1), 7, 3p are in AP, then
⇒ 7 – (2p – 1) = 3p – 7
⇒ 7 – 2p + 1 = 3p – 7
⇒ 7 + 1 + 7 = 3p + 2p
⇒ 5p = 15
⇒ p = 3
P = 3

Question 23.
Solution:

Question 24.
Solution:

d = T₂ – T₁ = 14 – 8 = 6
Common difference = 6

Question 25.
Solution:

Question 26.
Solution:

Question 27.
Solution:

Hope given RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.