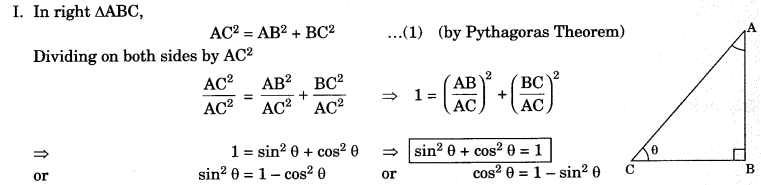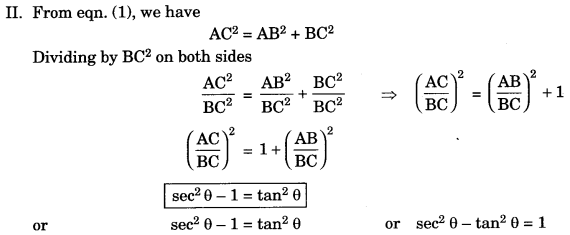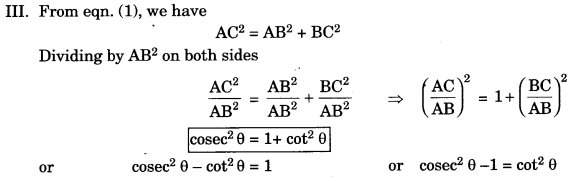Category: CBSE Class 10

On this page, you will find Introduction to Trigonometry Class 10 Notes Maths Chapter 8 Pdf free download. CBSE NCERT Class 10 Maths Notes Chapter 8 Introduction to Trigonometry will seemingly help them to revise the important concepts in less time.

CBSE Class 10 Maths Chapter 8 Notes Introduction to Trigonometry

Introduction to Trigonometry Class 10 Notes Understanding the Lesson

The word trigonometry is derived from the Greek words ‘Tri’ which means three, ‘gon’ means sides and metron meaning measure.

It means trigonometry is the study of relationship between the sides and angles

• The earliest work on trigonometry was recorded in Egypt and Babylon.
• Trigonometry was used by early astronomers to find out the distance of stars and planets from the earth.

Trigonometric Ratios

The ratios of the sides of a right triangle with respect to its acute angles are called trigonometric ratios.

1. In right triangle, side opposite to given acute angle will always be perpendicular.
2. Side opposite 90° will always be hypotenuse.
3. Remaining side will be base.
4. The sum of two angles (except right angle) is 90°
   i.e.,      ∠A + ∠C = 90°           ( ∵ ∠B = 90°)
   

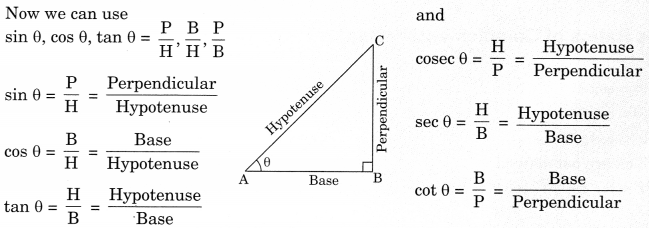
1. sin θ = sin θ = \(\frac{0}{\mathrm{H}}\) (O- side opposite to given angle i.e., acute angle)

2. cosine θ = cos θ = \(\frac{\mathrm{A}}{\mathrm{H}} \)(A-adjacent side) (H-Hypotenuse)

3. Tangent θ = tan θ =\(\frac{\mathrm{O}}{\mathrm{A}}\)
(O-side opposite to acute angle, A-adjacent side)

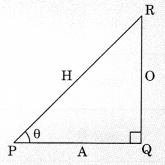
4. cosecant θ = cosec θ= \(\frac{\mathrm{H}}{\mathrm{O}}\)

5. secant θ = sec θ =\(\frac{\mathrm{H}}{\mathrm{A}}\)

6. cotangent θ= cot θ =\(\frac{\mathrm{A}}{\mathrm{O}}\)

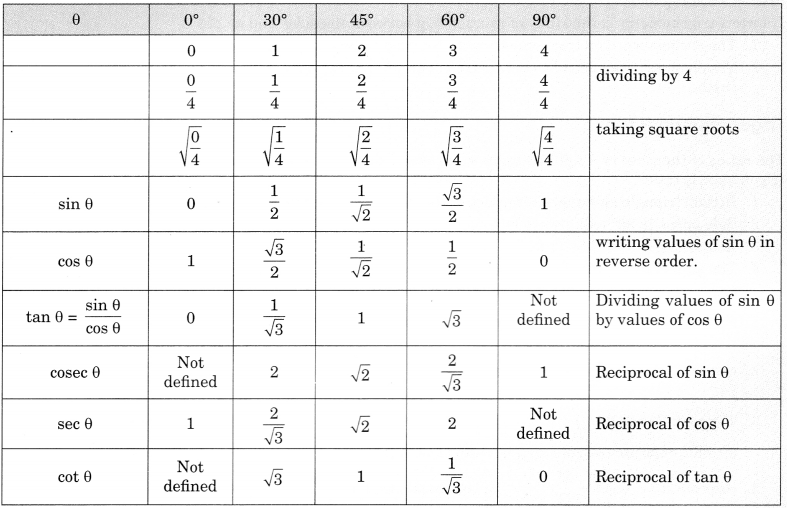
Trigonometric angles for some specific angles

Also we can find values for some special angles as follows:

Trigonometric Identities

Identity: That equation is called an identity. If it is true for all values of the variables which involved. I. In right ΔABC,

On this page, you will find Arithmetic Progressions Class 10 Notes Maths Chapter 5 Pdf free download. CBSE NCERT Class 10 Maths Notes Chapter 5 Arithmetic Progressions will seemingly help them to revise the important concepts in less time.

CBSE Class 10 Maths Chapter 5 Notes Arithmetic Progressions

Arithmetic Progressions Class 10 Notes Understanding the Lesson

We have observed many things in our daily life, follow a certain pattern.
(a) 1, 4, 7, 10, 13, 16, …….
(b) 15, 10, 5, 0, -5, -10,………….
(c) 1,\(\frac{1}{2}\),0,\(-\frac{1}{2}\)………………
These patterns are generally known as sequence. Two such sequences are arithmetic and geometric sequences. Let us investigate the Arithmetic sequence.

1. Sequence: A sequence is a ordered list of numbers.
Terms: The various numbers occurring in a sequence are called its terms. Terms of sequence are denoted by a₁ a₂, a₃, …………… a_n.

2. Arithmetic Progression: An arithmetic progression is a sequence of numbers such that the difference between the consecutive terms are equal.

3. Common difference: The difference between two consecutive terms of an arithmetic progression is called common difference.
d = a₂ – a₁
d  = a₃ – a₂
d = a₄ – a₃
……………..
……………..
d = a_n – a_n-1

4. Finite Arithmetic Progression: A sequence which has finite or definite number of terms is called finite sequence.
Example, (1, 3, 5, 7, 9)… which has 5 terms.

5. Infinite Arithmetic Progression: A sequence which has indefinite or infinite number of terms is called infinite arithmetic progression.
Example, 1, 2, 3, 4, 5, …

In general, arithmetic progression can be written as a, a + d, a + 2d, where a is the first term and d is called the common difference i.e. difference between two consecutive terms.

6. General form of an AP: Let a be the first term and d is the common difference then the AP is

Here
a₁ = a (we take) (a is first term of AP)
a₂ = a₁ + d = a + d
a₃ = a₂ + d = a + d + d = a + 2d
a₄ = a₃+ d = a + 2d + d = a + 3d
…………….
……………
a_n = a + (n – 1) d
i.e. AP is a, a + d, a + 2d, a + 3d,………… , a + (n – 1)d.
n^th term of AP = a + (n -1)d
Note: Common difference of AP can be positive, negative or zero.

1. n^th term or General term of an AP
n^th term of an AP = a + (n – 1) d where
a → first term of the AP
n → number of terms
d→common difference of an AP.

2. n^th term of an AP from the end: Let us consider an AP where first term a and common difference is If m is number of terms in the AP. then
n^th term from the end = [m – n + 1]^th term from the beginning.
n^th term from the end = a + (m-n +1 – 1)d – a + (m – n) d
It  l is the last term of the AP, then n^th term from the end is the n^th term of an AP where first term is l and common difference is – d
n^th term from the end – 1 + (n – 1) (-d)
= 1 – (n – 1) d

Sum of first n terms of an AP
Let S_n denote the sum of first n terms of an AP
S_n = a + a + d + a + 2d + a + 3d …. + a + (n – 1)d ……….. (1)
Rewriting the terms in reverse order.
S_n = a + (n – 1)    + a + (n – 2)d + a + (n-3)d + ………….+a ……… (2)
Adding equations (1) and (2)
2S_n = [2a + (n – 1)d] + [2a + (n-1)d] + … + [2a + (n – 1)d]
2S_n = n[2a + (n – 1)d]
S_n=\(\frac{n}{2}\)[2a+(n-1)d]
We can Write
S_n=\(\frac{n}{2}\)[a+a+(n-1)d] [l=a+(n-1)d]
S_n=\(\frac{n}{2}\)[a+l]

Note:
(i) The Tith term of an AP = S_n – S_n-1 or a_n = S_n+1 – S_n
Sum of first n positive integer
\(S_{n}=\frac{n(n+1)}{2}\)
(iii) Sum of n odd positive integer = n²
(iv) Sum of n even positive integer = n(n + 1)

On this page, you will find Coordinate Geometry Class 10 Notes Maths Chapter 7 Pdf free download. CBSE NCERT Class 10 Maths Notes Chapter 7 Coordinate Geometry will seemingly help them to revise the important concepts in less time.

CBSE Class 10 Maths Chapter 7 Notes Coordinate Geometry

Coordinate Geometry Class 10 Notes Understanding the Lesson

Distance formula

1. The distance between two points A(x₁, y₁) and B(x₂, y₂) is

2. The distance of point A(x, y) from origin 0(0, 0) is
\(\mathrm{AO}=\sqrt{x^{2}+y^{2}}\)

3. Three given points will form:

• Right angled triangle if sum of squares of any two sides is equal to the square of third (largest) side.
• Equilateral triangle if length of all three sides are equal.
• Isosceles triangle if length of any two sides are equal.
• A line or collinear if sum of two sides is equal to third side.

4. Four given points will form:

• Square if length of all four sides are equal and diagonals are equal.
• Rhombus if length of all four sides are equal.
• Rectangle if opposite sides are equal and diagonals are equal.
• Parallelogram if opposite sides are equal.

Section formula
I. If A(x₁, y₁) and BB(x₂, y₂)) are two points on a plane and P(x, y) divides AB internally in the ratio m : n, then co-ordinates of P are given by

Area of a Triangle

1. Area of ΔABC formed by vertices A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) is given by
Ar(ΔABC) =\(\frac{1}{2}\) (- y₃) + x₂ (y₃ – y₁)+ x₃(y₁ – y₂)]
[Only positive numerical value to be taken]

2. If Ar(ΔABC) = 0, then A, B and C are collinear points.

3. If‘C’ is centroid of a triangle, the median is divided in the ratio 2 : 1 by C and coordinates of C are
\(\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)\)

4. Area of quadrilateral LMNO = ar(ΔLMO) + ar(ΔNMO)

On this page, you will find Quadratic Equations Class 10 Notes Maths Chapter 4 Pdf free download. CBSE NCERT Class 10 Maths Notes Chapter 4 Quadratic Equations will seemingly help them to revise the important concepts in less time.

CBSE Class 10 Maths Chapter 4 Notes Quadratic Equations

Quadratic Equations Class 10 Notes Understanding the Lesson

1. Quadratic Equation: A quadratic equation in the variable x is of the form ax² + bx + c = 0, where a, b, c are real number and a ≠ 0.

2. Roots (or zeroes of a quadratic equation): A real number a is called the root of the quadratic equation
ax² + bx + c = 0 if aα² + bα + c = 0.

Alternatively, any equation of the form p(x) = 0, where p(x) is a quadratic polynomial is a quadratic equation and if p(α) = 0 for any real number a; the a is said to be the root (or zero) of p(x).

Solution of a quadratic equation by factorization
Finding the roots of a quadratic equation by the method of factorization means finding out the linear factors of the quadratic equation and equating it to zero, the roots can be found. i.e. ax² + bx + c = 0
(Ax + B) (Cr + D) = 0
where A, B, C and D are real numbers, A, C≠ 0.
We get Ax + B = 0 or Cx + D = 0
x =\(-\frac{B}{A}\) or x =\(-\frac{D}{C}\)
x =\(-\frac{\mathrm{B}}{\mathrm{A}},-\frac{\mathrm{D}}{\mathrm{C}}\) are the two roots of quadratic equation.

Solution of a quadratic equation by completing the square
For given quadratic equation ax²+ bx + c = 0
Divide the equation by a, so that the coefficient of x² becomes 1.
\(x^{2}+\frac{b}{a} x+\frac{c}{a}=0\)

Adding and subtracting \(\left(\frac{b}{2 a}\right)^{2}\) i.e., square of the half of the coefficient of x.
This formula is known as quadratic formula.
If α and β are roots of the given equation, then

ax² + bx + c = 0,
a ≠ 0, a, b, c ∈ R

Discriminant D = b² – 4ac

Condition exists  Nature of roots
(i) b² – 4ac > 0    Real and unequal
(ii) b² – 4ac = 0   Real and equal
(iii) b² – 4ac < 0  No real roots

 

 

On this page, you will find Pair of Linear Equations in Two Variables Class 10 Notes Maths Chapter 3 Pdf free download. CBSE NCERT Class 10 Maths Notes Chapter 3 Pair of Linear Equations in Two Variables will seemingly help them to revise the important concepts in less time.

CBSE Class 10 Maths Chapter 3 Notes Pair of Linear Equations in Two Variables

Pair of Linear Equations in Two Variables Class 10 Notes Understanding the Lesson

Two linear equations in the same two variables are called a pair of linear equations in two variables. The most general form of a pair of linear equation is
a₁x + b₁y + c₁ = 0
a₂x+ b₂y + c₂ = 0
where a₁,a₂, b_1,b₂, c₁ c₂ are real numbers. For the pair of linear equations, the following situations can arise:
(i) \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\) In this case, the pair of linear equations is consistent.

(ii) \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\) The pair of linear equations in inconsistent.

(iii) \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\) The pair of linear equations is consistent.

2. A pair of linear equations in two variables, can be represented, and solved by the

• Graphical method
• Algebraic method

3. Graphical Method: The graph of a pair of linear equations in two variables is represented by two lines, following three possibilities can occur.

• Two lines intersect at one point, then that point gives the unique solution of the two equations and the pair of equations is consistent.
• Two lines will not intersect, i.e. they are parallel, the pair of linear equations is inconsistent and the pair of equations will have no solution.
  
• The graph will be a pair of coincident lines. Each point on the lines will be a solution, so the pair of equations will have infinitely many solution and is consistent.

4. Algebraic Method: A pair of linear equations can be solved by any of the following three methods:

• Substitution method
• Elimination method
• Cross-multiplication method

5. Graphical Method of Solution of a pair of Linear Equations:

If the lines represented by the pair of linear equations in two variables are given by
a₁x + b₁y + c₁ = 0
a₂x+ b₂y + c₂ = 0

Following are the cases:

(i) If \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\) then the lines are intersecting lines and intersect at one point. In this case, the pair of  linear equations in consistent.

(ii) If \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\), then the lines are coincident. In this case, the pair of linear equation is consistent  (dependent)

(iii) If \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\) then the lines are parallel to each other. In this case, the pair of linear equations inconsistent.

On this page, you will find Polynomials Class 10 Notes Maths Chapter 2 Pdf free download. CBSE NCERT Class 10 Maths Notes Chapter 2 Polynomials will seemingly help them to revise the important concepts in less time.

CBSE Class 10 Maths Chapter 2 Notes Polynomials

Polynomials Class 10 Notes Understanding the Lesson

1. The value of the polynomial p(x) at x = a is p(a).

2. Zeroes of the polynomial p(x) can be find by equating p(x) to zero and solving the equation for

3. If for p(x) = ax² + bx + c = 0, a ≠ 0; α and β are the zeroes, then

4. If for p(x) = ax³ + bx² + cx + d = 0; a ≠ 0; α, β,γ are the zeroes, then
α + β + γ = \(\frac{-b}{a}\)
αβ+βγ + αγ = \(\frac{c}{a}\)
αβγ =\(\frac{-d}{a}\)

5. If α and β are the zeroes; then quadratic polynomial will be given by K[x² – Sx + P]
where
S = α +β
P = αβ
K (≠0) is real.

6. The cubic polynomial with zeroes α, β and γ is given by
K[x³ – S₁x² + S₁x² S₃]
where
S₁ = α + β + γ
S₂ = αβ + βγ + αγ
S₃= αβγ
K(≠ 0) is real.

Degree of a Polynomial:

1. The degree of a polynomial p(x) in x is the highest power of x in p(x)

Note: Expressions like \(\frac{1}{\sqrt{x}}, \frac{1}{x^{2}+1}, \sqrt{x+2}\)

2. (i) Polynomial with degree 1, i.e., polynomial of the form ax + b; a ≠ 0 is called linear polynomial.
(ii) Polynomial with degree 2, i.e., polynomial of the form ax2 + bx + c; a ≠ 0 is called quadratic polynomial.
(iii) Polynomial with degree 3, i.e. polynomial of the form ax³ + bx² + cx + d ; a ≠ 0 is called cubic polynomial.
(iv) Polynomial with degree 4, i.e. polynomial of the form ax⁴ + bx³ + cx² + dx + e; a ≠ 0 is called biquadratic polynomial.

Geometrical Meaning of the Zeroes of a Polynomial:

1. For any polynomial y = f(x), the number of points on which the graph of y = f(x) intersects at x-axis is called the number of the zeroes of the polynomial and the x-coordinates of these points are called the zeroes of the polynomial y = f(x).

2. Polynomial with degree ‘n’ has maximum ‘n’ number of zeroes. A constant polynomial has no zeroes.

3. Geometrical representation of a linear polynomial is always a straight line.

4. Geometrical representation of a quadratic polynomial is the graph of the shape either open upwards like ‘∪’ or open downwards like ‘∩’ according to a > 0 or a < 0. These curves are called Parabola.

Relationship Between Zeroes and Coefficient of a Quadratic Polynomial:

1. If α and β are the zeroes of the quadratic polynomial  p(x) = ax² + bx + c a≠0 then

Relationship Between Zeroes and Coefficient of a Cubic Polynomial

1. If α, β and γ are the zeroes of the cubic polynomial

2. A quadratic polynomial p(x) with zeroes α and β is given by
p(x) = K[x² – (α + β)x + αβ]
where K(≠0) is real.

3. A cubic polynomial p(x) with α, β and γ as zeroes is given by
p(x) = K[x³ – (α + β + γ)x² + (αβ +βγ + αγ)x – αβγ
where K(≠0) is real.

Division Algorithm for Polynomials:
If p(x) and g(x) are any two polynomials where g(x) ≠ 0. Then on dividing p(x) by g(x), we find other two polynomials q(x) and r(x) such that
p(x) = g(x) x q(x) + r(x);
where deg. of r(x) < deg. of gix)
or Dividend = Divisor x Quotient + Remainder

Note:

• If r(x) = 0, then g(x) will be a factor of p(x) otherwise not.
• If any real number ‘a’ is a zero of the polynomial p(x), then (x – a) will be a factor of p(x).

On this page, you will find Real Numbers Class 10 Notes Maths Chapter 1 Pdf free download. CBSE NCERT Class 10 Maths Notes Chapter 1 Real Numbers will seemingly help them to revise the important concepts in less time.

CBSE Class 10 Maths Chapter 1 Notes Real Numbers

Real Numbers Class 10 Notes Understanding the Lesson

In class X, we have study about real numbers and encountered irrational numbers. In this chapter we want to know about natural numbers, whole numbers, integers, rational numbers, irrational numbers and real numbers.

1. Natural numbers: Natural numbers are those used for counting. e.g.: 1, 2, 3, 4, 5,… (and so on).
Natural numbers are denoted by N.

2. Whole numbers: Whole numbers are simply the numbers 0, 1, 2, 3, 4, 5,… (and so on).
Counting numbers are whole numbers. Without zero we cannot count. Whole numbers are denoted by W.

3. Integer: The set of integers consist of zero 0, the natural numbers and the negative of natural numbers.
e.g.: …-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, … The integers are sometimes also called rational integers. Integers are denoted by Z. (Zahlen means to count)

4. Rational number: A rational number is any real number that can be expressed in the form \(\frac{p}{q} \)of R where q ≠ 0. Every integer is a rational number, the set of rational numbers is usually denoted by Q.
e.g : \(\frac{1}{2}, \frac{5}{1}, \frac{7}{9}\)
Note : The decimal expansion of rational number always either terminates after a finite number of digits, or they are non terminating and repeating decimals.

5. Irrational number: An irrational number is any real number that cannot be expressed as ratio of integers.
e.g : \(\sqrt{2}, \sqrt{3},\)π ,0.340440444…….. .These numbers cannot be represented as terminating or
repeating decimals.

6. Real number: The real number include all the rational numbers such as integers -5, -4, -1, 0, 1, 2,… and all fractions \(\frac{4}{3}, \frac{5}{11}, \ldots\) and all the irrational numbers such as \(\sqrt{2}, \sqrt{3}, \pi, \ldots\)

7. Algorithm: A set of rules for solving a problem in a finite number of steps.

8. Lemma: A lemma is a proven statement used for proving another statement.

9. Euclid Division Lemma: Euclid’s division lemma states that, for any two positive integers ‘o’ and ‘b’ there exists unique whole numbers q and r such that
a = bq + r, where 0 < r < b and a = dividend, b = divisor
q = quotient, r = remainder
i.e., Dividend = Divisor x Quotient + Remainder.
Euclid division lemma can be used to find the highest common factor (HCF) of any two positive integers.

9. Steps to obtain HCF using Euclid’s division lemma :
(i) Let us consider two positive integer a and b such that a >b.
Apply Euclid’s division lemma to the given integers a and b. Find two whole numbers q and r such that a = bq + r.

(ii) Now Check the value of r if r = 0 then b is the HCF of the given numbers. If r 0 then again apply Euclid’s division lemma to find the new divisor b and remainder r.

(iii) Continue the process till the remainder becomes zero. In that case the value of the divisor b is the HCF of a and b.
Note:

• HCF (a, b) = HCF (b, r)
• Euclid’s division algorithm can be extended for all integers except zero.
• Euclid’s division lemma and algorithm are so interlinked that people often call former as the division algorithm also.

10. Prime number: Any natural number which has exactly two factors is called prime number. e.g. 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, … etc.

11. Composite number: A composite number is a positive integer that has at least one positive divisor other than one or the number itself.
OR
A composite number is any positive integer greater than one that is not a prime number. e.g.: 4, 6, 8, 9, 10, 12, 14, 15, 16,… etc.

12. Co-prime numbers: A set of numbers which do not have any common factor other than one are called co-prime numbers.
Note: Two numbers are said to be co-prime if their HCF is 1. e.g. 1. All prime numbers are co-prime to each other

13. Consecutive integers are always co-prime.
Statement of fundamental theorem of arithmetic : Every composite number can be expressed as a product of primes and this factorisation is unique apart from the order in which the prime factors occur.
Note:

• The prime factorisation of natural number is unique except for the order of its factors.
• HCF of two numbers is equal to the product of the terms containing least power of common prime factors of the two numbers.
• The LCM of two number is equal to the product of the terms containing the greatest power of all prime factors of the two numbers.
• For any two positive integers a and b HCF (a, b) x LCM (a,b) = a x b
• For any three positive numbers a, b and c
  

Revisiting Irrational Numbers: We have already studied irrational numbers and many of their properties. Now in this section, we will prove \(\sqrt{2}, \sqrt{3}, \sqrt{5}, \sqrt{7} \)and in general, √P is irrational, where p is a prime.

(1) A number π is called irrational, if it can not be written in the form \(\frac{p}{q}\) where p and q are integers and q≠ 0.  An irrational number is a real number that can not be written as simple fraction.

Theorem: Let p be a prime number. If p divides a², then p divides a, where a is a positive integer.

Revisiting Rational Numbers and their Decimal Expansions

(1) Every rational number can be expressed as either terminating or non-terminating repeating decimal.

(2) Decimal expansion of every irrational number is non-terminating and non repeating.

(3) If the prime factorisation of denominator is of the form 2ⁿ x 5^m where n and m are non-negative integers, then rational number will have terminating decimal expansion.

(4) Let x be a rational number whose decimal expansion terminates. Then x can be expressed in the form x=\(\frac{p}{q}\), where p and q are co-prime and the prime factorisation of q is of the form 2ⁿ x 5^m where n and mare non-negative integers.

(5) Let x=\(\frac{p}{q}\) be a rational number, such that the prime factorisation of q is of the form 2ⁿ x 5^m, where Q n, m are non-negative integers, then the decimal expansion of x terminates. e.g :\(\frac{3}{8}=\frac{3 \times 5^{3}}{2^{3} \times 5^{3}}=\frac{375}{10^{3}}=0.375\)

(6) Let x=\(\frac{p}{q}\) be a rational number, such that the prime factorisation of q is not of the form 2ⁿ x 5^m , where n, m are non-negative integers, then x has a decimal expansion which is non-terminating (recurring) e.g : \( \frac{1}{7}=0 . \overline{142857}\)
Note: We conclude that decimal expansion of every rational number is either terminating or non-terminating recurring.

 

NCERT Notes for Class 10 Social Science

Class 10 History Notes

CBSE SST History Class 10 Notes

1. The Rise of Nationalism in Europe Class 10 Notes
2. The Nationalist Movement in Indo-China Class 10 Notes
3. Nationalism in India Class 10 Notes
4. The Making of Global World Class 10 Notes
5. The Age of Industrialisation Class 10 Notes
6. Work, Life and Leisure Class 10 Notes
7. Print Culture and the Modern World Class 10 Notes
8. Novels, Society and History Class 10 Notes

Class 10 Geography Notes

CBSE SST Geography Class 10 Notes

1. Resource and Development Class 10 Notes
2. Forest and Wildlife Resources Class 10 Notes
3. Water Resources Class 10 Notes
4. Agriculture Class 10 Notes
5. Minerals and Energy Resources Class 10 Notes
6. Manufacturing Industries Class 10 Notes
7. Lifelines of National Economy Class 10 Notes

Class 10 Civics Notes

CBSE SST Civics Class 10 Notes

1. Power Sharing Class 10 Notes
2. Federalism Class 10 Notes
3. Democracy and Diversity Class 10 Notes
4. Gender Religion and Caste Class 10 Notes
5. Popular Struggles and Movements Class 10 Notes
6. Political Parties Class 10 Notes
7. Outcomes of Democracy Class 10 Notes
8. Challenges to Democracy Class 10 Notes

Class 10 Economics Notes

CBSE SST Economics Class 10 Notes

1. Development Class 10 Notes
2. Sectors of Indian Economy Class 10 Notes
3. Money and Credit Class 10 Notes
4. Globalization and the Indian Economy Class 10 Notes
5. Consumer Rights Class 10 Notes

Chapter Wise Class 10 Maths Notes and Key Points for Class 10 Maths Pdf free download were prepared by expert teachers from the latest edition of NCERT books to get good marks in board exams. NCERT Class 10 Maths Notes part of Revision NCERT Notes for Class 10. Here we have given CBSE Class 10 Maths Notes PDF.

We recommend you to study NCERT Solutions for Class 10 Maths. According to the new CBSE Exam Pattern, MCQ Questions for Class 10 Maths pdf Carries 20 Marks.

CBSE Class 10 Maths Notes

1. Real Numbers Class 10 Notes
2. Polynomials Class 10 Notes
3. Pair of Linear Equations in Two Variables Class 10 Notes
4. Quadratic Equations Class 10 Notes
5. Arithmetic Progressions Class 10 Notes
6. Triangles Class 10 Notes
7. Coordinate Geometry Class 10 Notes
8. Introduction to Trigonometry Class 10 Notes
9. Some Applications of Trigonometry Class 10 Notes
10. Circles Class 10 Notes
11. Constructions Class 10 Notes
12. Areas related to Circles Class 10 Notes
13. Surface Areas and Volumes Class 10 Notes
14. Statistics Class 10 Notes
15. Probability Class 10 Notes

NCERT CBSE Important Questions for Class 10 Science: Students who are struggling to find out what are the important question asked in the annual exams? Here is the list of CBSE Class 10 Science Chapter Wise Question Bank Important Questions which are prepared by subject experts as per the latest CBSE syllabus curriculum. All these questions are designed after analyzing the previous questions papers & model papers. So, make sure to include practicing these NCERT extra important science questions and attain good marks in CBSE Board Exams.

Class 10 Science Important Questions with Answers PDF Download

Access all CBSE NCERT Chapter Wise Important Questions of Class 10 Science with answers and solutions by clicking on the particular chapter link available over here.

1. Chemical Reactions and Equations Class 10 Important Questions
2. Acids Bases and Salts Class 10 Important Questions
3. Metals and Non-metals Class 10 Important Questions
4. Carbon and its Compounds Class 10 Important Questions
5. Periodic Classification of Elements Class 10 Important Questions
6. Life Processes Class 10 Important Questions
7. Control and Coordination Class 10 Important Questions
8. How do Organisms Reproduce Class 10 Important Questions
9. Heredity and Evolution Class 10 Important Questions
10. Light Reflection and Refraction Class 10 Important Questions
11. Human Eye and Colourful World Class 10 Important Questions
12. Electricity Class 10 Important Questions
13. Magnetic Effects of Electric Current Class 10 Important Questions
14. Sources of Energy Class 10 Important Questions
15. Our Environment Class 10 Important Questions
16. Management of Natural Resources Class 10 Important Questions

More Resources

• NCERT Solutions for Class 10 Science
• NCERT Exemplar Solutions for Class 10 Science
• Value Based Questions in Science for Class 10
• HOTS Questions for Class 10 Science

We hope the given NCERT Important Questions for Class 10 Science CBSE Chapter Wise Pdf will help you. If you have any query regarding CBSE Chapter Wise Important Questions of Class 10 Science with answers and solutions, drop a comment below and we will get back to you at the earliest.

Value-Based Questions in Science for Class 10: Provided 10th Class Science CBSE Value Based Questions are free to download from this page. We have jotted down the class 10 science NCERT value-based important question for all chapters to help you score high marks in the annual examination. These NCERT CBSE value-based questions on Science ace up your exam preparation & make you feel confident to attempt any type of examinations.

Chapter Wise Solved CBSE Value Based Questions for Class 10 Science

All important class 10 science topics solved questions are given in this CBSE Value Based Questions Solutions PDF. Download Free PDF Value Based Questions in Science for Class 10 by using the below given accessible quick links.

1. Value Based Questions on Chemical Reactions and Equations Class 10
2. Value Based Questions on Acids, Bases and Salts Class 10
3. Value Based Questions on Metals and Non-metals Class 10
4. Value Based Questions on Carbon and Its Compounds Class 10
5. Value Based Questions on Periodic Classification of Elements Class 10
6. Value Based Questions on Life Processes Class 10
7. Value Based Questions on Control and Coordination Class 10
8. Value Based Questions on How do Organisms Reproduce? Class 10
9. Value Based Questions on Heredity and Evolution Class 10
10. Value Based Questions on Light Reflection and Refraction Class 10
11. Value Based Questions on Human Eye and Colourful World Class 10
12. Value Based Questions on Electricity Class 10
13. Value Based Questions on Magnetic Effects of Electric Current Class 10
14. Value Based Questions on Sources of Energy Class 10
15. Value Based Questions on Our Environment Class 10
16. Value Based Questions on Management of Natural Resources Class 10

More Resources

• Extra Questions
• Value Based Questions in Science for Class 10
• HOTS Questions for Class 10 Science
• NCERT Solutions for Class 10 Science
• NCERT Exemplar Solutions for Class 10 Science
• Previous Year Question Papers for CBSE Class 10 Science