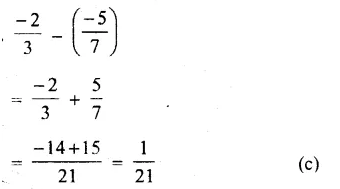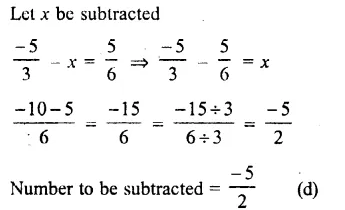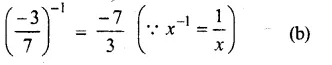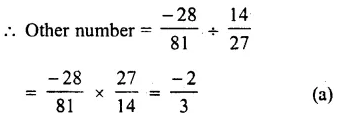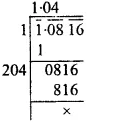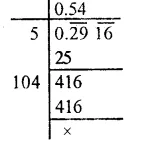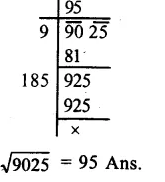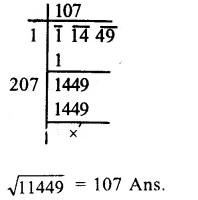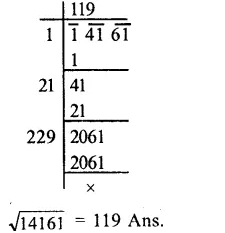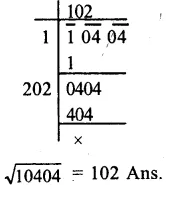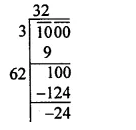RS Aggarwal Class 8 Solutions Chapter 2 Exponents Ex 2B

RS Aggarwal Class 8 Solutions Chapter 2 Exponents Ex 2B

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 2 Exponents Ex 2B.

Other Exercises

Question 1.
Solution:
(i) 57.36 = 5.736 x 101
(ii) 3500000 = 3.5 x 106
(iii) 273000 = 2.73 x 105
(iv) 168000000 = 1.68 x 108
(v) 4630000000000 = 4.63 x 1012
(vi) 345 x 105 = 3.45 x 102 x 105 = 3.45 x 107

Question 2.
Solution:
(i) 3.74 x 105
= \(\\ \frac { 374 }{ 100 } \) x 105
RS Aggarwal Class 8 Solutions Chapter 2 Exponents Ex 2B Q2.1
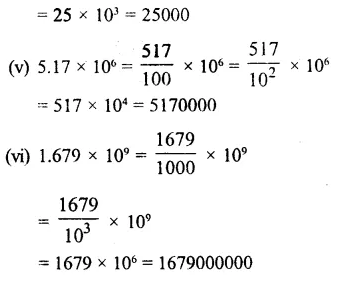
RS Aggarwal Class 8 Solutions Chapter 2 Exponents Ex 2B Q2.2

Question 3.
Solution:
(i) Height of Mount Everest = 8848 m
= 8.848 x 1000
= 8.848 x 103
(ii) Speed of light = 300000000 m/sec.
= 3.00000000 x 100000000
= (3 x 108) m/sec.
(iii) Distance between the earth and the sun = 149600000000 m
= (1.49600000000 x 100000000000)m = (1.496 x 1011) m

Question 4.
Solution:
Mass of earth = (15.97 x 1024) kg
and mass of moon = (7.35 x 1022) kg
= Total mass of earth and moon
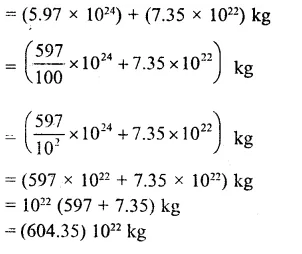
RS Aggarwal Class 8 Solutions Chapter 2 Exponents Ex 2B Q4.1

Question 5.
Solution:
(i) 0.0006
= \(\\ \frac { 6 }{ 10000 } \) = \(\frac { 6 }{ { 10 }^{ 4 } }\) = 6.10-4
RS Aggarwal Class 8 Solutions Chapter 2 Exponents Ex 2B Q5.1
RS Aggarwal Class 8 Solutions Chapter 2 Exponents Ex 2B Q5.2

Question 6.
Solution:
RS Aggarwal Class 8 Solutions Chapter 2 Exponents Ex 2B Q6.1

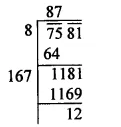
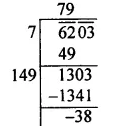
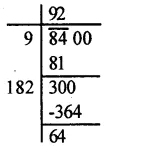
Question 7.
Solution:
(i) 2.06 x 10-5
RS Aggarwal Class 8 Solutions Chapter 2 Exponents Ex 2B Q7.1
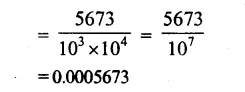
RS Aggarwal Class 8 Solutions Chapter 2 Exponents Ex 2B Q7.2

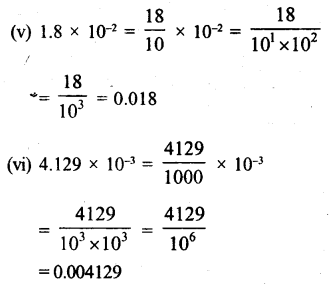
RS Aggarwal Class 8 Solutions Chapter 2 Exponents Ex 2B Q7.3

Hope given RS Aggarwal Solutions Class 8 Chapter 2 Exponents Ex 2B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 11 Arithmetic Progressions Ex 11B

RS Aggarwal Class 10 Solutions Chapter 11 Arithmetic Progressions Ex 11B

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11B.

Other Exercises

Question 1.
Solution:
(3k – 2), (4k – 6) and (k + 2) are three consecutive terms of an AP.
(4k – 6) – (3k – 2) = (k + 2) – (4k – 6)
⇒ 2(4k – 6) = (k + 2) + (3k – 2)
⇒ 8k – 12 = 4k + 0
⇒ 8k – 4k = 0 + 12
⇒ 4k = 12
k = 3

Question 2.
Solution:
(5x + 2), (4x – 1) and (x + 2) are in AP.
(4x – 1) – (5x + 2) = (x + 2) – (4x – 1)
⇒ 2(4x – 1) = (x + 2) + (5x + 2)
⇒ 8x – 2 = 6x + 2 + 2
⇒ 8x – 2 = 6x + 4
⇒ 8x – 6x = 4 + 2
⇒ 2x = 6
x = 3

Question 3.
Solution:
(3y – 1), (3y + 5) and (5y + 1) are the three consecutive terms of an AP.
(3y + 5) – (3y – 1) – (5y + 1) – (3y + 5)
⇒ 2(3y + 5) = 5y + 1 + 3y – 1
⇒ 6y + 10 = 8y
⇒ 8y – 6y = 10
⇒ 2y = 10
⇒ y = 5
y = 5

Question 4.
Solution:
(x + 2), 2x, (2x + 3) are three consecutive terms of an AP.
2x – (x + 2) = (2x + 3) – 2x
⇒ 2x – x – 2 = 2x + 3 – 2x
⇒ x – 2 = 3
⇒ x = 2 + 3 = 5
x = 5

Question 5.
Solution:
(a – b)², (a² + b²) and (a + b)² will be in AP.
If (a² + b²) – (a – b)² = (a + b)² – (a² + b²)
If (a² + b²) – (a² + b² – 2ab) = a² + b² + 2ab – a² – b²
2ab = 2ab which is true.
Hence proved.

Question 6.
Solution:
Let the three numbers in AP be
a – d, a, a + d
a – d + a + a + d = 15
⇒ 3a = 15
⇒ a = 5
and (a – d) x a x (a + d) = 80
a(a² – d²) = 80
⇒ 5(5² – d²) = 80
⇒ 25 – d² = 16
⇒ d² = 25 – 16 = 9 = (±3)²
d = ±3
Now, a = 5, d = +3
Numbers are 5 – 3 = 2
5 and 5 + 3 = 8
= (2, 5, 8) or (8, 5, 2)

Question 7.
Solution:
Let the three numbers in AP be a – d, a and a + d
RS Aggarwal Class 10 Solutions Chapter 11 Arithmetic Progressions Ex 11B 1

Question 8.
Solution:
Sum of three numbers = 24
Let the three numbers in AP be a – d, a, a + d
RS Aggarwal Class 10 Solutions Chapter 11 Arithmetic Progressions Ex 11B 2

Question 9.
Solution:
Let three consecutive in AP be a – d, a, a + d
a – d + a + a + d = 21
⇒ 3a = 21
RS Aggarwal Class 10 Solutions Chapter 11 Arithmetic Progressions Ex 11B 3

Question 10.
Solution:
Sum of angles of a quadrilateral = 360°
Let d= 10
The first number be a, then the four numbers will be
a, a + 10, a + 20, a + 30
a + a + 10 + a + 20 + a + 30 = 360
4a + 60 = 360
4a = 360 – 60 = 300
Angles will be 75°, 85°, 95°, 105°

Question 11.
Solution:
Let the four numbers in AP be a – 3d, a – d, a + d, a + 3d, then
a – 3d + a – d + a + d + a + 3d = 28
RS Aggarwal Class 10 Solutions Chapter 11 Arithmetic Progressions Ex 11B 4

Question 12.
Solution:
Let the four parts of 32 be a – 3d, a – d, a + d, a + 3d
RS Aggarwal Class 10 Solutions Chapter 11 Arithmetic Progressions Ex 11B 5

Question 13.
Solution:
Let the three terms be a – d, a, a + d
a – d + a + a + d = 48
⇒ 3a = 48
⇒ a = 16
and (a – d) x a = (a + d) + 12
⇒ a(a – d) = 4 (a + d) + 12
⇒ 16 (16 – d) = 4(16 + d) + 12
⇒ 256 – 16d = 64 + 4d + 12 = 4d + 76
⇒ 256 – 76 = 4d + 16d
⇒ 180 = 20d
⇒ d = 9
Numbers are (16 – 9, 16), (16 + 9) or (7, 16, 25)

Hope given RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1H

RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1H

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1H.

Other Exercises

Objective Questions :
Tick the correct answer in each of the following :

Question 1.
Solution:
Answer = (c)
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1H Q1.1

Question 2.
Solution:
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1H Q2.1

Question 3.
Solution:
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1H Q3.1

Question 4.
Solution:
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1H Q4.1

Question 5.
Solution:
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1H Q5.1

Question 6.
Solution:
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1H Q6.1

Question 7.
Solution:
Answer = (b)
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1H Q7.1

Question 8.
Solution:
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1H Q8.1

Question 9.
Solution:
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1H Q9.1

Question 10.
Solution:
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1H Q10.1

Question 11.
Solution:
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1H Q11.1

Question 12.
Solution:
Product of two numbers = \(\\ \frac { -28 }{ 81 } \)
One number = \(\\ \frac { 14 }{ 27 } \)
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1H Q12.1

Question 13.

Solution:
Answer = (c)
Let x be the required number, then
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1H Q13.1

Question 14.
Solution:
Answer = (d)
Let x is to be subtracted then
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1H Q14.1

Question 15.
Solution:
Answer = (c)
sum = -3,one number = \(\\ \frac { -10 }{ 3 } \)
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1H Q15.1

Question 16.
Solution:
Answer = (c)
We know that a number is called in standard form if the numerator and denominator has no common divisor except 1.
\(\\ \frac { -9 }{ 6 } \) is in standard form.

Question 17.
Solution:
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1H Q17.1

Question 18.
Solution:
Answer = (b)
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1H Q18.1

Question 19.
Solution:
Answer = (d)
Let x is required rational
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1H Q19.1

Question 20.
Solution:
Additive inverse of \(\\ \frac { -5 }{ 9 } \) is = – \(\left( \frac { -5 }{ 9 } \right) \)

Question 21.
Solution:
Reciprocal of \(\\ \frac { -3 }{ 4 } \) is \(\\ \frac { -4 }{ 3 } \)

Question 22.
Solution:
A rational number between = \(\\ \frac { -2 }{ 3 } \)
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1H Q22.1

Question 23.

Solution:
Answer: (b)
The reciprocal of a negative rational
the number is also a negative rational number.

Hope given RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1H are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3F

RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3F

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3F.

Other Exercises

Evaluate:

Question 1.
Solution:
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3F Q1.1

Question 2.
Solution:
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3F Q2.1
\(\sqrt { 33.64 } \) = 5.8

Question 3.
Solution:
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3F Q3.1

Question 4.
Solution:
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3F Q4.1

Question 5.
Solution:
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3F Q5.1

Question 6.
Solution:
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3F Q6.1
\(\sqrt { 10.0489 } \) = 3.17

Question 7.
Solution:
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3F Q7.1
\(\sqrt { 1.0816 } \) = 1.04

Question 8.
Solution:
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3F Q8.1
\(\sqrt { 0.2916 } \) = 0.54

Question 9.
Solution:
\(\sqrt { 3 } \) = 1.73
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3F Q9.1

Question 10.
Solution:
\(\sqrt { 2.8 } \) = 1.6733 = 1.67
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3F Q10.1

Question 11.
Solution:
\(\sqrt { 0.9 } \) = 0.948
= 0.95
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3F Q11.1

Question 12.
Solution:
Length of rectangle (l) = 13.6 m
and width (b) = 3.4 m
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3F Q12.1

Hope given RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3F are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1E

RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1E

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1E.

Other Exercises

Question 1.
Solution:
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1E Q1.1
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1E Q1.2

Question 2.
Solution:
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1E Q2.1
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1E Q2.2
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1E Q2.3

Question 3.
Solution:
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1E Q3.1
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1E Q3.2
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1E Q3.3
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1E Q3.4

Question 4.
Solution:
Product of two numbers = – 9
one number = – 12
Let second number = x
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1E Q4.1

Question 5.
Solution:
Product of two rational numbers = \(\\ \frac { -16}{ 9 } \)
One number = \(\\ \frac { -4 }{ 3 } \)
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1E Q5.1

Question 6.
Solution:
Let x be multiplied
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1E Q6.1

Question 7.
Solution:
Let x be multiplied
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1E Q7.1

Question 8.
Solution:
Let required number = x
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1E Q8.1

Question 9.
Solution:
sum of \(\\ \frac { 13 }{ 5 } \) and \(\\ \frac { -12 }{ 7 } \)
= \(\\ \frac { 13 }{ 5 } \) + \(\\ \frac { -12 }{ 7 } \)
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1E Q9.1

Question 10.
Solution:
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1E Q10.1

Question 11.
Solution:
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1E Q11.1
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1E Q11.2
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1E Q11.3

Question 12.
Solution:
(i) No, not always closed under division.
(ii) No, not always commutative.
(iii) No, not always associative.
(iv) No. It is not possible to divide any number by zero.

Hope given RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1E are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

NCERT Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms

NCERT Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms

These Solutions are part of NCERT Solutions for Class 9 Science. Here we have given NCERT Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms. LearnInsta.com provides you the Free PDF download of NCERT Solutions for Class 9 Science (Biology) Chapter 7 – Diversity in Living Organisms solved by Expert Teachers as per NCERT (CBSE) Book guidelines. All Chapter 7 – Diversity in Living Organisms Exercise Questions with Solutions to help you to revise complete Syllabus and Score More marks. Register for our free webinar class with best Science tutor in India.

More Resources

NCERT TEXT BOOK QUESTIONS

IN TEXT QUESTIONS

Question 1.
Why do we classify organisms ? (CCE 2012)
Answer:

  1. Identification is not possible without any system of classification.
  2. Classification helps in bringing out similarities and dissimilarities amongst organisms.
  3. Relationships are built up with the help of classification. They indicate the evolutionary pathways.
  4. Organisms of other localities and fossils can be studied only with the help of a system of classification.
  5. It is not possible to study every organism. Study of one or two organisms gives sufficient idea about other members of the group.
  6. Other branches of biology depend upon proper identification of the organism which is possible only through a system of classification.

Question 2.
Give three examples of the range of variations that you see in life forms around you.
Answer:

  1. Size: It varies from microscopic organisms (e.g., bacteria, size 0-5-5-0 pm) to very large sized animals (e.g, Blue whale, 30 metres long) and trees (e.g, Redwood tree, height 100 metres).
  2. Life Span: May fly lives for one day, most mosquitoes for a few days while some Pine trees live for thousands of years.
  3. Colour: Jelly fish and many worms are colourless. Birds, butterflies and flowers are variously coloured brightly.

Question 3.
Which do you think is a more basic characteristic for classifying organisms ?
(a) The place they live
(b) The kind of cells they are made of Why ? (CCE 2012)
Answer:
The kind of cells: Habitat is a place where diverse types of organisms live together. It cannot be used for classifying organisms. Cells have specific structure, prokaryotic in monerans and eukaryotic in the remaining organisms.
Organisms are unicellular in protista and multicellular in others. A cell wall is absent in animals. Cell wall contains chitin in fungi and cellulose in plants. Plastids occur in plant cells. They are absent in animal cells.

Question 4.
What is the primary characteristic on which the first division of organisms is made ? (CCE 2012)
Answer:
Type of cell, prokaryotic (genetic material or nucleoid free in cytoplasm) and eukaryotic (genetic material enclosed in nucleus).

Question 5.
On what basis are plants and animals put into different categories ? (CCE 2012)
Answer:
Plants and animals are placed in different categories because they differ in several characteristics.

  1. Shape: Animals have a definite shape while plants have less definite shape.
  2. Branching: Animals are unbranched (exception sponges), while plants are generally branched.
  3. Growth: Animals stop growing after reaching a certain size. Plants continue to grow till death.
  4. Locomotion: Animals can move from place to place (exception corals, sponges) while plants are fixed.
  5. Nutrition: Animals eat ready made food while plants manufacture their own food.
  6. Reserve Food: It is glycogen in animals and starch in plants.
  7. Cell Wall: Animal cells do not have a covering of wall while individual plant cells are surrounded by cell walls.
  8. Excretory Organs: They are present in animals but absent in plants.
  9. Sense Organs and Nervous System: They are found in animals but not in plants.

Question 6.
Which organisms are called primitive and how are they different from the so called advanced organisms ?
(CCE 2011, 2012)
Answer:
Primitive organisms are those organisms which have simple ancient body design with only basic characteristics of the group. There has been little change over a long period of time. Specialisations are fewer.
Advanced organisms are more recent organisms. They are also called higher organisms because they possess several specialisations. They have more complex structure and some new characteristics alongwith the basic ones.

Question 7.
Will advanced organisms be the same as complex organisms ? Why ? (CCE 2012, 2015)
Answer:
Yes. Advancement is based on development of specializations. Specialisation occurs where there is more elaboration and hence more complexity. However, there is likelihood of specialisation to lead to overspecialisation which becomes a hindrance to competitive nature of existence in the biosphere. Dinosaurs, giant crocodiles and mammoth have died down due to this reason. Therefore, advancement is possible only if specialisation leads to greater elaboration and efficiency.

Question 8.
What is the criterion for classification of organisms as belonging to kingdom Monera or Protista ?
(CCE 2012, 2014)
Answer:
Cell structure is used as a criterion for placing an organism in monera or protista. In monera the cells are prokaryotic. Membrane bound cell organelles are absent. In protista the cells are eukaryotic.
Membrane bound cell organelles are present. Protista contains only unicellular eukaryotes. Monera may have unicellular or multicellular forms.

Question 9.
In which kingdom will you place an organism which is single-belled, eukaryotic and photosynthetic ?
(CCE 2012, 2013)
Answer:
Protista.

Question 10.
In the hierarchy of classification, which grouping will have the smallest number of organisms with a maximum of characteristics in common and which will have the largest number of organisms.
(CCE 2011, 2012)
Answer:

  1. Small number (one) with maximum common characteristics— Species
  2. Largest number— Kingdom.

Question 11.
Which division among plants has the simplest organisms ?
Answer:
Thallophyta.

Question 12.
How are pteridophytes different from phanerogams ? (CCE 2012)
Answer:

Pteridophytes Phanerogams/Spermatophytes
1. Nature. They are seedless plants. Phanerogams are seed bearing plants.
2. Gametophyte. Gametophytes are small but independent. Gametophytes are nutritionally dependent upon the sporophyte.
3. Reproductive Organs. They are inconspicuous. Reproductive organs are quite conspicuous.
4. External Water. An external water is required for fertilization.
Examples. Ferns, Lycopodium.		 Fertilization does not require an external water.
Examples. Pinus, Maize.

Question 13.
How do gymnosperms and angiosperms differ from each other ? (CCE 2012)
Answer:

Gymnosperms Angiosperms
1. Sporophylls. They are aggregated to form cones. Sporophylls are aggregated to form flowers.
2. Seeds. The seeds are naked. The seeds are enclosed by fruit wall.
3. Microspores and Megaspores. The micro-spores and megaspores are produced by male and female cones. They are produced in the same or two different types of flowers.
4. Vascular Tissues. Xylem lacks vessels and phloem lacks companion cells. Xylem contains vessels and phloem contains companion cells.
5. Ovules. The ovules are not contained in the ovary. The ovules are enclosed in the ovary.
6. Endosperm. It is haploid. It is triploid.

Question 14.
How do poriferan animals differ from coelenterate animals ?
Answer:

Poriferans Coelenterates
1. Organisation. It is of cellular level. It is of tissue level.
2. Pores. A number of inhalent pores or ostia and a single exhalent pore or osculum are present. There is a single opening.
3. Digestion. It is intracellular. It is both intracellular and intercellular.
4. Muscle and Nerve Cells. They are absent. Primitive muscle and nerve cells appear for the first time in coelenterates.
5. Appendages. They are absent. Appendages are represented by tentacles.
6. Special Cells. The special cells are choanocytes or collar cells. Special cells are cnidoblasts.

Question 15.
How do annelid animals differ from arthropods ? (CCE 2012)
Answer:

Annelids Arthropods
1.      Appendages. They are unjointed.

2.       Circulation. Blood flows inside blood vessels (closed circulatory system).

3.       Coelom. True coelom is well-developed.

4.       Chitinous Exoskeleton. A chitinous exoskeleton is absent.

5.       Excretory Organs.
They are nephridia.

6.       Sensory System. It is less developed.

7.       Locomatory Organs. They are parapodia and setae.

 Appendages are jointed.

Blood flows through large fused sinuses or spaces (open circulatory system).

True coelom is small. Instead, blood filled false body cavity called haemocoel is present.

A chitinous exoskeleton is present.

Excretory organs are green glands and malpighian tubules.

Sensory system is well-developed.

They are legs and wings.

Question 16.
What are the differences between amphibians and Pisces? (CCE 2012)
Answer:

Pisces Amphibians
1. Scales. The body is covered by scales. 1. Scales are absent.
2. Mucous Glands. The skin does not possess mucous glands. 2. The skin has mucous glands that keep the skin moist and slippery.
3. Fins. Pisces possess fins for locomotion and steering 3. Fins may occur in larval stage. The adult does not possess fins. Limbs occur instead.
4. Heart. It is two chambered. 4. Heart is 3-chambered.
3. Lungs. Pisces do not have lungs. 5. Lungs are present.
Examples. Scoliodon, Labeo. Examples. Frog, Toad.

Question 17.
What are the differences between animals belonging to the aves group and those in mammalia group ? (CCE 2012)
Answer:

Aves Mammalia
1. Wings. Forelimbs are modified into wings. Wings are absent except in bats.
2. Feathers and Scales. The body is covered with feathers and scales. Feathers and scales are absent.
3. Skin Glands. Skin is dry. Only a single preen gland is present. Skin bears a number of sweat and oil glands.
4. Mammary Glands. They are absent. Female possesses mammary glands for feeding the young
5. Diaphragm. A diaphragm is absent. A partition called diaphragm is present between abdomen and thorax.
6. Beak. A toothless beak is present. Jaws do not form a beak. Teeth are present.
7. Bones. They are hollow or pneumatic. Bones do not possess air cavities.
8. Larynx/Syrinx. Larynx is non-functional. Instead syrinx is present. Larynx is functional. Syrinx is absent.
External air sacs do not occur over lungs.
9. Air Sacs. Lungs possess external air sacs.
10. Yolk. Eggs possess a lot of yolk (macrolecithal). Eggs have little yolk (alecithal).
11. Reproduction. Birds are oviparous. Mammals are viviparous with the exception of a few species.

NCERT CHAPTER END EXERCISES

Question 1.
What are the advantages of classifying organisms ? (CCE 2012, 2013, 2014)
Answer:

  1. Identification is not possible without any system of classification.
  2. Classification helps in bringing out similarities and dissimilarities amongst organisms.
  3. Relationships are built up with the help of classification. They indicate the evolutionary pathways.
  4. Organisms of other localities and fossils can be studied only with the help of a system of classification.
  5. It is not possible to study every organism. Study of one or two organisms gives sufficient idea about other members of the group.
  6. Other branches of biology depend upon proper identification of the organism which is possible only through a system of classification.

Question 2.
How would you choose between two characteristics to be used for developing a hierarchy in classification ?
Answer:
The character which is of fundamental importance, generally present in larger number of organisms, as a change in body design, is used in raising a higher category. The character of lesser importance, generally present in smaller number of individuals is used for raising lower category.

Question 3.
Explain the basis for grouping of organisms into five kingdoms. (CCE 2012, 2013)
Answer:
Four criteria have been used for grouping of organisms into five kingdoms—

  1. Procaryotic and eukaryotic nature
  2. Unicellular and multicellular nature
  3. Nutrition

Question 4.
How are criteria for deciding divisions in plants different from the criteria for deciding subgroups amongst animals ?
Answer:
Body design of plants is quite different from that of animals. Plants are anchored. They require organs for fixation and absorption. Plants are autotrophic. Reproductive organs, mechanical tissues and conducting tissues have evolved in higher plants. In animals the requirement is mobility for obtaining food and other necessities. Their evolution has occurred towards greater mobility, protection, increased efficiency in obtaining food and care of young ones. Therefore, criteria for deciding divisions or subgroups are different for plants and animals.

Question 5.
What are the major divisions in the plantae ? What is the basis for these divisions ? ( CCE 2015)
Answer:

  1. Multicellularity. Plantae includes multicellular organisms except for some primitive relatives of algae.
  2. They are eukaryotes, that is, with a nucleus and membrane bound cell organelles.
  3. Cell Wall. A cell wall generally containing cellulose occurs around cells.
  4. Central Vacuole. A mature cell commonly possesses a single large central vacuole.
  5. Food Reserve. It is starch and fat.
  6. They are double membrane covered cell organelles found in all plants. Some plastids possess photosynthesis pigments. They are called chloroplasts.

Kingdom plantae has three levels of classification:

  1. The first level of classification deals with presence or absence of well differentiated distinct parts. Undifferentiated plants are included amongst thallophyta.
  2. The second level of classification deals with presence or absence of vascular tissues.
  3. The third level of classification is based on the presence or absence of seeds and whether the seeds are exposed or enclosed inside fruits.

Question 6.
Explain how animals in vertebrata are classified into further subgroups.
Answer:
Vertebrata is divided into five classes—pisces, amphibia, reptilia, aves and mammalia on the basis of following characteristics :

  1. It consists of scales in fishes and reptiles, feathers in birds and hair in mammals. Skin is smooth and moist in amphibians.
  2. It is cartilaginous in chondrichthyes and bony in others.
  3. It occurs through gills in all fishes and larvae of amphibians. Other have lungs for breathing.
  4. Fishes and amphibians lay eggs in water. Reptiles and birds do so outside water.
  5. They occur in birds. Wings are used for flight.
  6. External Ears. They occur in mammals.
  7. Mammals generally show vivipary or give birth to young ones.

PRACTICAL BASED TWO MARKS QUESTIONS

Question 1.
The body of an organism is stream lined and is found in fresh water as well marine water. Identify the organism and write its one specific feature ? (CCE 2015)
Answer:
Fish, presence of fins, gills and scales.

Question 2.
Name the habitat of earthworms and how is it useful to them. (CCE 2015)
Answer:
Moist soil where they can obtain decaying organic matter as well as dig burrows easily.

Question 3.
Draw the diagram of a bony fish and write one of its adaptive feature. (CCE 2015)
Answer:
NCERT Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms image - 1
Adaptive feature : Presence of air bladder for remaining afloat inside water without spending energy.

Question 4.
After observing an earthworm carefully. Samir decided to place it in phylum Annelida. Which two features did he observe that helped him to do so ? (CCE 2015)
Answer:

  1. Elongated, cylindrical and segmented body,
  2. Presence of closed circulatory system with red-blood.

Question 5.
Mention two features adopted by birds which help them to fly.
(CCE 2015)
Answer:

  1. Fore limbs modified into wings,
  2. Stream-lined body with pneumatic bones.

Question 6.
Amita was shown the posterior parts of two cockroaches (I and II)
NCERT Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms image - 2
(a) She was asked to identify parts A and B.
(b) Which one of them is a male cockroach ?
(c) On which segment is part B present.
Write the correct answers. (CCE 2015)
Answer:
(a) A – anal cercus,
B – anal style.
(b) I is male cockroach
(c) Ninth segment.

Question 7.
Identify X and Y in the diagram of the part of earthworm drawn here. What function is performed by X ? (CCE 2015)
NCERT Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms image - 3
Answer:
X: Prostomium.
Y: Peristomium.
Functions of X:

  1. Sensory structure for receiving information about the environment.
  2. Pushing moist earth during digging of furrow.

Question 8.
What are the functions of modified hindlimbs of birds ? (CCE 2015)
Answer:

  1. Perching
  2. Walking
  3. Wading in aquatic birds.

Question 9.
Complete the following table (CCE 2016)
NCERT Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms image - 4
Answer:
1. Cockroach, chitinous exoskeleton (Arthropoda).
2. Earthworm, hydraulic skeleton (Annelida).

Question 10.
Give two identifying features of the phylum to which earthworm belongs. (CCE 2016)
Answer:
Annelida:

  1. Metameric segmentation
  2. Closed circulatory system.

Question 11.
State any two ways by which earthworm’s body is adapted to live in soil. (CCE 2016)
Answer:

  1. Elongated cylindrical body with moist skin
  2. Setae for firm grip
  3. Coelomic fluid developing hydraulic power for digging. /

Question 12.
(a) How are birds modified to reduce body weight for flying ? .
(b) Which part of the body is modified for flight ? (CCE 2016)
Answer:
(a) Hollow bones
(b) Fore limbs modified into wings.

Question 13.
Name any two characteristic features of class Reptilia. (CCE 2016)
Answer:

  1. Dry, nonglandular rough skin having scales
  2. Incompletely four-chambered heart.

Question 14.
The teacher had shown a student a specimen R and asked him it is a female Pinus cone. What feature will the student look for the identification of the specimen ? (CCE 2017)
Answer:

  1. Occurrence of megasporophylls and bract scales
  2. Presence of ovules or seeds (two) on the adaxial side of each magasporophyll (ovuliferous scale).

SELECTION TYPE QUESTIONS

Alternate Response Type Questions
(True/False. Right/Wrong-, Yes/No)

Question 1.
Prokaryotes do not have a true nucleus but possess all other types of organelles.
Question 2.
Paramecium possesses two types of nuclei, micronucleus and macronucleus.
Question 3.
Lichen is formed by symboitic association between an alga and a fungus.
Question 4.
Platypus and Echidna are reptiles that give birth to live young ones.
Question 5.
The largest bird is Ostrich.
Question 6.
Chameleon is an amphibian.
Question 7.
Angiosperms are also called flowering plants.
Question 8.
Algae are amphibians of plant kingdom.

Matching Type Questions :

Question 9.
Match the articles of the column I and II (single matching)
NCERT Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms image - 5

Question 10.
Match the contents of columns I, II and III (Double matching)
NCERT Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms image - 6

Question 11.
Which type of nutrition- autotrophic (A), decomposer (D), and holozoic (H) occurs in the organisms listed below (key or checklist items).
NCERT Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms image - 7

Question 12.
Match the Stimulus with Appropriate Response.
NCERT Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms image - 8

Fill In the Blanks

Question 13. Bird wings are modified ………….. limbs.
Question 14. …………… is a phylum of spiny skinned sea animals.
Question 15. Roundworm has ……………. symmetry.
Question 16. Gymnosperms have ……………. seeds.
Question 17. Fungi are …………….. organisms.

Answers:
NCERT Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms image - 9

SOME ACTIVITY BASED QUESTIONS

Question 1.
Give one point of difference between Gymnosperms and Angiosperms. (CCE 2012, 2014)
Answer:
Seeds are naked or exposed in gymnosperms but seeds are covered by fruit wall or pericarp in angiosperms.

Question 2.
Define phytogeny.
Answer:
The evolutionary history of organisms is termed as phylogeny.

Question 3.
Identify the animal group having :

  1. Body spiny and radial symmetry
  2. Bones light and hollow
  3. 4 pairs of jointed legs and no wings.
  4. Soft bodied animals supported by calcareous shells.
  5. External ear or pinna.

Answer:

  1. Echinodermata
  2. Aves
  3. Arachnida
  4. Mollusca
  5. Mammalia.

Question 4.
Give one point of difference between notochord and nerve cord.
Answer:
Notochord is an ensheathed flexible rod of turgid cells located along the back of chordate embryos and some prinitive adult chordates ventral to the nerve cord. It provides attachment to muscles. Notochord has given rise to jointed axial skeleton of cranium and vertebral column. Nerve cord is a collection of nerve fibres that runs throughout the length of an animal. It is hollow and dorsal in chordates where it gets modified into central nervous system of brain and spinal cord. Nerve cord is solid and ventral in nonchordates.

Question 5.
What is haemocoel ? Which groups of animals have haemocoel ?
Answer:
The blood filled cavity consisting of spaces in between the organs is known as haemocoel. Examples— Arthropoda and Mollusca.

Question 6.
Give one example of hemichordata, urochordata and cephalochordata.
Answer:

  1. Hemichordata- Balanoglossus.
  2. Urochordata— Herdmania.
  3. Cephalochordata- Amphioxus.

Question 7.
Differentiate the nature of skin in four classes of tetrapoda.
Answer:
The nature of skin in four classes of tetrapoda are—

  1. Class Amphibia- Thin, moist, glandular and respiratory skin.
  2. Class Reptilia— Dry and non-glandular skin with scales.
  3. Class Aves- Dry and non-glandular skin with feathers.
  4. Class Mammalia— Glandular skin with hairs.

Question 8.
Why whales are not grouped in the fishes ? (CCE 2012)
Answer:
Whales can swim in water like the fishes but are not fish as they respire with lungs, have four chambered heart, diaphragm and mammary glands. So they are mammals.

Question 9.
List a few flight/aerial adaptations in birds.
Answer:

  1. Forelimbs are modified into wings.
  2. Body is covered with exoskeleton of feathers.
  3. Long bones are pneumatic having air cavities.
  4. Body is stream-lined to reduce air resistance.
  5. Well developed flight muscles.
  6. Presence of air sacs to help in double respiration.
  7. Tail feathers form a steering apparatus.
  8. They have acute vision.

Question 10.
Give one example of each :

  1. Asymmetry, radial and bilateral symmetry
  2. Acoelomates, pseudocoelomate and haemocoelomate.

Answer:

  1. Amoeba, Hydra and a fish.
  2. Flatworms, Roundwarms and Arthropods.

Question 11.
In what way, amphibians are advanced than the fishes ?
Answer:
Amphibians have three-chambered heart and lungs for respiration, while fishes have two-chambered heart and gills for respiration.

Question 12.
Why is Euglena called dual organism! plant-animal ? (CCE 2012)
Answer:
Euglena is called plant-animal because it has characteristics of both plants and animals. Like plants, Euglena has chloroplasts with the help of which it performs photosynthesis. Like animals, it lacks cell wall, possesses pellicle, an anterior invagination, flagellum, eye spot, etc. and capable of obtaining ready made food in dark.

Question 13.
Why are protozoa called early animals ?
Answer:
Protozoa (pro-ancient, zoo—animal) are called early animals because like animals they have holozoic nutrition and glycogen as food reserve. They have, however, unicellular nature and are without an embryo stage. Protozoa evolved before the evolution of true animals or metazoa.

Question 14.
Name the organisms which has

  1. Setae and Parapodia
  2. Tube feet

Answer:

  1. Nereis
  2. Starfish

NCERT Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms

Hope given NCERT Solutions for Class 9 Science Chapter 7 are helpful to complete your science homework.

If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.

RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS

RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS

Other Exercises

Mark the correct alternative in each of the following:
Question 1.
In ∆ABC ≅ ∆LKM, then side of ∆LKM equal to side AC of ∆ABC is
(a) LX
(b) KM
(c) LM
(d) None of these
Solution:
Side AC of ∆ABC = LM of ∆LKM (c)
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS Q1.1

Question 2.
In ∆ABC ≅ ∆ACB, then ∆ABC is isosceles with
(a) AB=AC
(b) AB = BC
(c) AC = BC
(d) None of these
Solution:
∵ ∆ABC ≅ ∆ACB
∴ AB = AC (a)
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS Q2.1

Question 3.
In ∆ABC ≅ ∆PQR, then ∆ABC is congruent to ∆RPQ, then which of the following is not true:
(a) BC = PQ
(b) AC = PR
(c) AB = PQ
(d) QR = BC
Solution:
∵ ∆ABC = ∆PQR
∴ AB = PQ, BC = QR and AC = PR
∴ BC = PQ is not true (a)

Question 4.
In triangles ABC and PQR three equality relations between some parts are as follows: AB = QP, ∠B = ∠P and BC = PR State which of the congruence conditions applies:
(a) SAS
(b) ASA
(c) SSS
(d) RHS
Solution:
In two triangles ∆ABC and ∆PQR,
AB = QP, ∠B = ∠P and BC = PR
The condition apply : SAS (a)
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS Q4.1

Question 5.
In triangles ABC and PQR, if ∠A = ∠R, ∠B = ∠P and AB = RP, then which one of the following congruence conditions applies:
(a) SAS
(b) ASA
(c) SSS
(d) RHS
Solution:
In ∆ABC and ∆PQR,
∠A = ∠R
∠B = ∠P
AB = RP
∴ ∆ABC ≅ ∆PQR (ASA axiom) (b)
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS Q5.1

Question 6.
If ∆PQR ≅ ∆EFD, then ED =
(a) PQ
(b) QR
(c) PR
(d) None of these
Solution:
∵ ∆PQR = ∆EFD
∴ ED = PR (c)
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS Q6.1

Question 7.
If ∆PQR ≅ ∆EFD, then ∠E =
(a) ∠P
(b) ∠Q
(c) ∠R
(d) None of these
Solution:
∵ ∆PQR ≅ ∆EFD
∴ ∠E = ∠P (a)
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS Q7.1

Question 8.
In a ∆ABC, if AB = AC and BC is produced to D such that ∠ACD = 100°, then ∠A =
(a) 20°
(b) 40°
(c) 60°
(d) 80°
Solution:
In ∆ABC, AB = AC
∴ ∠B = ∠C
But Ext. ∠ACD = ∠A + ∠B
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS Q8.1
∠ACB + ∠ACD = 180° (Linear pair)
∴ ∠ACB + 100° = 180°
⇒ ∠ACB = 180°-100° = 80°
∴ ∠B = ∠ACD = 80°
But ∠A + ∠B 4- ∠C = 180°
∴ ∠A + 80° + 80° = 180°
⇒∠A+ 160°= 180°
∴ ∠A= 180°- 160° = 20° (a)

Question 9.
In an isosceles triangle, if the vertex angle is twice the sum of the base angles, then the measure of vertex angle of the triangle is
(a) 100°
(b) 120°
(c) 110°
(d) 130°
Solution:
In ∆ABC,
∠A = 2(∠B + ∠C)
= 2∠B + 2∠C
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS Q9.1
Adding 2∠A to both sides,
∠A + 2∠A = 2∠A + 2∠B + 2∠C
⇒ 3∠A = 2(∠A + ∠B + ∠C)
⇒ 3∠A = 2 x 180° (∵∠A + ∠B + ∠C = 180° )
⇒ 3∠A = 360°
⇒∠A = \(\frac { { 360 }^{ \circ } }{ 3 }\)  = 120°
∴ ∠A = 120° (b)

Question 10.
Which of the following is not a criterion for congruence of triangles?
(a) SAS
(b) SSA
(c) ASA
(d) SSS
Solution:
SSA is not the criterion of congruence of triangles. (b)

Question 11.
In the figure, the measure of ∠B’A’C’ is
(a) 50°
(b) 60°
(c) 70°
(d) 80°
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS Q11.1
Solution:
In the figure,
∆ABC ≅ ∆A’B’C’
∴ ∠A = ∠A
⇒3x = 2x- + 20
⇒ 3x – 2x = 20
⇒ x = 20
∠B’A’C’ = 2x + 20 = 2 x 20 + 20
= 40 + 20 = 60° (b)

Question 12.
If ABC and DEF are two triangles such that ∆ABC ≅ ∆FDE and AB = 5 cm, ∠B = 40° and ∠A = 80°. Then, which of the following is true?
(a) DF = 5 cm, ∠F = 60°
(b) DE = 5 cm, ∠E = 60°
(c) DF = 5 cm, ∠E = 60°
(d) DE = 5 cm, ∠D = 40°
Solution:
∵ ∆ABC ≅ ∆FDE,
AB = 5 cm, ∠A = 80°, ∠B = 40°
∴ DF = 5 cm, ∠F = 80°, ∠D = 40°
∴ ∠C =180°- (80° + 40°) = 180° – 120° = 60°
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS Q12.1
∴ ∠E = ∠C = 60°
∴ DF = 5 cm, ∠E = 60° (c)

Question 13.
In the figure, AB ⊥ BE and FE ⊥ BE. If BC = DE and AB = EF, then ∆ABD is congruent to
(a) ∆EFC
(b) ∆ECF
(c) ∆CEF
(d) ∆FEC
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS Q13.1
Solution:
In the figure, AB ⊥ BE, FE ⊥ BE
BC = DE, AB = EF,
then CD + BC = CD + DE BD = CE
In ∆ABD and ∆CEF,
BD = CE (Prove)
AB = FE (Given)
∠B = ∠E (Each 90°)
∴ ∆ABD ≅ ∆FCE (b)

Question 14.
In the figure, if AE || DC and AB = AC, the value of ∠ABD is
(a) 70°
(b) 110°
(c) 120°
(d) 130°
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS Q14.1
Solution:
In the figure, AE || DC
∴ ∠1 = 70° (Vertically opposite angles)
∴ ∠1 = ∠2 (Alternate angles)
∠2 = ∠ABC (Base angles of isosceles triangle)
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS Q14.2
∴ ABC = 90°
But ∠ABC + ∠ABD = 180° (Linear pair)
⇒ 70° +∠ABD = 180°
⇒∠ABD = 180°-70°= 110°
∴ ∠ABD =110° (b)

Question 15.
In the figure, ABC is an isosceles triangle whose side AC is produced to E. Through C, CD is drawn parallel to BA. The value of x is
(a) 52°
(b) 76°
(c) 156°
(d) 104°
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS Q15.1
Solution:
In ∆ABC, AB = AC
AC is produced to E
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS Q15.2
CD || BA is drawn
∠ABC = 52°
∴ ∠ACB = 52° (∵ AB = AC)
∴ ∠BAC = 180°-(52° +52°)
= 180°-104° = 76°
∵ AB || CD
∴ ∠ACD = ∠BAC (Alternate angles)
= 76°
and ∠BCE + ∠DCB = 180° (Linear pair)
∠BCE + 52° = 180°
⇒∠BCE = 180°-52°= 128°
∠x + ∠ACD = 380°
⇒ x + 76° = 180°
∴ x= 180°-76°= 104° (d)

Question 16.
In the figure, if AC is bisector of ∠BAD such that AB = 3 cm and AC = 5 cm, then CD =
(a) 2 cm
(b) 3 cm
(c) 4 cm
(d) 5 cm
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS Q16.1
Solution:
In the figure, AC is the bisector of ∠BAD, AB = 3 cm, AC = 5 cm
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS Q16.2
In ∆ABC and ∆ADC,
AC = AC (Common)
∠B = ∠D (Each 90°)
∠BAC = ∠DAC (∵ AC is the bisector of ∠A)
∴ ∆ABC ≅ ∆ADC (AAS axiom)
∴ BC = CD and AB = AD (c.p.c.t.)
Now in right ∆ABC,
AC2 = AB2 + BC2
⇒ (5)2 = (3)2 + BC2
⇒25 = 9 + BC2
⇒ BC2 = 25 – 9 = 16 = (4)2
∴ BC = 4 cm
But CD = BC
∴ CD = 4 cm (c)

Question 17.
D, E, F are the mid-point of the sides BC, CA and AB respectively of ∆ABC. Then ∆DEF is congruent to triangle
(a) ABC
(b) AEF
(c) BFD, CDE
(d) AFE, BFD, CDE
Solution:
In ∆ABC, D, E, F are the mid-points of the sides BC, CA, AB respectively
DE, EF and FD are joined
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS Q17.1
∵ E and F are the mid-points
AC and AB,
∴ EF = \(\frac { 1 }{ 2 }\) BC and EF || BC
Similarly,
DE = \(\frac { 1 }{ 2 }\) AB and DE || AB
DF = \(\frac { 1 }{ 2 }\) AC and DF || AC
∴ ∆DEF is congruent to each of the triangles so formed
∴ ∆DEF is congruent to triangle AFE, BFD, CDE (d)

Question 18.
ABC is an isosceles triangle such that AB = AC and AD is the median to base BC. Then, ∠BAD =
(a) 55°
(b) 70°
(c) 35°
(d) 110°
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS Q18.1
Solution:
In ∆ABC, AB = AC
AD is median to BC
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS Q18.2
∴ BD = DC
In ∆ADB, ∠D = 90°, ∠B = 35°
But ∠B + BAD + ∠D = 180° (Sum of angles of a triangle)
⇒ 35° + ∠BAD + 90° = 180°
⇒∠BAD + 125°= 180°
⇒ ∠BAD = 180°- 125°
⇒∠BAD = 55° (a)

Question 19.
In the figure, X is a point in the interior of square ABCD. AXYZ is also a square. If DY = 3 cm and AZ = 2 cm, then BY =
(a) 5 cm
(b) 6 cm
(c) 7 cm
(d) 8 cm
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS Q19.1
Solution:
In the figure, ABCD and AXYZ are squares
DY = 3 cm, AZ = 2 cm
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS Q19.2
DZ = DY + YZ
= DY + Z = 3 + 2 = 5 cm
In ∆ADZ, ∠2 = 90°
AD2 + AZ2 + DZ2 = 22 + 52 cm
= 4 + 25 = 29
In ∠ABX, ∠X = 90°
AB2 = AX2 + BX2
AD2 = AZ2 + BX2
(∵ AB = AD, AX = AZ sides of square)
29 = 22 + BX2
⇒ 29 = 4 + BX2
⇒ BX2 = 29 – 4 = 25 = (5)2
∴ BX = 5 cm (a)

Question 20.
In the figure, ABC is a triangle in which ∠B = 2∠C. D is a point on side BC such that AD bisects ∠BAC and AB = CD. BE is the bisector of ∠B. The measure of ∠BAC is
(a) 72°
(b) 73°
(c) 74°
(d) 95°
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS Q20.1
Solution:
In the figure, ∠B = 2∠C, AD and BE are the bisectors of ∠A and ∠B respectively,
AB = CD
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS Q20.2
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS Q20.3

Hope given RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3E

RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3E

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3E.

Other Exercises

Evaluate:

Question 1.
Solution:
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3E Q1.1

Question 2.
Solution:
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3E Q2.1

Question 3.
Solution:
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3E Q3.1

Question 4.
Solution:
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3E Q4.1

Question 5.
Solution:
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3E Q5.1

Question 6.
Solution:
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3E Q6.1

Question 7.
Solution:
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3E Q7.1

Question 8.
Solution:
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3E Q8.1

Question 9.
Solution:
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3E Q9.1

Question 10.
Solution:
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3E Q10.1

Question 11.
Solution:
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3E Q11.1

Question 12.
Solution:
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3E Q12.1

Question 13.
Solution:
Finding the square root of 2509 by division we find that 9 is left as remainder
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3E Q13.1
9 must be subtracted to get the perfect square 100.
Least number to be subtracted = 9

Question 14.
Solution:
Finding the square root of 7581 by division method, we find that 12 is left as remainder.
12 must be subtracted from 7581 to get a perfect square i.e., 7581 – 12 = 7569
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3E Q14.1
(i) The least number to be subtracted = 12
(ii) Perfect square = 7569
(iii) and square root = 87 Ans.

Question 15.
Solution:
Finding the square root of 6203 by division method, we find that 38 is to be added to get a perfect square.
(i) Least number to be added = 38
(ii) Perfect square = 6241
(iii) Square root = 79 Ans.
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3E Q15.1

Question 16.
Solution:
Finding the square root of 8400 by long division method, we find that 64 is to be added to 8400,
We, get 8400 + 64 = 8464
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3E Q16.1
Least number to be added = 64
Perfect square = 8464
Square root = 92 Ans.

Question 17.
Solution:
Least four-digit number = 1000
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3E Q17.1
Finding the square root of 1000 by the division method, we find that 24 must be added to get a perfect square of 4 digits.
Perfect square = 1000 + 24 = 1024 Ans.
square root of 1024 = 32
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3E Q17.2

Question 18.
Solution:
Greatest number of five digits = 99999
Finding the square root of 99999
We get remainder = 143
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3E Q18.1
Required perfect square = 99999 – 143 = 99856
and square root = 316 Ans

Question 19.
Solution:
Area of a square field = 60025 m²
Let its side = a
RS Aggarwal Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3E Q19.1

Hope given RS Aggarwal Solutions Class 8 Chapter 3 Squares and Square Roots Ex 3E are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula VSAQS

RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula VSAQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula VSAQS

Other Exercises

Question 1.
Solution:
In two congruent triangles ABC and DEF, if AB = DE and BC = EF. Name the pairs of equal angles.

In AABC and ADEF,
∆ABC ≅ ∆DEF
and AB = DE, BC = EF
∴ ∠A = ∠D, ∠B = ∠E and ∠C = ∠F
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula VSAQS Q1.1

Question 2.
Solution:
In two triangles ABC and DEF, it is given that ∠A = ∠D, ∠B = ∠E and ∠C = ∠F. Are the two triangles necessarily congruent?

No, as the triangles are equiangular, so similar.

Question 3.
Solution:
If ABC and DEF are two triangles such that AC = 2.5 cm, BC = 5 cm, ∠C = 75°, DE = 2.5 cm, DF = 5 cm and ∠D = 75°. Are two triangles congruent?
Yes, triangles are congruent (SAS axiom)
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula VSAQS Q3.1

Question 4.
Solution:
In two triangles ABC and ADC, if AB = AD and BC = CD. Are they congruent?
Yes, these are congruent
In two triangles ABC are ADC,
AB = AD (Given)
BC = CD (Given)
and AC = AC (Common)
∴ ∆sABC ≅ AADC (SSS axiom)
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula VSAQS Q4.1

Question 5.
Solution:
In triangles ABC and CDE, if AC = CE, BC = CD, ∠A = 60°, ∠C – 30° and ∠D = 90°. Are two triangles congruent?
Yes, triangles are congruent because,
In ∆ABC, and ∆CDE,
AC = CE
BC = CD ∠C = 30°
∴ ∆ABC ≅ ∆CDE (SAS axiom)
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula VSAQS Q5.1

Question 6.
Solution:
ABC is an isosceles triangle in which AB = AC. BE and CF are its two medians. Show that BE = CF.

Given : In ∆ABC, AB = AC
BE and CF are two medians
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula VSAQS Q6.1
To prove : BE = CF
Proof: In ∆ABE and ∆ACF.
AB = AC (Given)
∠A = ∠A (Common)
AE = AF (Half of equal sides)
∴ ∆ABE ≅ ∆ACF (SAS axiom)
∴ BE = CF (c.p.c.t.)

Question 7.
Solution:
Find the measure of each angle of an equilateral triangle.

In ∆ABC,
AB = AC = BC
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula VSAQS Q7.1
∵ AB = AC
∴ ∠C = ∠B …(i)
(Angles opposite to equal sides)
Similarly,
AC = BC
∴ ∠B = ∠A …(ii)
From (i) and (ii),
∠A = ∠B = ∠C
But ∠A + ∠B + ∠C = 180°
(Sum of angles of a triangle)
∴ ∠A + ∠B + ∠C = \(\frac { { 180 }^{ \circ } }{ 3 }\)  = 60°

Question 8.
Solution:
CDE is an equilateral triangle formed on a side CD of a square ABCD. Show that ∆ADE ≅ ∆BCE.

Given : An equilateral ACDE is formed on the side of square ABCD. AE and BE are joined
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula VSAQS Q8.1
To prove : ∆ADE ≅ ∆BCE
Proof : In ∆ADE and ∆BCE,
AD = BC (Sides of a square)
DE = CE (Sides of equilateral triangle)
∠ADE = ∠BCE(Each = 90° + 60° = 150°)
∴ AADE ≅ ABCE (SAS axiom)

Question 9.
Solution:
Prove that the sum of three altitude of a triangle is less than the sum of its sides.

Given : In ∆ABC, AD, BE and CF are the altitude of ∆ABC
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula VSAQS Q9.1
To prove : AD + BE + CF < AB + BC + CA
Proof : In right ∆ABD, ∠D = 90°
Then other two angles are acute
∵ ∠B < ∠D
∴ AD < AB …(i)
Similarly, in ∆BEC and ∆ABE we can prove thatBE and CF < CA …(iii)
Adding (i), (ii), (iii)
AD + BE -t CF < AB + BC + CA

Question 10.
Solution:
In the figure, if AB = AC and ∠B = ∠C. Prove that BQ = CP.
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula VSAQS Q10.1

Given : In the figure, AB = AC, ∠B = ∠C
To prove : BQ = CP
Proof : In ∆ABQ and ∆ACP
AB = AC (Given)
∠A = ∠A (Common)
∠B = ∠C (Given)
∴ ∆ABQ ≅ ∆ACP (ASA axiom)
∴ BQ = CP (c.p.c.t.)

Hope given RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12A

RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12A

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 12 Circles Ex 12A.

Other Exercises

Question 1.
Solution:
PT is the tangent to the circle with centre O and radius OT = 20 cm.
P is a point 29 cm away from O.
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12A 1
OP = 29 cm, OT = 20 cm
OT is radius and PT is the tangent
OT ⊥ PT
Now, in right ∆OPT,
OP² = OT² + PT² (Pythagoras Theorem)
⇒ (29)² = (20)² + PT²
⇒ 841 = 400 + PT²
⇒ PT² = 841 – 400
⇒ PT² = 441 = (21)²
⇒ PT = 21
Length of tangent PT = 21 cm

Question 2.
Solution:
P is a point outside the circle with centre O and OP = 25 cm
PT is the tangent to the circle and OT is the radius
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12A 2
OT ⊥ PT
PT = 24 cm
Now, in right ∆OPT,
OP² = OT² + PT² (Pythagoras Theorem)
⇒ 25² = OT² + (24)²
⇒ 625 = OT² + 576
⇒ OT² = 625 – 576 = 49 = (7)²
OT = 7 cm
or radius of the circle is 7 cm.

Question 3.
Solution:
Given : Two concentric circles with centre O and radii 6.5 cm and 2.5 cm respectively.
AB is a chord of the larger circle which touches the smaller circle at C.
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12A 3
To find : The length of AB.
Join OC, OA.
AB is tangent to the smaller circle and OC is the radius.
OC ⊥ AB and OC bisects AB at C.
AC = CB
OA = 6.5 cm, OC = 2.5 cm
Now, in right ∆OAC,
OA² = OC² + AC² (Pythagoras Theorem)
6.5² = 2.5² + AC²
⇒ 42.25 = 6.25 + AC²
⇒ AC² = 42.25 – 6.25 = 36 = (6)²
⇒ AC = 6
Length of chord AB = 2 x AC = 2 x 6 = 12 cm

Question 4.
Solution:
Given : In the given figure, a circle is inscribed in a triangle ABC which touches the sides AB, BC, CA at D, E and F respectively.
AB = 12 cm, BC = 8 cm and AC = 10 cm.
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12A 4
To find : Lengths of AD, BE and CF.
AD and AF are tangents to the circle from A.
AD = AF = x.
Similarly, BD and BE are tangents to the circle.
BD = BE = y
and CE and CF are tangents to the circle
CE = CF = z
x + y + 12 …(i)
y + z = 8 …(ii)
z + x = 10 …(iii)
Adding, 2(x + y + z) = 12 + 8 + 10 = 30
x + y + z = 15 …(iv)
Now, subtracting (ii), (iii) and (i) respectively from (iv)
x = 15 – 8 = 7
y = 15 – 10 = 5
z = 15 – 12 = 3
AD = 7 cm, BE = 5 cm and CF = 3 cm

Question 5.
Solution:
Given : In the given figure,
PA and PB are the tangents drawn from P to the circle with centre O.
OA and OB are joined.
To prove : A, O, B and P are concyclic.
Proof : PA is tangent and OA is the radius.
OA ⊥ PA
∠OAP = 90° …(i)
Similarly, OB is the radius and PB is the tangent
OB ⊥ PB
∠OBP = 90° …(ii)
Adding (i) and (ii)
∠OAP + ∠OBP = 90° + 90° = 180°
But these are the opposite angles of the quadrilateral AOBP
Quadrilateral AOBP is a cyclic
Hence A, O, B and P are concylic

Question 6.
Solution:
Given : In the given figure, chord AB of larger circle of the two concentric circles with centre O, touches the smaller circle at C.
To prove : AC = CB.
Construction : Join OC, OA and OB.
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12A 5
Proof: AB is tangent to the smaller circles and OC is the radius.
OC ⊥ AB.
In right ∆OAC and ∆OBC,
Hypotenuse OA = OB (radii of the same circle)
Side OC = OC (common)
∆OAC = ∆OBC (RHS axiom)
AC = CB (c.p.c.t.)

Question 7.
Solution:
Given : In the figure, from an external point P of the circle, PA and PB are tangents to the circle with centre O.
CD is a tangent at E.
PA = 14 cm.
To find : Perimeter of ∆PCD.
Proof: PA and PB are tangents from P to the circle.
PA = PB …(i)
CA and CE are tangents to the circle.
CA = CE …(ii)
Similarly,
DB = DE
Now, perimeter of ∆PCD
= PC + CD + PD
= PC + CE + ED + PD
= PC + CA + BD + PD
= PA + PB [From (i) and (ii)]
= 14 + 14 = 28 cm

Question 8.
Solution:
A circle with centre O, is inscribed in a ∆ABC touching it at P, Q, R respectively
AB = 10 cm, AR = 7 cm and CR = 5 cm
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12A 6
To find, the length of BC
AP and AR are the tangents to the circle
AP = AR = 7 cm
BP = AB – AP = 10 – 7 = 3 cm
BP and BQ are the tangents to the circle
BQ = BP = 3 cm
Similarly, CQ = CR = 5 cm
BC = BQ + CQ = 3 + 5 = 8 cm

Question 9.
Solution:
In the figure, a circle with centre O, touches the sides of a quadrilateral ABCD at P, Q, R and S respectively.
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12A 7
AB = 6 cm, BC = 7 cm and CD = 4 cm
To find, the length of AD.
We know that tangents from an external point to a circle are equal.
AP = AS, BP = BQ
CR = CQ and DR = DS
Now, AP + BP + CR + DR = AS + BQ + CQ + DC
⇒ (AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
⇒ AB + CD = AD + BC
⇒ AD = (AB + CD) – BC = (6 + 4 – 7) = 3 cm (AB = 6 cm, CD = 4 cm and BC = 7 cm)
Hence, AD = 3 cm.

Question 10.
Solution:
In the given figure, an isosceles ∆ABC in which AB = AC, is circumscribed a circle.
The circle touches its sides BC, CA and AB at P, Q and R respectively.
To prove : P bisects the base BC.
i.e. BP = PC
Proof : AR and AQ are tangents to the circle.
AR = AQ But AB = AC
AB – AR = AC – AQ
⇒ BR = CQ …(i)
BR and BP are tangents to the circle.
BR = BP …(ii)
Similarly,
CP and CQ are tangents
CP = CQ …(iii)
BR = CQ (proved)
From (ii) and (iii),
BP = CP or BP = PC
Hence, P is midpoint of BC.

Question 11.
Solution:
In the given figure, O is the centre of two concentric circles with radii 4 cm and 6 cm respectively.
PA and PB are the tangents drawn from P, to the outer circle and inner circle respectively.
PA = 10 cm
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12A 8
To find, the length of PB (upto one place of decimal)
OA and OB are the radii and PA and PB are two tangents to the circles respectively
OA ⊥ PA and OB ⊥ PB
In right ∆OAP,
OP² = OA² + PA² (Pythagoras Theorem)
= (6)² + (10)² = 36 + 100 = 136
Similarly, in right ∆OBP,
OP² = OB² + PB²
136 = (4)² + PB²
⇒ 136 = 16 + PB²
⇒ PB² = 136 – 16 = 120
PB = √120 cm = 2√30 cm = 2 x 5.47 = 10.94 = 10.9 cm

Question 12.
Solution:
In the given figure, ∆ABC circumscribed the circle with centre O.
Radius OD = 3 cm
BD = 6 cm, DC = 9 cm
Area of ∆ABC = 54 cm²
To find : Lengths of AB and AC.
Construction : Join OA, OB, OC, OE and OF.
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12A 9
Proof : OE = OF = OD = 3 cm, radii of the same circle.
BD and BF are tangents to the circle.
BD = BF = 6 cm
Similarly, CD = CE = 9 cm and AE = AF = x (Suppose)
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12A 10
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12A 11
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12A 12

Question 13.
Solution:
In the given figure, PQ is a chord of the circle with centre O.
TP and TQ are tangents, OP and OT are joined.
Radius of the circle is 3 cm and PQ = 4.8 cm.
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12A 13
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12A 14

Question 14.
Solution:
PQ and RS are two parallel tangents which
touches the circle at A and B. O is the centre of the circle.
OA and OB are joined.
To prove : AB passes through the centre O of the circle.
Construction : Draw OC || PQ or RS.
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12A 15
Proof : OA is radius and PQ is tangent.
OA ⊥ PQ ⇒ ∠OAP = 90°
Similarly, OB is radius and RS is the tangent
OB ⊥ RS ⇒ ∠OBR = 90°
PQ || OC
∠AOC + ∠OAP = 180° (Co-interior angles)
∠AOC + 90° = 180°
∠AOC = 180° – 90° = 90°
Similarly, ∠BOC = 90°
∠AOC + ∠BOC = 90° + 90° = 180°
AOB is a straight line.
Hence, AB passes through the centre of the circle.

Question 15.
Solution:
In the given figure, a circle with centre O, is inscribed in a quadrilateral ABCD.
The circle touches the siaes of quadrilateral at P, Q, R and S respectively.
AB = 29 cm, AD = 23 cm, ∠B = 90°
DS = 5 cm
To find : The radius of the circle.
Construction : Join OP and OQ.
Proof: Let OP = OQ = r
∠B = 90°
PBQO is a square.
DR and DS are the tangents to the circle.
DR = DS = 5 cm
AR = AD – DR = 23 – 5 = 18 cm
AR and AQ are tangents to the circle.
AQ = AR = 18 cm
QB = AB – AQ = 29 – 18 = 11 cm
PBQO is a square.
OP = OQ = BQ = 11 cm
Hence, radius of the circle (r) = 11 cm

Question 16.
Solution:
In the given figure, TP is the tangent from an external point T and ∠PBT = 30°.
To prove : BA : AT = 2 : 1
Proof: ∠APB = 90° (Angle in a semicircle)
∠PBT = 30° (given)
∠PAB = 90° – 30° = 60°
But, ∠PAT + ∠PAB = 180° (Linear pair)
⇒ ∠PAT + 60° = 180°
⇒ ∠PAT = 180° – 60° = 120°
and ∠APT = ∠PBA = 30° (Angles in the alternate segment)
In ∆PAT,
∠PTA = 180° – (120° + 30°) = 180° – 150° = 30°
PA = AT
In right ∆APB,
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12A 16

Hope given RS Aggarwal Solutions Class 10 Chapter 12 Circles Ex 12A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.6

RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.6

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.6

Other Exercises

Question 1.
In ∆ABC, if ∠A = 40° and ∠B = 60°. Determine the longest and shortest sides of the triangle.
Solution:
In ∆ABC, ∠A = 40°, ∠B = 60°
But ∠A + ∠B + ∠C = 180°
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.6 Q1.1
⇒ 40° + 60° + ∠C = 180°
⇒ ∠C = 180° = (40° + 60°)
= 180° – 100° = 80°
∵ ∠C = 80°, which is the greatest angle and
∠A = 40° is the smallest angle
∴ Side AB which is opposite to the greatest angle is the longest and side BC which is opposite to the smallest angle is the shortest.

Question 2.
In a ∆ABC, if ∠B = ∠C = 45°. which is the longest side?
Solution:
In ∆ABC, ∠B = ∠C = 45°
But ∠A + ∠B + ∠C = 180°
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.6 Q2.1
⇒ ∠A + 45° + 45° = 180°
⇒ ∠A + 90° = 180°
∴ ∠A = 180°-90° = 90°
∴∠A is the greatest
∴ Side BC opposite to it is the longest

Question 3.
In ∆ABC, side AB is produced to D so that BD = BC. If ∠B = 60° and ∠A = 70°, prove that :
(i) AD > CD
(ii) AD > AC
Solution:
Given : In AABC, side BC is produced to D such that BD = BC
∠A = 70° and ∠B = 60°
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.6 Q3.1
To prove :
(i) AD > CD (ii) AD > AC
Proof: In ∆ABC,
∠A = 70°, ∠B = 60°
But Ext. ∠CBD + ∠CBA = 180° (Linear pair)
∠CBD + 60° = 180° 3
⇒ ∠CBD = 180° – 60° = 120°
But in ∆BCD,
BD = BC
∴ ∠D = ∠BCD
But ∠D + ∠BCD = 180° – 120° = 60°
∴∠D = ∠BCD = \(\frac { { 60 }^{ \circ } }{ 2 }\)  = 30°
and in ∆ABC,
∠A + ∠B + ∠C = 180°
⇒ 70° + 60° + ∠C = 180°
⇒ 130° + ∠C = 180°
∴ ∠C =180°- 130° = 50°
Now ∠ACD = ∠ACB + ∠BCD = 50° + 30° = 80°
(i) Now in ∆ACB,
∠ACD = 80° and ∠A = 70°
∴ Side AD > CD
(Greater angle has greatest side opposite to it)
(ii) ∵ ∠ACD = 80° and ∠D = 30°
∴ AD > AC

Question 4.
Is it possible to draw a triangle with sides of length 2 cm, 3 cm and 7 cm?
Solution:
We know that in a triangle, sum of any two sides is greater than the third side and 2 cm + 3 cm = 5 cm and 5 cm < 7 cm
∴ This triangle is not possible to draw

Question 5.
In ∆ABC, ∠B = 35°, ∠C = 65° and the bisector of ∠BAC meets BC in P. Arrange AP, BP and CP in descending order.
Solution:
In ∆ABC, ∠B = 35°, ∠C = 65° and AP is the bisector of ∠BAC which meets BC in P.
Arrange PA, PB and PC in descending order In ∆ABC,
∠A + ∠B + ∠C = 180° (Sum of angles of a triangle)
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.6 Q5.1
⇒ ∠A + 35° + 65° = 180°
∠A + 100°= 180°
∴ ∠A =180°- 100° = 80°
∵ PA is a bisector of ∠BAC
∴ ∠1 = ∠2 = \(\frac { { 80 }^{ \circ } }{ 2 }\)  = 40°
Now in ∆ACP, ∠ACP > ∠CAP
⇒ ∠C > ∠2
∴ AP > CP …(i)
Similarly, in ∆ABP,
∠BAP > ∠ABP ⇒ ∠1 > ∠B
∴ BP > AP …(ii)
From (i) and (ii)
BP > AP > CP

Question 6.
Prove that the perimeter of a triangle is greater than the sum of its altitudes
Solution:
Given : In ∆ABC,
AD, BE and CF are altitudes
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.6 Q6.1
To prove : AB + BC + CA > AD + BC + CF
Proof : We know that side opposite to greater angle is greater.
In ∆ABD, ∠D = 90°
∴ ∠D > ∠B
∴ AB >AD …(i)
Similarly, we can prove that
BC > BE and
CA > CF
Adding we get,
AB + BC + CA > AD + BE + CF

Question 7.
In the figure, prove that:
(i) CD + DA + AB + BC > 2AC
(ii) CD + DA + AB > BC
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.6 Q7.1
Solution:
Given : In the figure, ABCD is a quadrilateral and AC is joined
To prove :
(i) CD + DA + AB + BC > 2AC
(ii) CD + DA + AB > BC
Proof:
(i) In ∆ABC,
AB + BC > AC …(i)
(Sum of two sides of a triangle is greater than its third side)
Similarly in ∆ADC,
CD + DA > AC …(ii)
Adding (i) and (ii)
CD + DA + AB + BC > AC + AC
⇒ CD + DA + AB + BC > 2AC
(ii) In ∆ACD,
CD + DA > CA
(Sum of two sides of a triangle is greater than its third side)
Adding AB to both sides,
CD + DA + AB > CA + AB
But CA + AB > BC (in ∆ABC)
∴ CD + DA + AD > BC

Question 8.
Which of the following statements are true (T) and which are false (F)?
(i) Sum of the three sides of a triangle is less than the sum of its three altitudes.
(ii) Sum of any two sides of a triangle is greater than twice the median drawn to the third side.
(iii) Sum of any two sides of a triangle is greater than the third side.
(iv) Difference of any two sides of a triangle is equal to the third side.
(v) If two angles of a triangle are unequal, then the greater angle has the larger side opposite to it.
(vi) Of all the line segments that can be drawn from a point to a line not containing it, the perpendicular line segment is the shortest one.
Solution:
(i) False. Sum of three sides of a triangle is greater than the sum of its altitudes.
(ii) True.
(iii) True.
(iv) False. Difference of any two sides is less than the third side.
(v) True.
(vi) True.

Question 9.
Fill in the blanks to make the following statements true.
(i) In a right triangle, the hypotenuse is the ……. side.
(ii) The sum of three altitudes of a triangle is ……. than its perimeter.
(iii) The sum of any two sides of a triangle is …….. than the third side.
(iv) If two angles of a triangle are unequal, then the smaller angle has the ….. side opposite to it.
(v) Difference of any two sides of a triangle is……. than the third side.
(vi) If two sides of a triangle are unequal, then the larger side has ……… angle opposite to it.
Solution:
(i) In a right triangle, the hypotenuse is the longest side.
(ii) The sum of three altitudes of a triangle is less than its perimeter.
(iii) The sum of any two sides of a triangle is greater than the third side.
(iv) If two angles of a triangle are unequal, then the smaller angle has the smaller side opposite to it.
(v) Difference of any two sides of a triangle is less than the third side.
(vi) If two sides of a triangle are unequal, then the larger side has greater angle opposite to it.

Question 10.
O is any point in the interior of ∆ABC. Prove that
(i) AB + AC > OB + OC
(ii) AB + BC + CA > OA + OB + OC
(iii) OA + OB + OC > \(\frac { 1 }{ 2 }\) (AB + BC + CA)
Solution:
Given : In ∆ABC, O is any point in the interior of the ∆ABC, OA, OB and OC are joined
To prove :
(i) AB + AC > OB + OC
(ii) AB + BC + CA > OA + OB + OC
(iii) OA + OB + OC > \(\frac { 1 }{ 2 }\) (AB + BC + CA)
Construction : Produce BO to meet AC in D.
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.6 Q10.1
Proof: In ∆ABD,
(i) AB + AD > BD (Sum of any two sides of a triangle is greater than third)
⇒ AB + AD > BO + OD …(i)
Similarly, in ∆ODC,
OD + DC > OC …(ii)
Adding (i) and (ii)
AB + AD + OD + DC > OB + OD + OC
⇒ AB + AD + DC > OB + OC
⇒ AB + AC > OB + OC
(ii) Similarly, we can prove that
BC + AB > OA + OC
and CA + BC > OA + OB
(iii) In ∆OAB, AOBC and ∆OCA,
OA + OB > AB
OB + OC > BC
and OC + OA > CA
Adding, we get
2(OA + OB + OC) > AB + BC + CA
∴ OA + OB + OO > \(\frac { 1 }{ 2 }\) (AB + BC + CA)

Question 11.
Prove that in a quadrilateral the sum of all the sides is greater than the sum of its diagonals.
Solution:
Given : In quadrilateral ABCD, AC and BD are its diagonals,
RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.6 Q11.1
To prove : AB + BC + CD + DA > AC + BD
Proof: In ∆ABC,
AB + BC > AC …(i)
(Sum of any two sides of a triangle is greater than its third side)
Similarly, in ∆ADC,
DA + CD > AC …(ii)
In ∆ABD,
AB + DA > BD …(iii)
In ∆BCD,
BC + CD > BD …(iv)
Adding (i), (ii), (iii) and (iv)
2(AB + BC + CD + DA) > 2AC + 2BD
⇒ 2(AB + BC + CD + DA) > 2(AC + BD)
∴ AB + BC + CD + DA > AC + BD

Hope given RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.6 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.