Prasanna

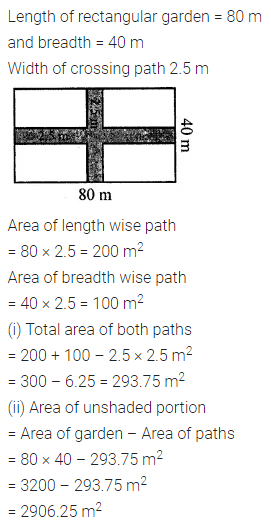
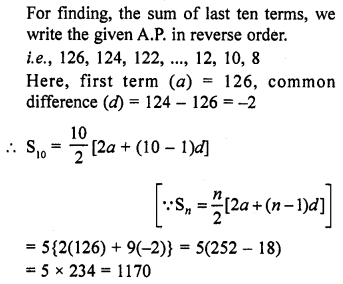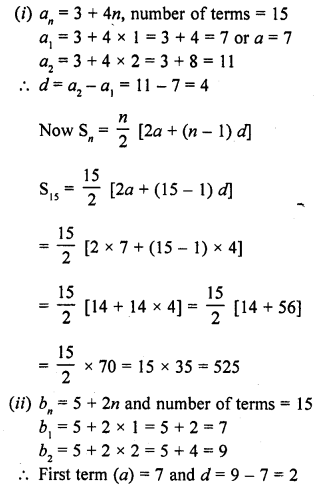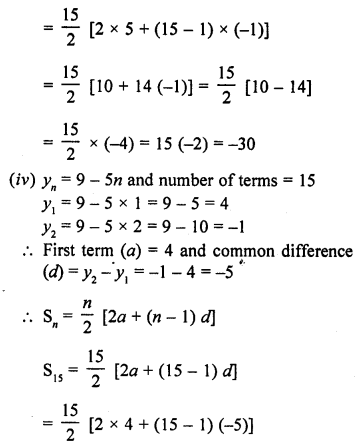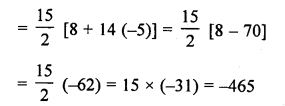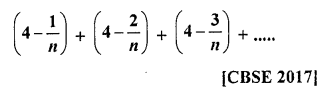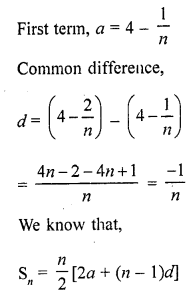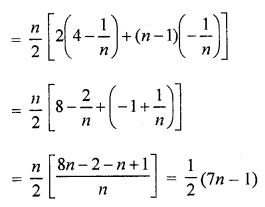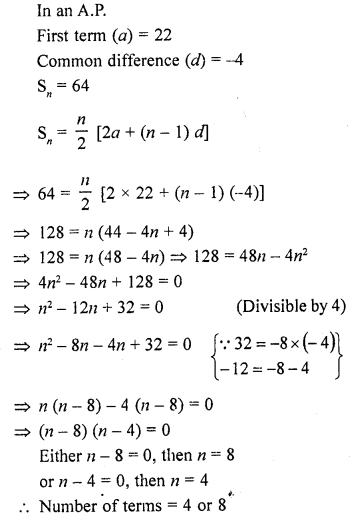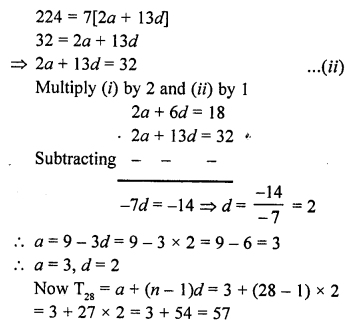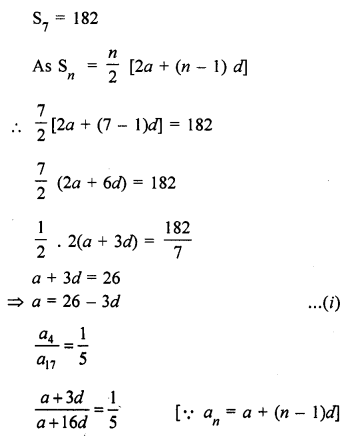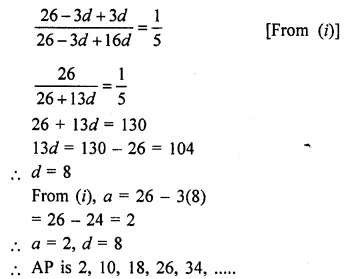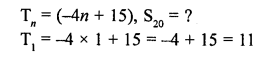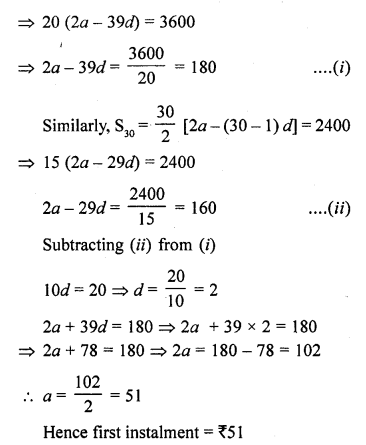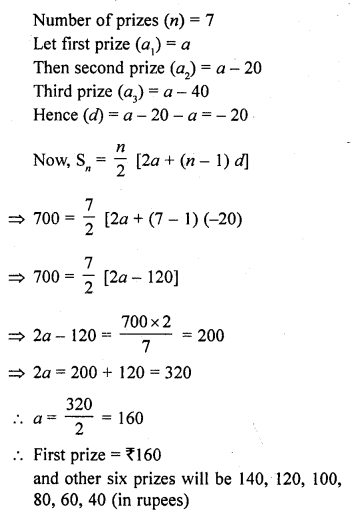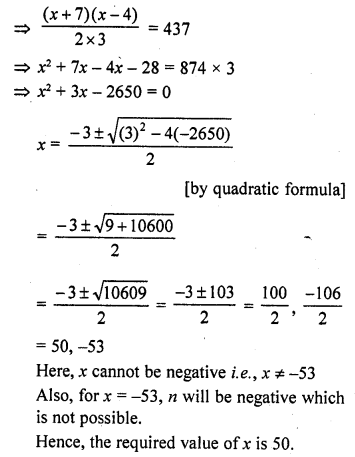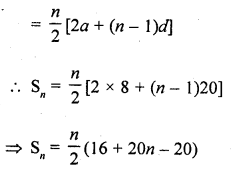Here we are providing Online Education NCERT Solutions for Class 12 English Flamingo Chapter 4 The Rattrap. Students can get Class 12 English The Rattrap NCERT Solutions, Questions and Answers designed by subject expert teachers.

Online Education Deep Water NCERT Solutions for Class 12 English Flamingo Chapter 4

The Rattrap NCERT Text Book Questions and Answers

The Rattrap Think as you read 

Question 1.
From where did the peddler get the idea of the world being a rattrap?
Answer:
The poor rattrap peddler struggled for his existence. He could not make both ends meet so he had to resort to both begging and petty thievery. Despite this, his condition was deplorable. Thinking of his miserable plight and his job, as he plodded on, he was struck by the idea that the whole world was nothing but a big rattrap. It baited people in the form of riches and joys, shelter and food, heat and clothing, just as the rattrap offered cheese and pork. Similarly, the moment one was tempted by the material joys, the world closed in on him and trapped him.

Question 2.
Why was he amused by this idea?
Answer:
The world had never been kind to him, so it gave him great joy to think ill of it. It became a treasured pastime for him to think of people he knew who had let themselves be caught in the dangerous trap, and of others who were still moving around the bait, ready to be trapped.

Question 3.
Did the peddler expect the kind of hospitality that he received from the crofter?
Answer:
When the peddler reached the little grey cottage by the roadside, he knocked on the door to ask for shelter for the night. He was surprised because, instead of the sour faces which ordinarily met him, this time he was welcomed by the owner, an old man.

Question 4.
Why was the crofter so talkative and friendly with the peddler?
Answer:
The crofter was an old man without wife or child. He was happy to get someone to talk to, in his loneliness. So, he welcomed the peddler. The old man was just as generous with his confidences as with his porridge and tobacco.

Question 5.
Why did he show the thirty kronor to the peddler?
Answer:
The old man was confiding and trusting. He told the peddler that he was no longer able to work as a day labour, and was supported by what he earned by selling his cow’s milk. The old man showed him the thirty kronor that he had received as payment from the creamery, to convince the peddler.

Question 6.
Did the peddler respect the confidence reposed in him by the crofter?
Answer:
No, the peddler did not respect the confidence reposed in him by the crofter because later, he went up to the window, smashed a pane and got hold of the pouch with the thirty kronor. He took the money and thrust it into his own pocket and went away.

Question 7.
What made the peddler think that he had indeed fallen into a rattrap?
Answer:
At first, the peddler was pleased with the money in his pocket; but he later got lost in the forest. All at once, he recalled his thoughts about the world being a rattrap. He felt that his end was near and that he had been fooled by a bait of thirty kronor.

Question 8.
Why did the ironmaster speak kindly to the peddler and invite him home?
Answer:
The owner of Ramsjo iron mill came into the forge on one of his night rounds of inspection and saw the peddler. The ironmaster walked close up to him, looked him over very carefully and mistook him for his friend, Nils Olof, and invited him home.

Question 9.
Why did the peddler decline the invitation?
Answer:
The peddler did not reveal his identity because he thought that the ironmaster might give him a couple of kronor. But, to go along up to the manor house and be received as his friend scared the peddler. He had stolen the thirty kronor from the old man and he felt that going up to the manor house would make him vulnerable. He merely wanted to sleep in the forge and then quietly sneak away.

Question 10.
What made the peddler accept Edla Willmansson’s invitation?
Answer:
When Edla Willmansson invited him, she looked at him compassionately. She also assured him that he would be allowed to leave just as freely as he came. She requested him to stay with them over Christmas Eve. She said this in such a friendly manner that the rattrap peddler felt reassured. Hence, he accepted Edla Willmansson’s invitation.

Question 11.
What doubts did Edla have about the peddler?
Answer:
When Edla Willmansson looked compassionately at the peddler, she noticed that the man was afraid. She at once knew that he had either stolen something or else had escaped from jail.

Question 12.
When did the ironmaster realise his mistake?
Answer:
When the ironmaster saw the stranger the day after, clean and well dressed, he realized his mistake. The valet had bathed him, cut his hair and shaved him. He was wearing clothes that belonged to the ironmaster. The ironmaster frowned as he realized that in the dimly-lit furnace, he had made a mistake. As the stranger stood there in daylight, it was impossible to mistake him for an old acquaintance.

Question 13.
What did the peddler say in his defence when it was clear that he was not the person the ironmaster had thought he was?
Answer:
When the ironmaster realized his mistake, the stranger made no attempt to hide or pretend. He said that it was not his fault as he had never pretended to be anything but a poor trader. He had pleaded and begged to be allowed to stay in the forge. He offered to put on his rags and go away.

Question 14.
Why did Edla still entertain the peddler even after she knew the truth about him?
Answer:
Edla entertained the peddler even after she knew the truth about him. She said that the whole year long the peddler roamed about without anyone welcoming him. He was forever afraid of being arrested and cross-examined. So, she felt compassion for the homeless tramp and wanted him to enjoy a day of peace with them. She also said that it was their mistake and they ought not to chase away a human being whom they had invited home and had promised Christmas cheer.

Question 15.
Why was Edla happy to see the gift left by the peddler?
Answer:
Edla gave a little cry of joy on seeing the gift, a small rattrap with three wrinkled ten kronor notes. Her deed of kindness had helped the poor peddler atone for his sin. He did not want her to be embarrassed in the Christmas season because of a thief. He said that the rattrap was a Christmas present from a rat who would have been caught in the world’s rattrap, had he not received kindness and honour from her. Ella felt satisfied at having helped someone rise above his faults.

Question 16.
Why did the peddler sign himself as Captain von Stahle?
Answer:
The peddler signed himself as Captain von Stahle because Edla had treated him as if he were a captain. He took away from the incident, the transient honour of having being treated like a captain. It inspired him to do good, and let go of his thieving ways.

The Rattrap Understanding the text

Question 1.
How did the peddler interpret the acts of kindness and hospitality shown by the crofter, the ironmaster, and his daughter?
Answer:
The peddler was granted shelter in a little cottage by the roadside. The crofter gave him food and trusted him by investing confidence in him. However, the peddler betrayed his trust and stole his money. Later, as he was lost in the forest, he felt trapped, and judged the kindness and money that came his way as nothing but a bait to trap him. He was also suspicious of the kindness showed to him by the ironmaster and his daughter. The peddler was convinced that any kindness shown to him was just a bait to trap him.

Question 2.
What are the instances in the story that show that the character of the ironmaster is different from that of his daughter in many ways?
Answer:
Despite a close relationship, the character of the ironmaster is shown to be different from that of his daughter. The ironmaster spoke to the peddler for some time but continued to mistake him for his friend Captain von Stahle, whereas, his observant daughter, who had never met his friend, within minutes, observed that either the peddler had stolen something or else he had escaped from jail.

When the ironmaster discovered that the peddler was not his friend, he wanted to hand him over to the sheriff but his daughter was more compassionate. She said that the peddler roamed without being welcomed anywhere. So, she wanted him to enjoy a day of peace with them. She also said that it was their mistake and they ought not to chase away a human being whom they had asked to come to their home and whom they had promised Christmas cheSr.

At church, they learnt that the rattrap peddler had robbed the crofter. The ironmaster wondered what all he had stolen from their cupboard and blamed the daughter for letting him in. However, she was repaid by the peddler for her trust that helped in reforming his character.

Question 3.
The story has many instances of unexpected reactions from the characters to others’ behaviour. Pick out instances of these surprises.
Answer:
The story does have many instances of unexpected reactions of the characters in response to others’ behaviour. The first was the crofter’s reaction to the peddler. Instead of the sour faces which ordinarily met him, the old man, without wife or child, was happy to get someone to talk to in his loneliness. He was very welcoming. But, the peddler, despite the hospitality, stole his money.

The second was the ironmaster, who mistook the peddler to be his friend Nils Olof, and tried to take him to his house. But, he was quick to turn his back when he realized his mistake.The third was the arrival of the ironmaster’s daughter, who realized that there was something amiss about the peddler but took him in. Even when the father and daughter found out the truth, the daughter stood by him. She wanted him to enjoy a day of peace with them.The peddler, in turn, surprised everyone when he returned his stolen booty. He honoured the trust reposed in him by Edla.

Question 4.
What made the peddler finally change his ways?
Answer:
Due to the trust and compassion shown by the ironmaster’s daughter Edla Willmansson, the peddler became a changed man. This was evident from the package he left for her before leaving. The package contained a small rattrap with three wrinkled ten kronor notes that the peddler left for her. In the rattrap, also lay a letter that revealed how he did not want her to be embarrassed in the Christmas season by a thief. He wanted her to return the money to the old man on the roadside. The rattrap was a Christmas present from him, who had been reformed and touched by the treatment he received from her.

Question 5.
How does the metaphor of the rattrap serve to highlight the human predicament?
Answer:
The peddler considered that the whole world was nothing but a big rattrap. Its only purpose was to set baits for people. It offered riches and joys, shelter and food, heat and clothing, exactly as the rattrap offered cheese and pork, and as soon as one let oneself be lured by the bait, it closed in. The peddler also told the ironmaster that the whole world was nothing but a big rattrap. All the good things that were offered were nothing but cheese rind and bits of pork, set out to drag people into trouble.

None escaped; one person falls into the trap one day and the other the next day. The only thing that could turn a person from rat-like ways was human kindness, something that he had received from Edla. Thus, in the end, the peddler left the rattrap as a Christmas present and called himself a rat who had been spared.

The metaphor of the rattrap highlights the theory of crime and punishment. Crimes, such as theft or giving in to temptation, are compared with a bait and the subsequent imprisonment in a trap. However, the human predicament forms the basis of the story where the story of the rattrap serves to bring out a lesson in moral values.

Question 6.
The peddler comes out as a person with a subtle sense of humour. How does this serve in lightening the seriousness of the theme of the story and also endearing him to us?
Answer:
The peddler has a good sense of humour and this diffuses the seriousness of the theme of the story, he also endears himself to the reader. Although he was a vagabond in pursuit of food and shelter, he found time to meditate on his philosophies and draw pleasure from the anticipated miseries of other people. He imagined people he knew to have landed in the trap and of others who were still circling around the bait.

The humour is brought out when at every occasion he lapsed into his theory of the rattrap. When his identity was discovered by the ironmaster, he said that a day would arrive when the ironmaster too might chase a big piece of pork, and get caught in the trap. He also signs off in the letter as “Captain von Stahle”, revealing how he held on to his sense of humour till the end.

The Rattrap Talking about the text

Discuss the following in groups of four. Each group can deal with one topic and present the views of the group to the whole class.

Question 1.
The reader’s sympathy is with the peddler right from the beginning of the story. Is the sympathy justified?
Answer:
The reader’s sympathy is with the peddler right from the beginning of the story for various reasons. It is justified.He is a victim of circumstances. He made rattraps with the material he got by begging in stores or at big farms. But even so, the business was not profitable. He had to resort to both begging and petty thievery for a living. His clothes were in rags, his cheeks were sunken, and hunger gleamed in his eyes. When he knocked on a door to ask for shelter at night, he was often refused and he “met sour faces”. Even when he stole the money from the crofter, he at once realized that his philosophy about the world as a rattrap had turned true for him. He had been caught with the bait of money. He regretted it and knew his own turn had come.
OR
It is not justified.
There were many who had lost their jobs. He stole money from the crofter who was hospitable to him. Secondly, he had the opportunity to tell the ironmaster of his true identity which he did not. He knew all along that if he did something wrong, he would be trapped, yet, he could not resist the bait.

Question 2.
The story also focuses on human loneliness and the need to bond with others. Discuss.
Answer:
The above statement is true for many characters in the chapters:
(a) The crofter, because of loneliness, lets the peddler in.

(b) The ironmaster at once bonded with the peddler without confirming his identity—“But of course it is you, Nils Olof!” he said. “How you do look!” and again “.. .We were just saying that it was too bad we didn’t have any company for Christmas.”

(c) Edla Willmansson sensed that all was not well, yet insisted that the peddler spend Christmas with them. When the ironmaster wanted to turn the peddler out, the daughter said, “I think he ought to stay with us today. I don’t want him to go.”

(d) The peddler, while leaving the ironmaster’s house left a message, “Written with friendship and high regard”.
The peddler was reformed by the kindness shown by Edla Willmansson. He wanted to be nice to her in return and did not want to embarrass her by his theft. He returned the stolen money, asking her to forward it to the old man. Human warmth and bonding enabled this change in him.

Question 3.
Have you known/heard of an episode where a good deed or an act of kindness has changed a person’s view of the world?
Answer:
The Bishop’s Candlesticks is one such episode that takes up on a similar theme.

The Rattrap Working with words

Question 1.
The man selling rattraps is referred to by many terms such as “peddler”, “stranger”, etc. Pick out all such references to him. What does each of these labels indicate about the context or the attitude of the people around him?
Answer:
He is referred to as a vagabond, intruder, tramp, ragamuffin and poor hungry wretch. These labels indicate the context or the attitude of the people around him. The people

• Had no respect for him.
• Felt he was a burden.
• Did not care to know him or his problems.
• Could pity him, but were not really compassionate.

Question 2.
You came across the words plod, trudge, stagger in the story. These words indicate movement accompanied by weariness. Write down five other words with a similar meaning.
Answer:
drag oneself, footslog, lumber, plod along, slog, stumble, traipse

The Rattrap Extra Questions and Answers

The Rattrap Short Answer Questions

Question 1.
What did the rattrap peddler do for a living?
Answer:
The rattrap peddler was an iron worker who lost his job to machines in an age of industrialization. Hence, he resorted to selling small rattraps of wire, and he obtained the required materials by begging. His business was not a profitable one, so he had no option but to beg and steal. His clothes were in rags, and his cheeks were sunken; he looked starved. He roamed alone like a vagabond.

Question 2.
How did the peddler get the idea of the world being a rattrap?
Answer:
The peddler struggled for his existence as selling rattraps was not a profitable business. He often resorted to begging and stealing. This led him to believe that the world was a big rattrap that sets baits for people. The moment one was tempted to reach out for the bait, the trap closed in on him.

Question 3.
Why was he amused by the idea of the rattrap?
Answer:
The peddler was amused by the idea of the rattrap because the world had been unkind to him. No one helped him; on the contrary, everyone shunned him. Hence, the peddler got joy in thinking ill of others. His treasured pastime consisted of thinking of people caught in the trap.

Question 4.
How was the crofter different from the kind of people the peddler usually met?
Answer:
The crofter was different from the kind of people the peddler usually met. The crofter invited him into his house, and unlike the usual people, he did not shun him. When the peddler went begging, the crofter offered him porridge, supper, and tobacco. He played cards with the peddler. Not only was he hospitable, but reposed a lot of trust in the peddler. He showed peddler where he kept his money.

Question 5.
Why did crofter show the thirty kronor to the peddler?
Answer:
The crofter showed the thirty kronor to the peddler because he was generous with his confidences. Moreover, he had told the peddler that he could not labour, but a cow supported him. When the peddler looked at him in disbelief, just to prove his point, he showed him the thirty kronor.

Question 6.
How did the peddler discover Ramsjo Ironworks?
Answer:
After stealing the crofter’s money, the peddler realized that he was lost. He had been walking around in the same area. Soon it became dark, and his fears and apprehensions increased. He felt he was caught in a rattrap. He sank down on the ground in gloom and dejection. When he put his head on the ground, he heard a hard, thumping sound. He was certain that the sound was produced by hammer strokes. So he mustered strength and moved in the direction of the sound.

Question 7.
What sight did the peddler see at the Ramsjo Ironworks?
Answer:
At the Ramsjo Ironworks, the peddler noticed that the master smith and his helper were sitting near the furnace. They were heating pig iron to put on the anvil. They wore nothing but a long shirt and a pair of wooden shoes. He also saw them get up every few minutes to stir the glowing mass with a long iron bar.

Question 8.
What was the blacksmith’s reaction to the peddler’s arrival at the forge?
Answer:
When the peddler entered the forge, the blacksmith failed to notice him right away as it was noisy and they were busy working. When the peddler stood close to the furnace, the blacksmith showed no reaction. It was a usual sight for the blacksmith to see vagabonds take shelter for the night at the forge. So he just glanced casually at the peddler and nodded a haughty consent, permitting him to spend the night.

Question 9.
How was the blacksmith’s reaction to the peddler different from that of the ironmaster? Why was it different?
Answer:
The blacksmith’s reaction was one of sheer indifference. He glanced casually and nodded a haughty consent. But the ironmaster noticed the tall stranger at once. He walked up to him, looked him over and called out, “Nils Olof!” The reactions were different because it was a usual sight for the blacksmith who often saw vagabonds come to spend the night there. But the ironmaster had mistaken him for his friend and hence invited him home.

Question 10.
Why did the rattrap peddler not reveal his identity to the ironmaster? Why did the peddler decline the invitation?
Answer:
The rattrap peddler realized the ironmaster’s mistake. He expected the ironmaster to give him a couple of kronor. He, however, felt discomforted to visit the ironmaster’s home with the mistaken identity. He also felt guilty having stolen thirty kronor. He felt going to the ironmaster’s house would be like throwing himself into the lion’s den. He just wanted to sleep in the forge that night and then sneak away.

Question 11.
What were the peddler’s feelings on his way to the ironmaster’s manor?
Answer:
On his way to the ironmaster’s manor, the peddler felt confidence in Edla. He followed her to the carriage. However, while travelling in the carriage, he had evil premonitions and regretted taking the crofter’s money. He could see himself in the trap. He felt he would never get out of it.

Question 12.
When the peddler was bathed and dressed, the ironmaster was not pleased. Why?
Answer:
The peddler had reached the ironmaster’s house looking like a vagabond. There, the valet helped the peddler dress. He had bathed him, cut his hair, and shaved him. The peddler was dressed in the ironmaster’s clothes. But when the peddler was bathed and dressed, the ironmaster was shocked. He then realized that this man was not his friend. In the dim light, he had mistaken him for his friend.

Question 13.
After the peddler’s identity was discovered, how did he spend the rest of his stay at the ironmaster’s house?
Answer:
After the peddler’s identity was discovered, he wondered why Edla had supported him. He sat and ate quietly. Through the morning he slept, and at noon they woke him for his share of the Christmas fare, after which he slept again. Feeling safe, he slept soundly like he had never slept before. He awoke in the evening, and after he had had his dinner, he thanked each one in the house and wished them for the night.

Question 14.
What did the ironmaster and Edla learn about the peddler at the church? How did they react?
Answer:
At the church, Edla received news of how the rattrap peddler had robbed the old crofter. The ironmaster was angry with Edla for letting the peddler stay. He was certain that the peddler might have had stolen things from the house while they were at the church. Edla was dejected, as well as embarrassed. She realized her mistake and was speechless.

Question 15.
What did the ironmaster and Edla discover when they went home?
Answer:
When ironmaster and Edla reached home, they expected the peddler to have escaped after robbing them. However, when they reached home, they discovered that the peddler had gone away, but much to their surprise, he had left a gift for Edla. The gift was a small rattrap with three wrinkled ten-kronor notes. Edla’s compassion had helped the poor peddler atone for his sin. The peddler also left a note saying he would have been caught in the world’s rattrap had he not been inspired and moved by Edla’s generosity.

The Rattrap Long Answer Questions

Question 1.
“The old man (crofter) was just as generous with his confidences as with his porridge and tobacco.” Justify.
Answer:
The crofter was as generous with his confidences as with his porridge and tobacco. It was out of a sense of hospitality that he looked after the vagabond as a guest. He had offered him porridge, supper and a big slice from his tobacco roll. After that they had played cards until bedtime. He discussed his life with the peddler and told him about his days of prosperity. He took him into confidence and told him that he earned a living by selling the milk his cow produced. The crofter had received a payment of thirty kronor. He also showed him the three ten-kronor bills and where he kept his money. The crofter was liberal with his hospitality and trust.

Question 2.
How did nature play against the peddler after he stole the crofter’s money?
Answer:
Nature seemed to penalize the peddler for stealing the crofter’s money. The peddler was initially pleased to get the money. He decided to steer away from the public highway for the fear of getting caught. So he went into the woods. The first hours of travel were easy, but later, the forest seemed like a labyrinth. The paths twisted back and forth strangely. The peddler walked on without coming to the end of the wood, He then realized that he had been walking around in the same area. At once, he recalled the rattrap theory he was baited with the thirty kronor.

Question 3.
Was the ironmaster a generous man? Why or why not?
Answer:
The ironmaster was a generous man. He mistook the rattrap peddler for an old acquaintance, Captain von Stahle, and coaxed him into going home with him. When the peddler refused, he sent his daughter to get him. He was also anxious that the peddler was looked after and comfortably dressed at his home. He also promised to try to get him a job. However, he felt cheated by the peddler once he found out his real identity.
OR
The ironmaster was not generous. He was a lonely man whose wife was dead and whose sons were abroad. He lived with his daughter. He had invited the peddler, mistaking him as an old friend, to alleviate his loneliness. Later, when he discovered his true identity, he wanted to get rid of him. In fact after discovering the truth about the peddler at the church, he was so angry and worried that he wanted to hand him over to the sheriff.

Question 4.
What kind of a girl was Edla? Give reasons for your answer.
Answer:
Edla was not pretty, but looked modest and shy. She was very hospitable and went to the forge to welcome her father’s guest. Her father was confident of her powers of persuasion and was sure that she would convince the guest to stay with them. Edla was also concerned and sensitive. She handed her big fur coat to the peddler to make him feel more comfortable and to cover his rags. She was polite and gentle.

She was, however, a keen observer. Unlike her father, she noticed that the peddler was afraid. She knew at once that either he had stolen something or had escaped from jail. She had the maturity to hide her emotions. She also assured the peddler that he would be allowed to leave just as freely as he had come. But, out of concern, she made him stay till Christmas.

Question 5.
What were the attitudes of the ironmaster and Edla toward the peddler before and after they discovered his identity?
Answer:
Before discovering the peddler’s identity, the ironmaster addressed the peddler as Nils Loft. He did not take the peddler’s reaction into account. He sensed that the peddler must have been uncomfortable because of the economic disparity between the two of them. The ironmaster also made sure that he was supplied with good meal and clothes. But once he discovered the case of mistaken identity, he immediately wanted to hand the peddler over to the sheriff. After he heard of the peddler in the church, he was furious and wondered what he had stolen from their cupboard. He blamed his daughter for letting him in.

Edla saw the peddler for the first time when she came to fetch him home. She noticed at once that the man was afraid. She guessed that he was either a thief or a runaway culprit. Despite this, she requested him to stay.

She was spontaneous and friendly, and coaxed the peddler into spending the Christmas with them. He also accepted the fur coat, and wore it over his rags. Edla expressed her surprise about his miserable plight and noticed that there was nothing to show that he was an educated man. When in the church, she realized that he was a thief; she never once expressed her fear. Her trust and compassion helped in reforming the peddler.

Question 6.
Was the case of mistaken identity the peddler’s fault?
Answer:
It was his fault.
The peddler let the ironmaster believe that he was an old acquaintance. He did so in order to get a couple of kronor from the ironmaster. He told the ironmaster that he was not doing well in life. His second chance to clear himself came when Edla came to invite him home. He kept quiet deliberately in the hope of material gain. He realized the risk of going to the manor house. Even when his identity was revealed, he behaved in a self-righteous fashion.
OR
It was not his fault.
The poor peddler stuggled to survive.
He had lost all ways of earning his livelihood and lived a life of hardship. He did not deliberately cheat them but merely kept quiet. He did try to avoid going to the iron master’s place many times, but starved as he was, and in rags, he was tempted to spend a comfortable day.

Question 7.
The story is both entertaining and philosophical. Discuss.
Answer:
The story has entertaining merit. The peddler has a pronounced sense of humour despite odds. He tends to philosophize even in the most difficult times. The reader is also kept in a ‘cliff hanging situation’ throughout the story. Every moment, the reader waits to know what would happen next. The story has entertaining moments like when the peddler’s identity is revealed after the valet had bathed him.
The philosophical message of the story is brought out in the theory of the rattrap— life is one big rattrap which closes in on an individual when he gives in to a temptation or steals or commits a crime. The story also elaborates the philosophy of second chances, stating that everyone should get another chance.

The Rattrap Value Based Question

Question 1.
The warmth of compassion extends its rays around the world, engraving mankind with its characteristic. Selma Lagerlof supports the theory of compassion in “Rattrap” which depicts the powerful and positive impact of such care. Discuss.
Answer:
The story revolves around the theory that life is one big rattrap. This implies that if one takes something wrongfully, the person will end up getting trapped in life as a consequence. The peddler felt that the whole world was a big rattrap that sets baits for people. The peddler earned his living by petty thievery. However, he turns over a new leaf when he receives compassion and trust from the ironmaster’s daughter. The protagonist believed till then in the dismal side of human nature.

His first “true” Christmas at the ironmaster’s . house egged him to change his ways and honour people’s trust in him. The story validates the concept that compassion revolves around humankind and the consideration of others. The peddler makes amends by returning the money he had previously stolen from the old man who had sheltered him. The tale also throws light on the value of second chances, stating that everyone should get another chance in life.

Online Education NCERT Solutions for Class 9 Hindi Sparsh Chapter 15 नए इलाके में … खुशबू रचते हैं हाथ

These Solutions are part of Online Education NCERT Solutions for Class 9 Hindi. Here we have given NCERT Solutions for Class 9 Hindi Sparsh Chapter 15 नए इलाके में … खुशबू रचते हैं हाथ.

पाठ्य-पुस्तक के प्रश्न-अभ्यास

(1) नए इलाके में

प्रश्न 1.
निम्नलिखित प्रश्नों के उत्तर दीजिए-
(क) नए बसते इलाके में कवि रास्ता क्यों भूल जाता है? [CBSE]
(ख) कविता में कौन-कौन से पुराने निशानों का उल्लेख किया गया है?
अथवा
कवि अपने गंतव्य तक पहुँचने के लिए कौन-कौन-सी निशानियाँ ढूँढता है? [CBSE]
(ग) कवि एक घर पीछे या दो घर आगे क्यों चल देता है? [CBSE]
(घ) “वसंत का गया पतझड़’ और ‘बैसाख का गया भादों को लौटा’ से क्या अभिप्राय है?
(ङ) कवि ने इस कविता में समय की कमी की ओर क्यों इशारा किया है? [CBSE]
(च) इस कविता में कवि ने शहरों की किस विडंबना की ओर संकेत किया है?
अथवा
यह कविता किस ओर इशारा करती है, स्पष्ट कीजिए। (CBSE]
उत्तर:
(क) नए इलाके में कवि इसलिए रास्ता भूल जाता है, क्योंकि-

• यहाँ रोज़ नए मकान बनते रहते हैं।
• पुराने मकान ढहाकर नए मकान बनाए जाते हैं।
• नए मकान बनाने के लिए पुराने पेड़ काटने से निशानी नष्ट हो जाती है।
• खाली जमीन पर कोई नया मकान बन जाता है।

(ख) कविता में निम्नलिखित पुराने निशानों का उल्लेख हुआ है-

• पीपल का पेड़
• ढहा घर या खंडहर
• जमीन का खाली टुकड़ा
• बिना रंग वाले लोहे के फाटक वाला इकमंजिला मकान

(ग) कवि एक घर आगे या दो घर पीछे इसलिए चल देता है, क्योंकि नए बस रहे उस इलाके में एक ही दिन में काफ़ी बदलाव आ जाता है। वह अपने घर को पहचान नहीं पाता है कि वह सवेरे किस घर से गया था।

(घ)  ‘वसंत का गया पतझड़’ और ‘बैसाख का गया भादों को लौटा’ से यह अभिप्राय है कि वहाँ एक ही दिन में इतना कुछ नया बन गया है, जितना बनने में पहले नौ-दस महीने या साल भर लगते थे। सुबह का निकला कवि जब शाम को वापस आता है तो एक ही दिन में नौ-दस महीने के बराबर का बदलाव दिखाई देता है।

(ङ) कवि ने कविता में समय की कमी की ओर इसलिए संकेत किया है क्योंकि तेज़ी से आ रहे बदलाव के कारण मनुष्य की व्यस्तता भी बढ़ती जा रही है। इससे उसके पास समय की कमी होती जा रही है।

(च) इस कविता में कवि ने शहरों की उस विडंबना की ओर संकेत किया है, जिसमें शहरों में हो रहे बदलाव, खाली जमीनों में टूटे मकानों की जगह इतने नित नए मकान बनते जा रहे हैं कि सुबह घर से निकले आदमी को शाम के समय अपना मकान खोजना पड़ता है, फिर भी उसे अपना मकान नहीं मिल पाता है।

प्रश्न 2.
व्याख्या कीजिए-
(क) यहाँ स्मृति का भरोसा नहीं
       एक ही दिन में पुरानी पड़ जाती है दुनिया
उत्तर:
नगरों में बसने वाली नई बस्तियाँ इस तरह तेजी से बढ़ती चली जा रही हैं कि आदमी को अपना घर तक ढूँढना कठिन हो गया है। वह कुछ ही दिन बाद अपनी बस्ती में लौटकर आए तो रास्ते तक भूल जाता है। उसकी पुरानी निशानियाँ देखते ही देखते नष्ट हो जाती हैं। इसलिए उसकी पुरानी स्मृतियाँ और निशानियाँ किसी काम नहीं आतीं। दुनिया इतनी तेजी से बदल-बन रही है कि जो निर्माण एक दिन पहले किया जाता है, दूसरे दिन तक पुराना पड़ चुका होता है। उसके बाद नए-नए निर्माण और खड़े हो जाते हैं।

(ख)  समय बहुत कम है तुम्हारे पास।
        आ चला पानी ढहा आ रहा अकास
        शायद पुकार ले कोई पहचाना ऊपर से देखकर
उत्तर:
देखिए व्याख्या क्र. 2..

योग्यता-विस्तार

प्रश्न 1.
पाठ में हिंदी महीनों के कुछ नाम आए हैं। आप सभी हिंदी महीनों के नाम क्रम से लिखिए।
उत्तर:
हिंदी महीनों के नाम-

1. चैत्र,
2. बैसाख,
3. ज्येष्ठ,
4. आषाढ़,
5. श्रावण,
6. भाद्रपक्ष,
7. आश्विन,
8. कार्तिक,
9. मार्गशीर्ष,
10. पौष,
11. माघ,
12. फाल्गुन

(2) खुशबू रचते हैं हाथ

प्रश्न 1.
निम्नलिखित प्रश्नों के उत्तर दीजिए-
(क) “खुशबू रचनेवाले हाथ’ कैसी परिस्थितियों में तथा कहाँ-कहाँ रहते हैं?
(ख) कविता में कितने तरह के हाथों की चर्चा हुई है?
(ग) कवि ने यह क्यों कहा है कि ‘खुशबू रचते हैं हाथ’?
(घ) जहाँ अगरबत्तियाँ बनती हैं, वहाँ का माहौल कैसा होता है?
(ङ) इस कविता को लिखने का मुख्य उद्देश्य क्या है?
उत्तर:
(क) खुशबू रचनेवाले हाथ अत्यंत कठोर परिस्थितियों में गंदी बस्तियों में, गलियों में, कूड़े के ढेर के इर्द-गिर्द तथा नाले के किनारे रहते हैं। वे अस्वच्छ एवं प्रदूषित वातावरण में जीवन बिताते हैं। वे इस दुर्गंधमय वातावरण में रहने को विवश हैं। वे सामाजिक और आर्थिक विषमता के शिकार हैं। दूसरों को खुशबू देने का काम करने । वाले इस प्रकार बदहाली का जीवन बिताते हैं।

(ख) कविता में निम्नलिखित तरह के हाथों की चर्चा हुई है-

1. उभरी नसोंवाले अर्थात् वृद्ध हाथ।
2. घिसे नाखूनोंवाले हाथ श्रमिक वर्ग को प्रतीक है।
3. पीपल के पत्ते जैसे नए-नए हाथ अर्थात् छोटे बच्चों के कोमल हाथ।
4. जूही की डाल जैसे खुशबूदार हाथ अर्थात् नवयुवतियों के सुंदर हाथ।
5. गंदे कटे-पिटे हाथ।
6. जखम से फटे हुए हाथ।

(ग) कवि ने ऐसा इसलिए कहा है क्योंकि इन गरीब मजदूरों के हाथ सुगंधित अगरबत्तियों का निर्माण करते हैं। तथा हमारे जीवन को सुख-सुविधाएँ उपलब्ध कराकर खुशबू से महकाते हैं जिससे ऐसा लगता है कि अत्यंत प्रदूषित वातावरण में रहकर भी इनके हाथ हमारे लिए सुख-सुविधाओं से भरी वस्तुओं का निर्माण करते हैं। जिससे समस्त प्राणियों के जीवन में सुगंध फैल जाती है। ये लोग स्वयं बदहाली का जीवन बिताकर दूसरे लोगों के जीवन में खुशहाली लाते हैं। इन शब्दों द्वारा कवि ने श्रमिकों के श्रम का गुणगान किया है।

(घ) जहाँ अगरबत्तियाँ बनती हैं वहाँ का वातावरण अत्यंत गंदगी भरा होता है। चारों ओर नालियाँ तथा कूड़े-करकट का ढेर जमा होता है। चारों ओर बदबू फैली होती है। ये सुगंधित अगरबत्तियाँ बनाने वाले ऐसे गंदे वातावरण में रहकर भी दूसरों के जीवन में खुशबू बिखेरते हैं पर ऐसे वातावरण में, ऐसी भयावह स्थितियों में रहनी इनकी विवशता है।

(ङ) इस कविता को लिखने का मुख्य उद्देश्य यह है कि हमारे समाज में सुंदरता की रचना करनेवाले गरीब
और उपेक्षित लोगों की ओर हमारा ध्यान आकर्षित करना है ताकि आम लोग इन गरीब मजदूरों के जीवन की वास्तविकता को जान लें और समाज में फैली विषमताओं तथा भेदभावों को मिटाने की कोशिश करें। मजदूरों और कारीगरों की दुर्दशा का चित्रण करना तथा लोगों में उनके उद्धार की चेतना जगाना भी है। कवि अगरबत्तियाँ बनानेवाले कारीगरों का प्रदूषित वातावरण में रहना दिखाकर यह कहना चाहता है कि इनके जीवन स्तर को ऊँचा उठाने के लिए हम सबको मिलकर प्रयास करना चाहिए ताकि इन्हें भी जीवन जीने के लिए। स्वच्छ वातावरण मिल सके।

प्रश्न 2.
व्याख्या कीजिए-
(क)
(i)  पीपल के पत्ते-से नए-नए हाथ
      जूही की डाल-से खुशबूदार हाथ
उत्तर:
अगरबत्ती बनाने वाले हाथों में कुछ के हाथ पीपल के नए-नए पत्तों के समान कोमल हैं। आशय यह है कि कुछ नन्हे-नन्हे बच्चे भी अगरबत्ती बनाने के काम में लगे हुए हैं। कुछ हाथ ऐसे हैं जिनमें से जूही की डालों जैसी खुशबू आती है। आशय यह है कि कुछ सुंदर युवतियाँ भी अगरबत्तियाँ बनाने में लगी हुई हैं।

(ii) दुनिया की सारी गंदगी के बीच
      दुनिया की सारी खुशबू
      रचते रहते हैं हाथे
उत्तर:
यद्यपि अगरबत्ती बनाने वाले कारीगर दुनिया भर को सुगंधित अगरबत्ती प्रदान करते हैं और वातावरण में सुगंध फैलाते हैं किंतु उन्हें स्वयं दुनिया भर की गंदगी के बीच रहना पड़ता है। उनके चारों ओर गंदगी का ही साम्राज्य रहता है। वे शोषित हैं, पीड़ित हैं।

(ख) कवि ने इस कविता में ‘बहुवचन’ का प्रयोग अधिक किया है? इसका क्या कारण है?
उत्तर:
कविता में ‘हाथ’ के लिए बहुवचन का प्रयोग किया गया है। इसके माध्यम से कवि बताना चाहता है कि यहाँ एक कारीगर या एक मजदूर की बात नहीं की जा रही। यह समस्या सब मज़दूरों की है।

(ग) कवि ने हाथों के लिए कौन-कौन से विशेषणों का प्रयोग किया है?
उत्तर:
कवि ने हाथों के लिए निम्नलिखित विशेषणों का प्रयोग किया है-

उभरी नसोंवाले
घिसे नाखूनोंवाले
पीपल के पत्ते-से नए-नए
जूही की डाल-से खुशबूदार
गंदे कटे-पिटे
ज़ख्म से फटे हुए।

योग्यता-विस्तार

प्रश्न 1.
अगरबत्ती बनाना, माचिस बनाना, मोमबत्ती बनाना, लिफ़ाफ़े बनाना, पापड़ बनाना, मसाले कूटना आदि लघु उद्योगों के विषय में जानकारी एकत्रित कीजिए।
उत्तर:
आस पड़ोस में रहने वाले किसी मज़दूर या कर्मचारी से बात करके जानिए और उनकी फैक्ट्री में जाकर देखिए। संभव हो तो घर में बनाने का प्रयास कीजिए।

Hope given NCERT Solutions for Class 9 Hindi Sparsh Chapter 15 are helpful to complete your homework.

If you have any doubts, please comment below. Learn Insta try to provide online tutoring for you.

We have given detailed Online Education NCERT Solutions for Class 7 Sanskrit Grammar Book अव्ययाः Questions and Answers come in handy for quickly completing your homework.

Online Education for Sanskrit Vyakaran Class 7 Solutions अव्ययाः

अव्यय – जो शब्द विभक्ति, वचन, लिंग एवं काल के अनुसार परिवर्तित नहीं होते हैं, अव्यय कहलाते हैं। इन शब्दों में कोई व्यय (विकार) नहीं होता, इसीलिए उन्हें ‘अव्यय’ कहा जाता है।
यथा- बालकः अधुना पठति।
वयम् अधुना पठामः।
मीता अधुना पठति।

यहाँ ‘अधुना’ में लिंग अथवा पुरुष से कोई परिवर्तन नहीं आया।
सः कुत्र गच्छति?
सः कुत्र अगच्छत्?
ते कुत्र अगच्छन्?
यहाँ ‘अधुना और कुत्र’ में काल अथवा वचन के कारण कोई विकार नहीं आया। अतः ‘अधुना’, ‘कुत्र’ जैसे शब्द अव्यय कहलाते हैं। अब निम्नलिखित अव्ययों को देखें और प्रयोग समझें।

अभ्यासः

प्रश्न 1.
(क) अव्ययपदं चित्वा लिखत। (अव्ययपद चुनकर लिखिए।) Pick out the indeclinables.
1. जलम् नीचैः वहति।
2. अलं कोलाहलेन।
3. शशक: शीघ्रं धावति।
4. वृद्धः शनैः चलति।
5. अहम् अपि तेन सह गमिष्यामि।
उत्तरम्-
नीचैः, अलम्, शीघ्रम्, शनैः, अपि, सह।

(ख) उचितेन अव्यय-पदेन रिक्तस्थानपूर्ति कुरुत- (उचित अव्यय पद द्वारा रिक्त स्थान पूर्ति कीजिए- Fill in the blanks with the appropriate indeclinables.)
यत्र-तत्र, यदा-तदा, एकदा ह्यः, तत्र
1. ___________ अहं विदेशम् अगच्छम्।
2. ___________ बालकाः ___________ कोलाहलः।
3. ___________ अहम् जन्तुशालाम् अगच्छम्।
4. ___________ अहम् विविधान् जन्तून् अपश्यम्।
5. ___________ वृष्टिः भवति ___________ मयूरः नृत्यति।
उत्तरम्-
1. एकदा
2. यत्र-तत्र
3. ह्यः
4. तत्र
5. यदा-तदा

(ग) प्रदत्तविकल्पेभ्यः उचितं पदं चित्वा वाक्यानि पूरयत-
(दिए गए विकल्पों से उचित पद चुनकर वाक्य पूरे कीजिए- Pick out the appropriate word from the options given and complete the sentences.)
1. अधुना वयम् क्रीडामः, त्वम् ___________ आगच्छ। (एव, अपि, मा)
2. ___________ वयम् खो-खो खेलम् खेलिष्यामः। (अद्य, ह्यः, श्व:)
3. ते बालकाः ___________ इतस्ततः भ्रमन्ति। (मृषा, वृथा, कुतः)
4. विद्यालयात् ___________ बसयानम् तिष्ठति। (अधुना, सर्वदा, बहि:)
5. पुत्र! अधुना त्वं ___________ आगच्छसि? (कुत्र, कुतः, कदा)
उत्तरम्-
1. अपि
2. श्वः
3. वृथा
4. बहिः
5. कुतः

Online Education HOTS Questions for Class 9 Science Chapter 4 Structure of the Atom

These Solutions are part of Online Education HOTS Questions for Class 9 Science. Here we have given HOTS Questions for Class 9 Science Chapter 4 Structure of the Atom

Question 1.
Both helium (He) and beryllium (Be) have two valence electrons. Whereas He represents a noble gas element, Be does not. Assign reason.
Answer:
The element He (Z = 2) has two electrons present in the only shell i.e., K-shell. Since this shell can have a maximum of two electrons only therefore, He is a noble gas element. The element Be (Z = 4) has electronic configuration as : 2, 2. Although the second shell has also two electrons but it is not complete. It can still accommodate six more electrons. Therefore, the element beryllium does not represent a noble gas element.

More Resources

• HOTS Questions for Class 9 Science
• NCERT Solutions for Class 9 Science
• Value Based Questions in Science for Class 9
• NCERT Exemplar Solutions for Class 9 Science
• Previous Year Question Papers for CBSE Class 9 Science

Question 2.
Study the data given below and answer the questions which follow :

1. Write the mass number and atomic number of the particles A, B, C and D.
2. Which represent a pair of isotopes ?

Answer:

1. Particle A : Mass number = 7 ; Atomic number = 3
   Particle B : Mass number = 17 ; Atomic number = 9
   Particle C : Mass number =16, Atomic number = 8
   Particle D : Mass number =18, Atomic number = 8
2. Particles C and D represent a pair of isotopes since they have same atomic number.

Question 3.
Which of the two will be chemically more reactive ; element X with atomic number 17 or element Y with atomic number 16 ?
Answer:
The electronic configuration of the two elements are as follows :
X(Z = 16): K (2), L(8), M(6) ;
Y(Z = 17): K(2), L(8), M(7)
The element X needs two electrons in the M shell to have the noble gas configuration of element, Ar (Z = 18). However, the element Y needs only one electron to achieve this. This means that the element Y has a greater urge or desire to take up one electron from an outside atom. It is therefore, more reactive than the element X which needs two electrons.

Question 4.
The number of protons, neutrons and electrons in particles from A to E are given below :

1. Which one is a cation ?
2. Which one is an anion ?
3. Which represent pair of isotopes ?

Answer:

1. B is a monovalent cation (B⁺)
2. E is a monovalent anion (E^–)
3. A and D represent pair of isotopes.

Question 5.
An atom of an element has three electrons in the third shell which is the outermost shell. Write

1. the electronic configuration
2. the atomic number
3. number of protons
4. valency
5. the name of the element
6. its nature whether metal or non-metal. (CBSE 2012)

Answer:
The third shell is M shell. If the atom of the element has three electrons in the third shell, this means that K and L shells are already filled.

1. Electronic configuration : 2, 8, 3.
2. Atomic number = No. of electrons =13
3. Number of protons = No. of electrons =13
4. Valency of the element = 3
5. The element with Z = 13 is aluminium (Al)
6. It is a metal.

Hope given HOTS Questions for Class 9 Science Chapter 4 Structure of the Atom are helpful to complete your science homework.

If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.