Prasanna

Here we are providing Online Education for What Happened to the Reptiles Extra Questions and Answers Class 6 English A Pact with the Sun, Extra Questions for Class 6 English was designed by subject expert teachers. https://ncertmcq.com/extra-questions-for-class-6-english/

Online Education for What Happened to the Reptiles Extra Questions and Answers Class 6 English A Pact with the Sun

What Happened to the Reptiles Extra Questions and Answers Short Answer Type

What Happened To The Reptiles Extra Questions Class 6 Question 1.
Why was Prem forced to leave the village?
Answer:
The communal riots in his village made life unsafe in the village. The people went mad, burnt houses and killed one another. So Prem left his village for good.

What Happened To The Reptiles Question Answer Class 6 Question 2.
What was unusual for Prem in Pambupatti village?
Answer:
In Pambupatti, there was no violence not even tension. People lived in peace. They also cared for the welfare of even stranger. This was something surprising for Prem.

What Happened To The Reptiles Question Answers Class 6 Question 3.
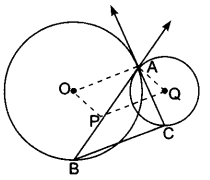
Who is Makara? What were the decision taken by him?
Answer:
Makara was the biggest crocodile. The reptiles in the forest included crocodiles, snakes, turtles and lizards. Makara being strong and selfish, drove all other reptiles out. He got rid of turtles, snakes and lizards one by one. But this created the problem of frogs and rats and other insects.

Extra Questions Of What Happened To The Reptiles Class 6 Question 4.
How did the forest become peaceful again?
Answer:
Crocodiles were facing tough times. A small crocodiles pointed out what had gone wrong. They knew that Makara was not all that strong and right. They called all their reptile friends back to Pambupatti. Their arrival marked the beginning of normal and peaceful life again in the forest.

What Happened To The Reptiles Class 6 Question Answer Class 6 Question 5.
What was the motive behind the story of the old man?
Answer:
The old man gave message through his story. This world belongs to all sorts of creatures. Together they keep a balance. Every kind of creature serves a useful purpose. It is sad that man is trying to kill all the species and rule over the world like a dictator. This is certainly not practicable or in his own interest. Our motto should be to ‘Live and Let Live’.

What Happened to the Reptiles Extra Questions and Answers Long Answer Type

What Happened To Reptiles Question Answer Class 6 Question 1.
‘A leader should be dynamic and protective’. Give your opinion, by taking example from the text.
Answer:
The leader has the capacity to bring changes in the lives of his followers. He is a torchbearer, so it is his duty to lead with dignity and dynamism. Step taken without thought is disastrous to a great extent. One should think of the consequences first only then he should act for the welfare of masses. Makara should have forseen the impact of his decision. He should have taken advice of some counsels before implementing on his decisions.

What Happened To The Reptiles Questions And Answers Class 6 Question 2.
‘Nature has given a rightful place for everyone and everything.’ Elaborate in context with the story.
Answer:
In the eyes of mother nature no One is superior or inferior. Whether a thing is big or small, has a rightful place. No discrimination is ever tolerated. Makara has taken advantage of his power and threw away other reptiles away from the forest. But he failed miserably. Discrimination amongst human being is to divide of caste, colour and creed often divide. But essential humanity brings them together.

What Happened To Reptiles Class 6 Question 3.
In what way is Pambupatti different from any other village?
Answer:
Unlike other villages, people of Pambupatti lived in peace. They did not fight in the name of religion or language. In this way, Pambhupatti is different from any other village.

What Happens To The Reptiles Class 6 Question 4.
Why is Prem determined not to return to his village?
Answer:
Prem determined not to return to his village because in his village people went mad and burnt down temple or mosque. There were religious crisis in the village and people started fighting with one another.

What Surprised Prem In Pambupatti Village Class 6 Question 5.
Why did Makara dislike tortoise, snakes and lizards? Write a line about each.
Answer:
Makara disliked tortoise because they were slow and stupid. They even carried their houses on their backs. He disliked snakes because they were slimy and they made funny noises. Makara disliked lizards because they were undependable changed colour.

Question Answer Of What Happened To The Reptiles Class 6 Question 6.
What went wrong when the tortoise, snakes and lizards left the forest?
Answer:
When the tortoises, snakes and lizards left the forest, rats multiplied in their absence, and eat the baby crocodile and millions of insects growing were bigger and nastier day by the day. The forest was full of bad smell of rotten fruits and animals.

Ncert Solutions For Class 6 English Chapter What Happened To The Reptiles Question 7.
Why do you think Prem wants to tell the story of the reptiles to the people of his village?
Answer:
The people of Prem’s village had gone mad. They fought with one another in the name of religion. The story of Pambupatti gave the message of peace and coexistence. It underlined the importance of living together. So Prem wanted to carry that message to his own village.

Question 8.
Do you agree that it is difficult not to go along with someone who is very strong and powerful? Express your views frankly and clearly.
Answer:
It is difficult not to go along with someone who is very strong and powerful. It is human nature to be on the safe side. Disagreeing with a powerful person is likely to call for trouble. Moreover, even if someone is bold enough to oppose him, it becomes a long fight. Such idealists may leave an impact on the society. But they do so at cost of their own ruin.

Question 7.
If you were a baby crocodile, would you tell Makara that he was wrong? What would you say to con.
Answer:
As a baby crocodile, I have a privilege to oppose my parents boldly. I would tell the elders that this world is a common property of living creatures. To convince my dad, Makara, that he is wrong. I will give him a couple of reasons. First, it is the duty of the strong to protect the weak, and not to harass them. Secondly, this Earth is not the sole property of any one person or animal. All are inter-dependent. Together, they make this Earth a place worth-living.

Here we are providing Online Education for A Pact with the Sun Extra Questions and Answers Class 6 English A Pact with the Sun, Extra Questions for Class 6 English was designed by subject expert teachers. https://ncertmcq.com/extra-questions-for-class-6-english/

Online Education for A Pact with the Sun Extra Questions and Answers Class 6 English A Pact with the Sun

A Pact with the Sun Extra Questions and Answers Short Answer Type

A Pact With The Sun Extra Questions Class 6 Question 1.
What was ‘the pact of the Sun’?
Answer:
The small girl Saeeda made a pact with the Sun. Her mother was not well. She needed the warmth of the Sun and fresh air. So she requested the rays of the Sun to come the next day to cure her mother.

Extra Questions Of A Pact With The Sun Class 6 Question 2.
How did the sunrays respond to Saeeda?
Answer:
The sunrays granted Saeeda’s request. They promised to reach the Earth at the fixed hour the next morning.

A Pact With The Sun Class 6 Extra Questions And Answers Question 3.
How did the sunrays keep their promise?
Answer:
The pathway to the Earth was blocked by thick, dark clouds. The Sun warned the rays to keep clear of the dark clouds. But all the rays refused to obey their father’s command. They got through the clouds and thus kept their word to Saeeda.

A Pact With The Sun Class 6 Chapter 1 Extra Questions Question 4.
How did Saeeda’s mother recovered?
Answer:
Saeeda’s mother felt the Sun on her face and she breathed in fresh air. She thought she was in a new world. Her eyes shone bright and she started recovering speedily.

A Pact With The Sun Extra Question Answer Class 6 Question 5.
What was the theme of the story?
Answer:
The story tells us Saeeda’s mother was denied healthy food, sunshine and fresh air. She remained sick. But her daughter made a pact with the sunrays to warm up the ailing old woman. And the results were wonderful.
Thus, A pact with the sun is an educative story. It tells us that fresh air, and sunshine in the open are the key to sound health. Even the sick people need these two things. They must not be kept confined in dark room. They should get normal food.

A Pact With The Sun Question Answer Class 6 Question 6.
What was Saeeda’s concern about her mother?
Answer:
Saeeda’s mother had been ailing for quite some time. No medicine proved effective. She was shut up in a small dark room. The cloudy weather continued for a few days. So, Saeeda, the little girl, made a request to the rays of the Sun to come down to the Earth and give warmth to the ailing woman.

Question 7.
How did Saeeda’s mother recover?
Answer:
The sunrays agreed and also kept their word. They came down in large numbers and gave new life to Saeeda’s mother. In this way Saeeda’s pact with the sunrays helped her mother to recovered soon.

A Pact with the Sun Extra Questions and Answers Long Answer Type

Question 1.
‘Children can communicate with a secret language’. Elucidate.
Answer:
Saeeda was listening to everything happening around her. She was worried but kept calm. She prayed to the departed rays of the Sun to come with warmth and brightness for well being of her mother. Her innocence and selfless love for her mother compelled the rays to fight with stubborn clouds. Thus her mother was recovered with her care.

Question 2.
‘The doctor advised her sunlight and normal diet’. Why the neighbors reacted differently?
Answer:
When a person fall sick, he is confined to a room with closed windows. Normal diet is restricted. But these things worsen the condition of the sick person. The doctor prescribed medicine and asked to provide Saeeda’s mother proper sunlight in the morning for faster recovery. The people were dubious. They thought that her cold and cough won’t get cured if she is not tended in a closed room. While others supported doctor’s advice.

Question 3.
The simplicity of a child is special for the heavens. Comment.
Answer:
The blessings of heaven is showered upon those who are innocent. Their prayers are heard and heavenly bodies keep their promises as the ray defied the orders of her father and shooed away the bewildered clouds their way to Saeeda’s house. So a child has a power to communicate with .heaven and their prayer are often heard.

Question 4.
What did the physician ask Saeeda’s mother to do to get well? Did their advice help her? If not, why?
Answer:
The physicians advised Saeeda’s mother not to take normal food, and to remain shut in a small dark room.

Question 5.
What did the specialist prescribe in addition to medicine?
Answer:
The specialist prescribed in addition to medicine to shift to a bigger room with open doors and windows. He also asked her to sit one hour daily in the sunshine and to breath in fresh air.

Question 6.
What did Saeeda tell the sunrays to do?
Answer:
Saeeda made a special request to the sunrays to help her mother get well. She asked them to come the next day with lots of warmth and brightness.

Question 7.
Why were the sunrays keen to go down to the Earth the next day?
Answer:
The sunrays had promise to Saeeda that they would come the next day. They feared that if they failed to reach on time the people would call them liars.

Question 8.
What is your own formula for keeping good health?
Answer:
Health is wealth, so I get up early do some exercises and yoga. I eat breakfast including fruits and whole grain. Than I go to school. I play in the evening and after taking my dinner, I go to sleep. I firmly believe that early to bed, and early to rise, makes a man healthy, wealthy and wise.

Question 9.
Who would you recommend to a patient in your neighbourhood the physicians contacted first or the specialist contacted next? Give reasons for your choice.
Answer:
The condition of Saeeda’s mother worsened because she was not taken to a specialist. When he examined her, he gave his expert advise and thus she was cured. So I would suggest any patient of my neighbourhood to contact a specialist for fast recovery.

Question 10.
When would you make a pact, with the sun? When you are going on a picnic, or when you are playing a cricket match? Think of other occasions.
Answer:
I am very fond of playing outdoors games. Generally most of us are forced to stay indoor to avoid exhaustion and heat stroke. So I will pact with the sun to remain hidden in clouds so that we could play more often for long hours atleast on Sundays.

In this page, we are providing Online Education for Sound Class 9 Extra Questions and Answers Science Chapter 12 pdf download. NCERT Extra Questions for Class 9 Science Chapter 12 Sound with Answers will help to score more marks in your CBSE Board Exams. https://ncertmcq.com/extra-questions-for-class-9-science/

Online Education for Class 9 Science Chapter 12 Extra Questions and Answers Sound

Extra Questions for Class 9 Science Chapter 12 Sound with Answers Solutions

Sound Class 9 Extra Questions Very Short Answer Type

Class 9 Science Chapter 12 Extra Questions And Answers Question 1.
What are longitudinal waves?
Answer:
A wave in which the particles of the medium vibrate back and forth in the ‘same direction’ in which the wave is moving, is called as a longitudinal wave.

Class 9 Science Chapter Sound Extra Question Answer Question 2.
What are transverse waves?
Answer:
A wave in which the particles of the medium, vibrate up and down ‘at right angle’ to the direction in which the wave is moving, is called a transverse wave.

Sound Class 9 Extra Questions Answers Question 3.
Define wavelength. What is its symbol and its SI unit?
Answer:
The distance between two consecutive compressions (C) or two consecutive rarefactions (R) is called the wavelength. The wavelength is denoted by (Greek letter ‘lambda’). Its SI unit is the metre (m).

Sound Class 9 Extra Questions Question 4.
Define frequency. What is its symbol and its SI unit?
Answer:
The number of complete waves (or cycles) produced per second is called a frequency of sound waves. It is denoted by f. The SI unit of frequency is hertz (Hz).

Sound Class 9 Worksheet With Answers Question 5.
What is one hertz?
Answer:
A vibrating body producing 1 wave per second is said to have a frequency of 1 Hz.

Sound Extra Questions And Answers Class 9 Question 6.
Define amplitude. What is its symbol and its SI unit?
Answer:
The magnitude of the maximum disturbance in the medium on either side of the mean value is called the amplitude of wave. It is denoted by A. The SI unit is the metre (m).

Sound Chapter Class 9 Extra Questions Question 7.
What is ‘audible’ sound?
Answer:
The sound which we are able to hear is called ‘audible’ sound. The audible range of sound for human beings extends from about 20 Hz to 20000 Hz.

Extra Questions On Sound Class 9 Question 8.
What do you mean by an echo?
Answer:
The repetition of sound caused by the reflection of sound waves is called an ‘echo’.

Numericals On Sound For Class 9 Question 9.
What do you understand by the terms “compression” and rarefaction?
Answer:
A region of high pressure of a medium when a sound wave travels through it is called compression.
A region of low pressure of a medium when a sound wave travels through it is called rarefaction.

Class 9 Science Sound Extra Questions Question 10.
What do you understand by the pitch of a sound?
Answer:
Pitch of a sound is the characteristic of sound that depends on the frequency received by a human ear.

Extra Questions Of Sound Class 9 Question 11.
What do you understand by the loudness of sound?
Answer:
The amplitude of the vibrating body determines the loudness of the sound. Larger the amplitude of vibration, larger the loudness of the sound produced.

Sound Chapter In Physics Class 9 Questions And Answers Question 12.
Define the characteristic “timbre” or “quality” of a sound.
Answer:
Quality or timbre is a characteristic of a sound which enables us to distinguish between two sounds of the same loudness and pitch.

Sound Class 9 Important Questions With Answers Question 13.
What is Sonar?
Answer:
Sonar is a device that uses ultrasonic wave to measure the distance, direction and speed of the underwater object.

Class 9 Sound Extra Questions Question 14.
What is Echocardiography?
Answer:
The technique of obtaining images of the heart by using the reflection of ultrasonic waves from various parts of the heart is called echocardiography.

Class 9 Science Chapter Sound Extra Question & Answer Question 15.
What is ultrasonography?
Answer:
The technique of obtaining images of internal organs of the body by using echoes of ultrasonic waves is called ultrasonography.

Question 16.
What is a stethoscope?
Answer:
The stethoscope is a medical instrument used for listening sounds produced within the body, chiefly in the heart or lungs.

Question 17.
What are infrasonic waves?
Answer:
The waves of frequency less than 20 Hz are called infrasonic waves.

Question 18.
What is ultrasound?
Answer:
The waves of frequency greater than 20,000 Hz are called ultrasonic waves or ultrasound.

Question 19.
Speed of sound is more on a hotter day. Explain why.
Answer:
Speed of sound increases with increase in temperature.

Question 20.
WrIte down the SI unit of (i) frequency (ii) wavelength.
Answer:
SI unit of wavelength is m and frequency is Hz.

Sound Class 9 Extra Questions Numericals

Question 1.
The sound produced by a thunderstorm is heard 10 s after the lightning is seen. Calculate the approximate distance of the thunder cloud. (Given the speed of sound = 340 ms’).
Ans. Given, t = 10 s
υ = 340 m/s
distance, x = υ x t = 340 x 10 = 3400 m.

Question 2.
What is the frequency of wave with time period 0.025 s?
Answer:
Given, t = 0.025 s
frequency, v = \(\frac{1}{t}=\frac{1}{0.025}\) = 40 Hz.

Sound Class 9 Extra Questions Short Answer Type 1

Question 1.
What is sound? When is the sound produced? Give examples.
Answer:
The sensation felt by our ears is called sound. A sound is a form of energy which makes us hear. When an object is set into vibrations, the sound is produced. For example, the vibrating diaphragm of a drum produces sound, the vibrating string of a guitar produces sound, the vibrating diaphragm of speakers of a radio produce sound, the vibrating end of a drilling machine produces sound, etc.

Question 2.
State the conditions to hear an echo.
Answer:
The conditions to hear an echo are:

1. Echo can be heard only if it is produced at least \(\frac {1}{10}\) th of a second (0.1 s) after the original sound.

2. The speed of sound in air is 344 m/s. Let us calculate the minimum distance from the reflecting surface, which is necessary to hear an echo.

∴ Distance travelled = 344 x \(\frac {1}{10}\) = 34.4 metres
Thus, the distance travelled by the sound in \(\frac {1}{10}\) th of a second is 34.4 m. This means that the minimum distance between the source of the sound and the listeners should be 17.2 metres.

3. Echo can be heard only if the reflecting surface is large.

Question 3.
Bats search out prey and fly in the dark night by emitting ultrasound. Explain.
Answer:
Bats search out prey and fly in the dark night by emitting and detecting reflections of ultrasonic waves. The high-pitched ultrasonic squeaks of the bat are reflected from the obstacles or prey and returned to bat’s ear. The nature of reflections tells the bat where the obstacle or prey is and what it is like.

Question 4.
Mention one advantage and one disadvantage of reverberation.
Answer:
A certain amount of reverberation improves the quality of sound of orchestral and choral music. However excessive reverberation makes the speech or music indistinct.

Question 5.
How does a megaphone works?
Answer:
A megaphone works on the principle of reflection of sound. In this instrument, a tube followed by a conical opening reflects sound successively to guide most of the sound from the source in the forward direction towards the audience.

Sound Class 9 Extra Questions Numericals

Question 1.
If the velocity of sound in air is 340 ms^-1. Calculate
1. wavelength when the frequency is 256 Hz.
2. frequency when the wavelength is 0.85 m.
Answer:
Given,
velocity of sound, υ = 340 m/s
1. v = 256 Hz
using, υ = λ v
λ = \(\frac {υ}{λ}\) = \(\frac {340}{256}\) = 1.33m

2. λ = 0.85
using, u = λv
λ = \(\frac {υ}{λ}\) = \(\frac {340}{0.85}\) = 400Hz

Question 2.
30 waves pass through a point in 3 seconds. If the distance between two crests is 2 m. Calculate
(a) frequency
(b) wavelength.
Answer:
30 waves in 3 seconds
υ = \(\frac {30}{3}\) = 10Hz
∴ λ = 2m.

Sound Class 9 Extra Questions Short Answer Type 2

Question 1.
What is the reflection of sound? State the laws of reflection.
Answer:
The bouncing back of sound from a hard surface is called a reflection of sound. The laws of reflection are:
1. The incident sound wave, the reflected sound wave and the normal at the point of incidence, all lie in the same plane.
2. The angle of incidence of sound is always equal to the angle of reflection of sound.

Question 2.
On what factor does the speed of sound depend?
Answer:
The speed of sound depends upon the following:

• The nature of the material (or medium) through which it travels. In general, sound travels fastest in solids, slower in liquids and slowest in gases.
• The humidity of the air. As the humidity of air increases, sound travels faster. Sound has more speed in humid air than in dry air.
• The temperature. The speed of sound in air at 0°C is 332 m/s whereas at 20°C, it is 344 m/s. Thus, as the temperature rises, the speed of sound also increases.

Question 3.
Write a note on ‘ultrasonic sounds’.
Answer:

• The sounds of frequencies higher than 20,000 Hz are known as ‘ultrasonic sounds’ (or just‘ultrasounds’).
• Human beings cannot hear ultrasonic sounds. Children under the age of five and some animals, such as dogs can hear sounds up to 25,000 Hz.
• As people grow older, their hearing sensation for higher frequencies becomes weaker.
• Ultrasonic sounds are used by dolphins, bats and porpoises to navigate in dark and to catch their prey.
• Some moths can hear high-frequency ultrasonic squeaks of the bat and know when a bat is flying nearby and are able to escape capture. Rats also play games by producing ultrasound.

Question 4.
Write three differences between transverse and longitudinal waves.
Answer:
Transverse waves:

• In the transverse waves, the particles of the medium vibrate perpendicular to the direction of wave motion.
• These waves travel in the form of alternate crest and trough.
• These waves can be transmitted through solid or liquid surfaces.

Longitudinal waves:

• In longitudinal waves, the particles of the medium vibrate along the direction of wave motion.
• These waves travel in the form of alternate compression and rarefactions.
• These waves can be transmitted through all the three types of media viz., solid, liquid and gases.

Question 5.
Write down three differences between a sound wave and lightwave.
Answer:
Sound wave:

• It travels in the form of longitudinal waves.
• It requires a medium for its propagation.
• It travels through air with a speed of 332 propagation. m/s at 0°C.

Lightwave:

• It travels in the form of a transverse wave.
• It does not require a medium for its propagation.
•  It travels through air with a speed of nearly 3 x 10⁸ m/s.

Sound Class 9 Extra Questions Long Answer Type

Question 1.
State three applications of reflection of sound.
Answer:
1. Megaphone and a bulb horn: Megaphones or loudhailers, horns, musical instruments such as trumpets and she Hana is, are all designed to send sound in a particular direction without spreading it in all directions, as shown in the figure. In these instruments, a tube followed by a conical opening reflects sound successively to guide most of the sound waves from the source in the forward direction towards the audience.

2. Stethoscope: Stethoscope is a medical instrument used for listening to sounds produced within the body, chiefly in the heart or lungs. In stethoscopes, the sound of the patient’s heartbeat reaches the doctor’s ears by multiple reflections of sound, as shown in the figure.

3. Soundboard: Generally the ceiling of concert halls, conference halls and cinema halls are curved so that sound after reflection reaches all corners of the hall, as shown in the figure. Sometimes a curved soundboard may be placed behind the stage so that the sound, after reflecting from the soundboard, spreads evenly across the width of the hail (Fig).

Question 2.
State the applications of ultrasound.
Answer:
Ultrasounds are high-frequency waves. Ultrasounds are able to travel along well-defined paths even in the presence of obstacles. Ultrasounds are used extensively in industries and for medical purposes.

1. Ultrasound is generally used to clean parts located in hard-to-reach places, for example, spiral tube, odd-shaped parts, electronic components, etc. Objects to be cleaned are placed in a cleaning solution and ultrasonic waves are sent into the solution. Due to high frequency, the particles of dust, grease and dirt get detached and drop out. The objects thus get thoroughly cleaned.

2. Ultrasounds can be used to detect cracks and flaws in metal blocks. Metallic components are generally used in the construction of big structures like buildings, bridges, machines and also scientific equipment. The cracks or holes inside the metal blocks, which are invisible from outside reduces the strength of the structure.

Ultrasonic waves are allowed to pass through the metal block and detectors are used to detect the transmitted waves. If there is even a small defect, the ultrasound gets reflected back indicating the presence of the flaw or defect.

3. Ultrasonic waves are made to reflect from various parts of the heart and form the image of the heart. This technique is called ‘echocardiography’.

4. An ultrasound scanner is an instrument which uses ultrasonic waves from getting images of internal organs of the human body. A doctor may image the patient’s organs such as liver, gall bladder, uterus, kidney, etc. It helps the doctor to detect abnormalities, such as stones in the gall bladder and kidney or tumours in different organs.

In this technique, the ultrasonic waves travel through the tissues of the body and get reflected from a region where there is a change of tissue density. These waves are then converted into electrical signals that are used to generate images of the
organ.

These images are then displayed on a monitor or printed on a film. This technique is called ‘ultrasonography’. Ulträsonography is also used for examination of the foetus during pregnancy to detect congenital defects and growth abnormalities.

5. Ultrasound may be employed to break small ‘stones’ formed in the kidneys into fine grains. These grains later get flushed out with urine.

Sound Class 9 Extra Questions HOTS

Question 1.
Why do we hear the sound produced by the humming bees while the sound of vibrations of a pendulum is not heard?
Answer:
This is because the frequency of the sound produced by humming bees lies in audible range and frequency of the sound of vibrations of pendulum lies in the infrasonic region.

Question 2.
Sounds of same loudness and pitch but produced by different musical instruments like a violin and flute are distinguishable.
Answer:
It is the quality of sound which enables us to distinguish between two sounds of the same loudness and pitch.

Question 3.
Which of the two graphs (a) and (b) shown in the figure below represents the human voice is likely to be the male voice? Give a reason for your answer. (NCERT Exemplar)

Answer:
Graph a represents the male voice because the frequency of male voice is less than that of the female voice.

Question 4.
The given graph (Fig.) shows the displacement versus time relation for a disturbance travelling with velocity 1500 ms^-1. Calculate the wavelength of the disturbance. (NCERT Exemplar)

Answer:
Here, frequency, u = \(\frac {1}{T}\)
T = 2 ms = 2 x 10^-6 s
Hence υ = \(\frac{1}{2 \times 10^{-6}}\) = 5 x 10⁵ Hz
using relation, λ. = \(\frac{v}{v}=\frac{1500}{5 \times 10^{5}}\) = 3 x 10^-2 m

Question 5.
For hearing the loudest ticking sound heard by the ear, find the angle x in the Figure. (NCERT Exemplar)

Answer:
Here angle of incidence,
i = 90° – 50° = 40°
Angle of incidence (i) or Angle of reflection (x)
x = i = 40°.

Sound Class 9 Extra Questions Value Based (VBQs)

Question 1.
Sumeet went to a hill station with his parents and elder sister Kirti. He was experiencing the scenic beauty of a hill station for the first time. One day they were walking in a forest area, Sumeet loudly called out ‘Kirti Didi’. He was surprised that he could distinctly hear the same sound twice. He discussed this with his sister and she explained the reason behind this echo.
Answer:
(a) The repetition of sound caused by the reflection of sound waves is called an echo.
(b) Kirti is intelligent and helpful.

Question 2.
Tinku studies in class 9th. Once he was suffering from cold and cough and was running a high temperature. His mother took him to a doctor. The doctor examined the chest and back of Tinku with the help of a device ‘stethoscope’. While examining with stethoscope doctor asked Tinku to take longer breaths. After examining Tinku, the doctor prescribed some drugs.

By regular use of these drugs, Tinku was normal within four days. But he could not understand the purpose of being examined by the use of a stethoscope. During winter break his cousin Honey, who was studying in a medical college, visited their place. On the request of Tinku, Honey explained the purpose of the stethoscope and its action.
(a) What is a stethoscope?
(b) What quality was shown by Honey?
Answer:
(a) The stethoscope is a medical instrument used for listening to sounds produced within the body, chiefly in the heart or lungs.
(b) Honey is intelligent and helpful.

Question 3.
On a hot summer afternoon, a man was shouting through a megaphone. He was ‘zip-repairer’. As Arshi was preparing for her examination, she got disturbed. She inquired her father about the instrument being used by the ‘zip-repairer’. The father told her that it was a megaphone also known as ‘loud hailer’.
(a) State the principle on which the megaphone works.
(b) Why did Arshi get disturbed?
Answer:
(a) Megaphone works on the principle of multiple reflections.
(b) Arshi got disturbed by noise pollution.

Question 4.
Reena’s grandmother took her mother to a doctor as she was four months pregnant for ultrasonography. But she showed her interest in determining whether the child is a boy or a girl. The doctor was annoyed and refused to disclose the gender of the child.
(a) What is ultrasonography?
(b) Write down the values shown by the doctor.
Answer:
(a) The technique of obtaining images of internal organs of the body by using echoes of ultrasound waves is called ultrasonography.
(b) A Doctor is a law-abiding person.

Here we are providing Online Education for Circles Class 10 Extra Questions Maths Chapter 10 with Answers Solutions, Extra Questions for Class 10 Maths was designed by subject expert teachers. https://ncertmcq.com/extra-questions-for-class-10-maths/

Online Education Extra Questions for Class 10 Maths Circles with Answers Solutions

Extra Questions for Class 10 Maths Chapter 10 Circles with Solutions Answers

Circles Class 10 Extra Questions Very Short Answer Type

Class 10 Circles Extra Questions Question 1.
If a point P is 17 cm from the centre of a circle of radius 8 cm, then find the length of the tangent drawn to the circle from point P.
Solution:

OA ⊥ PA (∵ radius is ⊥ to tangent at point of contact)
∴ In ∆OAP, we have
PO² = PA² + AO²
⇒ (17)² = (PA)² + (8)²
(PA)² = 289 – 64 = 225
⇒ PA = √225 = 15
Hence, the length of the tangent from point P is 15 cm.

Circle Class 10 Extra Questions With Solutions Question 2.
The length of the tangent to a circle from a point P, which is 25 cm away from the centre, is 24 cm. What is the radius of the circle?
Solution:

∵ OQ ⊥ PQ
∴ PQ² + QO² = OP²
⇒ 25² = OQ² + 24²
or OQ = √625 – √576
= √49 = 7 cm

Circles Extra Questions Class 10 Question 3.
In Fig. 8.6, ABCD is a cyclic quadrilateral. If ∠BAC = 50° and ∠DBC = 60° then find ∠BCD.
Solution:

Here ∠BDC = ∠BAC = 50° (angles in same segment are equal)
In ABCD, we have
∠BCD = 180° – (∠BDC + ∠DBC)
= 180° – (50° + 60°)= 70°

Extra Questions Of Circles Class 10 Question 4.
In Fig. 8.7, the quadrilateral ABCD circumscribes a circle with centre O. If ∠AOB = 115°, then find ∠COD.
Solution:

∵ ∠AOB = ∠COD (vertically opposite angles)
∴ ∠COD = 115°

Extra Questions On Circles Class 10 Question 5.
In Fig. 8.8, AABC is circumscribing a circle. Find the length of BC.

Solution:
AN = AM = 3 cm [Tangents drawn from an external point]
BN = BL = 4 cm [Tangents drawn from an external point]
CL = CM = AC – AM = 9 – 3 = 6 cm
⇒ BC = BL + CL = 4 + 6 = 10 cm.

Extra Questions For Class 10 Maths Circles With Solutions Question 6.
In Fig. 8.9, O is the centre of a circle, PQ is a chord and the tangent PR at P makes an angle of 50° with PQ. Find ∠POQ.
Solution:

∠OPQ = 90° – 50° = 40°
OP = OQ [Radii of a circle]
∠OPQ = ∠OQP = 40°
(Equal opposite sides have equal opposite angles)
∠POQ = 180° – ∠OPQ – ∠OQP
= 180° – 40° – 40° = 100°

Class 10 Maths Circles Extra Questions Question 7.
If two tangents inclined at an angle 60° are drawn to a circle of radius 3 cm, then find the length of each tangent.
Solution:

In Fig. 8.10
∆AOP ≅ ∆BOP (By SSS congruence criterion)
∠APO = ∠BPO = \(\frac{60°}{2}\) = 30°
In ∆AOP, OA ⊥ AP
∴ tan 30° = \(\frac{OA}{AP}\)
⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac{3}{AP}\)
⇒ AP = 3√3 cm

Circles Class 10 Important Questions Question 8.
If radii of two concentric circles are 4 cm and 5 cm, then find the length of each chord of one circle which is tangent to the other circle.
Solution:

OA = 4 cm, OB = 5 cm
Also, OA ⊥ BC
∴ OB² = OA² + AB²
⇒ 5² = 4² + AB²
⇒ AB = √25 – √16 = 3 cm
⇒ BC = 2 AB = 2 × 3 = 6 cm

Class 10 Maths Chapter 10 Extra Questions Question 9.
PQ is a tangent drawn from a point P to a circle with centre O and QOR is a diameter of the circle such that ∠POR = 120° then find ∠OPQ.
Solution:

∠OQP = 90°
∠QOP = 180° – 120° = 60°
∠OPQ = 180° – ∠OQP – ∠QOP
= 180° – 90° – 60°
= 30°

Circle Extra Questions Class 10 Question 10.
From an external point P, tangents PA and PB are drawn to a circle with centre O. If ∠PAB = 50°, then find ∠AOB.

Solution:
∵ PA = PB ⇒ ∠BAP = ∠ABP = 50°
∴ ∠APB = 180° – 50° – 50° = 80°
∴ ∠AOB = 180° – 80° = 100°

Circles Chapter Class 10 Extra Questions Question 11.
In PQ is a tangent at a point C to a circle with centre O. If AB is a diameter and ∠CAB = 30°, find ∠PCA.
Solution:

∠ACB = 90° (Angle in the semicircle)
∠CAB = 30° (given)
In ∆ABC,
90° + 30° + ∠ABC = 180°
⇒ ∠ABC = 60°
Now, ∠PCA = ∠ABC (Angles in the alternate segment)
∴ ∠PCA = 60°
or
Construction: Join O to C.
∠PCO = 90° [∵ Line joining centre to point of contact is perpendicular to PQ]
In ∆AOC, OA = OC [Radii of circle]
∴ ∠OAC = ∠OCA = 30° [Equal sides have equal opp. angles]
Now, ∠PCA = ∠PCO – ∠ACO
= 90° – 30° = 60°

Extra Question Of Circle Class 10 Question 12.
In fig. 8.16, there are two concentric circles with centre O. PRT and PQS are tangents to the inner circle from a point P lying on the outer circle. If PR = 5 cm, find the length of PS.
Solution:

PQ = PR = 5 cm [∵ Tangents drawn from external point are equal] PK
∴ PS = 2PQ = 10 cm [∵ Perpendicular drawn from centre to the chord bisects the chord]

Circles Class 10 Extra Questions Short Answer Type 1

State true or false for each of the following and justify your answer (Q. 1 to 3)

Circles Class 10 Extra Questions State Syllabus Question 1.
AB is a diameter of a circle and AC is its chord such that ∠BAC = 30°. If the tangent at C intersects AB extended at D, then BC = BD.
Solution:

True, Join OC,
∠ACB = 90° (Angle in semi-circle)
∴ ∠OBC = 180o – (90° + 30°) = 60°
Since, OB = OC = radii of same circle [Fig. 8.16]
∴ ∠OBC = ∠OCB = 60°
Also, ∠OCD = 90°
⇒ ∠BCD = 90° – 60° = 30°
Now, ∠OBC = ∠BCD + ∠BDC (Exterior angle property)
⇒ 60° = 30° + ∠BDC
⇒ ∠BDC = 30°
∵ ∠BCD = ∠BDC = 30°
∴ BC = BD

Class 10 Circles Important Questions Question 2.
The length of tangent from an external point P on a circle with centre O is always less than OP.

Solution:
True, let PQ be the tangent from the external point P.
Then ∆PQO is always a right angled triangle with OP as the hypotenuse. So, PQ is always less than OP.

Circles Class 10 Questions With Solutions Question 3.
If angle between two tangents drawn from a point P to a circle of radius ‘a’ and centre 0 is 90°, then OP = a√2.

Solution:
True, let PQ and PR be the tangents
Since ∠P = 90°, so ∠QOR = 90°
Also, OR = OQ = a
∴ PQOR is a square

Extra Questions Of Chapter Circles Class 10 Question 4.
In Fig. 8.20, PA and PB are tangents to the circle drawn from an external point P. CD is the third tangent touching the circle at Q. If PA = 15 cm, find the perimeter of ∆PCD.

Solution:
∵ PA and PB are tangent from same external point
∴ PA = PB = 15 cm
Now, Perimeter of ∆PCD = PC + CD + DP = PC + CQ + QD + DP
= PC + CA + DB + DP
= PA + PB = 15 + 15 = 30 cm

Chapter 10 Maths Class 10 Extra Questions Question 5.
In Fig. 8.21, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD.

Solution:
PA = PC + CA = PC + CQ [∵ CA = CQ (tangents drawn An from external point are equal)]
⇒ 12 = PC + 3 = PC = 9 cm
∵ PA = PB = PA – AC = PB – BD
⇒ PC = PD
∴ PD = 9 cm
Hence, PC + PD = 18 cm

Extra Questions Circles Class 10 Question 6.
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.

Solution:
Let the tangents to a circle with centre O be ABC and XYZ.
Construction : Join OB and OY.
Draw OP||AC
Since AB||PO
∠ABO + ∠POB = 180° (Adjacent interior angles)
∠ABO = 90° (A tangent to a circle is perpendicular to the radius through the point of contact)
90° + ∠POB = 180° = ∠POB = 90°
Similarly ∠POY = 90°
∠POB + ∠POY = 90° + 90° = 180°
Hence, BOY is a straight line passing through the centre of the circle.

Circles Class 10 Important Questions With Solutions Question 7.
If from an external point P of a circle with centre 0, two tangents PQ and PR are drawn such that QPR = 120°, prove that 2PQ = PO.

Solution:
Given, ∠QPR = 120°
Radius is perpendicular to the tangent at the point of contact.
∠OQP = 90°
⇒ ∠QPO = 60°
(Tangents drawn to a circle from an external point are equally inclined to the segment, joining the centre to that point)

2PQ = PO

Questions On Circles For Class 10 Question 8.
In Fig. 8.24, common tangents AB and CD to two circles with centres , and 0, intersect at E. Prove that AB = CD.

Solution:
AE = CE and BE = ED [Tangents drawn from an external point are equal]
On addition, we get
AE + BE = CE + ED
∠QPO = 60°
⇒ AB = CD

Circles Class 10 Extra Questions Pdf Download Question 9.
The incircle of an isosceles triangle ABC, in which AB = AC, touches the sides BC, CA and AB at D, E and F respectively. Prove that BD = DC.
OR
In Fig. 8.25, if AB = AC, prove that BE = EC.
[Note: D, E, F replace by F, D, E]

Solution:

Given, AB = AC
We have, BF + AF = AE + CE ….(i)
AB, BC and CA are tangents to the circle at F, D and E respectively.
∴ BF = BD, AE = AF and CE = CD ….(ii)
From (i) and (ii)
BD + AE = AE + CD (∵ AF = AE)
⇒ BD = CD

Question 10.
In Fig. 8.27, XP and XQ are two tangents to the circle with centre O, drawn from an external point X. ARB is another tangent, touching the circle at R. Prove that XA + AR = XB + BR.

Solution:
In the given figure,
AP = AR
BR = BQ
XP = XQ [Tangent to a circle from an external point are equal]
XA + AP = XB + BQ
XA + AR = XB + BR [AP = AR, BQ = BR]

Question 11.
In Fig. 8.28, a circle is inscribed in a AABC, such that it touches the sides AB, BC and CA at points D, E and F respectively. If the lengths of sides AB, BC and CA are 12 cm, 8 cm and 10 cm respectively, find the lengths of AD, BE and CF.

Solution:
Let AD = AF = x
∴ DB = BE = 12 – x
and CF = CE = 10 – x
BC = BE + EC
⇒ 8 = 12 – x + 10 – x
⇒ x = 7
∴ AD = 7 cm, BE = 12 – 7 = 5 cm, CF = 10 – 7 = 3 cm

Question 12.
In Fig. 8.29, AP and BP are tangents to a circle with centre 0, such that AP = 5 cm and ∠APB = 60°. Find the length of chord AB.

Solution:
PA = PB (Tangents from an external point are equal)
and ∠APB = 60°
⇒ ∠PAB = ∠PBA = 60°
∴ ∆PAB is an equilateral triangle.
Hence AB = PA = 5 cm.

Question 13.
In Fig. 8.30 from an external point P, two tangents PT and PS are drawn to a circle with centre 0 and radius r. If OP = 2r, show that ∠OTS = ∠OST = 30°.

Solution:
Let ∠TOP = θ
∴ cos θ = \(\frac{OT}{OP}\) = \(\frac{r}{2r}\) =\(\frac{1}{2}\)
⇒ cos θ = cos 60°
⇒ θ = 60°
Hence, ∠TOS = 120°
In ∆OTS, OT = OS [Radii of circle]
⇒ ∠OTS = ∠OST = \(\frac{60^{\circ}}{2}\) = 30°

Question 14.
In Fig. 8.31, are two concentric circles of radii 6 cm and 4 cm with centre O. If AP is a tangent to the larger circle and BP to the smaller circle and length of AP is 8 cm, find the length of BP.

Solution:
OA = 6 cm, OB = 4 cm, AP = 8 cm
OP² = OA² + AP² = 36 + 64 = 100
⇒ OP = 10 cm
BP² = OP² – OB² = 100 – 16 = 84
⇒ BP = 2√21 cm

Question 15.
In fig. 8.32, PQ is a tangent from an external point P to a circle with centre ( and OP cuts the circle at T and QOR is a diameter. If ∠POR = 130° and S is a point on the circle, find R 21 + 22.

Solution:
∵ ∠POR = 130o = ∠ROT [∵ Angle subtended by an arc at the centre is double than the angle subtended by it at any part of circumference]
∠2 = \(\frac{1}{2}\) ∠ROT = \(\frac{1}{2}\) × 130° = 65°
∠POQ = 180° – 130° = 50° [Linear pair]
and ∠Q = 90°
∴ ∠1 = 40°[∵ Line drawn from centre to the point of contact is perpendicular to the tangent]
Hence ∠2 + ∠1 = 65° + 40° = 105° .

Circles Class 10 Extra Questions Short Answer Type 2

Question 1.
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre 0 at a point so that OQ = 12 cm. Find the length of PQ.

Solution:
We have, ∠OPQ = 90°
OQ = 12 cm and OP = 5 cm
∴ By Pythagoras Theorem
OQ² = OP² + QP²
⇒ 122 = 52 + QP²
⇒ QP² = 144 – 25 = 119
= QP = √119 cm

Question 2.
From a point l, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. Find the radius of the circle.
Solution:

Let QT be the tangent and OT be the radius of circle. Therefore
OT ⊥ QT i.e., ∠OTQ = 90°
and OQ = 25 cm and QT = 24 cm
Now, by Pythagoras Theorem, we have
OQ² = QT² + OT²
⇒ 25² = 24² + OT²
⇒ OT² = 25² – 24²
⇒ 625 – 576
OT² – 49
∴ OT = 7 cm

Question 3.
In Fig. 8.35, if TP and TQ are the two tangents to a circle with centre 0 so that ∠POQ = 110°, then find ∠PTQ.
Solution:

Since TP and TQ are the tangents to the circle with centre O
So, OPIPT and OQ ⊥ QT
⇒ ∠OPT = 90°, ∠OQT = 90° and ∠POQ = 110°
So, in quadrilateral OPTQ, we have
∠POQ + ∠OPT + ∠PTQ + ∠TQO = 360°
⇒ 110° + 90° + ∠PTQ + 90° = 360°
⇒ ∠PTQ + 290° = 360°
∴ ∠PTQ = 360° – 290°
= ∠PTQ = 70°

Question 4.
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Solution:

Let AB be the diameter of the given circle with centre O, and two tangents PQ and LM are drawn at the end of diameter AB respectively.
Р. Now, since the tangent at a point to a circle is perpendicular to the radius through the point of contact.
Therefore, OA ⊥ PQ and OB ⊥ LM
i.e., AB ⊥ PQ and also AB ⊥ LM
⇒ ∠BAQ = ∠ABL (each 90°)
∴ PQ||LM (∵ ∠BAQ and ∠ABL are alternate angles)

Question 5.
If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80°, then find ∠POA.
Solution:

∵ PA and PB are tangents to a circle with centre O,
∴ OA ⊥ AP and OB ⊥ PB
i.e., ∠APB = 80°, ∠OAP = 90°, and ∠OBP = 90°
Now, in quadrilateral OAPB, we have
∠APB + ∠PBO + ∠BOA + ∠OAP = 360°
⇒ 80° + 90° + ∠BOA + 90o = 360°
⇒ 260° + ∠BOA = 360°
∴ ∠BOA = 360° – 260°
⇒ ∠BOA = 100°
Now, in ∆POA and APOB we have
OP = OP (Common)
ОА = ОВ (Radii of the same circle)
∠OAP = ∠OBP = 90°
∴ ∆POA ≅ APOB (RHS congruence condition)
⇒ ∠POA = ∠POB (CPCT)
Now, ∠POA = \(\frac{1}{2}\) = ∠BOA = \(\frac{1}{2}\) × 100 = 50°

Question 6.
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.

Solution:
Let O be the centre and P be the point of contact.
Since tangent to a circle is perpendicular to the radius through the point of contact,
∴ ∠OPA = 90° Now, in right ∆OPA we have
OA² = OP² + PA² [By Pythagoras Theorem]
5² = OP² + 4²
= 25 = OP² + 16
⇒ OP² = 25 – 16 = 9
∴ OP = 3cm
Hence, the radius of the circle is 3 cm.

Question 7.
Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Solution:

Let O be the common centre of two concentric circles and let AB be a chord of larger circle
touching the smaller circle at P. Join OP.
Since OP is the radius of the smaller circle and AB is tangent to this circle at P,
∴ OP ⊥ AB
We know that the perpendicular drawn from the centre of a circle to any chord of the circle bisects the chord.
Therefore, AP = BP
In right ∆APO we have
⇒ OA² = AP² + OP²
⇒ 5² = AP² + 3²
⇒ 25 – 9 = AP²
⇒ AP² = 16
⇒ AP = 4
Now, AB = 2.AP = 2 × 4 = 8 [∵ AP = PB]
Hence, the length of the chord of the larger circle which touches the smaller circle is 8 cm.

Question 8.
Prove that the tangents drawn at the ends of a chord of circle make equal angles with the chord.
Solution:

Given: A circle with centre O, PA and PB are tangents drawn at the ends A and B on chord AB.
To prove: ∠PAB = ∠PBA
Construction: Join OA and OB.
Proof: In ∆OAB we have
ОА = ОВ … (i) [Radii of the same circle]
∠2 = ∠1 … (ii) [Angles opposite to equal sides of a A]
Also (∠2 + ∠3 = ∠1 + 24) …(iii) [Both 90° as Radius ⊥ Tangent]
Subtracting (ii) from (iii), we have
∴ ∠3 = ∠4 = ∠PAB = ∠PBA

Question 9.
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.

Solution:
Let LM be tangent drawn at the point P on the circle with centre O. Join OP. If possible, let PQ be perpendicular to LM, not passing through O.
Now, since tangent at a point to a circle is perpendicular to the radius through the point.
∴ OP ⊥ LM ⇒ ∠OPM = 90°
Also, ∠QPM = 90° (as assumed above)
∴ ∠OPM = ∠QPM,
which is possible only when points O and I coincide
Hence, the perpendicular at the point of contact to tangent to a circle passes through the centre.

Question 10.
A quadrilateral ABCD is drawn to circumscribe a circle (Fig. 8.42). Prove that AB + CD = AD + BC.
OR
A circle touches all the four sides of a quadrilateral ABCD. Prove that AB + CD = BC + DA

Solution:
Since lengths of two tangents drawn from an external point of circle are equal,
Therefore, AP = AS, BP = BQ and DR = DS
CR = CQ (Where P, Q, R and S are the points of contact]
Adding all these, we have
(AP + BP) + (CR + RD) = (BQ + CQ) + (DS + AS)
⇒ AB + CD = BC + DA

Question 11.
A circle is touching the side BC of AABC at P and touching AB and AC produced at Q and R respectively. Prove that AQ = \(\frac{1}{2}\) (perimeter of ∆ABC).
Solution:

Since tangents from an exterior point to a circle are equal in length.
∴ BP = BQ [Tangents from B] …(i)
CP = CR [Tangents from C] … (ii)
and, AQ = AR [Tangents from A] …(iii)
From (iii), we have
AQ = AR
⇒ AB + BQ = AC + CR
AB + BP
⇒ AC + CP (Using (i) and (ii)] …(iv)
Now, perimeter of AABC = AB + BC + AC
= AB + (BP.+ PC) + AC
= (AB + BP) + (AC + PC)
= 2(AB + BP) [Uisng (iv)]
= 2(AB + BQ) = 2AQ [Using (i)]
AQ = \(\frac{1}{2}\) (Perimeter of ∆ABC)

Question 12.
The difference between the radii of the smaller circle and the larger circle is 7 cm and the difference between the areas of the two circles is 1078 sq. cm. Find the radius of the smaller circle.
Solution:
Given: r₂ – r₁ = 7 (r₂ > r₁) …(i)
and π(r₂² – r₁²) = 1078
π (r₂ – r₁) (r₂ + r₁) = 1078
π (r₂ + r₁) = 1078 [(From equation (i)]
⇒ r₂ + r₁ = \(\frac{1078 \times 7}{22 \times 7}\) = 49…(ii)
Adding (i) and (ii), we get
2r₂ = 56
⇒ r₂ = 28 cm
r₁ = 21 cm [From equation (ii)]
∴ Radius of smaller circle = 21 cm.

Circles Class 10 Extra Questions Long Answer Type 1

Question 1.
Prove that the tangent to a circle is perpendicular to the radius through the point of contact.
Solution:
Given: A circle C(O,r) and a tangent AB at a point P.
To Prove: OP ⊥ AB.
Construction: Take any point l, other than P, on the tangent AB. Join OQ. Suppose OQ meets the circle at R.
Proof: We know that among all line segments joining the point to a point on AB, the shortest one is perpendicular to AB. So, to prove that OP ⊥ AB it is sufficient to prove that OP is shorter than any other segment joining O to any point of AB.

Clearly, OP = OR [Radii of the same circle]
Now, OQ = OR + RQ
⇒ OQ > OR
⇒ OQ > OP [∵OP = OR]
Thus, OP is shorter than any other segment joining O to any point on AB.
Hence, OP ⊥ AB.

Question 2.
Prove that the lengths of two tangents drawn from an external point to a circle are equal.
Solution:

Given: AP and AQ are two tangents from a point A to a circle C (O, r).
To Prove: AP = AQ
Construction: Join OP, OQ and OA.
Proof: In order to prove that AP = AQ, we shall first prove that ∆OPA ≅ ∆OQA.
Since a tangent at any point of a circle is perpendicular to the radius through the point of contact.
∴ OP ⊥ AP and OQ ⊥ AQ
⇒ ∠OPA = ∠OQA = 90°
Now, in right triangles OPA and OQA, we have
OP = OQ [Radii of a circle]
∠OPA = ∠OQA [Each 90°]
and OA = OA [Common]
So, by RHS-criterion of congruence, we get
∆OPA ≅ OQA
⇒ AP = AQ [CPCT]
Hence, lengths of two tangents from an external point are equal.

Question 3.
Prove that the parallelogram circumscribing a circle is a rhombus.
Solution:

Let ABCD be a parallelogram such that its sides touch a circle with centre O.
We know that the tangents to a circle from an exterior point are equal in length.
Therefore, we have
AP = AS [Tangents from A]
BP = BQ [Tangents from B] …. (ii)
CR = CQ [Tangents from C] …. (iii)
And DR = DS [Tangents from D] …. (iv)
Adding (i), (ii), (iii) and (iv), we have
(AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
AB + CD = AD + BC
AB + AB = BC + BC [∵ ABCD is a parallelogram ∴ AB = CD, BC = DA]
2AB = 2BC ⇒ AB = BC
Thus, AB = BC = CD = AD
Hence, ABCD is a rhombus.

Question 4.
In Fig. 8.47, PQ is a chord of length 16 cm, of a circle of radius 10 cm. The tangents at P and Q intersect at a point T. Find the length of TP.
Solution:
Given: PQ = 16 cm
PO = 10 cm

Question 5.
If PQ is a tangent drawn from an external point P to a circle with centre O and QOR is a diameter where length of QOR is 8 cm such that ∠POR = 120°, then find OP and PQ.
Solution:
Let O be the centre and QOR = 8 cm is diameter of a circle. PQ is tangent such that ∠POR = 120°

Question 6.
In Fig. 8.49, two equal circles, with centres O and O’, touch each other at X.OO’ produced meets the circle with centre O’ at A. AC is tangent to the circle with centre 0, at the point C. O’D is perpendicular to AC. Find the value of \(\frac{DO’}{CO}\) .
Solution:

AC is tangent to circle with centre O.
Thus ∠ACO = 90°
In ∆AO’D and ∆AOC
∠ADO’ = ∠ACO = 90°
∠A = ∠A (Common)
∴ ∆AO’D – ∠AOC (By AA similarity)

Question 7.
In Fig. 8.50, O is the centre of a circle of radius 5 cm. T is a point such that OT = 13 cm and OT intersects circle at E. If AB is a tangent to the circle at E, find the length of AB, where TP and TQ are two tangents to the circle.

Solution:
In right ∆POT

TE = 8 cm
Let PA = AE = x
(Tangents from an external point to a circle are equal)
In right ∆AET
TA² = TE² + EA²
⇒ (12 – x)² = 64 + x²
⇒ 144 + x² – 24x = 64 + x²
⇒ x = \(\frac{80}{24}\)
⇒ x = 3.3 cm
Thus, AB = 6.6 cm

Circles Class 10 Extra Questions HOTS

Question 1.
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Solution:

Let a circle with centre O touches the sides AB, BC, CD and DA of a D quadrilateral ABCD at the points P, Q, R and S respectively. Then, we have to prove that
∠AOB + ∠COD = 180° and ∠AOD + ∠BOC = 180°
Now, Join OP, OQ, OR and OS.
Since the two tangents drawn from an external point to a circle subtend equal angles at the centre.
∴ ∠1 = ∠2, ∠3 = 24, 25 = 26 and 27 = 28 …(i)
Now, 21 + 22 +23 + 24 + 25 +26+ 27 + ∠8 = 360° … (ii)
[sum of all the angles subtended at a point is 360°]
⇒ 2(∠2 + ∠3 + ∠6 + ∠7) = 360° [using equation (i) and (ii)]
= (∠2 + ∠3) + (∠6 + ∠7) = 180°
∠AOB + ∠COD = 180°
again 2(∠1 + ∠8 +∠4 + ∠5) = 360° [from (i) and (ii)]
(∠1 + ∠8) + (∠4 + ∠5) = 180°
∠AOD + ∠BOC = 180°

Question 2.
A triangle ABC [Fig. 8.52] is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively. Find the sides AB and AC.
Solution:

Let ∆ABC be drawn to circumscribe a circle with centre O and radius 4 cm and circle touches the sides BC, CA and AB at D, E and 6 cm F respectively.
We have given that CD = 6 cm and BD = 8 cm
∴ BF = BD = 8 cm and CE = CD = 6 cm
{Length of two tangents drawn from an external point of circle are equal}
Now, let AF = AE = x cm
Then, AB = c = (x + 8) cm, BC = a = 14 cm, CA = b = (x + 6) cm
2s = (x + 8) + 14 + (x + 6) 25 = 2x + 28 or s = x + 14
s – a = (x + 14) – 14 = x
s – b = (x + 14) – (x + 6) = 8
s – c = (x + 14) – (x + 8) = 6

Squaring both sides, we have
48x (x + 14) = 16(x + 14)² = 48x (x + 14) – 16 (x + 14)² = 0
16 (x + 14) (3x – (x + 14)] = 0
⇒ 16(x + 14)(2x – 14) = 0
either 16(x + 14) = 0 or 2x – 14 = 0
⇒ x = -14 or 2x = 14
⇒ x = -14 or x = 7
But x cannot be negative so x ≠ – 14 .
∴ x = 7 cm
Hence, the sides AB = x + 8 = 7 + 8 = 15 cm
AC = x + 6 = 7 + 6 = 13 cm.

Question 3.
In Fig. 8.53, XY and X’Y are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and ∠X’Y at B. Prove that ∠AOB = 90°.
Solution:

Join OC. In ∆APO and ∆ACO, we have
AP = AC (Tangents drawn from external point A)
AO = OA (Common)
PO = OC (Radii of the same circle)
∴ ∆APO ≅ ∆ACO (By SSS criterion of congruence)
∴∠PAO = ∠CAO (CPCT)
⇒ ∠PAC = 2∠CAO
Similarly, we can prove that
∆OQB ≅ ∆OCB
∴∠QBO = 2CBO
⇒ ∠CBQ = 22CBO
Now, ∠PAC + ∠CBQ = 180° [Sum of interior angles on the same side of transversal is 180°]
⇒ 2∠CAO + 2∠CBO = 180°
⇒ ∠CAO + ∠CBO = 90°
⇒ 180° – ∠AOB = 90°
[∵ ∠CAO + ∠CBO + ∠AOB = 180°]
⇒ 180° – 90° = ∠AOB
⇒ ∠AOB = 90°

Question 4.
Let A be one point of intersection of two intersecting circles with centres O and Q. The tangents at A to the two circles meet the circles again at B and C respectively. Let the point P be located so that AOPQ is a parallelogram. Prove that P is the circumcentre of the triangle ABC.
Solution:

In order to prove that P is the circumcentre of ∆ABC it is sufficient to show that P is the point of intersection of perpendicular bisectors of the sides of AABC i.e., OP and PQ are perpendicular bisectors of sides AB and AC respectively. Now, AC is tangent at A to the circle with centre at 0 and OA is its radius.
∴ OA ⊥ AC
⇒ PQ ⊥ AC [∵ OAQP is a parallelogram so, OA ||PQ]
Also, Q is the centre of the circle
QP bisects AC [Perpendicular from the centre to the chord bisects the chord]
⇒ PQ is the perpendicular bisector of AC.
Similarly, BA is the tangent to the circle at A and AQ is its radius through A.
∴ BA ⊥ AQ [∵ AQPO is parallelogram]
BA ⊥ OP [∴ OP || AQ]
Also, OP bisects AB [∵ 0 is the centre of the circle]
⇒ OP is the perpendicular bisector of AB. Thus, P is the point of intersection of perpendicular bisectors PQ and PO of sides AC and AB respectively.
Hence, P is the circumcentre of ∆ABC.

Here we are providing Online Education for A Game of Chance Extra Questions and Answers Class 6 English Honeysuckle, Extra Questions for Class 6 English was designed by subject expert teachers.

Online Education for A Game of Chance Extra Questions and Answers Class 6 English Honeysuckle

A Game of Chance Extra Questions and Answers Short Answer Type

A Game Of Chance Class 6 Extra Questions Question 1.
What was Rasheed’s fault at the fair?
Answer:
Rasheed’s fault was that he did not pay heed to the advice of his uncle. He told him not to buy anything nor to go too far away in his absence.

A Game Of Chance Extra Questions Class 6 Question 2.
How did Rasheed lose all his money at the Lucky shop?
Answer:
Rasheed was tempted to try his luck and wanted win some big prize. He took several chances but won no expensive item. Thus he lost all his money.

Extra Questions Of A Game Of Chance Class 6 Question 3.
Was it Rasheed’s fault or he was tricked?
Answer:
Rasheed was neither unlucky nor foolish. He was an innocent boy while the shopkeeper was a cheat.

Game Of Chance Extra Questions Class 6 Question 4.
How did uncle explain the tricks of the shopkeeper?
Answer:
Uncle told Rasheed that the ‘Lucky Shop’ man had made fool of him. The old man and the boy who won costly things were in fact the shopkeeper’s friends. It was all a trick to tempt the customers.

A Game Of Chance Extra Questions And Answers Class 6 Question 5.
What lesson did the narrator learn from his experience at the fair?
Answer:
The narrator Rasheed went to the fair on the occasion of Eid. He was tempted to try his luck at a shop. He was too innocent. The shopkeeper was cheat. He lost all his little money in that game of chance. He learnt the lesson that he can be easily be fooled and robbed of his money by with shopkeepers.

A Game Of Chance Class 6 Extra Questions And Answers Question 6.
What trick did the shopkeeper play to allure his customers to play the losing game?
Answer:
The shopkeeper was rewarding the persons who staked their money with costly prizes. The game was played with six numbered discs. The winner claimed the article with the winning number. The tricky shopkeeper gave handsome prizes to his own friends. Rasheed too was tempted to try his luck. But he lost the last penny in that game of chance.

A Game Of Chance Extra Question Answer Class 6 Question 7.
Why do you think Rasheed’s uncle asked him not to buy anything in his absence?
Answer:
Rasheed’s uncle knew that many tradesmen and shopkeepers who made a fool of the gullible persons. Therefore, he asked Rasheed not to buy anything in his absence.

A Game Of Chance Question Answer Class 6 Question 8.
Why was the shop called ‘Lucky Shop’?
Answer:
The shop was called ‘Lucky Shop’ so as to attract the people to try their luck and win prizes.

Game Of Chance Class 6 Extra Questions Question 9.
An old man won a clock and sold it back to the shopkeeper. How much money did he make?
Answer:
The old man made 15 rupees by selling the clock back to the shopkeeper.

Question 10.
How many prizes did the boy win? What were they?
Answer:
The boy won four prizes. They were a comb, a fountain pen, a wrist watch and a table lamp.

Question 11.
Why was Rasheed upset?
Answer:
Rasheed was upset because he did not win any prize. All his money was lost at the ‘Lucky Shop’.

Question 12.
In what way did the shopkeeper make a fool of Rasheed?
Answer:
The shopkeeper played tricks to tempt to try his lucky by making him believe that it was luck that got the old man and the boy. theft- prizes but in reality they were friends of the shopkeeper. Therefore, Rasheed tried his luck again and again but only got some cheap things which he sold back to the shopkeeper and lost all his money.

A Game of Chance Extra Questions and Answers Long Answer Type

Question 1.
‘The game chance’ disheartened Rasheed: What role the elders should play in regaining the faith of a child’ like Rasheed, who had a bad experience?
Answer:
Rasheed tried his luck in ‘the Lucky Shop’ but he failed to win any reward. That was disheartening and demoralizing for the sensitive mind of the child. He felt that everyone around was making fun of him. Elders like Rasheed’s Uncle, without making fun of him, taught him not to embarrass himself. He asked him not to discuss about this act of various stupidity. To divert his attention from this episode, he bought him gifts. So that he won’t feel guilty. The lesson he learnt for life time was not to trust anybody blindly. His confidence was rebuilt by the faith his uncle reposed in him.

Question 2.
‘The owner of the shop played a mind game’. What impact would it have on a child’s mind?
Answer:
Children easily believe in what they see. When Rasheed was convinced that others are winning, he went ahead to try his luck as well. Initially he was optimistic to get reward by trying his luck. But later he felt discouraged. Nobody in the gathering came to comfort and console him. He was properly guided only by his uncle. He supported him unconditionally. The child would have personality disorders like lack of confidence. He might consider him unlucky as well. He was shattered by the whole incident. So, the society should own the responsibility of making confident citizens. If they observe anything wrong, they should raise the voice then and there.

A Game of Chance Extra Questions and Answers Reference to Context

Question 1.
Every year on the occasion of Eid, there was a fair in our village. Eid was celebrated only one day but the fair lasted many days. Tradesmen from far and wide came there with all kinds of goods to sell. You could buy anything from a small pin to a big buffalo. Uncle took me to the fair. Bhaiya, who worked for us at home, came with us. There was a big crowd at the fair. Uncle was leading us through the crowd when he met a few of his friends. They wanted him to spend some time with them.

(i) What was organised on the occasion of Eid?
(ii) What happen in the fair?
(iii) Who took Rasheed to the fair?
(iv) Whom did Uncle meet in the fair?
(v) Write the past participle of‘lead’.
Answer:
(i) A fair was organised on Eid.
(ii) Shops were set up by tradesmen for sale of goods.
(iii) Uncle took Rasheed to the fair.
(iv) Uncle met with his friends in the fair.
(v) led.

Question 2.
Uncle warned me neither to buy anything nor to go too far out while he was away. I promised that I . would wait for him. Bhaiya and I went from shop to shop. There were many things I would have liked to buy, but I waited for Uncle to return. Then we came to what was called the Lucky Shop. The shopkeeper was neither young nor old. He was a middle-aged man. He seemed neither too smart nor too lazy. Questions

(i) Who gave the warning?
(ii) What was the warning?
(iii) Why Rasheed couldn’t buy anything?
(iv) What was the name of the shop?
(v) Give antonym of lazy.
Answer:
(i) Uncle gave the warning.
(ii) Uncle warned him neither to buy anything nor to go too far out while he was away.
(iii) Rasheed couldn’t buy anything because he waited for his uncle to come.
(iv) ‘The lucky shop’ was the name of the shop.
(v) Active.

Question 3.
I wanted to try my luck too. I looked at Bhaiya. He encouraged me. I paid 50 paise and took six discs. My luck was not too good. I got two pencils. The shopkeeper bought them from me for 25 paise. I tried again. This time I got a bottle of ink, also of little value. The shopkeeper bought that too for 25 paise. I took a chance for the third time. Still luck was not with me.

(i) Who is T in above passage?
(ii) Who encouraged him to try his luck?
(iii) What did he win in the first chance?
(iv) What price did the shopkeeper pay for bottle of ink?
(v) What made Rasheed think that luck was not with him?
Answer:
(i) I is the boy Rasheed, named in the passage.
(ii) Rasheed’s bhaiya encouraged him to try his luck.
(iii) Rasheed .won two pencils only.
(iv) The shopkeeper paid 25 paise for the bottle of ink.
(v) Rasheed could manage to win things of little value only.

Question 4.
People were looking at me. Some were laughing at my bad luck, but none showed any sympathy. Bhaiya and! went to the place where Uncle had left us and waited for him to return. Presently he came. He looked at me and said, “Rasheed, you look upset. What is the matter?”

(i) Who were looking at him?
(ii) Why were they laughing?
(iii) Where did Rasheed and his Bhaiya return to?
(iv) What was the reason of his being upset?
(v) Change the noun into adjective for the word ‘sympathy’.
Answer:
(i) People were looking at him.
(ii) They were laughing at his bad luck.
(iii) Rasheed and his Bhaiya returned to the place where his uncle left him.
(iv) He was upset as he was befooled by the shopkeeper.
(v) Sympathic.